本文总结经典的背包问题。
四种基本模型: 01 背包、完全背包、多重背包、分组背包,不含优化。
参考书:《算法竞赛进阶指南》· 李煜东
背包问题的四种基本模型的代码有一定的规律,这也是本文要总结它的原因。
四种基本背包模型,都是 背包容积有限、最大化总价值,不同点在于物品的分布和选择方式。
以下的模型中,$f(j)$ 均定义为背包放入总体积为 $j$ 的物品时的最大价值。
01 背包 ¶
给定 $n$ 个物品,其中第 $i$ 个物品的体积为 $v_i$,价值为 $w_i$。有一个容积为 $m$ 的背包。要求选择一些物品放入背包, 使得物品总体积不超过 $m$ 的情况下,物品的总价值最高。
关键点:每个物品只可使用一次。
不断加入每一个物品 $i$,对于每一个总体积 $j$ 有两种情况:
- 不选第 $i$ 个物品,此时取值不变,仍为 $f(j)$。
- 选择第 $i$ 个物品,此时除去当前物品的体积后,即 $j-v_i$ 体积限制下的最大价值、再加上第 $i$ 个物品的价值 $w_i$。
所以推导方程是:
\[f(j) = \max_{v_i \leq j \leq m} { \{ f(j), f(j-v_i) + w_i \} }\]代码实现如下:
int f[MAX_M];
memset(f, 0xcf, sizeof f); f[0] = 0;
for (int i = 1; i <= n; i++) { // 物品
for (int j = m; j >= v[i]; j--) // 体积
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
int ans = 0;
for (int j = 0; j <= m; j++) ans = max(ans, f[j]);注意,其中标记部分使用了 倒序循环。
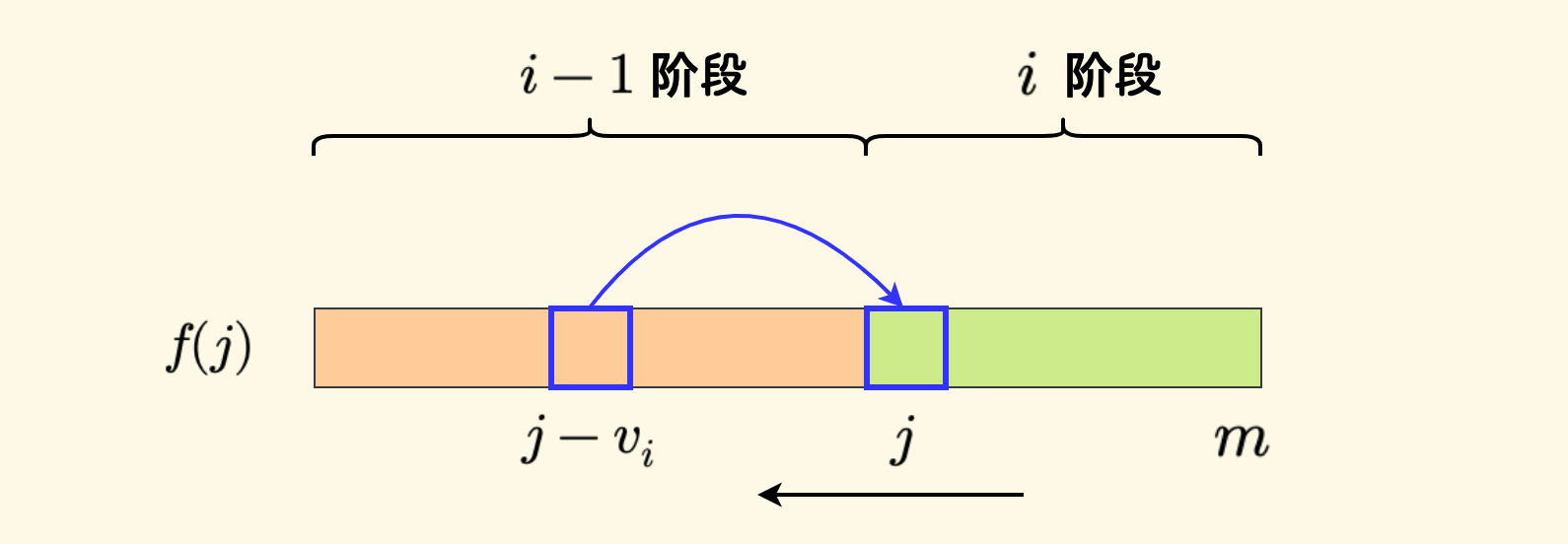
下图中:
- 左边是没有考虑加入当前物品的 $i-1$ 阶段
- 右边是已进入「加入了第 $i$ 个物品」的 $i$ 阶段
倒序遍历的时候,$f$ 数组上的 dp 过程就是从 $i-1$ 到 $i$ 阶段进行转移。
由于计算 $f(j)$ 时,左边的 $f(j-v_i)$ 仍处于 $i-1$ 阶段,所以对每个 $f(j)$ 来说,第 $i$ 个物品仅考虑了一次。
完全背包 ¶
给定 $n$ 种物品,其中第 $i$ 种物品的体积为 $v_i$,价值为 $w_i$,并且每种物品有无数个。有一个容积为 $m$ 的背包。 要求选择若干种物品放入背包,使得物品总体积不超过 $m$ 的情况下,物品的总价值最高。
关键点:每种物品可使用无限次。
和 01 背包的 dp 方程也一样,但是不同之处在于:内层循环正序。
int f[MAX_M];
memset(f, 0xcf, sizeof f); f[0] = 0;
for (int i = 1; i <= n; i++) { // 物品
for (int j = v[i]; j <= m; j++) // 体积
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
int ans = 0;
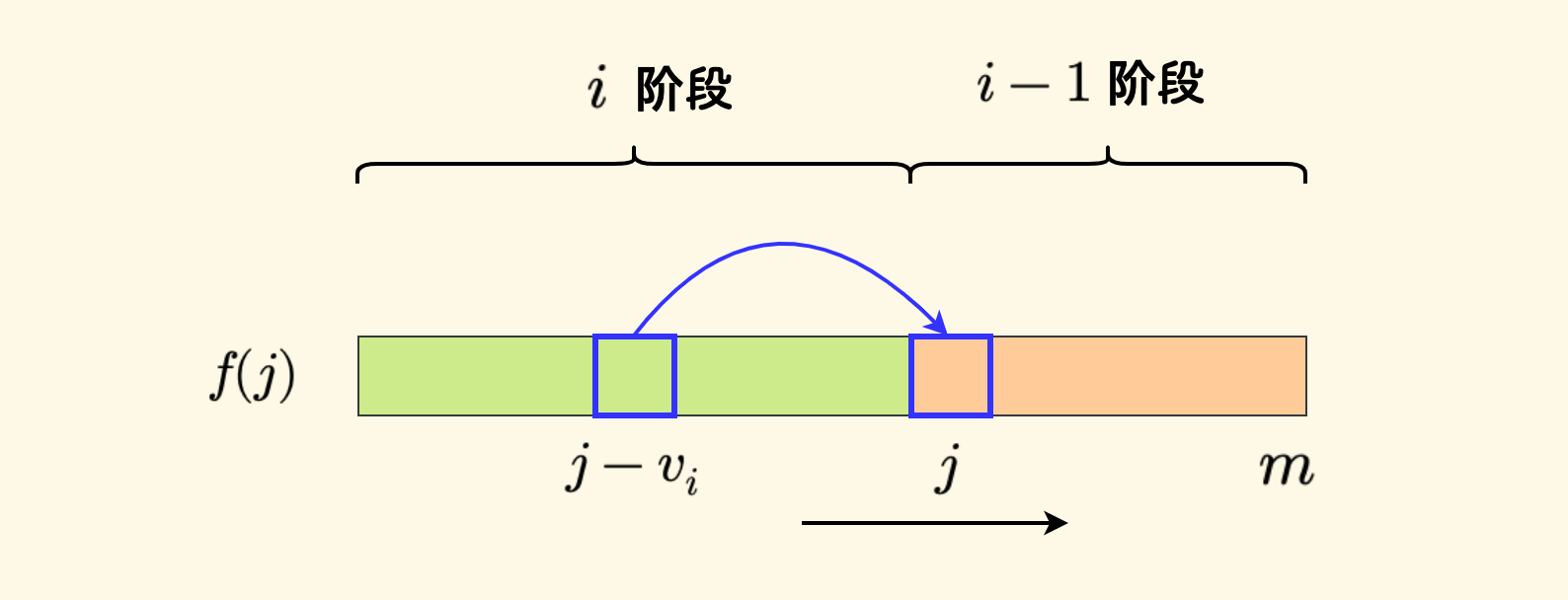
for (int j = 0; j <= m; j++) ans = max(ans, f[j]);类似于 01 背包的分析,从左向右正序遍历时,$f$ 数组上的 dp 过程就是从 $i-1$ 到 $i$ 阶段进行转移。
由于计算 $f(j)$ 时,左边的 $f(j-v_i)$ 已经处于 $i$ 阶段,所以对每个 $f(j)$ 来说,第 $i$ 种物品会被考虑多次。 而且,每种物品被被考虑使用多少次,是不加限制的。所以说,完全背包问题也叫做「无限制的背包问题」(Unbounded knapsack)。
多重背包 ¶
给定 $n$ 种物品,其中第 $i$ 种物品的体积为 $v_i$,价值为 $w_i$,并且有 $c_i$ 个。有一个容积为 $m$ 的背包。要求选择一些物品放入背包, 使得物品总体积不超过 $m$ 的情况下,物品的总价值最高。
关键点:每种物品只可使用给定次数。
多重背包,就是 01 背包基础上,每种物品重复了多次。
可直接把多重背包看成共有 $\sum^n_{i=1}{c_i}$ 个物品的 01 背包问题。
dp 定义和 01 背包是一样的。
下面代码中,高亮的两行即相当于 01 背包中的外层循环:
int f[MAX_M];
memset(f, 0xcf, sizeof f); f[0] = 0;
for (int i = 1; i <= n; i++) { // 物品种数
for (int k = 1; k <= c[i]; k++) // 每种物品的个数
for (int j = m; j >= v[i]; j--) // 体积
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
int ans = 0;
for (int j = 0; j <= m; j++) ans = max(ans, f[j]);这种方法时间复杂度较高,常用的优化手段是 二进制拆分 和 单调队列优化 $O(nm)$,本文暂不包含多重背包的优化内容。
分组背包 ¶
给定 $n$ 组物品,其中第 $i$ 组有 $c_i$ 个物品。第 $i$ 组的第 $k$ 个物品的体积为 $v_{ik}$,价值为 $w_{ik}$。 有一个容积为 $m$ 的背包。要求选择一些物品放入背包,每组至多选择一个物品,使得物品总体积不超过 $m$ 的情况下,物品的总价值最高。
关键点:每组至多选择一个物品。
考虑加入第 $i$ 组,对于每一个总体积 $j$ 有两种情况:
- 不选第 $i$ 组的物品,此时取值不变,仍为 $f(j)$。
- 选择第 $i$ 组的某个物品 $k$,此时除去此物品的体积后,即 $j-v_{ik}$ 体积限制下的最大价值、再加上当前选择物品的价值 $w_{ik}$。
推导方程如下,和 01 背包几乎一样:
\[f(j) = \max \begin{cases} f(j) &\\ \max_{1 \leq k \leq c_i} { \{ f(j-v_{ik}) + w_{ik} \}} &\end{cases}\]代码实现如下:
int f[MAX_M];
memset(f, 0xcf, sizeof f); f[0] = 0;
for (int i = 1; i <= n; i++) { // 物品
for (int j = m; j >= 0; j--) // 体积
for (int k = 1; k <= c[i]; k++)
if (j >= v[i][k])
f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
}
int ans = 0;
for (int j = 0; j <= m; j++) ans = max(ans, f[j]);相当于,内层循环在每个组里面选一个最优的代表元素。
对于每个目标体积 $j$,相当于对于组内每个物品 $v_{ik}$ 都倒序地推导一次 $f(j)$,这样 $f(j)$ 才可以取得整个第 $i$ 个小组加入后的总的最值。
对 $k$ 的循环必须放在内层,也就是说第 $i$ 组物品的枚举整体在 $j$ 的倒序循环之内,这样才可以保证整个组内最多挑选一个物品。
下图中,左侧黄色部分仍处于 $i-1$ 阶段,右侧绿色已经处于 $i$ 阶段,$k$ 的循环自上而下进行,转移总是从黄色区域(没考虑 $i$ 物品时)到绿色区域, 先自上向下、再自右向左,才确保每一组物品中最多使用一个。 如果把 $k$ 的循环放在 $j$ 循环的外面,就会存在绿色区域向黄色区域的转移了,打破了这一限制。
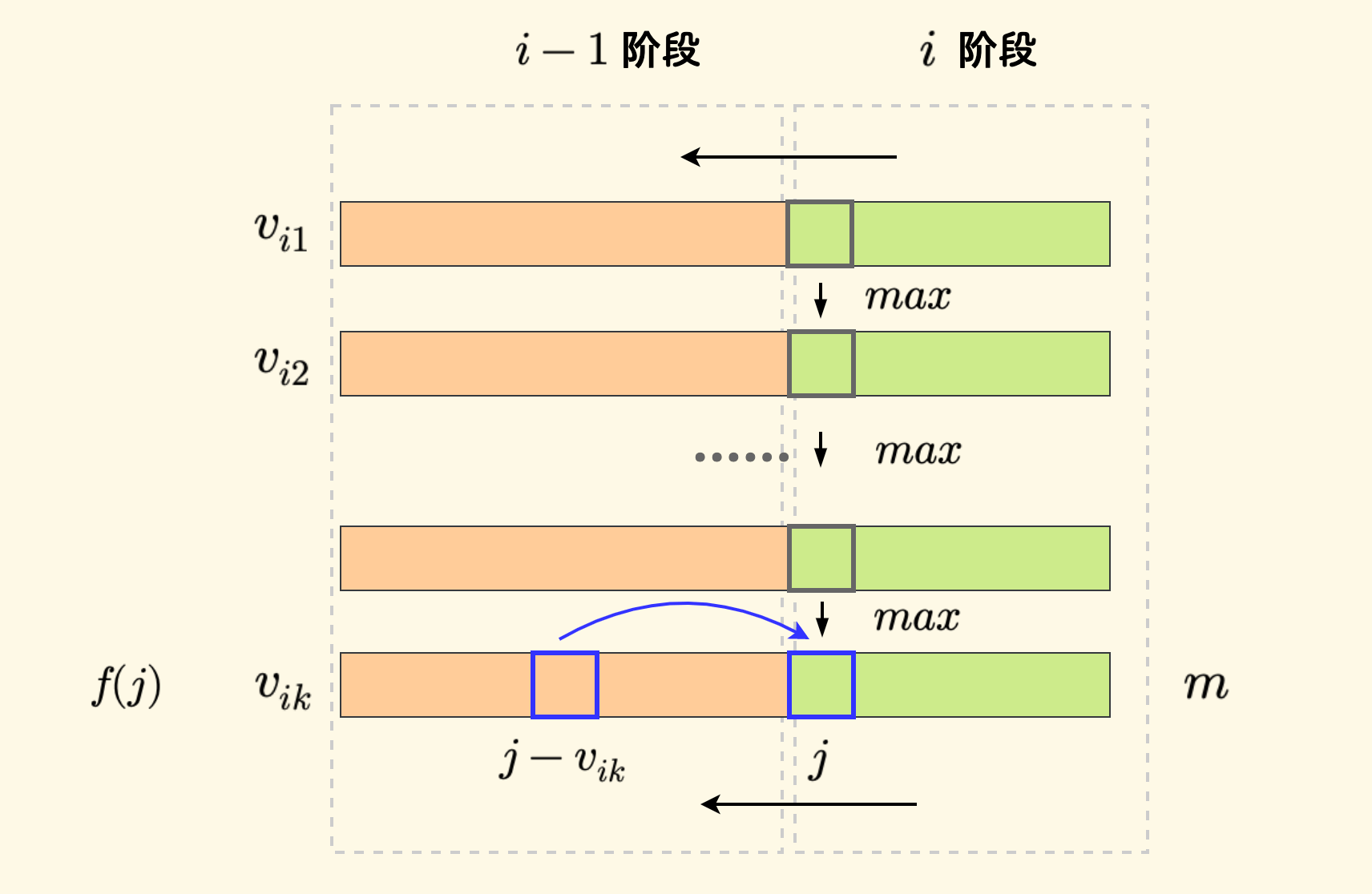
简而言之,分组背包是在 01 背包的基础上对每个目标体积对组内物品依次执行取最值。
混合背包 ¶
给定 $n$ 个物品,其中第 $i$ 个物品的体积为 $v_i$,价值为 $w_i$, 并且每个物品可以使用 $p_i$ 次。 有一个容积为 $m$ 的背包。要求选择一些物品放入背包,使得物品总体积不超过 $m$ 的情况下,物品的总价值最高。
其中 $p_i$ 取 $0$ 表示可以用无限次。
关键点:每个物品可使用的次数不再相同,而是由一个数组给出。
所谓「混合背包」,无非是前面基础背包模型的混合体。
无论是 01 背包、完全背包、多重背包,只是物品 $i$ 使用次数的限制不同,影响的是第 $i$ 个物品对 $f(j)$ 的转移方式。 根据物品 $i$ 可使用的次数来套入相应的模型即可。
代码形式如下:
int f[MAX_M];
memset(f, 0xcf, sizeof f); f[0] = 0;
for (int i = 1; i <= n; i++) {
if (p[i] == 0) { // 物品 i 使用次数无限制,套入 完全背包
for (int j = v[i]; j <= m; j++)
f[j] = max(f[j], f[j - v[i]] + w[i]);
} else if (p[i] == 1) { // 套入 01 背包
for (int j = m; j >= v[i]; j--)
f[j] = max(f[j], f[j - v[i]] + w[i]);
} else { // 套入 多重背包
for (int k = 1; k <= p[i]; k++)
for (int j = m; j >= v[i]; j--)
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
}二维费用背包 ¶
给定 $n$ 个物品,其中第 $i$ 个物品的体积为 $v_i$,重量为 $m_i$,价值为 $w_i$,每个物品仅可使用一次。 有一个容积为 $V$ 、最大承重 $M$ 的背包。要求选择一些物品放入背包,使得物品的总价值最高。
关键点:在 01 背包的基础上,新增了一个维度的限制。
原本的 01 背包,只有一个体积的限制,现在有两个限制:体积 和 重量。
先看代码形式:
int f[MAX_M][MAX_V];
memset(f, 0xcf, sizeof f); f[0][0] = 0;
for (int i = 1; i <= n; i++)
for (int j = V; j >= v[i]; j--) // 体积限制
for (int k = M; k >= m[i]; k--) // 重量限制
f[j][k] = max(f[j][k], f[j - v[i]][k - m[i]] + w[i]);可以从 DP 的转移含义来理解这个代码。
不断加入每个物品 $i$,依次考察每个总体积 $j$、每个总重量 $k$,都有两种情况:
- 不选第 $i$ 个物品,此时取值不变,仍为 $f(j,k)$。
- 选择第 $i$ 个物品,此时除去当前物品的体积和重量后,即 $j-v_i$ 体积限制下、$k-m_i$ 重量限制下的最大价值、再加上第 $i$ 个物品的价值 $w_i$。
两种限制要同时满足才可以,所以写成嵌套的两层循环,由于是 01 背包,所以都要倒序遍历。
二维费用背包的一个模板题:acwing 8。
一些题目 ¶
数字组合
给定 $N$ 个正整数 $A_1$, $A_2$, …, $A_N$, 从中选出若干个数,使它们的和为 $M$,求有多少种选择方案。
-- 来自 《算法竞赛进阶指南》, acwing 278
每个元素只可利用一次,属于 01 背包问题,只是取最值变成了求和。
定义 $f(j)$ 表示凑出来和为 $j$ 的时候的方案数。
要凑出来 $j$,就要考虑每个 $j-a_i$ 的方案数,然后求和。
\[f(j) = \sum_{a_i \leq j \leq m} { f(j-a_i) }\]最开始,$f(0)$ 的方案数钦定为 $1$,只是为了递推式的合法性,你可以代入 $i=1$ 的情况,来分析 $i=0$ 的情况 $f$ 的合理取值。
数字组合 - C++ 代码
const int N = 110;
const int M = 10010;
int n, m;
int a[N];
int f[M];
int solve() {
memset(f, 0, sizeof f);
f[0] = 1;
for (int i = 1; i <= n; i++)
for (int j = m; j >= a[i]; j--)
f[j] += f[j - a[i]];
return f[m];
}
自然数拆分
给定一个自然数 $N$,要求把 $N$ 拆分成若干个正整数相加的形式,参与加法运算的数可以重复。
-- 来自 《算法竞赛进阶指南》, acwing 279
每个参与计算的自然数可以重复使用,是完全背包问题。
此时每个自然数 $i$ 的体积就是 $i$ 本身,总体积限制就是 $n$。
推导的方程式和 数字组合 问题是类似的:
\[f(j) = \sum_{i \leq j \leq n} { f(j-i) }\]只需要把内层变为正序循环:
自然数拆分 - C++ 代码
using ull = unsigned long long;
const ull mod = 2147483648;
int solve(int n) {
ull f[n + 1];
memset(f, 0, sizeof f);
f[0] = 1;
for (int i = 1; i < n; i++) {
for (int j = i; j <= n; j++) {
f[j] += f[j - i] % mod;
}
}
return f[n] % mod;
}
砝码称重
有 1g、2g、3g、5g、10g、20g 的 6 种砝码,其中第 $i$ 种砝码有 $a_i$ 种。 总重量不超过 1000g。可以表示成多少种重量?
-- 来自 洛谷 P2347 砝码称重
总重量限制 $M=1000$,每种物品有 $a_i$ 个,定义 $f(j)$ 表示拼成总重量为 $j$ 的方案数,最后统计 $f$ 非 $0$ 的 $j$ 的个数即可,属于多重背包问题,套入模型即可。
前面已说过,朴素的多重背包就相当于把「每种物品重复的多次」展开后的 01 背包问题。
砝码称重 - C++ 代码
const int M = 1000;
int a[7]; // 第 i 种物品有 a[i] 个
int v[7] = {0, 1, 2, 3, 5, 10, 20}; // 每种物品的重量,即模型中的「体积」
int f[M + 1]; // f[j] 表示拼成重量 j 的方案数
int solve() {
memset(f, 0, sizeof f);
f[0] = 1;
for (int i = 1; i <= 6; i++)
for (int k = 1; k <= a[i]; k++)
for (int j = M; j >= v[i]; j--)
f[j] += f[j - v[i]];
int ans = 0;
for (int j = 1; j <= M; j++) if(f[j]) ans ++;
return ans;
}
樱花
现有 $n$ 颗樱花树,第 $i$ 颗的美学价值是 $w_i$,最多可以观赏 $p_i$ 次($p_i$ 取 0 表示不限制观赏次数),观赏需要 $t_i$ 时间。
小明总共有空余时间 $m$ 分钟,求能观赏到的最大美学价值是多少。
-- 来自 洛谷 P1833 樱花
非常板的混合背包问题,无需多言,直接套模型即可。
樱花 - C++ 代码
const int N = 10000 + 1;
const int MAX_M = 1001;
int f[MAX_M];
int p[N], v[N], w[N]; // 次数限制数组, 体积数组, 价值数组
int n, m; // m 是总的分钟数
int solve() {
memset(f, 0xcf, sizeof f);
f[0] = 0;
for (int i = 1; i <= n; i++) {
if (p[i] == 0) { // 完全背包
for (int j = v[i]; j <= m; j++) {
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
} else if (p[i] == 1) { // 01 背包
for (int j = m; j >= v[i]; j--) {
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
} else { // 多重背包
for (int k = 1; k <= p[i]; k++) {
for (int j = m; j >= v[i]; j--) {
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
}
}
}
int ans = 0;
for (int j = 0; j <= m; j++) ans = max(ans, f[j]);
return ans;
}
一和零
给定一个字符串数组 $strs$,其中每个字符串都只包含 $0$ 和 $1$ 两种字符。
找出这个数组的最大子集的长度,要求满足其中所有字符串中的 $0$ 的个数不超过 $m_1$、$1$ 的个数不超过 $m_2$。
-- 来自 leetcode 474. 一和零
可以预处理这个数组,得到两个体积数组 $v1$ 和 $v2$:
一和零 - 预处理体积数组 - C++ 代码
int v1[N], v2[N];
for (int i = 0; i < strs.size(); i++) {
auto& s = strs[i];
v1[i] = count(s.begin(), s.end(), '0');
v2[i] = s.size() - v1[i];
}
问题即转化为,选出一些字符串,要求同时满足:
- $0$ 的个数不超过 $m_1$,也就是,$v1$ 的体积总和不超过 $m_1$。
- $1$ 的个数不超过 $m_2$,也就是,$v2$ 的体积总和不超过 $m_2$。
题目要求「子集」的长度最大,那么以「子集的长度」作为价值,也就是说每个字符串的价值都是 $1$。
这样,即转化为「二维费用01背包问题」,套入模型即可。
一和零 - C++ 代码
const int N = 601;
const int M1 = 101;
const int M2 = 101;
class Solution {
public:
int findMaxForm(vector<string>& strs, int m1, int m2) {
// 预处理体积数组, 分别是 0 和 1 的
int v1[N], v2[N];
for (int i = 0; i < strs.size(); i++) {
auto& s = strs[i];
v1[i] = count(s.begin(), s.end(), '0');
v2[i] = s.size() - v1[i];
}
// 01 背包
int f[M1][M2];
memset(f, 0xcf, sizeof f);
f[0][0] = 0;
for (int i = 0; i < strs.size(); i++) {
for (int j = m1; j >= v1[i]; j--) { // 限制 0 的个数
for (int k = m2; k >= v2[i]; k--) { // 限制 1 的个数
f[j][k] = max(f[j][k], f[j - v1[i]][k - v2[i]] + 1);
}
}
}
int ans = 0;
for (int j = 0; j <= m1; j++)
for (int k = 0; k <= m2; k++)
ans = max(ans, f[j][k]);
return ans;
}
};
分割等和子集
给你一个只包含正整数的非空数组。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
-- 来自 leetcode 416
这个问题和 数字组合 十分相似,属于 01 背包问题。
定义 $f(j)$ 表示凑出来和为 $j$ 的方案是否可行,方程式如下:
\[f(j) = \forall_{a_i \leq j \leq m} { \{ f(j) \lor f(j-a_i) \} }\]代码实现如下,同样注意钦定初始 $f(0)$ 是 $true$:
分割等和子集 - C++ 代码
class Solution {
public:
bool canPartition(vector<int>& a) {
int n = a.size();
int sum = accumulate(a.begin(), a.end(), 0);
if (sum & 1) return false; // 奇数不行
int m = sum / 2;
bool f[m + 1];
memset(f, 0, sizeof f);
f[0] = true;
for (int i = 1; i < n; i++) {
for (int j = m; j >= a[i]; j--)
f[j] |= f[j - a[i]];
}
return f[m];
}
};
目标和
给你一个非负整数数组
a和一个整数target。向数组中的每个整数前添加
+或-,然后串联起所有整数,可以构造一个表达式:例如,
nums = [2, 1],可以在 2 之前添加+,在 1 之前添加-,然后串联起来得到表达式+2-1。返回可以通过上述方法构造的、运算结果等于
target的不同 表达式 的数目。-- 来自 leetcode 494. 目标和
比如说,a=[1,1,1,1,1] 且 target=3 的情况,共有 5 种方案:
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3
这个题目挺巧妙的,关键点在于识破问题的转化玄机。
如果全部填入 + 号,那么计算结果就是总和 sum:
+1 + 1 + 1 + 1 + 1 = 5
那么,把其中一部分加号,变成 - 号,来凑 tagert,比如下面就是一种方案:
+1 + 1 + 1 + 1 + 1 = 5
// =>
+1 + 1 + 1 + 1 - 1 = 3
加号变减号,其实是减去了两倍的数值,假设总共要减去两倍的 m 的数值才可以凑成:
sum - 2*m = target
问题可以转化为:
从原数组中挑选一部分数字,应用上减号,使得总体减去的结果是
m=(sum-target)/2。
如此,即转化成计算拼成和为 m 的 01 背包问题,其他不必赘述。
目标和 - C++ 代码
class Solution {
public:
int findTargetSumWays(vector<int>& a, int target) {
int sum = accumulate(a.begin(), a.end(), 0);
int m = (sum - target);
if (m & 1 || m < 0) return 0; // 非法情况,拼不成
m >>= 1; // 除以 2
int n = a.size();
// 01 背包
int f[2001];
memset(f, 0, sizeof f);
f[0] = 1;
for (int i = 0; i < n; i++)
for (int j = m; j >= a[i]; j--)
f[j] += f[j - a[i]];
return f[m];
}
};
最大约数和
选取和不超过 $S$ 的若干个不同的正整数,使得所有数的约数(不含它本身)之和最大。
-- 来自 洛谷 P1734
例如,$S=11$ 时,取 $4$ 和 $6$,结果是:
(1 + 2) + (1 + 2 + 3) = 9 // 注意 1 的约数是自己,不符合要求,所以不含在内
对于每个不超过 $S$ 的整数 $i$,定义其价值为它所有的约数之和 $w_i$,即可转化为 01 背包问题。
比如 $4$ 的价值是 $1+2=3$,再比如 $6$ 的价值是 $1+2+3=6$。但是注意 $1$ 的价值是 $0$。
求每个整数的价值 $w_i$ 时,只需遍历到 $\sqrt{i}$ 即可,细节是,注意排除自身。
最大约数和 - 预处理价值数组 - C++ 代码
const int N = 1000 + 1;
int w[N]; // 价值数组
memset(w, 0, sizeof w);
for (int i = 1; i <= S; i++) {
if (i > 1) w[i] += 1; // i > 1 时,约数至少包含 1
// 2~sqrt(i) 范围内的约数 j 和 i/j
int j = 2;
for (; j * j < i; j++)
if (i % j == 0) w[i] += j + i / j;
// 完全平方数时注意防止重复,sqrt(i)
if (j * j == i) w[i] += j;
}
以 $S$ 作为体积限制,物品 $i$ 的体积是 $i$,价值是 $w_i$,求最大价值。因为要求取不同的若干个数,所以是 01 背包模型,直接套入求解即可。
最大约数和 - 01 背包 - C++ 代码
int f[N]; // 01 背包 dp 数组
memset(f, 0xcf, sizeof f); f[0] = 0;
for (int i = 1; i <= S; i++) {
for (int j = S; j >= i; j--)
f[j] = max(f[j], f[j - i] + w[i]);
}
int ans = 0; // 答案是 f 的最大值
for (int j = 0; j <= S; j++) ans = max(ans, f[j]);
return ans;
完全平方数
输入一个不超过 $10000$ 的正整数 $m$,求它可以表示成最少几个平方数的和(不包括 $0$)。
比如 $m=12$ 时的答案是 $3$,表示方式是 $4+4+4$。
-- 来自 leetcode 279. 完全平方数
洛谷上有一个类似的题目: 洛谷 1679 神奇的四次方数 。
把每个完全平方数看做背包体积,预处理出来物品的体积数组:
完全平方数 - 预处理体积数组 C++ 代码
const int K = 100 + 5;
int v[K]; // 体积数组
// 预处理体积数组, 最多到 k=sqrt(m)
int k = 1;
while (1) {
int s = k * k;
if (s > m) break;
v[k++] = s;
}
背包的总体积限制是 $m$,定义 $f(j)$ 表示拼成 $j$ 的最少的平方数的个数。
那么转移方程仍然是,依次考虑每个数字 $i$,选或者不选它:
\[f(j) = \min { \{ f(j), f(j-v_i) + 1 \}}\]由于目标是取最小值,所以初始化 $f(j)$ 数组到无穷大。
最初的情况,$f(0) = 0$。
每个数字的使用次数不加限制,代入完全背包模型即可,$f(m)$ 即是答案。
完全平方数 - C++ 代码
const int K = 100 + 5;
const int M = 10000 + 5;
int f[M];
int v[K]; // 体积数组
class Solution {
public:
int numSquares(int m) {
// 预处理体积数组, 最多到 sqrt(m)
int k = 1;
while (1) {
int s = k * k;
if (s > m) break;
v[k++] = s;
}
// 代入完全背包
memset(f, 0x3f, sizeof f);
f[0] = 0;
for (int i = 1; i < k; i++) {
for (int j = v[i]; j <= m; j++) {
f[j] = min(f[j], f[j - v[i]] + 1);
}
}
return f[m];
}
};
数组的均值分割
将整数数组
a分割为两个非空子数组,使得各自的平均值相等。如果可以如此分割,则返回
true,否则返回false。
a的元素大小范围在[0, 10^4]内,元素个数不超过30个。-- 来自 leetcode 805. 数组的均值分割
比如说,a 取 [1,2,3,4,5,6,7,8] 的时候,可以分割为:[1,4,5,8] 和 [2,3,6,7]。
首先,数组大小 n 是 1 的时候肯定是不行的,特判排除。
假设分割后的两个子数组的平均数是 t(它可能是个小数), 并假设其中一个数组的大小是 k,整个数组的和是 s,那么有:
t * k + t * (n-k) = s
// =>
t = s/n
也就是说,这个平均值一定是整个数组的平均值。
但是,每个数组的和不一定是 s/2,个数也不一定相等,比如 [5,3,11,19,2]。
不过,其中肯定有一个子数组的和是不大于 s/2 的。
这和 分割等和子集 问题非常相似,只是要求更严格一点,可以基于 01 背包来考虑。
定义 $f(j, k)$ 表示使用 $k$ 个元素拼成和为 $j$ 是否可行的布尔值。
这里,相对于原本的 01 背包模型,新加入一个维度 $k$ 以方便计算平均数来验证答案。
不断放入 $a_i$,对于和为 $j$ 的推导,需要考虑每一个可能的 $k$:
- 不选 $a_i$ 时,$f(j, k)$ 不变。
- 选择 $a_i$ 时,剔除 $a_i$ 元素后、应该考虑 $f(j-a_i, k-1)$ 是否可行。
不过,目前 $f$ 只描述了拼成目标和是否可行,要进一步验证平均数是否为 $s/n$。
初版代码实现如下:
数组的均值分割 - 优化前 - C++ 代码
const int M = (1e4 * 30) / 2 + 1;
class Solution {
public:
bool splitArraySameAverage(vector<int>& a) {
int n = a.size();
int s = accumulate(a.begin(), a.end(), 0);
if (n == 1) return false;
// 肯定有一个子数组和不大于 s/2, 足够
int m = s / 2;
// 拼成和 m 且花费 k 个数字是否可行
bool f[M][30];
memset(f, 0, sizeof f); f[0][0] = true;
for (int i = 0; i < n; i++) {
for (int j = m; j >= a[i]; j--)
for (int k = 1; k <= n - 1; k++) {
f[j][k] |= f[j - a[i]][k - 1];
// 验证 j/k == s/n
if (f[j][k] && (j * n == s * k))
return true;
}
}
return false;
}
};
这个实现可以勉强 AC,考虑到 $k$ 的取值范围肯定不大于 30,可以考虑二进制优化。
定义 $f(j)$ 为一个整数,其低位起第 $k$ 个比特是 $1$ 表示拼成和为 $j$ 且花费 $k$ 个数字是可行的。
如此一来,原本最内层的循环可以简化,就是说 $k$ 从 $1…n-1$ 的 dp 转移过程,可以简化成一个语句:
f[j] |= f[j - a[i]] << 1;
验证环节则可以通过依次检查每个 $j$ 的每一个比特来进行。
最终优化后的代码实现如下:
数组的均值分割 - 优化后 - C++ 代码
const int M = (1e4 * 30) / 2 + 1;
class Solution {
public:
bool splitArraySameAverage(vector<int>& a) {
int n = a.size();
int s = accumulate(a.begin(), a.end(), 0);
if (n == 1) return false;
// 肯定有一个子数组和不大于 s/2, 足够
int m = s / 2;
// f[j] 的第 k 位 bit 是 1 表示拼成和 m 且花费 k 个数字可行
int f[M];
memset(f, 0, sizeof f); f[0] = 1;
for (int i = 0; i < n; i++)
for (int j = m; j >= a[i]; j--)
f[j] |= f[j - a[i]] << 1;
// 验证
for (int j = 0; j <= m; j++) {
for (int k = 1; k <= n - 1; k++) {
if ((f[j] & 1 << k) && (j * n == s * k))
return true;
}
}
return false;
}
};
组合总和
给你一个由 不同 整数组成的数组
a,和一个目标整数m。请你从a中找出并返回总和为m的元素组合的个数。-- 来自 leetcode 377. 组合总和 Ⅳ
例如:a 取 [1,2,3],m 取 4 时有 7 种可行组合:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
这个问题非常具有迷惑性,注意所谓的「组合」,其实根本不是组合,而是「排列」。比如说 (1,2,1) 和 (2,1,1) 算作两种可行方案。
所以这不算一个背包问题,拿完全背包模型去做是错误的,会少算。
这个问题类似经典的 爬楼梯问题 (是不是没想到)。
定义 $f(j)$ 为总和为 $j$ 的时候的方案总数。
要想获得 $j$,就要考虑从前面的 $f$ 转移而来,转移的方式,就是考虑 每个数字 $a_i$ 作为转移路径:
\[f(j) = \sum_{0 \leq i \leq n} { f(j-a_i) }\]这好比说,要爬到 $j$ 层楼梯,可行的爬楼梯步数从数组 $a$ 中获取,一共有多少种方案。
代码实现如下:
const int N = 201;
const int M = 1001;
unsigned int f[M];
memset(f, 0, sizeof f);
f[0] = 1;
for (int j = 0; j <= m; j++)
for (int i = 0; i < a.size(); i++)
if (j >= a[i]) f[j] += f[j - a[i]];
return f[m];
这看起来和完全背包问题很像,但是不同点在于:每次计算一个 $f(j)$ 都要考虑全部的数字 $a_i$。 而完全背包模型只能考虑当前阶段 $i$ 之前的物品。
下面的图可以清晰地看到二者的差别,其中绿色区域是可行的转移来源:
- 左边的是当前的问题,转移路径可以来自全部物品,不同的路径也会有相同的 dp 值,所以适合当前的「排列」计数问题。
- 右边的是完全背包问题,因为每次转移都只能从左下方而来,所以转移路径是「上坡线」,只会有一条,也就是与排列无关。
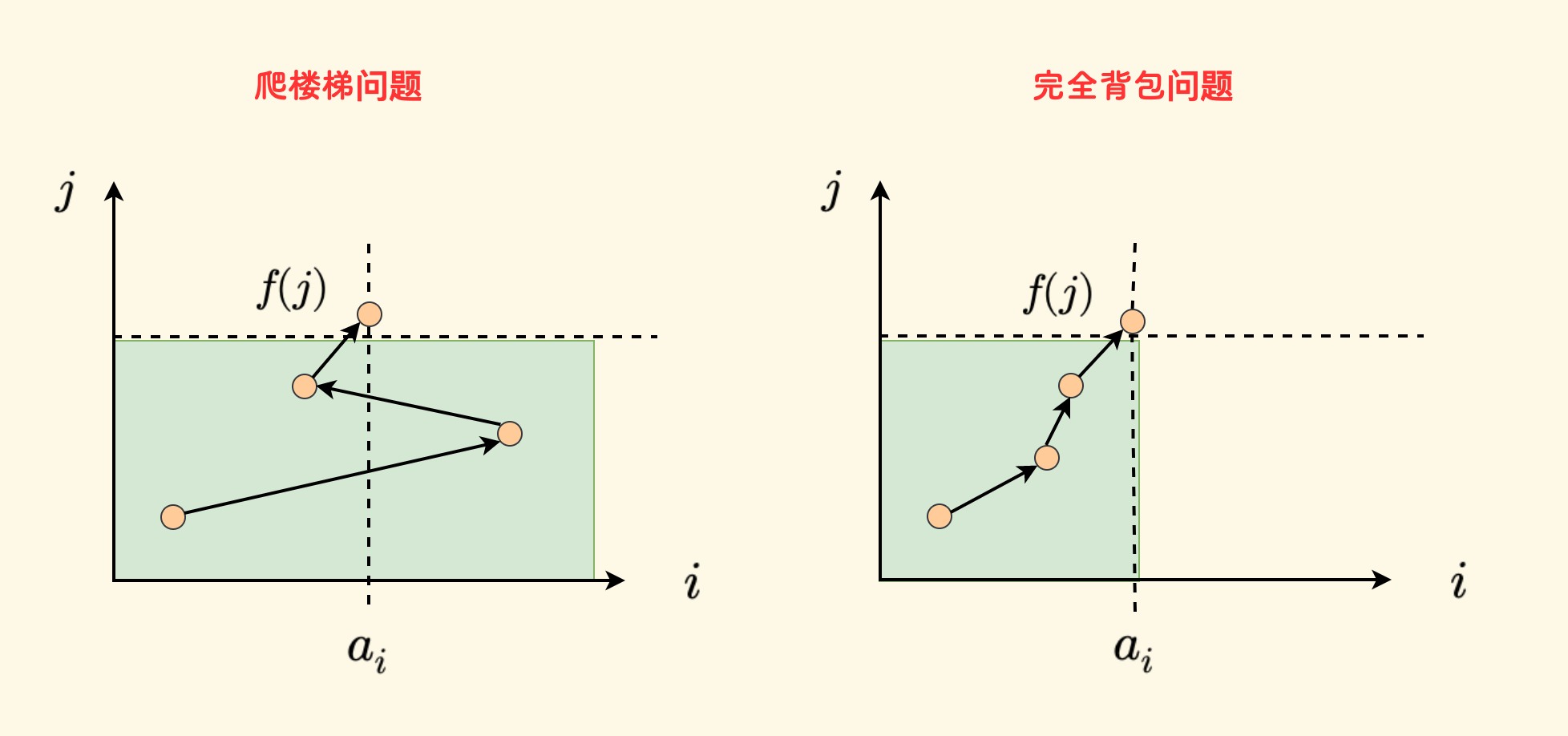
从动态规划的角度来看,二者的 阶段划分 和 转移方式 不同:
- 完全背包问题,是以物品 $a_i$ 来划分阶段,再考虑每个体积 $j$ 的转移。
- 这个爬楼梯问题,是以目标 $j$ 来划分阶段,使用每个 $a_i$ 来转移。
从代码上来看,区别仅在于 内外层循环的对象不同: 求排列数的时候外层循环目标体积、内层循环物品。背包问题则反之。
硬币
给定 $N$ 种硬币,其中第 $i$ 种硬币的面值为 $A_i$,共有 $C_i$ 个。 从中选出若干个硬币,把面值相加,若结果为 $S$ ,则称 “面值 $S$ 能被拼成”。 求 $1∼M$ 之间能被拼成的面值有多少个。
-- 来自 《算法竞赛进阶指南》, acwing 281
一眼多重背包,此外和 分割等和子集 问题类似,是判定性问题。
前面说过,多重背包的外两层循环可以看成 01 背包的外层循环。
定义 $f(j)$ 为是否可以拼成面值为 $j$ 的布尔值,则 dp 方程为:
\[f(j) = \forall_{1 \leq k \leq c_i} \forall_{a_i \leq j \leq m} { \{ f(j) \lor f(j-a_i) \} }\]代码实现如下:
硬币 - C++ 代码
const int N = 101;
const int M = 1e5 + 10;
const int C = 1001;
int n, m;
int a[N], c[N];
bool f[M];
int solve() {
memset(f, 0, sizeof f);
f[0] = true;
for (int i = 1; i <= n; i++)
for (int k = 1; k <= c[i]; k++)
for (int j = m; j >= a[i]; j--)
f[j] |= f[j - a[i]];
int ans = 0;
for (int i = 1; i <= m; i++) ans += f[i];
return ans;
}
这样可以通过测试用例的正确性,但是会超时,复杂度太高。
注意到,当前问题是一个「可行性」问题,而不是最优化问题。
因为只关心 $f(j)$ 是否为 $true$,其实不必每个阶段把 $c_i$ 个硬币都循环一次。
首先,如果在放入第 $i$ 种硬币时,$f(j)$ 已经是 $true$,那么没必要再考虑它了。
接下来 $f(j)$ 只有可能由 $f(j-a_i) = true$ 的情况转移而来。
如果转换一下思路,不直接基于多重背包模型,而是基于完全背包模型。
更严格地说,是 「使用次数受限制的」完全背包模型:
for (int i = 1; i <= n; i++) {
for (int j = v[i]; j <= m; j++) // 注意是正序
if (!f[j] && f[j-a[i]] && check(j))
f[j] = 1;
}其中的 check 函数用以限制第 $i$ 种硬币的使用次数不得超过 $c_i$。
假设一个数组 $used(j)$ 表示在考虑放入第 $i$ 种硬币时、要拼成面值 $j$ 所需的硬币 $i$ 的最少个数。
如果面值 $j-a_i$ 可以拼成,只需再使用一次硬币 $i$,那么面值 $j$ 也可以拼成,所以 $used$ 数组的递推关系式如下:
\[used(j) = used(j-a_i) + 1\]那么 check 函数实际上就是要检查 $used(j) < c_i$ 的限制。
最终核心代码如下:
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= m; j++) used[j] = 0;
for (int j = a[i]; j <= m; j++)
if (!f[j] && f[j - a[i]] && used[j - a[i]] < c[i]) {
f[j] = true;
used[j] = used[j - a[i]] + 1;
}
}优化掉了一层循环的根本原因在于:这是个可行性判断问题:
原本的多重背包模型,对每个阶段 $i$ 都会跑 $c_i$ 次 $f$ 数组依次进行转移。 因为多重背包模型需要求出 $f(j)$ 的具体取值。但是可行性判断只需要判断真假, 对于每个 $f(j)$ 而言,仅当面值 $j$ 从未被拼成出来时,才考虑转移。只要拼成功过,就不再考虑这个 $j$ 了。
而每个硬币的使用次数 $c_i$ 的限制,可以使用辅助数组 $used$ 来保证,同时此数组可以随着 $j$ 的循环同步递推。
硬币 - 优化后完整 C++ 代码
#pragma GCC optimize(3)
using namespace std;
const int N = 101;
const int M = 1e5 + 10;
const int C = 1001;
int n, m;
int a[N], c[N];
bool f[M];
int used[M];
int solve() {
memset(f, 0, sizeof f);
f[0] = true;
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= m; j++) used[j] = 0;
for (int j = a[i]; j <= m; j++)
if (!f[j] && f[j - a[i]] && used[j - a[i]] < c[i])
f[j] = true, used[j] = used[j - a[i]] + 1;
}
int ans = 0;
for (int i = 1; i <= m; i++) ans += f[i];
return ans;
}
简单总结 ¶
- 四种背包问题模型的代码实现有一定规律,其中 01 背包 和 完全背包是基础。
- 多重背包可以看做对每种物品重复执行了多次的 01 背包问题。
- 分组背包可以看做在 01 背包基础上,对每个目标体积、对组内每个物品依次推导,取总的最值。
- 多重背包问题下,如果不计算具体值,而只判断可行性,可以尝试改造为「受次数限制的完全背包问题」。
- 混合背包只是在转移上依据设定的次数限制来套入不同的基础背包模型。
- 二维费用背包是在基础背包上多加了一个维度的限制。
(完)
更新日志:
- 2024/02/12:添加「数组的均值分割」问题
- 2024/02/06:添加「组合优化」问题,并解释了它和完全背包的区别。
- 2024/02/22:添加问题「最大约数和」。
- 2024/02/24:添加问题「砝码称重」、「完全平方数」
- 2024/03/12:添加「二维费用背包」、「混合背包」、问题「一和零」、「樱花」
- 2024/03/12:文章标题从「背包问题的简单总结」更改为「背包问题的整体总结」
相关文章:树上背包 - 有依赖的背包问题
本文原始链接地址: https://writings.sh/post/knapsack
