我想再次引用 《通灵芯片》 中的这句话:
有限状态机为何如此有用,其原因之一是它们能识别序列。
正则表达式的背后就是状态机。
本文只讲关键过程,基本概念则不再说明。
前面的话 ¶
正则表达式引擎的构造可以分三步:
- 通过 双栈法 解析正则表达式,构造等价的 NFA 。
通过子集构造法,将 NFA 转化为等价的 DFA 。
这并非必需,虽然 NFA 也能识别字符串,但 DFA 跑起来更快。
- 通过 Hopcroft 算法, 化简 DFA 到最小状态数目。这一步也非必需,只是让空间占用更优。
另外,实际的代码实现可能稍复杂,为叙述上的简明,文中将采用类似 Python 的伪代码来示意, Python 和 C++ 的具体代码则放在 文尾链接。
要实现的正则表达式非常简单,它只支持以下几种规则:
ab连接两个表达式串a|b两个表达式取「或」的关系,匹配其中任一即可a*克林闭包,即重复 0 次或多次a?表示可有可无,即出现 0 次或 1 次a+表示重复 1 次或多次,其实即aa*[0-9]表示命中某个范围内的字符, 比如[a-zA-Z]表示命中大小写字母(ab)括号表示其中的表达式优先结合
举例来说:(a|b)*ab 可以匹配字符串 aaab,但是无法匹配 bbba。再比如 [0-9]* 可以匹配数字串 123,但是无法匹配 abc 。
闭包类操作符的优先级应该比其他操作符要高,把优先级量化的表格 precedence 如下:
| 操作 | 优先级(越高越大) |
|---|---|
ab | 1 |
a|b | 1 |
a* | 2 |
a? | 2 |
a+ | 2 |
在数据结构上,不论是 NFA 状态还是 DFA 状态,都至少有两个字段:
id是状态的唯一标识。is_end来表示此状态是否是一个终态。
把结构 State 作为状态基类,NfaState 和 DfaState 都将继承自它。
State 状态基类的代码表示
class State:
id: int
is_end: bool
接下来,将展开讲三个过程。
构造 NFA ¶
同一个输入符号下,NFA 状态目标状态可能有多个,因此 NFA 状态的结构设计如下:
NfaState 状态的代码表示
class NfaState(State):
# 跳转表, { Char => { Target States... }}
transitions: dict[C, set[NfaState]] = {}
def add_transition(self, ch, to):
self.transitions[ch].add(to)
if self.is_end:
self.is_end = False
其中 add_transition 方法负责添加一条从当前状态到目标状态的跳转关系。
NFA 和 DFA 有一个不同之处,就是 NFA 可以添加空边。 在本文中采用符号 epsilon 也就是希腊字母 ε 来表示空符号。
空边意味着,可以在不输入符号的情况下,沿着它前进。如果目标状态也有空边,那么这种跳转可以递归进行。 比如下图中,1 号状态可以在不输入任何符号的情况下,不断向前跳转。
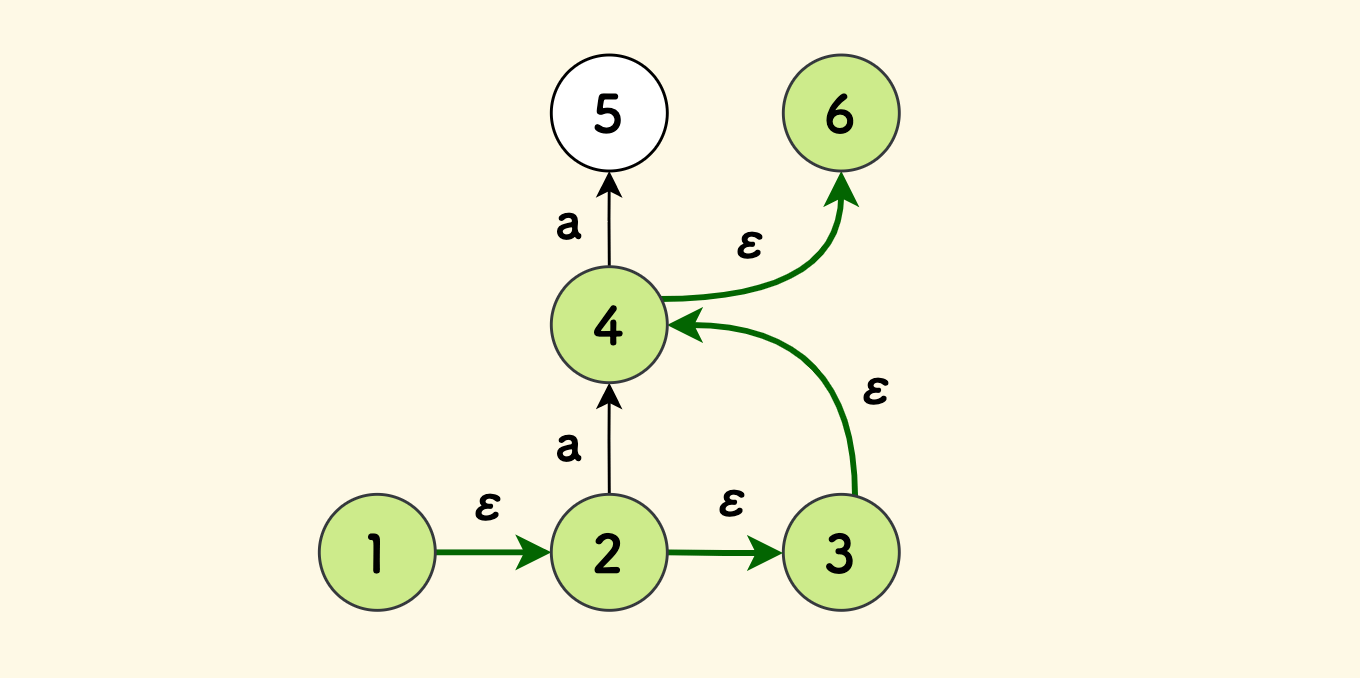
NFA 的起始状态只有一个,但是终态可以有多个。 不过,将 NFA 的结构设计为只有一个终态的话,会简化问题, 因为有多个终态的 NFA 可以通过添加空边的方式转化为等价的只有一个终态的 NFA 。
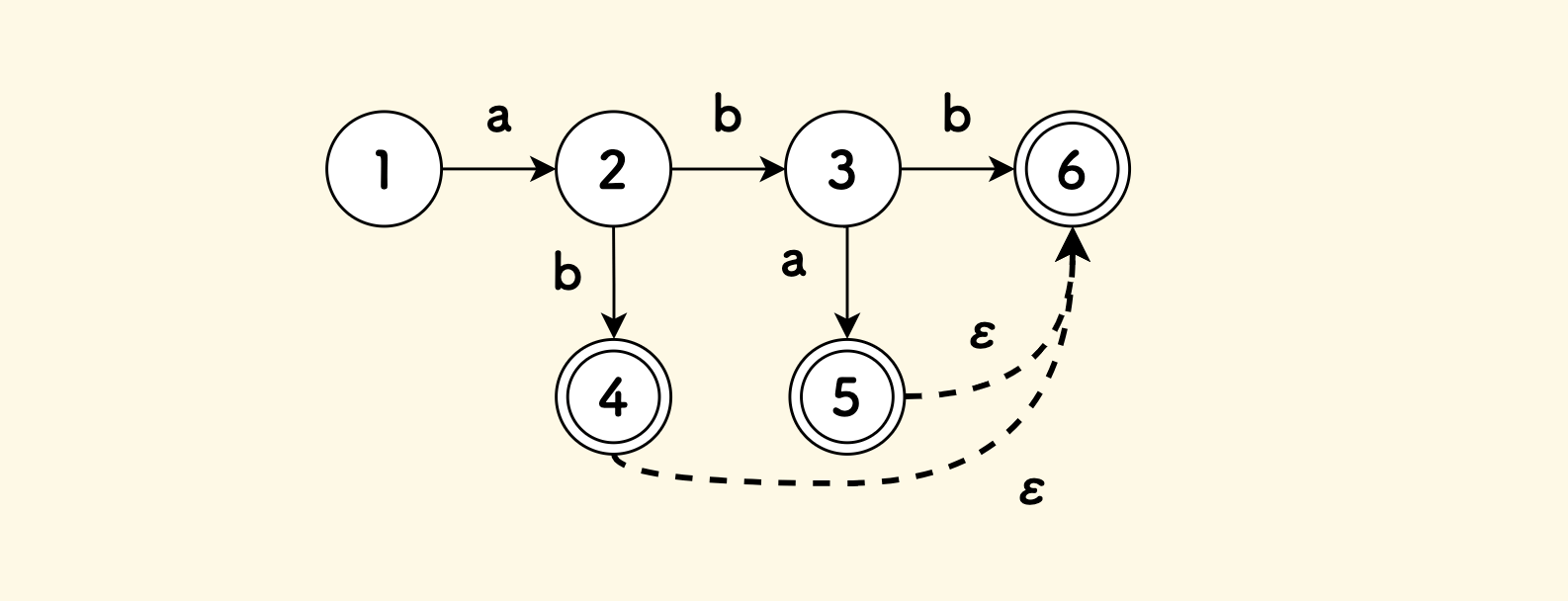
Nfa 状态机的代码表示
class Nfa:
start: NfaState
end: NfaState
正则表达式构造 NFA 有两个关键点:
- 采用双栈法、自底向上地解析正则表达式
- 在解析过程中,针对不同规则,不断构造 NFA
这个构造过程,将实现在一个叫做 NfaParser 的类中。
NfaParser 的代码结构
class NfaParser:
id: int = 0 # 状态计数
def parse(self, s):
# 解析正则表达式字符串,返回一个 NFA
pass
先定义一个基本方法 new_state 来对新建的状态计数,方便在新建 NfaState 时给 id 字段初始值。
NfaParser 的 new_state 方法
def new_state(self, is_end):
self.id += 1
return NfaState(self.id, is_end)
接下来,依次看如何处理每一个正则表达式规则。
每一个正则表达式背后是一个 NFA,正则操作符都是在通过添加空边来组合和变形这些 NFA。
首先,一个简单的输入符号
a可以表达为一个最简单的 NFA ,其中2号状态是终态:
从单个输入符号构造 NFA 的伪代码
def create_nfa_from_symbol(self, ch): start = self.new_state(False) end = self.new_state(True) start.add_transition(ch, end) return Nfa(start, end)对于连接操作符,
ab可以表达为a和b两个 NFA 的串联:
连接操作符 nfa_concat 的伪代码实现
def nfa_concat(self, a, b): # 添加一条空边跳转 2->3 a.end.add_transition(epsilon, b.start) return Nfa(a.start, b.end)对于或操作符,
a|b可以表达为a和b两个 NFA 的并联:
或操作符 nfa_union 的伪代码实现
def nfa_union(self, a, b): start = self.new_state(False) # 5 end = self.new_state(True) # 6 start.add_transition(epsilon, a.start) # 5->1 start.add_transition(epsilon, b.start) # 5->3 a.end.add_transition(epsilon, end) # 2->6 b.end.add_transition(epsilon, end) # 4->6 return Nfa(start, end)对于克林闭包,
a*可以表达为:
克林闭包 nfa_closure 的伪代码实现
def nfa_closure(self, a): start = self.new_state(False) # 3 end = self.new_state(True) # 4 a.end.add_transition(epsilon, a.start) # 2->1 start.add_transition(epsilon, a.start) # 3->1 a.end.add_transition(epsilon, end) # 2->4 start.add_transition(epsilon, end) # 3->4 return Nfa(start, end)类似的,
a?可以表达为:
nfa_optional 的伪代码实现
def nfa_optional(self, a): start = self.new_state(False) # 3 end = self.new_state(True) # 4 start.add_transition(epsilon, a.start) # 3->1 a.end.add_transition(epsilon, end) # 2->4 start.add_transition(epsilon, end) # 3->4 return Nfa(start, end)a+很简单,可以直接表达为aa*:nfa_plus 的伪代码实现
def nfa_plus(self, a): return self.nfa_concat(a, self.nfa_closure(a))对于
[0-9a-z]一类的字符范围语法糖,其实是在创建一个多条边的 NFA :create_nfa_from_ranges 的伪代码实现
def create_nfa_from_symbols(self, chs): start = self.new_state(False) end = self.new_state(True) if chs: for ch in chs: start.add_transition(ch, end) else: start.add_transition(epsilon, end) return Nfa(start, end) def create_nfa_from_ranges(self, ranges): chs = set() for r in ranges: start, end = r for x in range(ord(start), ord(end) + 1): chs.add(chr(x)) return self.create_nfa_from_symbols(chs)
举例来看,比如表达式 (a|b)*ab ,将它一步一步演化成为最终的 NFA 状态机的过程如下图:
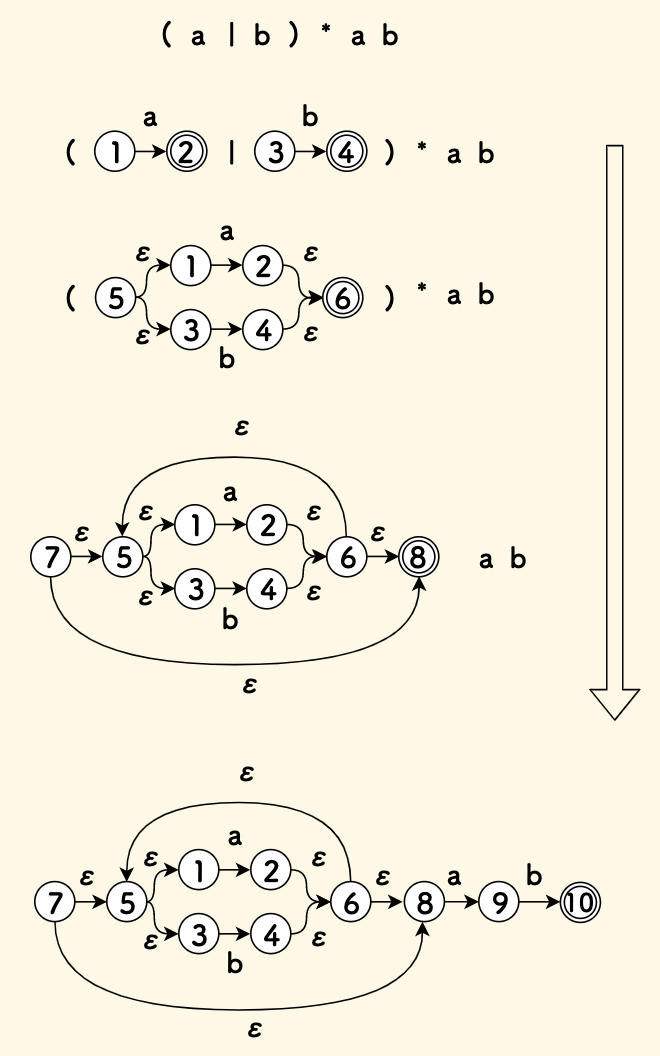
下面的问题是,如何解析正则表达式字符串?
这是一种 Parsing 过程,将采用 dijkstra 双栈算法, 它是为算术表达式解析而生,但是也适用于任何有操作符优先级关系的表达式解析。
双栈法本质上是一种自底向上的 shift-reduce 解析过程。
双栈的意思是,一个栈存放生成的 NFA 状态机,另一个栈存放操作符(比如 |, * 等)。
解析过程有两种动作:
- shift 移入动作:将新构造的 NFA 或者操作符压入到相应栈中
- reduce 归约动作:如果时机合适,则弹出栈顶的操作符和相应数量的 NFA ,进行计算。 计算就是上面所讲的
nfa_union,nfa_concat之类的函数。
使用栈的原因在于,操作符之间有优先级关系,存在需要先等待、后归约的情况。 而使用两个栈的原因在于,我们要不断考察栈顶的操作符,如果只采用一个栈, 栈顶不确定是 NFA 还是 操作符的话,就会不方便。
仍以 (a|b)*ab 为例,它的 shift-reduce 解析过程如下图所示,其中:
- 遇到字符
a,b时,应用create_nfa_from_symbol函数,得到新的 NFA 入栈。 - 计算
(a|b):将a和b的 NFA 出栈、操作符|出栈,应用nfa_union函数,得到新的状态机p,入栈。 - 计算
p*:将p出栈、操作符*出栈,应用nfa_closure函数,得到新的状态机q,入栈。 - 计算
qa: 将q和a的 NFA 出栈,应用nfa_concat函数,得到新的状态机r,入栈。 - 如此,进一步应用连接规则,将
rb归约为状态机s,即最终结果。
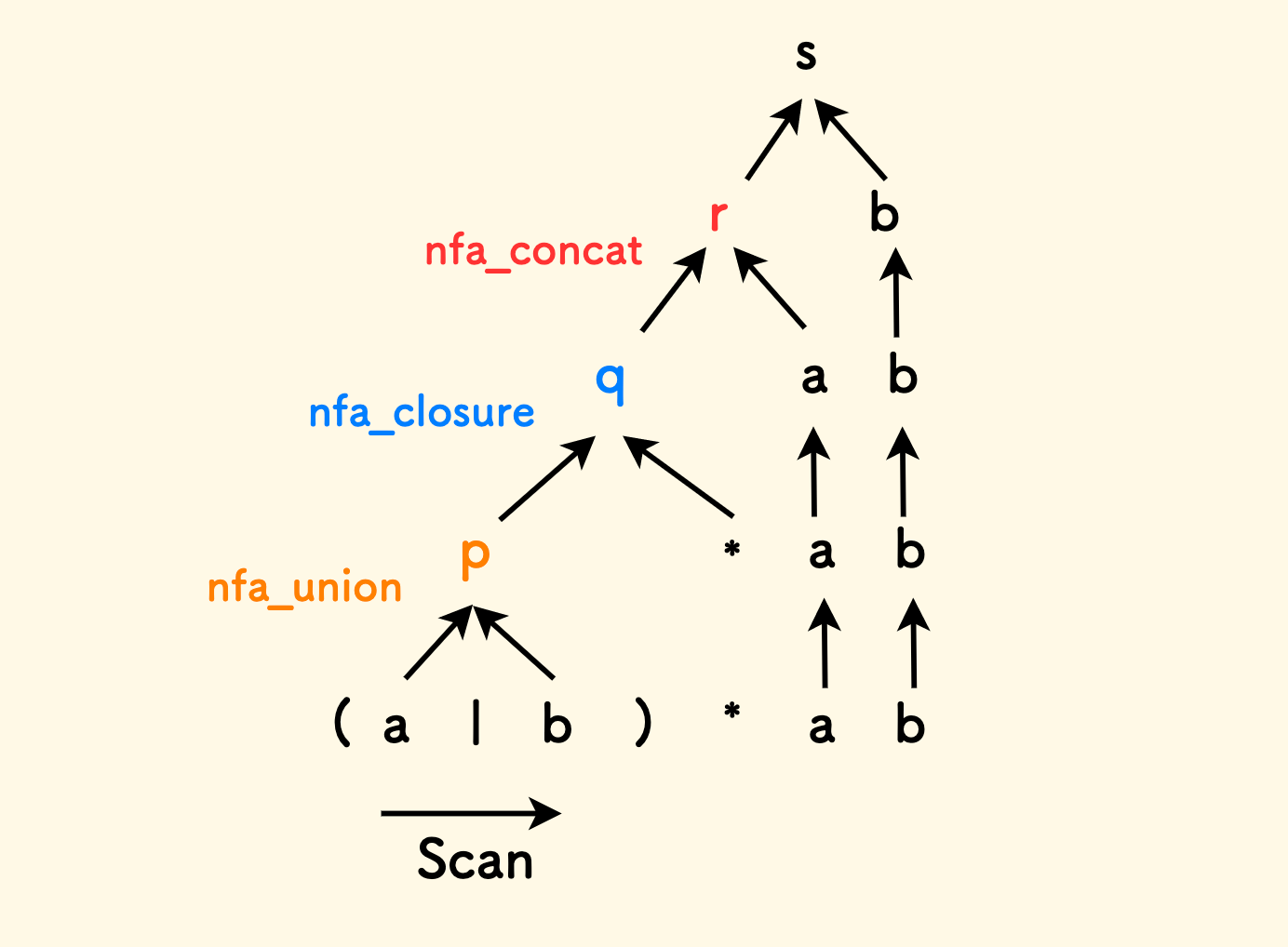
从这个例子,可以看到,shift-reduce 是一个自底向上的解析过程,向右移入,向上归约。
解析算法的详细过程:
- 定义两个栈:一个用来存放 NFA、另一个存放操作符
定义进行计算的子过程:
弹出栈顶操作符,弹出相应数量的 NFA,计算后结果入栈。
比如对于操作符
|、操作符*来说:def calc(self, nfa_stack, op_stack): op = op_stack.pop() if op == '|': b = nfa_stack.pop() a = nfa_stack.pop() nfa_stack.push(self.nfa_union(a, b)) elif op == '*': a = nfa_stack.pop() nfa_stack.push(self.nfa_closure(a)) # 其他操作符的情况...自左向右地,每扫描到一个字符
ch:如果遇到非操作符的字符,则应用
create_nfa_from_symbol函数构造一个新的 NFA 入栈。遇到范围语法糖,也是如此,不过是应用
create_nfa_from_ranges函数。如果遇到操作符,是否需要归约取决于优先级关系:
如果操作符栈顶优先级更高,则先计算、再入栈。
先计算栈顶,直到栈顶优先级比当前操作符低为止;再把当前操作符入栈。
否则 先入栈、后面等机会再计算。
用代码来示意就是:
while precedence(op_stack.top()) >= precedence(ch): calc(nfa_stack, op_stack) op_stack.push(ch)- 如果遇到左括号,直接入操作符栈,以等待右括号闭合。
如果遇到右括号,则不断出栈进行计算,直到左括号出栈。
用代码来示意就是:
while op_stack.top() != ')': calc(nfa_stack, op_stack) op_stack.pop() # 丢弃左括号
- 最后
nfa_stack中应该仅剩余一个元素,即计算结果。
这里面有一些细节需要说明:
正则表达式的连接操作符,实际上没有「真身」。我们可以将正则表达式事先预处理,相当于给它定义一个符号,比如
&。举例来说,
(a|b)*ab可以预处理为(a|b)*&a&b,这样解析过程就方便了。实际中还要考虑到转义字符的情况,具体处理可以参考文尾代码实现链接中的处理。
计算的时机中并没有考虑输入终止时的情况。输入结束时,栈中可能残留待计算的操作符和 NFA 。 那么需要再输入结束后,检查下操作符栈是否非空,将其计算完即可。
至此,我们已可以将一个正则表达式转化为非确定性有限自动机 NFA。
NFA 转化为 DFA ¶
对于 DFA 状态来说,同一个输入符号下,可能的目标跳转状态最多只有一个。 因此 DfaState 的结构设计如下:
DfaState 状态的代码表示
class DfaState(State):
# 跳转表, { Char => Target State }
transitions: dict[C, DfaState] = {}
DFA 状态机的起始状态只有一个,终态可以有多个,那么其结构设计为:
Dfa 状态机的代码表示
class Dfa:
start: DfaState
# 所有的状态集合, 方便匹配函数使用
states: set[DfaState]
如果不介意 NFA 相比 DFA 在匹配上的时间开销的话,我们可以仅用第一部分解析到的 NFA 来匹配字符串。 由于 NFA 的状态在同一个输入字符下,可以到达的目标状态可以有多个,所以要检查到每一个可能的跳转路径。 另外,由于有空边的存在,所以要递归向前沿着空边找到所有可能的目标状态。
这两点都造成了一个问题:NfaState 在同一输入下的目标状态是不唯一的。 这也是采用 NFA 来匹配会比 DFA 来匹配更慢的原因。
子集构造法 处理的就是这个问题,它的做法是:
- 一个状态可到达的所有状态,都加入一个集合,作为 DFA 中的一个新状态。
- 存在空边的情况下,不断沿着空边把途经状态也加入这个集合。
如此一来,会有两个效果:
- 集合到集合之间的跳转变的唯一了。
- 消除了空边。
也就是说,这样就构造了 DFA 。
值得说明的是, NFA 总可以转化为一个与其能力等价的 DFA。 子集构造法是通用的,并不局限于正则表达式这一场景。
以一个例子来说明子集构造法的过程,如下图所示,左侧是 NFA,右侧是构造的 DFA:
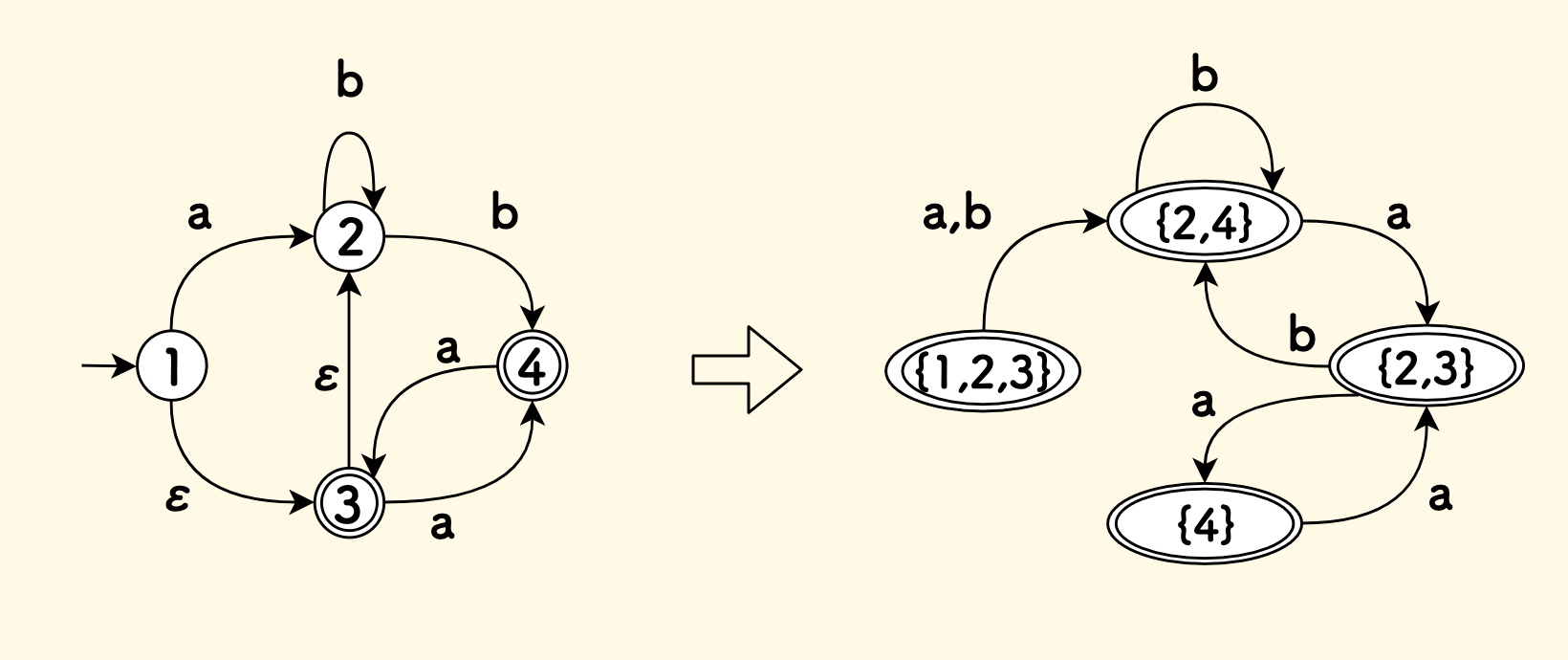
- 最开始,将初始状态自己构造一个集合
{1},沿着空边递归寻找可达状态,加入2和3号状态,得到{1,2,3} 考察
{1,2,3}所有的非空出边(就是考察集合中每个状态的非空出边):- 对于字符
a来说,可以到达的有{2,4}, 沿着空边扩充,仍然是{2,4} - 对于字符
b来说,可以到达的有{2,4}, 沿着空边扩充,仍然是{2,4}
- 对于字符
考察
{2,4}所有的非空出边:- 对于字符
a来说,可以到达的有{3},沿着空边扩充,得到{2,3} - 对于字符
b来说,可以到达的右{2,4}, 沿着空边扩充,仍然是{2,4}
- 对于字符
考察
{2,3}所有的非空出边:- 对于字符
a来说,可以到达的有{4}, 沿着空边扩充,仍然是{4} - 对于字符
b来说,可以到达的有{2,4}, 沿着空边扩充,仍然是{2,4}
在这一步,没有产生新的集合,所以结束。
最终得到了四个新的集合,每一个集合就是一个
DfaState。此外,包含终态的集合在 DFA 中也是终态。
- 对于字符
我们可以把 NFA 转 DFA 的过程实现在一个叫做 DfaBuilder 的类中。
上面例子中,有两个主要过程:
每次跳转到一个集合,都沿着空边进行扩充。
我们可以把状态集合
N沿着空边不断扩充后的集合叫做N的空边闭包ε-closure(N)。要沿着空边递归扩充,可以采用深度优先的方式,代码示意如下:
epsilon_closure 函数的伪代码实现
def epsilon_closure(self, N): # 原地沿空边递归扩充 NfaState 集合 # N 中的所有 NfaState 入栈 stack = [] for s in N: stack.push(s) # DFS 深度优先遍历 while stack: s = stack.pop() # 沿着空边,找所有可以到达的状态,加入集合 for t in s.transitions[epsilon]: if t not in N: N.add(t) # 压入栈中 stack.push(t)如果产生一个新的集合,都将它加入处理队列。
构造的主过程则是:
- 最开始,以 NFA 的初始状态构造起始集合
{1} 对于每个可能非空字符出边,考察其可到达的状态的集合。这个跳转动作叫做
move函数:move 函数的伪代码实现
def move(self, S, ch): # move(S, ch) 返回从状态 S 经过非空边 ch 跳转到的目标状态 N = self.d[S.id][ch] self.epsilon_closure(N) # 沿空边扩充 id = self.make_dfa_state_id(N) if id not in self.states: # 如果已经生成过,则返回,不再新建 self.make_dfa_state(N, id=id) return self.states[id]其中有个细节是,如果一个集合(或者叫
DfaState)已经存在了,就不要再新建了。- 如果
move到达的目标集合还没有处理过,那么加入处理队列。
这个处理过程是广度优先的,代码可以实现如下:
DfaBuilder 构造 DFA 的主过程伪代码实现
def build(self):
# 初始状态: 从 NFA 的开始状态沿空边可达的整个闭包
N0 = {self.nfa.start}
self.epsilon_closure(N0)
S0 = self.make_dfa_state(N0)
# q 是待处理的队列,先进先出,也即广度优先
# 所谓 "处理", 就是给每个 DfaState S 填写非空边的跳转表
q = [S0]
# q_d 是已经在队列中的所有状态的 ID
# 如果已经加入到队列了,就不必重复加入了
# 实际上 q 是一种 unique 队列
q_d = {S0.id}
# 最终要构建的 DFA
dfa = Dfa(S0)
while q:
# 弹出一个待处理的状态 S
S = q.pop(0)
q_d.remove(S.id)
# 对于每一个可能的 **非空** 跳转边 ch
for ch in self.d.get(S.id, {}):
# 跳入的是一个其他状态 T
T = self.move(S, ch)
# 记录跳转边
S.add_transition(ch, T)
if T not in dfa.states:
if T.id not in q_d:
# T 尚未打标,加入队列
q.append(T)
q_d.add(T.id)
# S 已处理完成,放入 dfa
dfa.states.add(S)
return dfa
最后,我们前面解析正则表达式 (a|b)*ab 得到的 NFA 构造为 DFA 的过程如下图所示。 这个图每一步中处于同一个集合的 NfaState 会被染成绿色。 可以看到,这个表达式所等价的 DFA 仅包含三个状态。
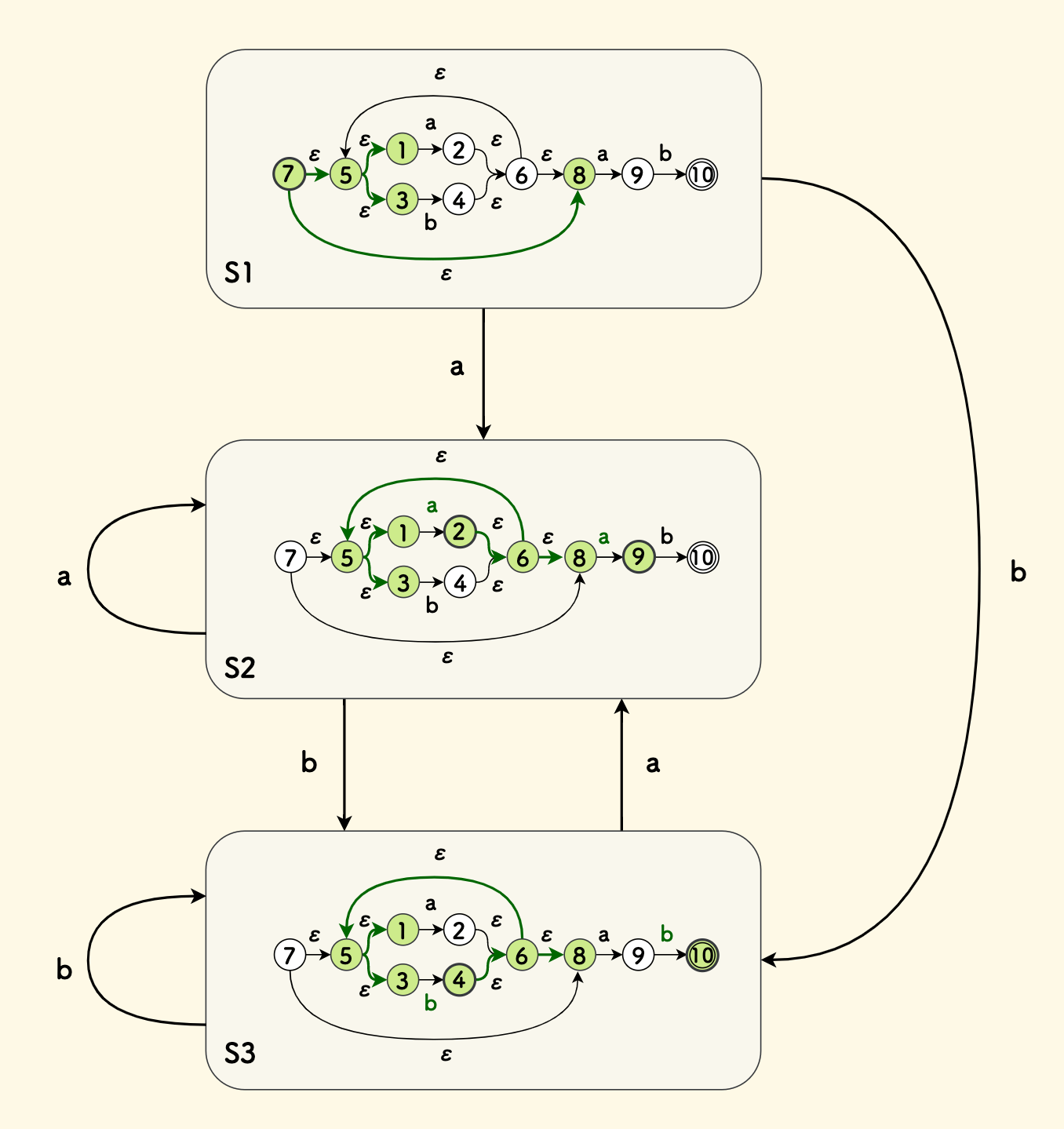
至此,我们可以把一个正则表达式转化到 DFA 了,也可以写出匹配函数了: 不断输入字符,根据输入字符跳转状态,输入结束时,如果到达了一个终态,就表示匹配成功。
DFA 匹配函数 match
class DFA:
def match(self, s: str):
st = self.start
for x in s:
if x not in st.transitions:
return False
st = st.transitions[x]
return st.is_end
化简 DFA ¶
最后,如何将一个 DFA 的状态数最小化呢?
我们可以做的有三个事:
- 清理死状态,也就是去除那些没有出边的非终态。
- 清理无法到达的状态。
- 合并等价的状态。
前两点非常容易理解,不再展开讨论。
第三点,采用的是 Hopcroft DFA 最小化算法。这个算法非常巧妙:
- 首先,先假定 DFA 的所有状态分为两个小组,比如将所有终态分成一组,其他的一组。
在每个小组中,找到可以「区分」的状态,执行分割。
如何区分的关键在于:如果对于某个输入字符,两个状态的目标跳转状态不在同一个小组, 那么这两个状态也不应该在同一个小组,就应该分割这个小组。
- 不断重复第三步,直到不再存在可以分割的情况,这些小组就构成了最终的最小化的 DFA 。
看一个例子:
初始情况,所有状态都在一个小组内。下图中左边是原本的 DFA ,右边是分组情况。

先把终态
E分割出去,形成了两个小组{A, B, C, D}和{E}。小组
{E}只有一个状态成员,无需考虑分割。- 依次考察小组
{A, B, C, D}的每个状态,比如A。 - 再依次考察每个输入字符
a和b。 - 如果存在这种情况,一个状态的目标状态和
A的目标状态不在同一个小组,将其收集起来。 所有这种状态构成一个新的小组,分割出去。
在下图中,
D在字符b输入的情况下跳转到E,和A的目标状态不在同一个小组, 所以将{D}分割出去。
- 依次考察小组
同样的思路,可以把
{B}从{A, B, C}中分割出去:考察状态
A和C,到达的目标状态都在小组{A, B, C}中。但是状态
B在输入字符b的情况下,目标状态D在小组{D}中。
目前有四个小组。按照同样的思路,无法再找到可以分割的情况。所以算法结束。
这四个小组,就是最终新的 DFA 的四个状态。

状态化简结束的同时,需要维护好跳转关系。
只需要根据原来
DfaState之间的跳转关系, 把它们小组之间的跳转关系补上即可:原状态A可以经过边a到达状态B的话,就在二者所在小组之间添加一条边a。另外,包含终态的小组,在新的 DFA 中也是终态。
这个例子最终得到的化简后的 DFA 如下图:

最后来分析一下代码实现。
将 DFA 化简的过程实现在一个叫做 DfaMinifier 的类中:
最开始的时候,初始化为两个分组。
不断执行
refine函数,进行分割,直到无法分割。DfaMinifier 主过程 minify 函数
class DfaMinifier: dfa: Dfa # 要化简的原始 DFA def minify(self): # 所有终态在一个小组 g1 = self.make_group({s for s in self.dfa.states if s.is_end}) # 其他状态在一个小组 g0 = self.make_group(self.dfa.states - g1) # 初始分为两组 gs = {g0, g1} # 不断分割,直到无法分割 while self.refine(gs): pass # 重写 DFA self._rewrite_dfa(gs)refine函数负责检查每个小组是否可以分割,并执行分割。refine 函数代码实现
def refine(self, gs): for g in gs: # 检查每个小组 for a in g: # 找到小组内与 a 不同的状态集合 g2 = self.find_distinguishable(g, a) if g2: # 执行切分 g1 = self.make_group(g - g2) # 加入新的小组,移除废弃的分组 gs.remove(g) gs.add(g1) gs.add(g2) # 发生了分割 return True # 未发生分割 return Falsefind_distinguishable是refine函数的子过程,负责收集与给定状态「不同的」状态, 构成一个可以分割出去的小组。:find_distinguishable 函数代码实现
def find_distinguishable(self, g, a): # 在小组 g 中找到和 a 不等价的所有其他状态 b 的集合 g2 # 如果不存在,返回的就是空集合 x = set() for ch in a.transitions: # 对于 a 有出边的情况, 考察每个出边所到达的目标状态 ta = a.transitions[ch] # 检查同小组的每个其他状态 b for b in g: if b != a: # tb 是 b 在此符号下的目标状态, 注意可能是 None tb = b.transitions.get(ch, None) if tb is None or self.group(ta) != self.group(tb): # 目标状态所在小组不同, 记录一下 x.add(b) if x: # 对于一个出边,可以区分,就直接 break break return self.make_group(x)
最后,重新生成一个 DFA 的过程,比较简单,不再展开。
代码实现 ¶
完整的代码实现,放在了 github 上:
Update @2023-09-03:
我实现了一个 C++20 的编译时正则表达式引擎: compile_time_regexp.hpp
(完)
相关阅读:
本文原始链接地址: https://writings.sh/post/regexp