摩尔投票算法和 N/K 推广 (Boyer Moore)

摩尔投票算法，也叫多数投票算法，可以在常数空间内在大小为 N 的序列中找到可能最多 K 个出现次数超过 N/K 次的元素。

找众数问题，可以很容易地用哈希表计数来求解，但是摩尔投票算法的特点在于：常数级别的空间复杂度。不过，它只适用于事先知道众数元素出现次数不少于一定比例的情况。

这个算法非常巧妙，值得写一篇文章说道说道。

给定一个大小为 n 的数组 nums ，返回其中的多数元素。多数元素是指在数组中出现次数大于 [n/2] 的元素。给定的数组总是存在多数元素。
尝试设计时间复杂度为 O(n)、空间复杂度为 O(1) 的算法解决此问题。

采用摩尔投票算法的思路是：

初始化一个候选元素。
迭代这个数组，遇到相同的元素，则投票增加、反之减少。
投票清零之时，更换候选元素为当前元素。

N/2 情况下的摩尔投票 C++ 代码

int majorityElement(vector<int>& nums) {
    // 当前考察的候选元素
    int v = 0;
    // 当前候选元素的票数
    int vote = 0;

    for (auto i = 0; i < nums.size(); i++) {
        if (vote == 0) v = nums[i];  // 更换候选数字
        if (nums[i] == v) vote++; // 投票
        else vote--; // 抵消
    }
    return v;
}

看上去很神奇！细想一下，也容易理解的。

这里有个概念值得体会体会：抵消。因为存在一个元素出现次数超过一半，所以此元素的票可以和其他元素的票抵消，最终一定胜出。

事实上，这个算法可以推广到 N/K 的情况。

直接来看一个 N/3 的情况，题目 leetcode 229.多数元素 II :

给定一个大小为 n 的整数数组，找出其中所有出现超过 [n/3] 次的元素。

这样的众数元素最多有 2 个，但是请注意, 目标众数也可能不存在，或者只有一个。

这一次，采用摩尔投票算法的思路是：

初始化两个候选元素 , 并追踪它们的票数。
迭代数组时，遇到相同的元素，则相应候选元素的投票增加。
如果遇到的元素不在两个候选元素之中，则两个候选元素的票数都减少。
任一个候选元素的票数清零之时，更换它为当前元素。

和 N/2 的情况不同的是，现在是两个候选人, 而且投票抵消的规则有所变化。

N/3 情况下的摩尔投票 C++ 代码

int majorityElement(vector<int>& nums) {
    // 两个候选元素 和 各自票数
    int a, b;
    int va = 0, vb = 0;

    for (auto v : nums) {
        if (va > 0 && v == a) va++;  // va > 0 确保此候选元素仍然有效
        else if (vb > 0 && v == b) vb++;
        else if (va == 0) {
            a = v;
            va = 1;
        } else if (vb == 0) {
            b = v;
            vb = 1;
        } else {
            va--;
            vb--;
        }
    }
    // todo: 需要进一步校验最终的候选元素是否是目标众数
}

但是，这一次似乎不那么容易理解了。

不要着急，我画个图，一图胜千言。

假设数组是 [A, B, A, B, C, B, C, D, B], 下面模拟整个投票过程，左边的三列分别是两个候选者和抵消者，右边是当前轮次的输入。

每输入一个元素，都会根据规则更新左边的棋盘情况：

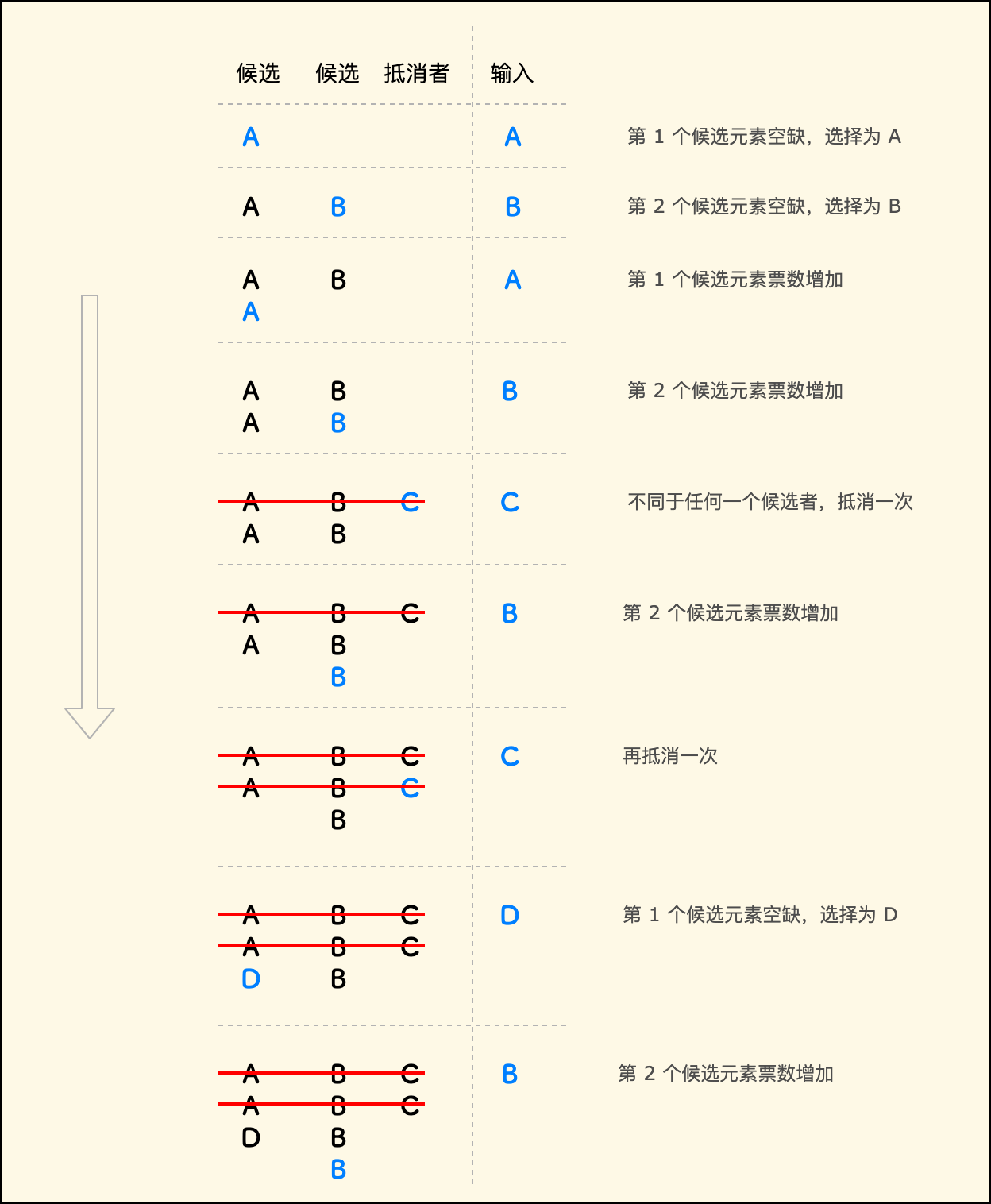
观察最后一轮的情况，可以知道：

最终的候选者并不一定是要找的众数，比如 D 。
但是消掉的数字一定不是要找的众数。
因为，无论我们前面如何抵消，最终的棋盘应该类似下面的图，字母 X 表示所有被抵消的元素（它们具体是什么并不重要）。
在这个图中，X 矩阵的个数不超过 N, 一共有三列。
而抵消的时机是一行中的三个元素互不相同，那么一个元素在 X 矩阵中的每一行中至多出现一次。也就是说 X 矩阵中的任一个数字的出现次数都不会超过 N/3 次。
摩尔投票最后的棋盘
也就是说，X 矩阵排除了不可能成为目标众数的元素。剩下的两个候选元素是仅剩的可能。

显然，这个分析可以直接推广到 N/K 的情况。

需要强调的是，从分析中可以看到，摩尔投票算法仅仅排除了不可能的元素，它并没有保证剩余的元素就是目标众数。我们还需要再实际统计验证一下。因为最终要验证的候选元素的个数是常数的 K 个，所以最终总的时间复杂度也不会超过 O(N) 。

N/3 情况下的摩尔投票 C++ 代码 (摩尔 + 检查)

vector<int> majorityElement(vector<int>& nums) {
    // 两个候选者 a 和 b， 手里各自有 va 和 vb 张票
    int a, b;
    int va = 0, vb = 0;

    for (auto v : nums) {
        if (va > 0 && v == a) va++;  // va > 0 确保此候选元素仍然有效
        else if (vb > 0 && v == b) vb++;
        else if (va == 0) {
            a = v;
            va = 1;
        } else if (vb == 0) {
            b = v;
            vb = 1;
        } else {
            va--;
            vb--;
        }
    }

    // 检查
    vector<int> ans;
    int na = 0, nb = 0;
    for (auto v : nums) {
        if (v == a) na++;
        if (v == b) nb++;
    }

    if (va > 0 && na > nums.size() / 3) ans.push_back(a);
    if (vb > 0 && nb > nums.size() / 3) ans.push_back(b);
    return ans;
}

（完）

本文原始链接地址： https://writings.sh/post/boyer%E2%80%93moore-majority-vote

摩尔投票算法 和 N/K 推广 (Boyer Moore)

摩尔投票算法和 N/K 推广 (Boyer Moore)