本文记录一种简洁优美的无旋平衡树 fhq treap 的结构和原理。
其最大优点就是:代码量比较短,但是功能却很强劲。
因为它的所有能力最终都基于两个基本的操作: 分裂 和 合并。
文章较长,图片较多。
前置说明 ¶
先回顾 二叉搜索树 和 堆 的性质,然后 Treap 是二者之结合。
二叉搜索树 BST ¶
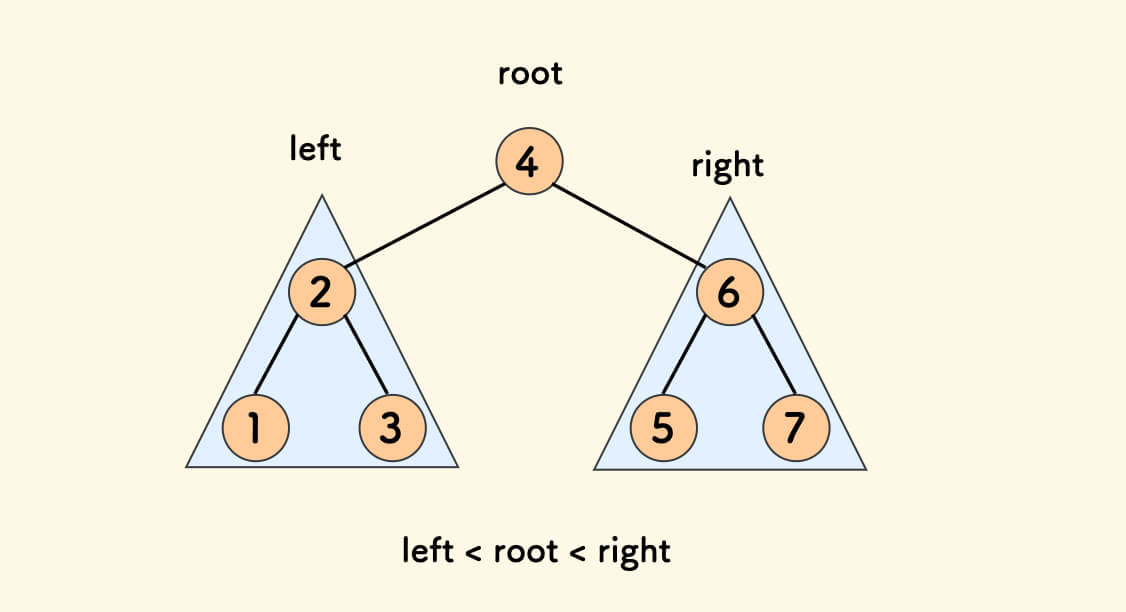
二叉搜索树(BST)[1] 的性质:
- 任意左子树上的所有节点值 小于 它的根节点的值。
- 任意右子树上的所有节点值 大于 它的根节点的值。
简而言之:left < root < right。
堆 Heap ¶
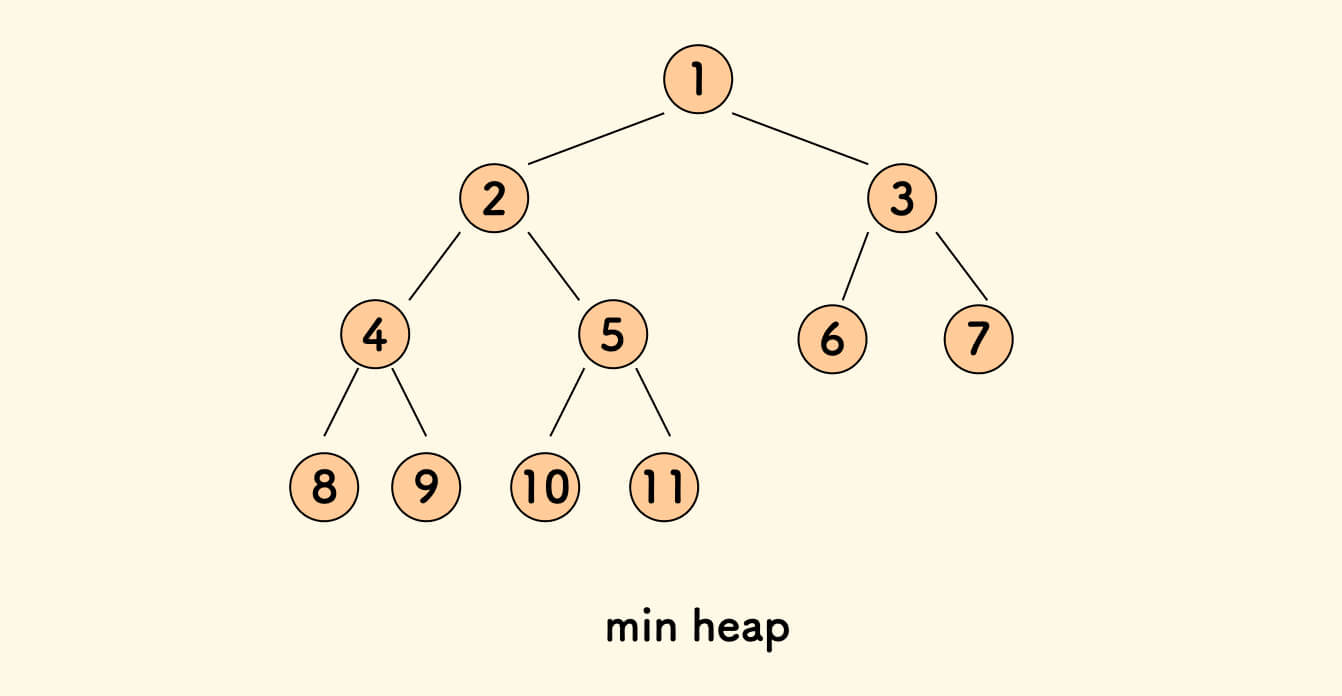
堆(Heap)[2] 的性质: 所有父亲节点的值不大于其孩子节点的值的完全二叉树。
简而言之:root <= left 且 root <= right。
树堆 Treap ¶
树堆(Treap)= 二叉搜索树(BST)+ 堆(Heap)。
树堆 [3] 的节点维护两个信息:
- 权值
val- 按此值形成 BST - 随机值
rnd- 按此值形成 Heap,以实现随机平衡(弱平衡)。
FHQ Treap 是一种最常用的无旋 Treap,核心操作只有两个:
- 分裂:按权值
val分裂,递归过程。 - 合并:按随机值
rnd合并,递归过程。
其他功能全部是基于这两种基本操作的。
核心操作 ¶
结构定义 ¶
静态开一个数组来存储节点:
const int N = 10005;
struct {
int l, r; // 左右孩子的下标
int val; // BST 的权值
int rnd; // 堆的随机值
int size; // 树的大小
} tr[N];
int root = 0, n = 0; // 根节点, 最新节点的下标
pushup 函数 ¶
在递归的过程中,后序地综合左右子树的信息、维护父树的信息。
只维护子树大小 size 信息的 pushup 函数代码如下:
// 父树内的节点数 = 左子树的节点数 + 右子树的节点数 + 1 (根节点本身)
void pushup(int p) {
tr[p].size = tr[tr[p].l].size + tr[tr[p].r].size + 1;
}
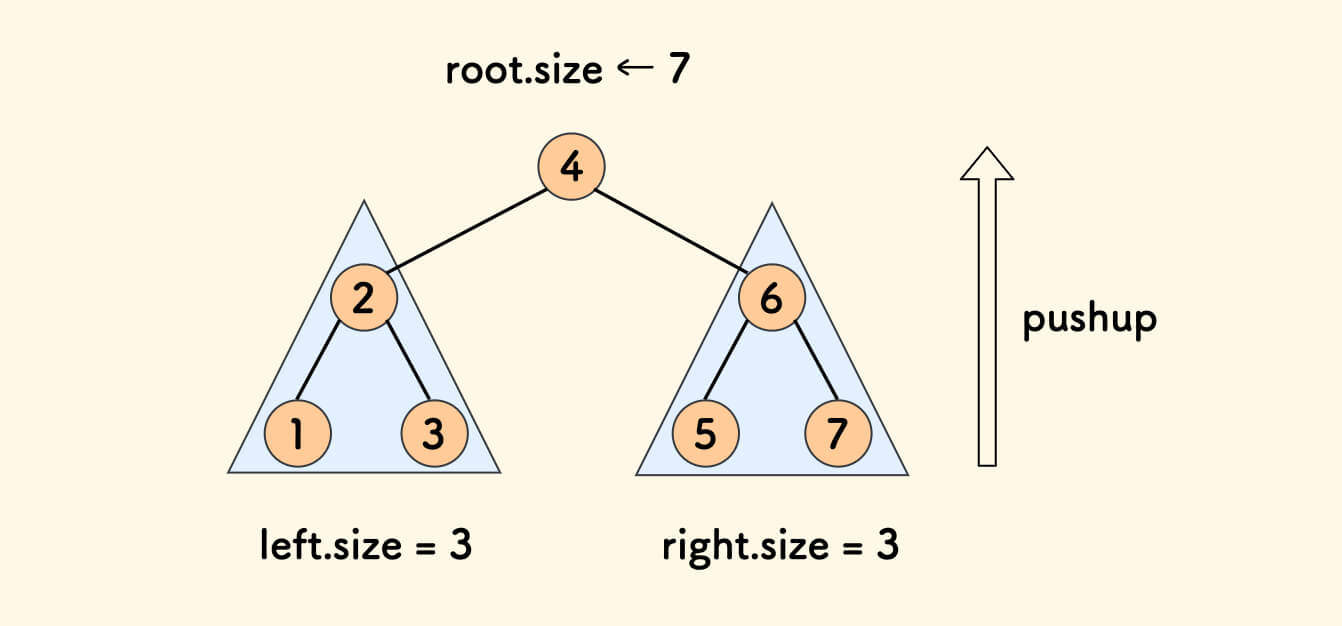
pushup 跟随在递归之后,自底向上进行,在 分裂 和 合并 过程中都会调用。
伪代码示意如下:
void dfs(...) {
dfs(...);
// 因为子树结构可能变化,需要在递归后,维护树 p 的信息
pushup(p);
}在实际场景中,也可以借路 pushup 函数维护其他信息,比如用 treap 来优化 DP 转移的时候, 常涉及维护某个值域范围上的最值、求和等信息。
分裂 split ¶
分裂函数 split(p, v, &x, &y) 的含义是:
- 把树
p按值v分裂成两颗子树:左边的x和 右边的y。 - 使得分裂后子树
x中的权值全部不大于v,子树y中的权值全部大于v。
先看代码实现,注意传参 x 和 y 是引用:
分裂函数 split 的 C++ 实现
void split(int p, int v, int &x, int &y) {
if (!p) { x = y = 0; return; }
if (tr[p].val <= v) {
x = p;
split(tr[p].r, v, tr[p].r, y);
} else {
y = p;
split(tr[p].l, v, x, tr[p].l);
}
pushup(p);
}
简单分析代码中的第一种情况,第二种情况是类似的,可以结合下面的图示来理解。
如果给定的值 v 不小于当前节点 p 的权值,那么:
p的左子树中的权值肯定全部小于v,分裂后属于x。此时,x可确定为p。- 只需要继续递归分裂
p的右子树。但是y还未确定,需要继续向下带。
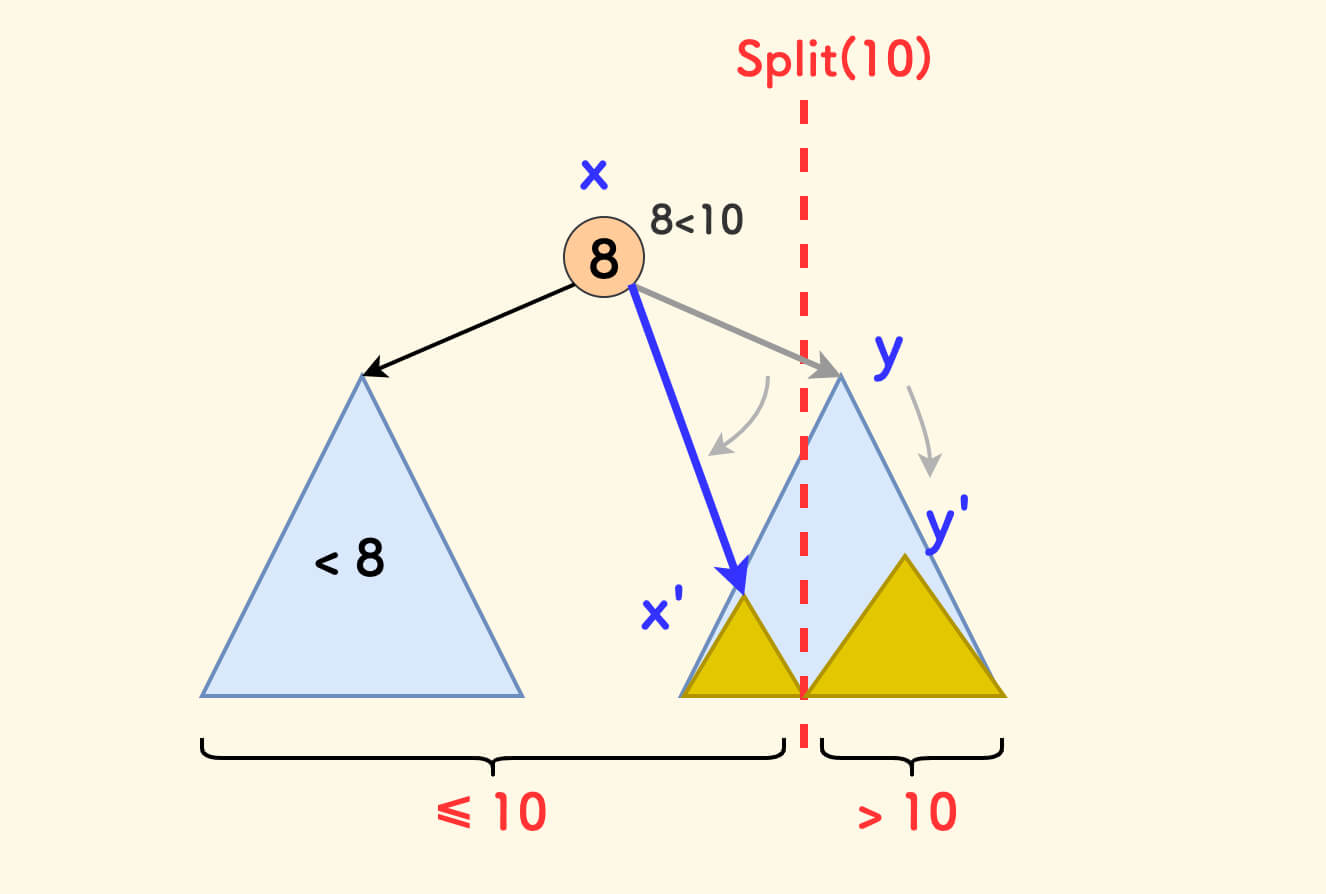
假设下一层递归分裂后的左右子树是 x' 和 y',那么:
y应该指向y'x'应该作为x的右子树,因为都≤ v
简而言之,此时 要递归分裂右子树,进而得到的左子树成为当前节点的右子树。
因此,这种情况下的递归代码如下,注意第 3、4 个参数是引用:
if (tr[p].val <= v) {
// x 可以确定为 p
x = p;
// 继续递归分裂右子树
// y 需要指向 y'
// x 的右孩子需要指向 x'
split(tr[p].r, v, tr[p].r, y);
}
另一种情况,是类似的道理,不再赘述。
显然,分裂后的两颗子树也是 treap。
分裂操作的动态示意图如下:
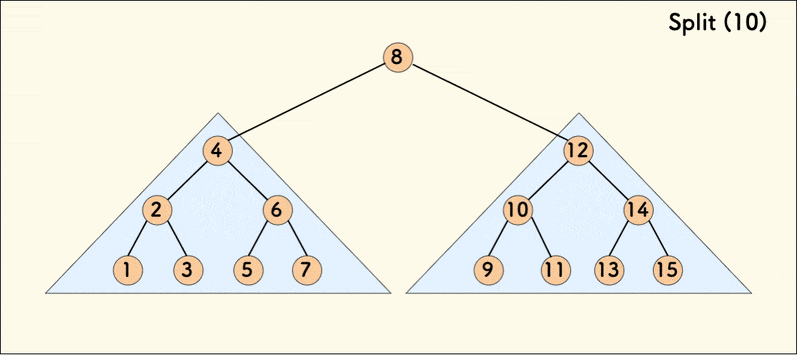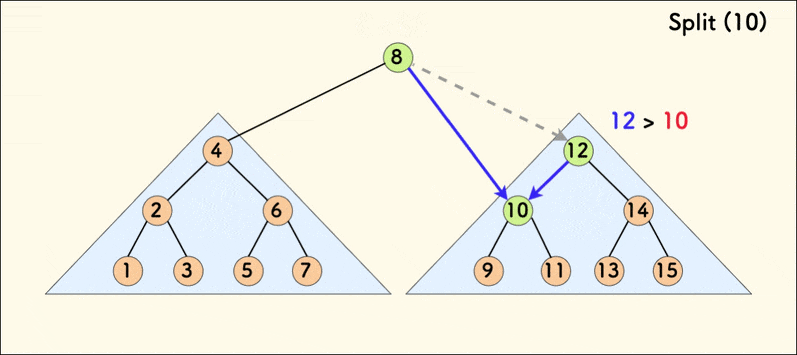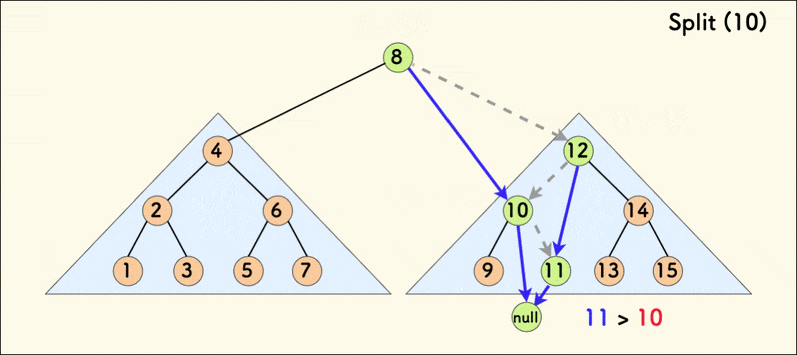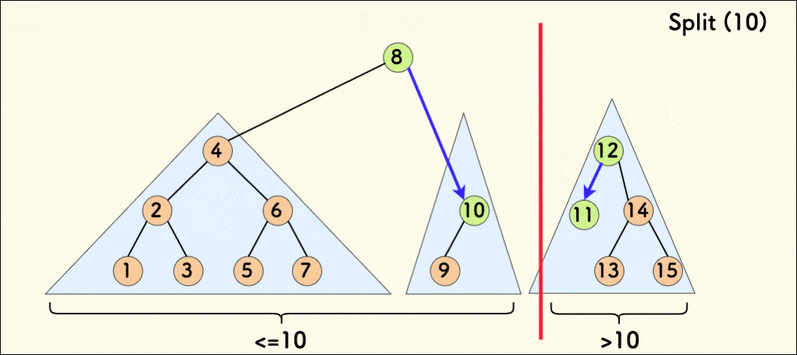
在树相对平衡的情况下,分裂的平均时间复杂度是 $O(\log{n})$。
可以看到,分裂操作只利用了二叉搜索树的性质。
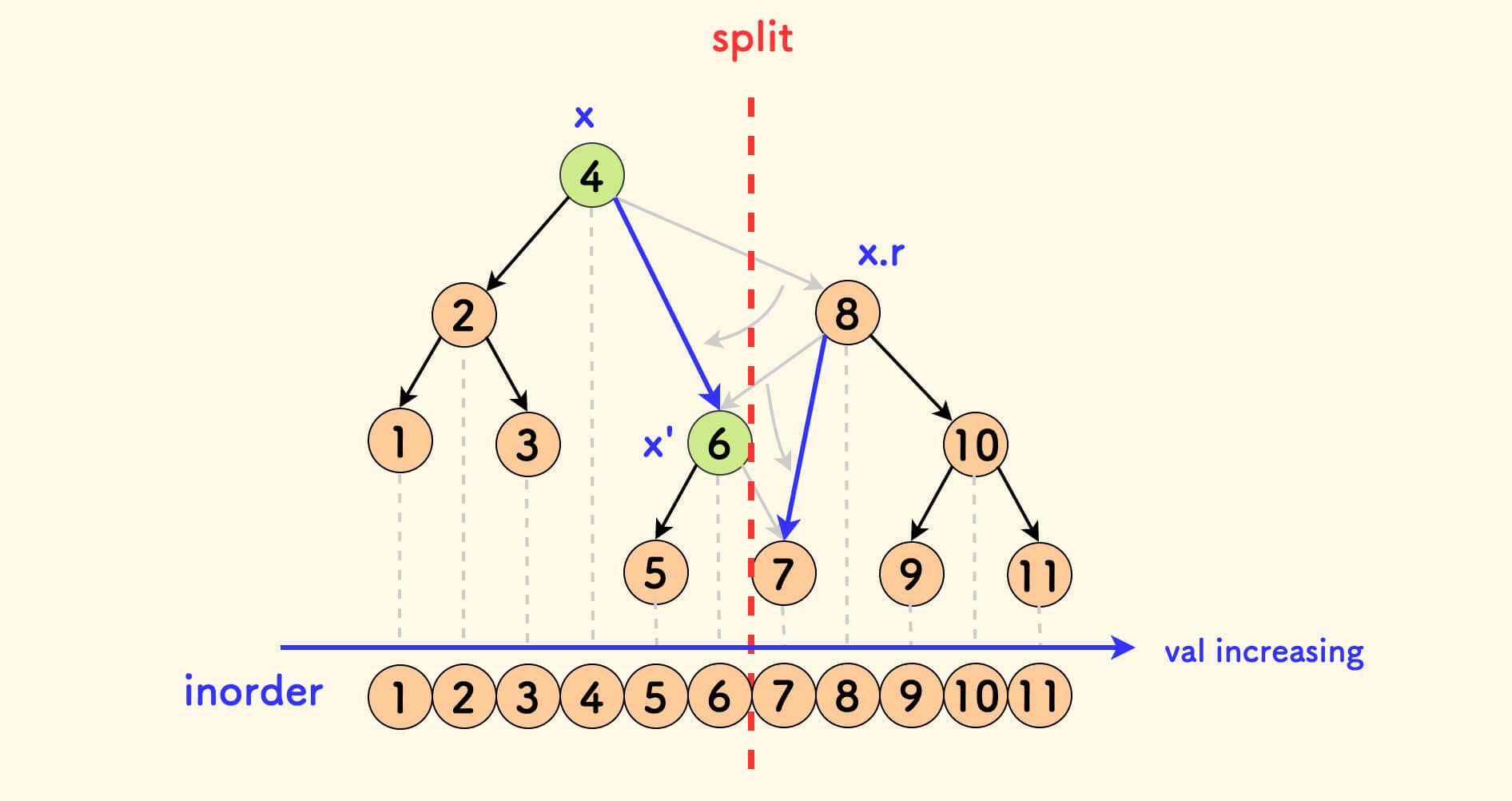
一个重要的性质是,分裂不改变中序遍历。详细点说是,分裂不会改变任意两个节点在中序遍历中位置的相对顺序。
在下图中,中序遍历的结果可以映射到一根数轴上,可以看到分裂并不影响中序。
分裂操作不影响中序顺序的详细解释
严格一点分析的话,仍然看第一种情况,即 tr[p].val <= v 的这个逻辑分支。
下图中,在分裂后 x 节点指向了 x',但是 x' 一定来自 x 原来的右子树中,所以 x' 在中序遍历中一定仍位于 x 之后。
同样的分析可以适用另一种情况。
分裂路径上只有这两种情况,因此所涉及的节点在中序中的相对顺序并不会改变。
合并 merge ¶
合并函数 merge(x, y) 的含义是:
- 按堆的随机值
rnd合并两颗 treapx和y,使得合并后成为一颗新的 treap - 入参要求:
x中全部节点的权值 要全部不大于y中全部节点的权值。
显然 split 函数分裂得到的两颗子树,是满足 merge 的入参要求的。
事实上,fhq treap 的大部分上层能力都是「先分后合」的套路。
合并的核心逻辑是,比较 x 和 y 的随机值的大小,rnd 小的放在上面。
先看代码实现:
合并函数 merge 的 C++ 实现
int merge(int x, int y) {
if (!x || !y) return x + y;
if (tr[x].rnd < tr[y].rnd) {
tr[x].r = merge(tr[x].r, y);
pushup(x);
return x;
} else {
tr[y].l = merge(x, tr[y].l);
pushup(y);
return y;
}
}
只讨论第一种情况,另一种情况是类似的。
如果 x.rnd 更小,那么:
- 应该把
x节点放上面,也就是 要选择x作为新树的根。 - 因为
x中的权值全部小于y的,所以要把y放在x的(新的)右子树中。 - 先把
x原来的右子树x.r和y合并,得到新的树y',即成为x新的右子树。
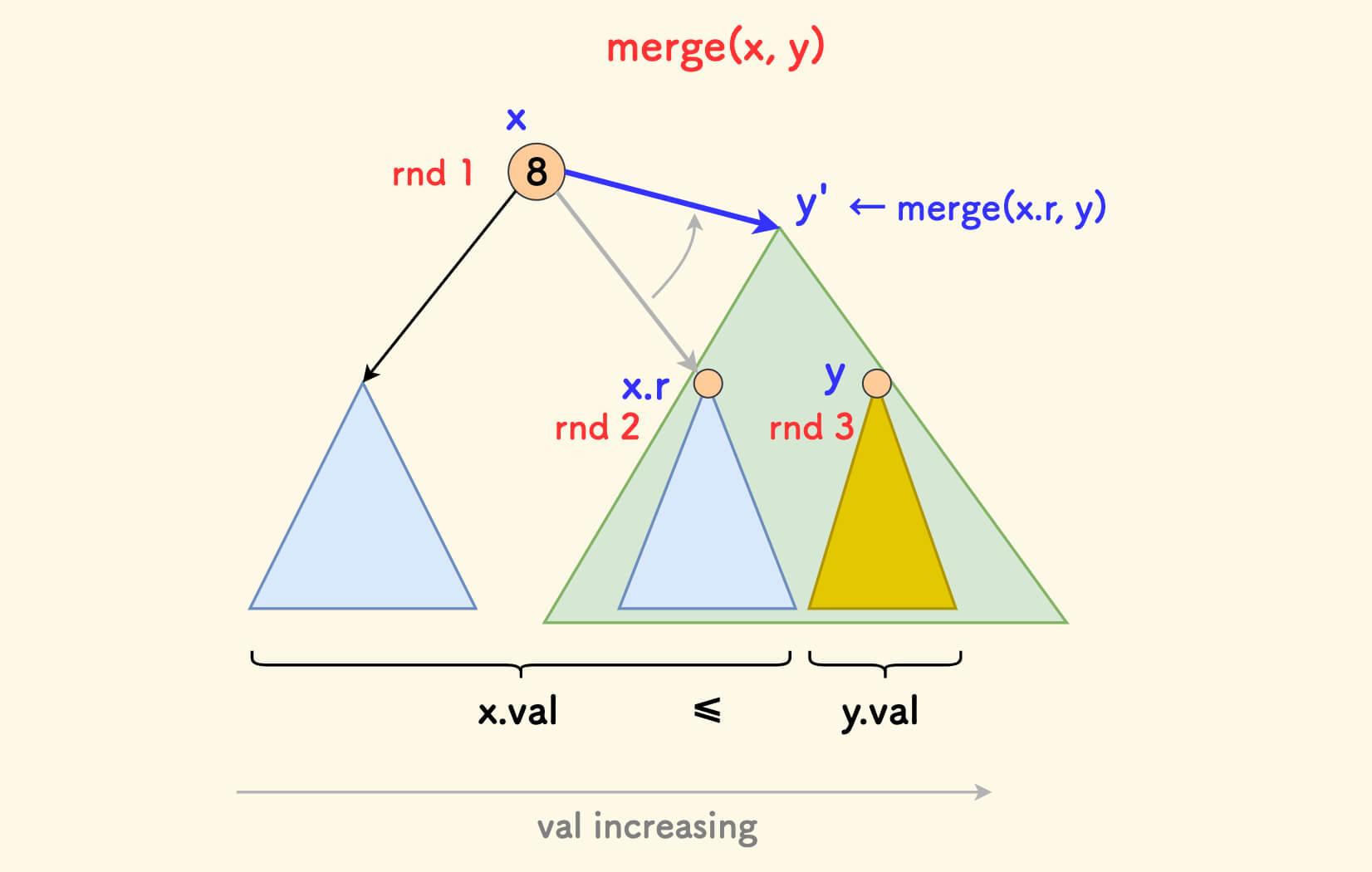
简而言之,此时 要先递归合并 x 的右子树和 y,然后成为 x 新的右子树。
这种情况代码注释如下:
if (tr[x].rnd < tr[y].rnd) {
// 递归合并 x 的原右子树 和 y,记作 y'
// y' 成为 x 新的右子树
tr[x].r = merge(tr[x].r, y);
// 因为 x 树内的结构发生了变化,所以要后序维护 x 的信息
pushup(x);
return x;
}
一个细节是,原来的右子树 x.r 的全部权值是不大于 y 的全部权值的, 递归调用时满足 merge 的入参要求。
另一种情况,是类似的道理,不再赘述。
合并操作的动态示意图如下:
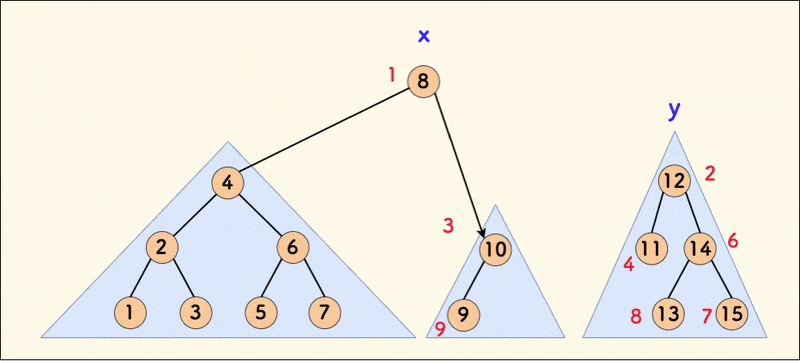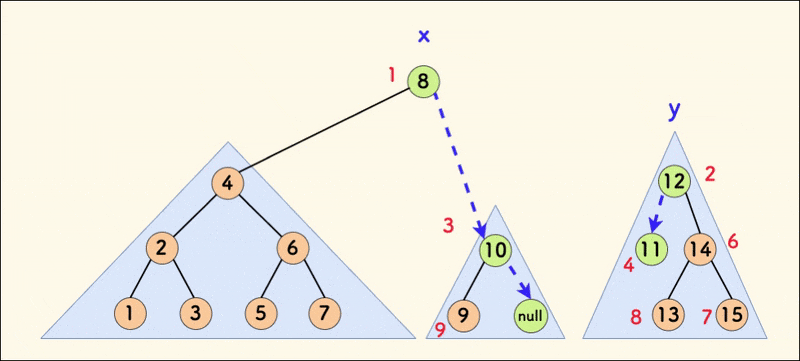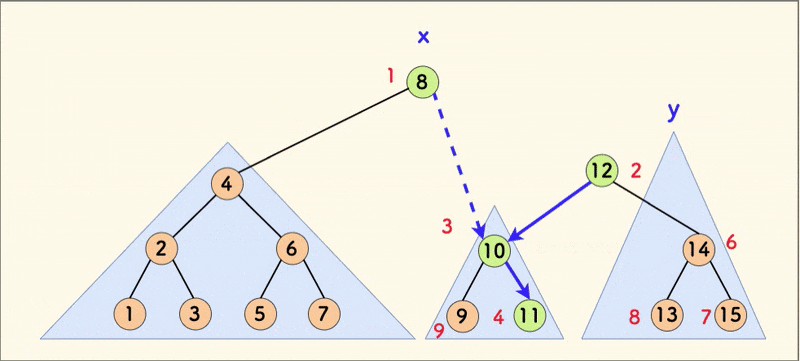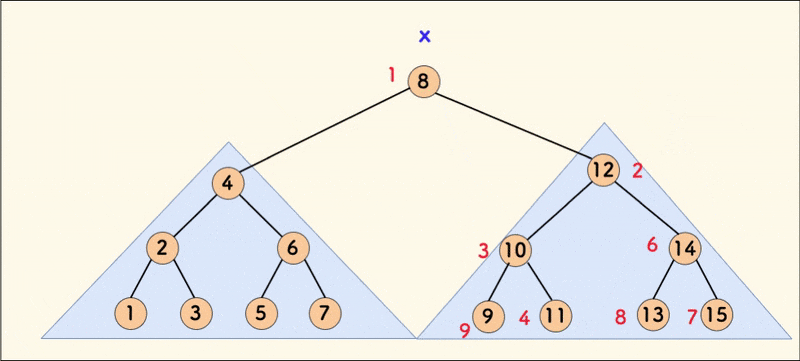
在树相对平衡的情况下,合并的平均时间复杂度是 $O(\log{n})$。
可以看到,合并操作保障了堆的性质,进而让 treap 平衡(绝大多数情况下)。
同样,一个重要的性质是,合并不改变中序遍历。
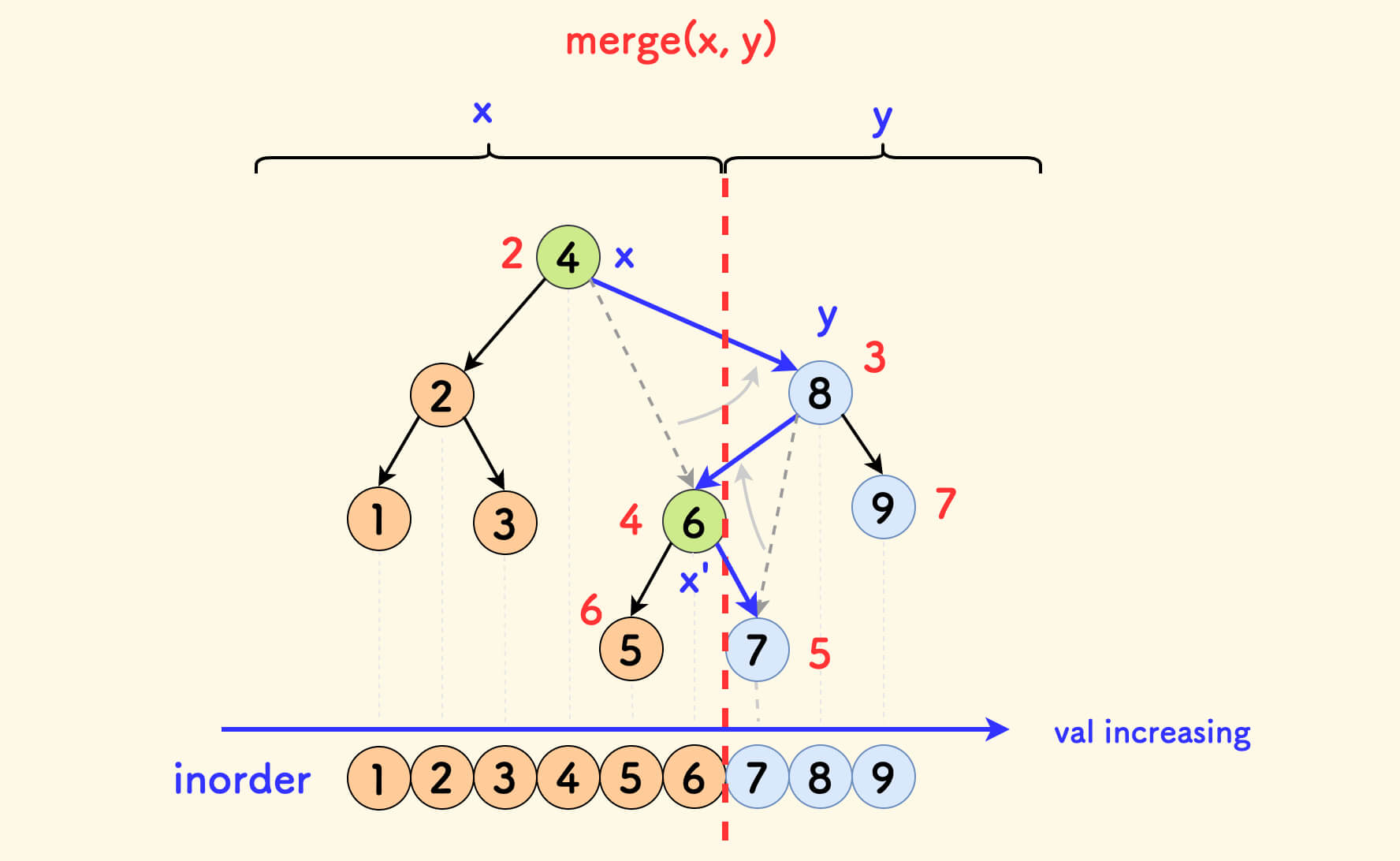
下图中,中序遍历的结果映射到一根数轴上,在满足 x 的权值全部不大于 y 的权值的情况下, 合并操作并不影响中序(其中,节点旁边的红色数字是随机值)。
合并操作不影响中序顺序的详细解释
严格一点的分析,仍然看第一种情况,即 x 放上面的这个逻辑分支,那么最终 x 的右孩子一定指向 y。
下图中,假设在合并前 x 的右孩子原本指向 x',那么合并之后 x' 一定存在于 y 的子树之中。 可以看下面的代码来帮助理解这一点。
if (tr[x].rnd < tr[y].rnd) {
// x 放上面,那么先递归合并 x 的右子树 和 y,再作为 x 的右子树。
tr[x].r = merge(tr[x].r, y);
pushup(x);
return x;
}
也就是说,x' 原本是 x 的右孩子节点,合并后会在 x 的右子树之中,那么 x' 在中序遍历中仍然位于 x 之后。
所以,对于这一种情况,合并操作不会影响节点在中序遍历中的相对顺序。
另一种情况可类似地分析。
合并的路径上,可能发生顺序变化的节点只有这两种情况,结论得证。
常用操作 ¶
大部分都是「先分后合」,切入点在于如何剖出目标子树。
插入 insert ¶
要插入一个权值为 v 的新节点:
- 先按
v分裂成x和y两个子树. - 新建一个权值为
v的节点z. - 先合并
x和z,再合并y.
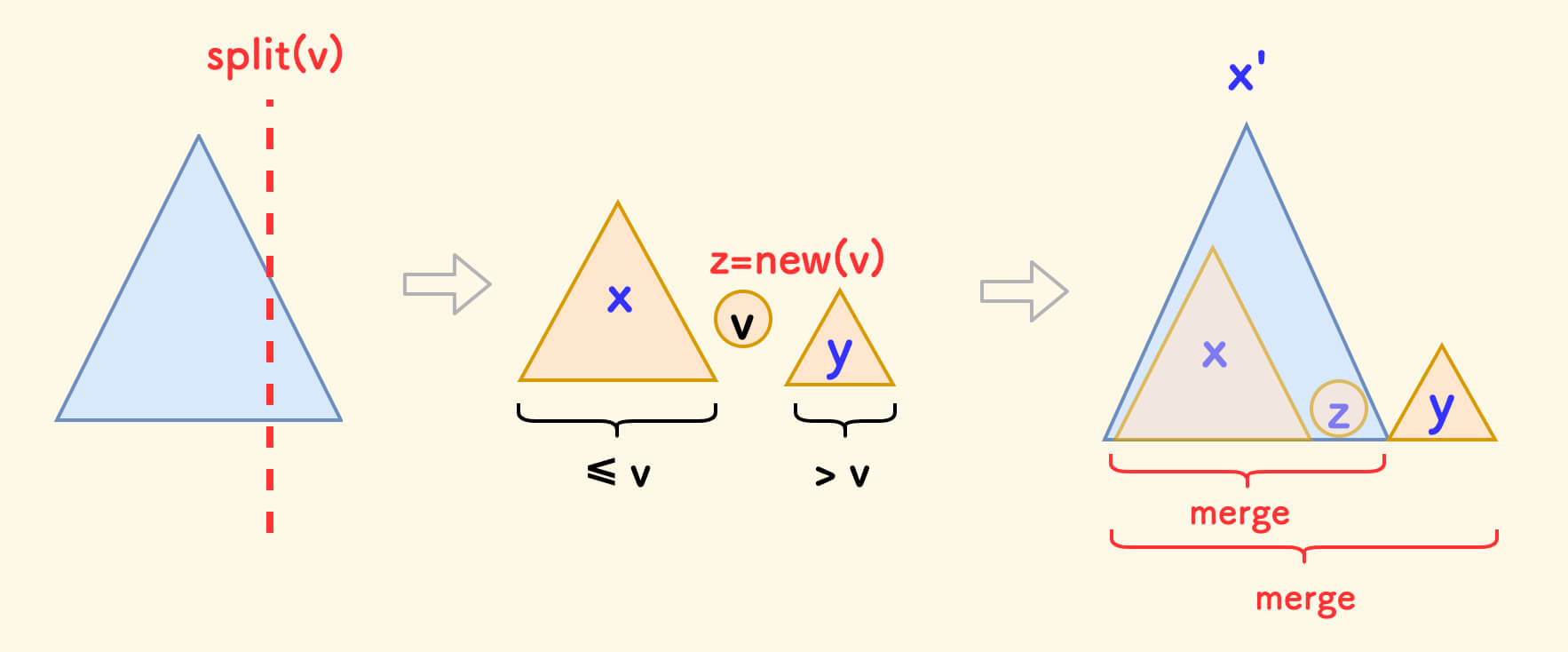
其中的一个细节是,合并时的顺序是满足 merge 函数的入参要求的。
insert 函数 C++ 实现
// 插入一个权值为 v 的新节点
void insert(int v) {
// 按 v 分裂, 找到插入点 x <=v < y
int x, y;
split(root, v, x, y);
// 新建节点
int z = newnode(v);
// 依次合并 x, z 和 y (权值 val 也满足如此顺序)
root = merge(merge(x, z), y);
}
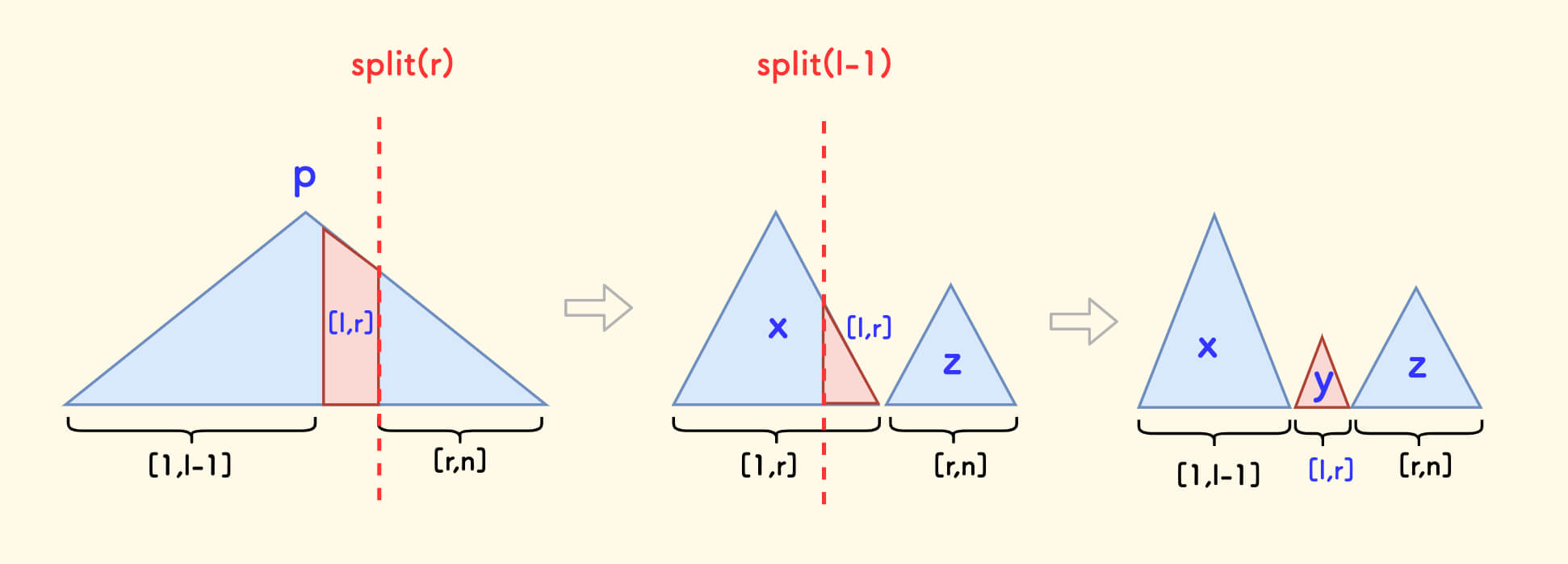
删除 del ¶
del(v) 函数负责删掉树中权值为 v 的一个节点。
和 insert 函数一样,关键是如何剖出目标子树:
- 先按值
v分裂出左右子树x和z。 - 再按值
v-1分裂子树x,分成x和y。
现在,子树 y 中的全部节点的值都是 v。
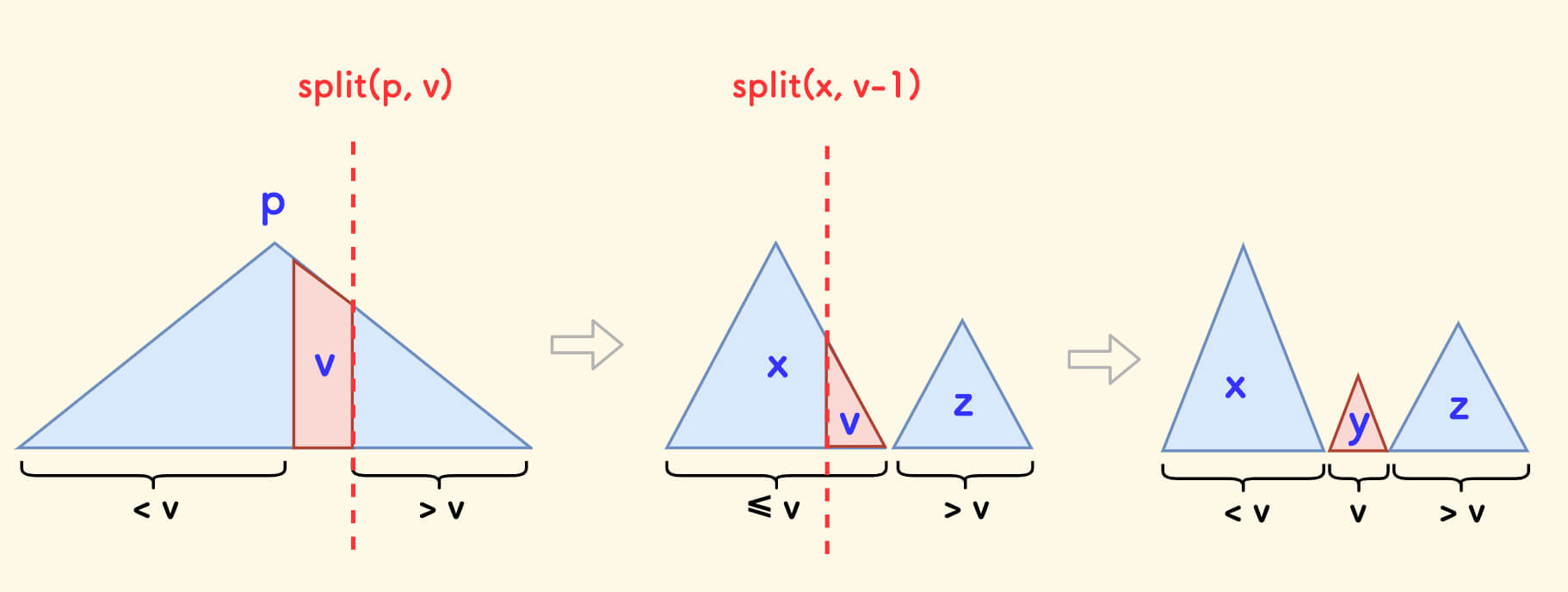
如果把所有权值是 v 的节点删除,那么只需要 merge(x, z) 即可。
现在,我们只删除一个值为 v 的节点,把 y 的根删掉,只需要把其左右子树合并:
y = merge(tr[y].l, tr[y].r);
最后,再依次把 x, y, z 合并起来,即可。
如果 y 是空树呢?也就是 v 不存在的情况。
上面的代码实现中,合并空树的两个子树,得到的也是空树。 所以,如果找不到 v,就相当于没有删除任何节点,符合预期。
del 函数 C++ 实现
// 删除一个权值是 v 的节点
void del(int v) {
int x, y, z;
// 先找到 v 的分割点 => x <= v < z
split(root, v, x, z);
// 再按 v-1 分裂 x 树 => x <= v-1 < y <= v
split(x, v - 1, x, y);
// y 就是值等于 v 的节点, 删除它
// 如果找不到 v, y 就是空树, 其左右孩子都是 0, 不影响
y = merge(tr[y].l, tr[y].r);
// 再把 x, y, z 合并起来
root = merge(merge(x, y), z);
}
排名 rank ¶
rank 函数的含义是,返回权值为 v 在树中的排名。
比如,假如树中的节点的权值是 3,5,2,1,3,那么 3 在其中的排名是 3。
排名其实就是 小于 v 的节点个数再加一。
按 v-1 分裂出左子树 x,答案就是 x.size + 1。
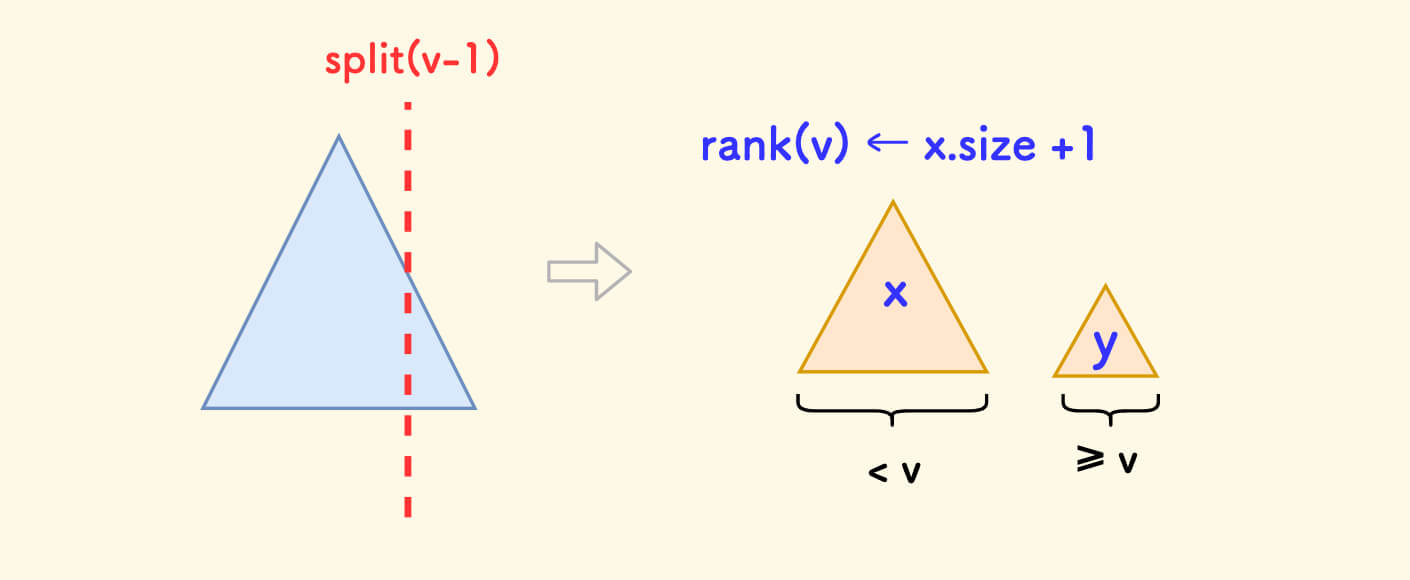
搞完以后,要记得合并回去。
rank 函数 C++ 实现
// 查找排名, 满足 < v 的个数+1
int rank(int v) {
int x, y;
split(root, v - 1, x, y);
int ans = tr[x].size + 1;
root = merge(x, y);
return ans;
}
第 k 小 topk ¶
topk 函数的含义是:查找出树中第 k 小的权值。
比如,假如树中的节点的权值是 3,5,2,1,3,那么 topk(4) 的权值是 3。
只需要利用 treap 的二叉搜索树性质。
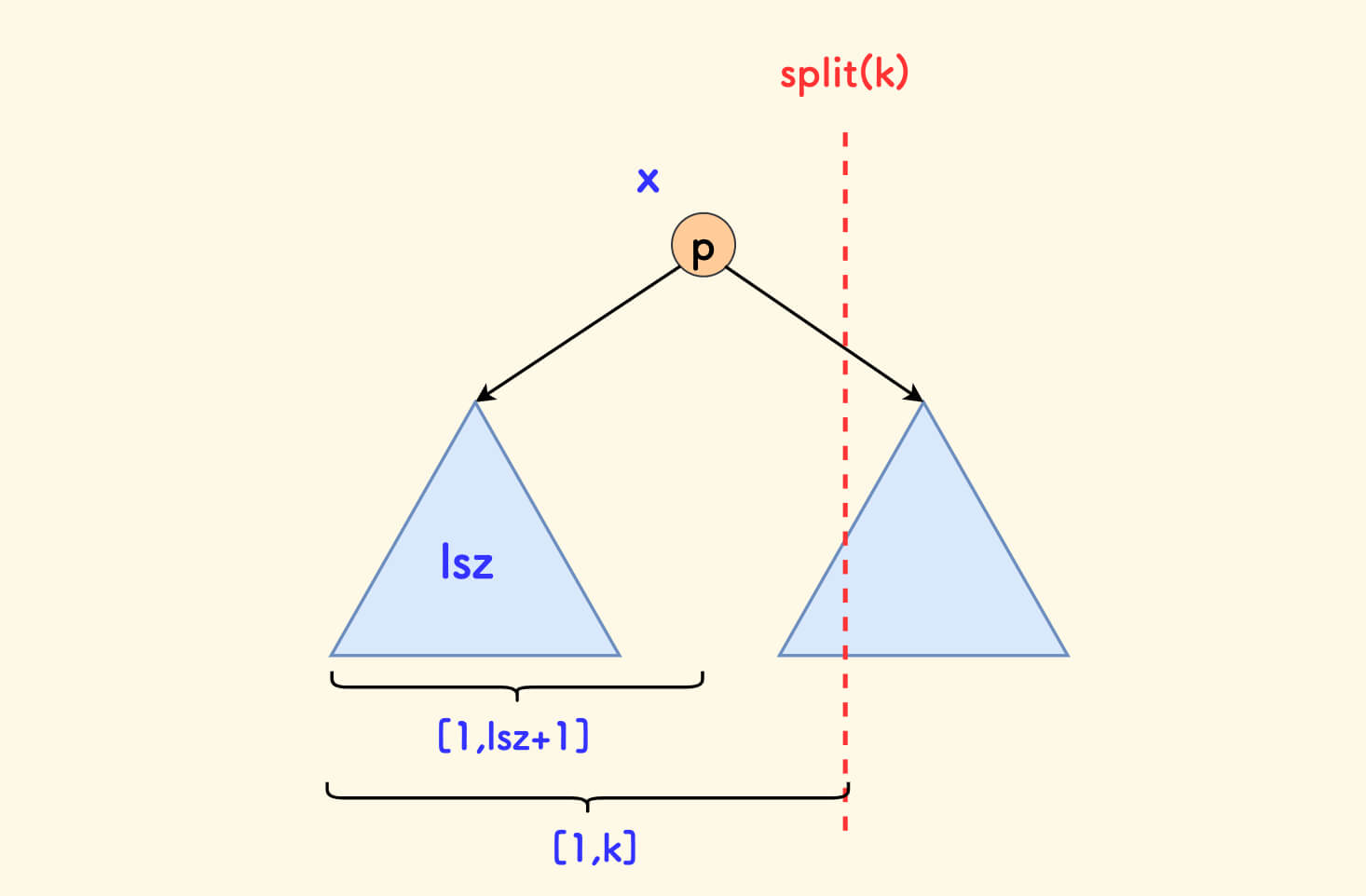
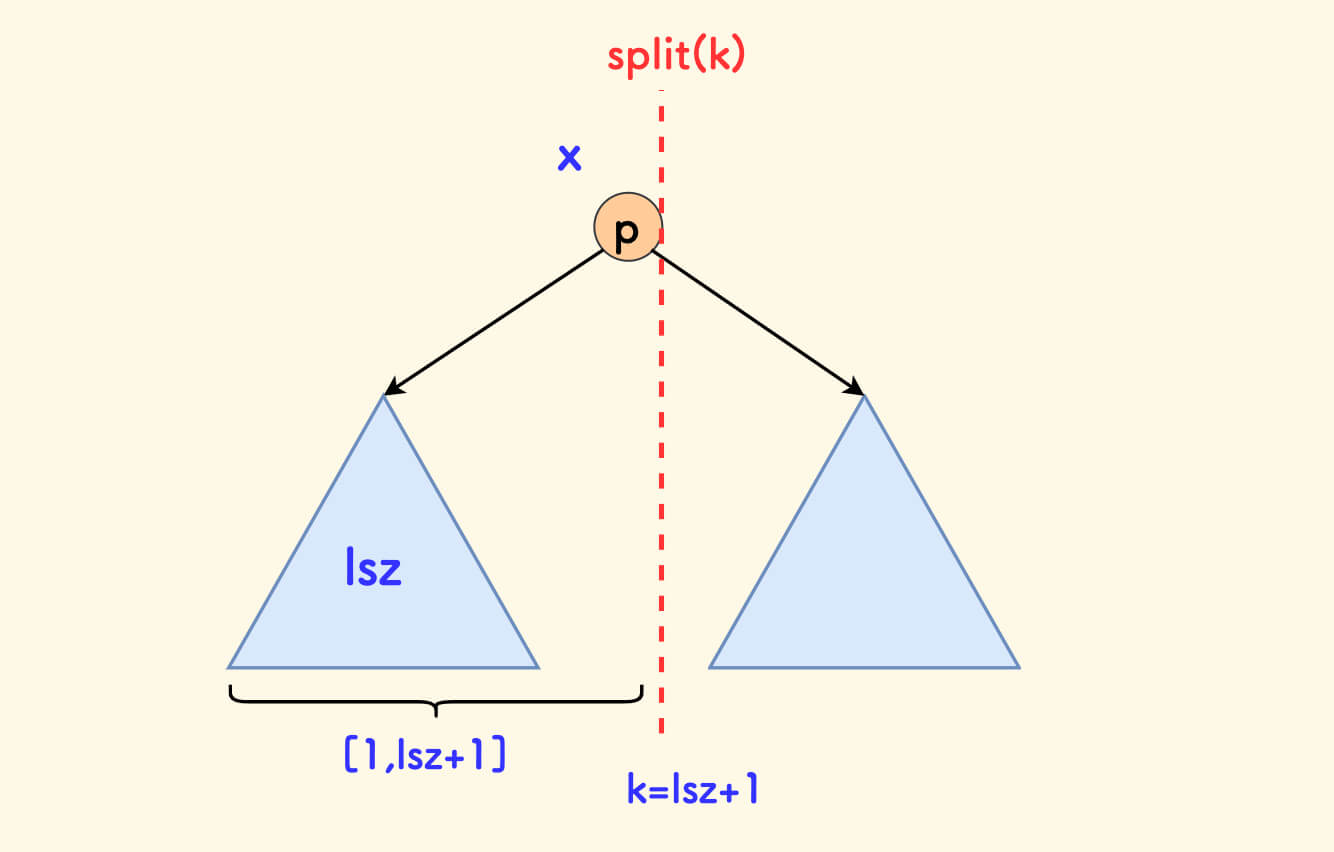
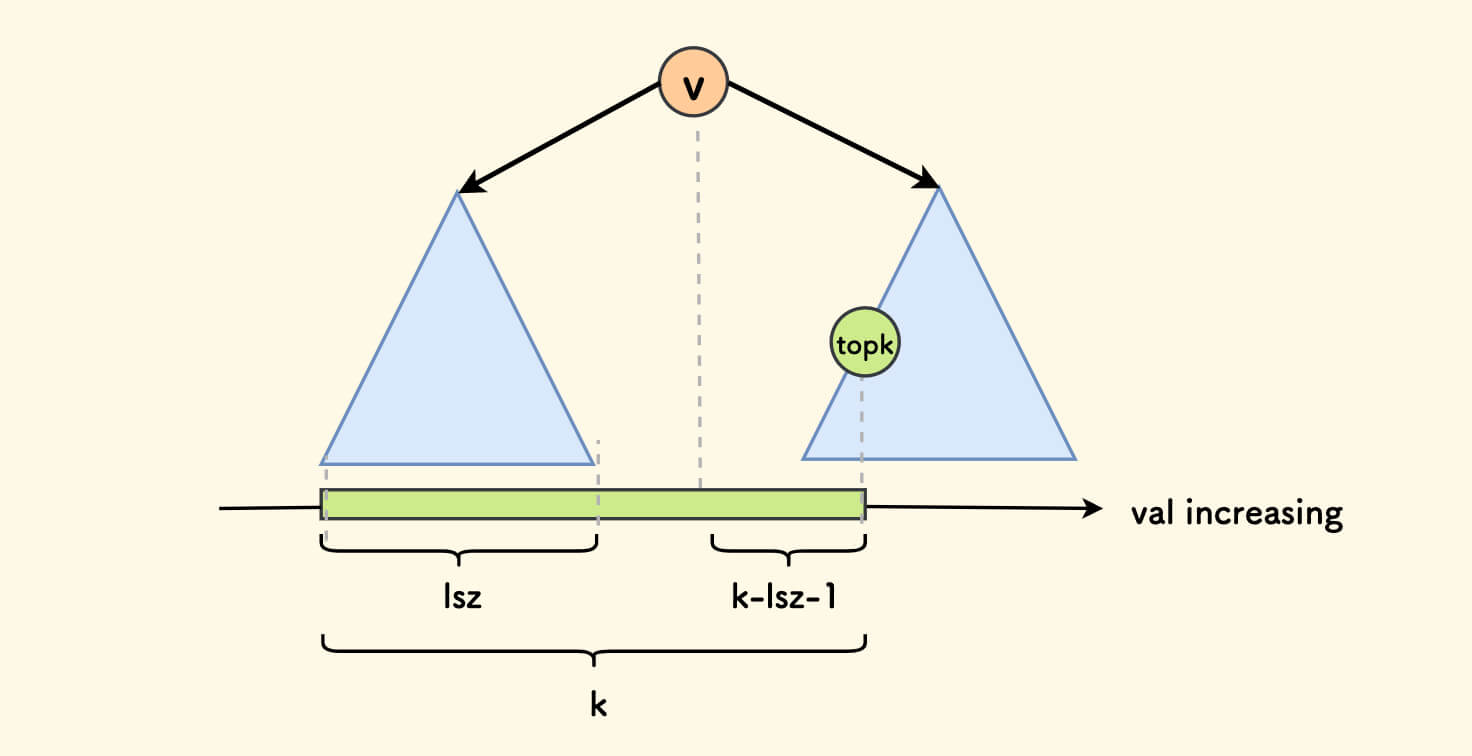
假设当前节点的左子树的大小是 lsz,分情况讨论:
- 如果
lsz+1恰好是k,那么当前节点的权值就是第k小。 - 如果
k<lsz+1,因为左子树的权值全部小于根节点,那么需要继续递归向左子树查找第k小。 - 如果
k>lsz+1,因为左子树已经占了lsz个,再排除根节点,需要继续向右子树查找第k-lsz-1小。
下图是第 3 种情况的示意图,其他两种情况也是显然的。
把二叉搜索树的中序遍历结果映射到一根数轴上看,结论会非常明显。
topk 函数 C++ 实现
int topk(int p, int k) {
int lsz = tr[tr[p].l].size;
if (k == lsz + 1) return tr[p].val;
if (k <= lsz) return topk(tr[p].l, k);
return topk(tr[p].r, k - lsz - 1);
}
前驱、后继 ¶
前驱函数 get_pre(v) 的含义是:找出树中严格小于 v 的最接近的权值。
后继函数 get_suc(v) 的含义是:找出树中严格大于 v 的最接近的权值。
两个函数思路相似,只说明前驱函数的实现:
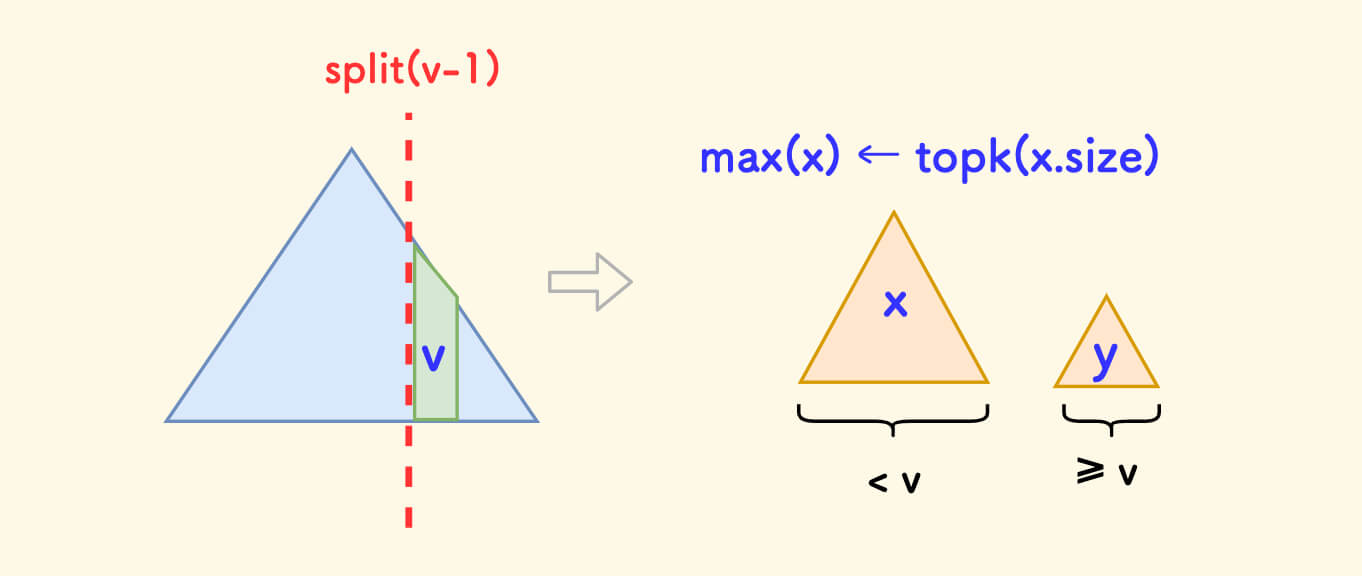
- 先按
v-1分裂,剖出小于v的子树x,然后返回其中最大值。 - 找子树
x最大值的过程,可以利用topk函数,也就是topk(x.size)。
前驱函数 pre 和 后继函数 suc 的 C++ 实现
// 前驱, 严格 <v 的值
int get_pre(int v) {
int x, y;
split(root, v - 1, x, y);
int ans = topk(x, tr[x].size);
root = merge(x, y);
return ans;
}
// 后继, 严格 > v 的值
int get_suc(int v) {
int x, y;
split(root, v, x, y);
int ans = topk(y, 1);
root = merge(x, y);
return ans;
}
模板代码 ¶
支持上述操作的一般叫做「普通平衡树」:题目 P6136、代码
区间操作 ¶
下面的部分,相较于普通的 fhq treap,难度稍大一点。
要支持一个数组上的区间操作,主要有两点要修改:
- 原来是按值分裂,现在 要按位置分裂。
- 要实现「区间更新」的话,需要 延迟标记 的机制来优化。
将分别展开讨论。
按位置分裂 ¶
分裂的依据
前面有说过,分裂 和 合并 操作都不会影响中序遍历结果 [4] [5]。
现在,放弃 treap 对权值形成二叉搜索树的性质,变为 对下标形成二叉搜索树。
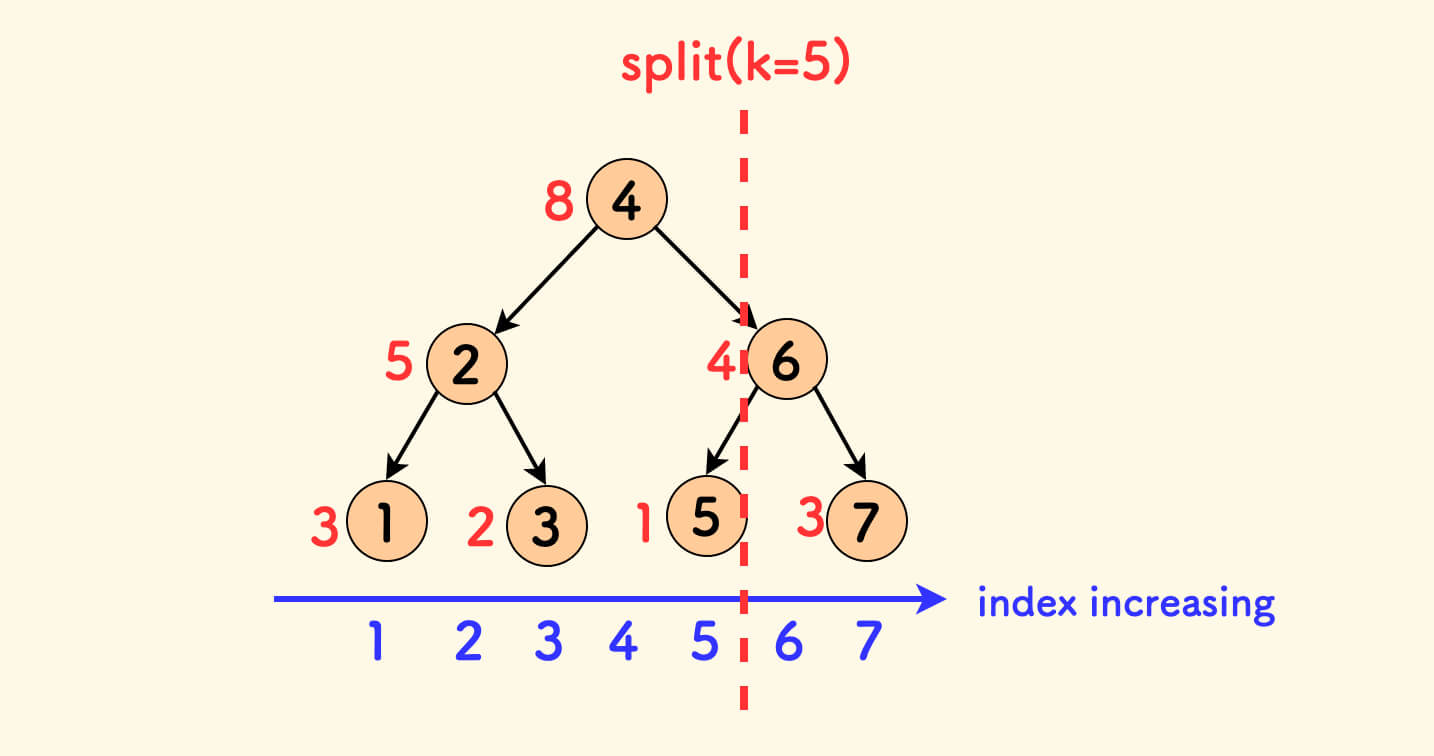
举例,数组 [3,5,2,8,1,4,3],将它按组织成一棵树,如下图所示,其中节点内的黑色数字表示下标、旁边红色的数字表示元素值。 因为下标是严格有序的,所以这颗树对下标的中序遍历就是下标的递增序列。
按位置 k 对这棵树进行分裂,分裂后下标的中序顺序不会变化,亦即分裂不会打乱下标顺序。
对于合并操作,因为合并只利用了随机值,与权值无关,所以可继续沿用,代码无需变化。 同样,合并操作不会影响下标的中序顺序。
综之,按下标分裂 和 合并 这两种核心操作,都不会改变下标的顺序,这是其能够维护区间的根本原因。
看做「区间树」
其实,修改后的 treap 可以看做一种「区间树」,这和线段树很像:
- 每一个节点代表原数组上的一段区间。
- 父节点的区间 = 左孩子的区间 + 父节点本身 + 右孩子的区间。
- 并非每一段区间都有一个节点来代表。
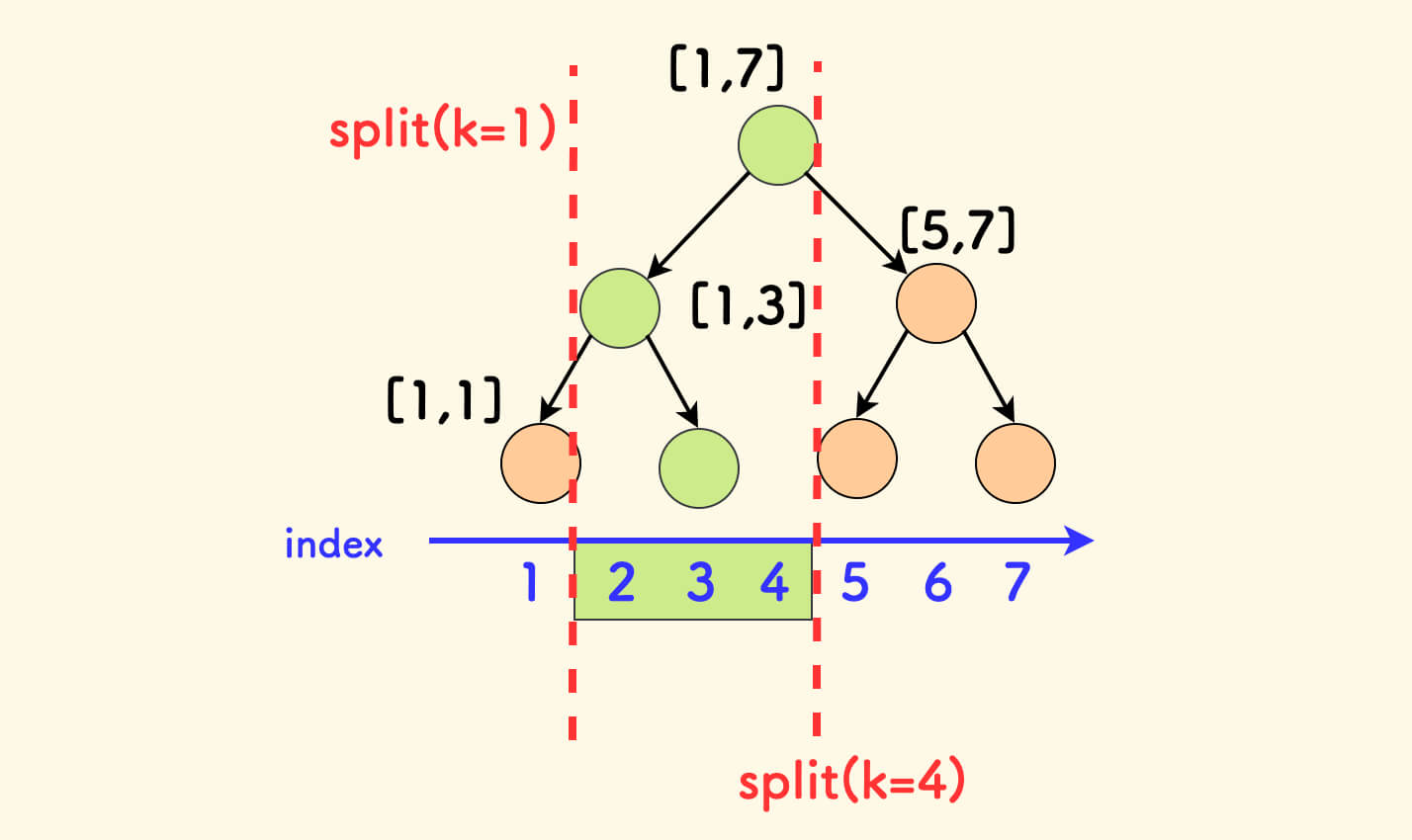
- 但是总可以剖分出一颗子树来代表任一段区间。
比如下图中可以分裂两次来得到绿色的子树,它对应着绿色区间 [2,4]:
新的分裂函数
现在分裂函数 split(p, k, &x, &y) 的含义是:
- 在位置
k处分裂树p为两颗子树x和y. - 使得:
- 左边的树
x中节点在原数组中的位置 全部不大于k - 右边的树
y中节点在原数组中的位置 全部大于k.
- 左边的树
节点结构的定义无需新增字段,「按位置分裂」可以转化为「按子树的大小分裂」。
可直接看代码实现,和原来的分裂函数只有稍许不同。
按位置分裂的 split 函数 - C++ 代码
#define ls tr[p].l
#define rs tr[p].r
void split(int p, int k, int &x, int &y) {
if (!p) { x = y = 0; return; }
pushdown(p); // pushdown 函数在延迟标记中会讲
if (tr[ls].size < k) {
x = p;
k -= tr[ls].size + 1;
split(rs, k, rs, y);
} else {
y = p;
split(ls, k, x, ls);
}
pushup(p);
}
如不尽理解可点开下方详细说明。
新的分裂函数的详细解释
假设当前节点的左子树的大小是 lsz,分情况讨论:
- 如果
lsz ≥ k,说明位置k在左子树中,递归分裂左子树,此时y可确定为p. 如果
lsz+1 < k,说明位置k在右子树中,如下图所示:但是,注意
k的含义是:当前树中的中序位置,但是它要和树的大小作比较, 所以进入右子树递归时要排除左子树和根节点,变成在右子树中找位置k-(lsz+1)。此时
x可确定为p.
左子树大小 +1 严格小于 k 的情况的示意图 如果
lsz+1恰好等于k,说明可以直接在p处分裂完成。此时
x确定为p,以保证x子树内的节点在原数组中的位置不超过k.也就是说,确切的分裂点是在
p节点的紧右侧。此时和第 2 点情况一样,向右子树递归,
x可确定为p.
左子树大小+1 恰好等于 k 的情况的示意图
第 2, 3 点其实可以统一为 lsz+1<=k 也就是 lsz < k 的情况,所以总共有两种情况。
关于分裂函数如何维护和孩子节点的关系,和 普通的分裂函数 完全一致 [跳转],说明完毕。
剖分区间 ¶
剖分出一个子树来代表一个给定的区间
[l,r]。
先剖分出区间 [1,r],再从中剖分 [l,r]。
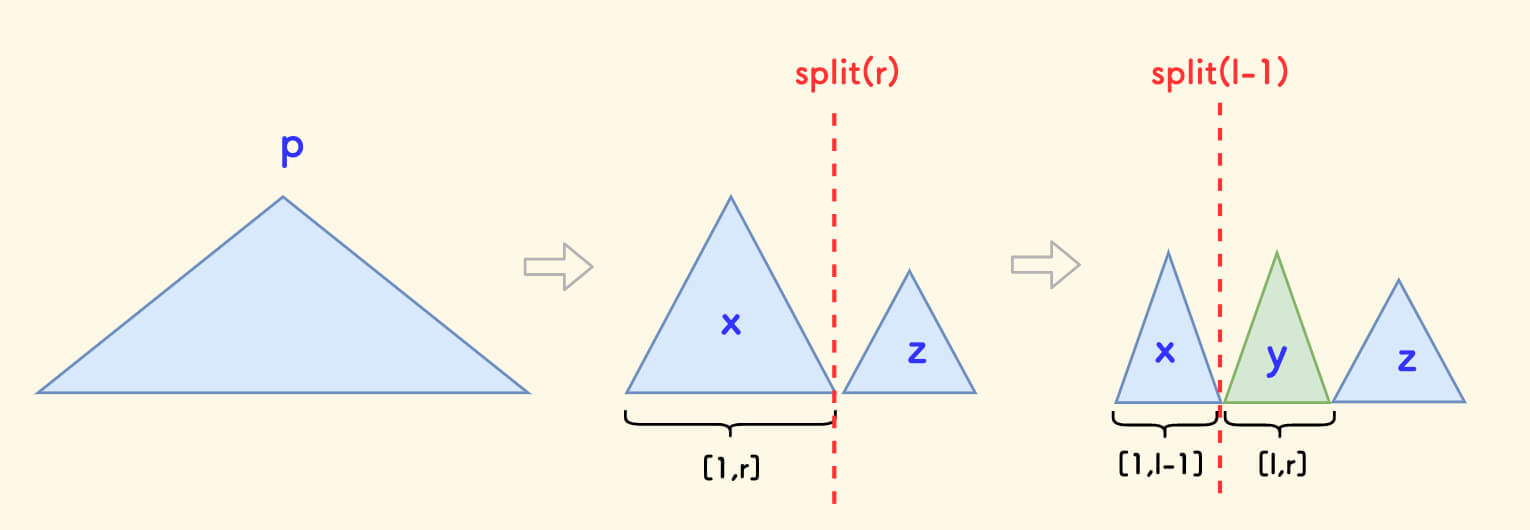
代码实现如下:
int x, y, z;
split(root, r, x, z);
split(x, l - 1, x, y);
// 此时 y 代表区间 [l,r]
延迟标记 ¶
有的人也叫这种机制为「懒标记」,在线段树中也有应用。
主要优化的场景是 区间更新。
这里说的「区间更新」,是区别于「单点更新」而言的,比如 区间翻转、区间推平 都算作区间更新,着重强调对整个目标区间的写操作。
以区间推平为例:
将区间
[l,r]内的元素值全部变为c。
朴素的做法是:先剖分出来目标区间的子树,然后把每个节点的权值依次更新为 c。
如下图所示,需要操作的是所有绿色的节点,时间复杂度最差是 $O(n\log{n})$:
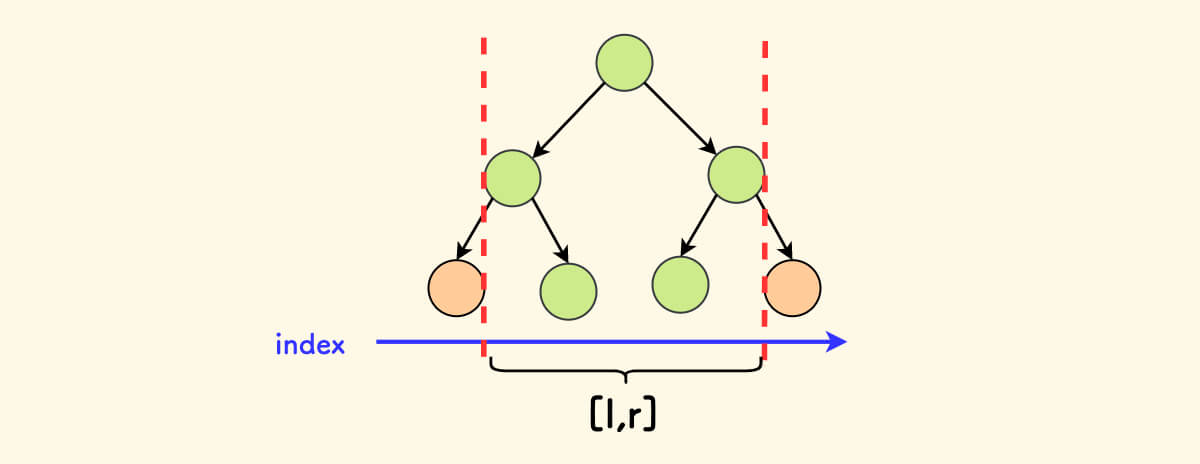
延迟标记的思路则是:
- 先不要更新,而是先打标记。
- 下次访问到的时候,再执行更新,并把标记下传到下一层孩子。
所谓「延迟更新」,不管下次是「读」还是「写」,总之下次访问到打了标记的节点,才执行更新,并下传标记。
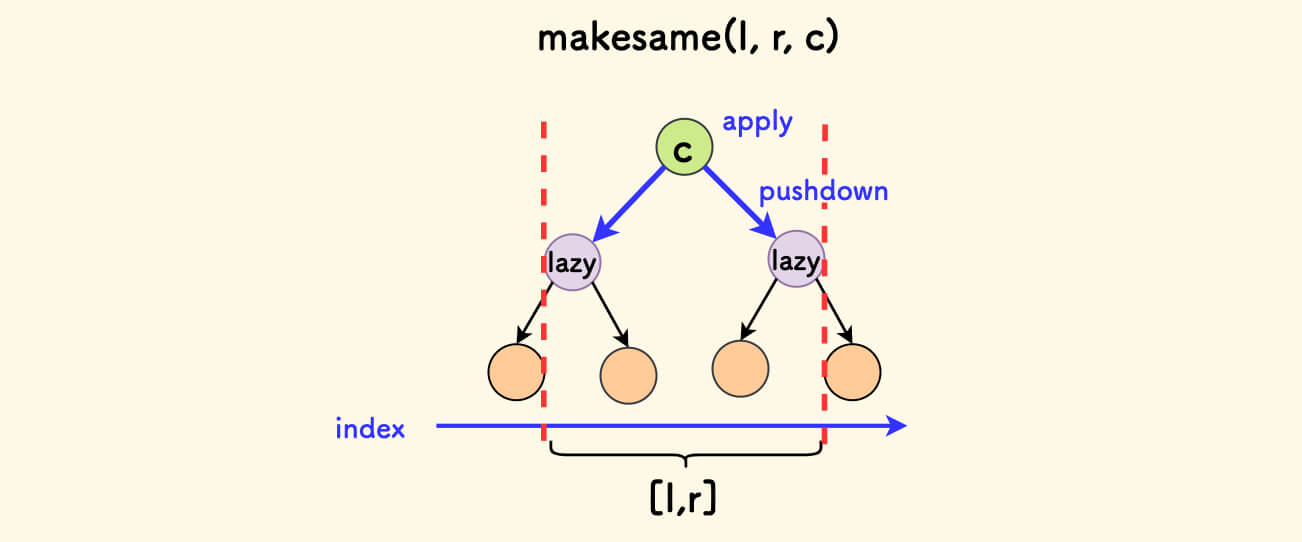
fhq treap 的核心操作只有两种:分裂 和 合并。那么只要在其中埋上延迟更新的逻辑即可,也就是 pushdown 函数。
首先,仍以「区间推平」为例,节点的结构体定义上要加两个新字段:
节点新增两个字段 - C++ 代码
struct {
int l, r; // 左右孩子
int val; // 节点权值
int rnd; // 随机值
int size; // 子树大小
int cov_tag; // 覆盖延迟标记
int cov_val; // 覆盖更新的值
} tr[N];然后,做一个 pushdown 函数,如果存在标记,就执行更新,再下传打标:
pushdown 函数 - C++ 代码
void do_cover(int p) {
if (!tr[p].cov_tag) return;
// 修改当前节点的权值
int c = tr[p].val = tr[p].cov_val;
// 下传标记到孩子节点
tr[ls].cov_tag = 1, tr[ls].cov_val = c;
tr[rs].cov_tag = 1, tr[rs].cov_val = c;
// 清理当前节点的标记
tr[p].cov_tag = 0;
tr[p].cov_val = 0;
}
void pushdown(int p) {
if (!p) return;
do_cover(p);
}
最后把 pushdown 加入到 分裂 和 合并 的递归下降的过程中即可:
split 和 merge 函数加入 pushdown 函数 - C++ 代码
void split(int p, int k, int &x, int &y) {
if (!p) { x = y = 0; return; }
pushdown(p);
if (tr[ls].size < k) {
x = p;
k -= tr[ls].size + 1;
split(rs, k, rs, y);
} else {
y = p;
split(ls, k, x, ls);
}
pushup(p);
}
int merge(int x, int y) {
if (!x || !y) return x + y;
if (tr[x].rnd < tr[y].rnd) {
pushdown(x);
tr[x].r = merge(tr[x].r, y);
pushup(x);
return x;
} else {
pushdown(y);
tr[y].l = merge(x, tr[y].l);
pushup(y);
return y;
}
}本质上说,延迟标记的机制是,延迟地按需逐层更新。
延迟标记的部分说明完毕。
题目:维护数列 ¶
下面的所有操作都围绕题目 洛谷 P2042 - 维护数列 来展开:
维护一个数列,支持以下 6 种操作:
- 插入
INSERT:在数列的第k个数字后插入tot个数字,tot=0表示在数列头插入。- 删除
DELETE:从数列的第k个数字开始连续删除tot个数字。- 修改
MAKE-SAME:把数列的第k个数字开始的连续tot个数字全部修改为c。- 翻转
REVERSE:把数列的第k个数字开始的连续tot个数字翻转。- 求和
GET-SUM:对数列的第k个数字开始的连续tot个数字求和。- 求最大子段和
MAX-SUM:求出当前数列中和最大的一段子列的和。
这个题的坑点很多。
首先,节点的定义会丰富如下,新字段的具体含义会在后面依次介绍:
节点的定义 - 添加了新字段 - C++ 代码
struct {
int l, r; // 左右孩子
int val; // 节点权值
int rnd; // 随机值
int size; // 子树大小
int rev_tag; // 翻转延迟标记
int cov_tag; // 覆盖延迟标记
int cov_val; // 覆盖更新的值
int sum; // 子树所代表的区间的和
int mpre; // 区间的最大前缀和
int msuf; // 区间的最大后缀和
int msum; // 子树内最大的区间和
} tr[N];
另外,题目中最常见的描述是「从第 k 个开始的 tot 个数字」, 那么先封装一个辅助函数 help_split 来做剖分区间:
辅助函数 help_split - C++ 代码
// 剖分出子树 x, y, z
// y 是从第 k 个开始的 tot 个数字的区间
void help_split(int &x, int &y, int &z, int k, int tot) {
int l = k, r = k + tot - 1;
split(root, r, x, z);
split(x, l - 1, x, y);
}
批量插入 ¶
在数列的第
k个数字后插入tot个数字,tot=0表示在数列头插入。
朴素的做法是,先剖分出子树 [1,k],然后依次合并每个新节点。
批量插入的朴素做法 - C++ 代码
void insert(int k, int tot) {
int x, y;
split(root, k, x, y);
for (int i = 1; i <= tot; i++)
x = merge(x, newnode(to_inserts[i]));
root = merge(x, y);
}
这样做的时间复杂度是 $O(m\log({n+m}))$,其中 m 代表要插入的个数 tot。
一种更优的做法是:先对 tot 个数字分治建树,然后再合并进来。
具体来说,把要插入的数组 to_inserts 不断二分,然后再两两合并。
过程和归并排序一样:
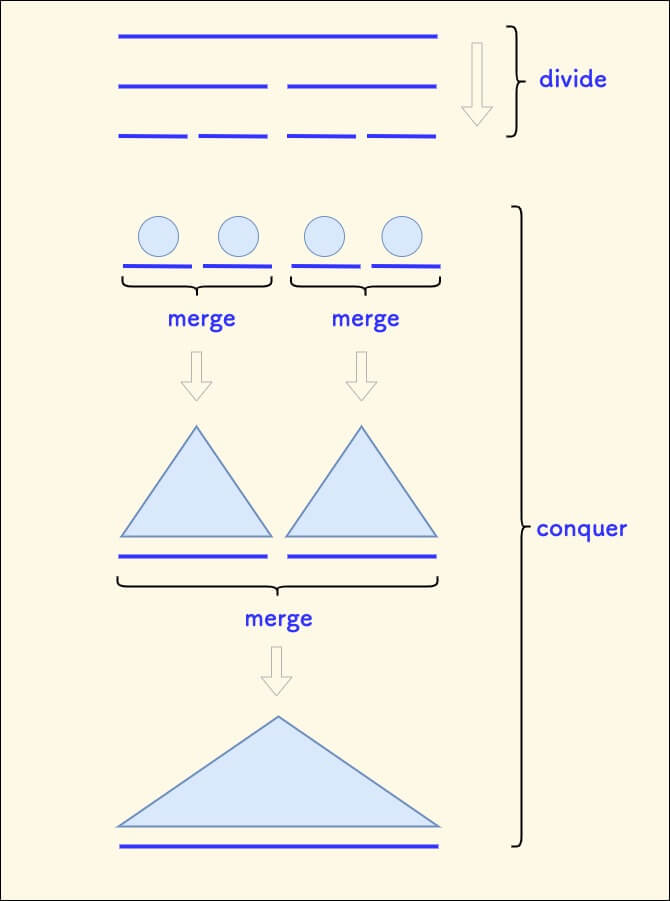
批量插入的分治建树做法 - C++ 代码
int build(int l, int r) {
if (l == r) return newnode(to_inserts[l]);
int mid = (l + r) >> 1;
return merge(build(l, mid), build(mid + 1, r));
}
void insert(int k, int tot) {
int x, y;
split(root, k, x, y);
int z = build(1, tot);
root = merge(merge(x, z), y);
}
分治建树的时间复杂度,等价于归并排序,是 $O(m\log{m})$。 最终批量插入的时间复杂度是 $O(m\log{m} + \log{n})$ 或者 $O(m\log{m} + \log{m})$ ,比朴素的做法更小。
建树还有更优的线性时间复杂度的做法,借助于单调栈 [6]。
批量删除 ¶
从数列的第
k个数字开始连续删除tot个数字。
这个是比较简单的:
- 先剖分出三棵树
x,y,z,其中y表示目标区间。 - 然后合并
x,z,舍弃中间要删除的区间y即可。
P2042 的内存限制是比较严格的,由于采用静态数组来存放树,可以尝试复用已经删除的槽位。
垃圾回收机制
新建一个栈,来追踪已经删除的空闲的节点标号:
// 垃圾回收栈
int gc_stack[N];
int gc_top = 0;
在删除一颗子树的时候,需要递归地将子树的每个节点放入 gc 回收池:
void gc(int p) {
if (!p) return;
gc_stack[gc_top++] = p;
gc(ls), gc(rs);
}
在新建节点时,优先复用回收池中的节点:
int newnode(int val) {
// 复用已回收的节点, tt 追踪 tr 数组中的最新下标
int i = gc_top ? gc_stack[--gc_top] : ++tt;
memset(&tr[i], 0, sizeof tr[i]);
// 暂时省略其他初始化项 ...
return i;
}
最终,采用垃圾回收的批量删除实现如下:
批量删除 - C++ 代码
void del(int k, int tot) {
int x, y, z;
// 剖分目标子树 y
help_split(x, y, z, k, tot);
// 回收整颗子树 y
gc(y);
// 合并 x, z
root = merge(x, z);
}
区间求和 ¶
对数列的第
k个数字开始的连续tot个数字求和。
首先,对每个节点添加一个字段 sum,来表示其子树上所有节点的元素值之和:
struct {
// ... 省略其他字段
int sum; // 子树的区间和
} tr[N];
这个字段的维护,只需要借路 pushup 函数,和 size 的维护如出一辙:
void pushup(int p) {
tr[p].size = tr[ls].size + tr[rs].size + 1;
tr[p].sum = tr[ls].sum + tr[rs].sum + tr[p].val;
}要查询一个区间上的和,只需要先剖出这个子树,然后取树根上的 sum 字段即可。
getsum 区间和函数 - C++ 代码
int getsum(int k, int tot) {
int x, y, z;
help_split(x, y, z, k, tot);
int ans = tr[y].sum;
root = merge(merge(x, y), z);
return ans;
}
延伸一下,如果要维护区间最值,也是类似的做法,可以借路 pushup 函数。
最大子段和 ¶
这 6 种操作中最难的一个:
求出当前数列中和最大的一段子列的和。
需要额外定义三个字段:
struct {
// 省略其他字段...
int sum; // 所代表的区间的和
int mpre; // 所代表的区间的最大前缀和
int msuf; // 所代表的区间的最大后缀和
int msum; // 所代表的区间内的最大子段和
} tr[N];前提,时刻注意 treap 的区间树的视角:
父节点代表的区间 = 左孩子的区间 + 父节点 + 右孩子的区间。
和区间求和一样,可以在 pushup 函数中维护最大子段和 msum。
对于节点 p,它所代表的区间内的最大子段和有两种情况:
路过
p的情况:此时,最大子段和等于下面两种子情况之最大:
- 左孩子区间的最大后缀和 +
p的值 + 右孩子区间的最大前缀和。 - 或者只取
p单个节点本身。

// 路过 p 的情况 tr[p].msum = max(tr[ls].msuf + tr[p].val + tr[rs].mpre, tr[p].val);- 左孩子区间的最大后缀和 +
不路过
p的情况:此时,容易知道
p.msum来自左、右孩子的msum之最大者。
// 不路过 p 的情况, 取左右孩子之最大 msum if (ls) tr[p].msum = max(tr[p].msum, tr[ls].msum); if (rs) tr[p].msum = max(tr[p].msum, tr[rs].msum);
两种情况,不断综合取最值即可。
但是,还要维护父节点 p 的 mpre 和 msuf 字段:
求父节点
p的最大后缀和msuf:同样有两种情况,包含
p和不包含p的情况,两种情况取最值。
tr[p].msuf = max({ tr[rs].sum + tr[p].val + tr[ls].msuf, tr[rs].msuf, 0 });求父节点
p的最大前缀和mpre,一样的分析。
tr[p].mpre = max({ tr[ls].sum + tr[p].val + tr[rs].mpre, tr[ls].mpre, 0 });
其中有一个细节点是,mpre 和 msuf 要时刻保证至少为 0,因为我们只考虑计算非负的求和成分。
maxsum 函数 和 pushup 维护- C++ 代码
void pushup(int p) {
tr[p].size = tr[ls].size + tr[rs].size + 1;
tr[p].sum = tr[ls].sum + tr[rs].sum + tr[p].val;
tr[p].mpre = max({tr[ls].mpre, tr[ls].sum + tr[p].val + tr[rs].mpre, 0});
tr[p].msuf = max({tr[rs].msuf, tr[rs].sum + tr[p].val + tr[ls].msuf, 0});
tr[p].msum = max(tr[ls].msuf + tr[p].val + tr[rs].mpre, tr[p].val);
if (ls) tr[p].msum = max(tr[p].msum, tr[ls].msum);
if (rs) tr[p].msum = max(tr[p].msum, tr[rs].msum);
}
// 返回整个树上的最大子段和
int maxsum() { return tr[root].msum; }
int newnode(int val) {
// 其他代码省略...
tr[i].msum = tr[i].sum = tr[i].val = val;
tr[i].mpre = tr[i].msuf = max(0, val); // 注意至少取 0
return i;
}区间推平 ¶
把数列的第
k个数字开始的连续tot个数字全部修改为c。
如前面所说,这是一种区间更新,需要用到延迟标记 [跳转] 的优化。
不过,延迟更新会影响区间求和,需要稍加修改。
如果仅仅对一个节点做了延迟标记,而没有做更新,那么 pushup 维护区间和的过程会算错。
比方说,对节点 p 打了延迟更新的标记,它的父节点是 q,另一个孩子是 r,如果下一次 分裂 或者 合并 只路过了 r,而没有路过 p, 延迟更新就不会触发,pushup 函数对 q 节点的求和就会算错。
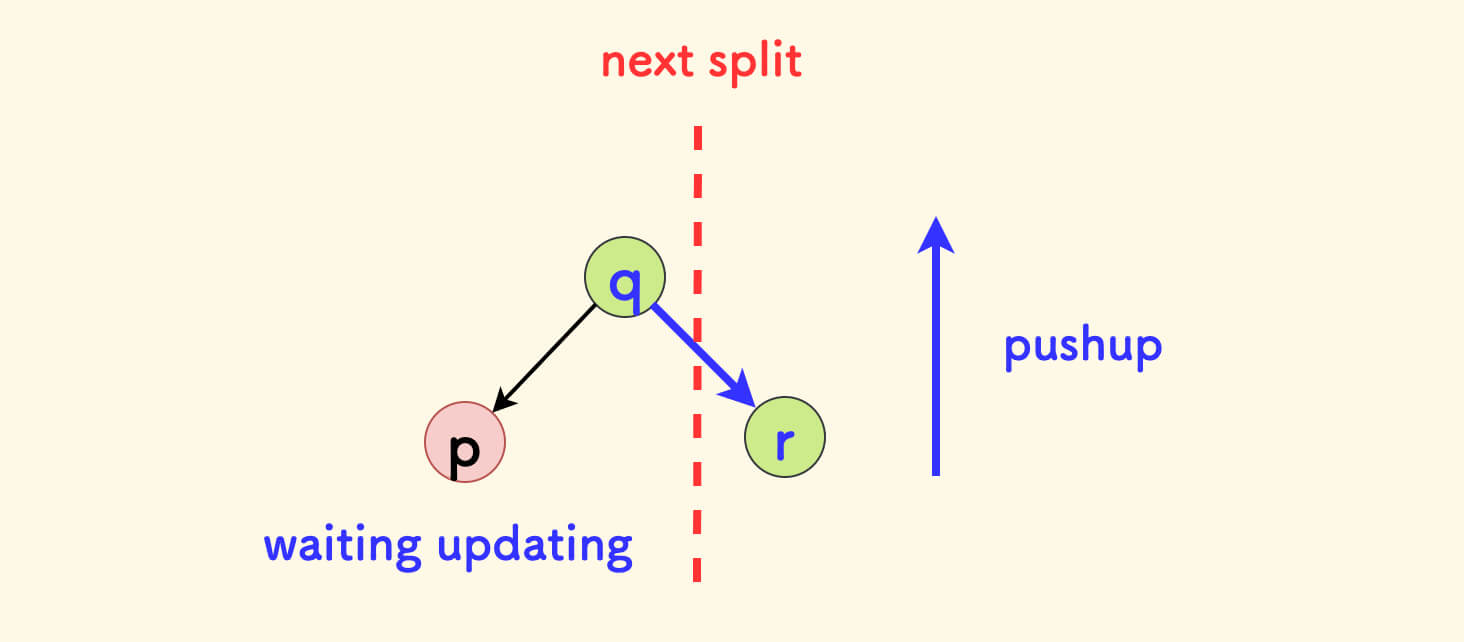
同样的原因,对于 pushup 函数所维护的 mpre、msuf 和 msum 都会出错。
解决的办法是,不要只打标,也要提前向下执行一层。
同样,在 pushdown 函数中下放标记时,也是要向下执行一层。
这样,可以确保:向上维护的祖先节点的信息不会出错,只有其子树内的节点才会延迟更新。
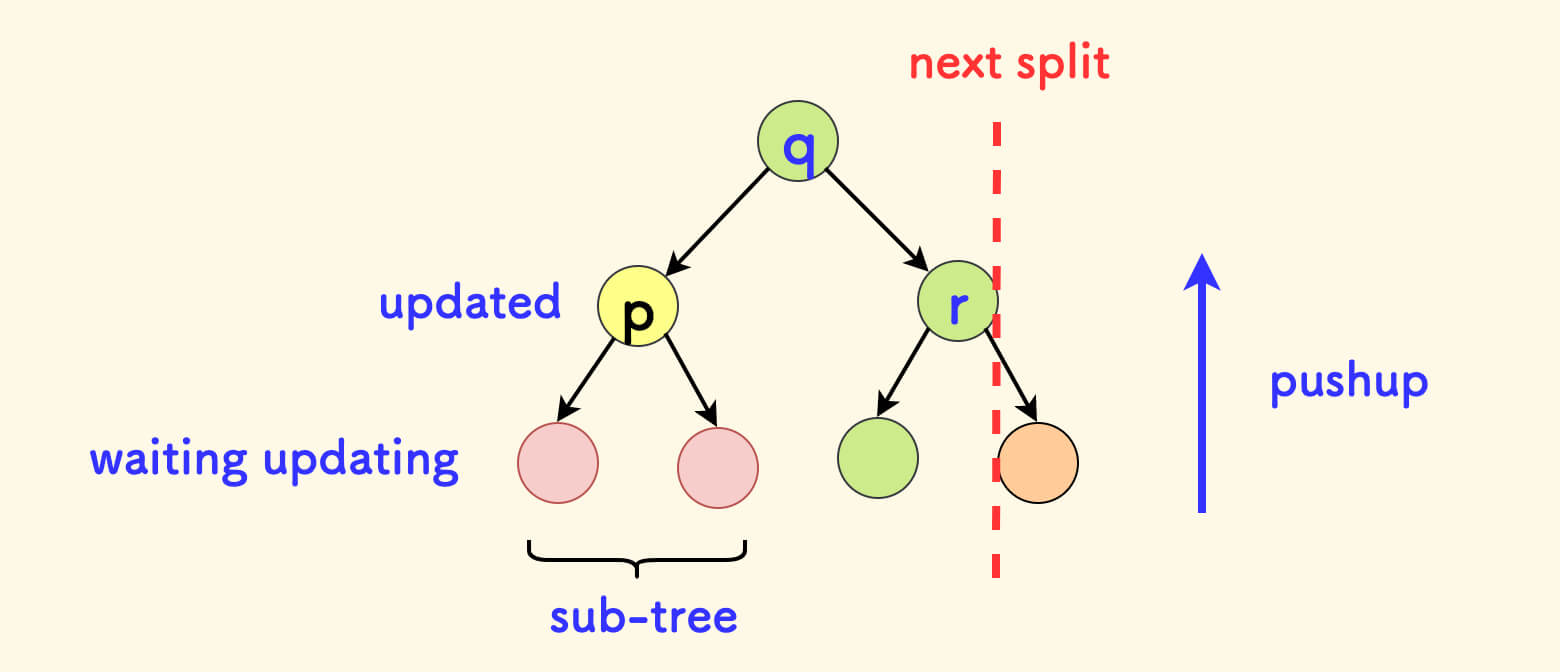
如此一来,延迟标记的机制不会受太多影响,只是提前向下多走了一层。对 pushup 维护信息造成的耦合问题也得以消除。
makesame 函数 - C++ 代码
void do_cover(int p) {
if (!tr[p].cov_tag) return;
// 修改当前节点的值
int c = tr[p].val = tr[p].cov_val;
// 因为采用延迟更新, 所以子树的和不再等于: 左右子树的和+p.val
// 这里要同步修改掉区间和 sum 和依赖它的 mpre, msuf 和 msum
int s = tr[p].sum = c * tr[p].size;
tr[p].mpre = tr[p].msuf = max(0, s);
tr[p].msum = max(c, s);
// 下传标记
tr[ls].cov_tag = 1, tr[ls].cov_val = c;
tr[rs].cov_tag = 1, tr[rs].cov_val = c;
// 清理当前标记
tr[p].cov_tag = 0;
tr[p].cov_val = 0;
}
void pushdown(int p) {
if (!p) return;
// 当前节点执行区间覆盖
do_cover(p);
// 提前向下执行一层
if (ls) do_cover(ls);
if (rs) do_cover(rs);
}
void makesame(int k, int tot, int c) {
int x, y, z;
help_split(x, y, z, k, tot);
// 打标
tr[y].cov_tag = 1;
tr[y].cov_val = c;
// 提前向下执行一层
do_cover(y);
root = merge(merge(x, y), z);
}
区间翻转 ¶
把数列的第
k个数字开始的连续tot个数字翻转。
区间翻转也是一种区间更新操作,也需要使用 延迟标记机制 来优化。
区间翻转,可以逐层交换左右子树来逐步完成。
假设已经把目标区间的子树剖分出来,下图演示了这个子树的翻转过程:
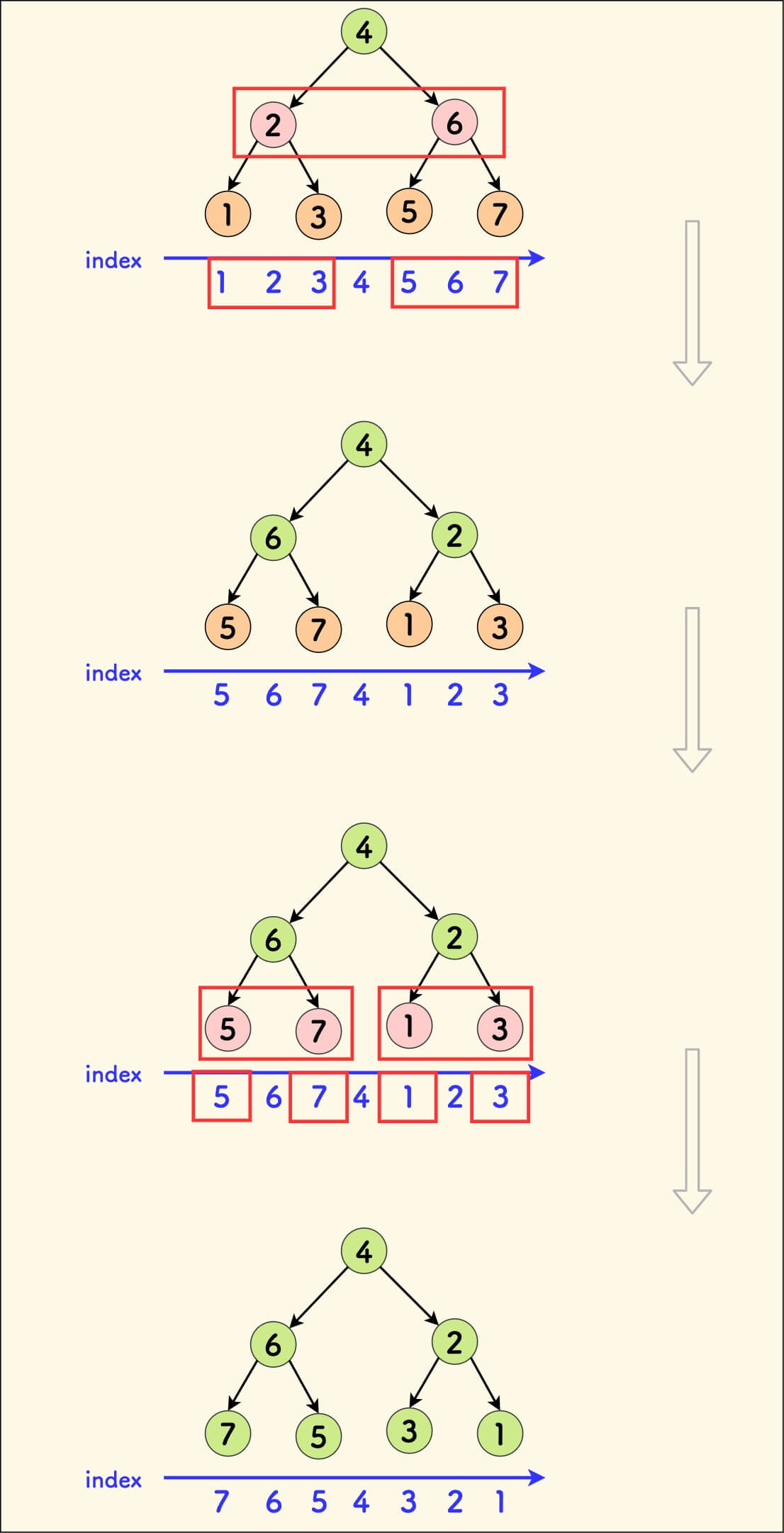
也就是说,pushdown 下行过程中,只需要每次交换左右子树即可。
给节点新增一个字段 rev_tag,它是 0 或者 1,如果对一段区间连续做了偶数次翻转,即可消除翻转标记。
struct {
// 省略其他字段
int rev_tag; // 翻转延迟标记
} tr[N];
// 打标记采用异或
rev_tag ^= 1;交换左右子树会影响到 最大前缀和 mpre 和 最大后缀和 msuf 的含义,所以要一并维护。
// 交换左右孩子子树
swap(ls, rs);
// 还要交换前后缀和
swap(tr[p].mpre, tr[p].msuf);
同样地,向下多执行一层,以杜绝对 pushup 过程中维护的最大子段和信息的影响。
reverse 函数区间翻转 - C++ 代码
void do_reverse(int p) {
if (!tr[p].rev_tag) return;
// 交换左右孩子
swap(ls, rs);
// 还要交换前后缀和
swap(tr[p].mpre, tr[p].msuf);
// 下传标记
tr[ls].rev_tag ^= 1;
tr[rs].rev_tag ^= 1;
// 清理当前标记
tr[p].rev_tag = 0;
}
void pushdown(int p) {
if (!p) return;
do_reverse(p);
// 向下标记, 多执行一层
if (ls) do_reverse(ls);
if (rs) do_reverse(rs);
}
// 在 k 处翻转 tot 个
void reverse(int k, int tot) {
int x, y, z;
help_split(x, y, z, k, tot);
// 打标
tr[y].rev_tag ^= 1;
// 提前执行一层
do_reverse(y);
root = merge(merge(x, y), z);
}
至此,6 种区间操作都说明完毕。
模板代码 ¶
结尾语 ¶
fhq treap 真是一个性价比很高的数据结构,核心操作只有两种,其他操作都是在此基础之上构建。
最后做一些总结。
普通平衡树 treap:
- Treap 是 BST 和 Heap 的结合。
- 能力都是基于两个核心操作:分裂 和 合并。
- 如何剖出目标子树是关键。
- 分裂 和 合并 都不影响中序遍历的相对顺序。
支持区间操作的 treap:
- 进行区间操作,要按位置分裂。
- 看做区间树:任一个区间都可以剖分出一颗子树与之对应。
- 进行区间更新,可以采用「延迟标记」优化。
- 分治建树。
- 适合借路
pushup函数的:区间查询操作。 - 适合借路
pushdown函数的:区间更新的延迟标记下传。 - 延迟标记机制会带来和
pushup向上维护的逻辑耦合,解决办法:提前向下执行一层。
脚注 ¶
(完)
相关阅读:
本文原始链接地址: https://writings.sh/post/fhq-treap