LIS 计数问题的树状数组和平衡树解法

本文简记最长上升子序列 LIS 的个数问题的树状数组和平衡树两种解法。

问题描述
树状数组解法
平衡树解法

此外，求解 LIS 个数，还有另一种基于分层 DAG 模型的解法。

建议先读前置文章：求 LIS 长度的 dp 转移优化。

问题描述 ¶

leetcode 上有这个题 673 最长递增子序列的个数：

给定一个未排序的整数数组 a ，返回最长严格递增子序列的个数。

比如 [1,3,5,4,7] 的最长递增子序列的个数是 2，分别是 [1,3,4,7] 和 [1,3,5,7]。

容易想到 $O(n^2)$ 的 DP 做法，不再说明。

本文要讨论的是两种用数据结构来优化的 $O(n\log{n})$ 的解法。

树状数组解法 ¶

前置知识：树状数组的原理。

先回顾求 LIS 长度的情况 ^[2]。

假设 dp[x] 表示以值 x 结尾的 LIS 的长度，dp 转移关系如下：

// v 是已经扫描过的 且 < x 的 a[j] 的值
dp[x] = max(dp[v], for each v < x) + 1;

用树状数组来维护 dp 数组的前缀最值，代码非常简洁：

树状数组求解 LIS 长度的主过程 - C++

int mx = max(a); // 最大值
int dp[mx];

for (auto x : a) update(x, ask(x-1) + 1);
ans = ask(mx); // 答案

现在要进一步求 LIS 的个数，就要一边维护最值的同时、一边维护最值的个数。

这里和一般用树状数组的情况稍有不同，要修改代码模板：把原本调用 max 函数的地方「丰富」一下，不止要维护最值，还要追踪最值的个数。

树状数组维护前缀最值的 C++ 模板

int ask(int x) {
    int ans = 0;
    for (; x; x -= x & -x)
        ans = max(c[x], ans); // 修改点：统计最值的个数
    return ans;
}
void update(int x, int v) {
    for (; x <= n; x += x & -x)
        c[x] = max(c[x], v); // 修改点：维护最值个数
}

树状数组中每一项 c[x] 代表着一个小区间 [x-lowbit(x)+1,x] 的信息 ^[1]。

如果树状数组是维护前缀和的，那么每个 c[x] 的值就是小区间上的区间和。

如果树状数组是维护前缀最值的，那么每个 c[x] 的值就是小区间上的区间最值。

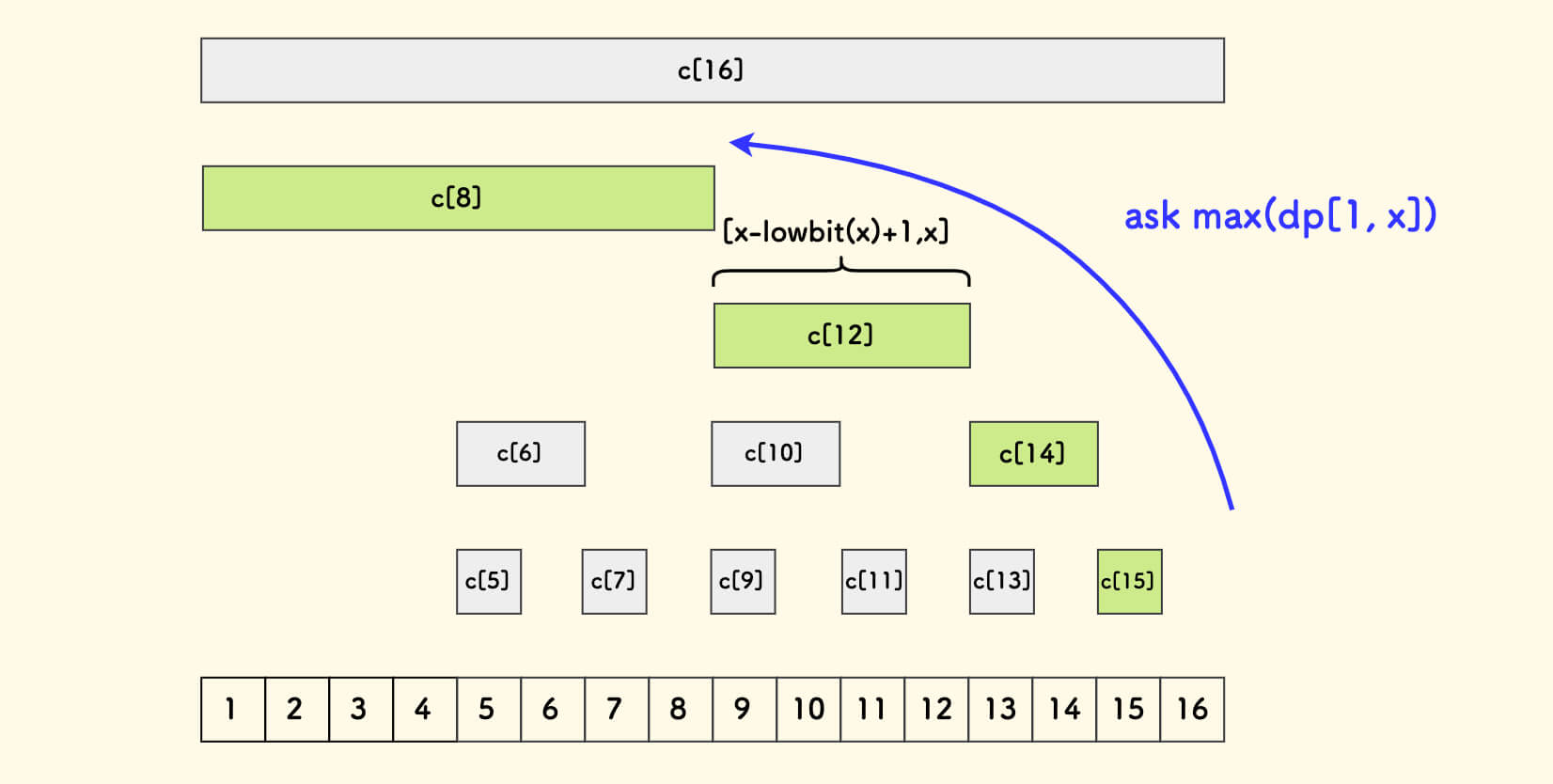
树状数组的本质，就是把信息打散到长度倍增的小区间去维护，这样平衡了查询和维护的时间到 $O(\log{n})$。

那么，在本题中，做一个结构体 P 来作为树状数组维护的信息：

struct P { int f, g; };

vector<P> c(n+1);

f 是 LIS 长度，也就是小区间内的 x 中最大的 dp[x]。
g 是 LIS 个数，也就是小区间内的最大 dp 值的出现次数。

接下来，分别讨论如何修改 ask 和 update 函数。

ask(x) 函数的含义是：查询前缀值域区间 [1,x] 上的总信息，是一个自右向左的爬树过程。不断检查途径的小区间，综合其最大值 f，同时维护其计数 g。

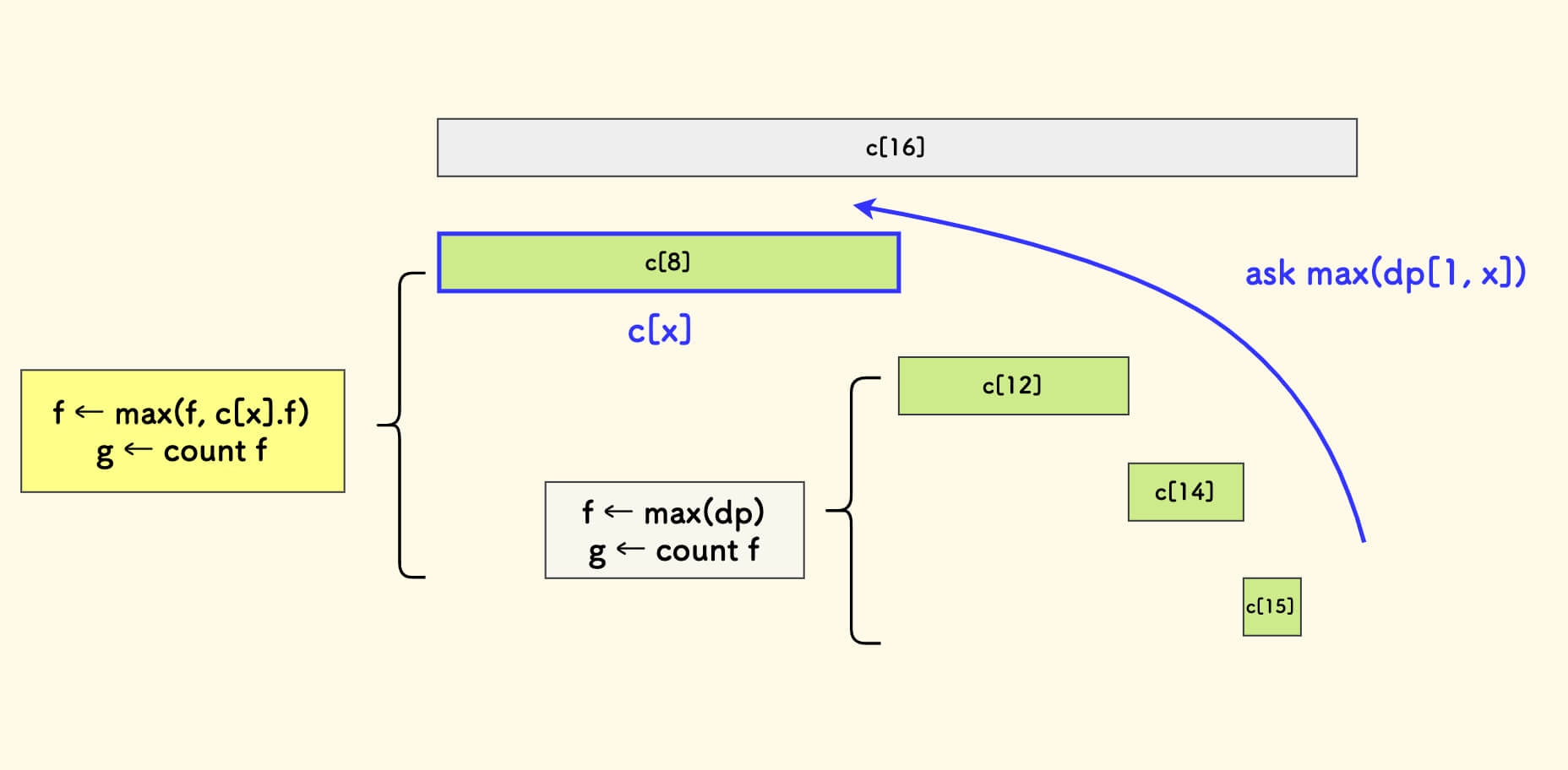
ask 函数的 C++ 实现（说明见注释）

P ask(int x) {
    // f 和 g 分别表示 [1,x] 上的 LIS 长度 和 个数
    int f = 0, g = 0;

    for (; x; x -= lowbit(x)) {
        // 预判当前最大的 f 是否更换

        // f 肯定会被换掉，清零计数
        if (f < c[x].f) g = 0;

        // 此时 c[x].f 必定取胜，添加其计数到统计值 g
        if (f <= c[x].f) g += c[x].g;

        // 否则，如果 f > c[x].f，
        // 说明答案 f 无需变化，个数也无需变化

        // f 取最大者即可
        f = max(f, c[x].f);
    }

    return {f, g};
}

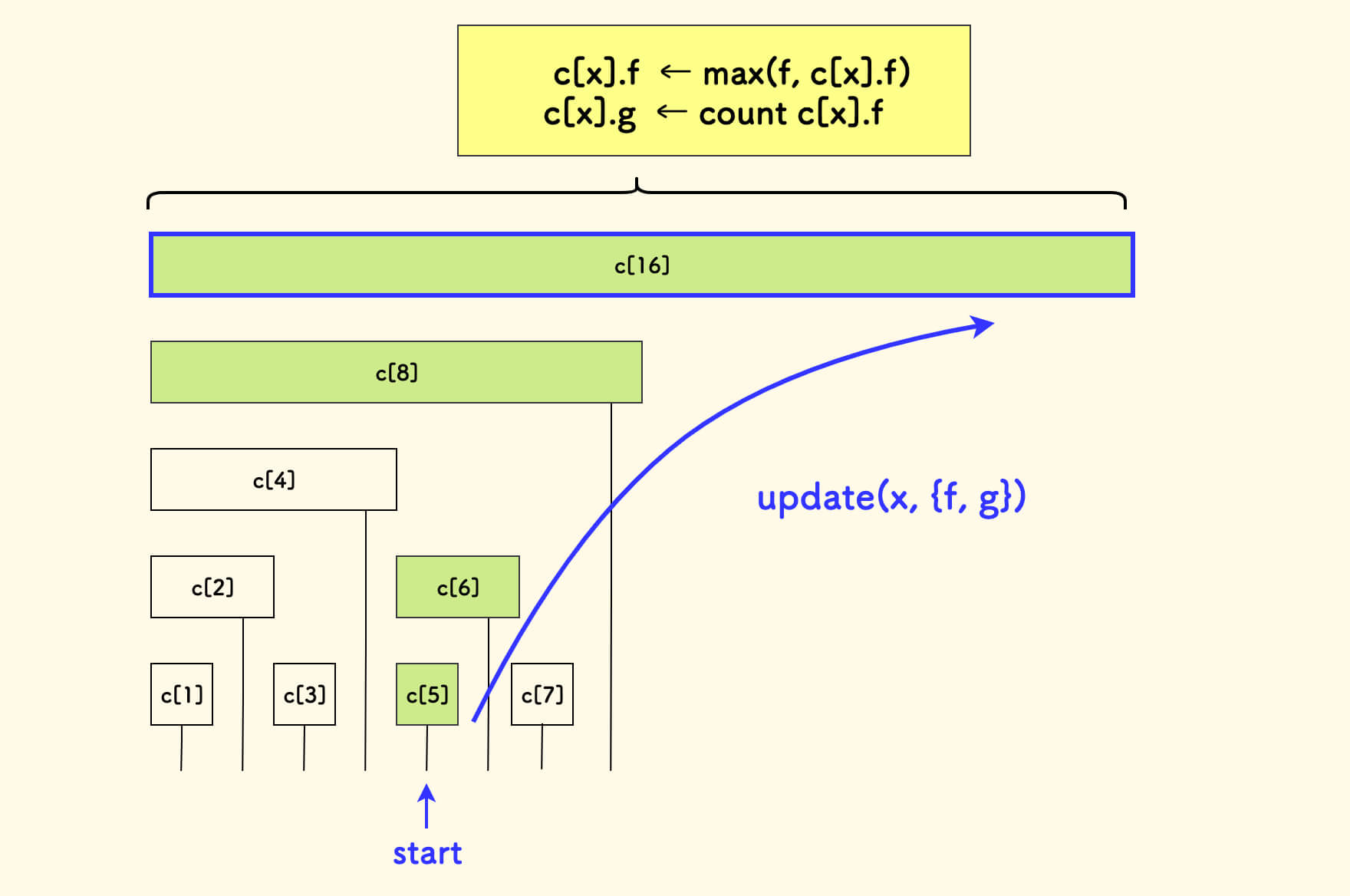
update 函数也是如法炮制：修改单元素的小区间 [x,x] 上的信息，不断向上更新其祖先区间，维护各个祖先区间上的最值 f 和其计数，是一个自左向右的爬树过程。

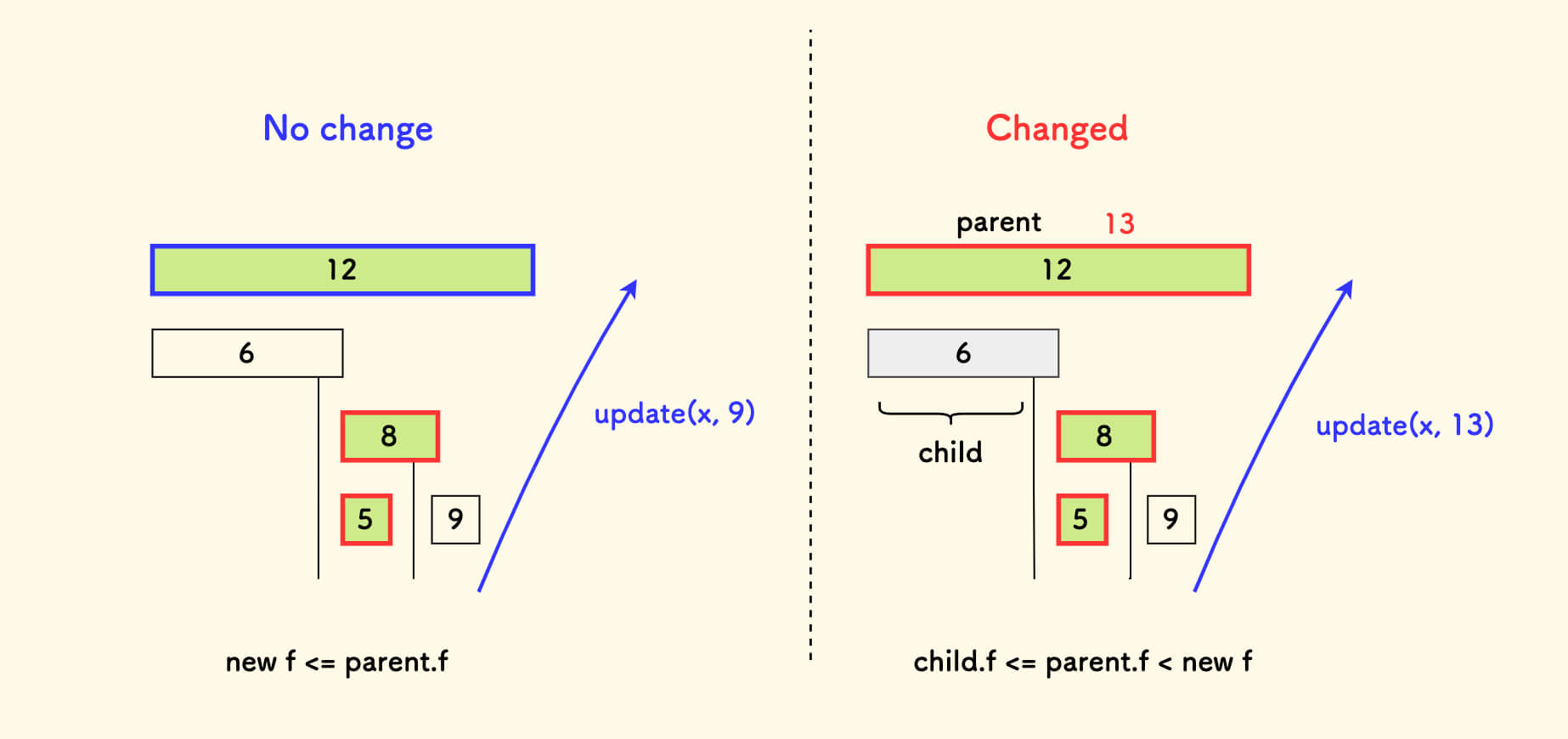
这里面其实有两种情况，需要冷静分析一下，对于每个祖先区间来说：

如果区间上的 c[x].f 最值没有变化，对应下图中左边的情况，继续细分两种情况：
1. 如果输入的 f 严格更小，那么祖先区间上的计数无需变化。
2. 如果输入的 f 恰好等于祖先区间维护的 f，那么加上新增的数量 g。
但是，如果输入的 f 更大，导致区间的 f 更新。如何对 f 在这个祖先区间内计数呢？
对应下图中右边的情况，因为祖先区间原本维护的 f 一定比子孙小区间的 f 都大。那么如果输入的新的 f 更大的话，自然所有计数只可能来自于爬坡途径的小区间。其他子孙小区间是不可能有这么大的 f 的，也就无需统计它们。

update 函数的 C++ 实现（说明见注释）

void update(int x, const P& p) {
    for (; x <= n; x += lowbit(x)) {
        // 更新前，预判小区间的 f 是否即将变化
        // c[x].f 肯定会更换，清零计数
        if (c[x].f < p.f) c[x].g = 0;

        // 新的 p.f 必定取胜，添加其计数的贡献
        // 否则，c[x].f 不会变，c[x].g 也无须变化
        if (c[x].f <= p.f) c[x].g += p.g;

        c[x].f = max(c[x].f, p.f);
    }
}

最后来到主过程，依次迭代原数组中的元素 x：

查询小于 x 的最大 dp 值，以及其个数 g。
也就是查询 [1,x-1] 区间上的 {f,g}。
新的以当前值 x 结尾的 LIS 的长度就是 f+1。
原来能以小于 x 的值结尾的 LIS 的长度是 g 的话，那么添加了更大的 x 后，LIS 的个数也是 g。
比如下图中例子，蓝色框表示值域 [1,x-1]，里面最大 LIS 长度是 f=3，有 g=2 个。新加入的 x 可以跟其中每一个形成以 x 结尾的长度是 f+1 的 LIS，个数也是 g。
唯一注意的细节是，g 要保证至少为 1。

问题的答案就是整个树状数组上的 g。

此外，要注意提前做离散化，总体时间复杂度是 $O(n\log{n})$。

代码实现如下，看起来也很简洁：

int n = a.size(), m = discrete(a);
BIT b(m);
for (auto x : a) {
    auto [f, g] = b.ask(x - 1);
    b.update(x, {f + 1, max(g, 1)});
}
return b.ask(m).g;

可以看到，本题目中对树状数组的使用方式是非常新颖的！

最终完整的代码实现见 Github - LIS 个数的树状数组解法完整 C++ 代码

平衡树解法 ¶

这里说的平衡树是指 fhq treap ^[3]。

仍然是基于求 LIS 长度的情况来考虑（前置阅读 - 求 LIS 长度的平衡树解法）。

和前面一样，假设 dp[x] 表示以值 x 结尾的 LIS 的长度，dp 转移关系如下：

// v 是已经扫描过的 且 < x 的 a[j] 的值
dp[x] = max(dp[v], for each v < x) + 1;

fhq treap 的核心操作 split 会根据一个给定的数值 v，把树分成两个子树，使得左子树中所有节点的权值全部不大于 v，右子树中所有节点的权值全部大于 v。

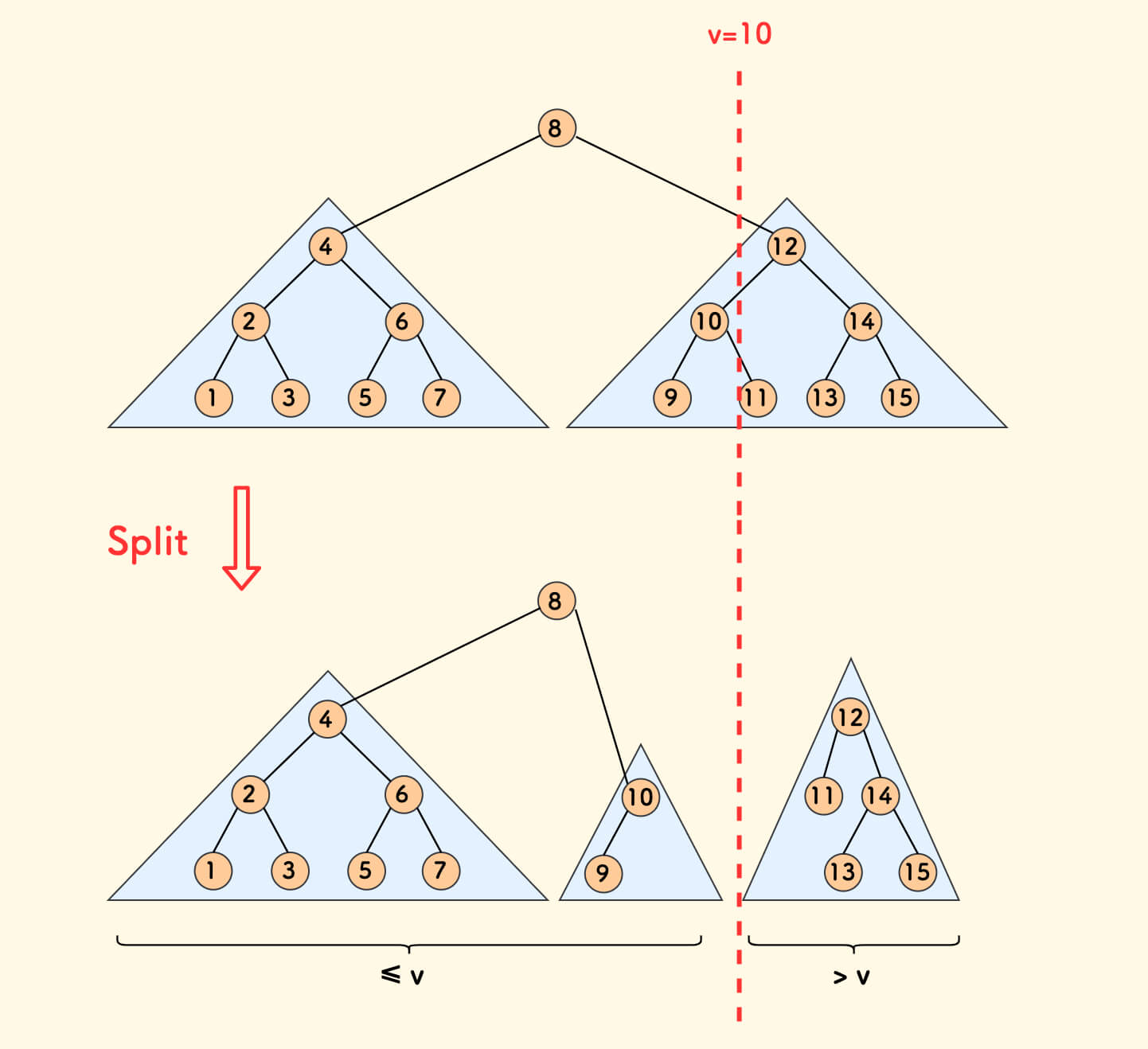
如果在每个节点上维护 dp 值，那么可以先按 x-1 分裂，取左子树上所有节点的最大的 dp 值，再加一即可得到新的 LIS 长度。

回到当前题目，可以在 treap 的每个节点额外维护 4 个信息：

len - 表示以当前节点的权值 val 结尾的 LIS 的长度, 也就是 dp[val]
mxlen - 表示以当前节点为根的子树中最大的 len 的值
num - 表示以 val 结尾的 LIS 的个数
mxnum - 表示以当前节点为根的子树中最大的 LIS 的个数

fhq treap 中的节点 C++ 定义

struct {
    int l, r;   // 左右孩子
    int val;    // BST 的权值
    int rnd;    // 堆的随机值
    int size;   // 树的大小
    int len;    // 以 val 结尾的 lis 的长度
    int mxlen;  // 子树中的最大的 lis 长度
    int num;    // 以 val 结尾的 lis 的个数
    int mxnum;  // 子树中最大的 lis 的个数
} tr[N];

现在考虑如何维护这些信息。

和 treap 求 LIS 长度的方法 ^[4] 中一样，可以在 pushup 函数中插入维护逻辑。

原本的 pushup 函数在分裂和合并操作后，自下而上地综合左右子树信息来维护父树信息。

最初始的用途是维护树的大小 size，代码如下：

fhq treap 中的分裂、合并和 pushup 函数 C++

void pushup(int p) {
    tr[p].size = tr[tr[p].l].size + tr[tr[p].r].size + 1;
    // 在这里加逻辑
}

// 按给定的 v 值来分裂成两个子树 x 和 y
// 分裂后 x 的所有权值都 <= v，y 的所有权值都 > v
void split(int p, int v, int &x, int &y) {
    if (!p) {
        x = y = 0;
        return;
    }
    if (tr[p].val <= v) {
        x = p;
        split(tr[p].r, v, tr[p].r, y);
    } else {
        y = p;
        split(tr[p].l, v, x, tr[p].l);
    }

    // pushup 是自底向上的穿插
    pushup(p);
}

// 合并两个子树 x 和 y
// 注意要求：x 中的所有权值要不大于 y 中的
int merge(int x, int y) {
    if (!x || !y) return x + y;
    if (tr[x].rnd < tr[y].rnd) {
        tr[x].r = merge(tr[x].r, y);
        pushup(x);
        return x;
    } else {
        tr[y].l = merge(x, tr[y].l);
        pushup(y);
        return y;
    }
}

借路 pushup 函数来维护 mxlen 和 mxnum 字段，如图所示。

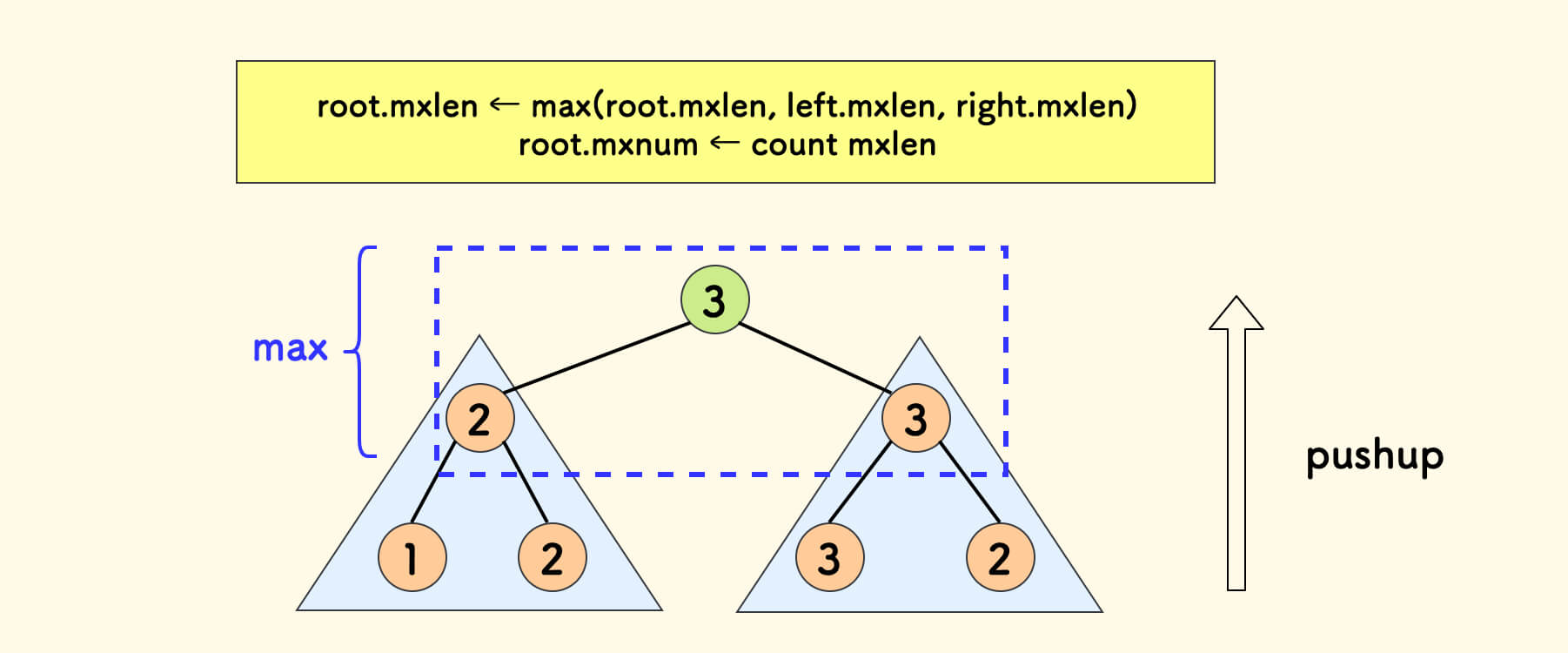
可以直接看代码实现：

pushup 维护 mxlen 和 mxnum 字段 - C++ 代码

void pushup(int p) {
    tr[p].size = tr[tr[p].l].size + tr[tr[p].r].size + 1;

    // 更新最大长度 和 其个数
    tr[p].mxlen = tr[p].len;
    tr[p].mxnum = tr[p].num;

    // 左右子树最大的 dp 值
    int lmaxlen = tr[p].l ? tr[tr[p].l].mxlen : 0;
    int rmaxlen = tr[p].r ? tr[tr[p].r].mxlen : 0;

    // 统计最终取胜的 mxlen 的个数 mxnum
    if (tr[p].mxlen < lmaxlen || tr[p].mxlen < rmaxlen)
        tr[p].mxnum = 0;
    if (tr[p].mxlen <= lmaxlen && rmaxlen <= lmaxlen)
        tr[p].mxnum += tr[tr[p].l].mxnum;
    if (tr[p].mxlen <= rmaxlen && lmaxlen <= rmaxlen)
        tr[p].mxnum += tr[tr[p].r].mxnum;

    tr[p].mxlen = max({lmaxlen, rmaxlen, tr[p].mxlen});
}

其中一个细节是，统计个数时，只有 pushup 途径的子树才会对父树的 mxnum 有贡献，而无需统计其他子树。这一点可以分情况讨论一下，和树状数组中的讨论雷同 ^[5]，这里略去不讲。

下面考虑主过程，是比较简单的。

顺序扫描原数组的每一项 x：

查询小于 x 的最大 dp 值，以及其个数信息。

也即是查询 <=x-1 的子树上的信息，可以走 split 函数。

构造一个询问函数 ask(v)，它返回权值不大于 v 的子树上最大的 LIS 长度 mxlen 和其个数：

ask 函数的 C++ 实现

pair<int, int> ask(int v) {
  // 先分裂为左子树 x 和右子树 y
  int x, y;
  split(root, v, x, y);
  // 此时左子树 x 的所有权值 val 都不大于 v
  int mxlen = tr[x].mxlen, mxnum = tr[x].mxnum;
  // 搞完以后，要记得把两个子树再合并回去
  root = merge(x, y);
  return {mxlen, mxnum};
}

只需要执行 ask(x-1) 获取到 mxlen 和 mxnum。

mxlen+1 就是新的以当前值 x 结尾的 LIS 的长度。

原来能以小于 x 的值结尾的 LIS 的长度是 mxnum 的话，那么添加了更大的 x 后，LIS 的个数也是一样的。

比如下图中的例子，蓝色框中 <x 的最大 LIS 长度是 3，有 2 个。新加入的 x 可以跟其中每一个形成一个新的 LIS，个数也是 2。

插入新节点的实现代码如下：

insert 函数的 C++ 实现

int newnode(int v, int len, int num) {
    tr[++n].val = v;
    tr[n].rnd = rand();
    tr[n].size = 1;
    tr[n].len = len;
    tr[n].mxlen = len;
    tr[n].num = num;
    tr[n].mxnum = num;
    return n;
}

void insert(int v, int len, int num) {
    int x, y;
    split(root, v, x, y);
    int z = newnode(v, len, num);
    root = merge(merge(x, z), y);
}

最终的答案是树根上的 mxnum。

求解主流程代码如下，时间复杂度是 $O(n\log{n})$。

int findNumberOfLIS(vector<int> &a) {
    FHQ treap;
    for (auto x : a) {
        auto [mxlen, mxnum] = treap.ask(x - 1);
        treap.insert(x, mxlen + 1, max(mxnum, 1));
    }
    return treap.tr[treap.root].mxnum;
}

完整的代码实现见 Github - LIS 个数的 Treap 解法完整 C++ 代码。

结尾语 ¶

两种解法都有一个特点：用数据结构来优化 DP，同时统计其个数。

而且，统计个数的逻辑还要嵌入到数据结构的代码之中，借路来维护。都要修改代码模板，比较新颖。

（完）

LIS 计数问题的 树状数组 和 平衡树 解法

问题描述 ¶

树状数组解法 ¶

平衡树解法 ¶

结尾语 ¶

LIS 计数问题的树状数组和平衡树解法