关于 2D 平面上检测两个矩形是否重叠的一篇小短文。
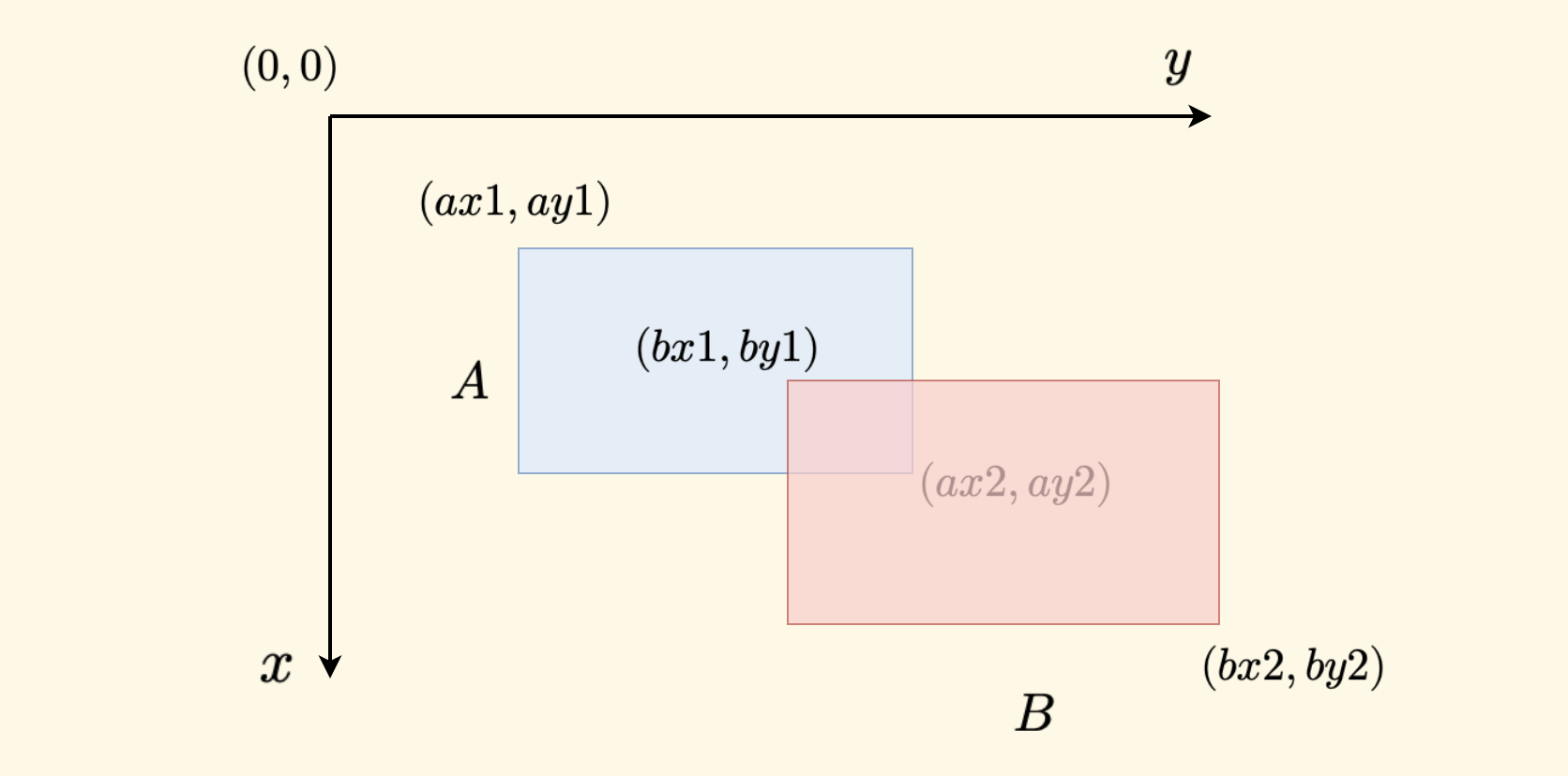
假设要检测的两个矩形是 $A$ 和 $B$,我们的坐标系是左上角为原点,向右算作 $y$, 向下算作 $x$ 。
每个矩形用左上角和右下角的坐标来描述,两个矩形分别表示为 $(ax1, ay1), (ax2, ay2)$ 和 $(bx1, by1), (bx2, by2)$ 。
检测是否重叠的代码十分简短,只有一行:
bool isOverlap = ax1 <= bx2 && ax2 >= bx1 && ay1 <= by2 && ay2 >= by1;
充分性 ¶
下面来解释这行代码:
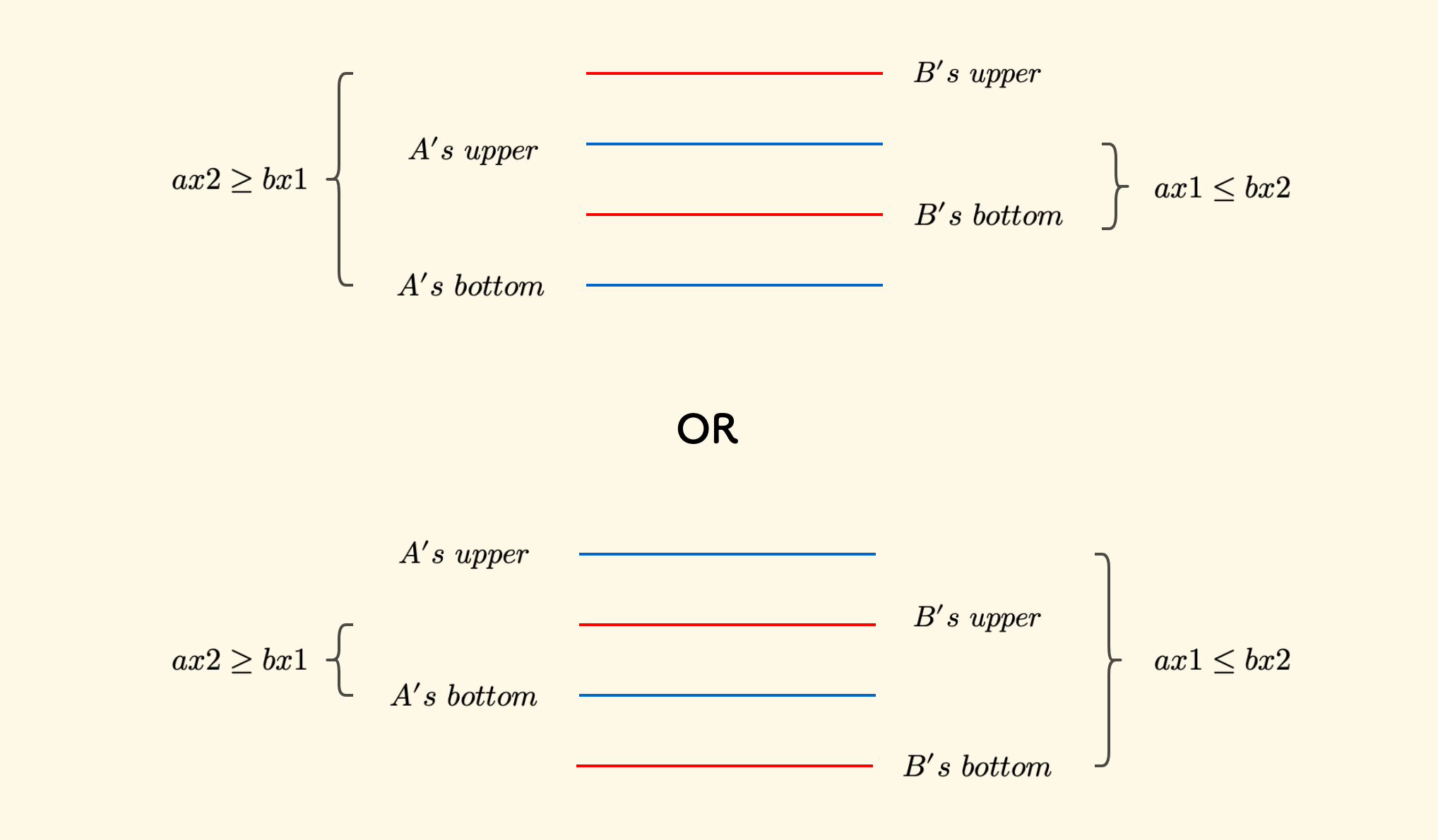
- $ax1 \le bx2$ 意思是说, $A$ 的上边界在 $B$ 的下边界的上边
- $ax2 \ge bx1$ 意思是说, $A$ 的下边界在 $B$ 的上边界的下边
要同时符合这俩条件,只有两种情况:
同样道理,对于纵轴的两个条件:
- $ay1 \le by2$ 意思是说,$A$ 的左边界在 $B$ 的右边界的左边
- $ay2 \ge by1$ 意思是说,$A$ 的右边界在 $B$ 的左边界的右边
这时,也有两种情况:
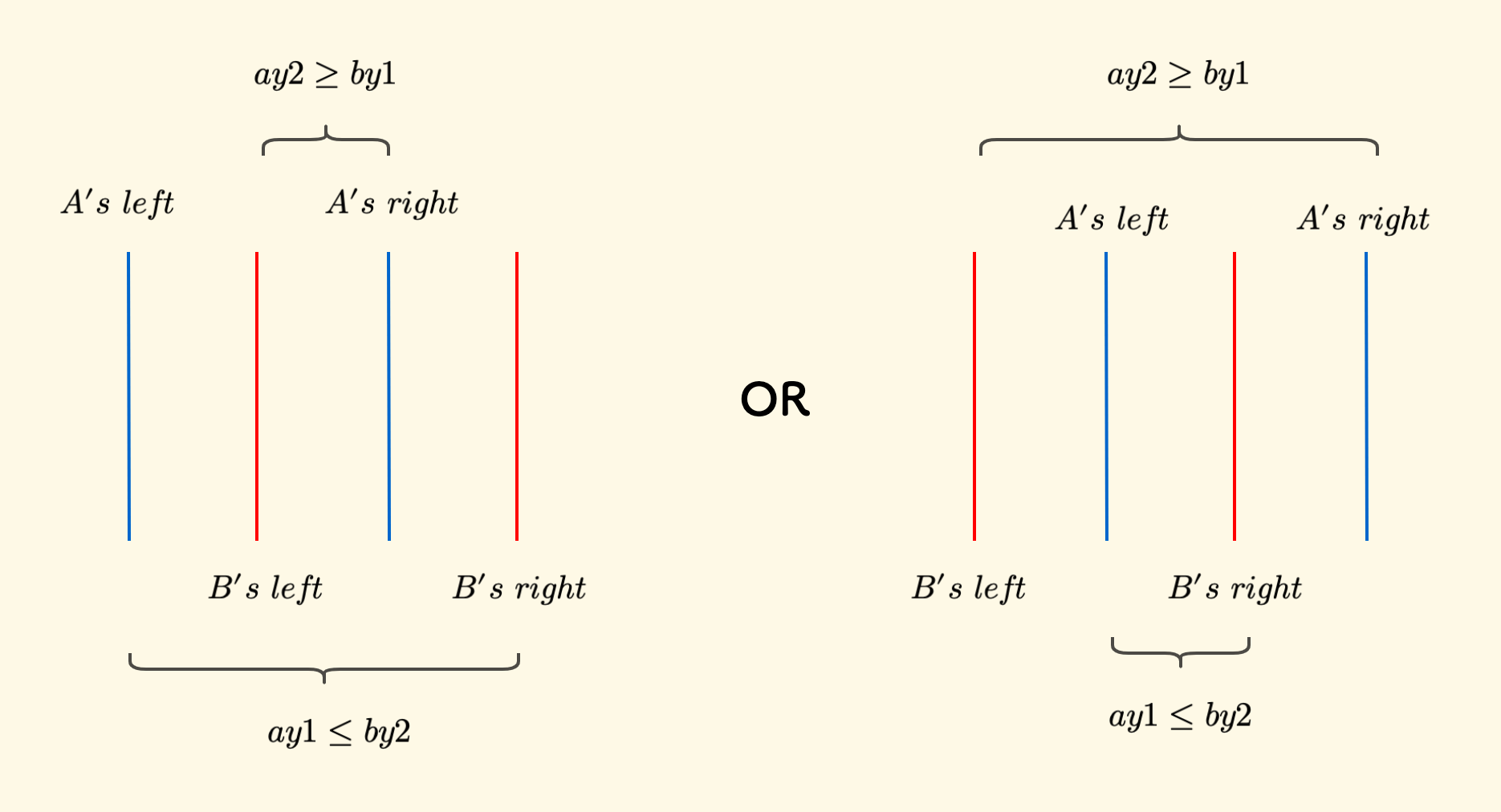
那么,上面的两种情况、结合下面的两种情况,任意组合一下,就会有 $4$ 种情况:
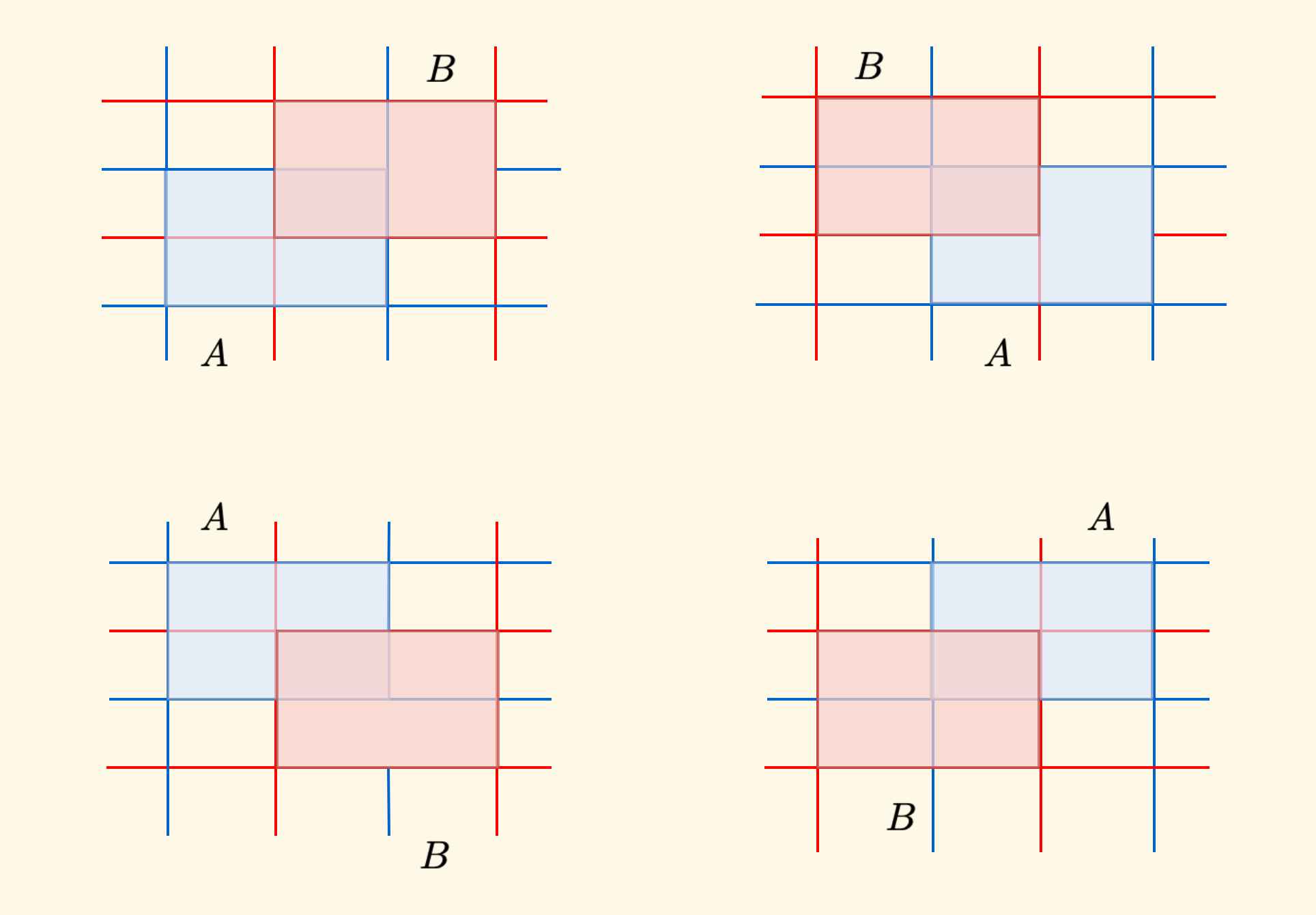
可以看到,$4$ 种情况下都相交,也就是说,只要这四个条件同时满足,那么必定存在重叠部分。
注意的是,这 $4$ 种情况说明了,无论两个矩形在平面上的相对位置如何,$A$ 和 $B$ 在这个公式中角色互换也好,只要这四个条件满足,就必定相交。
充分性得以说明。
必要性 ¶
必要性是说,这四个条件中,但凡其中一个不满足,那么就肯定不相交。
如果 $ax1 \le bx2$ 不满足,也就是说 $ax1 > bx2$, 意思是说 $A$ 的上边界在 $B$ 的下边界的下边。 那么,此时整个 $A$ 必然位于 $B$ 的下方,肯定无法相交。如下图所示。
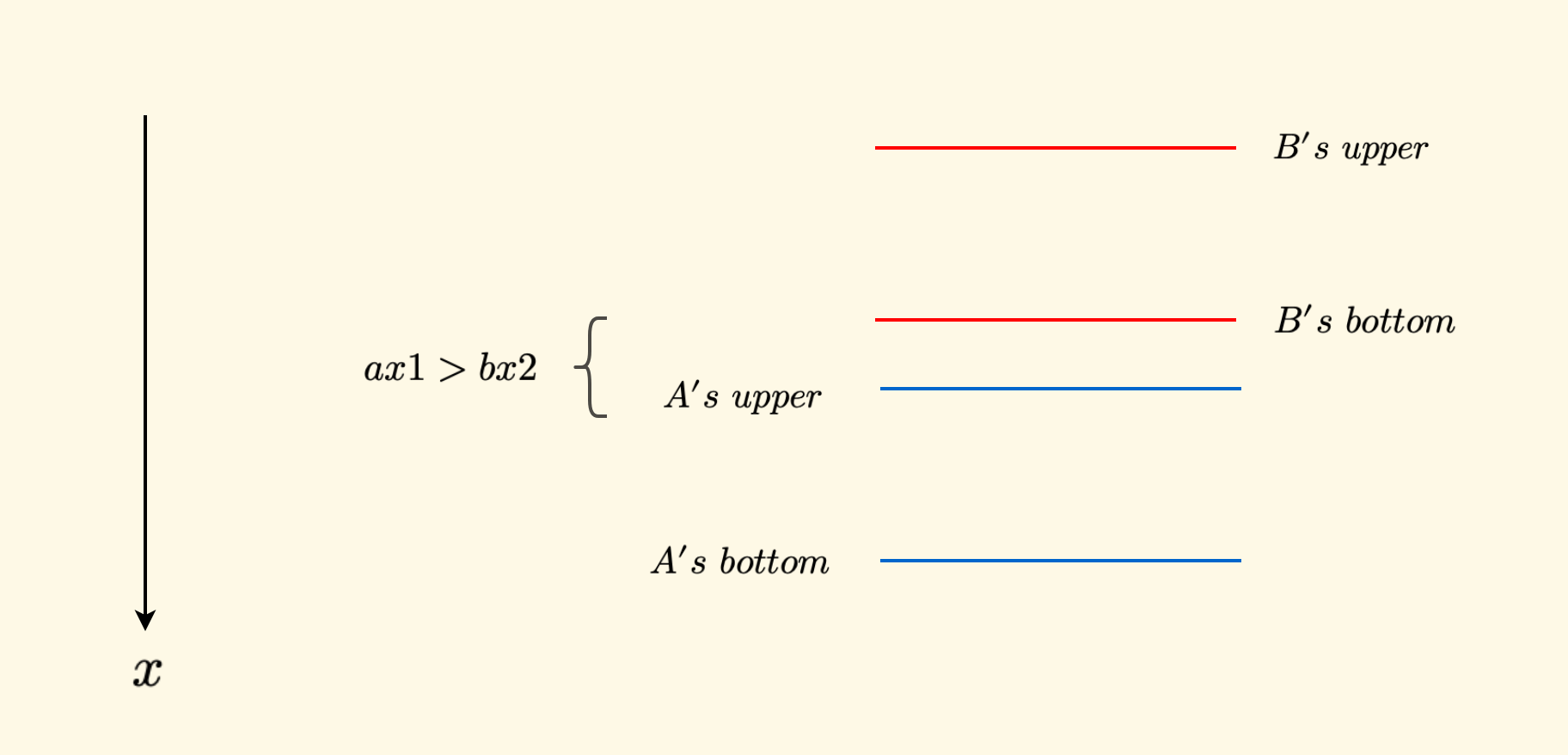
其余条件也可以类似思路来证明,不再展开。
以上,综合了充分性和必要性说明了 AABB 检测代码的正确性。
最后贴一个链接,可以看 DEMO: https://silentmatt.com/rectangle-intersection/
(完)
本文原始链接地址: https://writings.sh/post/aabb
