本文记录最大连续子序列和问题的两种解法:前缀和方法 和 动态规划方法。
问题 ¶
从一个可能包含负数的整数数组中,找出其连续子数组的和的最大值。
例如,对于 [-2,1,-3,4,-1,2,1,-5,4] 来说,连续子数组 [4,-1,2,1] 的和最大,为 6 。
前缀和方法 ¶
前缀和 sum(i) 是指以位置 i 结尾的前缀子数组的求和结果:
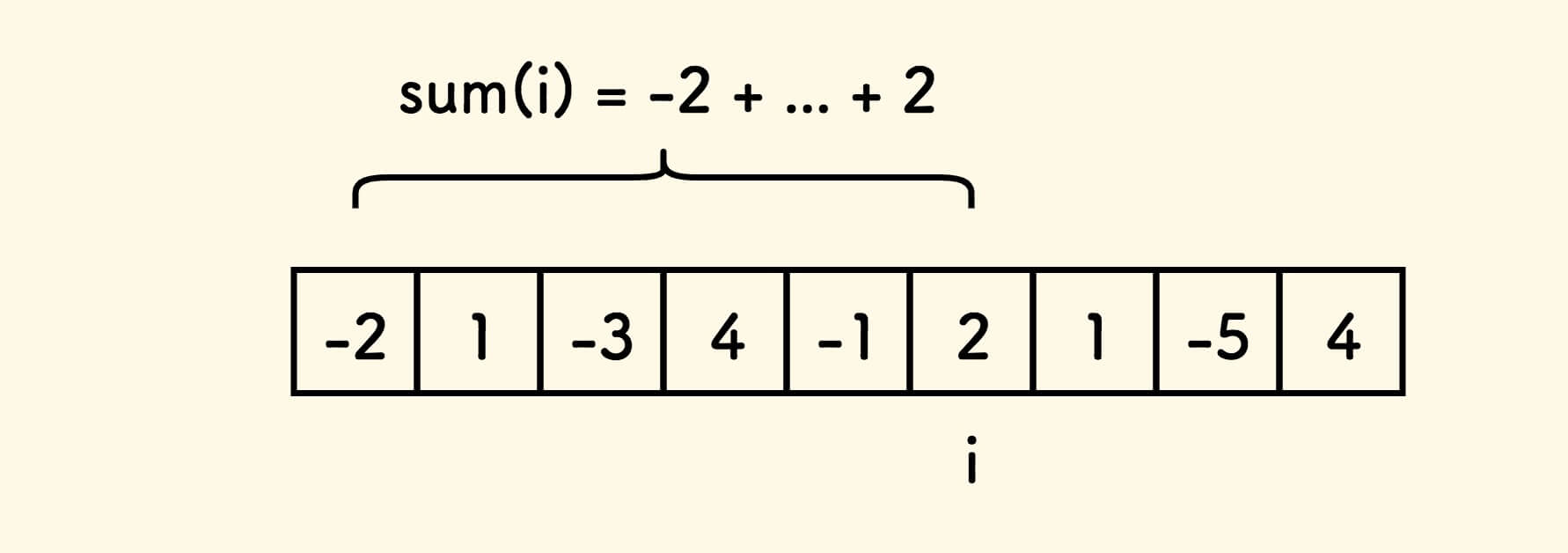
如此,任意一个连续数组 [i..j] 之和可以表达为 sum(j) - sum(i-1) :
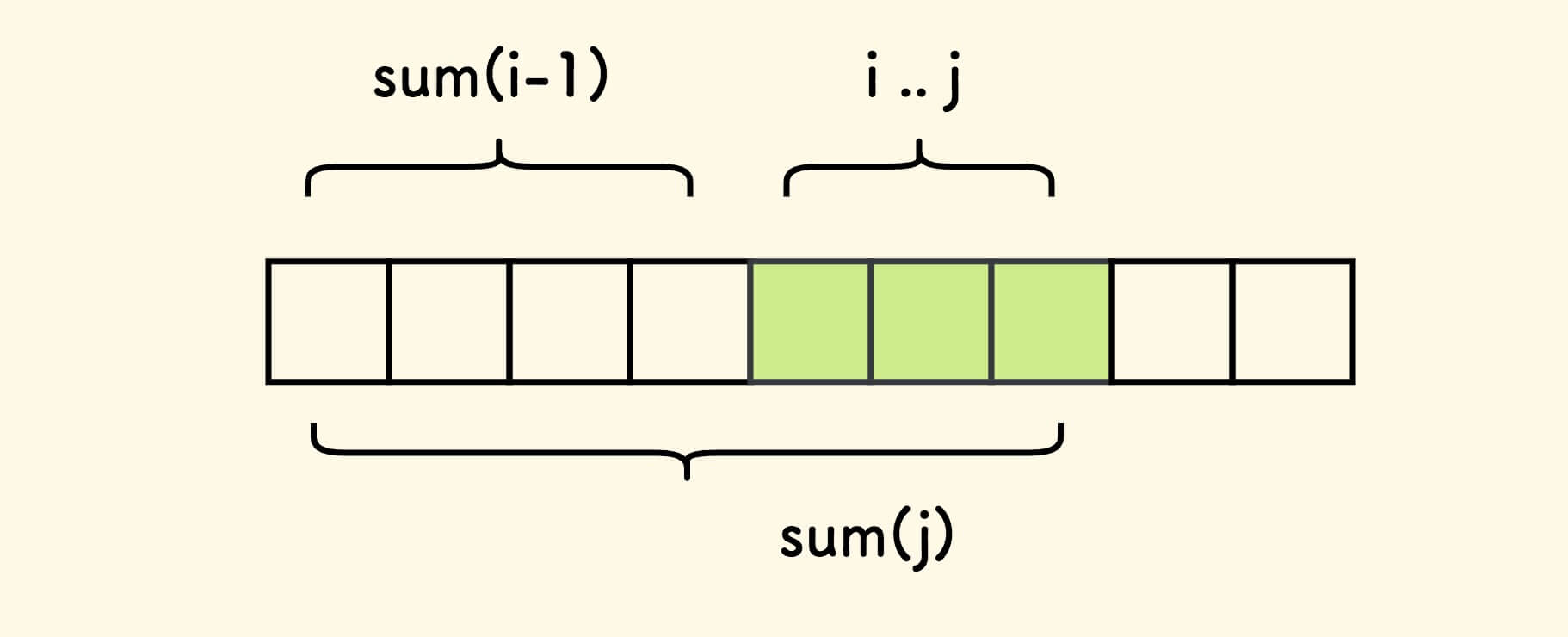
对于一个确定的 j ,假设前缀和 sum(j) 已知。
要使右侧区间内数字之和最大, 势必要求左侧前缀和 sum(i-1) 最小。
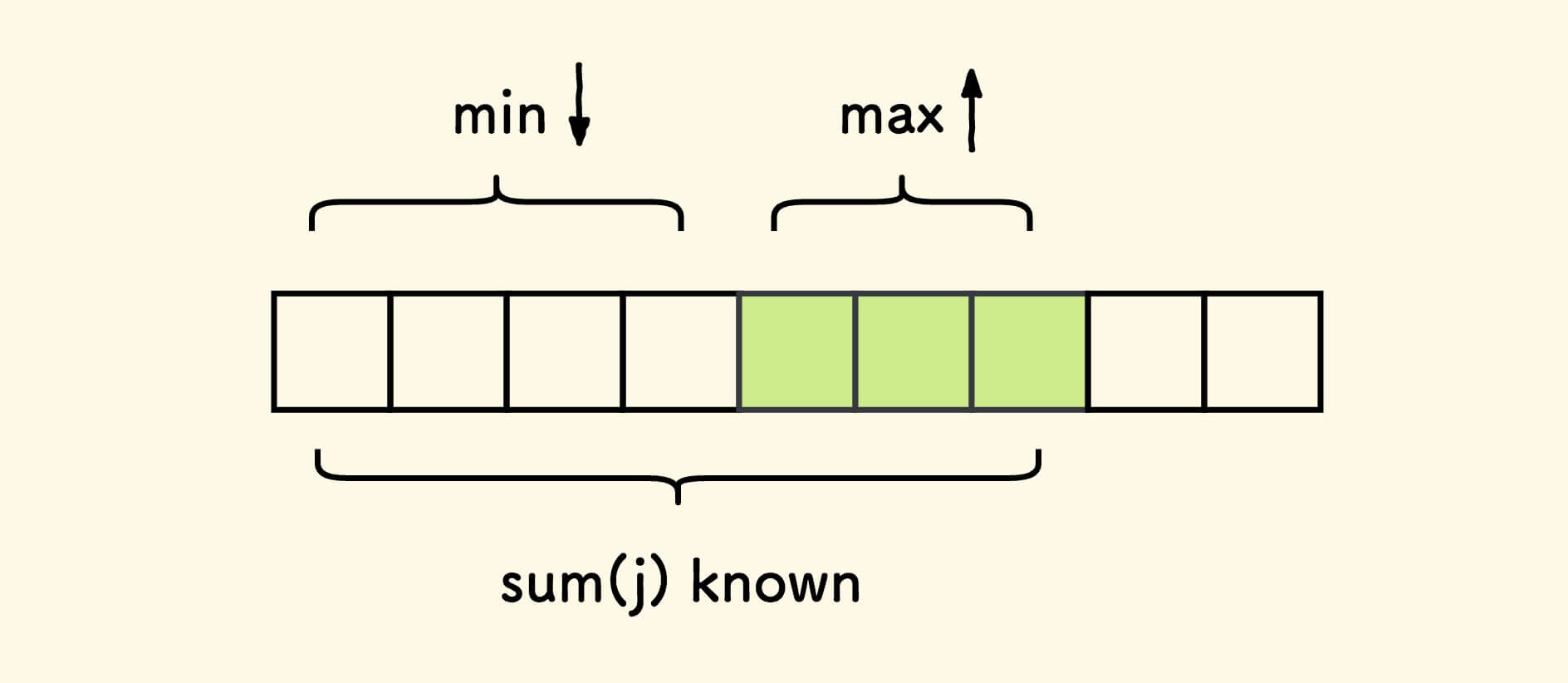
也就是,要找出 j 左边的前缀和的最小值,它可以在计算前缀和的过程中记录下来。
最后,对所有 j 找出其右侧区间的最大和 ,记录其中最大的即结果。
最大子序列和问题 - 前缀和方法 - C 语言实现
// 返回给定整数数组的最大连续子序列的和。
int LargestSumContiguousSubarray(int nums[], int length) {
// Sum of 1..j
int sum = 0;
// Min value of sum(i), where i < j.
int min = 0;
// Max value of delta, where delta = sum(j) - min.
int max = nums[0];
for (int j = 0; j < length; j++) {
sum += nums[j];
int delta = sum - min;
if (delta > max) max = delta;
if (sum < min) min = sum;
}
return max;
}
时间复杂度是 O(n) ,空间复杂度是 O(1) 。
动态规划方法 ¶
任何连续数组,都可以表达为:以位置 i 结尾的连续数组。
假设函数 dp(i) 是所有以位置 i 结尾的连续数组的和的最大值。
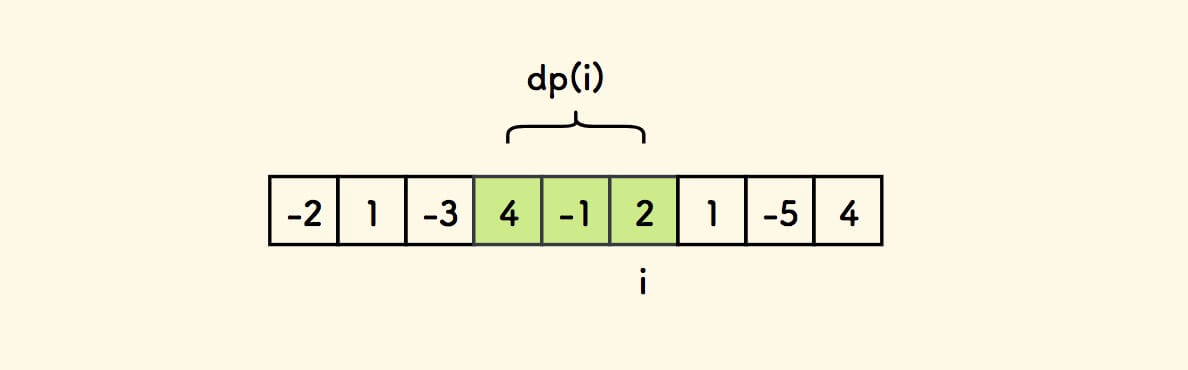
由定义可知, nums[i] 是所考虑的连续数组的结尾元素,因此 dp(i) 必然包含 nums[i] 作为成分。
假设已知 dp(i-1),考虑其递推到 dp(i):
- 如果
dp(i-1)是正数,考虑到要求最大和,因此将它吸收,即dp(i) = dp(i-1) + nums[i] - 否则,不吸收
dp(i-1),即dp(i) = nums[i]
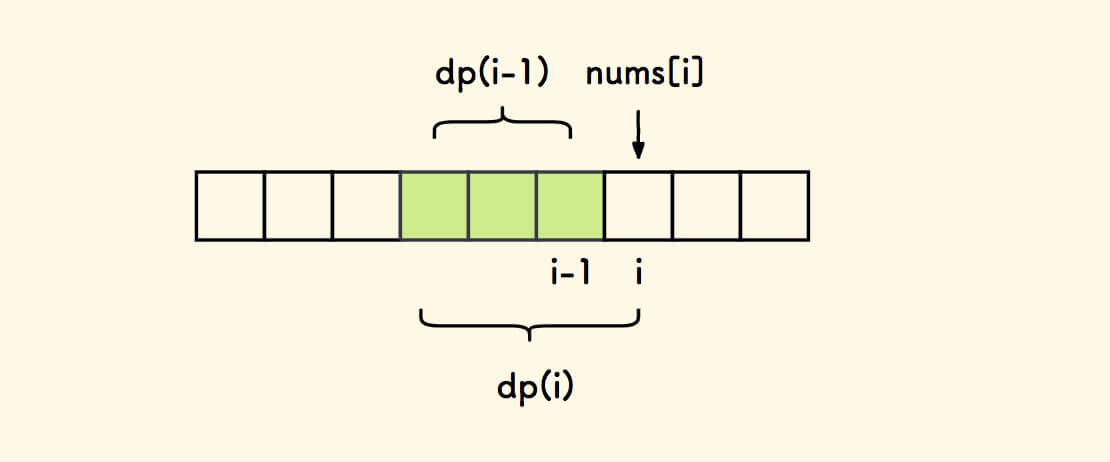
对所有 0..n-1 的 i 求解其 dp(i) ,找出其中最大值即结果。
最大子序列和问题 - 动态规划方法 - C 语言实现
// 返回给定整数数组的最大连续子序列的和。
int LargestSumContiguousSubarray(int nums[], int length) {
if (length <= 0) return 0;
int max = 0;
int dp[length];
dp[0] = nums[0];
for (int i = 1; i < length; i++) {
if (dp[i - 1] > 0)
dp[i] = dp[i - 1] + nums[i];
else
dp[i] = nums[i];
if (max < dp[i]) max = dp[i];
}
return max;
}
最大子序列和问题 - 动态规划方法 - C 语言实现 - 空间 O(1)
// 返回给定整数数组的最大连续子序列的和。
int LargestSumContiguousSubarraySpaceO1(int nums[], int length) {
if (length <= 0) return 0;
int dp = nums[0];
int max = dp;
for (int i = 1; i < length; i++) {
if (dp > 0)
dp += nums[i];
else
dp = nums[i];
if (max < dp) max = dp;
}
return max;
}
时间复杂度是 O(n) ,空间复杂度是 O(n) 或 O(1)。
(完)
本文原始链接地址: https://writings.sh/post/algorithm-largest-sum-contiguous-subarray
