本文记录一些基本的数论类算法。
内容包括:
最大公约数 ¶
最大公约数 是指能够整除两个或多个整数的最大正整数。
两个整数 $a$ 和 $b$ 的最大公约数一般记作 $gcd(a, b)$ ,例如 $gcd(54, 24) = 6$ 。
一般采用 欧几里得算法 ,或叫做「辗转相除法」。
欧几里得算法是所有算法的鼻祖,因为它是现存最古老的非凡算法。
--- 《计算机程序设计艺术》· 高德纳
算法内容
两个整数的最大公约数等于其中较小的那个数和两数相除余数的最大公约数 。
用数学符号来表达即:
如果 $a \geq b$ ,那么 $gcd(a, b) = gcd(b, a \% b)$ 。
举例来说:
\[gcd(54, 24) = gcd(24, 54 \% 24) = gcd(24, 6) = gcd(6, 24 \% 6) = gcd(6, 0) = 6\]根据算法描述可以很快给出代码实现:
欧几里得算法 - 最大公约数 - 递归版本 - C 语言实现
// 辗转相除法 - 最大公约数
int Gcd(int a, int b) {
if (a < b) return Gcd(b, a);
if (b > 0) return Gcd(b, a % b);
return a;
}
欧几里得算法 - 最大公约数 - 循环版本 - C 语言实现
// 辗转相除法 - 最大公约数 - 循环版本
int Gcd(int a, int b) {
if (a < b) return Gcd(b, a);
while (b > 0) {
int m = a % b;
a = b;
b = m;
}
return a;
}
正确性说明
假设 $g$ 是 $a$ 和 $b$ 的公因数,那么 $a$ 可以表示为 $a = gk_1$ ,$b$ 可以表示为 $b = gk_2$ 。
如果 $a$ 对 $b$ 的余数是 $m$ ,那么 $a$ 也可以表示为 $a = kb + m$ 。
于是有 $gk_1 = gk_2k + m$ ,所以 $m = g(k_1 - k_2k)$ ,因此 $g$ 也是余数 $m$ 的因数。
即 $a$ 和 $b$ 的公因数也是余数 $m$ 的因数 ,因此 $gcd(a, b)$ 可以转化为 $gcd(b, m)$ 。
注意,这里只在说 两个数的因数同时也是其余数的因数 ,没有说互素性相关的事。
直到余数是 $0$ 时,即 $gcd(a, b)$ 变化成 $gcd(b, 0)$ 时,留下的第一个参数就是结果。
余数变 $0$ ,意味着某一时刻发生了 $gcd(a, b) \rightarrow gcd(b, a\%b) = gcd(b, 0)$ , 此时 $b$ 可以整除 $a$ 。$g$ 是 $a$ 和 $b$ 的最大公因数, 所以 $g \leq b \leq a$ ,而 $b$ 可以整除 $a$ ,所以 $g$ 就是 $b$ 。 就是说,下一时刻留下的数就是 $g$ 。
此外,算法必然是可以结束的:
由于每一步转化,余数 $m$ 必然严格小于 $b$ ,即每一步的算法的第二个输入项 $b$ 都在严格减小, 而且余数非负,所以必然在某一步达到 $b = 0$ ,此时算法终止。
复杂度分析
首先,对于任意两个整数 $x$ 和 $y$ ,如果 $x > y$ 的话,那么一定有 $x \% y < \frac {x} {2}$ ,是因为:
- 如果 $y > \frac {x} {2}$ ,则 $x \% y \leq x - y < \frac {x} {2}$ .
- 如果 $y \leq \frac {x} {2}$ ,则 $x \% y < y < \frac {x} {2}$ .
观察欧几里得算法的两步迭代:
\[gcd(a, b) = gcd(b, a \% b)\] \[gcd(b, a \% b) = gcd(a \% b, b \% (a \% b))\]可以看到第二个参数由 $b$ 变为 $b \% (a\%b)$ ,它不大于 $\frac {b} {2}$ 。
第二个参数每两步迭代,会减少到不超过原来的 $\frac {1} {2}$ ,直到为 $0$ 时算法结束。 因此,欧几里得算法的时间复杂度不超过 $O(2logb)$ ,其中 $b$ 是两个参数中较小的那个数。
最小公倍数 ¶
最小公倍数 是指两个给定整数可以同时整除的最小的整数。
两个整数 $a$ 和 $b$ 的最小公倍数一般记作 $lcm(a, b)$ ,例如 $lcm(54, 24) = 216$ 。
最小公倍数和最大公约数有以下关系:
\[lcm(a, b) = \frac {|a \cdot b|} {gcd(a, b)}\]最小公倍数 - C 语言实现
int Lcm(int a, int b) { return a * b / Gcd(a, b); }
素数测试 ¶
如何判断一个给定的整数 a 是否是素数?
如果 $a$ 是一个合数,那么必然有一个因数不大于 $\sqrt a$ 。
此方法是 素数测试 的最简单的办法。
素数测试 - C 语言实现
bool IsPrime(int a) {
if (a < 2) return false;
for (int i = 2; i * i <= a; i++) {
if (a % i == 0) return false;
}
return true;
}
此算法的时间复杂度是 $O(\sqrt n)$ 。
不过,在素数测试领域中,一般考虑 $n$ 位长度的整数的时间复杂度,如此一来, 此算法的时间复杂度则是指数级别的 $O(\sqrt {2^n})$ 即 $O(2^{n/2})$ 。
AKS 素数测试 是第一个多项式时间内确定性的素数测试算法。
埃拉托斯特尼素数筛法 ¶
如何找出一个给定的自然数 n 内的所有素数?
算法步骤
埃拉托斯特尼筛法 是解决这一问题的经典算法,简称埃氏筛:
把不大于 $\sqrt n$ 的所有素数的倍数剔除,剩下的就是素数 。
算法的步骤说明:
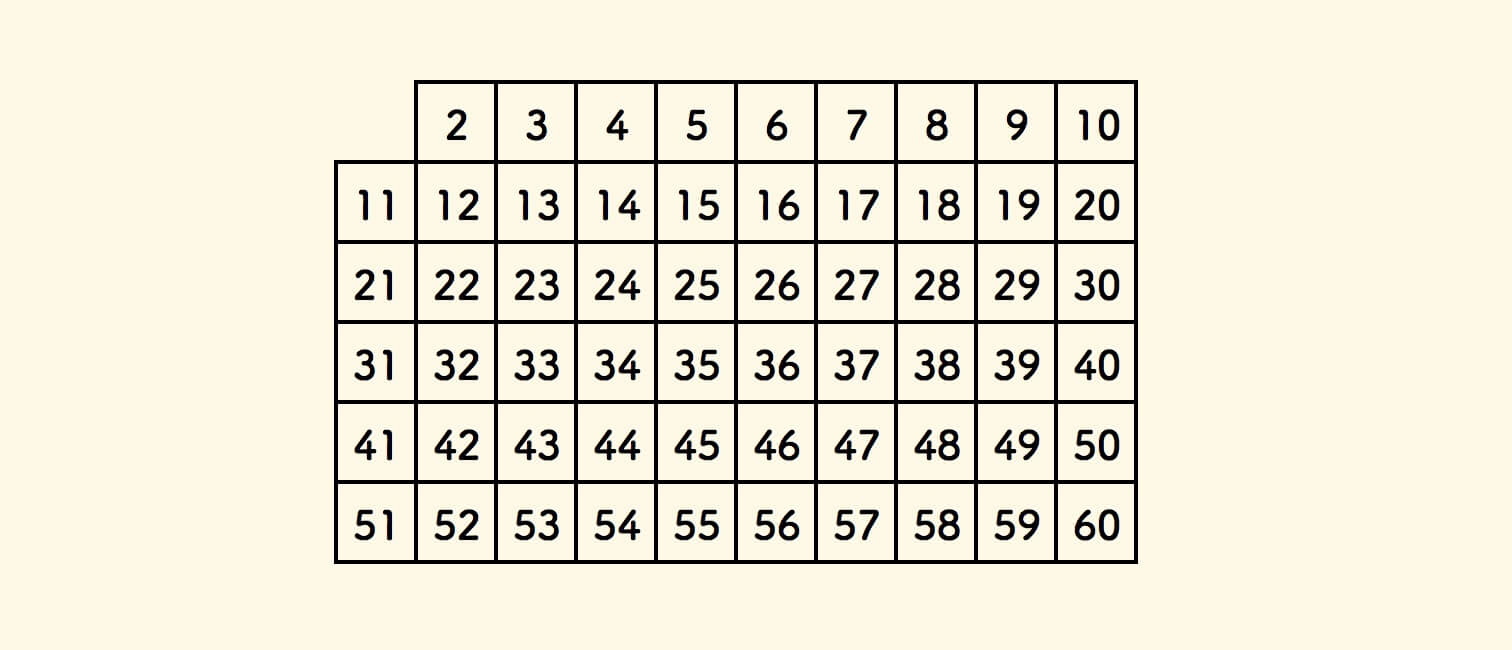
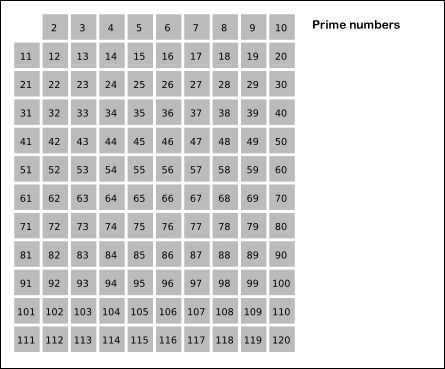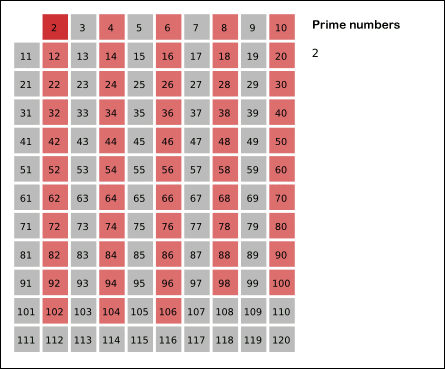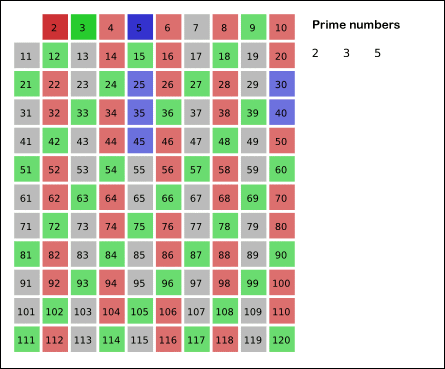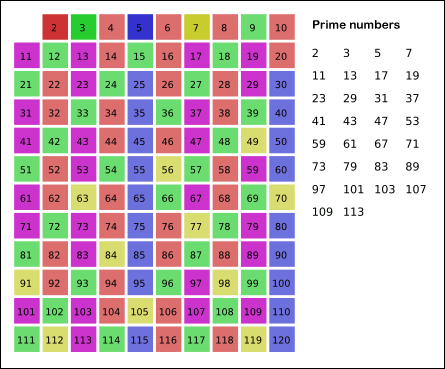
准备一个表格如下,所有方格标记为真,即认为表格中所有数字都是素数,将从中筛除合数:

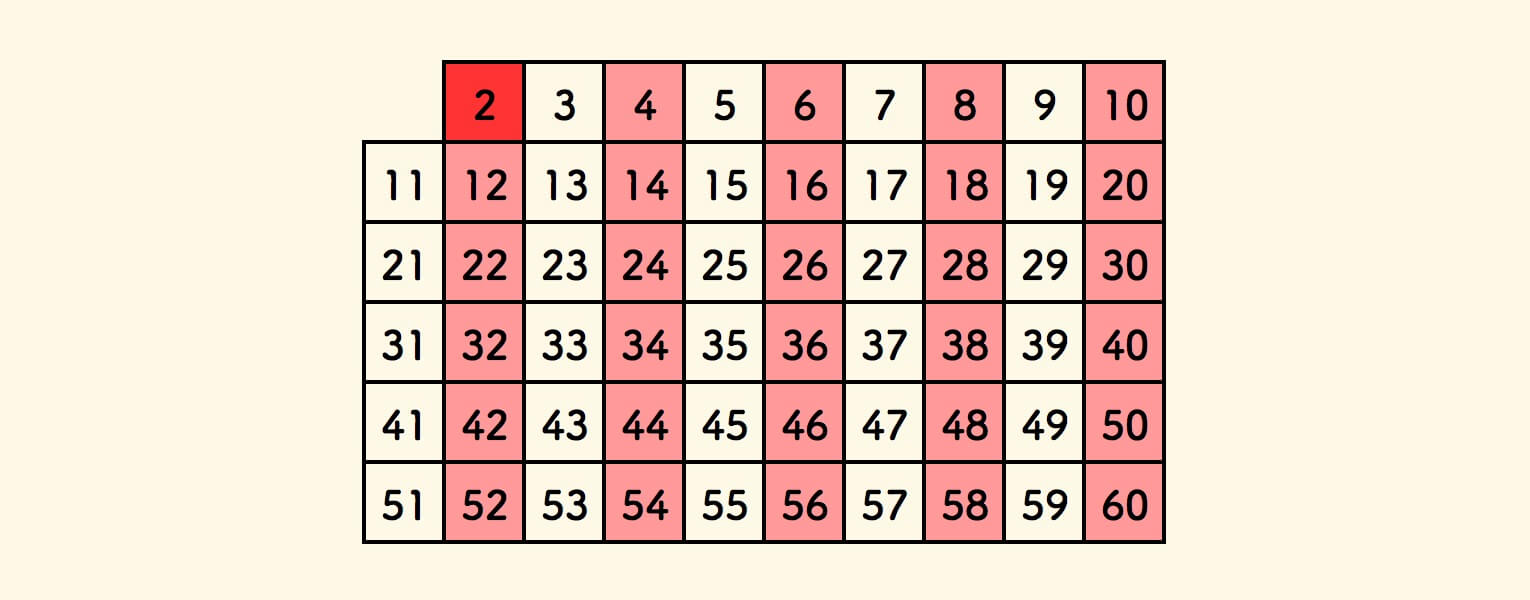
当前表格中最小的标记是真的数是 $2$ ,取 $2$ 叫做 筛子,筛除 $2$ 的所有倍数。
即标记 $2$ 的所有倍数为假。

接下来表格中最小的标记是真的数是 $3$ ,同样地,取 $3$ 为筛子,筛除 $3$ 的所有倍数。

如此反复进行。
因为小于 $n$ 的合数必然有不大于 $\sqrt n$ 的素因数,所以,当筛子达到 $\sqrt n$ 时,结束算法。
对于本例来讲就是到 $\sqrt {61}$ ,取整后 $7$ ,此时算法结束。

此外:
每一轮筛除时,因为当前筛子是表格中未被更小的、先前的筛子筛除的数字,所以它一定是一个素数, 即 筛子是素数。
在使用筛子 $p$ 进行筛选时,对于它的倍数 $pq$ ,如果 $q < p$ :
- 如果 $q$ 是一个素数,则必然 $pq$ 已经被 $q$ 筛除。
- 否则 $q$ 是一个合数,也必然存在一个更小的素数筛子把 $q$ 和 $pq$ 都筛除了。
所以,此类 $p$ 的倍数无需再次考虑。
即 每次使用筛子 $p$ 时,只需从 $p^2$ 处开始筛除倍数即可。
整个筛选过程的动态图示如下:
算法实现
埃拉托斯特尼素数筛法 - C 语言实现
// 埃拉托斯特尼筛法
// 输入上限整数 n 和 大小为 n 的筛表
// 筛表中位置为素数的项会被设置 true
void Eratosthenes(int n, bool table[]) {
if (n <= 0) return;
for (int i = 0; i < n; i++) table[i] = true;
if (n >= 1) table[0] = false;
if (n >= 2) table[1] = false;
for (int i = 2; i * i < n; i++) {
if (table[i]) {
for (int j = i * i; j < n; j += i) table[j] = false;
}
}
return;
}
算法复杂度
埃氏筛法对于每个素数筛子 $p$ ,会筛除 $n/p$ 个合数,因此步骤数是:
\[\frac {n} {2} + \frac {n} {3} + \frac {n} {5} + \ldots = n \sum_{p \leq n} {\frac {1} {p}}\]根据 Mertens’ theorems :
\[\lim_{n \rightarrow \infty } \left( \sum_{p \leq n} {\frac {1} {p}} -\ln{\ln {n}} - M \right) = 0\]其中 $M$ 是一个 常数 , 因此,其时间复杂度是 $O(n\log{\log{n}})$ 。
快速素数筛法 ¶
快速素数筛法是 埃氏筛 的一种优化筛法,也叫做欧拉筛,或者线性筛。
埃氏筛 的时间复杂度是比线性的 $O(\log {n})$ 大的,是因为 重复标记了一些合数 。
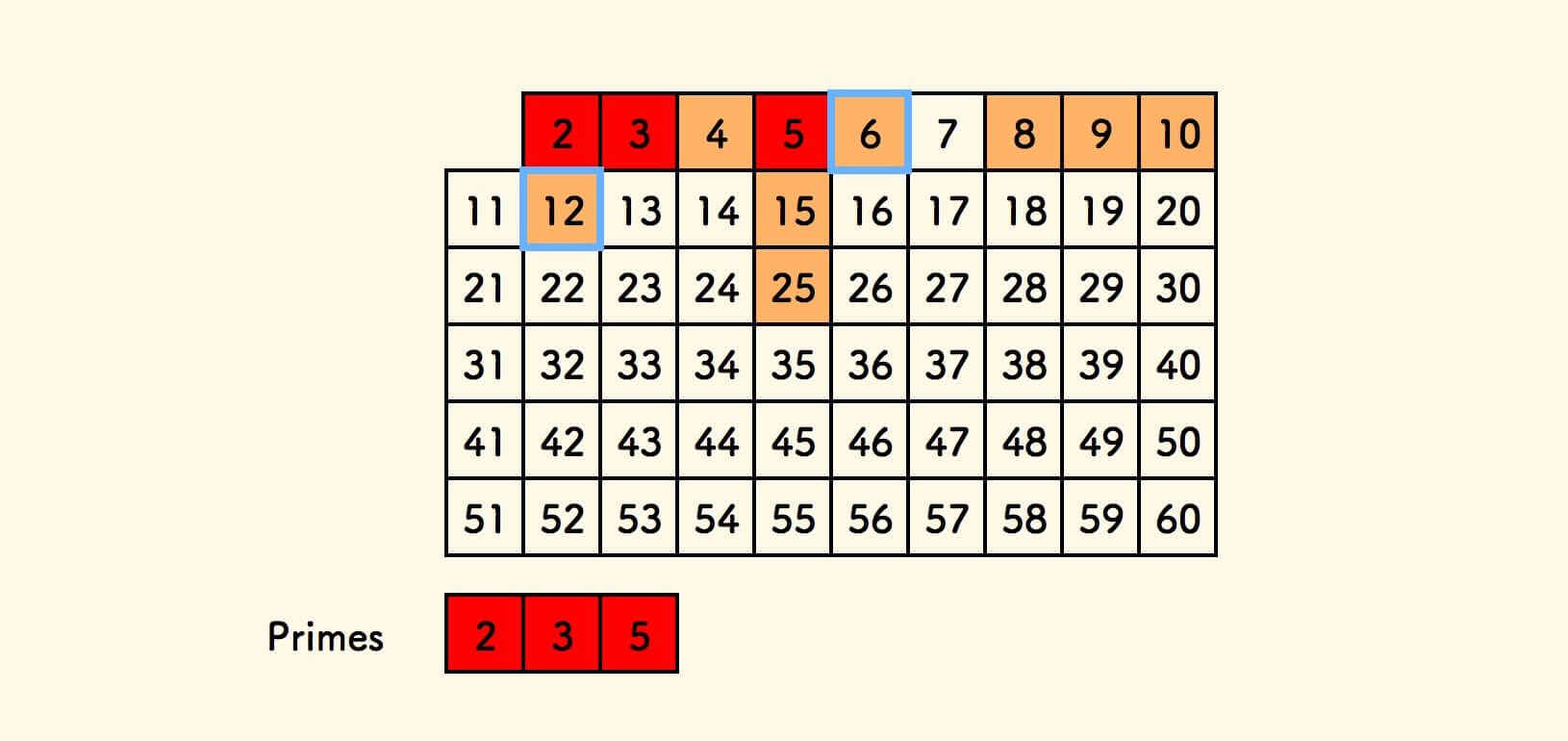
例如,在使用筛子 $3$ 进行合数标记的时候,数字 $12$ 会被重复标记,因为它已经被 $2$ 标记过一次:
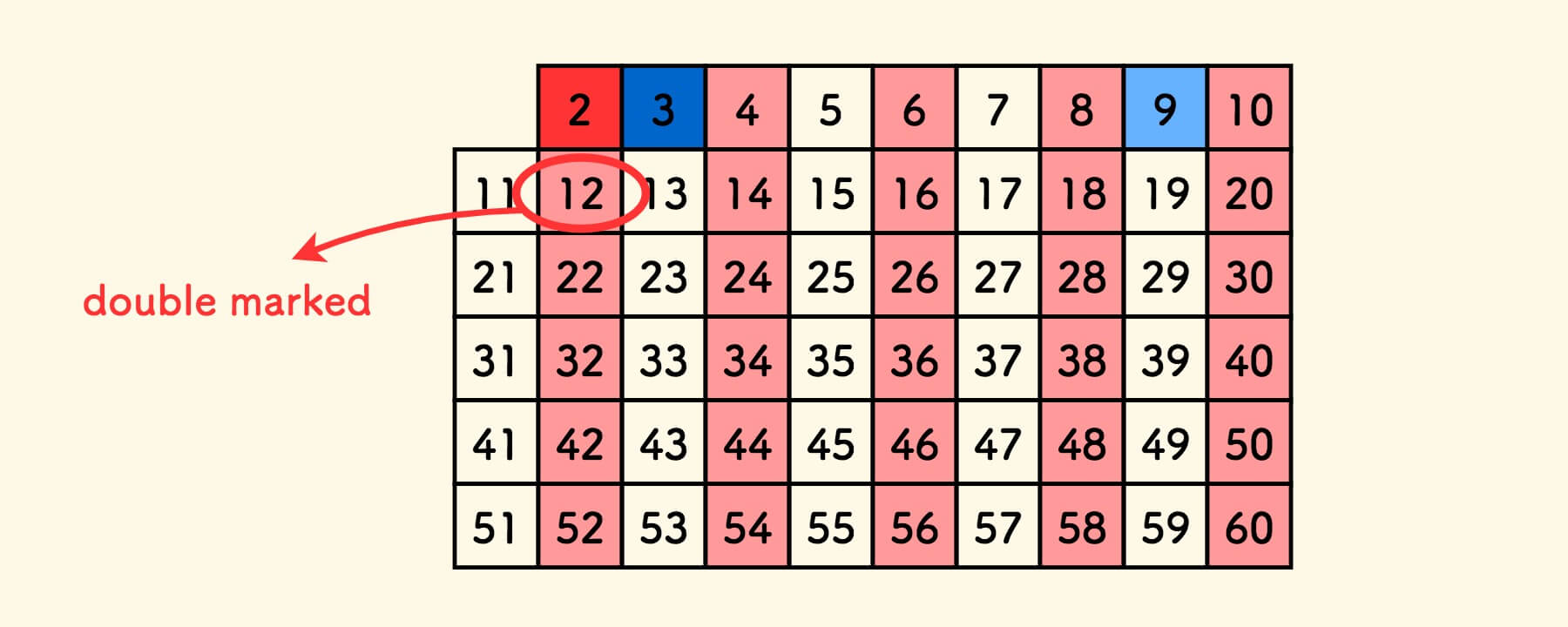
如果避免掉重复标记,时间复杂度就有希望降低到 $O(n)$ 。
算法步骤
快速筛的思路是,让每个合数只被它最小的素因数筛掉 。
快速筛的实施步骤,稍不同于埃氏筛:
和埃氏筛一样,准备相同的一张表格,从中筛去合数。
初始化,仍然所有方格标记为真,即认为表格中所有数字都是素数。
不同点是,同时准备一个数组,记录已经找到的素数。
遍历表格中的数字,对于 $2$ ,当前表格中的标记是真,说明是一个素数 。
把 $2$ 加入素数数组,筛去 $2 \times 2 = 4$ 。

对于 $3$ ,当前表格中的标记是真,说明是一个素数 。
把 $3$ 加入素数数组,筛去 $2 \times 3 = 6$ 、 $3 \times 3 = 9$ 。
上面的过程,是对当前遍历的数字 $k = 3$ ,乘上已知的每一个素数 $p$,对 $pk$ 进行筛除。
这个筛除过程,可以叫做 素数 $p$ 筛除了 $pk$ 。

对于 $4$ ,当前表格中的标记是假,说明是一个合数。
筛去 $2 \times 4 = 8$ ,即 素数 $2$ 筛除了 $8$ 。
但是由于 $4$ 是 $2$ 的倍数 ,此时终止筛除,不再筛除 $3 \times 4 = 12$ ,是因为, 我们希望 $12$ 被它最小的素因数 $2$ 筛除,而不是被素数 $3$ 筛除。

对于 $5$ ,加入素数数组,筛去 $2 \times 5$ 、$3 \times 5$ 、$5 \times 5$ 。

对于 $6$ ,筛去 $2 \times 6$ 。
此时, $12$ 被素数 $2$ 筛除。

对于 $7$ ,加入素数数组,筛去 $2 \times 7$ 、$3 \times 7$ 、$5 \times 7$ 、$7 \times 7$ 。

重复如上,直到遍历完表格中的数字,即得到小于 $n$ 的所有素数。

其中的疑问点可能在于:
为何当前数字 $k$ 是当前素数 $p$ 的倍数的时候,要停止筛除?
如果当前的数字 $k$ 是当前素数 $p$ 的倍数,那么 $k$ 可以表示为 $k = mp$ 。
对于比 $p$ 更大的素数比如 $q$ 而言,采用素数 $q$ 继续进行筛除合数 $qk = qmp$ 违背了算法的设计初衷,因为 $qmp$ 应该由更小的素数 $p$ 来筛除。
另外, 合数 $qmp$ 将在后面,当 $k = qm$ 的时候,最终被素数 $p$ 筛除 。
快速筛和埃氏筛虽然都是筛去合数、留下素数的过程,但是具体的方法确是不同的。
对于快速筛的方法步骤总结如下:
- 建立表格 $table$ ,所有方格初始化为真,即最开始认为所有数字是素数,考虑筛除合数。
- 建立素数数组 $primes$ ,保存已知的素数。
- 对于从 $2$ 到 $n-1$ 的每一个数字 $k$:
- 如果 $table[k]$ 是真,即 $k$ 是一个素数,将 $k$ 加入到素数数组。
- 对于已知的每一个素数 $p$:
- 筛除合数 $pk$ ,即标记 $table[pk]$ 为假。
- 如果 $k$ 是 $p$ 的倍数,则终止此轮筛除。
- 此外,当 $pk >= n$ 时,显然可以直接终止此轮筛除。
- 数组 $primes$ 中的数字即小于 $n$ 的全部素数。
算法实现
快速素数筛法 - C 语言实现
// 快速素数筛法 - 欧拉筛法
// 输入上限整数 n 、大小为 n 的筛表 table 和 接收返回结果的素数表 primes.
void EulerSieve(int n, bool table[], int primes[]) {
if (n <= 0) return;
for (int i = 0; i < n; i++) table[i] = true;
if (n >= 1) table[0] = false;
if (n >= 2) table[1] = false;
int j = 0; // 记录已知素数的多少
for (int i = 0; i < n; i++) primes[i] = 0;
for (int k = 2; k < n; k++) {
if (table[k]) primes[j++] = k;
for (int i = 0; i < j; i++) {
int p = primes[i];
if (p * k < n)
table[p * k] = false;
else
break;
if (k % p == 0) break;
}
}
return;
}
算法复杂度
虽然,快速筛法有两层循环, 算法的内层循环,存在多次迭代的情况, 但也存在立即退出的情况。 每个合数只被筛除了一次 , 时间复杂度是 $O(n)$ 。
相关阅读: 如何算法实现加减乘除四则运算
(完)