有序二维矩阵搜索问题

问题 ¶

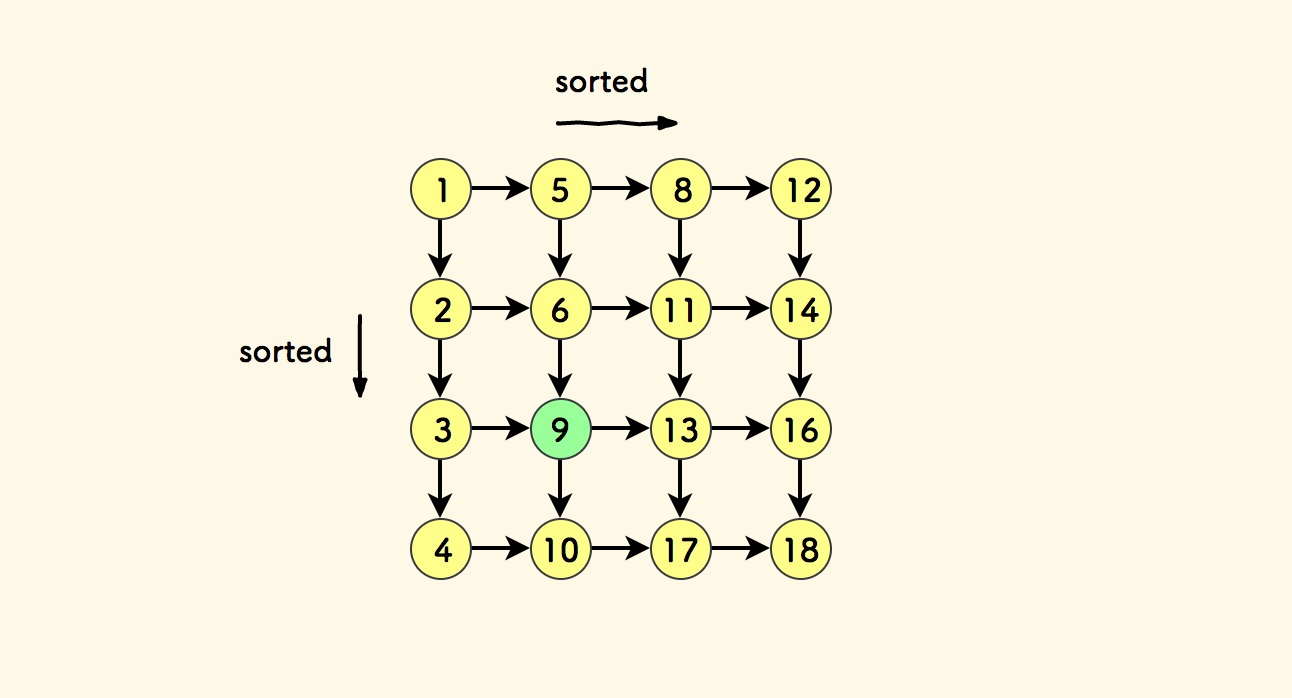
在一个大小为 rows x cols 的二维矩阵中查找目标值 target ， 已知此矩阵的每一行、每一列的数字都是有序的。

leetcode 题目 - 搜索二维矩阵

算法思路 ¶

问题中所说的矩阵在数学上被称为 杨氏矩阵 。

从右上角的视角看矩阵，考虑右上角的顶点 vertex 。

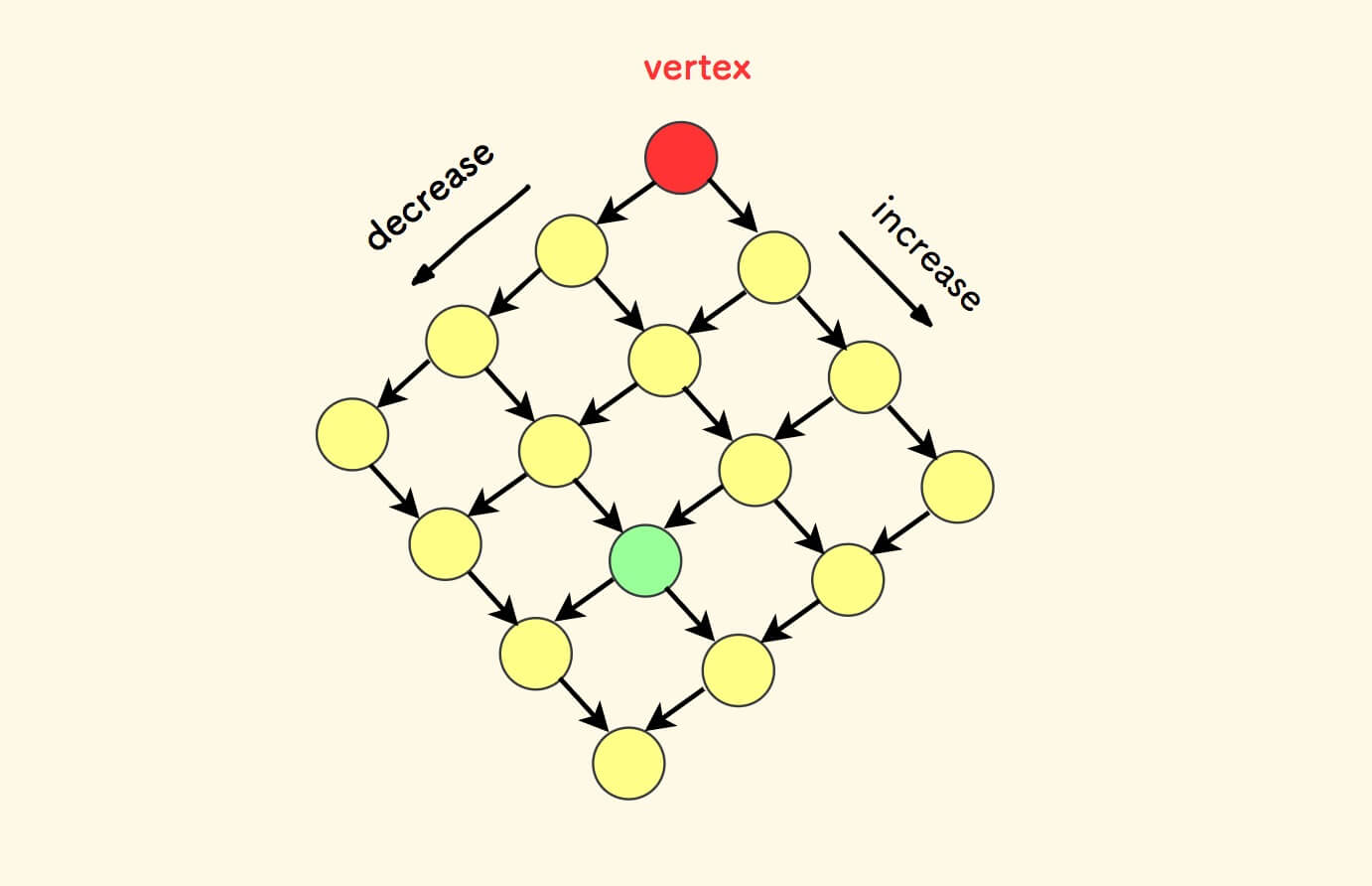
右上角顶点有如下性质：

• 是第一行的最大值
• 是最后一列的最小值

假设要找的数字是 target：

• 如果 target < vertex ，即 target 比最后一列的最小值还要小 ， 即可排除最后一列。

  

• 如果 target > vertex ，即 target 比第一行的最大值还要大 ， 即可排除第一行。

  

排除完成后，继续取剩余矩阵的右上角顶点，不断应用此过程：

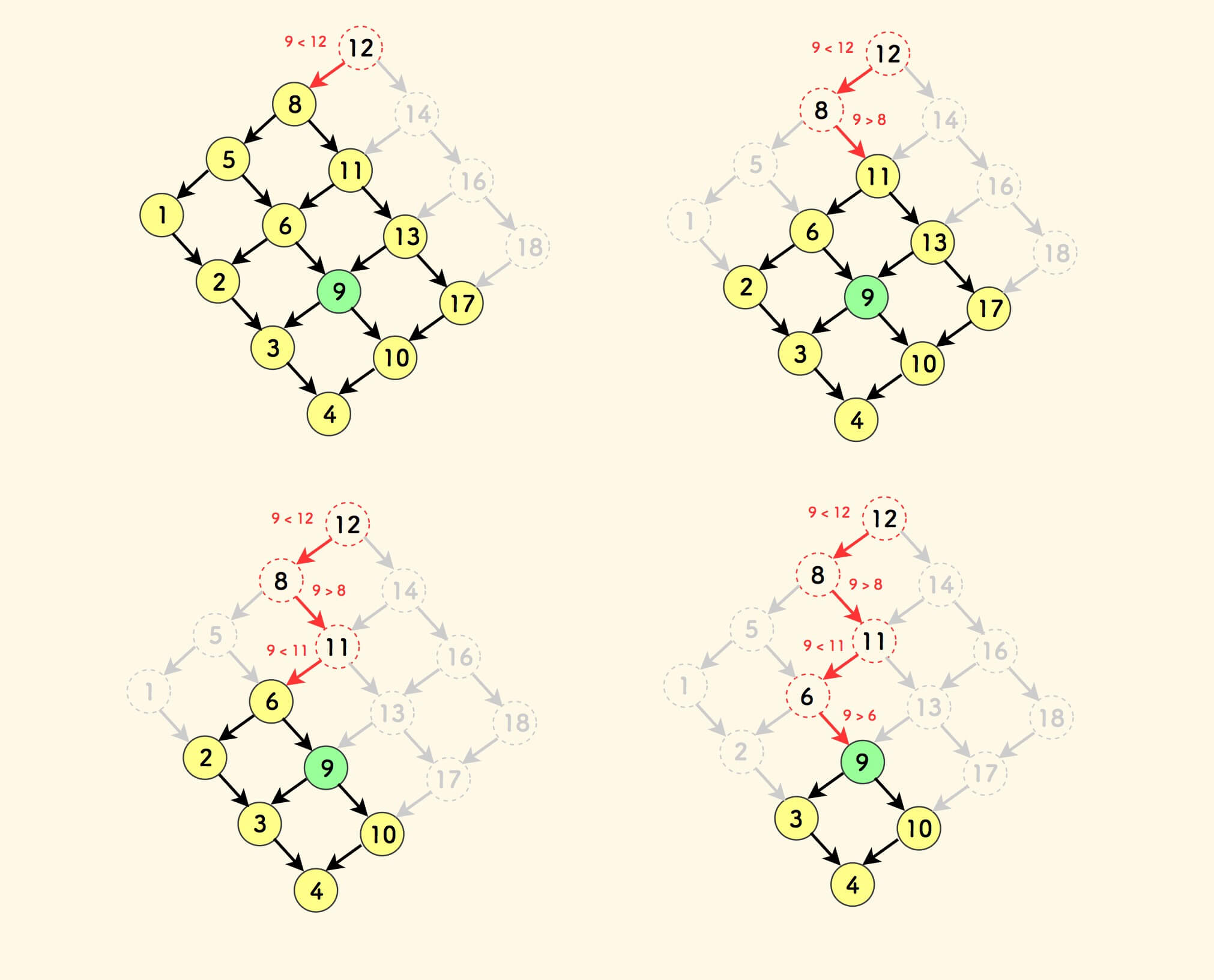
算法过程：

1. 设当前矩阵的顶点为 vertex = matrix[row][col] ，初始条件下：col = cols - 1 ，row = 0 。

2. 将目标值 target 和顶点的值 vertex 进行比较：

   1. 如果 target < vertex ，则排除顶点的列，即 col-- 。
   2. 如果 target > vertex ，则排除顶点的行，即 row++ 。
   3. 否则，命中结果。

3. 不断重复前两步，直到无法继续查找为止。

   当 row 达到 rows ，或者 col 递减为 0 的时候，结束比较，未找到。

C 语言实现 ¶

bool SearchSortedMatrix(int rows, int cols, int matrix[rows][cols],
                        int target) {
    if (rows <= 0 || cols <= 0) return false;

    int row = 0;
    int col = cols - 1;

    while (row < rows && col >= 0) {
        int vertex = matrix[row][col];

        if (target < vertex) {
            col--;
        } else if (target > vertex) {
            row++;
        } else {
            return true;
        }
    }
    return false;
}

复杂度分析 ¶

最差情况，找到目标值需要排除 rows 个行， cols 个列，因此时间复杂度是 O(rows + cols) 。

相似问题 ¶

leetcode 上有一个类似的问题 - 1351. 统计有序矩阵中的负数：

给你一个 m * n 的矩阵 grid，矩阵中的元素无论是按行还是按列，都以非递增顺序排列。 请你统计并返回 grid 中 负数 的数目。

采用类似的思路，可以从右上角顶点出发，此时右上角始终有这样的性质: 当前行最小值、当前列最大值。

class Solution {
   public:
    int countNegatives(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        int i = 0;
        int j = n - 1;
        int count = 0;
        // 右上角性质: 当前行最小值、当前列最大值
        while (i < m && j >= 0) {
            if (grid[i][j] < 0) {
                // 当前列此行以下的部分肯定全部 < 0
                count += m - i;
                // 排除当前列
                j--;
            } else {
                // 当前行左边的部分肯定都 >= 0
                // 排除当前行
                i++;
            }
        }
        return count;
    }
};

结语 ¶

不过，需要指出，本方法虽然简洁优美，但是，在矩阵比较大的情况下，它不是时间复杂度最优的方法。 参考 再探有序二维矩阵搜索问题之分治解法。

（完）

本文原始链接地址： https://writings.sh/post/algorithm-search-sorted-2d-matrix