算术表达式求值（双栈法）

如何求解一个算术表达式的值？比如字符串 3+1+(2x(2+1-2x1+1)) 的值应该为 8。

本文介绍用于表达式求值的 dijkstra 双栈算法。

这个算法不仅仅适用于算术运算，也适用于有优先级关系的任何表达式形式，比如逻辑运算、正则表达式等。

初步思路 ¶

关键点在于优先级的处理。

比如说，考虑一个简单的表达式 5+3x2，我们要先计算后面的乘法。

但对于另一个表达式例子 2+5+3x2 来说，我们可以先计算前面的加法。

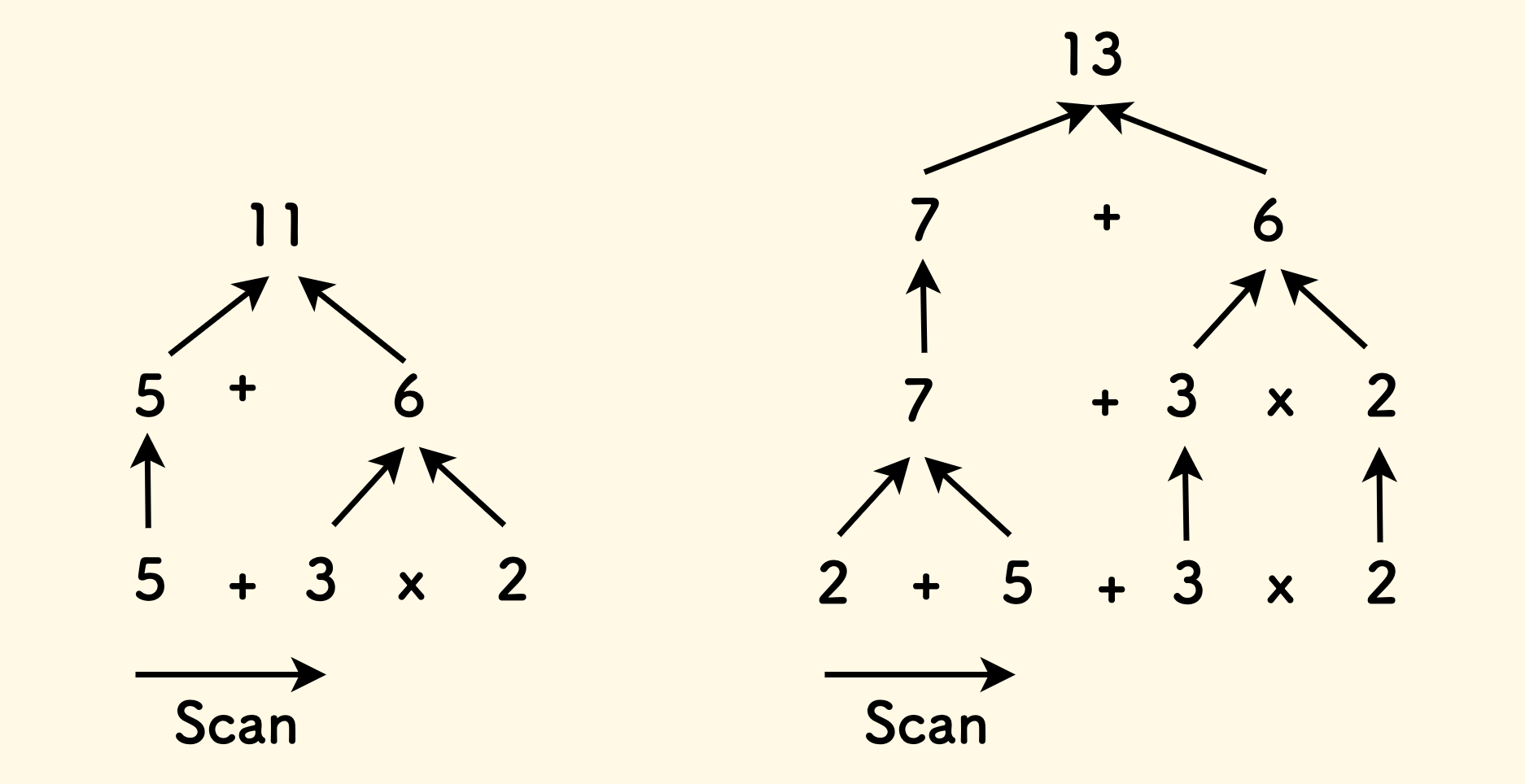
这说明两个问题：

遇到运算符时不要直接计算，而是要稍等一下后面的运算符优先级是不是更高。
这种优先级的作用距离很短，仅影响相邻运算符。

另一种优先级是括号，比如说 (5+3)x2 ，我们要先计算括号内的部分，而可以无视后面乘法运算符优先级关系。

稍复杂点，比如 (3x(3+2))+1，我们应先计算内层括号，再考虑外层的括号，因为内层的括号先闭合。也就是说，遇到闭合的右括号，括号内部分可以计算完毕，并舍弃这对括号。

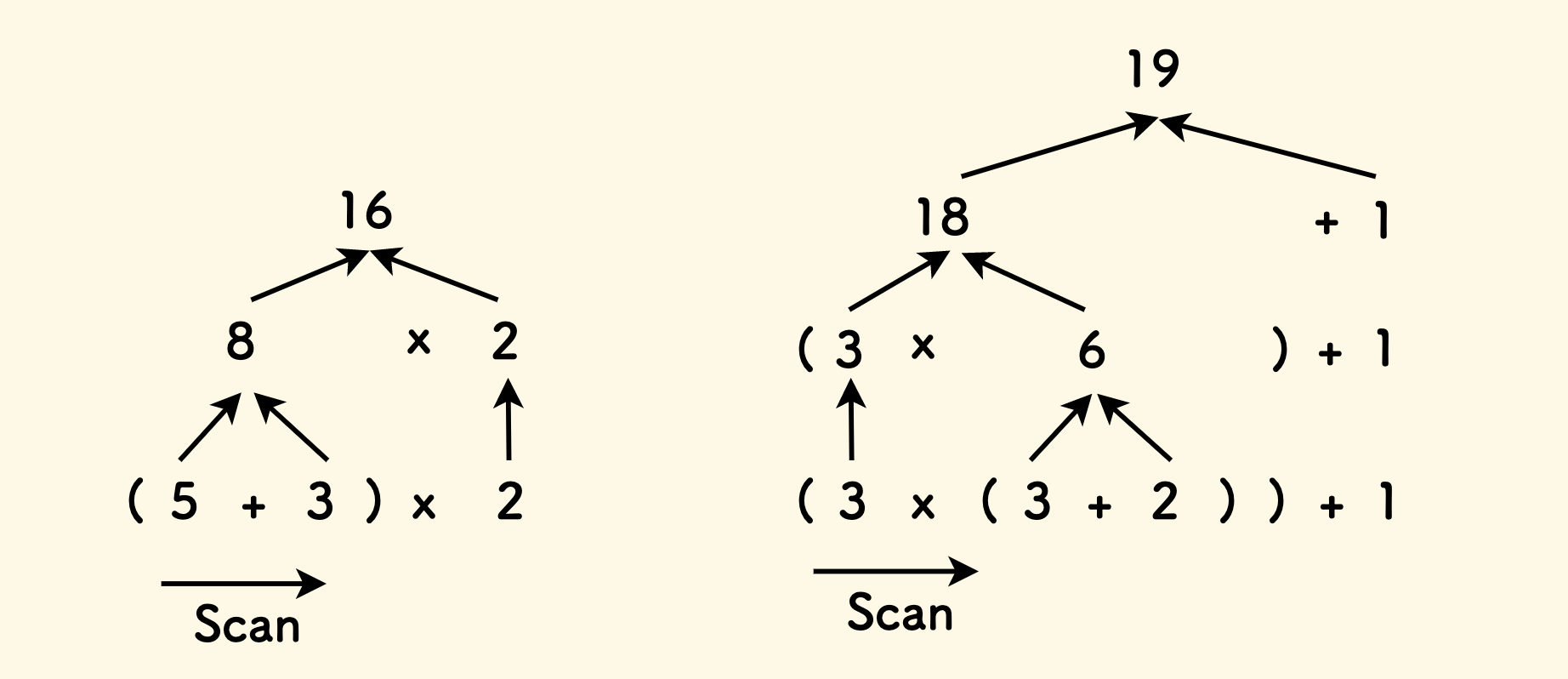
总而言之，计算的时机在于：

当前运算符优先级比接下来的运算符高（不低）时。
遇到括号，在括号闭合时才计算。

因为要处理这两种「等待」，所以需要用到栈。

算法思路 ¶

事实上，前面的两张示意图，已经暗示了，算术表达式求值可以表达为一个自底向上的过程。

实际上也是一种 shift-reduce 移入归约过程：所谓「shift 移入」是指输入符号入栈，「reduce 归约」是指符号出栈计算、结果再入栈。

算法过程:

移入：遇到输入符号，则入栈。
归约：遇到运算符，考察栈顶运算符：
- 如果其优先级比当前运算符不低，则出栈计算，计算结果入栈。
- 否则，先入栈，等待后面有机会再计算。
归约：遇到右括号，栈内元素出栈，直至左括号出栈，计算后结果入栈。

回到文首提出的表达式 3+1+(2x(2+1-2x1+1)) ，其 shift-reduce 过程如下图所示。其中栈在横向上，遇到符号则入栈扩展，达到归约条件则向上归约。

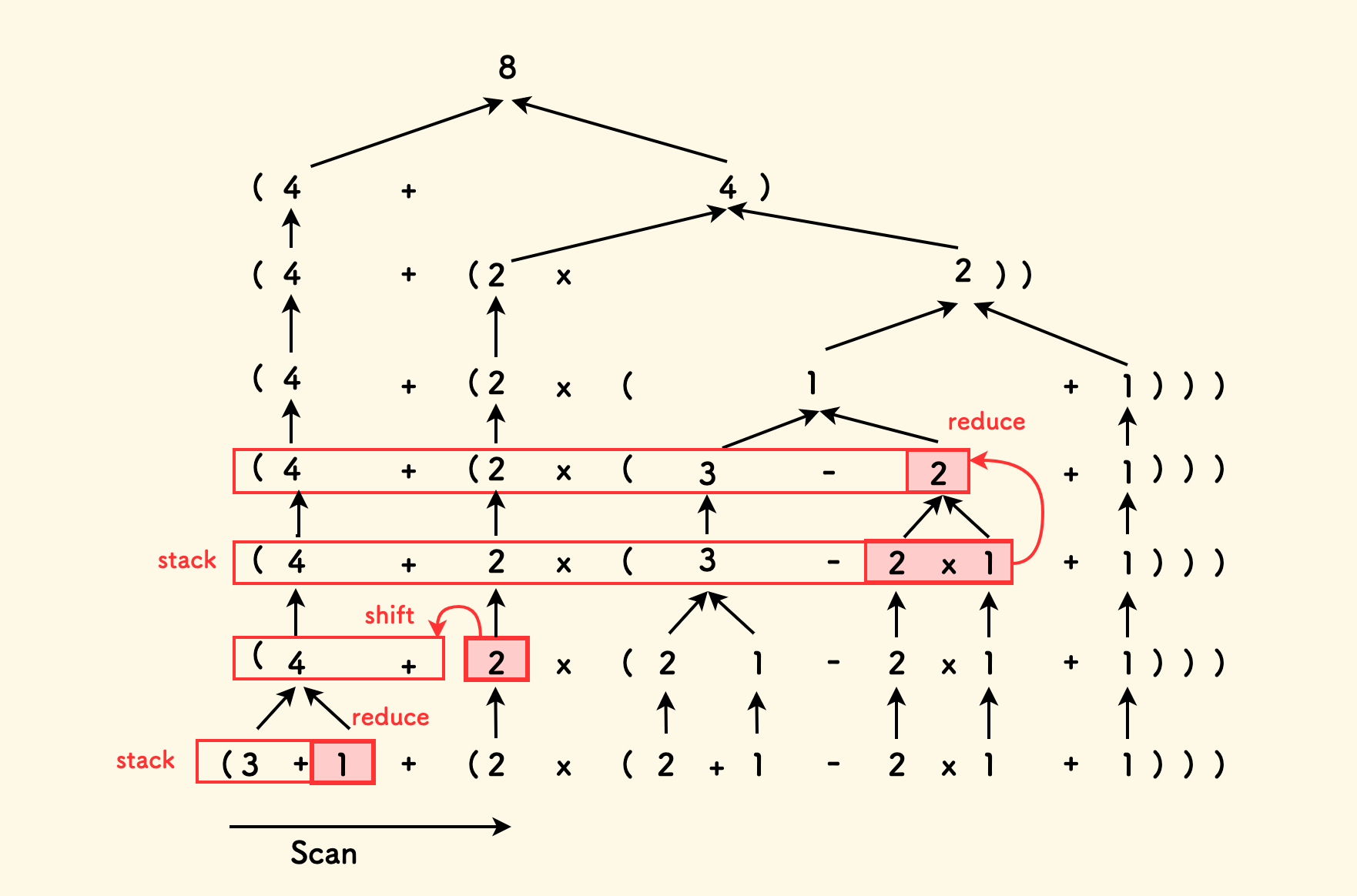
但是，因为我们要考察「栈顶」的运算符，如果栈顶可能是数字、也可能是运算符，就不大好弄。所以要采用两个栈，一个用来存放数字，另一个来存放运算符。

最终，dijkstra 双栈算法的详细过程：

定义两个栈：一个用来存放数字、另一个存放运算符

定义进行计算的子过程：

弹出栈顶运算符，弹出相应数量的数字，计算后结果入数字栈。

比如对于减法来说：

void calc(op_stack, num_stack) {
  op = op_stack.pop();

  switch(op) {
    case '-':
      b = num_stack.pop();
      a = num_stack.pop();
      num_stack.push(a - b);
      break;
     // 其他运算符...
  }
}

自左向右地，每扫描到一个字符 ch：
1. 如果遇到数字，直接入数字栈
2. 如果遇到四则运算符：
  1. 如果运算符栈顶优先级更高，则先计算、再入栈。
    先计算栈顶，直到栈顶优先级比当前运算符低为止；再把当前运算符入栈。
  2. 否则先入栈、后面等机会再计算。
  用代码来示意就是:
```
 while (precedence(op_stack.top()) >= precedence(ch))
   calc(op_stack, num_stack);
 op_stack.push(ch);
```
3. 如果遇到左括号，直接入运算符栈，以等待右括号闭合。
4. 如果遇到右括号，则不断出栈进行计算，直到左括号出栈。
  用代码来示意就是:
```
while (op_stack.top() != ')')
  calc(op_stack, num_stack);
op_stack.pop();  // 丢弃左括号
```
最后数字栈中应该仅剩余一个元素，即计算结果。

沿着这个算法过程，前面所说的表达式 3+1+(2x(2+1-2x1+1)) 的计算步骤如下图所示。其中shift 就是入栈；每一个归约点，就是一次计算：

实际中，还要考虑到多位数字、忽略空白字符的情况。

此外，一个细节点是，计算的时机中并没有考虑输入终止时的情况。输入结束时，栈中可能残留待计算的运算符和数字。

解决办法可以有两种：

预处理表达式字符串，比如将 1x(3+2) 整体带上括号，转化为 (1x(3+2))，这样就可以在最终的右括号闭合时调用计算。
另一种方法，则无需拷贝内存：输入结束后，如果运算符栈非空，则继续计算完它即可。
用代码来示意就是：
```
// 字符串读取迭代结束后
while (op_stack.size() > 0)
  calc(op_stack, num_stack);
```

代码实现 ¶

代码实现放在了 Github 上：

出于最近学习 C++ 的兴趣，我还做了一份 C++ 编译期算术表达式计算的实现：

C++ 语言版本编译时算术表达式计算 - arithmetic-expression-cpp-compiletime - github

最后，值得再说明一次的是，这个算法不仅仅适用于算术表达式的求值，也适合诸如正则表达式、逻辑表达式等带有优先级关系的表达式形式。

它本质上是一种自底向上的移入归约解析过程。

（完）

相关阅读: 实现一个简单的正则表达式引擎

本文原始链接地址： https://writings.sh/post/arithmetic-expression