本文是 双向 BFS 的简单笔记。
双向 BFS 是指,在起点和终点(目标)都确定的情况下,两端交替地、对向进行广度优先搜索、直至相遇的搜索策略。
感性的理解 ¶
相比单向的 BFS,双向 BFS 为什么会更快呢?
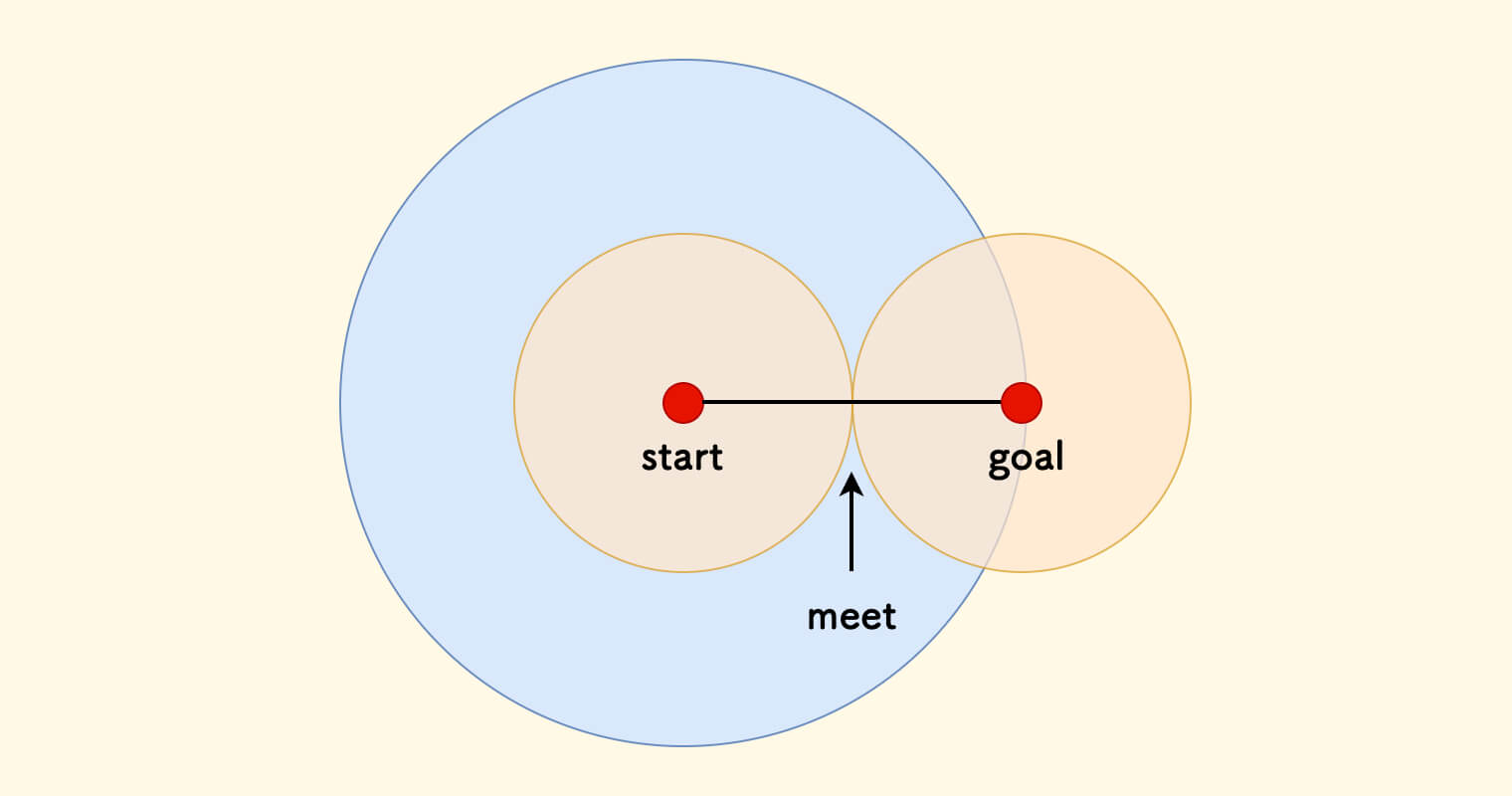
比如说,搜索从起始状态 start 演进到目标状态 goal 的最少步数, 如下图所示。
一种感性的理解是:
- 单向 BFS 扫描过的所有状态可以表达为大圆的面积。
- 双向 BFS 扫描过的所有状态可以表达为两个小圆的面积之和。
两个小圆的面积会比一个大圆的面积要小,也就是说,双向 BFS 扫描的状态数会更少。
这种理解很巧妙,只是一种「感性」的理解,并非严格。
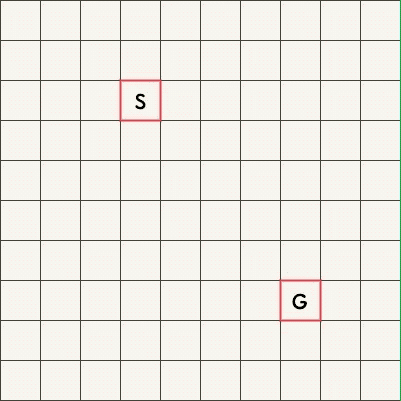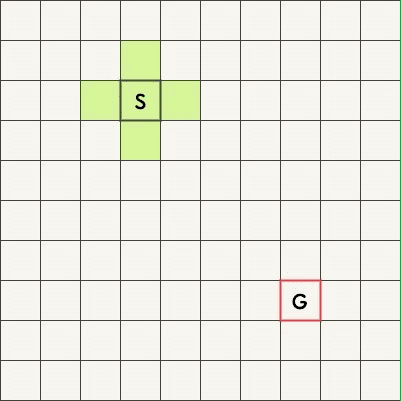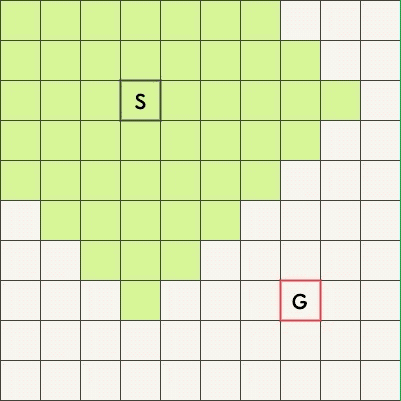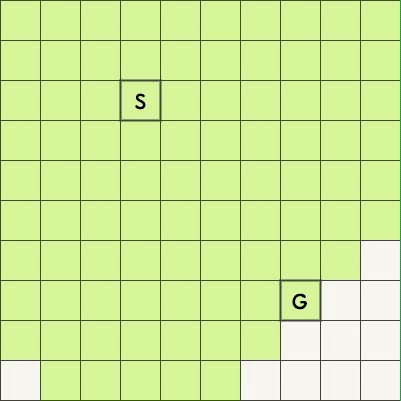
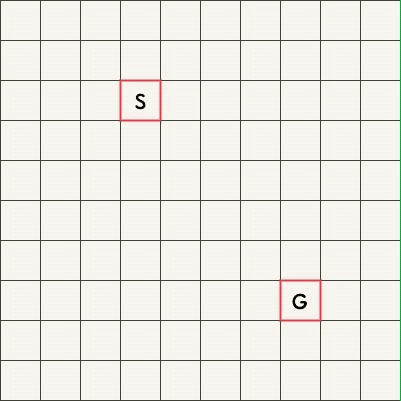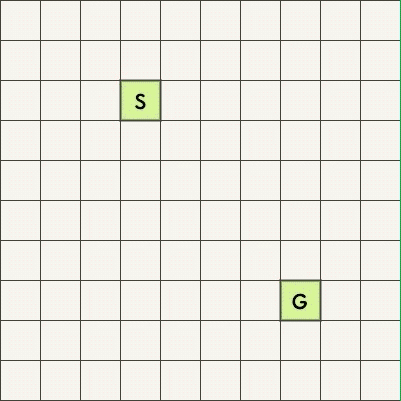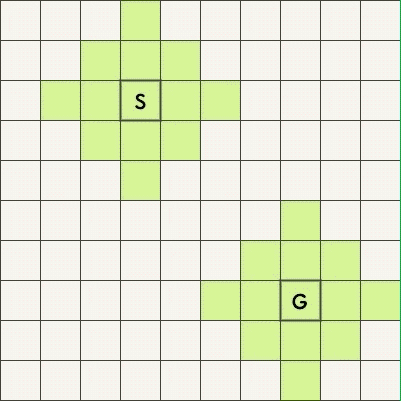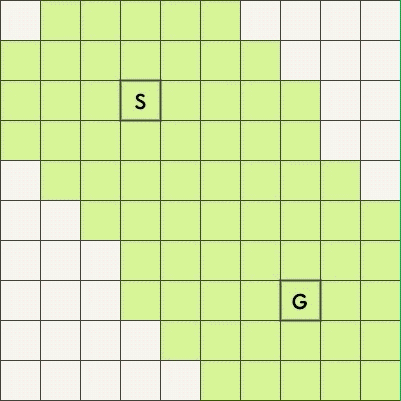
BFS 适合最短路问题,下面两张图是搜索从起始点 S 到终点 G 的最短路的过程,上图是单向 BFS、下图是双向 BFS。
可以看到,双向 BFS 扫描过的方格明显更少。
代码形式 ¶
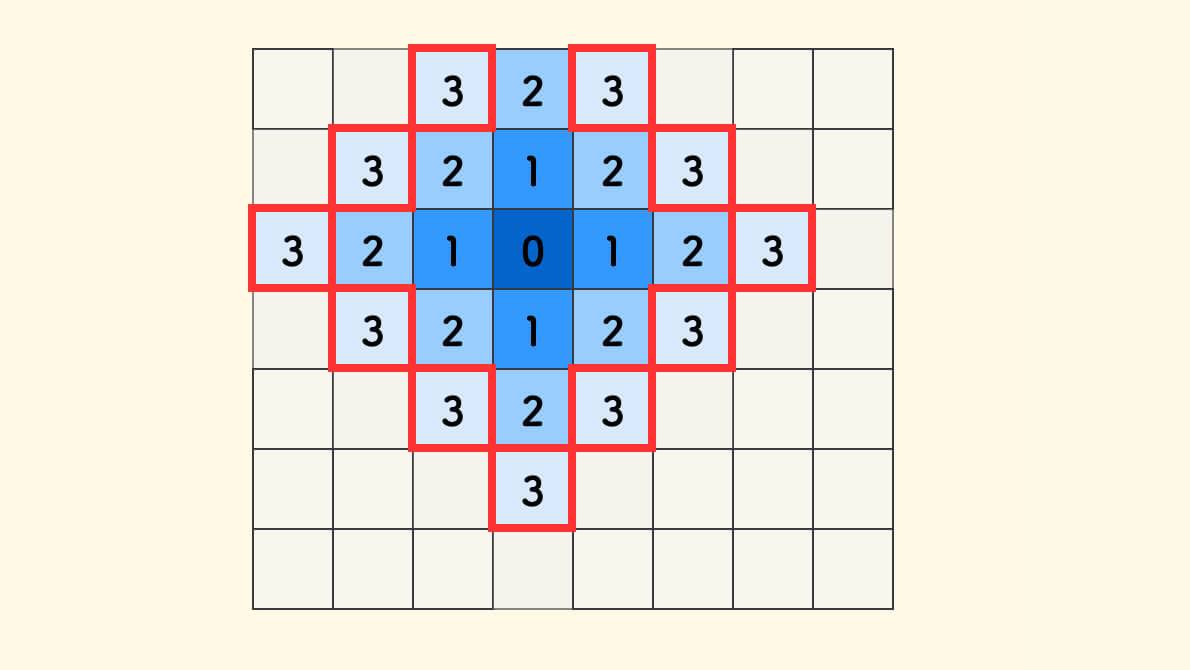
BFS 是一种逐层搜索的方式,一般借助队列来实现,边消费、边生产。 消费完当前层后,把下一层加入到队列中。
下面的例图中,从内向外逐层搜索,队列中存放的,可以理解为最外层的方格。
双向 BFS 的伪代码形式如下,每次选择更小的队列进行扩展:
queue<int> q1, q2;
q1.push(start), q2.push(goal);
int steps = 0; // 答案, 最少步数
while (!q1.empty() && !q2.empty()) {
// 每次选择更小的队列进行扩展
if (q1.size() > q2.size()) swap(q1, q2);
steps++;
if (extend(q1)) return steps;
}
bool extend(queue<int>& q) {
int n = q.size();
while (n--) {
auto x = q.front();
q.pop();
// TODO: 判断是否和对面相遇,相遇则返回 true
// TODO: 向外扩展一层, 加入队列
}
return false;
}
一个例题 ¶
给定一个元素互不相同的整数数组
nums和 两个整数start和goal。要经过一系列运算,把
start转换到goal,可执行的运算是,选择数组中任一元素,做下面三种运算之一:
x + nums[i]x - nums[i]x ^ nums[i](按位异或)注意,使
x越过0 <= x <= 1000范围的运算同样可以生效,但该该运算执行后将不能执行其他运算。返回将
start转化为goal的最小操作数;如果无法完成转化,则返回-1。
注意到,三种运算的逆运算也在其中,也就是说,使用这三种运算也可以反过来把 goal 运算到 start 。
那么,可以选择用双向 BFS,相遇时结束搜索。
相遇的条件可以用 hash set 来判断。
另外,注意判重,已经处理过的数字就无需再入队了。
leetcode 2059. 转化数字的最小运算数 - C++ 实现
(完)
