本文简记二叉树的遍历,笔记目的。
深度优先 dfs ¶
深度优先遍历二叉树,可分为:前序(先序)、中序 和 后序 三种情况。
前中后序遍历 ¶
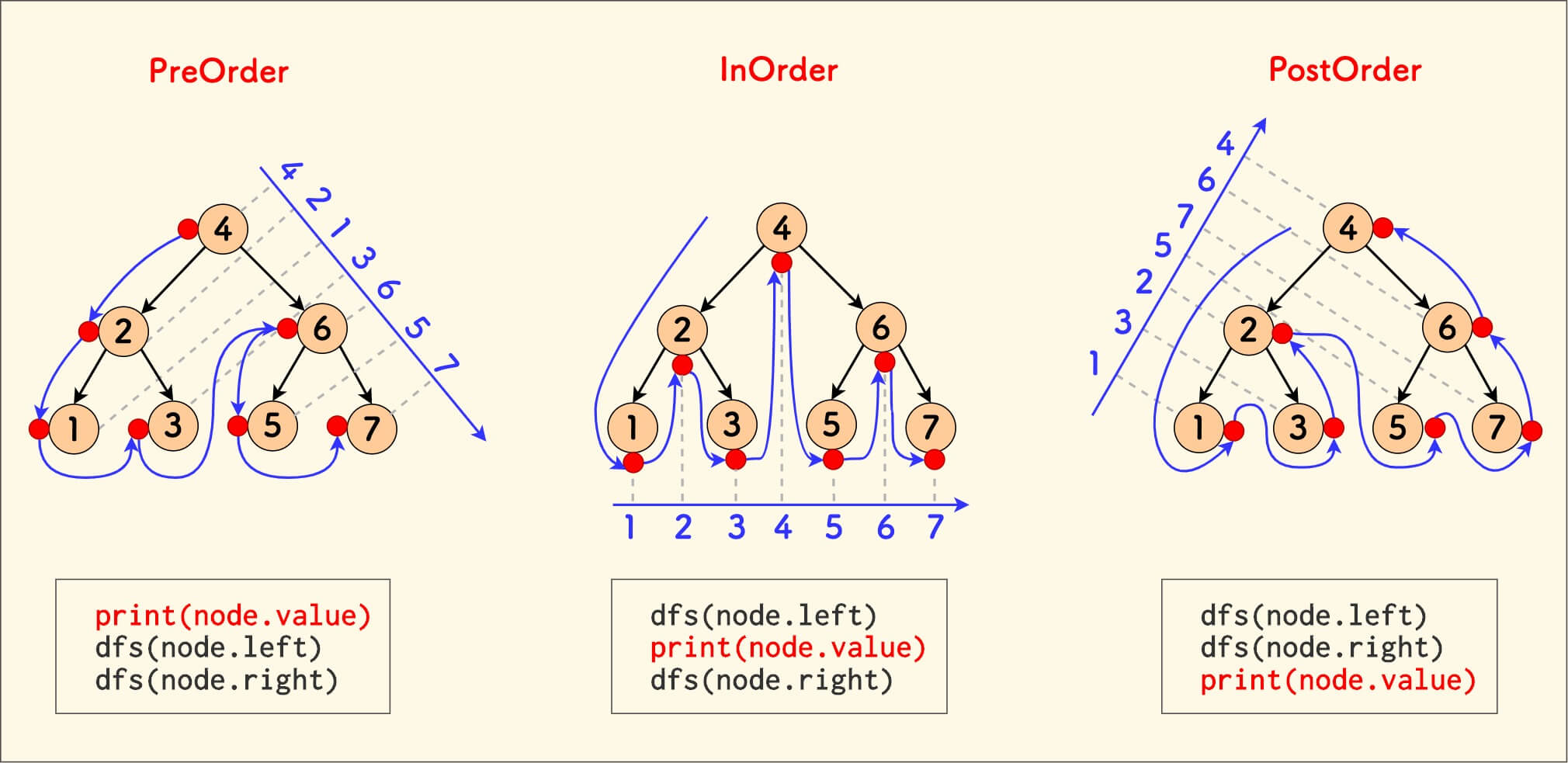
前中后序的遍历效果,一图以蔽之,见下方,快捷的记忆方式可以有两种:
- 节点边上小红点的位置,各自代表一种遍历序。
遍历序就是节点映射到蓝色数轴上的顺序,只是数轴的方向和摆放位置不同。
特殊地,二叉搜索树的中序遍历是有序的(下图中的就是二叉搜索树)。
递归写法:
二叉树前中后序的递归写法 - C++
// 先序遍历/前序遍历 (递归)
void PreOrder(Node* root, vector<int>& ans) {
if (root == nullptr) return;
ans.push_back(root->val);
PreOrder(root->left, ans);
PreOrder(root->right, ans);
}
// 中序遍历 (递归)
void InOrder(Node* root, vector<int>& ans) {
if (root == nullptr) return;
InOrder(root->left, ans);
ans.push_back(root->val);
InOrder(root->right, ans);
}
// 后序遍历 (递归)
void PostOrder(Node* root, vector<int>& ans) {
if (root == nullptr) return;
PostOrder(root->left, ans);
PostOrder(root->right, ans);
ans.push_back(root->val);
}非递归写法 ¶
建立一个栈来模拟递归,存储两个信息:
node- 等待处理的节点visited- 此节点是否访问过
每个节点会入栈两次:先访问,再处理。
下方是对前序遍历的一部分过程的栈模拟示意图,其中黄色表示第一次访问、绿色表示第二次访问(即 visited 是 true 的情况):
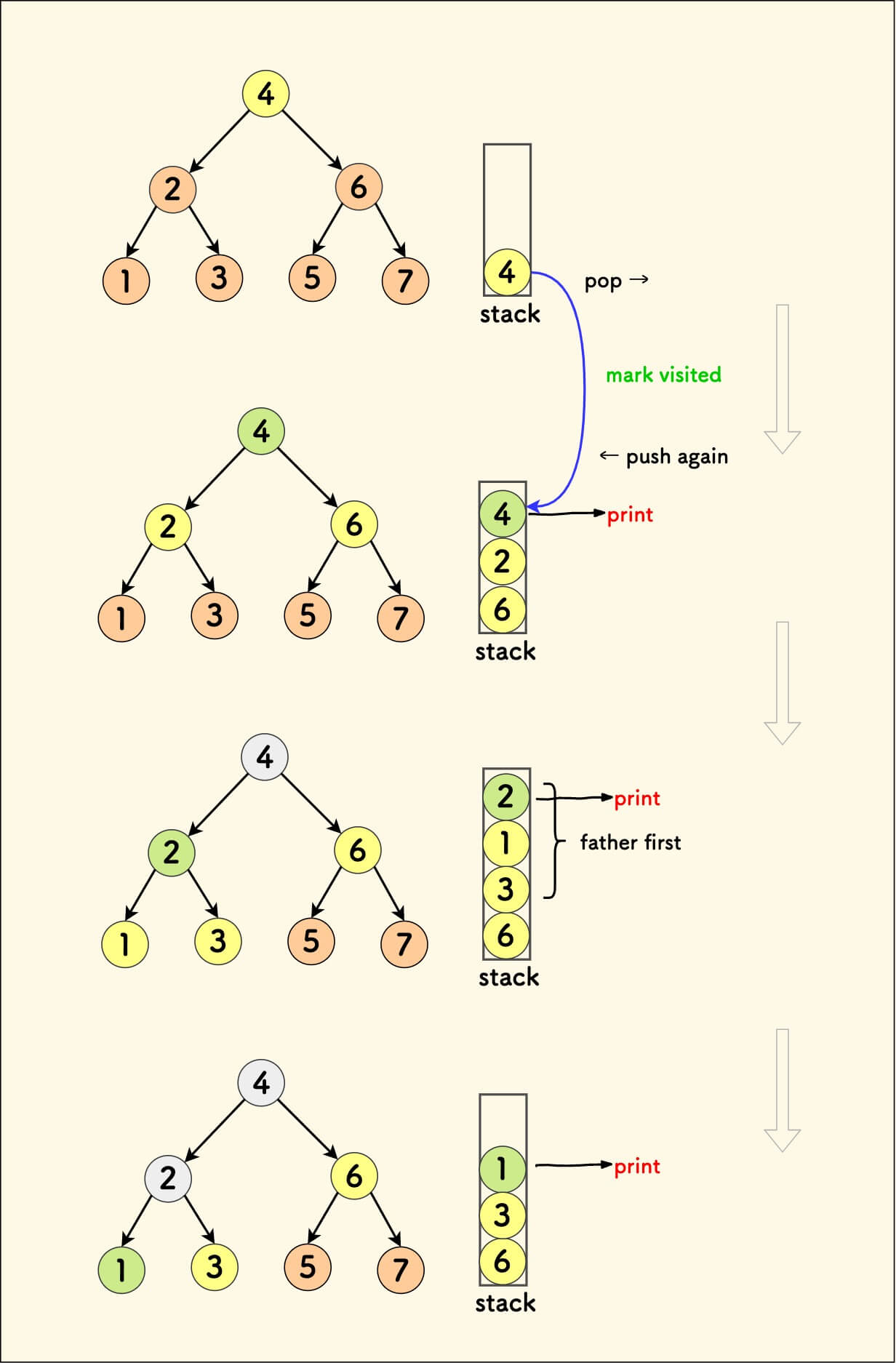
统一的非递归写法来描述前中后三种遍历序,不同点仅在于父子节点入栈的顺序:
二叉树前中后序的非递归写法 - C++
// 先序遍历/前序遍历 (非递归)
vector<int> PreOrder(Node* root) {
if (root == nullptr) return {};
vector<int> ans;
stack<pair<Node*, bool>> s;
s.push({root, false});
while (!s.empty()) {
auto [node, visited] = s.top();
s.pop();
if (node == nullptr) continue;
if (!visited) {
// 最后再访问孩子
s.push({node->right, false});
s.push({node->left, false});
// 先处理父节点
s.push({node, true});
} else {
// 第二次访问时执行处理
ans.push_back(node->val);
}
}
return ans;
}
// 中序遍历 (非递归)
vector<int> InOrder(Node* root) {
if (root == nullptr) return {};
vector<int> ans;
stack<pair<Node*, bool>> s;
s.push({root, false});
while (!s.empty()) {
auto [node, visited] = s.top();
s.pop();
if (node == nullptr) continue;
if (!visited) {
// 最后访问右孩子
s.push({node->right, false});
// 再处理父节点
s.push({node, true});
// 先访问左孩子
s.push({node->left, false});
} else {
// 第二次访问时执行处理
ans.push_back(node->val);
}
}
return ans;
}
// 后序遍历 (非递归)
vector<int> PostOrder(Node* root) {
if (root == nullptr) return {};
vector<int> ans;
stack<pair<Node*, bool>> s;
s.push({root, false});
while (!s.empty()) {
auto [node, visited] = s.top();
s.pop();
if (node == nullptr) continue;
if (!visited) {
// 最后处理父节点
s.push({node, true});
// 再访问右孩子
s.push({node->right, false});
// 先访问左孩子
s.push({node->left, false});
} else {
// 第二次访问时执行处理
ans.push_back(node->val);
}
}
return ans;
}广度优先 bfs ¶
和图一样,广度优先要借助一个队列来实现,是一种自顶向下逐层遍历的过程。
处理完当前节点后,弹出它,并把其孩子节点顺序加入队尾。
是一种 边消费、边生产 的过程。
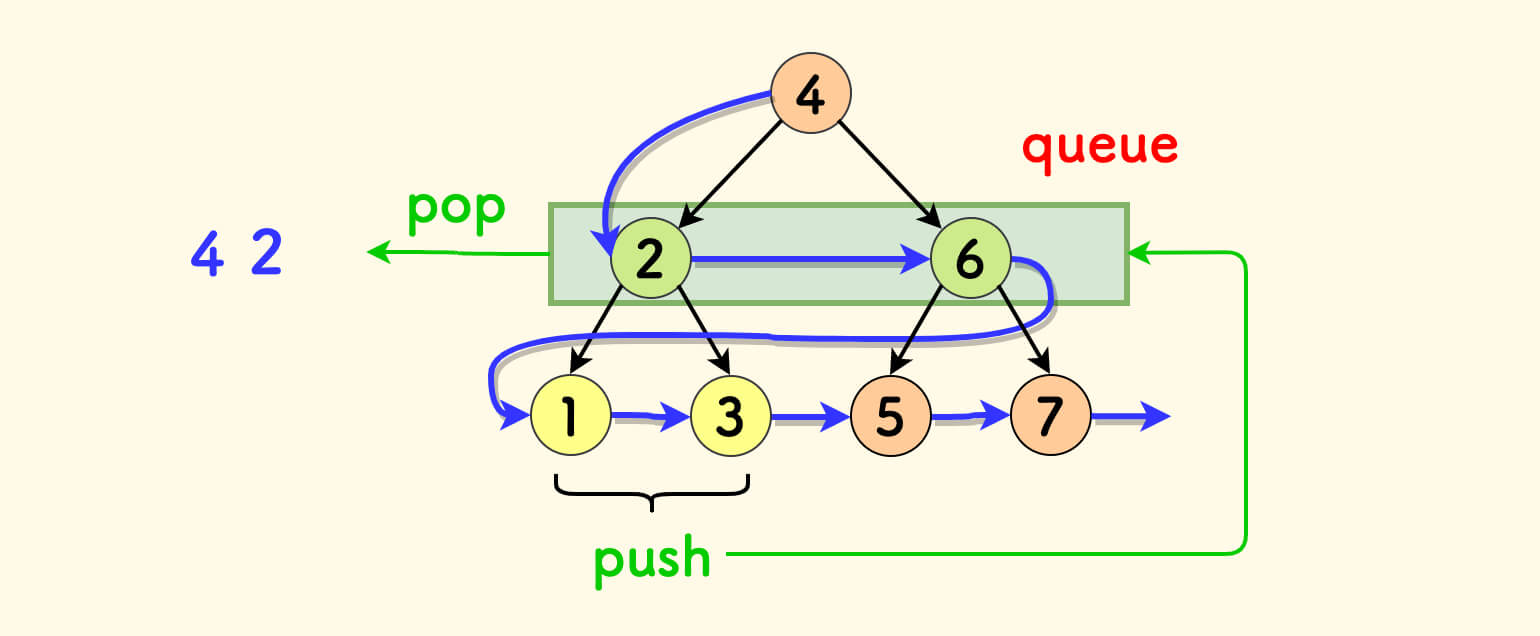
二叉树的广度优先遍历 - C++
vector<int> BFS(Node* root) {
vector<int> ans;
queue<Node*> q;
q.push(root);
while (!q.empty()) {
auto node = q.front();
q.pop();
if (node == nullptr) continue;
ans.push_back(node->val);
// 处理下一层
q.push(node->left);
q.push(node->right);
}
return ans;
}
层序遍历 ¶
要求输出一个二维数组,把每一层的节点放在一起,然后返回所有层作为答案。
例如,下图的二叉树的层序遍历结果是 [[4], [2,6], [1,3,5,7]]。
在广度优先遍历基础上,拆一层子循环,每当消费完上一层的节点后,新开一层。
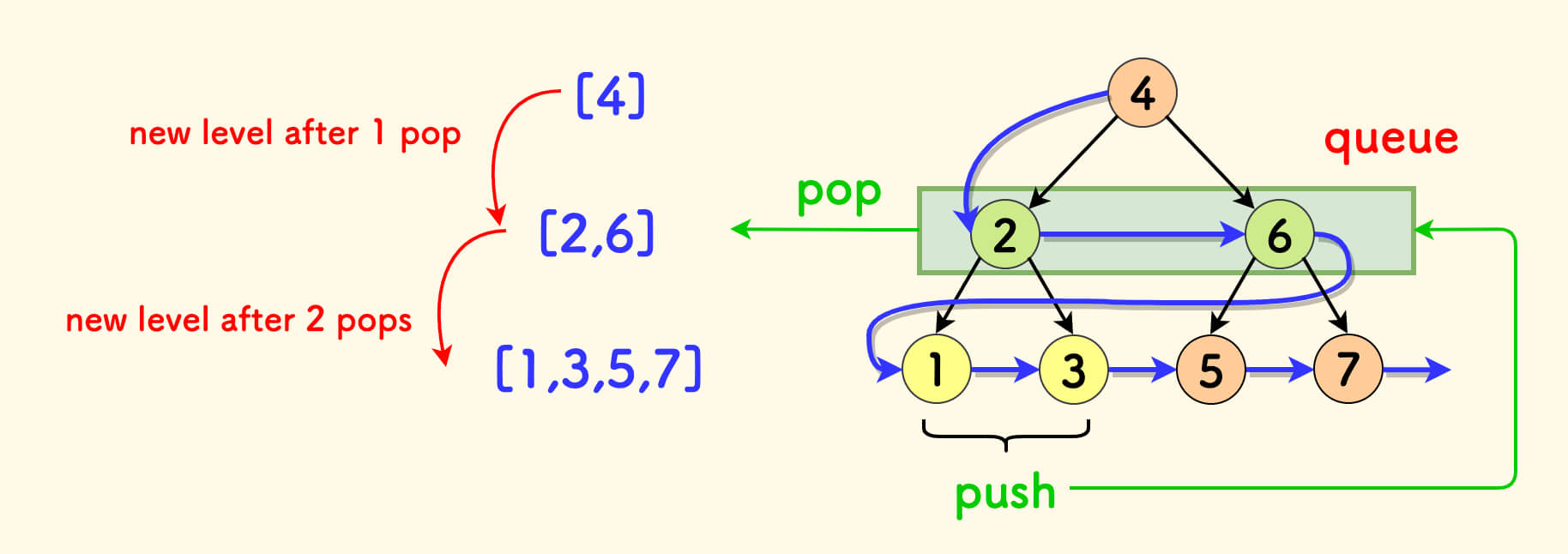
二叉树的层序遍历 - C++
vector<vector<int>> LevelOrder(Node* root) {
if (root == nullptr) return {{}};
vector<vector<int>> ans;
ans.push_back({});
queue<Node*> q;
q.push(root);
while (!q.empty()) {
int n = q.size(); // 上一层的数量
while (n--) {
auto node = q.front();
q.pop();
if (node == nullptr) continue;
ans.back().push_back(node->val);
// 处理下一层
if (node->left != nullptr) q.push(node->left);
if (node->right != nullptr) q.push(node->right);
}
// 新建一层
if (!q.empty()) ans.push_back({});
}
return ans;
}
本文二叉树的所有代码已放到 github:code-snippets/binary-tree
(完)
