对我思维模式影响非常大的一本科普书,是我在做机器人群体协作的时候阅读的,对我设计多机器人协作的系统有很多思维启迪的作用。 这本书被称为最好的复杂性科学的科普读物之一。 非常感兴趣的部分有元胞自动机、分形、小世界网络、无尺度网络、遗传算法等等, 非常好奇和神往的点在于 大自然的复杂系统的运作逻辑、复杂系统对自然界系统的刻画,以及对我们建模上、思维方式上的启发。 世界有太多的系统是自组织的, 很多自组织的个体形成了复杂甚至智能的集体表现。 本书涉猎面很广,有很多点都值得继续深挖学习下去。 这一本书有益于一览复杂性世界的历史演进、浅尝复杂系统相关的有趣的研究方法,是一本复杂系统方向的非常好的科普书。
豆瓣链接: 《复杂》·梅拉妮·米歇尔

复杂性 ¶
- 复杂系统是由大量个体组成的网络,不存在中央控制,通过简单的运作规则产生出复杂的集体行为和复杂的信息处理,并通过学习和进化产生出适应性。
- 如果系统有组织的行为不存在内部和外部的控制者或领导者,则也成为自组织的。
混沌和预测 ¶
- 对于非线性系统,整体不等于部分之和。
- 混沌系统:对于其初始位置和动量的测量如果有极其微小的不精确也会导致对其长期观测结果产生巨大误差。即对初始条件的敏感依赖性。 著名的蝴蝶效应 是一种混沌现象。
最简单的混沌系统:逻辑斯蒂映射 (logistic map)
\[x_{ i+1 } = Rx_{ i }(1-x_{i})\]这里 $x_{i}$ 是区间 $[0,1]$ 上的一个小数。
- 混沌系统的共性:
- 倍周期: 随着参数控制参数$R$的增大,系统吸引子的震荡周期成倍增加的现象。 倍周期是一种典型的系统走向混沌的方式。 下图是逻辑斯蒂映射的分叉图,图中吸引子 $x$ 是 控制参数 $r$ 的函数:

- 费根鲍姆常数: 倍周期分叉中两个相邻分叉点间隔的比例收敛于一个常数$4.6692016$, 也就是第一费根鲍姆常数(上图中左侧,开始的分叉点之间的水平距离之比的极限) , 上图中,竖直方向上特定的分叉点之间距离之比的极限也就是第二费根鲍姆常数 $2.50290787$. 另外,具有自相似性质的著名的曼德博集合 的缩放速率接近费根鲍姆常数

曼德博集合示意图
对于混沌思想的三点总结:
- 看似混沌的行为可能来自确定性系统,无须外部的随机源。
- 一些简单的确定性系统的长期变化,由于对初始条件的敏感依赖性,即使在原则上也无法预测。
- 虽然混沌系统的具体变化无法预测,但是存在普适共性,比如倍周期分岔和费根鲍姆常数。虽然在细节上无法预测,但是在更高的层面上混沌系统是可以预测的。
信息与熵 ¶
熵:是一种测量在动力学方面不能做功的能量总数。
在统计学意义上,熵度量的是系统的无序度,也就是说,系统越杂乱无章,它的熵值越大。
放在宇宙上看,世界是走向无序的。
- 熵增定律 · 热力学第二定律:
热力学系统从一个平衡态到另一平衡态的过程中,其熵永不减少:若过程可逆,则熵不变;若不可逆,则熵增加。
注意,关键描述: 孤立系统的熵不自动减小。 对于生命体,薛定谔在其 《生命是什么》 提到:
生命以负熵为生。 生命体不断的吸收低熵物质,放出高熵物质, 总体仍然满足熵增定律。
信息熵 | 香农熵: 接收的每条消息中(相对于信息接收者)包含的信息的平均量。
熵越高,则能传输越多的信息,熵越低,则意味着传输的信息越少。
推论:任何无损压缩技术不可能缩短任何消息。
熵最好理解为不确定性的量度而不是确定性的量度,因为越随机的信源的熵越大。
简而言之:信息熵就是信息量的数学期望。
计算 ¶
- 哥德尔不完备定理: 存在命题,不可证明,也不可证否。 算术要么不一致,要么不完备。
这个命题是不可证的。
- 图灵机:
- 一个无限长的纸带`.
- 一个读写头.
- 一组有限的规则集合,根据当前机器所处状态和当前读写头的指向符号来决定接下来读写头的操作。

因为图灵机的描述规则有限,因此图灵机本身可以编码为字符串。
因此可以设计图灵机U来存储另一个图灵机M编码后的程序,并模拟M的运作。 现代电子计算机其实就是通用图灵机。
停机问题:
判断任意一个程序是否能在有限的时间之内结束运行的问题。 或者说: 是否存在一个程序P,对于任意输入的程序w, 能够判断w会在有限时间内结束或者死循环。
图灵证明:不存在解决停机问题的通用算法。 停机问题包含了自指,本质上是一种悖论。 关键点在于「程序本身也是一种数据」, 证明详见维基百科(反证法)。
从而: 不存在明确程序能判定任意数学命题是否为真。
进化 ¶
如果要我选择一个历史上最重要的思想,我认为不是牛顿,也不是爱因斯坦,或是其他人,而是达尔文。 – 哲学家·丹内特
- 存在进化,所有物种都来自共同祖先。
- 资源有限,竞争导致了自然选择。
- 生物性状会变异,变异是随机的,并不必然会增加适应性。
- 进化是通过细微的有利变异不断积累形成的。
- 生命的熵的减少,是自然选择的结果,即自然选择做了功。
度量复杂性 ¶
描述复杂性的方式:
- 信息熵
- 算法信息量: 能够产生对事物完整描述的最短计算机程序的长度。
- 用逻辑深度描述复杂性: 越复杂的事物越难构造。
- 用计算能力度量复杂性:沃尔夫勒姆提出,系统的计算能力如果等价于通用图灵机的计算能力,就是复杂系统。
- 统计复杂性:度量用来预测系统将来的统计行为所需的系统过去行为的最小信息量。
分形 ¶

在任何尺度上都有微细结构的几何形状,具有 自相似性 和 无尺度性。分形也被称为扩展对称或展开对称。 如果在每次放大后,形状的重复是完全相同的,这被称为自相似。
科赫曲线 是一种分形结构: 将各边分成3等份,不断重复这个过程。
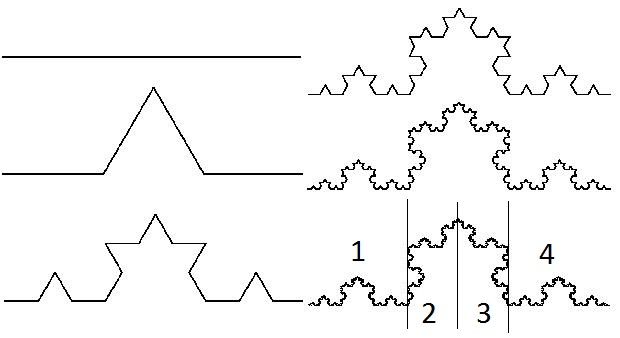
每条科赫曲线的长度是无限大(但面积是有限的),它是连续而无处可微的曲线。
分形维数 也叫做 豪斯多夫维数: 一个几何结构(线段/图案/立体结构)分形放大了$X$次后,其占有的空间(对应的:长度/面积/体积)比原来放大了 ${X}^{N}$倍,那么这个$N$就定义为这个分形结构的维度 (参考知乎链接)。
特殊的,对于科赫曲线,参考图示得知,如果将它放大3倍,长度会增加4倍,所以维数: ${3}^{N}=4$ 即得到 $N={log}_{3}4$ 。
简而言之:
- 分形维数决定了物体的自相似拷贝的数量。
- 同样也决定了随着层次的变化,物体总大小会如何改变。
自我复制的计算机程序 ¶
就算深蓝赢了卡斯帕罗夫,它也不会有快乐的感觉。
自我复制的程序通常叫做 quine.
自我复制的程序通过两种方式来使用内存中的信息:既作为执行的指令,又作为这些指令使用的数据。
信息的双重使用是哥德尔悖论的核心。
若人们不相信数学简单,只因他们未意识到生命之复杂。 – 冯诺依曼
遗传算法 ¶
遗传算法是一种进化算法,用于解决最优化问题, 步骤:
- 生成初始群体,大量随机个体(个体即候选解)。
- 计算群体中各个个体的适应度。
- 进化:
- 根据适应度选择一对个体A和B作为父母,个体的适应性越高,被选中的概率越高
- 父母交配产生两个子代个体
- 让子代个体以很小的概率发生变异
- 将产生的个体放入新群体中
- 回到第2步,继续循环下去.
关键点:
- 如何编码所有的个体(策略),并定义交合、变异?
- 如何评价适应度?
进化算法是探索设计死角的伟大工具。 – Jason Lohn
元胞自动机 ¶
元胞自动机: 由元胞组成的网格,每个元胞都根据邻域的状态来选择自己的状态,所有的元胞遵循同样的规则, 规则根据各个元胞邻域的当前状态决定元胞的下一步状态。
下图是元胞自动机的例子: 生命的游戏
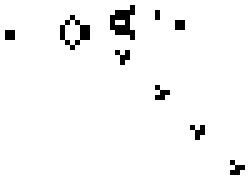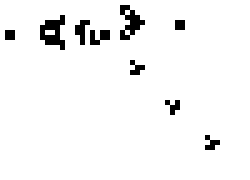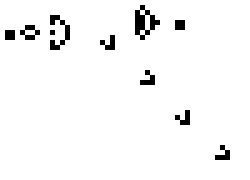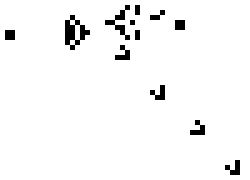
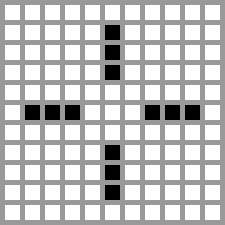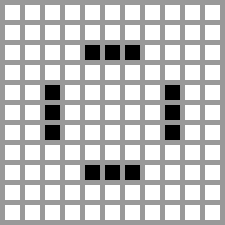
元胞自动机也是由大量简单个体组成,不存在中央控制,每个个体都只与少量其他个体交互。
冯诺依曼曾给出了一个等价于通用图灵机的元胞自动机。
元胞自动机的三个特征:
- 平行计算:每个元胞个体都同时同步的改变。
- 局部的:元胞的状态变化只受周围元胞的影响。
- 一致性:所有元胞受同样的规则所支配。
4类元胞自动机:
- 类型1(不动点): 不管初始状态如何,最后停止在不变的图样上。
- 类型2(交替态): 不管初始状态如何,最后要么停在不变的图样上,要么在几个图样之间循环。
- 类型3(随机态): 几乎所有的初始形态将会演变成一个伪随机或混沌的形式。
- 类型4(复杂态): 最有趣的一种。 几乎所有的初始模式将会演变成相互作用的复杂和有趣的方式结构,并且局部结构的形成能够长时间存在。
这里推荐下玩一下模拟生命样貌的元胞自动机: Lenia,下图是Lenia的一个示例图
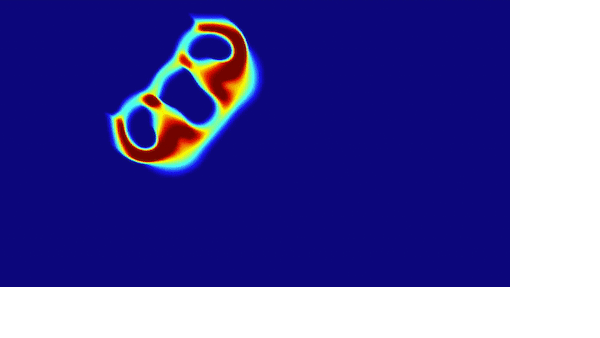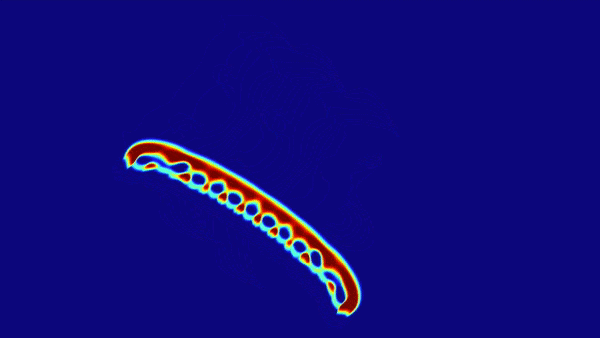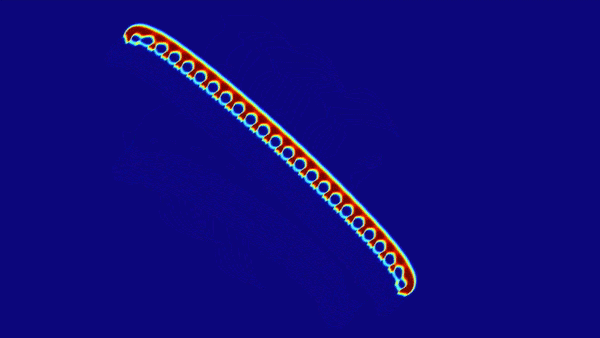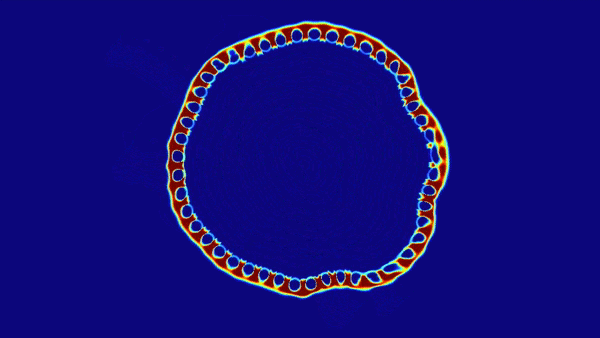
沃尔夫勒姆的一位助手库克证明了规则110是通用的。
沃尔夫勒姆的计算等价原理:
- 思考自然界中的过程的正确方法是将它们视为计算。
- 像规则110这样极为简单的规则(或程序)都能进行通用计算,这表明通用计算的能力在自然界中广泛存在。
- 通用计算是自然界计算的复杂性的上限,即自然界中不存在「不可计算」的行为。
- 自然界中各个过程实现的计算在复杂程度上都是等价的。
自然界的过程就是计算 – 沃尔夫勒姆
生命系统中的信息处理 ¶
那自然系统的计算指的是什么呢?
- 计算是复杂系统为了成功适应环境而对信息进行的处理。
- 元胞自动机的信息就是元胞格子在每一步的状态组合。
蚁群算法: 是一种用来在图中寻找优化路径的机率型算法。
蚂蚁随机朝一个方向搜索,如果遇到食物,就返回蚁穴,沿途留下作为信号的化学物质 - 信息素。当其他蚂蚁发现了信息素, 就有可能沿着信息素的轨迹前进。信息素的浓度越高,蚂蚁就越有可能跟着信息素走,如果蚂蚁找到了食物,就返回巢穴。这样, 信息素的轨迹增强,如果信息素的轨迹得不到增强,就会消失。
信息是如何被传递和处理的?
- 没有哪个个体能感知或传达系统状态的”宏观画面”。 信息必须通过空间和时间采样来传递。
- 由于获得的信息具有统计性,个体的信息面不对称,行为就必然有随机成分。
- 微粒化探测(并行级差扫描): 大量个体同时并行的对许多可能性进行探测,虽然搜索是并行的,但是存在级差, 即并非所有可能都以同样的速度和深度进行探测,及时利用搜索结果的信息不断调整探测从而有所侧重。
- 分散探测与集中行动之间的互动: 系统既要探测信息,又要对信息加以利用,不断调整适应。 在分散探测和集中行动之间进行平衡可能是适应性和智能系统的共性。
侯世达的并行级差扫描: 许多可能性被并行地进行探索,用获得的最新信息不断对各种可能性的收益进行估计,并根据反馈分配资源。
合作的进化 ¶
问题:
为什么由自私个体组成的群体中会进化出合作?
有一部书叫做 《合作的进化》,专门在讨论这个话题。
囚徒困境: 是博弈论的非零和博弈中具代表性的例子,反映个人最佳选择并非团体最佳选择。
| 乙沉默(合作) | 乙认罪(背叛) | |
| 甲沉默(合作) | 二人同服刑半年 | 甲服刑10年;乙即时获释 |
| 甲认罪(背叛) | 甲即时获释;乙服刑10年 | 二人同服刑5年 |
可以看到,囚徒困境的典型特点是,个人最好的选择并不是团体最好的选择。
每个人从自私的角度考虑:
- 如果对方指证我的话,我需要指证对方而不至于判10年,可以判5年。
- 如果对方没有选择指证我的话,我更好的选择是指证对方,这样可以直接获释(而不至于服刑半年)。
每个人都追求自利,使得所有人的利益都受损。 — 阿克塞尔罗德
公地悲剧:个人利益与公共利益对资源分配有所冲突的社会陷阱。
结论:
- 如果只进行一个回合,则两方的最好策略是背叛。
- 但如果有多个回合,则总是背叛的参与者的收益会远低于学会了相互合作的参与者。
在多次、长期的非零和博弈中,不管对手的策略如何变化,合作策略比非合作策略的收益要更高。
阿克塞尔罗德的《合作的进化》一书,详细记录了多回合囚徒困境的 计算机模拟和结论,总而言之: 以善报善,以牙还牙 (也常称为: 一报还一报)
- 不首先背叛
- 对于对方的合作和背叛都有回报: 对方合作,回之以合作;对方背叛,回之以背叛。
- 宽恕:背叛后再次选择合作的对手, 回之以合作。
这个策略是所有模拟囚徒困境中的计算机程序中得分最高的策略,同时也是遗传算法演化出来的策略。它的显著特点:
- 善良性: 不首先背叛
- 报复性: 人若犯我,我必犯人
- 宽容性: 宽恕背叛后再次合作的对手
- 清晰性: 行为明确,具有可预见性
阿克塞尔罗德的结果颇具哲学意味,对于无论是计算机场景下、还是政治、经济、生活中常见的「个体利益和团体冲突」的 多轮非零和博弈过程,「友善、报复、宽恕、明确」都是一个非常好的原则!
合作的进化是非常出色的计算机建模案例,关于计算机建模:
- 计算机模型必须是可重复的。
- 建模的艺术是去除实际中与问题无关的部分,但有可能有风险遗漏至关重要的因素。
网络 ¶
什么是网络思维?
网络思维: 关注的不再是事物本身,而是事物之间的关系。
网络 是由边连接在一起的节点组成的集合。
小世界网络 ¶
小世界网络 是一类特殊的复杂网络结构,在这种网络中大部分的节点彼此并不相连,但绝大部分节点之间经过少数几步就可到达。
一个网络如果只有少量长程连接,相对节点数量来说平均路径却很短,则为小世界网络。
六度分割理论: 世界上任何互不相识的两人,只需要很少的中间人就能够建立起联系。 并不是说任何人与人之间的联系都必须要经过6步才会达到,而是表达了这样一个重要的概念: 在任何两位素不相识的人之间, 通过一定的联系方式,总能够产生必然联系或关系。
我的朋友的朋友也很可能是我的朋友。
小世界网络的判定准则有两个:
- 特征路径长度短: 两个节点的路径长度的平均值短。
- 高集聚系数: “抱团”现象。
无尺度网络 ¶
无尺度网络 是带有一类特性的复杂网络,其典型特征是在网络中的大部分节点只和很少节点连接, 而有极少的节点与非常多的节点连接。
典型的带有无尺度特性的网络:万维网。
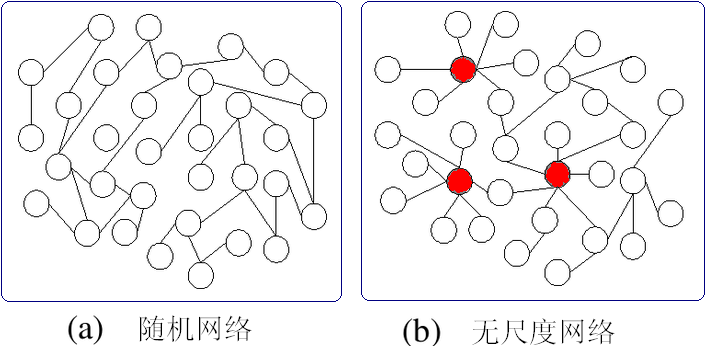
无尺度网络的度分布(在网络中随机抽取一个节点,它的度是多少呢?这个概率分布就称为节点的度分布), 符合幂律分布。
另外,幂律分布本身具有无尺度特点,延伸:80/20法则。
下图a是随机网络的度分布,b是无尺度网络的度分布,可以看出b是符合幂律分布的,幂律分布本身也是无尺度的,具有标度不变性。
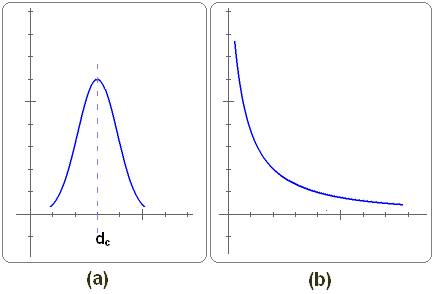
所有的无尺度网络也具有小世界特性,但是并不是所有具有小世界特性的网络都是无尺度的。
无尺度网络的重要特点: 稳健性。 如果随机删除一些节点,不会改变网络的基本特点,因为大量节点是低连接度的节点。
关于互联网的无尺度研究:
- 入度为$k$的网页数量正比于 $\frac { 1 }{ { k }^{ 2 } }$ (同样具有无尺度、自相似的分布特点)
- 大部分网页为低连接数的,极少部分网页具有高连接度 (仍然是幂律分布的特点)。
无尺度网络是如何产生的?
偏好附连 (马太效应) 连接度高的节点比连接度低的节点更有可能得到新的连接。
比例之谜 ¶
克莱伯定律: 代谢率正比于体重的$3/4$.
这个定律背后的原因非常有趣,也就是幂律分布和分形结构的关系: 分形结构正是产生幂律分布的一种方式。
齐普夫定律: 在自然语言的语料库里,一个单词出现的频率与它在频率表里的排名成反比。 所以,频率最高的单词出现的频率大约是出现频率第二位的单词的2倍,而出现频率第二位的单词则是出现频率第四位的单词的2倍。 注意,齐夫定律是一个实验定律,而非理论定律。
齐普夫定律也是一个幂律分布。
这个定律的解释:
- 最省力原则,一旦用到一个词,对类似的意思用这个词要比换其他词要省力。
- 信息量的角度:信息发送者在将信息量最大化的同时,尽量将发送信息的成本最小化。
秩序的起源 ¶
生命具有复杂化的内在趋势(区别于自然选择),而且可能自组织才是进化的主导作用。 —— 考夫曼
考夫曼认为,生命具有复杂化的内在趋势,而独立于自然选择。
豆瓣链接: 《The Origins of Order》
复杂性的未来: 等待卡诺。
值得继续探索的部分 ¶
- 元胞自动机
- 幂律分布
- 哥德尔不完备定理
- 分形
- 合作的进化
- 遗传算法
- 自组织的世界观
– 毕 《复杂》笔记。
本文原始链接地址: https://writings.sh/post/complexity-a-guided-tour-notes



