值域离散化 | 春水煎茶

离散化就是把一个给定的数据集映射到更小的、无重复值的数据集上，保持相对大小关系不变。

常作为一种预处理手段。

一般来说，遇到数据范围很大、或者有负数的情况，而实际问题的求解和元素的值具体多少无关，只是和它们的相对大小有关时，可以把它映射到 [1,m] 的正整数区间。

比如，把数组 [-9281903, 5, 290389, 99298348, -88723, 17300284, 5, 290389] 离散化后，应该是 [1,3,4,6,2,5,3,4]。

离散化的步骤，简单说就是，先排序、再去重、再替换。

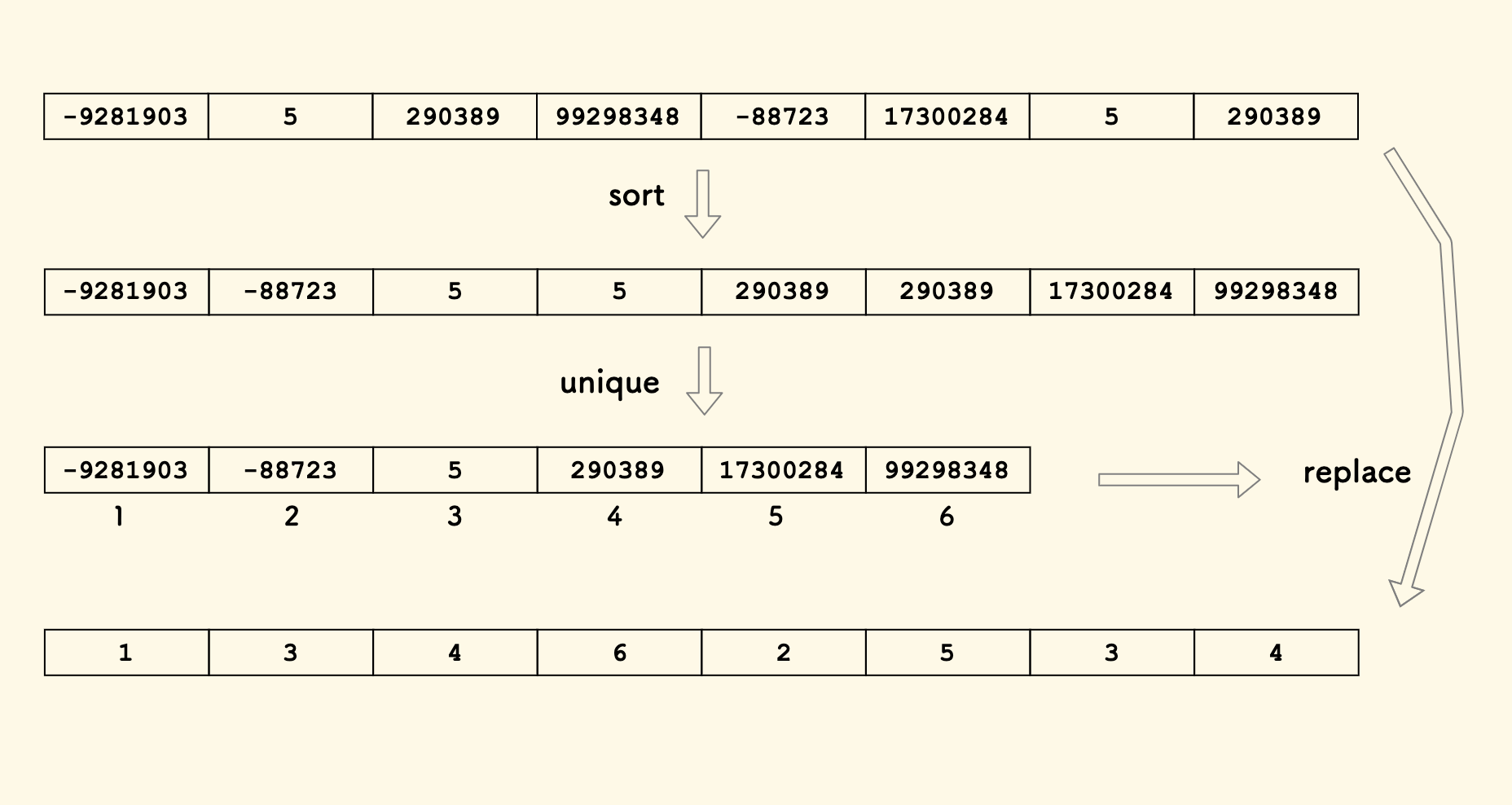
展开来说，假设要离散化的数组是 a[i]：

从 a 复制一个数组，记为 p。
对 p 进行排序（为了去重）。
对 p 进行去重，去重后大小为 m。
遍历原数组 a，将 a[i] 替换为其在 p 中的左界位置，因为 p 已经有序，所以可以二分。

其中，最后一步是可选的，视情况决定要不要原地替换掉原数据，有时离散化只是要构造一个原数组的有序且无重复的排列。

下面是一个 C++ 版本的原地离散化实现，其时间复杂度是 $O(n\log{n})$。

// 原地离散化，返回离散化后的值域最值 m
// 假设原数组 a 下标从 0 开始
int discrete(vector<int>& a) {
    // ①  拷贝一份
    vector<int> p(a.begin(), a.end());

    // ② 排序
    sort(p.begin(), p.end());

    // ③ 去重
    int m = unique(p.begin(), p.end()) - p.begin();

    // ④ 找左界，原地替换为下标
    for (int i = 0; i < a.size(); i++) {
        // 映射到 1~m
        a[i] = lower_bound(p.begin(), p.begin() + m, a[i])
            - p.begin() + 1;
    }
    return m;
}

（完）

本文原始链接地址： https://writings.sh/post/discrete