Arithmetic Expression Evaluation (Double Stack Method)

How to evaluate the value of an arithmetic expression? For example, the value of the string 3+1+(2x(2+1-2x1+1)) should be 8.

This article introduces Dijkstra’s double-stack algorithm for expression evaluation.

This algorithm is not only applicable to arithmetic operations, but also to any expression form with priority relationships, such as logical operations, regular expressions, etc.

Preliminary Ideas ¶

The key point lies in handling precedence. .

For example, consider a simple expression 5+3x2. We need to calculate the multiplication at the end first.

But for another expression example 2+5+3x2, we can calculate the addition at the beginning first.

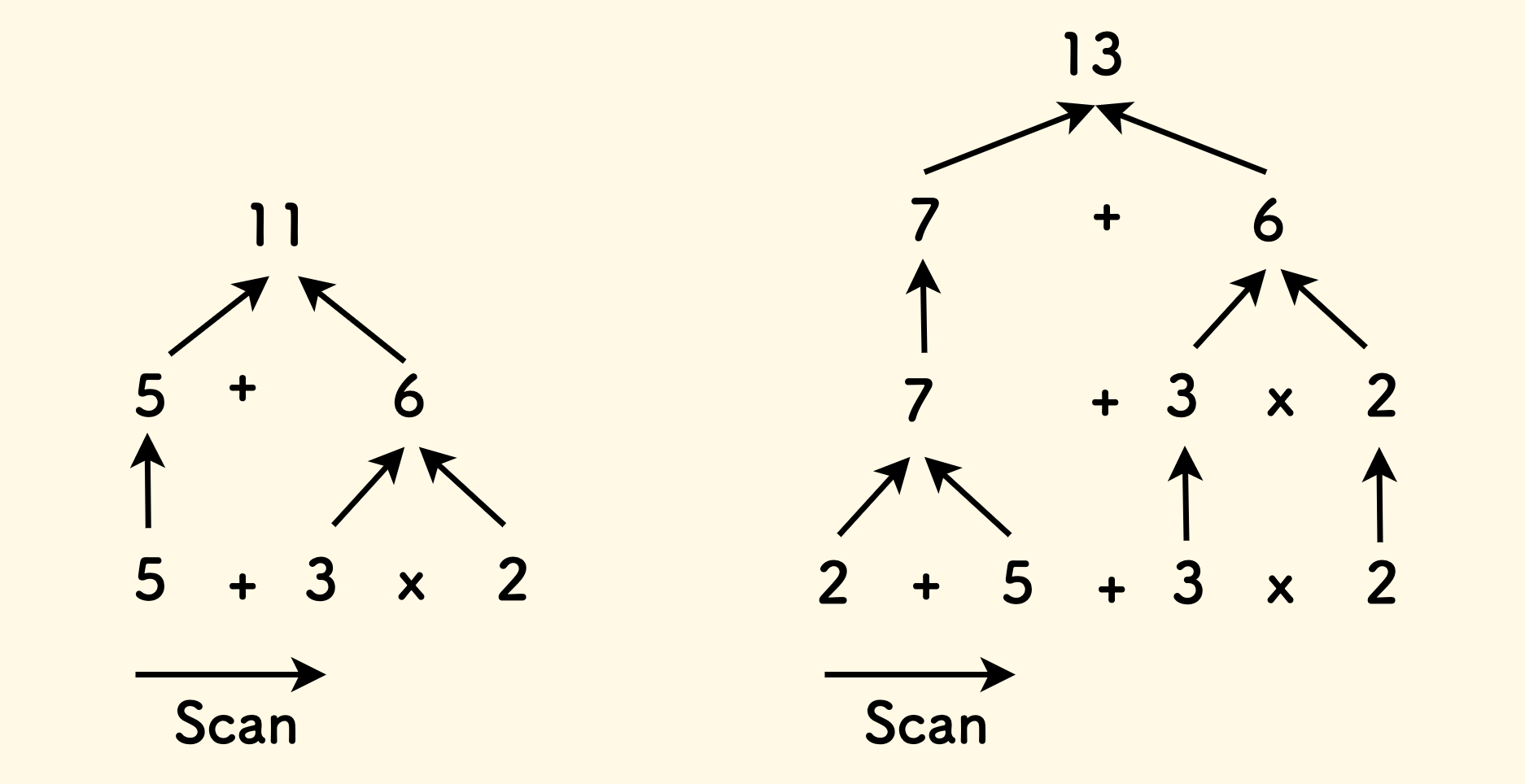
This illustrates two points:

Don’t calculate directly when you encounter an operator, but wait a bit to see if the precedence of the following operator is higher.
The effective range of this precedence is very short, only affecting adjacent operators.

Another type of precedence is parentheses. For example, in (5+3)x2, we need to calculate the part inside the parentheses first, ignoring the precedence of the multiplication operator later.

A slightly more complex example, like (3x(3+2))+1, we should first calculate the inner parentheses, and then consider the outer parentheses, because the inner parentheses close first. That is, when a closing right parenthesis is encountered, the part inside the parentheses can be completely calculated, and the pair of parentheses is discarded.

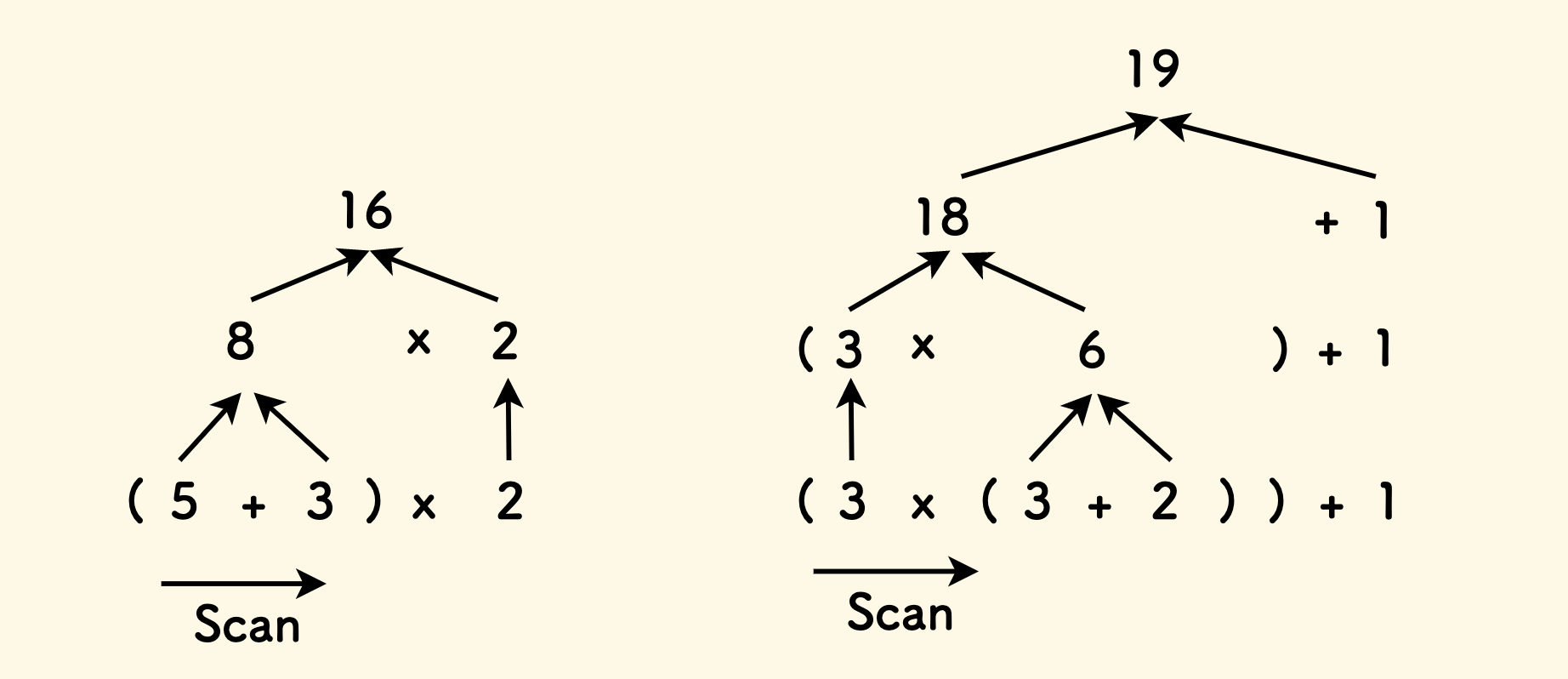
In summary, the timing for calculation is:

When the precedence of the current operator is higher (or not lower) than the next operator.
When parentheses are encountered, calculate only when the parentheses are closed.

Because these two types of “waiting” need to be handled, a stack is required.

Algorithm Idea ¶

In fact, the previous two schematic diagrams have already implied that arithmetic expression evaluation can be expressed as a bottom-up process.

It is also a type of shift-reduce parsing process: The so-called “shift” refers to input symbols entering the stack, and “reduce” refers to symbols leaving the stack for calculation, and the result then entering the stack.

Algorithm process:

Shift: When an input symbol is encountered, it is pushed onto the stack.
Reduce: When an operator is encountered, examine the operator at the top of the stack:
- If its precedence is not lower than the current operator, pop it from the stack for calculation, and push the result onto the stack.
- Otherwise, push it onto the stack first, waiting for a later opportunity to calculate.
Reduce: When a right parenthesis is encountered, pop elements from the stack until the left parenthesis is popped. Calculate the result and push it onto the stack.

Returning to the expression proposed at the beginning of the article, 3+1+(2x(2+1-2x1+1)), its shift-reduce process is shown in the figure below. The stack is horizontal. When a symbol is encountered, it is pushed onto the stack and expanded. When a reduction condition is met, it is reduced upwards.

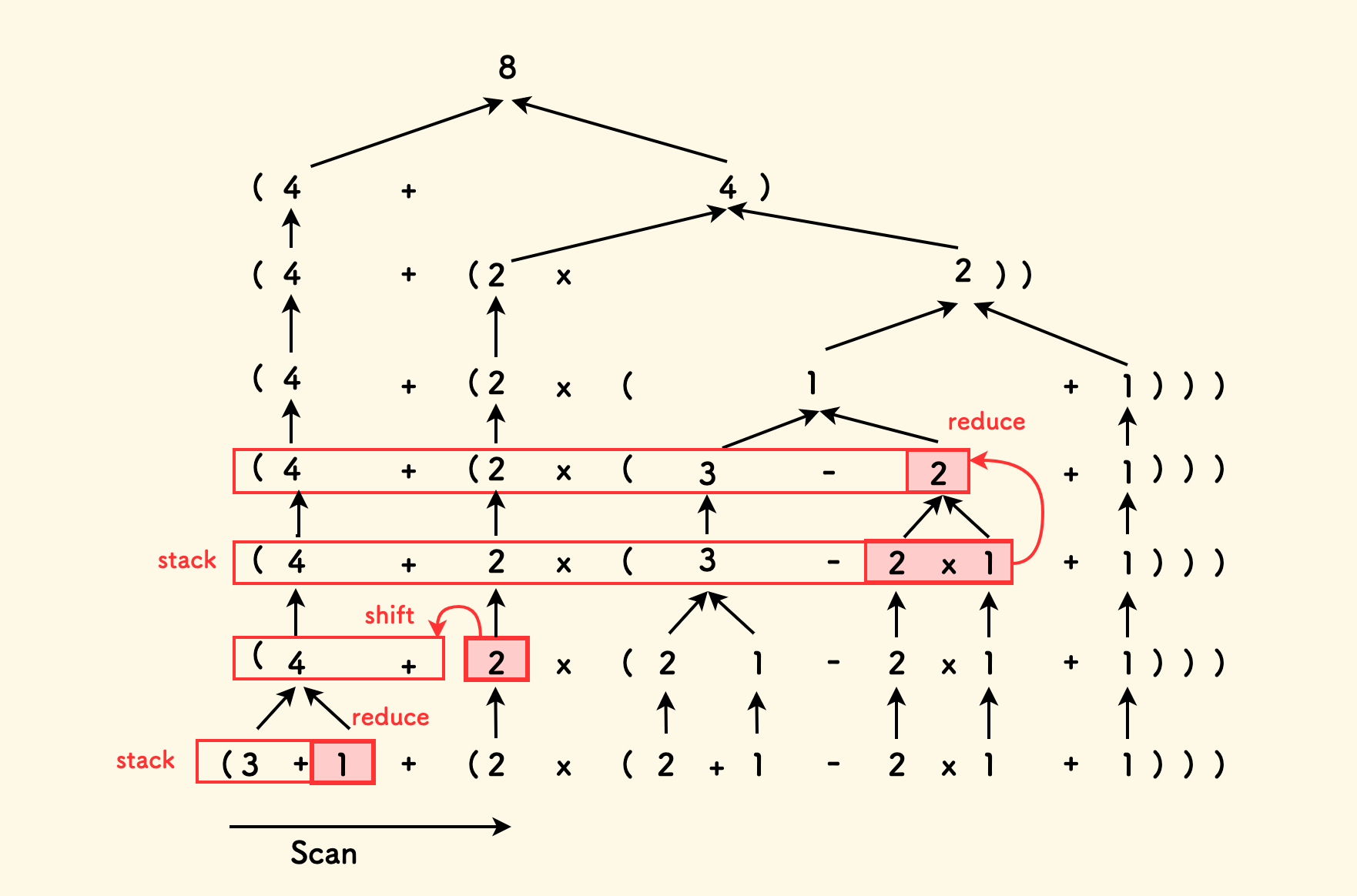
However, because we want to examine the “top” operator of the stack, it would be difficult to handle if the top of the stack could be a number or an operator. So, two stacks should be used, one to store numbers and the other to store operators.

Finally, the detailed process of Dijkstra’s double-stack algorithm:

Define two stacks: one for storing numbers and the other for storing operators.

Define a sub-process for performing calculations:

Pop the operator at the top of the operator stack, pop the corresponding number of numbers, and push the calculated result onto the number stack.

For example, for subtraction:

void calc(op_stack, num_stack) {
  op = op_stack.pop();

  switch(op) {
    case '-':
      b = num_stack.pop();
      a = num_stack.pop();
      num_stack.push(a - b);
      break;
     // Other operators...
  }
}

From left to right, for each scanned character ch:
1. If a number is encountered, push it directly onto the number stack.
2. If an arithmetic operator is encountered:
  1. If the operator at the top of the operator stack has higher precedence, then calculate first, then push onto the stack.
    Calculate the top of the stack first until the precedence of the top of the stack is lower than the current operator; Then push the current operator onto the stack.
  2. Otherwise, push it onto the stack first, and wait for an opportunity to calculate it later.
  The code would look like this:
```
 while (precedence(op_stack.top()) >= precedence(ch))
   calc(op_stack, num_stack);
 op_stack.push(ch);
```
3. If a left parenthesis is encountered, push it directly onto the operator stack to wait for the right parenthesis to close.
4. If a right parenthesis is encountered, continuously pop elements from the stack and perform calculations until the left parenthesis is popped.
  The code would look like this:
```
while (op_stack.top() != '(')
  calc(op_stack, num_stack);
op_stack.pop();  // Discard the left parenthesis
```
Finally, the number stack should contain only one element, which is the calculation result.

Following this algorithm process, the calculation steps of the aforementioned expression 3+1+(2x(2+1-2x1+1)) are shown in the figure below. Shift means push onto the stack; each reduction point is a calculation:

In practice, you also need to consider the case of multi-digit numbers and ignoring whitespace characters.

In addition, one subtle point is that the case where input terminates is not considered in the timing of the calculation. When the input ends, there may be operators and numbers left in the stack waiting to be calculated.

There are two ways to solve this:

Pre-process the expression string, for example, enclose 1x(3+2) with parentheses to transform it into (1x(3+2)), so that the calculation can be called when the final right parenthesis closes.
Another method does not require copying memory: After the input ends, if the operator stack is not empty, continue to complete the calculation.
The code would look like this:
```
// After the string reading iteration is over
while (op_stack.size() > 0)
  calc(op_stack, num_stack);
```

Code Implementation ¶

The code implementations are placed on Github:

Out of a recent interest in learning C++, I also made a C++ compile-time arithmetic expression calculation implementation:

C++ Language Version Compile-time Arithmetic Expression Calculation - arithmetic-expression-cpp-compiletime - github

Finally, it is worth stating once again that this algorithm is not only applicable to the evaluation of arithmetic expressions, but also to expressions with priority relationships such as regular expressions, and logical expressions.

It is essentially a bottom-up shift-reduce parsing process.

(End)

Please note that this post is an AI-automatically chinese-to-english translated version of my original blog post: http://writings.sh/post/arithmetic-expression.

Original Link： https://writings.sh/post/en/arithmetic-expression