在阅读 《通灵芯片》 的时候, 书中提到一个关于有限状态机的冷门但是有趣的问题,叫做 射击队同步问题 :
假设你是一名将军,指挥排成长长一行队伍的士兵。由于队伍太长, 你无法大声下达「开火」命令,于是你只好向队伍中的第一名士兵下达命令,要他传给第二个, 再依次传递下去。难的是,全队士兵必须同时开火。虽然有节奏的战鼓响个不停,但你不能指望规定在多少点鼓声之后一齐开火, 因为你并不清楚到底有多少士兵。
这个问题的实质就是设计一排相同的有限状态机,每个状态机只能看到其相邻状态机的情况。 在每一帧时钟前进时,每个状态机都可以跳转一次状态。 需要满足,对于无论多少个士兵的情况,当一端收到开始命令后,总能在时钟前进有限次数后, 所有士兵都运转到同一个状态。
这个问题并不容易,是一个有名的难题。
射击队同步问题在 1957 年提出,第一个解决方案由计算机科学家 约翰·麦卡锡 和 马文·闵斯基 在 1962 年给出,包含 15 个状态,也就是本文中讲述的方案。
解决思路 ¶
推荐一个此问题的视频:Firing Squad synchronization problem - Youtube , 结合此视频看,对于理解这个问题本身、和此解决方案有许多帮助。
首先介绍士兵的几种状态:

I- 静止状态 IdleF- 开火状态 FireR- 举起右手 Hand right raised.L- 举起左手 Hand left raised.A- 右腿迈一步 Right leg at step 1st.B- 右腿迈两步 Right leg at step 2nd.C- 右腿迈三步 Right leg at step 3rd.a- 左腿迈一步 Left leg at step 1st.b- 左腿迈两步 Left leg at step 2nd.c- 左腿迈三步 Left leg at step 3rd.
最开始所有人都出于静止状态。
如果一个士兵看到他左边的人举起右手,那么他就举起右手
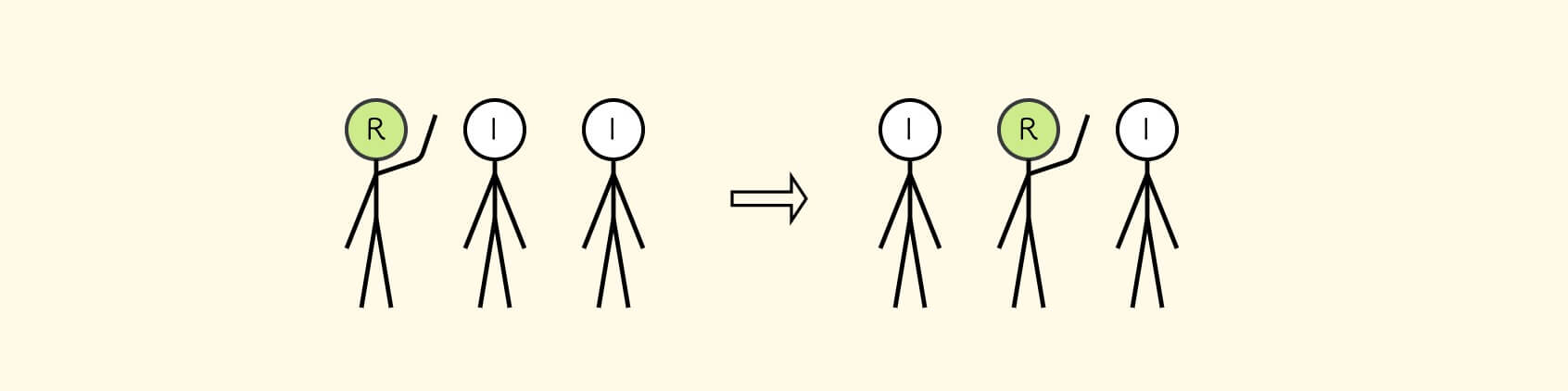
如果右手边没有人,那么换举左手。
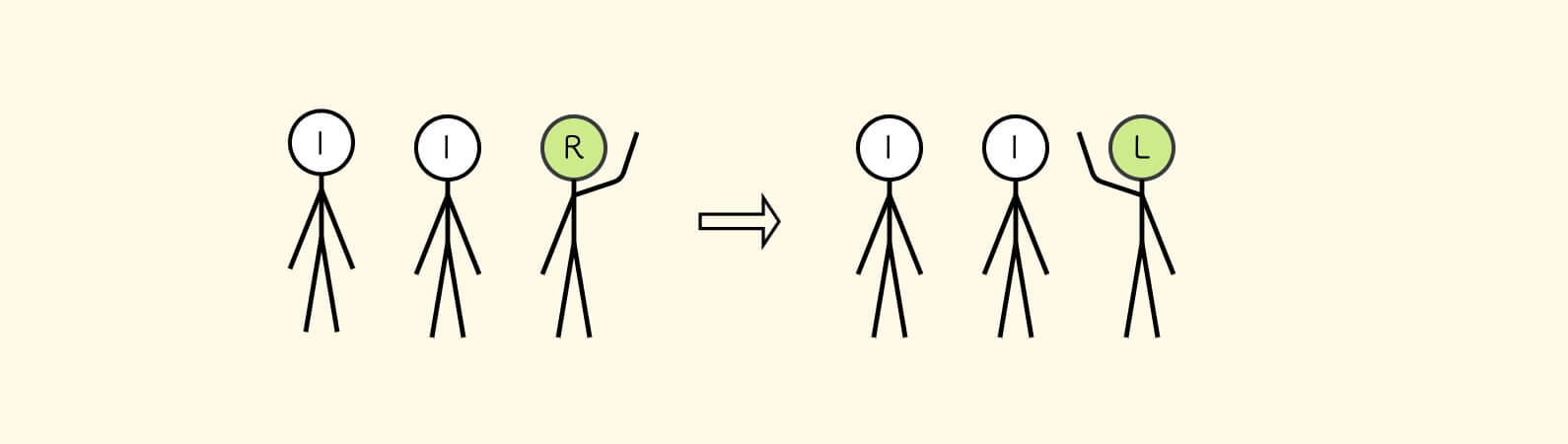
就是说, 举右手的动作一路向右传播,到队尾后,换举左手 。
同理对于左手的情况,会向左一路传到队头,换举右手,不再赘述。
不像举手的动作那样简单,迈腿的动作则分为三步:
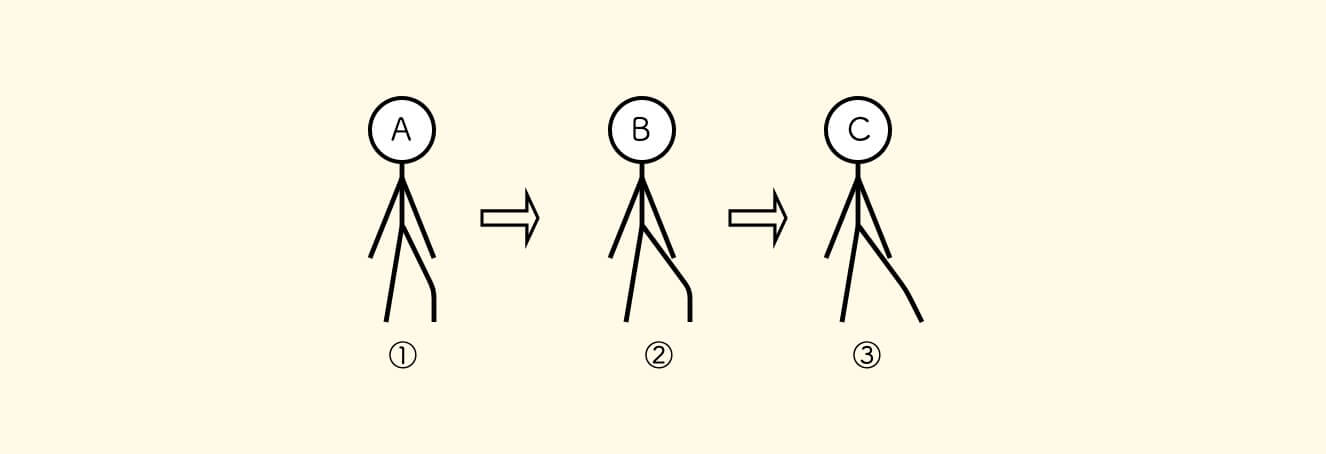
如果一个士兵看到他左边的人在 C 状态,那么他就进入 A 状态。 通俗点说,左边的人迈右腿快结束了,我才开始迈右腿。
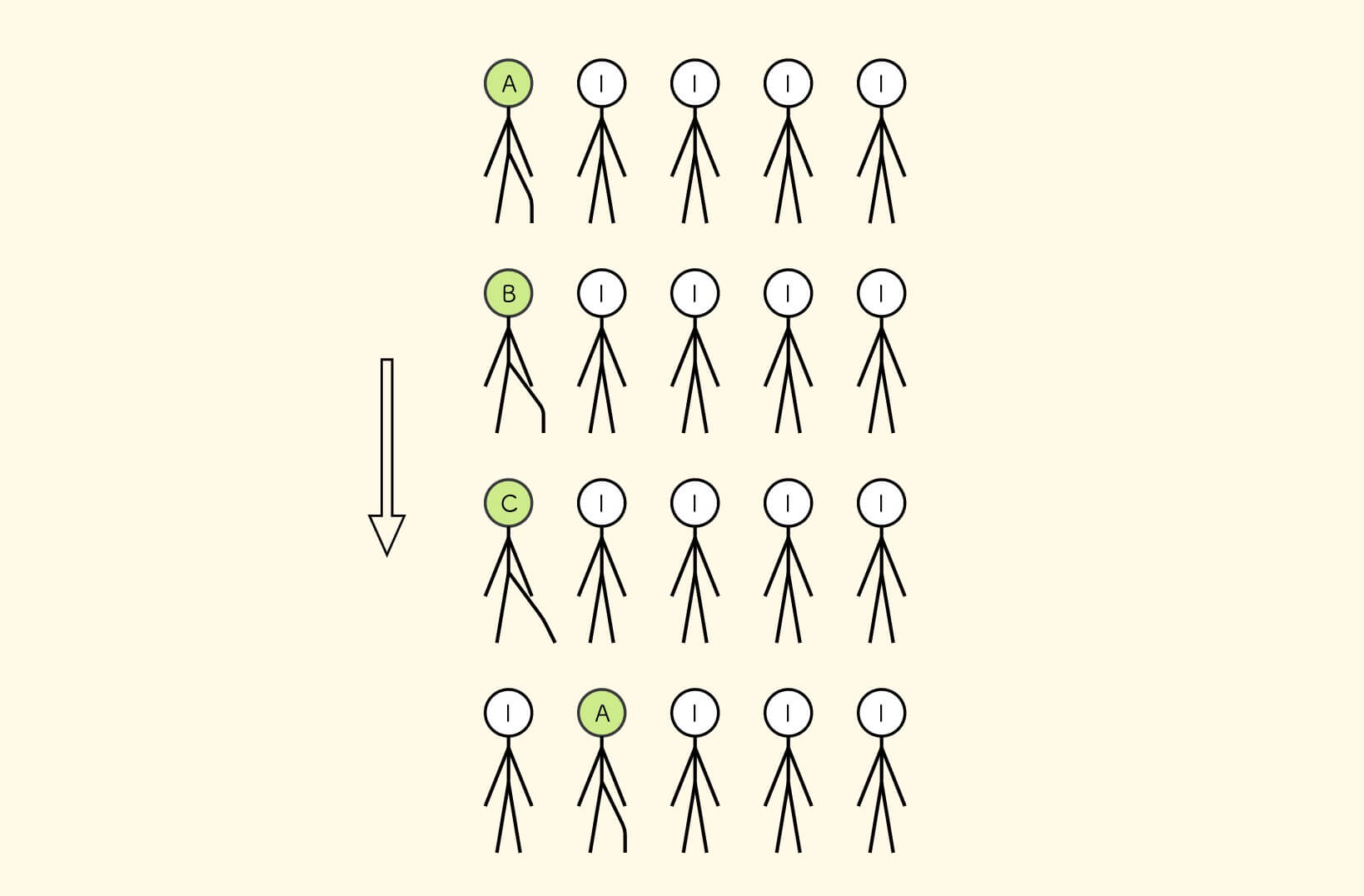
ABC 是迈右腿、向右传播,abc 则是迈左腿,向左传播。
可以知道,迈腿的传播速度更慢,是举手的传播速度的三分之一。
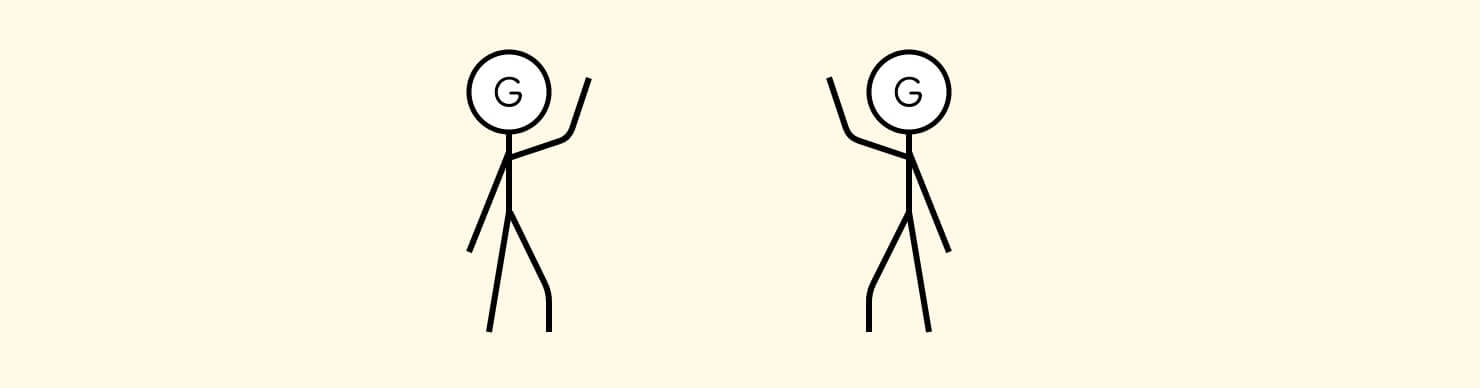
最开始的时候,让队头的士兵举右手、抬右腿,此时称他是一个将军 General,即处于 G 状态; 同样,对于举左手、抬左腿的情况,也是 G 状态。 凡是手脚并用的情况,都叫将军状态。
现在我们看下 8 个士兵的情况下,一帧一帧地推演,会发生什么?

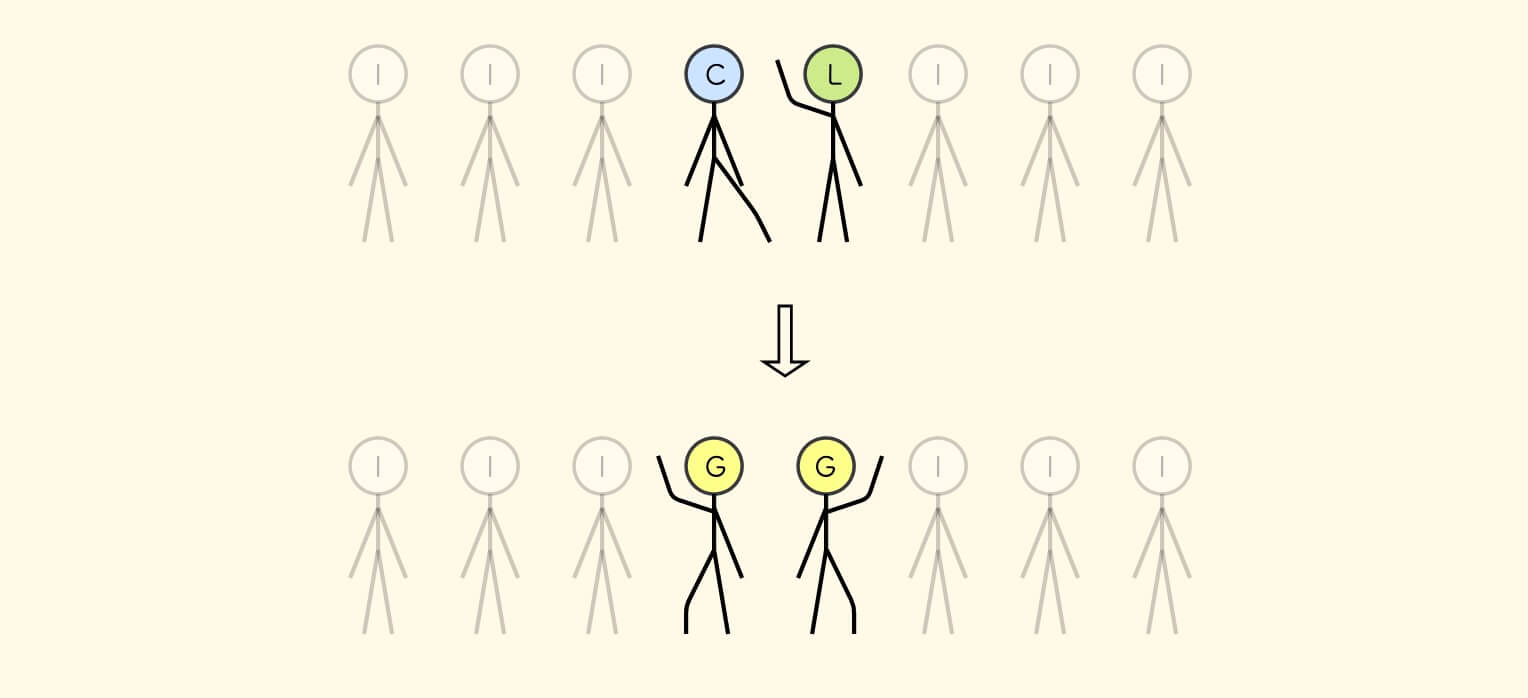
这是一幅很长的图,可以看到,由于举手比迈腿的传播快三倍,举手的动作传播到队尾后, 又反射回来,正好和迈腿动作在队列中点相遇。 此时,我们让这两个士兵都成为将军,进入 G 状态:
同样,对于 R 和 c 相遇的情况,也会使得两个士兵都成为将军。
凡是举手和迈腿两种信号相遇的情况,都会促发将军的诞生。
一个将军会把举手和迈腿的信号向相应方向传播,G 是传播的起点。
如此一来,动作可以分别向左右传播,整个队伍一分为二,左右开弓!
现在,套用前面所说的规则,继续对 8 个士兵的情况推演:

可以看到,经过不断的二分,最终所有士兵都成为了将军。
如果一个士兵自己是将军,且两边的士兵也都是将军,那么他可以开火。
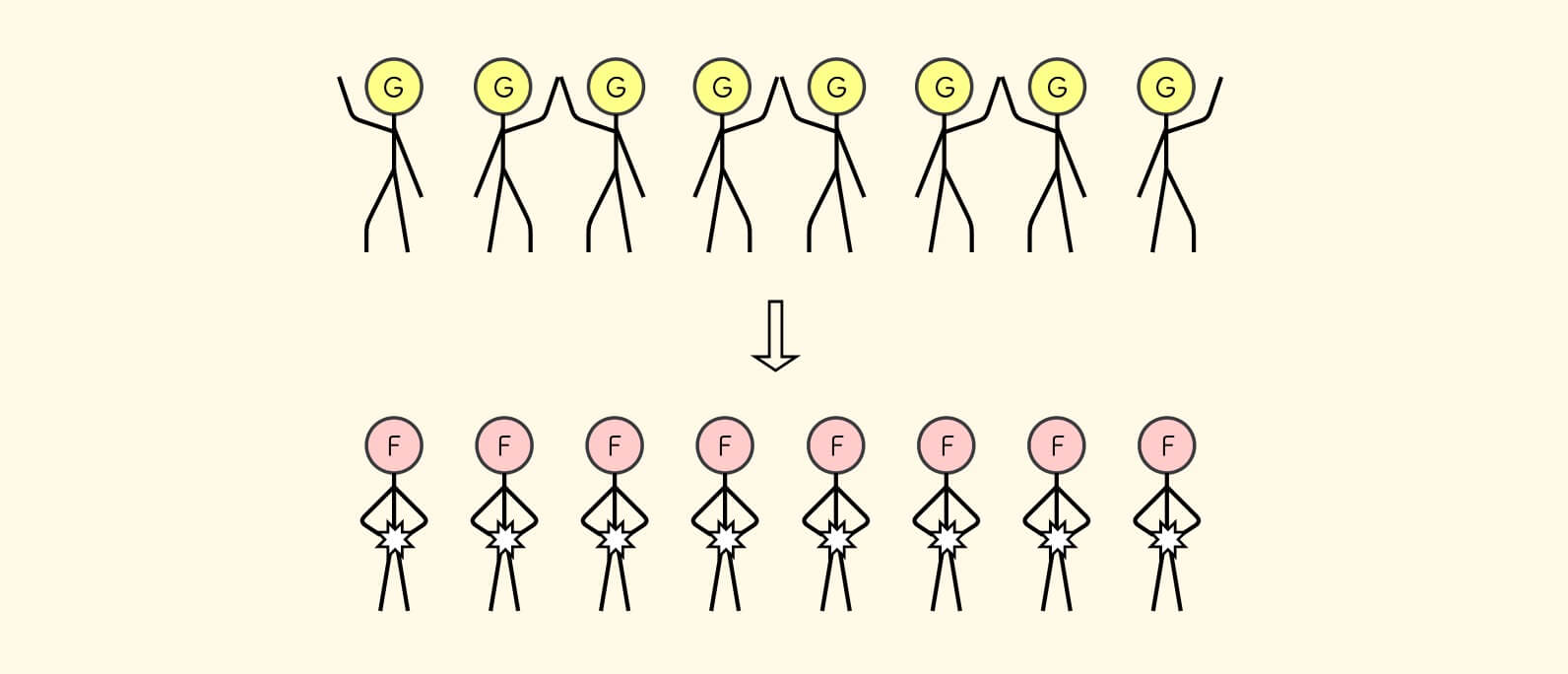
最后把所有步骤连起来看一下:

至此,我们已经知道 8 个士兵的队伍如何运作了。
8 是个特殊的数字,它是 2 的次幂。我们知道 8 个士兵的情况后, 也就知道了 4 个、16 个、32 个士兵 … 的情况了。
不过,奇数个士兵的情况要稍微复杂一点。我们如果知道奇数个士兵的情况如何解决, 那么就知道所有的情况了。
奇数个士兵的情况 ¶
来推演一下 7 个士兵的情况。
在最开始的阶段,和前面 8 个士兵的情况差不多,不同的是,这一次是 A 和 L 相遇。

A 和 L 相遇,也算是迈腿和举手两种动作传播的碰撞,不同的是这一次只需要 A 变为 G , 这样,才得以使队伍一分为二。
可以看到这个将军状态和前面的不太一样,他双手举起、双腿迈出。
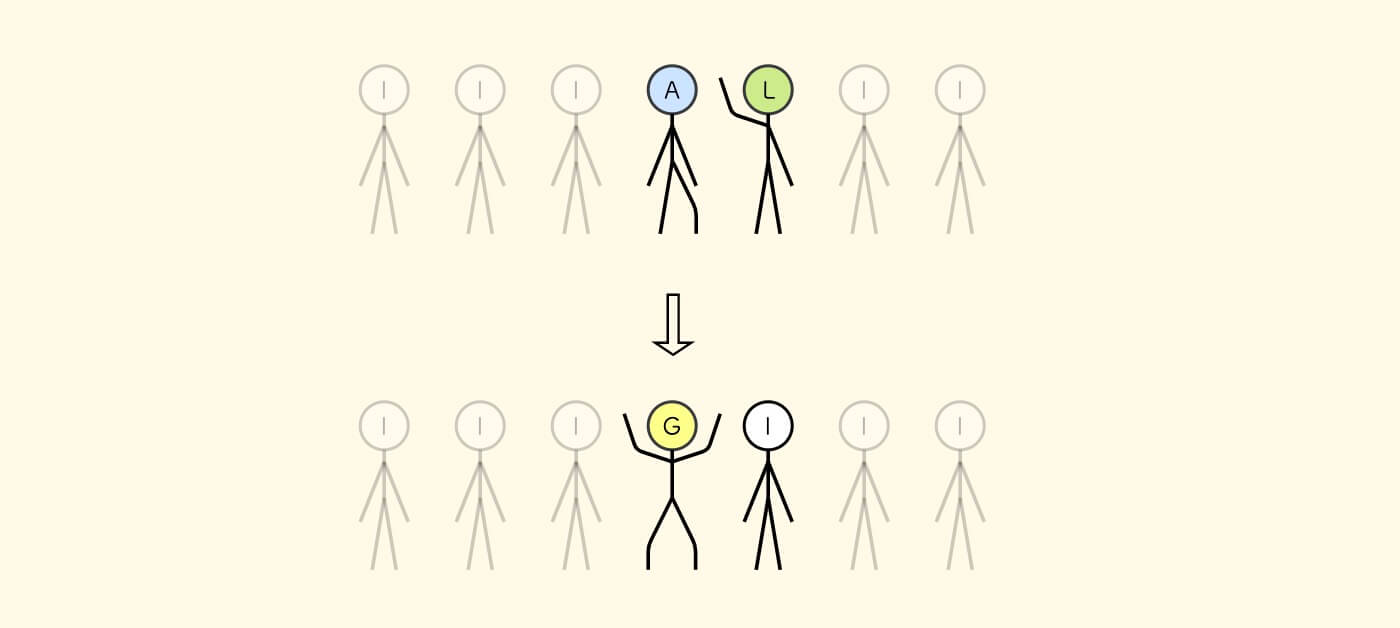
我们可以把这种 G 状态,看成两个将军的综合:
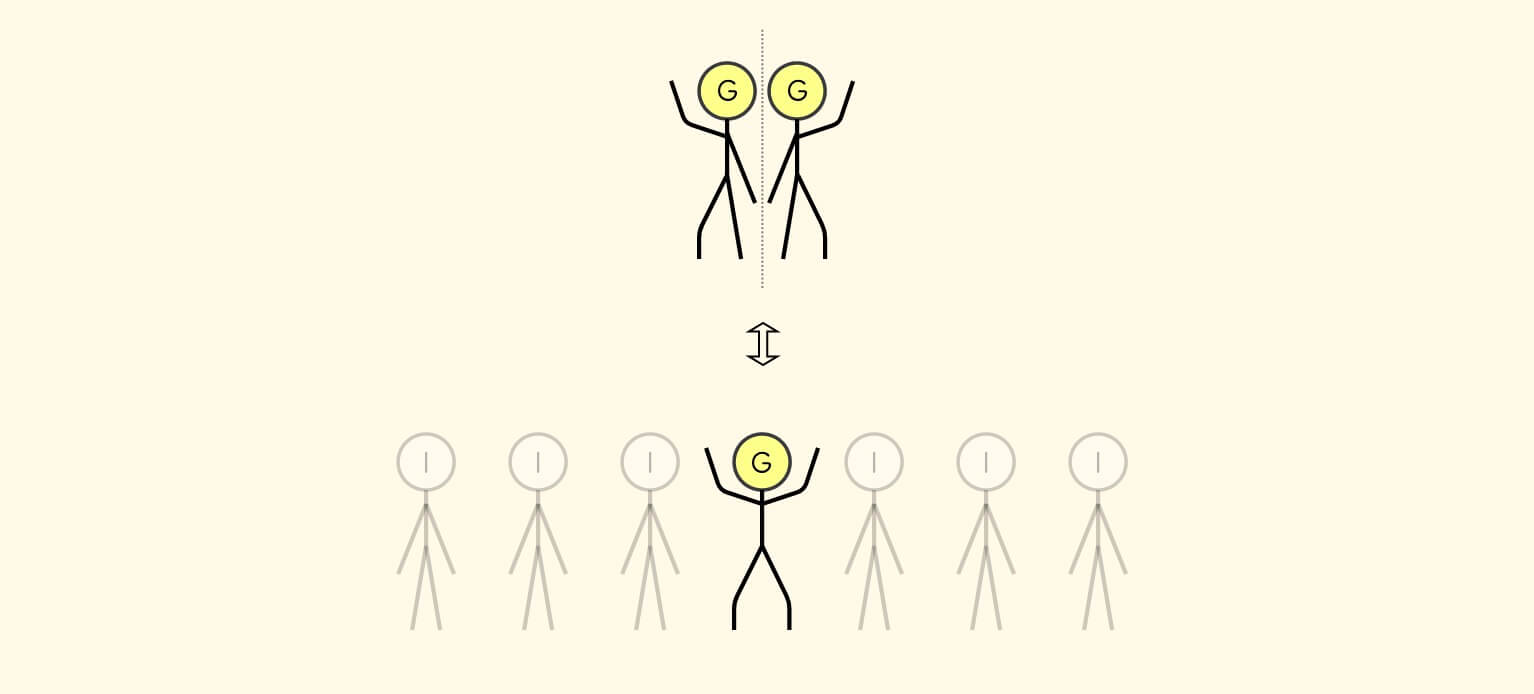
这样,两个将军将分别向左右传播举手和迈腿的动作,达到二分的目的!
同样地,R 和 a 相遇,也会让 a 变为 G 。
现在继续推演,可以看到新增了两个状态:

新增的两个状态是 bB 和 cC ,它们也可以看做两个士兵的综合:
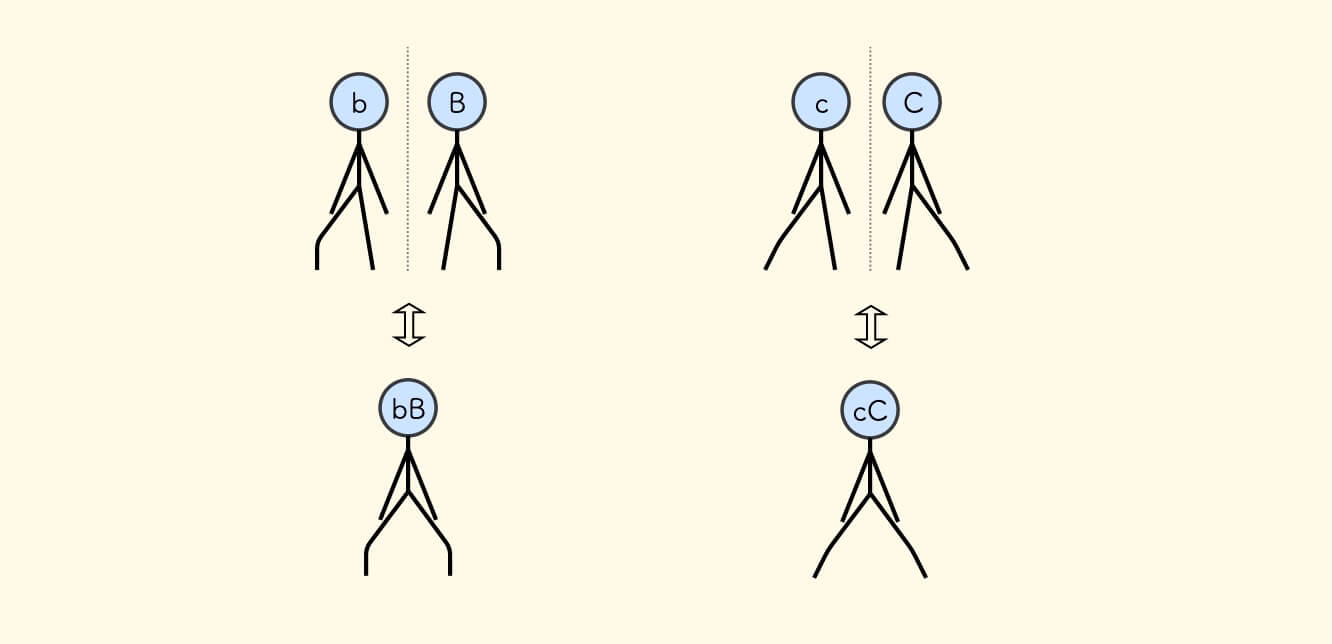
回到图 2.1 继续推演 7 个士兵的情况:

最终,7 个士兵全部运转到同一个状态。
其中,可以看到两个新的状态 RL 和 LR ,这两个组合状态,也可以看做两个士兵的综合, 状态转变就是交换左右手,不再赘述。
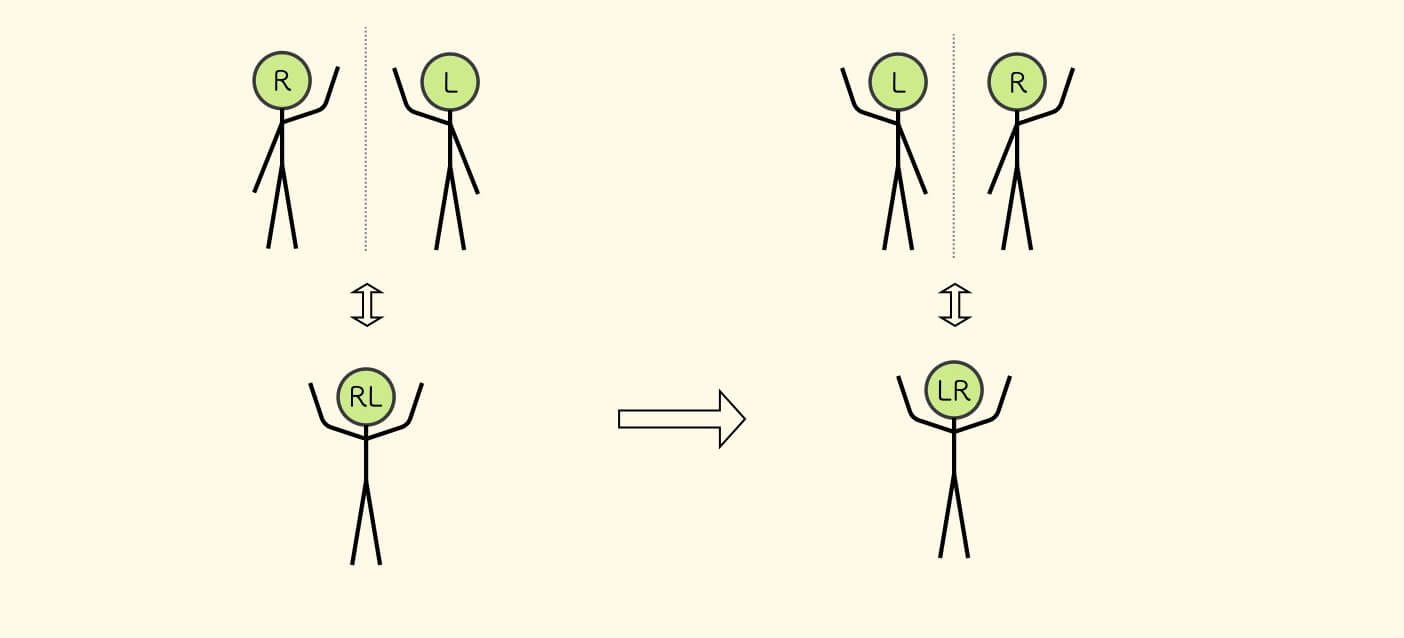
最后把所有步骤连起来看一下:

奇数个士兵的情况已经解决,综合前面 2 的次幂的情况下的思路, 我们已经完成全部情况的思路。
至此,我们一共使用了 15 个状态 (三个将军状态算作一种),让它们集中亮个相吧!
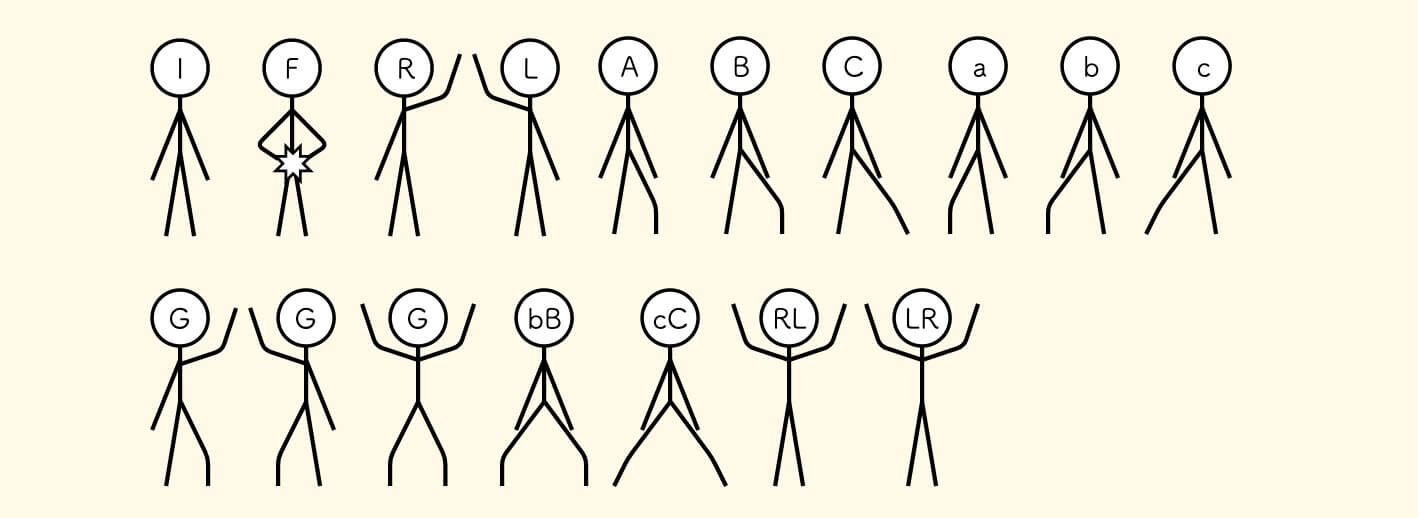
我们真的可以把三种 G 状态算作一个吗?
事实上,三种 G 的传播方向不同,有向左传播的、有向右传播的,还有两边传播的; 并且,三种 G 状态的后续状态也不一样。
但是,可以根据左右邻居的状态判断接下来的传播方向和后续状态。
如果当前士兵处于 G 状态,那么:
- 如果两边的士兵都是静止状态,那么就是双向传播,也即转换为
bB状态。 - 如果只有左边的士兵是静止状态,那么就向左传播,也即转换到
b状态。 - 如果只有右边的士兵是静止状态,那么就向右传播,也即转换到
B状态。
更多的示例 ¶
下面分别是 8 个、7 个、13 个士兵 的情况:

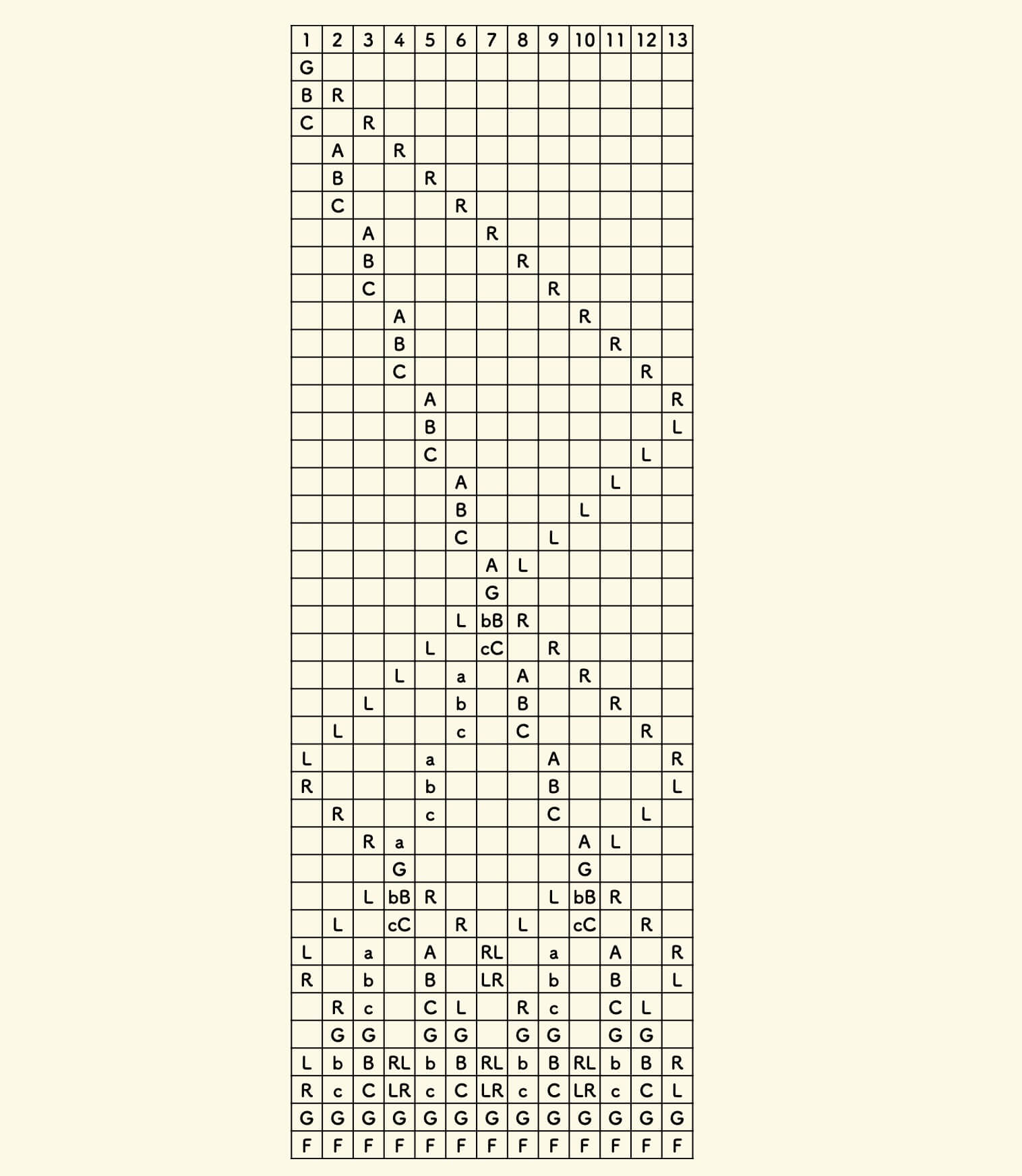
可以看到,这个解决方案的精髓,就是用两个信号的碰撞,不断二分的过程。
时间复杂度 ¶
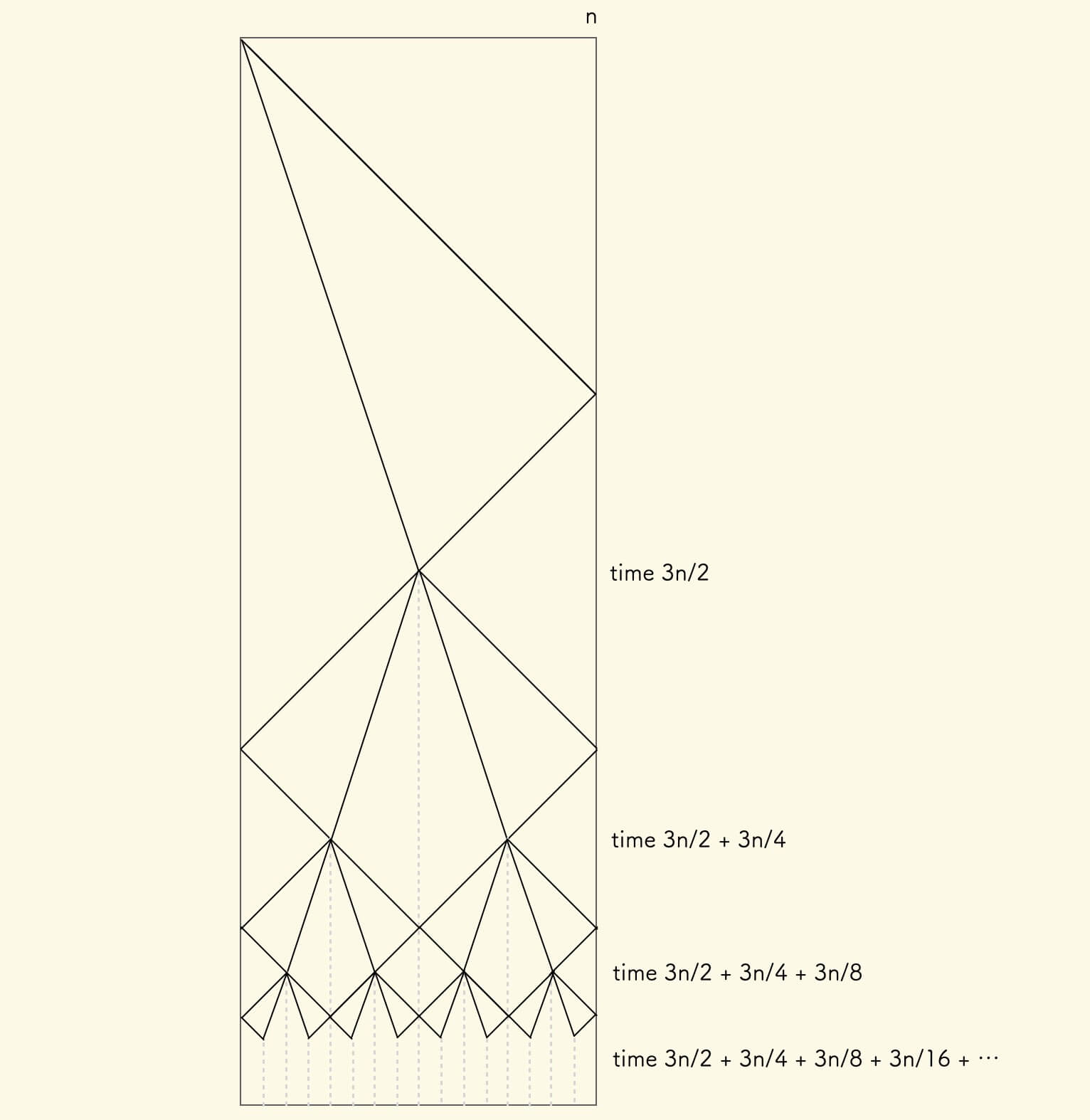
假设士兵的总人数是 n ,那么采用当前方案,到达开火状态的时间开销可以计算得出, 注意 几何级数 收敛:
也就是说,n 个士兵的队伍,在当前方案下,需要 3n 帧时间后才可以开火。
程序实现 ¶
思路清楚后,程序实现并不难, 分析出每个状态机的跳转函数是关键的, 不止需要关注前面所讲的跳转条件,还有 “放下手”、”收回腿” 等隐性的状态跳转。
射击队问题 - 状态跳转函数 - Python
def next(l, s, r):
if s == A:
if r[0] == "L":
return G
return B
if s == B:
return C
if s == C:
if r[0] == "L":
return G
return I
if s == a:
if l[-1] == "R":
return G
return b
if s == b:
return c
if s == c:
if l[-1] == "R":
return G
return I
if s == "bB":
return cC
if s == "cC":
if l[-1] == "R":
return G
if r[0] == "L":
return G
return I
if s == G:
if (l + r) in ("$$", "$G", "G$", "GG"):
return F
if r == I and l == I:
return bB
if r == I:
return B
if l == I:
return b
if s == L:
if l == "$":
return R
if l[-1] == "R":
return R
if l[-1] == "C":
return G
if r == G:
return L
return I
if s == R:
if r == "$":
return L
if r[0] == "L":
return L
if r[0] == "c":
return G
return I
if s == LR:
if l[-1] == "C" or r[0] == "c":
return G
return I
if s == RL:
return LR
if s == I:
if l == G or l[-1] == "R":
if r == G or r[0] == "L":
return RL
return R
if r == G or r[0] == "L":
if l == G or l[-1] == "R":
return RL
return L
if l[-1] == "C":
return A
if r[0] == "c":
return a
return s
源码参见 Firing_squad_synchronization_problem - github 。
最后,这个问题非常有趣!
参考链接:
- Firing squad synchronization problem - Wikipedia
- [Confetti] Firing Squad synchronization problem
- Firing Squad Synchronization Problem - New solutions
(完)
本文原始链接地址: https://writings.sh/post/firing-squad-synchronization-problem
