约瑟夫环问题（线性解法和对数解法）

本文是对约瑟夫环问题的两种解法的简单笔记。

问题 ¶

$0 \sim n-1$ 共 $n$ 个数字围成一圈，从 $0$ 开始计数，排到第 $k$ 个的数字被剔除，然后从下一个数字重新开始计数，如此反复。 找到最后剩下的一个数字。

如果数字是从 $1$ 开始编号的，即 $1 \sim n$ 的 $n$ 个数字的话，答案加一即可。

OJ 题目链接：

• 洛谷 P8671
• leetcode LCR 187. 破冰游戏
• leetcode 1823. 找出游戏的获胜者

线性解法 ¶

定义 $f_k(n)$ 为 $n$ 个数字情况下每 $k$ 个数字剔除一位的问题答案。

首项易得 $f_k(1)=0$，递推式如下，将稍后说明：

代码实现如下，时间复杂度是 $O(n)$ 且与 $k$ 无关：

int josephus1(int n, int k) {
    int f = 0;
    for (int i = 2; i <= n; i++)
        f = (f + k) % i;
    return f;
}

下面是这个递推式的说明。

每次剔除一个数字，问题的规模即减一。

反向思考，已知 $n-1$ 规模的答案，把剔除的数字放回来，得到 $n$ 规模的情况。

下图中，$Case(n-1)$ 是问题规模为 $n-1$ 的情况，目前位于 ① 号状态。

假设此时已知最后剩下的数字是 $f_k(n-1)$。

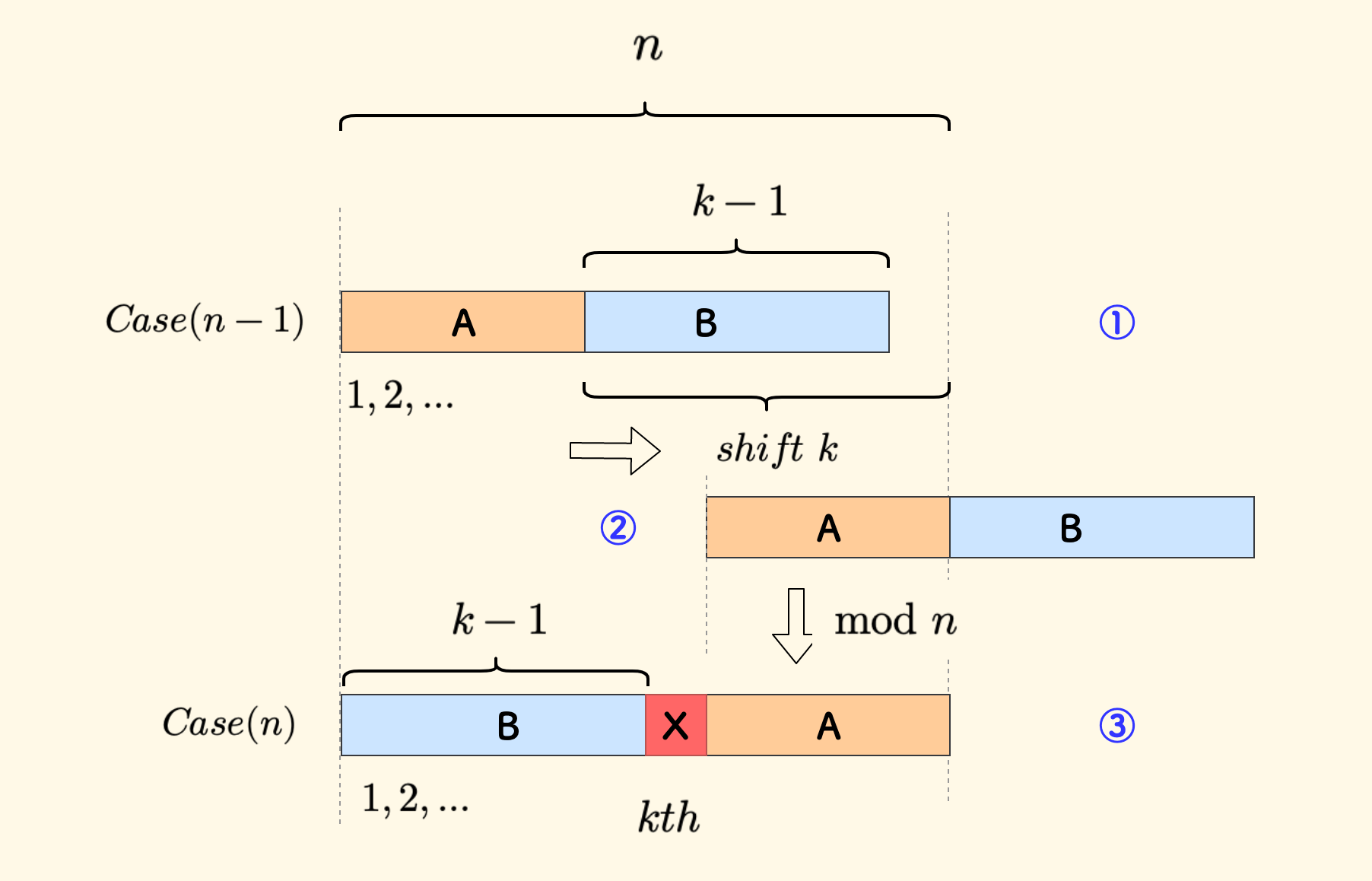
1. 把数列分成 A 和 B 两部分，其中 B 中有 $k-1$ 个数字。
2. 整个数列右移 $k$ 位，来到 ② 号状态。
3. 整个数列再对 $n$ 取模，会来到 ③ 号状态，此时即是问题规模为 $n$ 的情况。

在 ② 号状态下 A 中每个数字都仍小于 $n$，所以取模后不会变。但是 B 中的都会不小于 $n$，取模后会来到头部。

另外，此时 B 尾部和 A 之间会恰好有一个空位。 ③ 号状态下开始计数，这个空缺恰好是第 $k$ 个元素（图中红色的 X），也就是 $Case(n)$ 情况下要删除的数字。

说明按这种映射方法，可以正确地把 $n-1$ 的约瑟夫问题映射到 $n$ 的约瑟夫问题上。

因此，从 $f_k(n-1)$ 反推到 $f_k(n)$ 的时候，每个数字的变化可以描述为下式，最后幸存的数字亦是如此：

初始情况 $f(1)=0$，即唯一的数字 $0$ 就是最后幸存者。从 $f(1)$ 倒推到 $f(n)$ 就得到了答案。

这个说明并不严格，但是应该可以帮助理解的。

总而言之，约瑟夫环问题的线性解法，是一种关于数字规模的反向线性递推方法，$n-1$ 的情况后移 $k$ 位即倒推回了 $n$ 的情况。

对数解法 ¶

前面的线性解法是从 $n-1$ 的情况反推，下面的对数解法是从 $n-n/k$ 的情况反推。

本部分参考文章 cp-algorithms - josephus problem。

这种解法只可优化 $k$ 小于 $n$ 的情况。

考虑 $Case(n)$ 的情况，尽可能不要回头跑完一趟，剔除尽可能多的数字。

最多可以删掉的数字个数是 $p=n/k$ 个（向下取整），余下 $n \% k$ 个数字。

新的计数起点从下图中 A 处开始，每两个删除的数字中间有 $k-1$ 个数字的间隔。

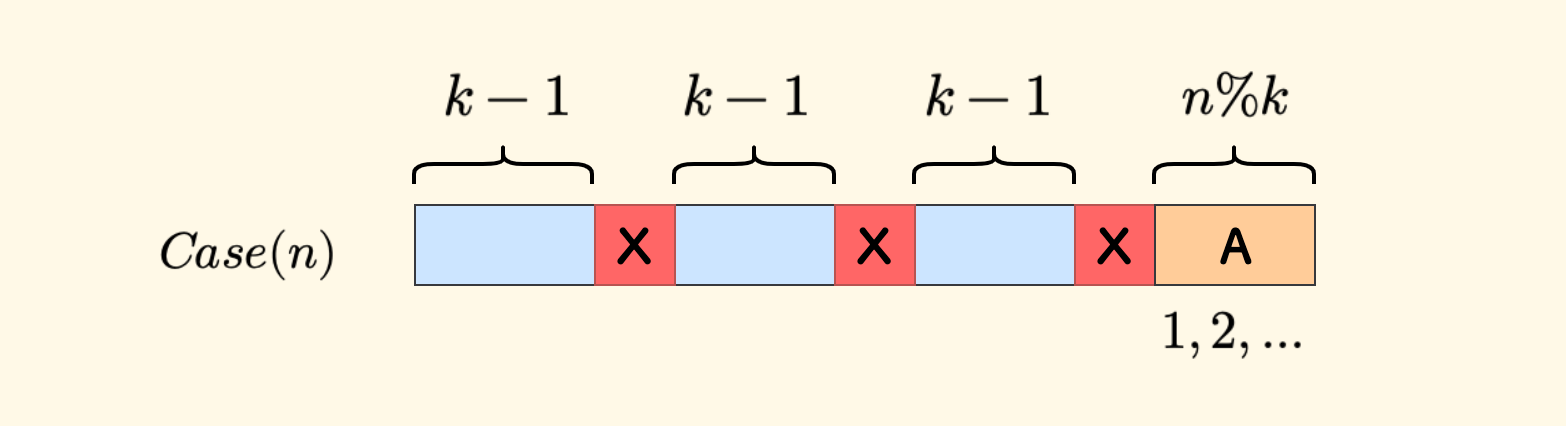
现在看 $Case(n-p)$ 的情况，把数列分成两部分 A 和 B，其中 A 的长度是 $n\%k$。

此时 A 和 B 中的数字都是幸存者，将还原每一个幸存者 F 在 $Case(n)$ 情况下的标号，把删掉的 $p$ 个数字放回来。

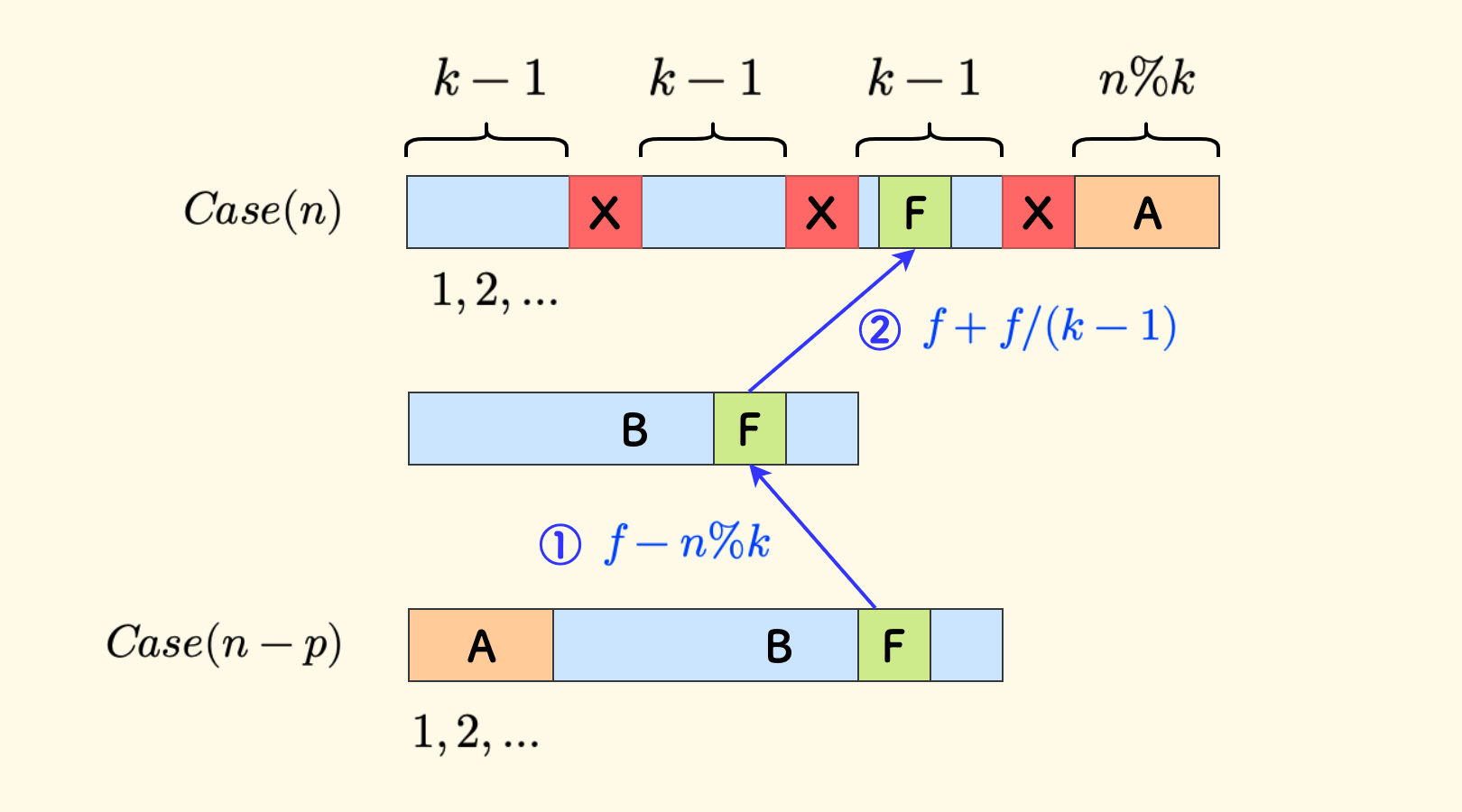
先考虑 F 在 B 中的情况：

1. 第 ① 步，因为 A 中没有被删除的数字，不参与分摊，所以将蓝色的 B 左对齐：

   \[f \leftarrow f - n \% k\]

2. 第 ② 步，把 F 左边被删除的数字补回来，因为每间隔 $k-1$ 个 B 中的数字就删除一个红色的 X，那么 F 左侧一共分摊 $f/(k-1)$ 个：

   \[f \leftarrow f + f/(k-1)\]

还有一种情况是 F 在 A 中的时候，可以尝试兼容一下。

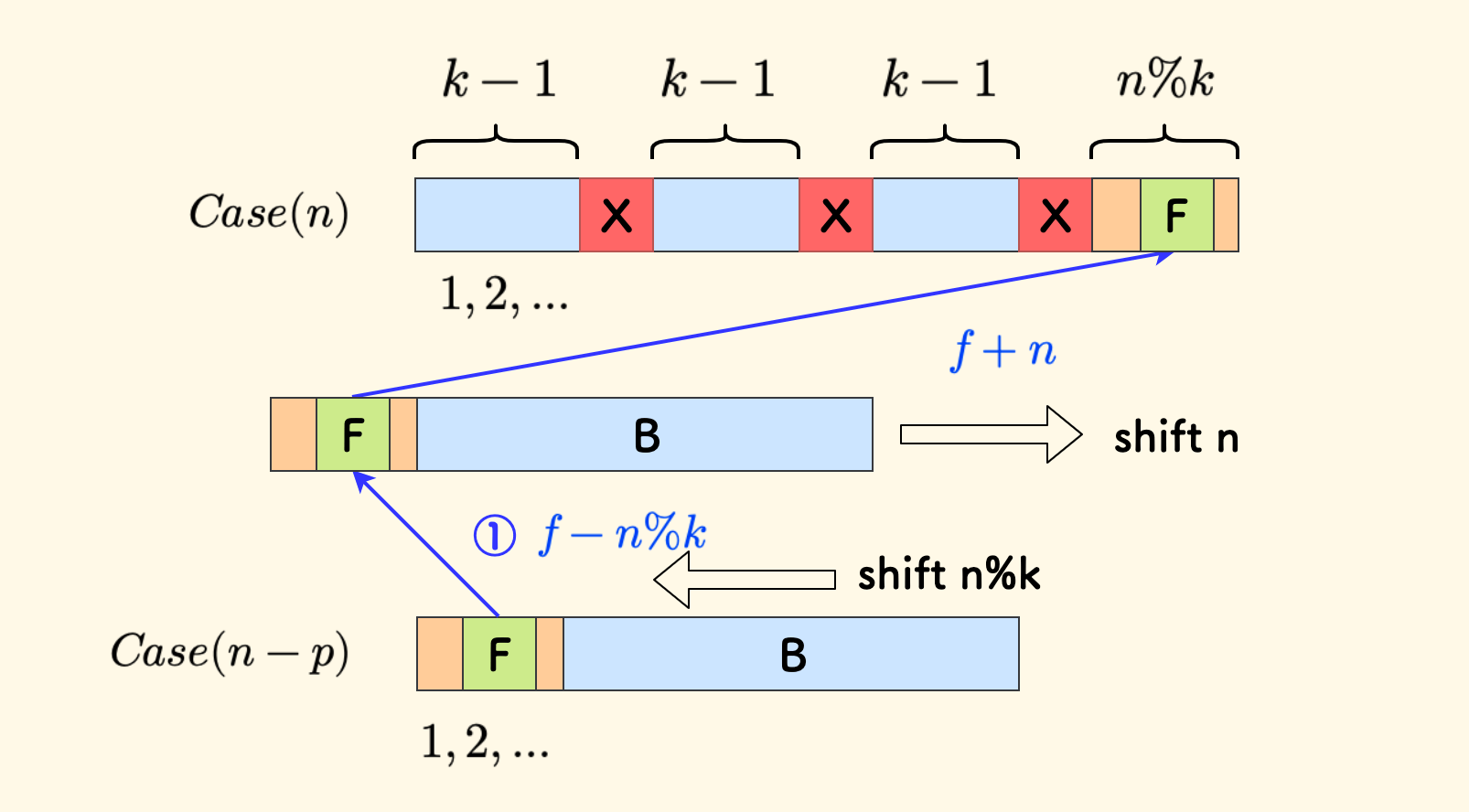
仍然坚持让整个数列左移 $n\%k$，此时 A 中的数字会变成负数，不过没关系，直接再右移 $n$ 就和 $Case(n)$ 中的对齐了。

这是因为 A 的长度就是 $n\%k$，左移这么多，再右移 $n$ 就会跟 $n$ 的数列右端对齐。

注意考虑两个特例：

• $k = 1$ 时，除数 $k-1$ 变成 $0$ 失效，此时答案可特判为 $n-1$，相当于依次删除，最后一个数字一定是最终幸存者。
• $k > n$ 时，此时 $n/k$ 整数是 $0$，问题规模没有减小，此时要退化到线性解法。

综合来看，代码实现如下：

int josephus2(int n, int k) {
    if (n == 1) return 0;
    if (k == 1) return n - 1;
    if (k > n) return (josephus2(n - 1, k) + k) % n;
    int f = josephus2(n - n / k, k) - n % k;
    return f + (f < 0 ? n : (f / (k - 1)));
}

复杂度分析上，只分析 $k$ 小于 $n$ 的情形，每次会剩余 $n(1-\frac{1}{k})$ 个数字，假设迭代 $x$ 次，那么：

中间计算省去不会（可参考 cp-algorithms），最终的结果是 $x \approx k\log{n}$。

也就是时间复杂度是 $O(k\log{n})$。

using ll = unsigned long long;
int josephus3(int n, int k, ll q) {
  if (k == 1) return n - 1;
  for (q = q * k + k - 1; q >= n; q = q - n + (q - n) / (k - 1));
  return q;
}

benchmark ¶

我简单地对约瑟夫问题的三种解法（包括 MaskRay 博客的那个对数解法 ^[1]）做了一下 benchmark，代码和结果在 code-snippets - github。

大概结论是：

1. $k$ 比较小的时候（小于 $n$）：对数解法比线性解法快 10 倍左右，但是二种对数解法差距不大。
2. $k$ 比较大的时候（大于 $n$）：线性解法最优，对数解法由于会降级到线性解法，表现和线性解法接近。MaskRay 博客的那个对数解 法^[1] 会严重恶化。

从复杂度来看，线性解法的时间复杂度是和 $k$ 的大小无关的，而对数解法的复杂度则是 $O(k\log{n})$，所以 $k$ 大于 $n$ 时对数解法不如线性解法。

一种比较好的策略是：$k < n$ 时用对数解法，否则用线性解法。

（完）

本文原始链接地址： https://writings.sh/post/josephus