逻辑时钟是描述分布式系统中时序和因果关系的一种机制。 由于网络延迟、时钟漂移等现实问题,我们无法建立一个全局物理时钟来描述时序, 因此区别于物理时钟的「逻辑时钟」机制应运而生。 第一个逻辑时钟算法是由分布式领域的大神 Lamport 在1978年提出的 lamport 时钟算法。

本文将从一个基础问题的讨论切入,逐步介绍:
- 为什么需要逻辑时钟 – 物理时钟是否可行?
- 相对论是带来了什么启示 – 事件的相对性
- 最早期的逻辑时钟算法什么特点 – Lamport逻辑时钟
- 后续改进的算法有哪些 – 「向量时钟」和「版本向量」等等
逻辑时钟的思想有趣而深刻,值得探究。
本文内容非常长,需要读者静心阅读。
如何确定分布式系统中事件的发生顺序? ¶
首先,我们来观察一个「如何确定分布式系统中事件的发生顺序」的问题:
在这个分布式系统中,有三个独立的进程A、B、C:
- 首先,进程A中发生了一个事件$a$,并把这个事件消息同步给另外两个进程B和C。
- B收到消息后,发生了一个事件$b$,并把这个事件消息同步给进程C。
- 但是由于无法确定的网络延迟原因,导致进程A发出的消息到达C晚于进程B发出的消息到达C,这样 进程C的视角上,最终看到的事件顺序是 $b, a$,但是这与事实是相悖的。
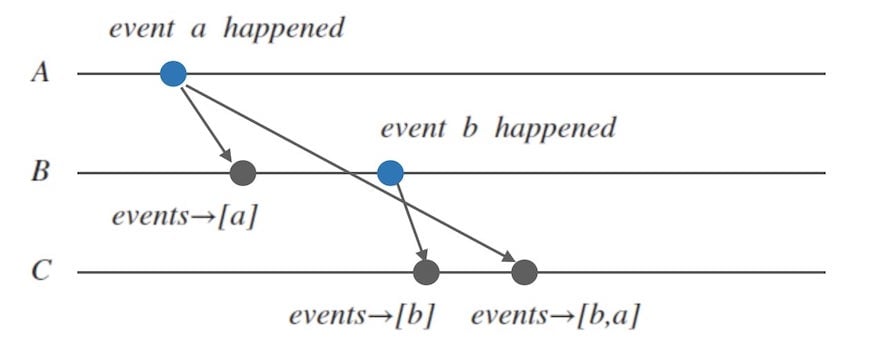
可以看到,在分布式通信中,由于网络延迟的不确定性, 仅仅以接收顺序作为整个分布式系统中事件的发生顺序是不可取的。
下面我们再观察一个稍微现实点的例子。
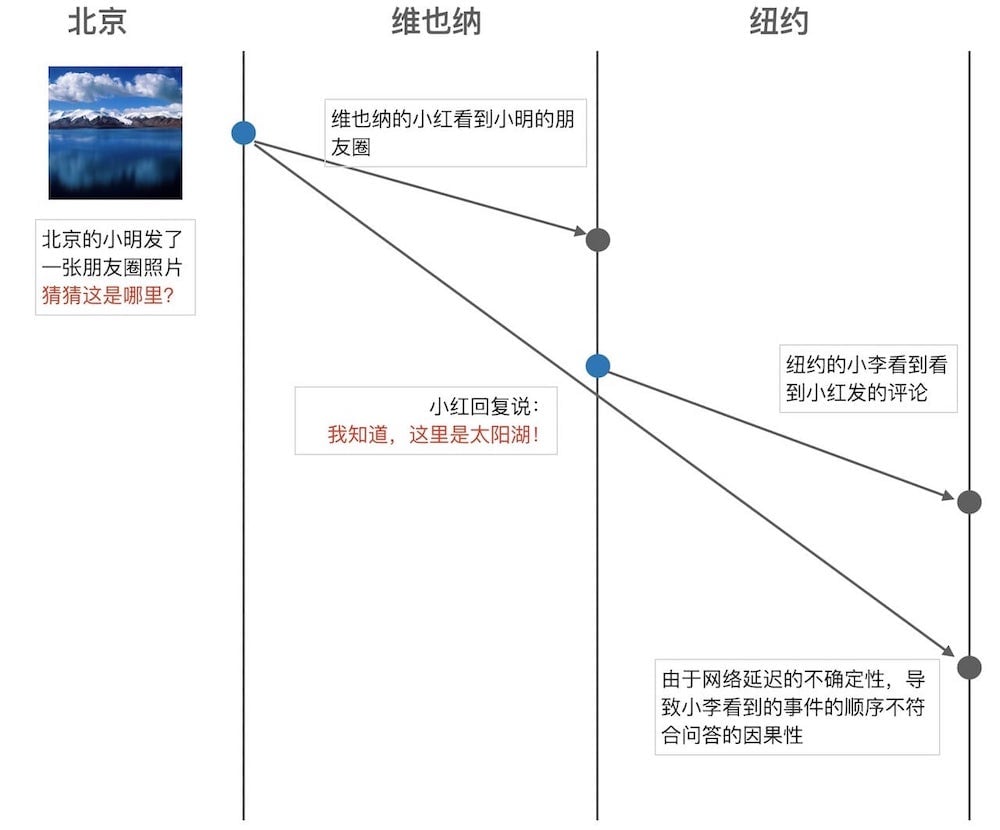
- 假设朋友圈有三个数据中心,分别在北京、维也纳和纽约。
- 北京小明在朋友圈中发了一张风景图,并问到「猜猜这里是哪里?」,这条消息被扩散到其他数据中心。
- 维也纳的小红看到这个消息后,回复说她知道。这条回复也被扩散到其他数据中心。
- 但是由于无法确定的网络延迟的原因,导致纽约的数据中心先收到小红的回复,而后收到了原始的提问消息。 这样,导致最终小李看到的问答顺序是不符合问答的因果一致性的。
下面是微信朋友圈架构设计的两个关于因果一致性算法设计的PPT截图(来自《微信朋友圈技术之道》,链接已经损坏):

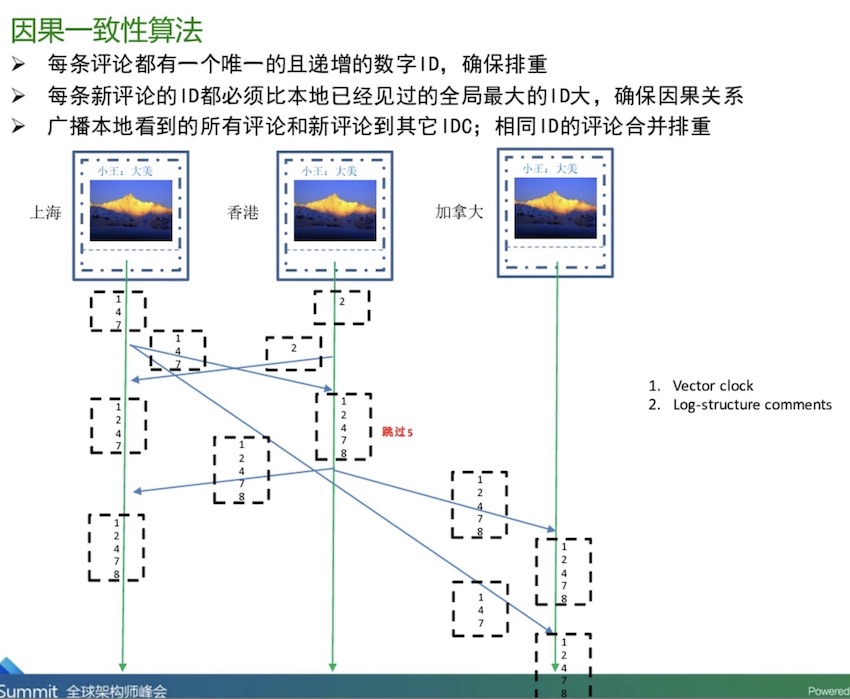
在腾讯的分享PPT中,提到了「向量时钟」, 不过我们稍后再揭开它的神秘面纱。
而这两个例子中,我们面临的要解决的问题, 其实是分布式系统中的因果一致性, 换句话说,就是如何准确刻画分布式中的事件顺序, 显然仅仅简单地依靠进程接收到的(看到的)事件发生顺序是不准确的。
全局物理时钟 ¶
对于上面提到的两个问题,我们试图解决的一个天然想法是, 记录每个分布式进程中发生事件的原始时间戳, 并把它连同事件本身扩散到其他节点,这样其他节点的视角上就可以观察到完整的因果顺序了?
If you have one clock, you know what the time is. If you have two, you are not sure.
大家都清楚的一点是,不同节点的物理时钟其实是不一致的,而且无法做到精确一致。
其原因:
- 仍然是由于网络延迟的不确定,我们无法通过网络同步时间来获取一个全局一致的物理时钟。
- 现实中的多个时钟,即使时间已经调成一致,但是由于日积月累的计时速率的差异,会导致时钟漂移而显示不同的时间。
如此看来,寄希望于一个全局的时钟来对事件顺序做全局标定也是不现实的。
参考链接:
全序和偏序 ¶
在数学上,「顺序」是如何描述的?
我们看下序理论中的两种序关系:偏序(partial ordering) 和 全序 (total ordering).
偏序: 假设 $\le$ 是集合$S$上的一个二元关系,如果 $\le$ 满足:
- 自反性: 对$S$中任意的元素$a$,都有 $a\le a$.
- 反对称性: 如果对于$S$中的两个元素 $a$ 和 $b$, $a\le b$ 且 $b\le a$,那么 $a=b$
- 传递性: 如果对于$S$中的三个元素,有$a\le b$ 且 $b\le c$, 那么 $a \le c$
以上的数学内容其实不那么重要~ 关键理解: 偏序关系是一种序关系,但只是部分元素有序,并不是全部元素都可以比较。
全序则比偏序的要求更为严格一些, 在偏序的基础上,多了一个完全性的条件:
- 完全性: 对于$S$中的任意$a$ $b$元素,必然有 $a \le b$ 或 $b \le a$.
可以看出,实际上, 全序就是在偏序的基础上,要求全部元素都必须可以比较。
总结来看,简短说: 偏序是部分可比较的序关系,全序是全部可比较的序关系。
举例来看:
- 自然数集合中的比较大小的关系,就是一种全序关系。
- 集合之间的包含关系,则是一种偏序关系(集合之间可以有包含关系,也可以没有包含关系)。
- 复数之间的大小关系,是一种偏序关系,而复数的模的大小关系,则是一种全序关系。
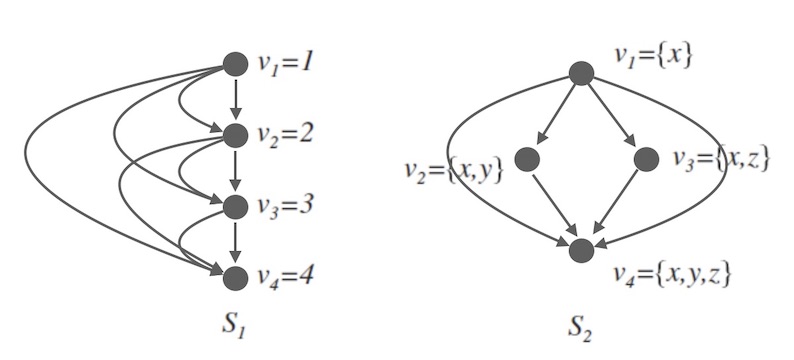
下面用简单的有向图(哈斯图)来描述下全序和偏序的区别:
图5中$S_{1}$上的图示关系,描述的是整数之间的大小顺序,是一种全序关系,可以看到任意两个元素之间都可以比较顺序。
而$S_{2}$上的关系,描述的是集合之间的包含关系,是一种偏序关系,其中 $v_{2}$ 和 $v_{3}$ 是不可比较的。
现在我们回头看,寻求全局时钟为分布式节点中的时间做顺序标定的方式, 其实是在寻求一种全序关系来描述分布式中的事件顺序, 而且是严格对齐真实的物理时钟的全序关系。
事件先后的相对性 ¶
逻辑时钟的概念是由著名的分布式系统科学家 Leslie Lamport (2013年图灵奖得主) 提出的, 在他的那篇著名的论文「Time, Clocks and the Ordering of Events in a Distributed System」 的介绍上,lamport提到了著名的狭义相对论:
Special relativity teaches us that there is no invariant total ordering of events in space-time; different observers can disagree about which of two events happened first. There is only a partial order in which an event e1 precedes an event e2 iff e1 can causally affect e2.
Leslie Lamport 《Time, Clocks and the Ordering of Events …》
爱因斯坦的狭义相对论告诉我们,时空中不存在绝对的全序事件顺序, 不同的观察者可能对哪个事件是先发生的无法达成一致。 但是有偏序关系存在,当事件e2是由事件e1引起的时候,e1和e2之间才有先后关系。
对于「不同的观察者可能对哪个事件是先发生的无法达成一致」这个说法, 我们从同时的相对性开始说起:
根据狭义相对论,发生在空间中不同位置的两个事件,它们的同时性并不具有绝对的意义, 我们没办法肯定地说它们是否为同时发生。若在某一参考系中此两事件是同时的,则在另一相对于原参考系等速运动的新参考系中, 此两事件将不再同时。
维基百科「同时的相对性」
因为狭义相对论最基本的假设,光速不变原理: 无论在何种惯性参考系下,光在真空中的传播速度相对观察者都是一个常数。所以「同时」这个概念也是相对的。
关于同时的相对性,有一个著名的火车思想实验:
有一个观察者$A$在移动的火车中间,有另一位观察者$B$在地面上的月台上, 当两个观察者相遇时,一道闪光从火车的中央发出。
对于火车上的观察者$A$而言,由于火车头和火车尾距离光源的距离是相同的, 因此观察到了光同时到达了车头和车尾。
但是对于月台的观察者$B$而言,火车的尾部会迎向光移动,而车头会远离光移动, 而且光速是有限的,且相对于两个观察者都是相同的常数,所以$B$认为光会先到达车尾,后到达车头。
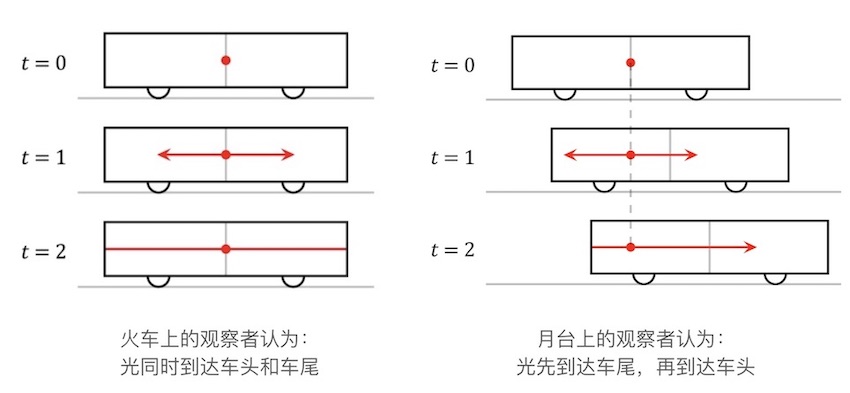
这样,对于不同参照系的观察者而言,事件的顺序并没有一个一致性的结论。 之所以得出这样神奇的结论,仍然是因为关键的「光速不变原理」。 但是,这并不意味着发生了因果上的逻辑矛盾, 我们在这种情况下,只是无法在不同的参照系下观察到一致性的事件顺序。
我们经验上所说的「同时发生」,是因为光速太大,或者我们生活的尺度太小, 所以同时是一种近乎同时。
相对论告诉我们,光速是物质移动的最大速度,信息传播的速度不可能超过这个速度。 假如太阳消失了,地球上的我们也要在8分钟之后感知到太阳消失了。
也就是说,一个事件$A$发生后, 载有这个事件信息的光(引力、无论什么,快不过光速)到达观察者之前, 观察者是无法没有任何感知的, 这时我们就无法定义事件的顺序。 而当信息最终传播到达观察者时, 这个事件也就对观察者发生了影响, 造成了一个新的事件$B$,叫做「观察到了事件$A$的事件$B$」。 这时我们才有 $A$ happened before $B$ 的因果关系。
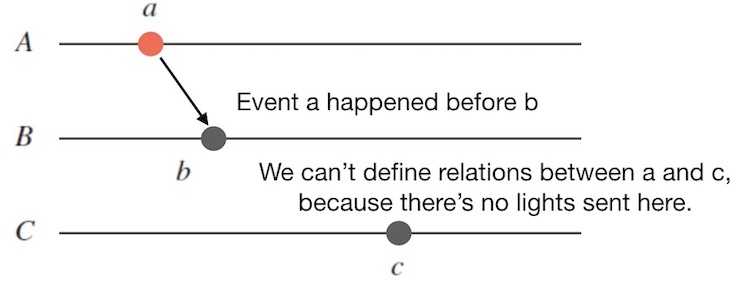
可以看到,时空对于描述事件顺序的「happened before」同样是偏序关系。
因为事件$A$的发生, 造成了事件$B$的发生(包括$B$这种观察$A$而发生的事件),那么$A$和$B$就存在因果关系。
Lamport受相对论中事件顺序的相对性的启发,创造了Lamport Logical Clocks。
我们的分布式系统,和相对论有很多相似之处:
- 在物理时空中,信息是通过光速传播的,而在分布式系统中,信息是通过网络传播的。
- 在物理时空中,不同参照系下的观察者可能对于事件顺序无法达成一致, 而在分布式系统中,由于全局物理时钟无法实现,不存在进程拥有全局视角。 而如果进程间的事件没有因果关系,那么就无法达成顺序上的一致性。
- 在物理时空中,由于光速限制,观察者在观察到事件$A$的时候,才确定了事件$B$和$A$的因果关系。 那么在分布式系统中,我们同样可以通过消息传递来创造因果关系。
总体来说, 逻辑时钟尝试用「通过进程间创造通信以添加因果关系」的方式来对分布式中的事件顺序做描述。
下面,我们来看下,「通过通信创造因果关系」 这个设计对于刻画分布式系统中的事件顺序有多么重要。
观察下面图8中的两个图:
- 红色的点表示自发性事件。 黑色的表示『观察到其他进程事件』而发生的事件。
- 横向黑色实线代表物理时钟。
- 带箭头的线表示进程中一个事件发生时,向另外一个进程传播这个事件。
我们试着从每个进程的视角,依次对图$S_{1}$和$S_{2}$进行推导一下,会发现, 其实两个图所描述的事件顺序,在进程的相对视角中,是一样的。
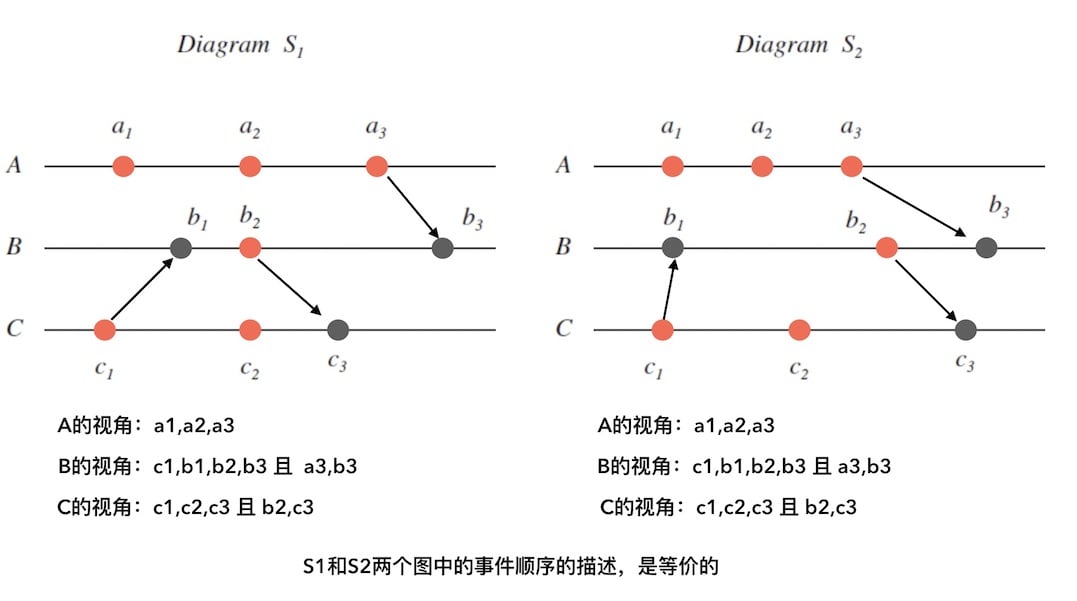
我们的逻辑时序应该越接近物理时序越好,然而两个图对时序的刻画, 出现了歧义(比如无法确定 $a_{3}$ 和 $b_{2}$ 的顺序)。 根本上是没有做充分的消息传递来添加因果关系。
逻辑时钟(Lamport’s timestamp) ¶
现在,我们开始讨论Lamport的逻辑时钟算法。
首先我们需要明确一点: 逻辑时钟并不度量时间本身,仅区分事件发生的前后顺序。
那么,「事件」是如何分类的:
- 进程内自发的事件(如下图中的红色标记的事件)。
- 发送一个消息,是一个事件(如下图中的蓝色标记的事件)。
- 接收一个消息,是一个事件 (如下图中的黑灰色标记的事件)。
我们上面有提到「happened before」的关系,我们知道,因果关系是推导「happened before」关系的重要一环:
if $e_{i}$ causes $e_{j}$, then $e_{i}$ must happen before $e_{j}$ – Logical Time
道理是显然的:如果事件$e_{i}$导致了事件$e_{j}$,那么一定$e_{i}$发生在$e_{j}$之前。
我们现在给「happened before」这个关系一个记号: $\rightarrow$, 事件$a$在事件$b$之前发生则表示为 $a \rightarrow b$, 那么我们有:
- 如果 $a$ 和 $b$ 是同一个进程内的事件,并且 $a$ 在 $b$ 之前发生,则 $a \rightarrow b$。
- 如果事件 $a$ 是「发送了一个消息」,而事件 $b$ 是接收了这个消息,则 $a \rightarrow b$。
- 如果 $a \rightarrow b$ 并且 $b \rightarrow c$ ,那么 $a \rightarrow c$ (即传递性)。
那么,是否存在两个事件并无顺序关系吗? 经过前面的讨论,答案当然是肯定的。
如果两个事件无法推导出顺序关系的话,我们称两个事件是并发的,记作 $a \parallel b$。
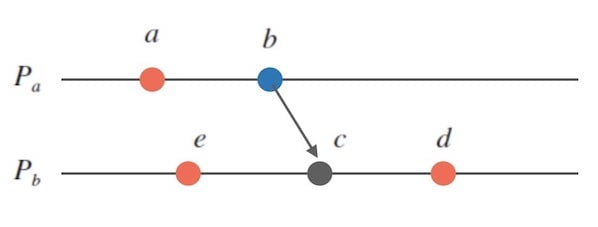
这样,我们可以这样描述上面的图9中存在的事件顺序:
- $a \rightarrow b \rightarrow c \rightarrow d$
- $e \rightarrow c \rightarrow d$
- $a \parallel e$
- $b \parallel e$
可以看出, 「 happened before」$\rightarrow$ 是一个偏序关系。
Lamport的时钟算法:
- 每个进程 $P_{i}$ 内维护本地一个计数器 $C_{i}$ ,初始为$0$.
- 每次执行一个事件,计数器 $C_{i}$ 自增 (假设自增量为$1$).
- 进程 $P_{i}$ 发消息给进程 $P_{j}$ 时,需要在消息上附带自己的计数器 $C_{i}$.
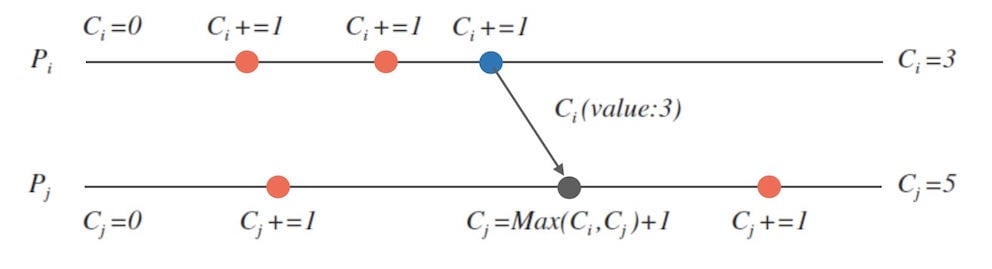
- 当进程 $P_{j}$ 接收到消息时,更新自己的计数器 $C_{j}=Max(C_{i}, C_{j})+1$
下面的图10是这个算法的示意图,可以推算最后的时钟计数器的值:$C_{i}=3$, $C_{j}=5$
下面,将证明:如果 $a \rightarrow b$,那么一定有 $C_{a} < C_{b}$。
- 假设 $a$ 和 $b$ 发生在同一个进程内,显然 $C_{a} < C_{b}$.
假设 $a$ 和 $b$ 分别处在不同的进程内,如 $P_{a}$ 和 $P_{b}$,
根据事件先后的定义,必然存在一个不早于 $a$ 且 不晚于 $b$ 的由 $P_{a}$ 到 $P_{b}$ 的通信 (否则 $a \parallel b$ ,矛盾)。
那么假设两个进程在 $a$ 和 $b$ 之间最近一次通信是由 $P_{a}$ 向 $P_{b}$ 发送了消息 $a \rightarrow b$: 易得 $a \rightarrow c \rightarrow d \rightarrow b$ (其中可能 $a=c$ 或者 $d=b$) 。根据算法定义,得:
- $C_{a} \le C_{c}$ (进程内计数器自增).
- $C_{d} \le C_{b}$ (进程内计数器自增).
- $C_{c} < C_{d}$ (进程间通信,观察者事件已经严格大于发生者事件的计数器)。
那么,最终推导出 $C_{a} < C_{b}$(严格小于)。

图11 - 事件 $a$ 和 $b$ 在不同进程的情况下,中间一定有消息传递,否则两个事件并发
以上,得证 $a \rightarrow b \Rightarrow C_{a} < C_{b}$。
但是,如果我们已知 $C_{a} < C_{b}$ 的话,是否可以推导出 $a \rightarrow b$ 呢?
悲哀的是,不能。 下面的图12是个反例:
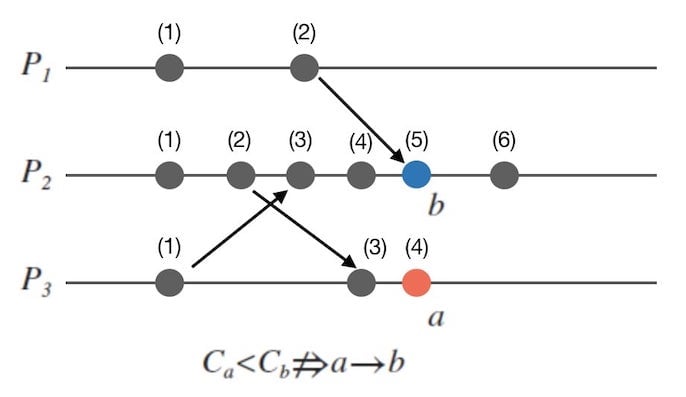
这样,我们反证了 $C_{ a } < C_{ b } \nRightarrow a \rightarrow b$。
我们无法推导出 $C_{ a } < C_{ b } \Rightarrow a \rightarrow b$ 的原因,在于 $a$ 可能和 $b$ 并发。
但是, 如果 $C_{ a } < C_{ b }$,一定不会有 $b \rightarrow a$ 的关系存在。
Lamport的逻辑时钟算法构建了一个全序(total ordering)时钟来描述事件顺序, 但是我们知道「happened before」是一个偏序关系, 用全序关系的一维计数器来描述「happened before」的话, 就会导致无法等价化描述的结果, lamport时钟的缺陷在于:如果两个事件并不相关,那么这个时钟给出的大小关系则没有意义, 这个缺陷其实恰好就是全序和偏序的不同点而已。
所以,要准确描述事件顺序,我们终究要寻求偏序方法。
于是,我们继续探讨向量时钟。
向量时钟 (Vector Clocks) ¶
向量时钟,其实是对Lamport的时钟的一个延伸思考,算法结构一致,只是多传了一部分信息。
对每个进程,定义一个向量 $VC$ ,向量的长度是 $n$, $n$ 是进程数目。
- 初始化各个进程 $P_{i}$ 的向量, 全部抹零: ${VC}_{i} = [0,…,0]$。
- 进程 $P_{i}$ 每发生一个事件时, 其向量的第 $i$ 个元素自增: ${VC}_{i}[i] += 1$。
- 当进程 $P_{i}$ 发消息给进程 $P_{j}$ 时,需要在消息上附带自己的向量 ${VC}_{i}$。
当进程 $P_{j}$ 接收到消息时,对齐对方的时钟,并在自己的时钟上自增:
对 $[0, n)$ 上的任意一个整数 $k$ 执行 $VC_{j}[k] = Max(VC_{j}[k], VC_{i}[k])$ ,
接着,对应第2点: $ {VC}_{j}[j]+=1 $ 。
下面图13是一个向量时钟算法的示意图:
- 和lamport时钟算法示意图一样:(红色点、蓝色点、黑灰色点..)
图的右方部分,总结了这个算法对不同事件的操作:
- 对于红色和蓝色,也就是进程内自发性事件和发送消息的事件,向量内相应的计数器自增。
- 发送消息的时候,需要传播出去自己的整个向量(也就是广播自己对整个系统的视角)。
- 接收到消息的时候,也就是蓝色事件,需要对齐对方的向量,并应用第一条规则,即自己的向量内相应计数器自增。
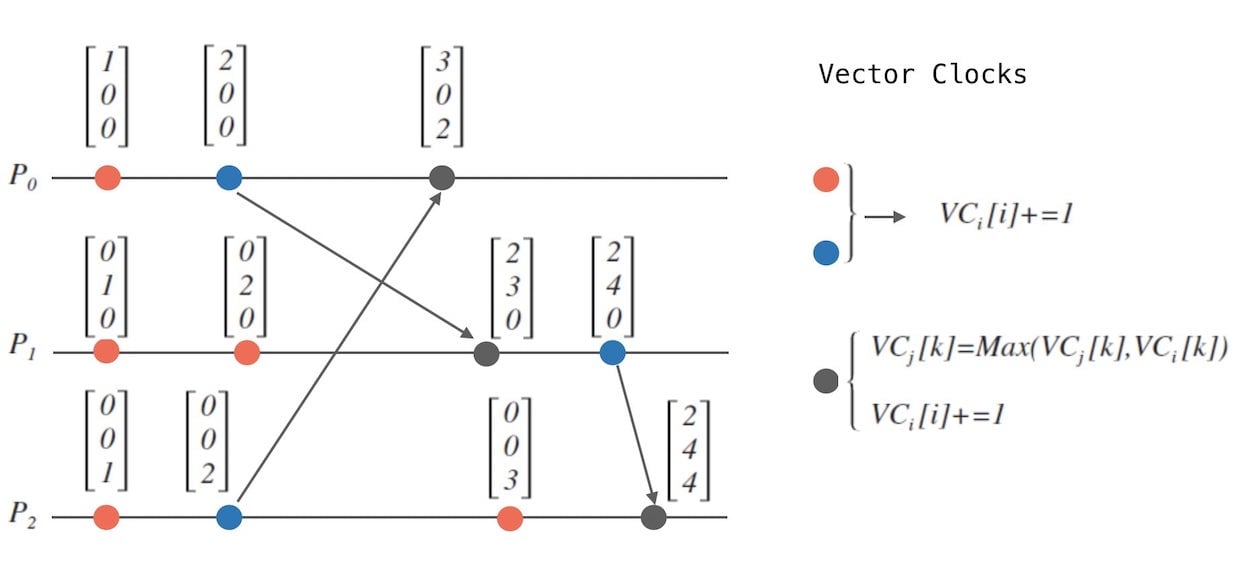
可以发现,向量时钟和lamport的时钟算法结构一样, 不同的点在于: lamport时钟只是在对齐时钟的计数器, 而向量时钟是在对齐各自对整个系统的视角。
我们可以推导出来关于向量时钟比较大小的几个性质:
向量的各维相等,则向量相等。 这个是显而易见的。
向量时钟是有序的 (充要),即:
$VC_{i}$ 的各维上的值不大于 $VC_{j}$ 对应维上的值, 则认为 $VC_{i}$ 不大于 $VC_{j}$ 。
向量时钟有序性质的进一步细化,定义了严格小于:
如果 $VC_{i}$ 不大于 $VC_{j}$ , 并且至少存在一个维,在这个维上 $VC_{i}$ 的值严格小于 $VC_{j}$ 在这个维上的值, 则认为 $VC_{i}$ 小于 $VC_{j}$。
如果两个向量不存在大小关系,则认为两个向量平行,记作 $VC_{i} \parallel VC_{j}$.
这几个性质看起来复杂,其实都是在定义向量时钟之间的大小关系。 我们可以得出一个结论:
向量时钟之间的大小关系是一种偏序关系。
和lamport时钟一样,我们可以利用类似的推导方式,证明 $ a \rightarrow b \Rightarrow VC_a < VC_b$ 。 这里不再描述证明思路。
我们接下来要花一定篇幅论证下 $VC_a < VC_b \Rightarrow a \rightarrow b$ 。
- 如果 $a$ 和 $b$ 两个事件处在同一个进程中,显而易见 $a \rightarrow b$ 。
假设 $a$ 和 $b$ 分别处在不同的进程内,如 $P_a$ 和 $P_b$ ,
设 $VC_a = [m,n]$ , $VC_b = [s,t]$ 。
因为 $VC_a < VC_b$ ,所以 $m \le s$, 所以必然在 不早于 $a$ 之前 和 不晚于 $b$ 之后的时间内, $P_a$ 向 $P_b$ 发送了消息 (否则 $P_b$ 对 $P_a$ 的计数器得不到及时刷新,$s$ 就不会不小于 $m$ )。

图14 - 中间必然存在$P_a$向$P_b$发送了消息 实际上,可以分为以下几种情况:

图15 - 可能出现的4种情况 - 当 $a = c$ 且 $d = b$ , 易得 $a \rightarrow b$.
- 当 $a = c$ 且 $d \rightarrow b$ ,由传递性,得 $a \rightarrow b$ .
- 同样对于 $d = b$ 且 $a \rightarrow c$ 的情况.
- 当 $a \rightarrow c$ 且 $d \rightarrow b$ ,根据进程内的算法逻辑和传递性,也很容易得出结论。
综上: $VC_a < VC_b \Rightarrow a \rightarrow b$ 得证。
进一步的,我们可以得出这样的结论:
向量有序,则事件有序(充要):
$VC_a < VC_b \Leftrightarrow a \rightarrow b$
向量平行,则事件并发(充要):
$VC_a \parallel VC_b \Leftrightarrow a \parallel b$
是的,向量时钟可以准确刻画事件顺序。
其本质在于将lamport时钟的全序计数器的方式改造成向量时钟的偏序大小关系。
向量时钟看前面的问题 ¶
现在我们回到文中一开始提到的问题。
由于网络延迟的不确定性, 我们在文章开始提出了一个$A$, $B$, $C$三个进程中如何确定事件顺序的问题。
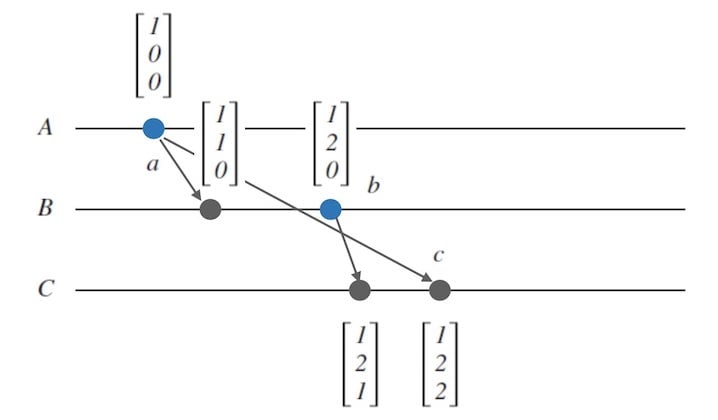
我们可以从下面的图16中看出, $VC_{a} < VC_{b} < VC_{c}$,那么可以确定 $a \rightarrow b \rightarrow c$。 也就是我们找到了一种方法来描述这种情况下的事件顺序。 进程$C$的视角下观察 $a$ 和 $b$ 的顺序的问题也有了明确的答案。
最后,我们回到朋友圈的例子。 下面图17中可以看出, $VC_{a} < VC_{b} < VC_{c} < VC_{d} < VC_{e}$, 显然可以确定 $a \rightarrow b \rightarrow c \rightarrow d \rightarrow e$ 。
在小李看到小明的朋友圈和小红的评论的时候,也收到了这两条数据的向量, 我们可以根据向量时钟来确定事件的先后关系,从而不会显示出因果矛盾。
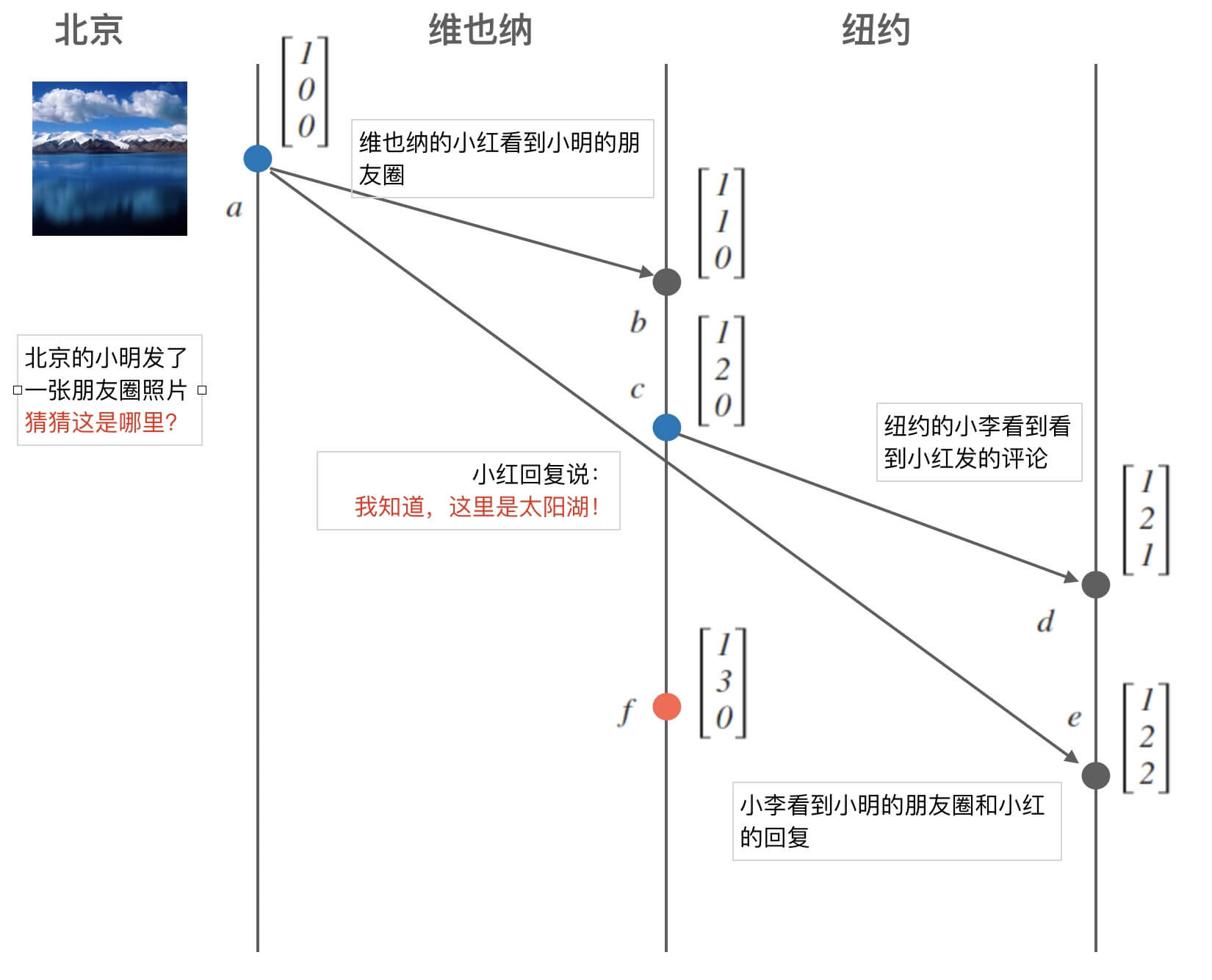
图17中还有一个事件 $f$, 它的发生可能是小红又发了一条评论。 我们可以看到 $VC_{f} \parallel VC_{e}$。 这时候,无法确定事件 $f$ 和 $e$ 的先后关系,也就是说 $f \parallel e$。
但是,这时候小李还没有看见这个事情。所谓「因果」:有因才有果。 看见也是一个事件的果。 这样说, $f$ 和 $e$ 没有因果关系, 因为小李还没有看见这个事件。 所以讨论也就没有意义。
版本向量 (Version Vectors) ¶
版本向量 Version Clocks 是一种工程上用来同步分布式数据的算法, 和向量时钟非常相似,以至于人们经常混淆这两种算法。 但是二者却有不同的地方 (Version Vectors are not Vector Clocks)。
我们注意到在向量时钟算法中, 消息传播后,发送方的向量一定会小于接收者的向量, 是因为接收者对齐了发送者的原因。
版本向量在此基础上,做了一点小的加强:
消息传播后,发送方也对齐接收者的向量, 也就是双向对齐,在版本向量中,叫做同步。
用数学语言描述的话,向量时钟算法的第三点,改成:
对 $[0, n)$ 上的任意一个整数 $k$ 执行 $VC_{i}[k]=VC_{j}[k]=Max(VC_{j}[k], VC_{i}[k])$
除了这个关键性区别外, 版本向量还和向量时钟算法有一点细微的区别:
发送消息和接收消息的时候不再自增向量中的自己的计数器,而是只做双方的向量对齐操作。 也就是,只有在更新数据的时候做向量自增。
版本向量是针对数据的更新和同步的协调算法,那么我们把数据操作的事件分为以下两种:
- 更新数据的事件, 即图18中红色的点。
- 同步数据的事件, 发送数据 和 接收数据, 分别为蓝色和黑灰色的点。
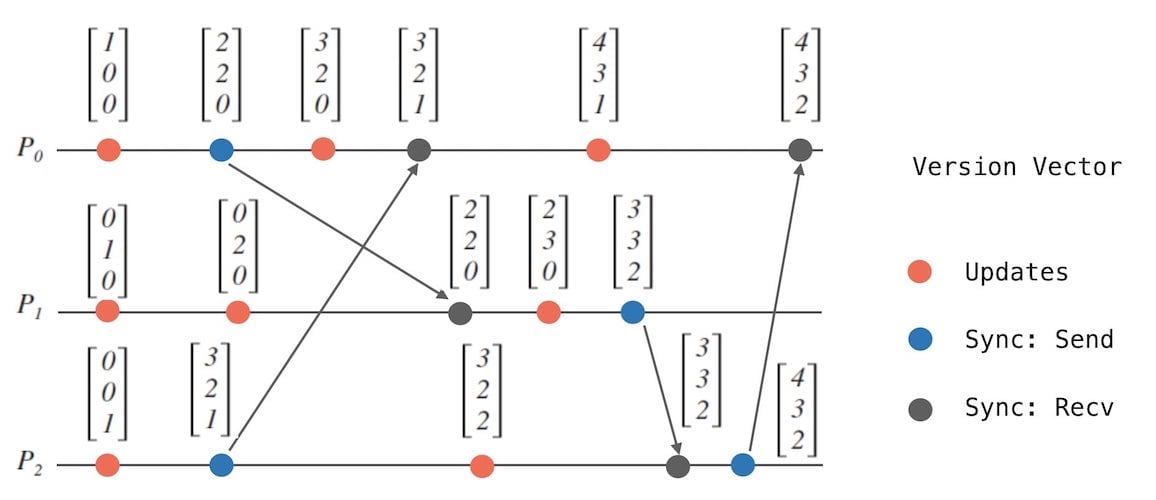
我们可以看到,在进行一次同步操作后,双方进程的版本向量会变成一样。
在我们熟知的网络通信方式上(比如TCP,UDP),同步操作可以做成原子的 , 比如接收进程对收到的消息进行消息反写。
向量时钟的不足 ¶
我们再次回到向量时钟,可以看出它的两点不足:
只考虑了固定数量的节点,没有考虑节点的动态添加和销毁。
如果我们考虑用类似Hashtable而不是Vector的描述方式的话, 我们还需要事先给每个节点定义一个全局唯一标识。
现代解决方案: 区间树时钟 - Interval Tree Clocks。 这个论文我没有看明白 T_T。
大概是每个时间戳设定为 $(Id, Event)$, 而 $Id$ 和 $Event$ 都用区间树的数据结构来做。 而区间树是可以在 $[0,1]$ 实数域上无限二分的。
文中建立了一个通用的时钟模型叫做「Fork-Event-Join Model」,
新加入一个节点的时候,我们找一个节点进行
fork,fork则将当前节点的时间戳的Id二分、 Event 克隆,作为新节点的初始时间戳。当一个节点要移出的时候, 我们把它合并到一个其他节点,
join类似fork的一个 反向操作, 类似一个取最大者的方式进行合并。区间树时钟算法消去了向量时钟对全局唯一节点标识的依赖。
假设节点数量是 $N$ , 那么每个节点需要维护的空间复杂度是 $O(N)$。 通信的信息量的复杂度也是 $O(N)$ 。
关于这个话题,有个文章可以看下: Causality Is Expensive. 文中提到:
Causality can be characterized only by vector timestamps of size N.
也就是这个 $O(N)$ 的复杂度,不能再小了。
2019年新鲜出炉的一个寻求优化时钟空间的算法,布隆时钟 - Bloom Clocks。
总结与感想 ¶
- 现实中,无法构建精确的全局时钟来描述事件顺序。
- 受狭义相对论的启发,我们用因果关系来描述事件顺序。
- 因果关系是一种偏序关系。
- Lamport时钟构造的计数器之间的大小关系是一种全序关系,无法准确刻画事件顺序的偏序关系。
- 向量时钟是一种对lamport时钟的延伸,以偏序关系准确刻画了事件的因果顺序。
此外,向量时钟给我一种感想,对每个分布式节点来说:
- 我把我的视角分享给其他节点。
- 我对齐我看到的其他节点的视角。
本质上,是在做 视角对齐。
这自然地,让我想起了Gossip谣言传播算法。 Gossip算法如其名,每个分布式参与者都在散播自己视角的信息,以达到谣言扩散的效果。 同样是在做 视角对齐。
对于分布式系统中的事件顺序的刻画,就讨论到这里。
– 毕 「逻辑时钟」
本文原始链接地址: https://writings.sh/post/logical-clocks



