分酒问题的图论建模 🍷

在读《算法概论》时，碰到一个有趣的问题，值得一记。叫做 “注水问题”, 也常称 “分酒问题” 或 “倒酒问题” ，描述如下：

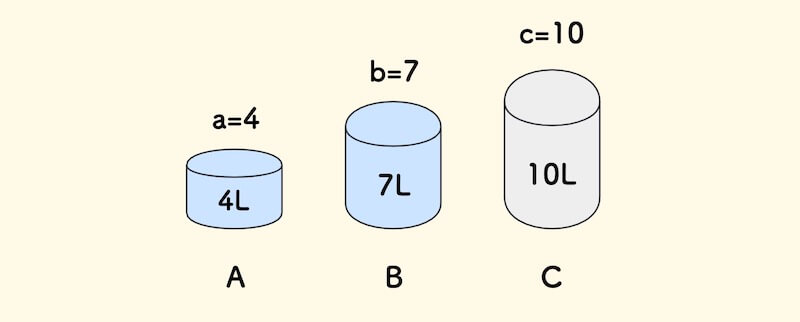
现在有三个容器，容积分别为 4 品脱，7 品脱, 10 品脱。其中 4 品脱和 7 品脱的容器是满的， 10 品脱的容器是空的。目前我们只能进行一种操作：将一个容器的水注入另一个容器，注水操作只能在源容器已空或者目标容器已满的情况下停止。我们要知道，是否存在一个合理的注水顺序，使得 4 品脱或 7 品脱的容器中恰好剩余 2 品脱的水?

这是道并不稀罕的数学趣味题，本文将对此问题建模成一个图论问题，并用图的搜索算法 (BFS 或 DFS) 来解决。

首先，我们将 4L, 7L, 10L 的三个瓶子依次标号为 A, B, C 。

用 a, b, c 三个变量来追踪三个容器中的水的余量, 初始情况下, a=4, b=7, c=0 。

我们要求解的是，是否可以经过一系列注水操作后，使得 a 和 b 中的至少一个等于 2? 更进一步地，如果存在的话，具体的倒水步骤是什么？

显然，总的水量 a + b + c 一定是 11, 就是说，一旦 a 和 b 确定，c 也就确定了。因此，可以取 (a,b) 作为状态，当做有向图的顶点。我们总的思路就是，从初始顶点 (4,7) 出发，探索所有可能的注水路径，判断是否可以到达 (2,x) 或 (x,2) 的顶点。这个探索的过程，采用 BFS 广度优先搜索或者 DFS 深度优先搜索均可。

下图是这个分酒问题建模成一个有向图的局部情况的示意，其中顶点 (a,b) 表示容器 A 和容器 B 的余量，边的意思是，以 A → B 为例，表示从 A 容器注入 B 容器直到源容器空或目标容器满为止。

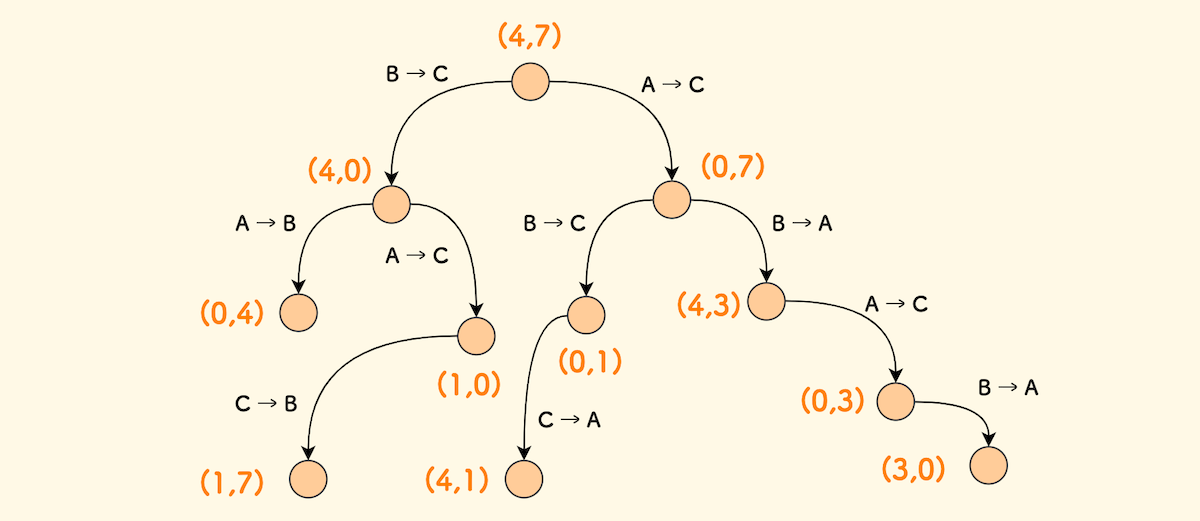
我们可以枚举出来所有可能的注水操作，共有 6 种：

ACTION_A_TO_B: A 注入 B
ACTION_A_TO_C: A 注入 C
ACTION_B_TO_A: B 注入 A
ACTION_B_TO_C: B 注入 C
ACTION_C_TO_A: C 注入 A
ACTION_C_TO_B :C 注入 B

此外，还有初始化操作 ACTION_INIT 和空标志 ACTION_VOID 两个特殊的动作。

需要注意的是，注水操作必须满足两个条件:

源容器有余量的水
目标容器有空闲容积

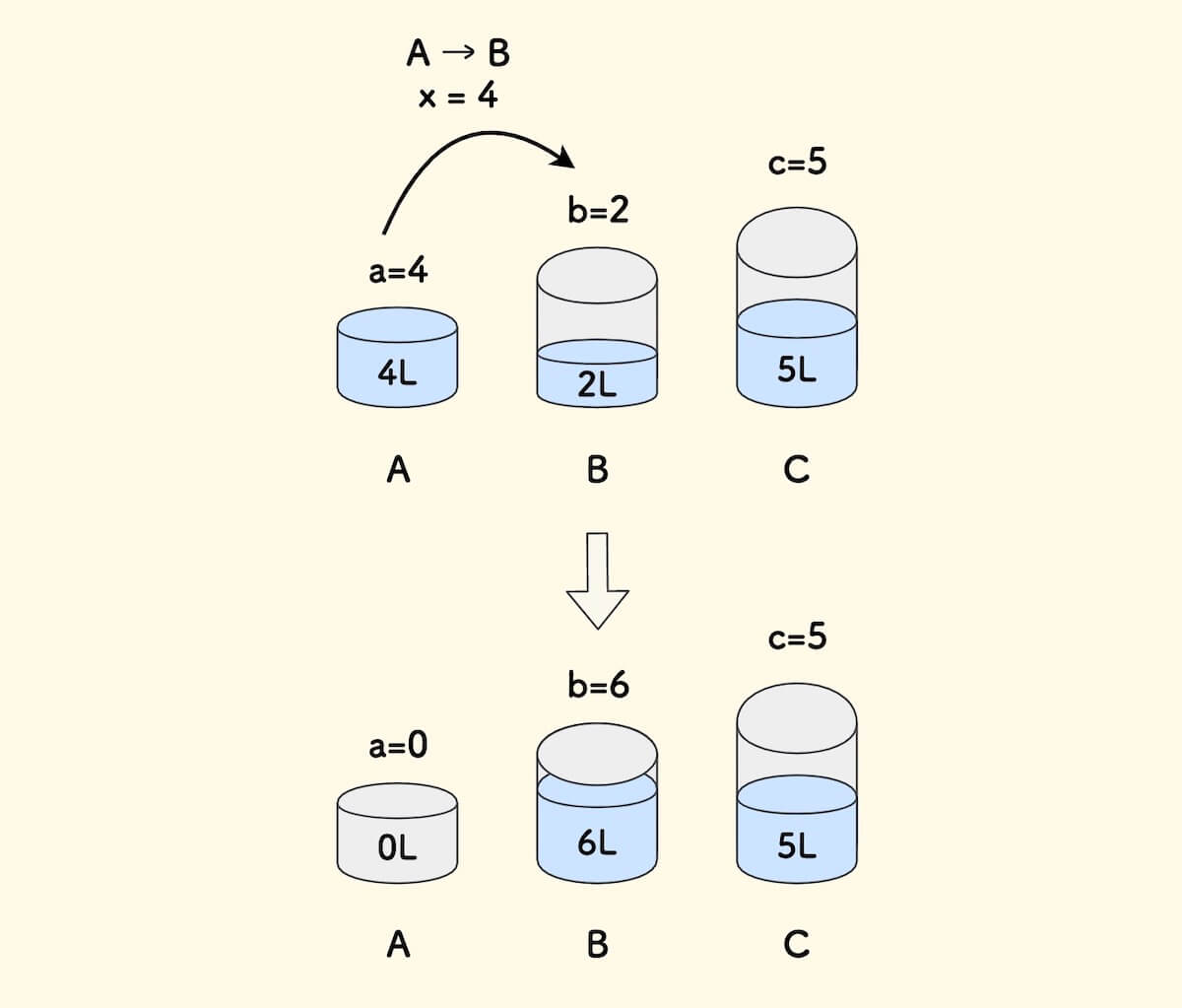
举例来说，假设目前的状态 (a,b) 是 (4,2) ，即 A 和 B 容器分别有 4L 和 2L 水，此时可知 c = 11 - 4 - 2 = 5，即 C 容器有 5L 水。

现在的情况下，可知容器 A 已满无法再注入水。我们可以继续的操作只能是 A → B, A → C, C → B 和 B → C 。

此时，以 A → B 注水为例，可注水的量 x 只能是 4L ，这取决于源容器中水的余量和目标容器的空闲容积，二者的最小值。在注水操作完成后，(a,b) 的状态变为 (0,6) 。如此，就完成了一次从顶点 (4,2) 到另一个顶点 (0,6) 的推导。

从当前顶点出发，对每个可能的操作，计算出可以注水的量 x ，即可推导出下一目标顶点，不断进行下去，即可推导出来所有可以到达的顶点。

推导的方式无非两种：深度优先 DFS 和广度优先 BFS ，回忆下 DFS 和 BFS 的代码范式：

深度优先搜索 DFS 的范式 - 循环版本

stack = [root]
while not stack.empty():
    v = stack.pop()
    if visited(v):
        continue
    for ch in v.children():
        stack.push(ch)

广度优先搜索 BFS 的范式 - 循环版本

queue = [root]
while not queue.empty():
    v = queue.popleft()
    if visited(v):
        continue
    for ch in v.children():
        queue.push(ch)

需要注意的是，可以用一个二维数组 visited[a][b] 标记已访问过的节点，避免进入回环带来的无限循环。

更推荐采用 BFS 广度优先的方式，它可以给出更短的操作序列，这是因为 BFS 更适合最短路径的探索。

在迭代过程中，可以一同收集动作序列，即可知道每个顶点可以经由哪些步骤到达。 Python 版本的代码实现如下，也放在了 github 上。

分酒问题 - BFS 广度优先探索 - Python 实现

# 倒酒的动作
ACTION_VOID = ""  # 空标志
ACTION_INIT = "(init)"  # 初始标志
ACTION_A_TO_B = "(A->B)"  # A容器倒入B容器，以下雷同
ACTION_A_TO_C = "(A->C)"
ACTION_B_TO_A = "(B->A)"
ACTION_B_TO_C = "(B->C)"
ACTION_C_TO_A = "(C->A)"
ACTION_C_TO_B = "(C->B)"


def pour_visited_matrix_bfs():
    # 共六种倒酒情况: A->B, A->C, B->C, B->A, C->A, C->B
    # a, b, c 记录每个状态下的酒的容量
    # 采用 BFS 广度优先遍历的方式，计算所有可能的状态

    # d 是访问数组，d[a][b], a, b 确定后，即可确定 c
    # 初始化为 void
    d = [[ACTION_VOID for _ in range(8)] for _ in range(5)]

    # 起始情况，a=4, b=7
    # 入队 A, B 容器的现状 和 当前累积的动作
    s = [[4, 7, ACTION_INIT]]
    d[4][4] = ACTION_INIT

    while len(s) > 0:
        # 获取队头 a, b
        a, b, actions = s.pop(0)
        # 推导当前第三个容器的状态
        c = 11 - a - b

        if d[a][b] != ACTION_VOID:
            # 如果访问过，则不再访问
            continue

        d[a][b] = actions
        print(f"{a},{b}=> {actions}")

        # A -> B
        if a > 0 and b < 7:
            x = min(a, 7 - b)
            a1 = a - x
            b1 = b + x
            s.append([a1, b1, actions + ACTION_A_TO_B])
        # A -> C
        if a > 0 and c < 10:
            x = min(a, 10 - c)
            a1 = a - x
            c1 = c + x
            b1 = 11 - a1 - c1
            s.append([a1, b1, actions + ACTION_A_TO_C])
        # B -> A
        if b > 0 and a < 4:
            x = min(b, 4 - a)
            a1 = a + x
            b1 = b - x
            s.append([a1, b1, actions + ACTION_B_TO_A])
        # B -> C
        if b > 0 and c < 10:
            x = min(b, 10 - c)
            c1 = c + x
            b1 = b - x
            a1 = 11 - b1 - c1
            s.append([a1, b1, actions + ACTION_B_TO_C])
        # C -> A
        if c > 0 and a < 4:
            x = min(c, 4 - a)
            a1 = a + x
            c1 = c - x
            b1 = 11 - a1 - c1
            s.append([a1, b1, actions + ACTION_C_TO_A])
        # C -> B
        if c > 0 and b < 7:
            x = min(c, 7 - b)
            b1 = b + x
            c1 = c - x
            a1 = 11 - b1 - c1
            s.append([a1, b1, actions + ACTION_C_TO_B])

    return d


if __name__ == "__main__":
    d = pour_visited_matrix_bfs()

    # 是否存在 (2,x) 和 (x,2) 的情况?
    for a in range(5):
        for b in range(8):
            if (a == 2 or b == 2) and d[a][b] != ACTION_VOID:
                print(f"a={a},b={b}:", d[a][b])

执行这个代码后，可以看到 BFS 推导出来的所有可能的状态，以及对应的注水步骤:

4,7 => (init)
0,7 => (init)(A->C)
4,0 => (init)(B->C)
4,3 => (init)(A->C)(B->A)
0,1 => (init)(A->C)(B->C)
0,4 => (init)(B->C)(A->B)
1,0 => (init)(B->C)(A->C)
0,3 => (init)(A->C)(B->A)(A->C)
4,1 => (init)(A->C)(B->C)(C->A)
1,7 => (init)(B->C)(A->C)(C->B)
3,0 => (init)(A->C)(B->A)(A->C)(B->A)
0,5 => (init)(A->C)(B->C)(C->A)(A->B)
3,7 => (init)(A->C)(B->A)(A->C)(B->A)(C->B)
4,5 => (init)(A->C)(B->C)(C->A)(A->B)(C->A)
4,6 => (init)(A->C)(B->A)(A->C)(B->A)(C->B)(B->A)
2,7 => (init)(A->C)(B->C)(C->A)(A->B)(C->A)(A->B)
0,6 => (init)(A->C)(B->A)(A->C)(B->A)(C->B)(B->A)(A->C)
2,0 => (init)(A->C)(B->C)(C->A)(A->B)(C->A)(A->B)(B->C)
4,2 => (init)(A->C)(B->A)(A->C)(B->A)(C->B)(B->A)(A->C)(B->A)
0,2 => (init)(A->C)(B->C)(C->A)(A->B)(C->A)(A->B)(B->C)(A->B)

回到问题本身:

“是否存在一个合理的注水顺序，使得 4 品脱或 7 品脱的容器中恰好剩余 2 品脱的水?”

显然是存在的，而且我们可以给出具体的注水步骤。

（完）

本文原始链接地址： https://writings.sh/post/pour-problem