幂律分布 - 比例之谜

幂律分布是自然界广泛存在的一种分布形式，各种各样的物理、生物、社会现象的分布都遵循着幂律，比如牛顿万有引力定律、月球坑大小的分布、语言的用词频率等等。

在数学上描述为：

\[f(x)=ax^{k}+\varepsilon\]

其中， $a$和$k$都是常数，$\varepsilon $是一个渐近微小函数.

下图是一个幂律分布的图样(展示人气排名的规律)：

在统计学中，幂律是两个量之间的函数关系，其中一个量的相对变化会导致另一个量的相应幂次比例的变化.

幂律分布是一种分布形式，帕累托分布、齐普夫定律、克莱伯定律等都是一种幂律分布。

标度不变性 ¶

幂律分布具有标度不变性，就是说变量$x$的变化将会导致函数值 $f(x)$ 的相应幂次比例的变化，且与初值无关。

那么，什么是标度不变性？

标度不变性 (Scale invariance) 也称为尺度不变性、无尺度性。用来形容结构、形状或者规律并不随变量的尺度的变化的影响的特性。

简而言之：形式不随尺度变化。

例如，正方形的面积$S$与边长$X$的平方关系 $S = X ^ 2$，是具有标度不变性的，边长扩大2倍，面积则扩大4倍：

分形具有标度不变性，更确切地，是具有自相似特点。

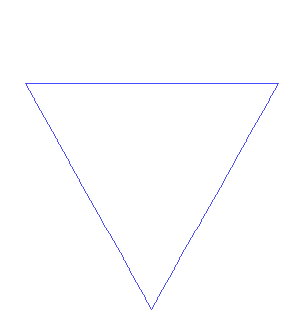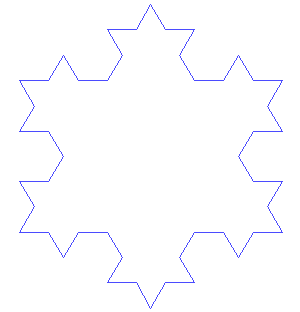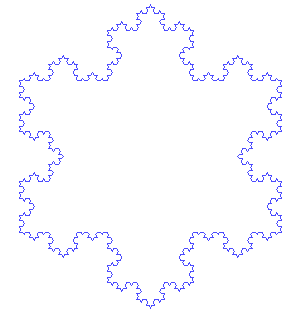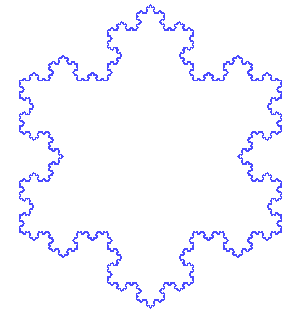
下面的科赫曲线是一个典型的分形图形，它具有标度不变性，在任意大小的尺度上，都有相似的结构：

齐夫定律 ¶

齐夫定律 Zipf’s law 是描述自然语言中单词出现的频率的分布规律的实验性质的定律。

一个单词出现的频率与它在频率表里的排名成反比.

频率最高的单词出现的频率大约是出现频率第二位的单词的2倍，而出现频率第二位的单词则是出现频率第四位的单词的2倍。

下图是维基百科排名前100的最常用词和它们的出现频率的分布图，符合一个幂律分布（幂指数小于1）：

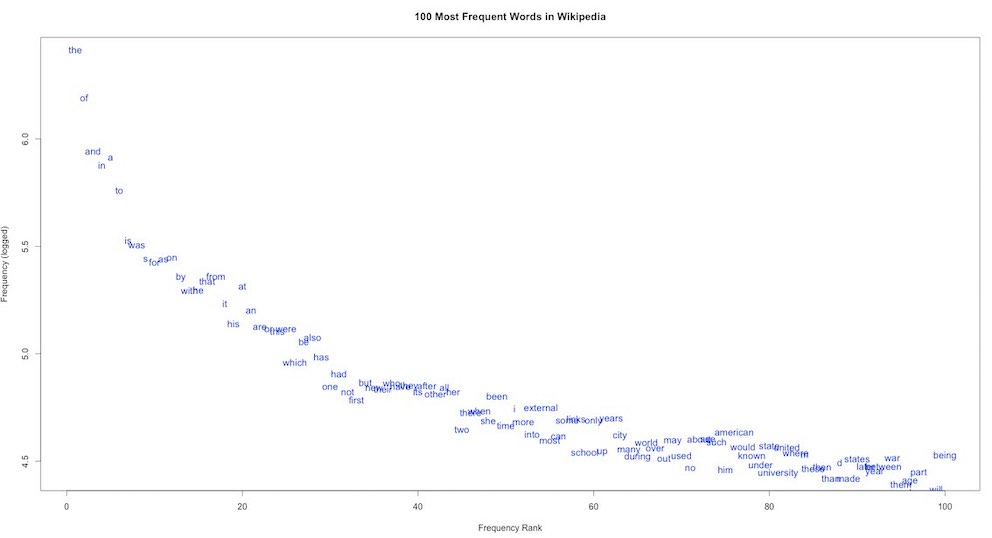
齐夫定律，不仅适用于语料全体，也适用于单独的一篇文章。

但注意的是，齐夫定律是一种实验性质的定律，并不是理论定律。

齐夫定律是如何形成的呢？有很多种解释。齐夫本人的解释是这样的：

一方面，人们都遵循「最省力原则」，也就是说，一旦用到一个词表达一个意思，对类似的情况自然用仍用这个词更省力。
另一方面，人们希望语言没有歧义，这又需要用不同的词表达相似但是又不完全一样的意思。

齐夫在数学上证明了上面两种原因会产生幂律分布。

曼德布罗特从信息量的角度给出了一种解释：信息发送者在将信息量最大化的同时，尽量将发送信息的成本最小化。并证明了，如果同时优化信息量和传输成本，就会导致齐夫定律。

有趣的是，心理学家乔治米勒使用简单的概率论证明，猴子在键盘上随意敲击，如果偶然敲到了空格键就断词，这样得到的文本同样遵循齐夫定律。

克莱伯定律 ¶

克莱伯定律(Kleiber’s law)，也叫做代谢比例理论，描述了动物的代谢率和体重的幂次关系：

根据观测数据提出，对于很多动物，其基础代谢率水平与体重的$3/4$次幂成正比.

用数学式来表达就是：

\[R ∝ M^{3/4}\]

下图是代谢率和动物体重的关系的双对数图，两边同时取对数得 $log({R}) ∝ {3/4} log({M})$，可以看到是一个正比直线，直线的斜率就是幂律的指数，这里是$3/4$ (图来自The Kleiber Law)

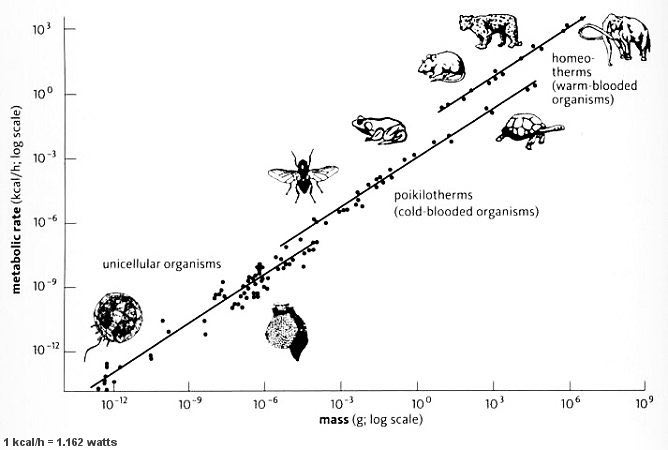
代谢比例理论，对于生物学的重要性就好比牛顿的发现对于物理学的重要性。

为什么是$3/4$？定律背后的原因非常有趣，和分形结构有关。

生命体的主要器官和结构都是具有自相似特征的分形结构，例如人体的肺器官：

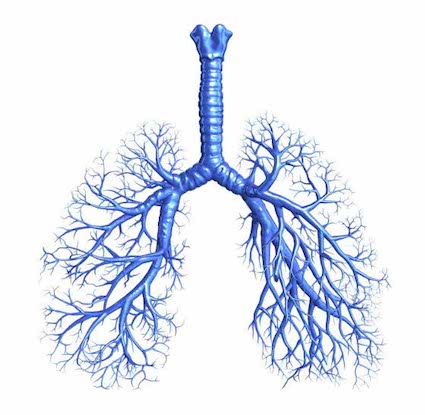
在《复杂》一书中，关于克莱伯定律，给出了这样的说法，『分形给了生物第四维』：

虽然生物是三维的，内部的生理结构和运作却表现为四维… 分形几何给了生命额外一个维度。 – 《复杂》

对克莱伯定律详细的解释见下面的「克莱伯定律的解释」部分。

分形和分形维数 ¶

在上面的克莱伯定律中，提到了分形维数的概念。那分析维数是什么呢？首先，要了解下分形结构。

分形是在任何尺度上都有微细结构的几何形状，具有 自相似性 和 无尺度性。分形也被称为扩展对称或展开对称。如果在每次放大后，形状的重复是完全相同的，这被称为自相似。分形在不同的缩放级别上可以是近似相似的。

著名的分形结构有科赫曲线，康托尔集等.

下面是一个科赫曲线的分形过程示例：每个线段都三等分，不断重复这个过程。

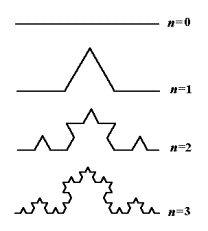
可以看到，科赫曲线拥有自相似的特点，尺度的缩小和放大，并不影响它的形状。

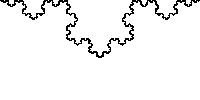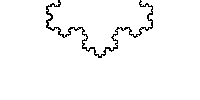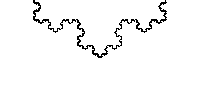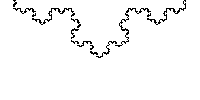
另外，科赫曲线的长度是无限大的，连续而无处可微。

分形维数一般是指豪斯多夫维数：一个几何结构（线段/图案/立体结构）分形放大了$L$次后，其占有的空间（对应的：长度/面积/体积）比原来放大了 ${L}^{D}$倍，那么这个$D$就定义为这个分形结构的维度。

让我们考虑下规则分形下的维数。

一维图形：长度为$l$的线段，放大后，长度放大了2倍，为 $2l$.
二维图形：长度为$l$的正方形，放大后，面积放大了4倍，为 $4l^2$.
三维图形：长度为$l$的正方体，放大后，体积放大了8倍，为 $8l^3$.

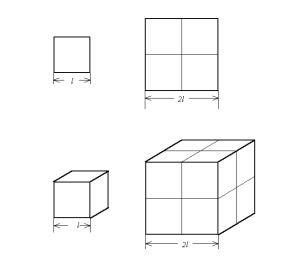
如果将边长变化的倍数记$L$ , 放大后整个图形结构变化的倍数记作 $K$，则上述关系可以表达为：

\[{L}^{D} = {K} \quad (D=1,2,3)\]

这个$D$就是豪斯多夫维数，那么 $D$ 可以写作：

\[{D} = \frac { \log{K} }{ \log { L } }\]

这就是豪斯多夫维数的一般性的定义形式。

对于规则图形， $D$正好为整数，也就是欧几里得维数(计盒维数).

但是，分形维数不一定永远是整数。

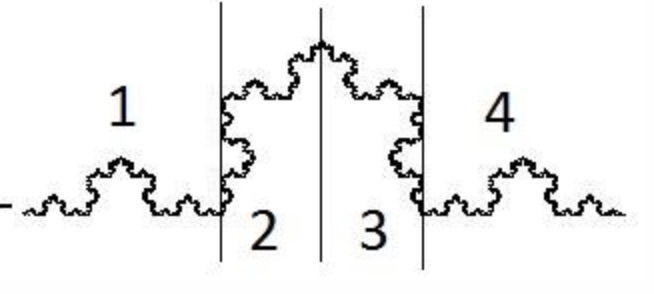
对于科赫曲线，如下面图例可知，如果将它放大3次，长度会增加4倍，所以维数是 $\frac {\log{4}} {\log{3}}$ 大约是 $1.26$ (一个无理数).

对于康托尔集 (给定初始一个线段点集，每次分形都去掉每一段一条线段的中间三分之一)，对于每次三等分操作之后剩下的两个小线段，我们把它们放大三倍，会得到两个三等分操作之前的大线段。也就是说，小的局部放大3倍，原来的图形长度上放大了2倍，所以，维数是 $\frac {\log{2}} {\log{3}}$，大约是 $0.63$。

$K = L^D$ 本身即形成了一个幂律关系，其中分形维数 $D$ 就是幂次指数。

可以看出，分形是产生幂律的一种原因。

克莱伯定律的解释 ¶

生命体中的很多器官、组织都是分形分支结构，分形分支结构是具有自相似特征的，在所有尺度上都自相似意味着空间在所有尺度上都被同等填充，那就是说，分形分支结构是在尽可能填充空间的每一个角落。换句容易理解的话说，动物体内的分形网络其实是高效利用空间的，大肠表面充满了分形褶皱，使得二维面积在三维空间最大化填充。而动物体积的增大，使得三维分支在四维空间最大化填充。

我们现在反过来看克莱伯定律，先观察立方体的表面积和体积的幂次关系:

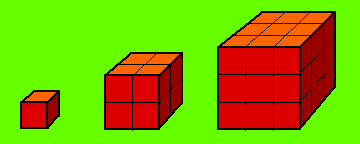
	小立方体	中立方体	大立方体
边长	1	2	3
表面积	6	24	54
体积	1	8	27

我们可以总结出一个规律，就是： 表面积与体积的 $2/3$ 次幂成比例。

这个结论当然也可以直接由体积和表面积公式推导得出（你也可以用球而不是立方体，会有同样的结论）。

不过，我们这里通过分形维数的概念，推导一下，体积每次扩大为 $(2L)^3$ 倍的时候，表面积会相应扩大为 $6{(2L)}^2$，现在来计算表面积相对体积的维数$D$：

体积扩大的倍数 $N = \frac {(2L)^3} {L^3}$ 即 $8$.
面积扩大的倍数 $K = \frac {6{(2L)}^2} {6L^2}$ 即 $4$.
因此 $D = \frac {\log K} {\log N} = \frac {\log 4} {\log 8} = \frac {2\log 2} {3\log 2} = 2/3$

那么，进一步推广到四维呢？可以得出四维的表面积相对于四维的体积的维数应该是 $3/4$。换句话说，四维的表面积(其实就是三维体积)和四维的体积的 $3/4$ 次幂成比例。

所谓的新陈代谢生物体只是一个包含了时间的四维空间中的一个区域，而如果我们再把生物体的新陈代谢看作是生物体所对应的三维空间中的体积(速率一说除去了时间维度)，就会有代谢速率正比于四维体积$3/4$幂次的关系了。再假设体液（血液等）的总体积正比于体重，即可得出克莱伯定律。

当然，这个角度的解释非常粗糙。不过，我一定要介绍它的原因是因为它让人充满了幻想~。

关于这个角度的解释可以参考：

《复杂》 - 章节：比例之谜
生命之流 - 流动与时间的赛跑：四维角度

更为准确些（没那么魔)的解释，要看维基百科的「定律背后原因」的部分，实际上是通过假设：

体液总体积$V$正比与体重。
代谢率正比于体液总流量。
循环系统由许多微管组成，因此继续假设：
1. 微管的体液流量正比于微管体积, 所以微管总数 $N$ 正比于体液总流量。
2. 微管组成分形结构，有自相似特点，所以 $N^{4}$ 正比于 $V^{3}$

基于以上的假设和推论，最终可以推导出克莱伯定律。

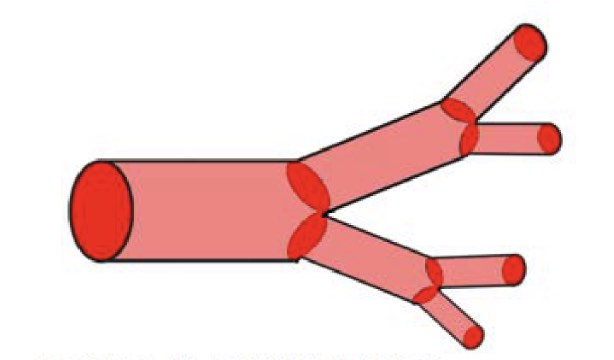
对于维基百科这个解释，其中至于为什么得出 “$N^{4}$ 正比于 $V^{3}$” 的结论，真的没看懂！不过维基百科给了一个论文链接)，貌似这是一个叫做「WBE分形网络模型 (West, Brown and Enquist’s Mode)」，一个圆柱连接成的自相似结构的网络模型，推导出来的数学推论。

另外一个有趣解说的思路，值得看一下： The 3/4 Law

无论如何，还是要推一下当年三位科学家对这个现象做出了很大努力后的解释稿原文吧： life’s universal scaling laws - West,James,Brown

万维网的幂律分布 ¶

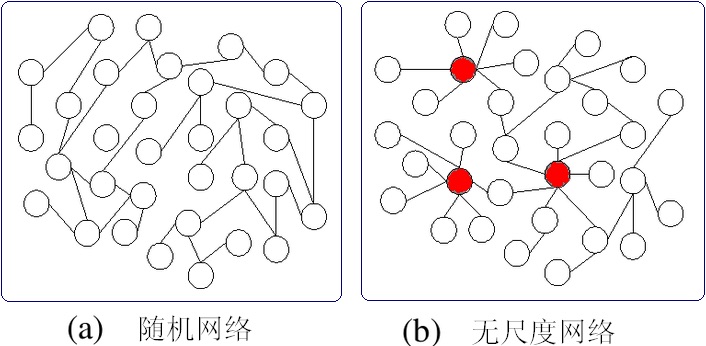
万维网是一种典型的无尺度网络。

所谓无尺度网络，即具有标度不变性(尺度无关)的复杂网络，其典型特征是在网络中的大部分节点只和很少节点连接，而有极少的节点与非常多的节点连接。

相比于随机网络而言，无尺度网络中有这样的特征：少量的枢纽节点拥有大量的连接，例如流量很大的 Google 就是万维网的一个枢纽节点。

研究发现，入度为$k$的网页数量正比于$\frac {1} {k^2}$。 (入度是指指向本网页的链接数量)。

这一现象，仍然是一个幂律分布。 无尺度网络一定遵循连接度幂律分布，同样拥有自相似特性和无尺度特性。

背后的原因也可以猜测一下：越流行的网站，越容易拿到其他网页的流入链接，仍然是偏好附连。这让我想起了「马太效应」: 强者愈强、弱者愈弱的累积反馈现象。

此外，所有的无尺度网络还有「小世界特性」 (但是注意不是所有的小世界网络都是无尺度网络)。

帕累托分布 ¶

说到幂律分布，不得不提经济学著名的帕累托分布，是从大量真实世界的现象中发现的幂定律分布，这个分布因其著名的而又发人深省的推论「80%的财富掌握在20%的人手中」而闻名。

数学上的帕累托分布：

\[P(X>x)=(\frac { x }{ { x }_{ min } } )^{ -k }\]

其中 $x$ 是任何一个大于$x_{min}$的数， $x_{min}$ 是 $x$ 最小的可能值（正数）， $k$是为正的参数。帕累托分布曲线族是由两个数量参数化的：${x}_{min}$ 和 $k$。

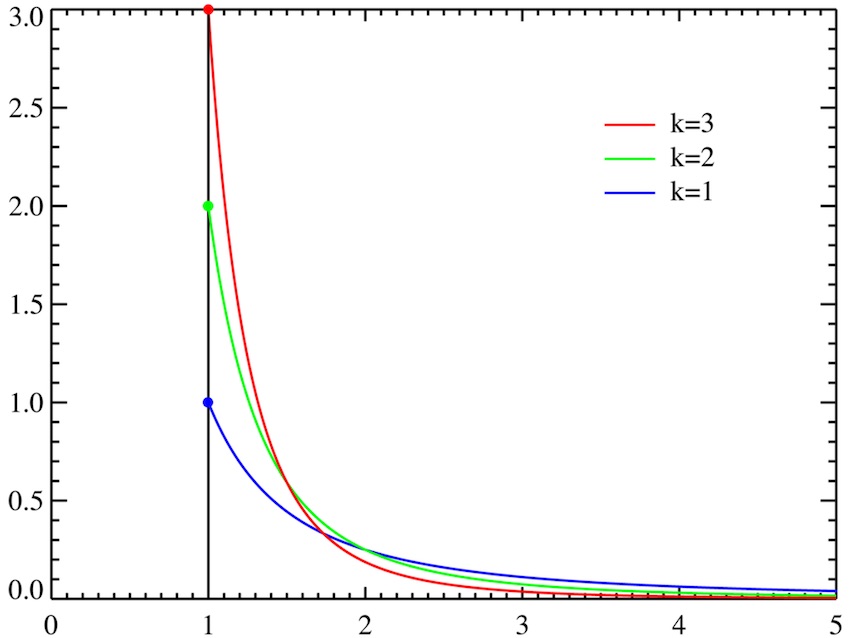
帕累托分布经常用来描述经济上财富在个体上的分布关系，一个著名的应用是帕累托法则，也就是我们常说的二八法则：

在任何一组东西中，最重要的只占其中一小部分，约20%，其余80%尽管是多数，却是次要的。

经常用二八法则描述的现象：

80%的财富掌握在20%的人手里。
80％的销售额来自20％的客户。
意大利约有80％的土地由20％的人口所有。
20%的品牌占据了80%的市场。

而对于我们的人生启示..

我们应该把80%的精力放在20%的主要事务上。

长尾理论 ¶

帕累托法则认为企业界80%的业绩来自20%的产品。然而，长尾理论则关注其余的80%的”冷门”产品：

由于成本和效率的因素，当商品储存流通展示的场地和渠道足够宽广，商品生产成本急剧下降以至于个人都可以进行生产，并且商品的销售成本急剧降低时，几乎任何以前看似需求极低的产品，只要有卖，都会有人买。这些需求和销量不高的产品所占据的共同市场份额，可以和主流产品的市场份额相比，甚至更大。

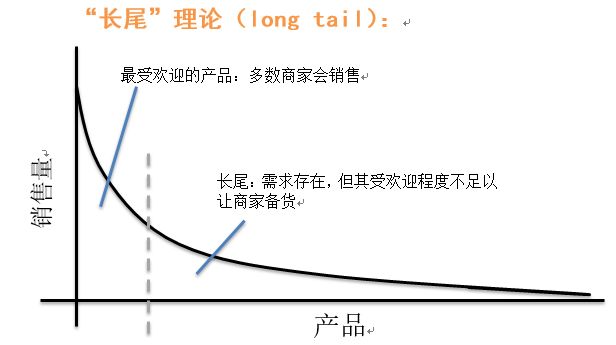
上图表达：将庞大的长尾利基商品量乘以相当小的单项长尾商品销售量，其获利仍极为可观。

说简单些：长尾效应认为小众需求的总和仍然是个大市场！

但是注意长尾的应用条件： 极地的成本、 宽广的渠道。在生产成本下降、渠道大幅打开的情况下（富余时代），人们的个性化需求的市场总和才足以和主流市场匹敌。

例如：亚马逊一半左右的销售来自于比较热门的商品，而另一半却来自相对不那么热门的商品。

长尾理论看似是对二八法则的挑战，事实上，二者同源，都是幂律现象。

对于二八法则和长尾理论的辩证看法：

二八法则：稀缺经济下，边际成本高，符合大众需求的产品有更大的机会卖出，因此商家重视20%的畅销品，而小众需求被抑制。「边际成本高，小众产品的供给压力大」
长尾理论：丰饶经济下，边际成本极低，大众需求可以得到完全满足，小众需求供给压力得到释放，出现长尾市场。「边际成本低，小众产品的供给压力降低」

对我们的启示而言：

在资源有限、或者边际成本高昂的条件下，精力关注在主要矛盾上。
在资源充裕、或者边际成本低廉的条件下，主要矛盾可以被解决，进而向利基市场要效益。

幂律成因仍是未决之谜 ¶

幂律分布在自然、经济和社会活动中广泛存在，除了以上这些，在城市规模、收入、地震、心率变化、股市波动等现象中都发现了幂律分布。但是对于幂律分布的根本成因，目前却在一定程度上仍然是一个迷。

现在已经出现的各种解释方式有：偏好附连（优先连接）、分形结构、自组织临界性、随机过程等等，但是哪种机制根本上导致了幂律现象没有统一的共识。

理解幂律分布的根源、意义和在各学科中的共性，是目前许多复杂系统研究领域最为重要的未解决的问题。 – 《复杂》

从我个人上的感觉，幂律形成的一个重要原因是「不断的正反馈」机制。如果个体之间相互影响，造成了循环性的正反馈作用导致细节因素不独立，会形成幂律现象。