原地旋转矩阵

一个经典的算法问题 leetcode 48. 旋转矩阵：

给定一个 n × n 的二维矩阵 g。请你将它原地顺时针旋转 90 度。

比如，下图是一个矩阵的翻转情况：

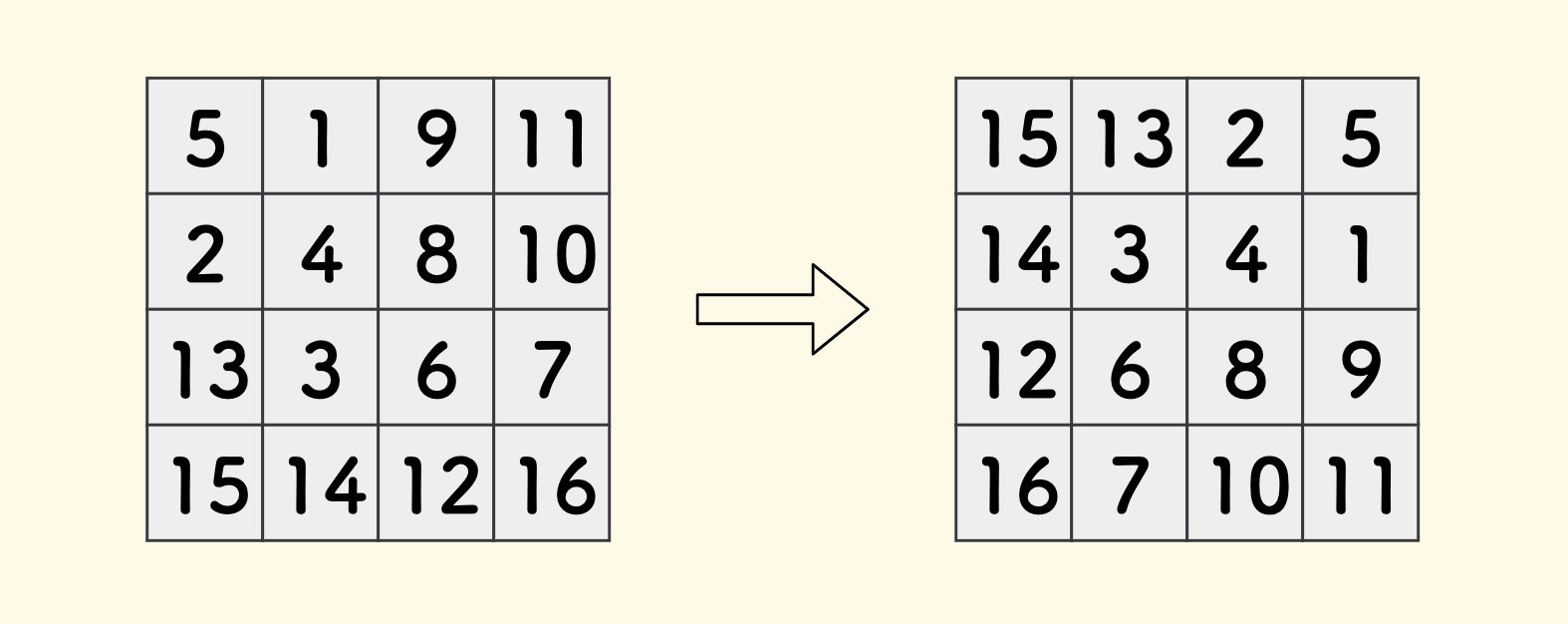
这个旋转是有规律的，染色后可以清晰地看出：

1. 原来的第 i 行，在旋转后变成了从右向左的第 i 列，也就是从左向右的第 n-1-i 列。

   

2. 原来的第 j 列，在旋转后变成了从上到下的第 j 行。

   

综合可以得到一个规律：

原来位置在 (i,j) 的元素，旋转后的位置是 (j,n-1-i)。

模拟旋转的主要思路： 将自外向内地旋转，然后枚举上方横边的每个元素、一次性连续旋转 4 次。

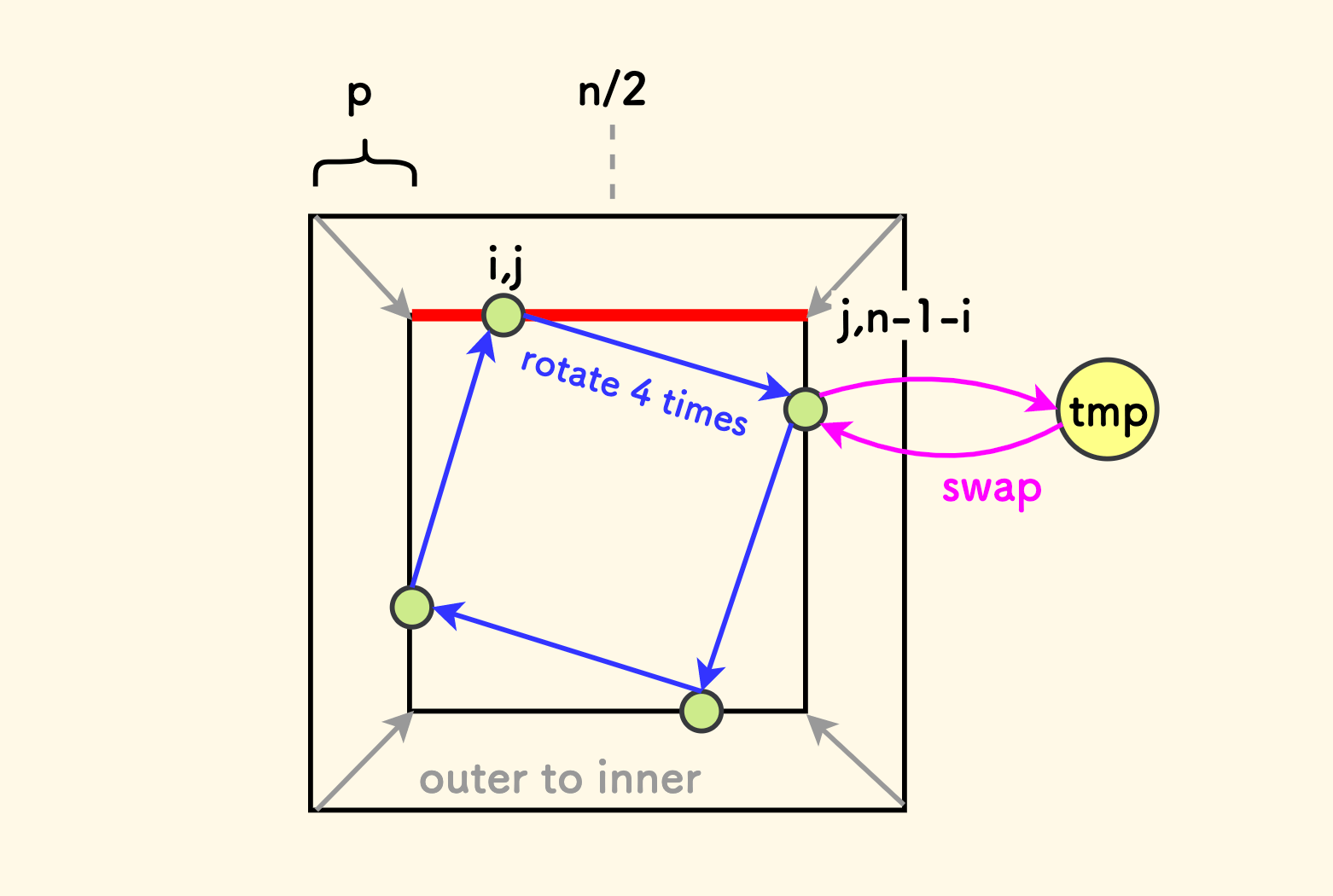
具体地讲，如下图中所示：

1. 从外向内考虑每个小的子矩阵，命一个变量 p 表示当前考虑的小矩阵距离原矩阵外框的边距。其迭代范围是 [0,n/2]。
2. 当固定好一个 p 时，需要把图中红色的边上的每个元素 [i,j] 不断旋转 4 次，即可完成这个子矩阵的所有周边上的元素的旋转。
3. 可以设置一个临时变量 tmp 来方便原地交换。当把一个元素置入新位置时，把这个位置上的原元素取出放到 tmp 暂存一下，相当于临时交给 tmp 倒一下手， 不断如此进行下去即可。

C++ 代码实现如下，整个过程是原地进行的，时间复杂度是 O(n^2)：

void rotate(vector<vector<int>>& g) {
  int n = g[0].size();

  // 从外围向内围进行, p 是当考虑的小矩阵距离原矩阵的边距
  for (int p = 0; 2 * p <= n; p++) {
    // 考虑红色上边框上的每个元素
    // 从 [p, p] 到 [p, n-1-p] 依次开始转
    // 注意避开行尾 (即 j 严格小于 n-1-p)
    for (int i = p, j = p; j < n - 1 - p; j++) {
      // 把元素 [i,j] 连续旋转 4 次,
      // tmp 用来临时存储目标位置上的原元素
      for (int x = i, y = j, tmp = g[i][j], k = 0; k < 4; k++) {
        int tx = y, ty = n - 1 - x;
        std::swap(tmp, g[tx][ty]);
        x = tx, y = ty;
      }
    }
  }
}

还是挺有趣的。

（完）

本文原始链接地址： https://writings.sh/post/rotate-matrix