状态机 DP 的笔记 | 春水煎茶

本文是对状态机 DP 的笔记。

状态机 DP ¶

状态机 dp 一般属于线性 dp，即可以按问题规模线性地划分阶段，每个阶段又可以划分为几个小状态，组成一个状态机，每个小状态代表一种可能情况，对应一个 dp 值。

随着 dp 阶段的推进，每个小状态的 dp 值从前一个阶段的一个或多个状态转移过来。

本文中，一般用 $i$ 来表示阶段，用 $j$ 来表示状态，$f_i(j)$ 或 $f(i,j)$ 等来表示 $i$ 阶段下状态 $j$ 的 dp 值。

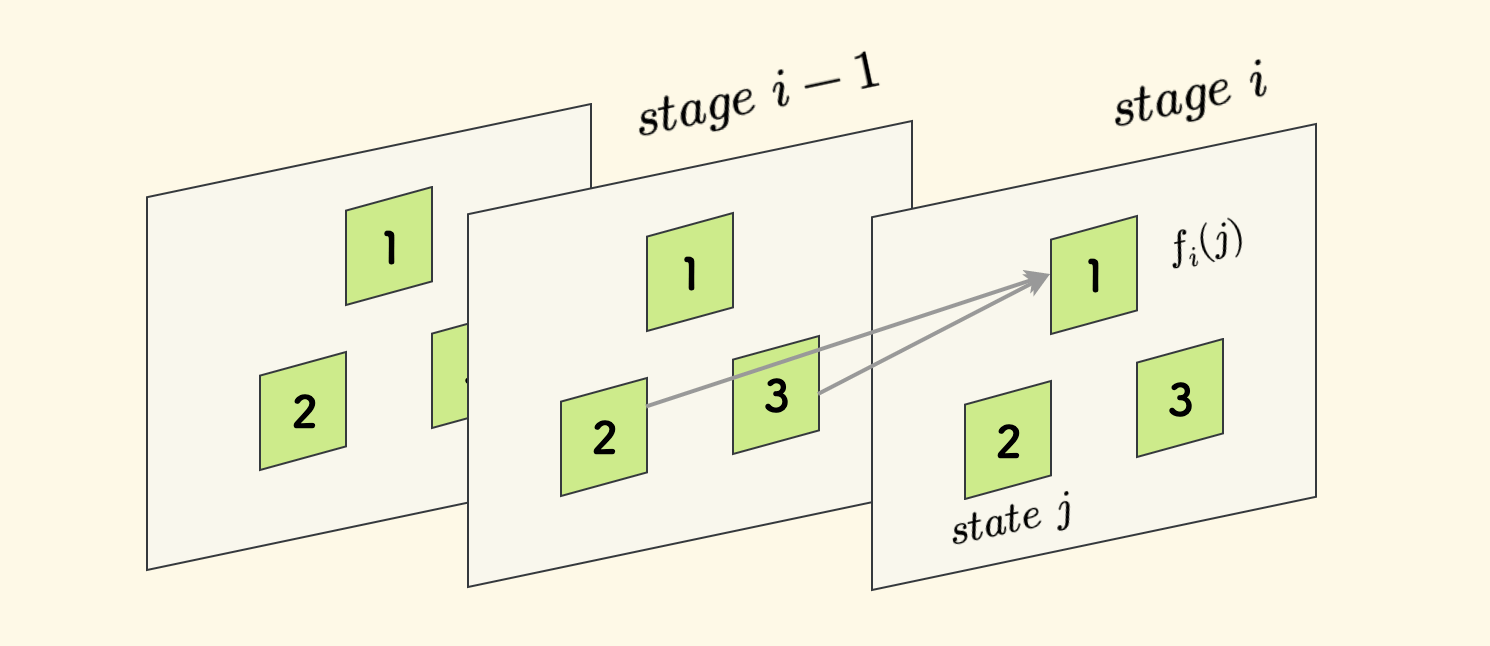
因为一般转移只和前一个阶段有关，所以可以用滚动数组的方式来优化，只需关注最新情况。通俗地说，只需要一个固定数组 $f(j)$ 来存各个小状态的 DP 值，可以省去阶段 $i$ 这个维度。

采用滚动数组转移时的一个细节注意点

采用滚动数组的方式时，由于是拿 dp 数组的一项去更新另一项，要注意转移语句的顺序，以避免同一阶段内转移的级联影响。

有时需要暂记上一个阶段的 dp 值来作为转移的起点，以避免小状态转移之间的相互影响。比如用 $f(a)$ 更新了 $f(b)$，稍后又用 $f(b)$ 来更新 $f(c)$ 的这种情况，实际可能执行了错误的转移，因为 $f(c)$ 包含了当前阶段的 $f(a)$ 的影响，这可能并非想要的。

下面是一个代码示意：

int f[MAX_J + 1]; // f[j] 表示最新的状态 j 下的 DP 值

f[j] = 0; // 初始化 i = 0 时, f[j] 的取值

for (int i = 1; i <= n; i++) {  // 考虑每个阶段 i
    // 先暂记当前各个状态的转移起点
    int f0 = f[0], f1 = f[1], ...;
    // 考虑每个状态 j 可能转移自哪些状态
    // 转移时，视情况综合各个状态来源、比如取最值之类的
    f[j] = max(f0, f1, ...);
    ...
}

// 最后，问题规模达到 n 后，综合考虑各个状态，给出答案
ans = max(f);

解决这一类问题，要首先分析出最小的状态集、转移条件，画出状态机，即可进行 DP 求解。

粉刷房子 ¶

有 $n$ 个房子排成一排，每个房子可被粉刷成红、蓝和绿这三种颜色中的一种，但是要求相邻的两个房子的颜色不同。
第 $i$ 个房子粉刷成颜色 $j$ 的成本是 $C(i,j)$，求最小的总粉刷成本。
-- 来自 leetcode LCR. 粉刷房子

考虑第 $i$ 个房子，有 $3$ 种可能的状态，要把它刷成颜色 $j$，就要考虑前一个房子已经刷成另外 $2$ 种颜色的最小成本，再加上粉刷成颜色 $j$ 的成本。

定义 $f(j)$ 表示当前房子刷成第 $j$ 个颜色的最小成本，转移如下：

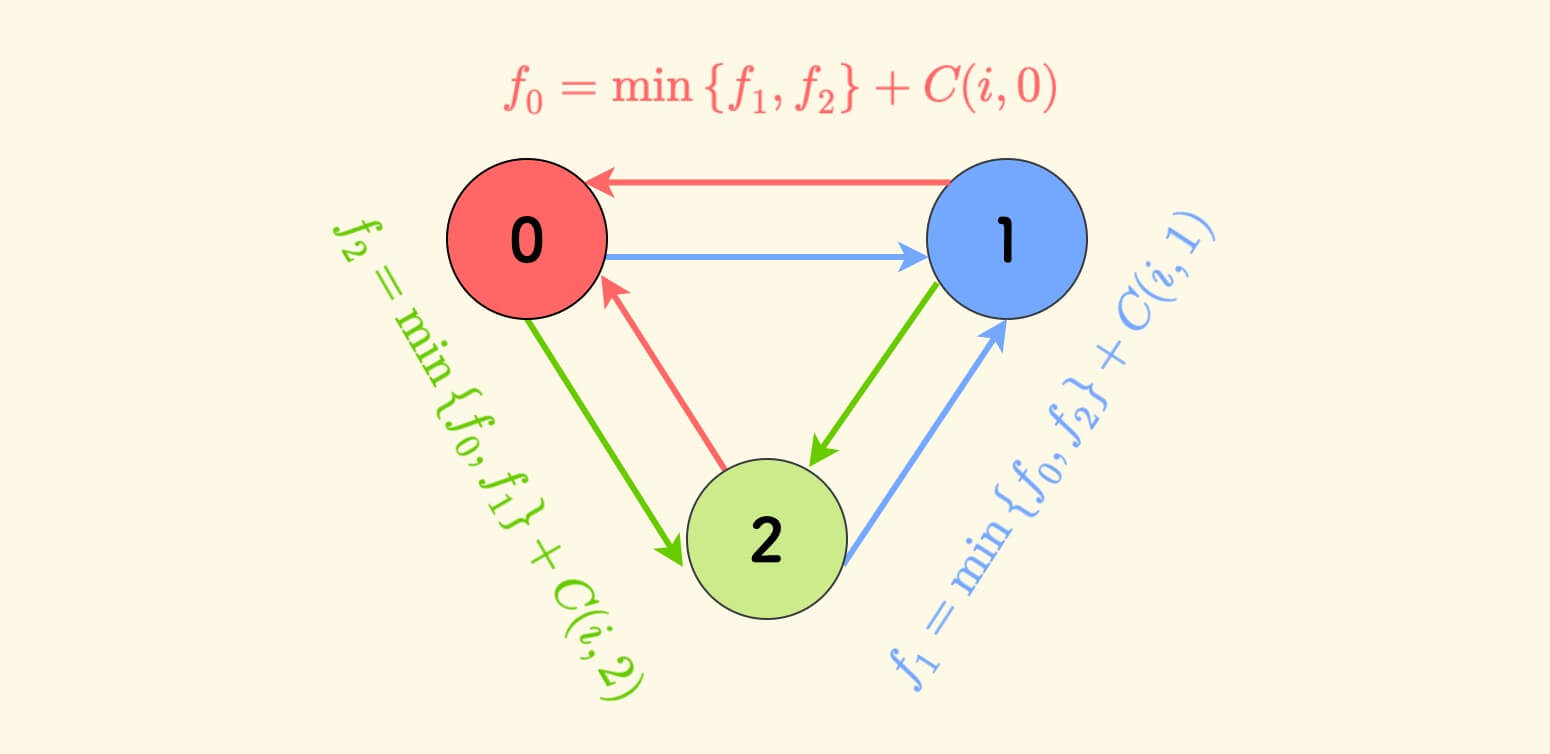
\[\begin{split} f_0 &= \min {\{ f_1, f_2 \}} + C(i,0) \\ f_1 &= \min {\{ f_0, f_2 \}} + C(i,1) \\ f_2 &= \min {\{ f_0, f_1 \}} + C(i,2) \end{split}\]

容易钦定初始情况：$f_j = C(0,j)$。

具体实现见下方，时间复杂度是线性的 $O(n)$。

一个细节是，滚动更新 $f$ 时要注意避免三个转移的相互影响，应取出上一个阶段的值后暂记、再用之来更新 $f$。

粉刷房子 - C++ 代码

class Solution {
   public:
    int minCost(vector<vector<int>>& C) {
        int f[3] = {C[0][0], C[0][1], C[0][2]};

        for (int i = 1; i < C.size(); i++) {
            int f0 = f[0], f1 = f[1], f2 = f[2];
            f[0] = min(f1, f2) + C[i][0];
            f[1] = min(f0, f2) + C[i][1];
            f[2] = min(f0, f1) + C[i][2];
        }
        return min({f[0], f[1], f[2]});
    }
};

可被三整除的最大和 ¶

找出一个整数数组中最大的能被三整除的元素和。
-- 来自 leetcode 1262. 可被三整除的最大和

比如数组 [3,6,5,1,8]，应该选 [3,6,1,8]，它们的和是 18，是可以被 3 整除的最大的元素和。

每个元素和有三种情况，即除以 3 后分别余 0，1 和 2。

定义 $f(j)$ 是除以 $3$ 后余 $j$ 的最大的元素和。

那么，依次考虑每个元素 $x$ 时，状态 $j$ 会转移到状态 $k=(j+x)\%3$。

答案则是取最值，更大则更新：

\[f(k) = \max {\{ f(k), f(j) + x \}}\]

具体来说，当前每个状态下的最大元素和 $f_j$，加上 $x$ 后的和记为 $s_j$ ：

int s0 = f[0] + x;
int s1 = f[1] + x;
int s2 = f[2] + x;

然后，各自转移到目标状态 $s_{j \% 3}$ 上去：

f[s0 % 3] = max(f[s0 % 3], s0);
f[s1 % 3] = max(f[s1 % 3], s1);
f[s2 % 3] = max(f[s2 % 3], s2);

依次遍历每个元素执行这个过程即可，最终 $f(0)$ 即是整除 $3$ 的最大元素和。

初始情况下，可以设定 $f(j)$ 全部为 0，从数组的第 0 项开始转移。

可能被三整除的最大和 - C++ 代码

class Solution {
   public:
    int maxSumDivThree(vector<int>& a) {
        int f[3] = {0, 0, 0};

        for (auto x : a) {
            int s0 = f[0] + x;
            int s1 = f[1] + x;
            int s2 = f[2] + x;

            f[s0 % 3] = max(f[s0 % 3], s0);
            f[s1 % 3] = max(f[s1 % 3], s1);
            f[s2 % 3] = max(f[s2 % 3], s2);
        }

        return f[0];
    }
};

股票买卖（k次交易） ¶

给定一个整数数组 $prices$ 表示某支股票第 $i$ 天的价格 $prices[i]$，最多可以买 $k$ 次、卖 $k$ 次。但是再次购买之前必须卖出手上的股票。求可以获取到的最大利润。
$k$ 是给定的一个 $[1,100]$ 范围内的整数。
-- 来自 leetcode 买卖股票的最佳时机 IV

因为再次购买股票前，必须卖掉手上持有的，所以可以划分为两类状态：手上持有现金和手上持有股票。

DP 定义如下：

$f_0(j)$ 表示当前进行了 $j$ 次买入后，手上持有现金的情况下获取的最大利润。
$f_1(j)$ 表示当前进行了 $j$ 次买入后，手上持有股票的情况下获取的最大利润。

初始情况下，第 $0$ 天的情况：

手上持有现金，未参与任何交易，盈利是 $f_0(0)=0$。
购入当日股票，盈利是负的，即 $f_1(1) = -prices[0]$。

也就是说，定义一个二维数组：

int f[2][101];

f[0][0] = 0;
f[1][1] = -prices[0];

下面考虑转移，考虑第 $i$ 天的情况：

要到达持有现金的状态，可以由两种情况转移而来：
1. 目前手上持有股票，卖掉股票，盈利 $prices[i]$。
2. 目前在手上持有现金，保持不变。
综合取最值：
\[f_0(j) = \max { \{ f_0(j), f_1(j) + prices[i] \}}\]
要到达持有股票的状态，也可以由两种情况转移而来：
1. 目前手上持有股票，保持不变，即不卖。
2. 目前在手上持有现金，购入股票，盈利 $-prices[i]$，并且消耗一次购买机会。
综合取最值：
\[f_1(j) = \max { \{ f_1(j), f_0(j-1) - prices[i] \}}\]

状态机的转移图示：

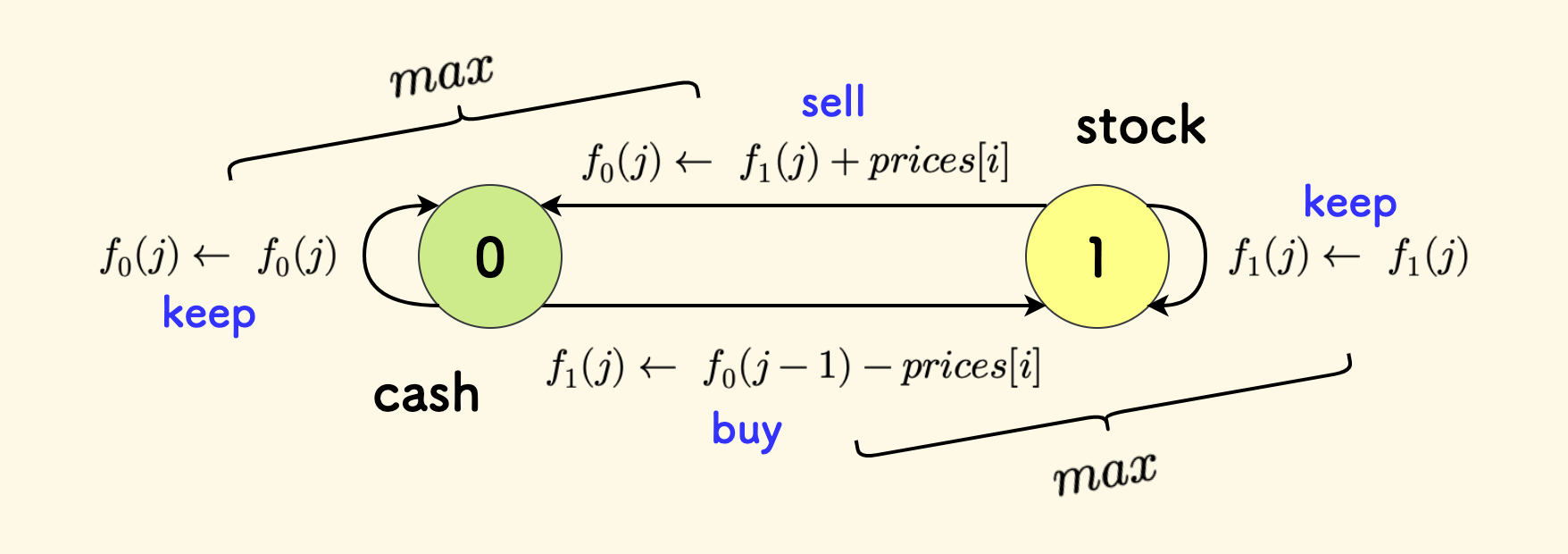
最终的答案应该取手持现金情况下的最大利润，即各个 $f_0(j)$ 的最值。

买卖股票的最佳时机 IV - C++ 代码

class Solution {
public:
    int maxProfit(int k, vector<int>& prices) {
        int f[2][101];
        memset(f, 0xcf, sizeof f);

        f[0][0] = 0;
        f[1][1] = -prices[0];

        for (int i = 1; i < prices.size(); i++) {
            for (int j = 1; j <= k; j++) {
                f[0][j] = max(f[0][j], f[1][j] + prices[i]);
                f[1][j] = max(f[1][j], f[0][j - 1] - prices[i]);
            }
        }
        return max(0, *max_element(begin(f[0]), end(f[0])));
    }
};

两个思考点：

为什么没有暂记上一阶段的 DP 值？

观察实现代码，可以看到并没有暂记滚动数组的上一个阶段的 DP 值，这是因为：

先计算的 $f_0(j)$ 不会对下面一行的 $f_1(j)$ 的计算造成影响。
$f_1(j)$ 真正依赖的是 $f_0(j-1)$，目前是正向循环 $j$，考虑下面的转移情况：
```
// j-1 时, 以今日价格卖出股票
f[0][j-1] = f[1][j] + prices[i];
// j 时, 以今日价格买入股票
f[0][j] = f[0][j-1] - prices[i];
```
虽然确实存在了两类状态在同一阶段内的级联影响，但是这个情况正好代表了：当天卖出后立即买入的情况，题目没有限制这种情况，所以是希望包括进去的。

如果不限制交易次数呢？

不限制交易次数的时候，会变的更简单，直接舍弃 $j$ 这个维度即可。

也就是只有两种状态，$f_0$ 表示手持现金状态下的最大获利，$f_1$ 表示手持股票状态下的最大获利。

转移是类似的，可以看做是当前问题的简化版：

int f[2] = {0, -prices[0]};

for (int i = 1; i < n; i++) {
    f[0] = max(f[0], f[1] + prices[i]);
    f[1] = max(f[1], f[0] - prices[i]);
}

retrun f[0];

股票买卖（含冷冻期） ¶

给定一个整数数组 $prices$ 表示某支股票第 $i$ 天的价格 $prices[i]$，可以买卖任意多次。
但是卖出股票后，无法在第二天买入股票，也就是存在 $1$ 天的冷冻期。
求可以获取到的最大利润。
-- 来自 309. 买卖股票的最佳时机含冷冻期

和前面的问题的区别就是：

去掉了交易次数的限制，简化了状态数 ^[1]。
增加了冷冻期的限制：卖出后无法立即购买。

实际上相当于新增了状态，现定义 $3$ 种状态：

$f(0)$ 表示：手持现金，昨日存在卖出，现在不可以买入，即处于冷冻期。
$f(1)$ 表示：手持现金，昨日无卖出，现在可以买入。
$f(2)$ 表示：手持股票。

下面分析转移：

要到达手持股票的状态：
1. 要么不买（已经处于手持股票状态，保持不变）。
2. 要么买（手上现金、但是不处于冷冻期），此时花费 $prices[i]$。
综合取最大值：
\[f(2) = \max \left\{ f(2),\ f(1)-prices[i]\right\}\]
要到达手持现金的自由状态：
1. 前面即已经手持现金自由，保持不变。
2. 从冷冻期转移而来（解冻）。
综合取最大值：
\[f(1) = \max \left\{ f(1), f(0) \right\}\]
要想到达冷冻期，只有一条路：卖出股票，此时获得盈利。
\[f(0) = f(2) + prices[i]\]

状态转移图见下方：

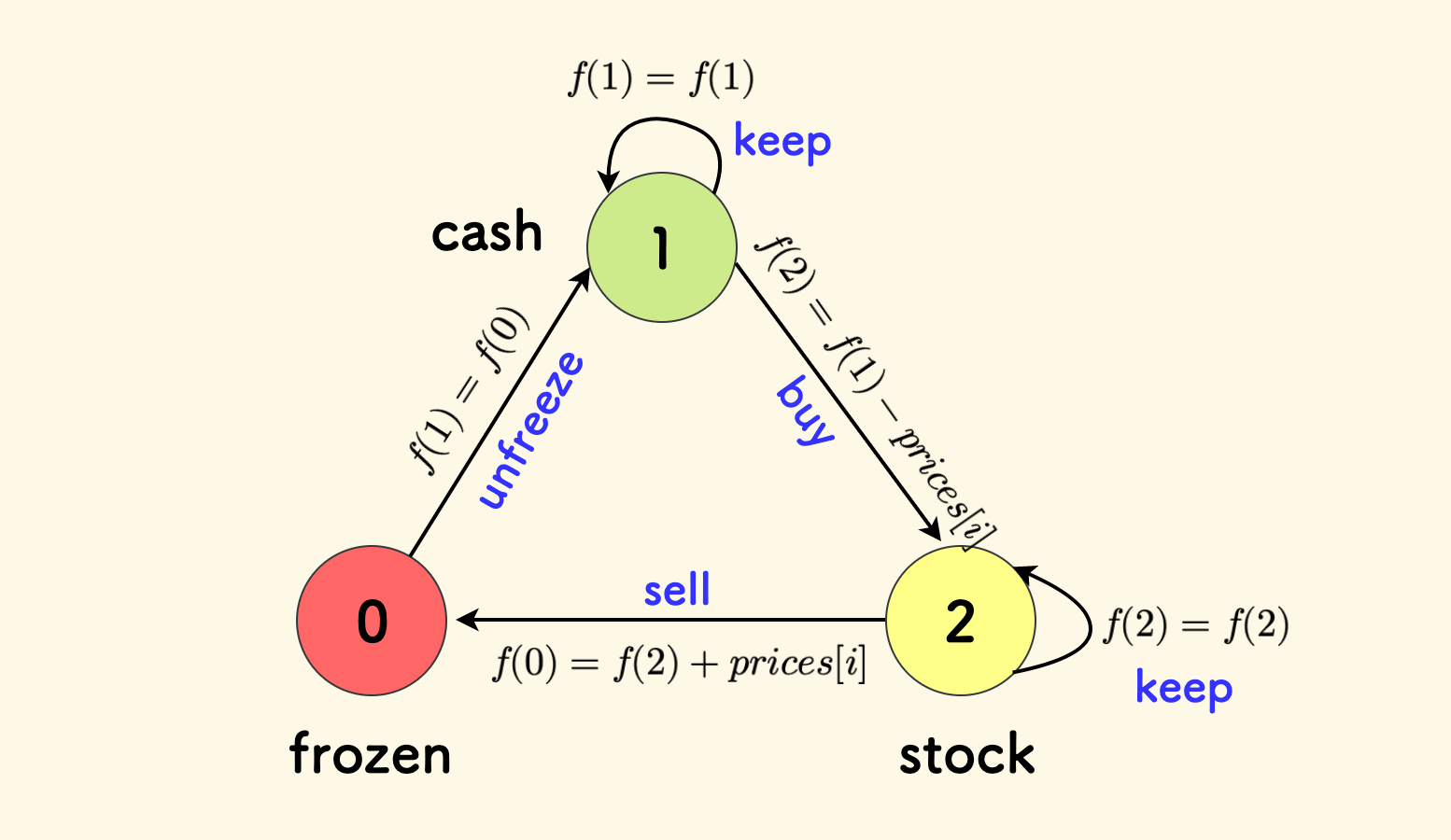
特别注意的是，冷冻期不可保持，一天之后必定解冻，没有自旋的状态转移。

接下来考虑下转移顺序，不像前面 ^[2] 了，当前的问题中状态的转移顺序至关重要。

在一天之内（也就是一个阶段内）：

允许买入之后、立即卖出：
也就是下图中，允许 ① 号转移对 ③ 号转移形成影响，就是说 ① 要放在 ③ 前面进行转移。
冷冻期为 1 天：
任何经过状态 $0$ 的转移，都不可以在当天内级联式地流转。
也就是，② 号转移必须在 ① 号转移后面，这样不至于 ② 对 ① 形成影响。
同样，③ 号转移必须在 ② 号转移后面，这样 ③ 才不会对 ② 形成影响。

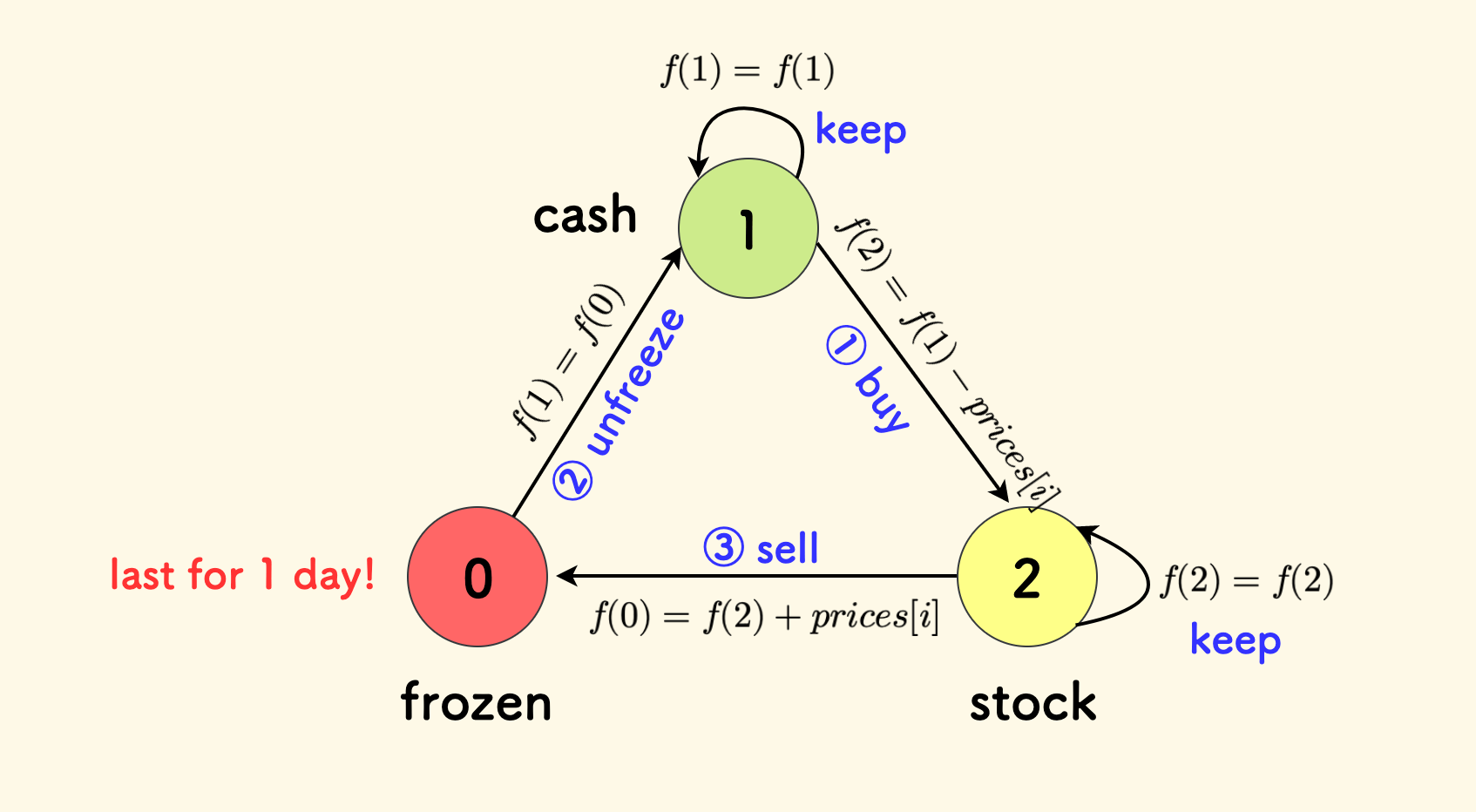
综合下来，转移的顺序只能是：

for (int i = 1; i < prices.size(); i++) {
  // 保持手持股票 or 买入 ①
  f[2] = max(f[2], f[1] - prices[i]);
  // 保持自由 or 刚解冻  ②
  f[1] = max(f[1], f[0]);
  // 卖出后进入冷冻期  ③
  f[0] = f[2] + prices[i];
}

通俗地来看，今日（阶段 $i$）卖出后，次日（阶段 $i+1$ ）进入冷冻期，再一天（阶段 $i+2$）后恢复购买自由，冷冻期恰好为 $1$ 天。

这里分析转移顺序的技巧是：讨论在同一阶段内，是否允许转移之间的级联式影响。

买卖股票的最佳时机含冷冻期 - C++ 代码

class Solution {
   public:
    int maxProfit(vector<int>& prices) {
        int f[3] = {0};
        f[2] = -prices[0];  // 第一天买入的话,盈利是负的
        for (int i = 1; i < prices.size(); i++) {
            // 转移顺序不可更换
            f[2] = max(f[2], f[1] - prices[i]);
            f[1] = max(f[1], f[0]);
            f[0] = f[2] + prices[i];
        }
        return max({0, f[0], f[1]});
    }
};

将字符串翻转到单调递增 ¶

给一个只包含字符 0 和 1 的字符串 s，你可以翻转多次，一次翻转是指把一个字符从 0 变为 1 或者从 1 变为 0。
求把字符串 s 变成单调递增的最小翻转次数。
单调递增是说，形如 00..0011..11 这种形式，也可以没有 0，也可以没有 1，总之不能递减。
-- 来自 leetcode 926. 将字符串翻转到单调递增

比如说：s="00110" 时，只需要翻转一次，即翻转最后一个 0，变成 00111。

这个问题和下面的使序列递增的最小交换次数十分相似。

定义两个状态，考虑第 $i$ 个元素：

$f_0$ 表示当前元素没有发生翻转的情况
$f_1$ 表示当前元素发生了翻转的情况

$f$ 的值是两种情况下子字符串 $s[0..i]$ 形成单调递增的最小翻转次数。

一个字符翻转多于两次是没有意义的，所以我们只需要考虑这两种状态。

此外，由于我们会考虑每个字符是否会翻转，必定不会遗漏任何情况。

初始情况下，容易钦定 $f_0 = 0$ 且 $f_1 = 1$。

现在，假定已经完成了前面 $i-1$ 个字符的推导，考虑下面第 $i$ 个字符的情况：

如果第 $i-1$ 个字符是 0，第 $i$ 个字符也是 0，也就是最近的两个字符是 00：
1. 要想保持 $s_i$ 不翻转，势必 $s_{i-1}$ 也不可翻转，转移方程如下：
  \[f_0 = f_0\]
2. 要想翻转 $s_i$ 为 1，那么 $s_{i-1}$ 可翻转、也可不翻转，综合取最小。
  并且此时增加了一次翻转次数，转移方程如下：
  \[f_1 = \min{ \{ f_0, f_1 \}} + 1\]
继续类似的讨论，可以推导其他三种情况：
1. 相邻字符是 10 的情况：
  \[\begin{split} f_0 &= f_1 \\ f_1 &= \min { \{ f_0, f_1 \} } + 1 \end{split}\]
2. 相邻字符是 01 的情况：
  \[\begin{split} f_0 &= \min { \{ f_0, f_1 \} } \\ f_1 &= f_0 + 1 \end{split}\]
3. 相邻字符是 11 的情况：
  \[\begin{split} f_0 &= \min { \{ f_0, f_1 \} } \\ f_1 &= f_1 + 1 \end{split}\]

至此，两个状态随着阶段 $i$ 的转移方程已全部推出。

一个细节仍然是，因为采用了滚动数组，所以要注意提前暂记上一个阶段的 dp 值，防止一个阶段内的小状态之间的级联转移。

最后的答案是，$f_0$ 和 $f_1$ 之中的最小者。

将字符串翻转到单调递增 - C++ 代码

class Solution {
   public:
    int minFlipsMonoIncr(string s) {
        int f[2];  // f[0] 表示不翻 s[i], f[1] 表示翻 s[i] 的最少次数
        f[0] = 0;
        f[1] = 1;

        for (int i = 1; i < s.size(); i++) {
            int f0 = f[0], f1 = f[1];
            if (s[i - 1] == '0' && s[i] == '0') {  // 00
                f[0] = f0;
                f[1] = min(f0, f1) + 1;
            } else if (s[i - 1] == '1' && s[i] == '0') {  // 10
                f[0] = f1;
                f[1] = min(f0, f1) + 1;
            } else if (s[i - 1] == '0' && s[i] == '1') {  // 01
                f[0] = min(f0, f1);
                f[1] = f0 + 1;
            } else {  // 11
                f[0] = min(f0, f1);
                f[1] = f1 + 1;
            }
        }
        return min(f[0], f[1]);
    }
};

使序列递增的最小交换次数 ¶

给定两个长度相等的整数数组 $a$ 和 $b$，可以进行如下交换操作：
选定一个下标 $i$，交换 $a[i]$ 和 $b[i]$。
返回使 $a$ 和 $b$ 都严格递增的最小交换次数，测试用例保证可以实现。
-- 来自 leetcode 801. 使序列递增的最小交换次数

线性划分阶段，每个阶段有两种状态，即有无交换了 $a_i$ 和 $b_i$。

DP 定义：

$f_0(i)$ 为第 $i$ 个元素没发生交换的情况
$f_1(i)$ 为第 $i$ 个元素发生了交换的情况

$f$ 的值是两种情况下前 $a[0..i]$ 和 $b[0..i]$ 形成严格递增时的最小交换次数。

考虑从 $i-1$ 阶段向 $i$ 阶段转移，此时 $0..i-1$ 都已经严格递增。

如果 $a$ 和 $b$ 的第 $i$ 项恰好也满足递增，那么，可以都交换，也可以都不交换。

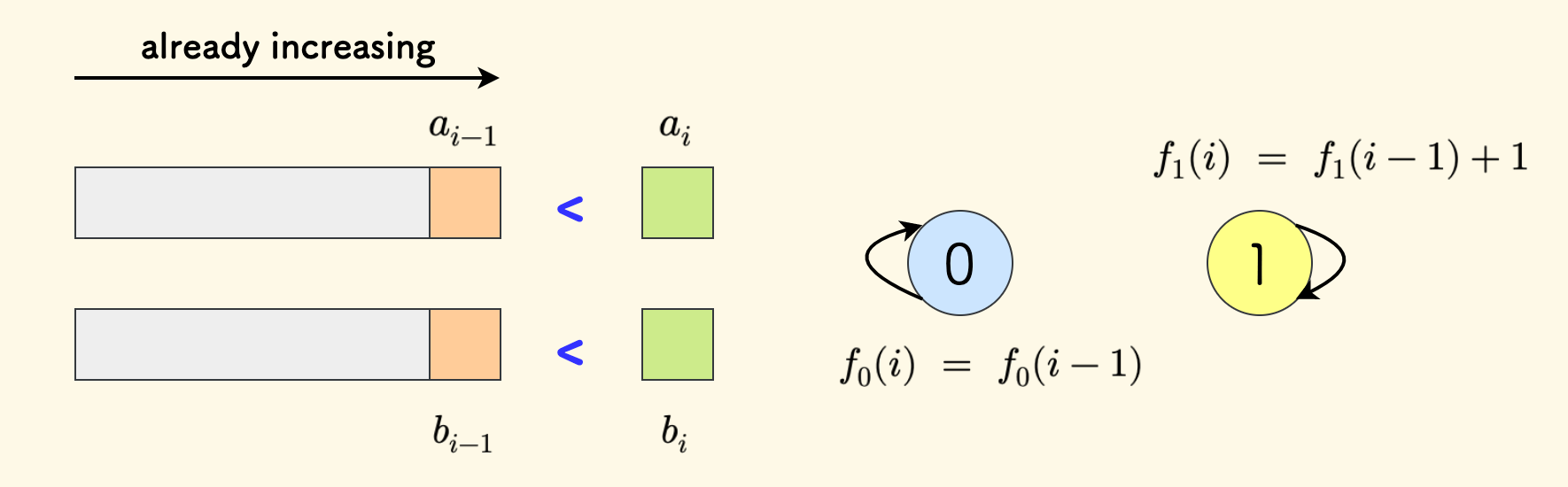
即，当 $a_{i-1} < a_i$ 且 $b_{i-1} < b_i$ 时：

选择都不交换，也就是基于 $i-1$ 阶段不交换的情况下，继续保持不交换。
\[f_0(i) = f_0(i-1)\]
选择都交换，相当于基于 $i-1$ 阶段交换的情况下，再执行一次交换，则：
\[f_1(i) = f_1(i-1) + 1\]

还有一种情形，就是当 $a_{i-1} < b_{i}$ 且 $b_{i-1} < a_{i}$ 的时候，此时只需要交换一对。

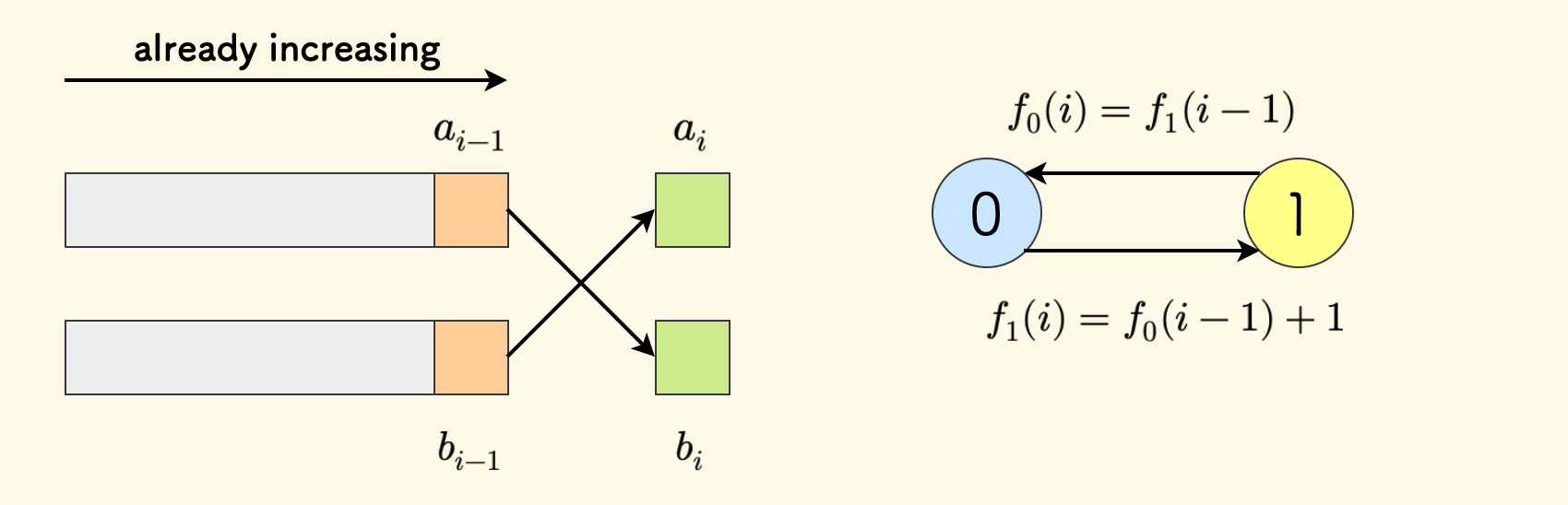
如果 $a_{i-1}$ 和 $b_{i-1}$ 没有执行过交换，那么就交换 $a_i$ 和 $b_i$，交换次数增加。
\[f_1(i) = f_0(i-1) + 1\]
如果 $a_{i-1}$ 和 $b_{i-1}$ 执行过交换，那么就不要交换 $a_i$ 和 $b_i$，交换次数不变。
\[f_0(i) = f_1(i-1)\]

这两种情形，可能同时满足，就要综合取最小值。

状态转移图综合来看如下图：

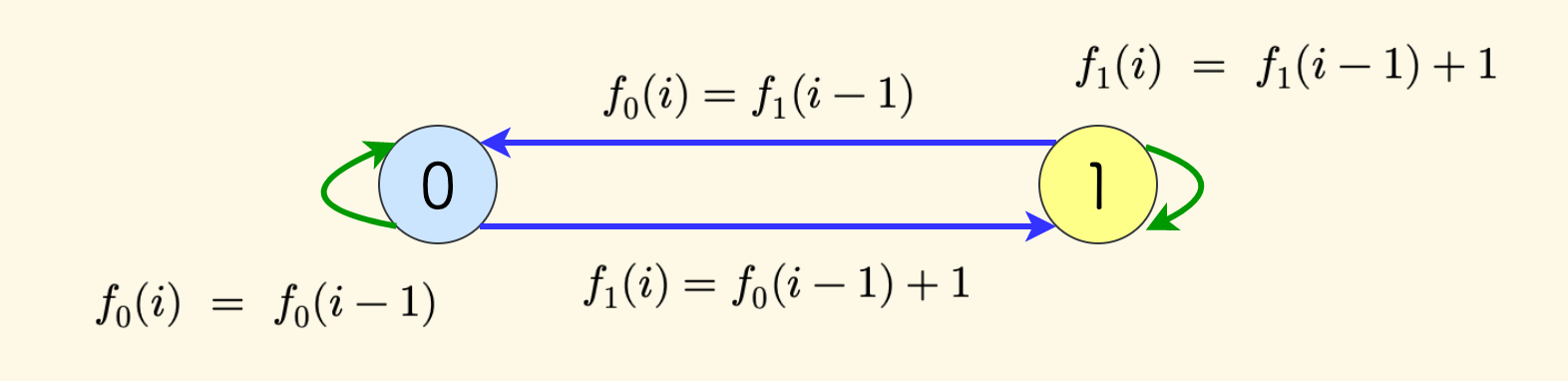
我们采用的线性阶段划分，而且当前阶段的情况只和上一个阶段有关，所以也可以用滚动数组的方式。采用滚动数组的时候，仍然要注意暂记一下上一个阶段的 DP 值。

代码实现如下：

使序列递增的最小交换次数 - C++ 代码

class Solution {
   public:
    int minSwap(vector<int>& a, vector<int>& b) {
        // f[0] 表示不交换 i, f[1] 表示交换 i 的最小次数
        int f[2] = {0, 1};

        for (int i = 1; i < a.size(); i++) {
            int f0 = f[0], f1 = f[1];
            // 注意先放大, 以便取到正确的 min
            memset(f, 0x3f, sizeof f);

            int a1 = a[i - 1], a2 = a[i], b1 = b[i - 1], b2 = b[i];

            if (a1 < a2 && b1 < b2) { // 都交换 or 都不交换
                // 都不交换, f[0] 不变
                f[0] = f0;
                // 都交换, 也就是基于上一次的交换下, 继续交换一次, f[1] 增加
                f[1] = f1 + 1;
            }
            // 注意和前面的取最小, 两种情况可能同时存在
            if (a1 < b2 && b1 < a2) { // 只可以交换一对
                // 基于上一次不交换, 进行交换一次
                f[1] = min(f[1], f0 + 1);
                // 或者基于上一次交换,这一次不交换
                f[0] = min(f[0], f1);
            }
        }
        return min(f[0], f[1]);
    }
};

最长非递减子序列 ¶

给定一个只包含 $1$ 和 $2$ 两种元素的数组 $a_1,a_2,…,a_n$。你可以最多选择一个区间 $[l,r]$ 进行翻转，使得翻转后整个数组 $a$ 中的最长非递减子序列的长度最长（这里的子序列不要求连续）。求这个最长非递减子序列的长度。
-- 来自 codeforces 933 A，acwing 3549

$a$ 中只有 $1$ 和 $2$ 两种元素，那么一个非递减子序列肯定是形如以下形式的：

1 1 ... 1 2 2 ... 2

要想进行最多一次翻转（也可以不翻转），到达这种形式，只有四种来源的可能：

.1                // state1，不翻转
.12..2            // state2，不翻转
.12..21..1        // state3，翻转 2..21..1
.12..21..12..2    // satte4，翻转 2..21..1

那么问题可以转化为：

在数组 $a$ 中找出形如以上 4 种形式的最长的子序列。

考虑依次遍历数组的每个元素 $a_i$，这 4 种子序列其实可以互相转化。

定义 $f(i)$ 表示第 $i$ 种 state 形式的子序列的最大长度。

如果新增的 $a_i$ 是 $1$，那么：

$state1$ 只可以继续由其本身转移而来。
```
1...1 1
```
\[f(1) = f(1) + 1\]
$state3$ 可以由：
1. $state2$ 添加一个 1 转移而来。
```
1..12..2 1
```
2. 也可以由 $state3$ 继续添加一个 1 转移而来。
```
1..12..21..1 1
```
  综合取最大值：
  \[f(3) = \max { \{ f(2) + f(3) \} } + 1\]

类同的分析，$a_i=2$ 的情况：

$state2$ 可以由 $state1$ 和其本身转移而来：
```
1..1 2
1..12..2 2
```
\[f(2) = \max { \{ f(1) + f(2) \} } + 1\]
$state4$ 可以由 $state3$ 和其本身转移而来：
```
1..12..21..1 2
1..12..21..12..2 2
```
\[f(4) = \max { \{ f(3) + f(4) \} } + 1\]

至此，4 种形式的子序列的转移情况已经分析完毕，状态机图示如下：

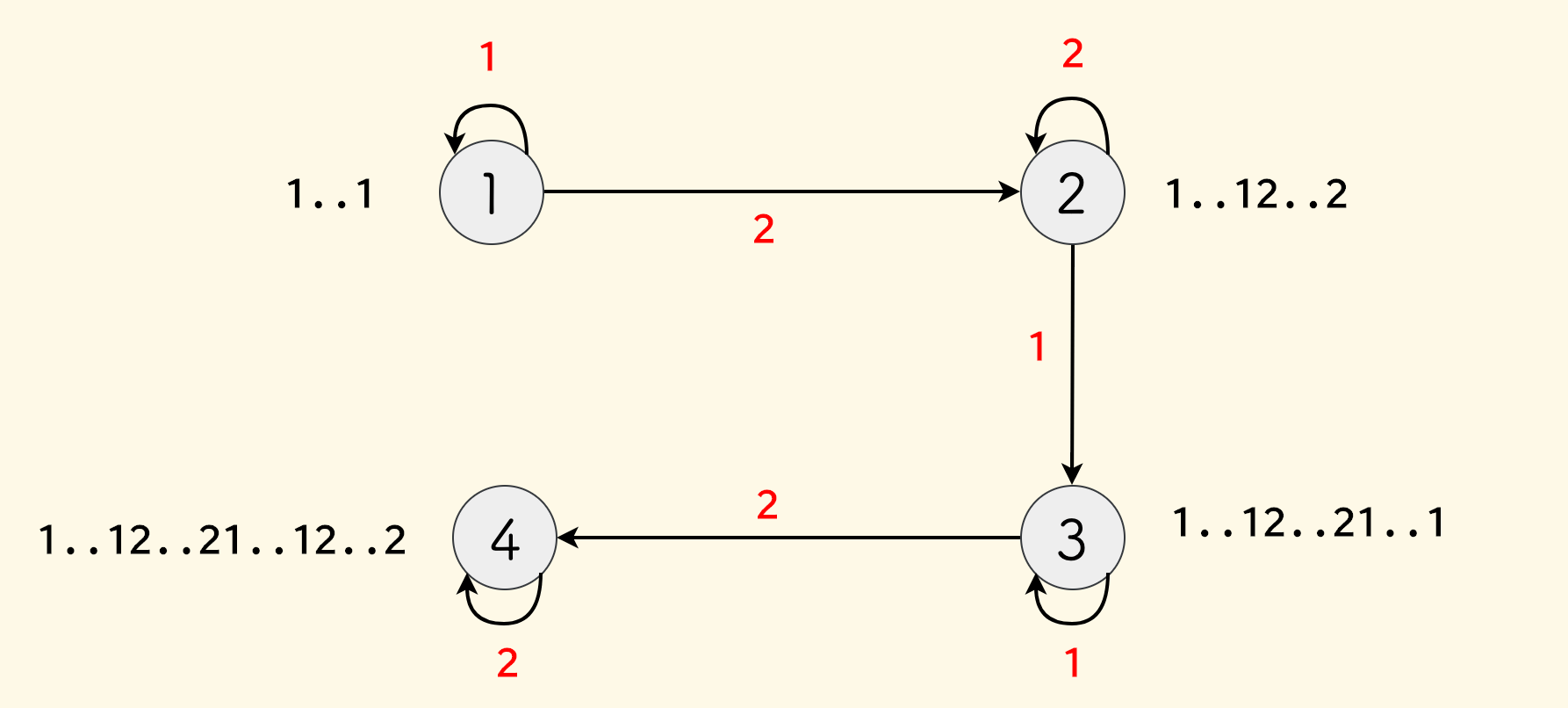
依次遍历每个 $a_i$，不断转移 dp 即可。最终 $f$ 数组的最大值就是答案。

最长非递减子序列 - C++ 代码

// state1    1..1
// state2    1..12..2
// state3    1..12..21..1
// state4    1..12..21..12..2
const int N = 2001;
int n;
int a[N]; // 下标从 1 开始
int f[5];

int solve() {
    memset(f, 0, sizeof f);

    for (int i = 1; i <= n; i++) {
        if (a[i] == 1) {
            f[1]++;
            f[3] = max(f[2], f[3]) + 1;
        } else {  // a[i] = 2
            f[2] = max(f[1], f[2]) + 1;
            f[4] = max(f[3], f[4]) + 1;
        }
    }
    int ans = 0;
    for (int j = 1; j <= 4; j++) ans = max(ans, f[j]);
    return ans;
}

简单总结 ¶

状态机 DP 一般是线性 dp。
先理清楚状态集合、转移条件和初始状态。
状态机 DP 可以采用滚动数组来做。
务必理清同一阶段内不同转移之间的顺序和相互影响。
分析状态善用倒推，要想到达 $j$ 状态，可能的来源有哪些。

（完）

更新日志：

2024/02/25 - 新增问题「将字符串翻转到单调递增」。

本文原始链接地址： https://writings.sh/post/statemachine-dp