黄金分割法,又称 0.618 法, 在数学上用于搜索一维单峰函数的极值的方法,和 二分法 类似, 是一种区间缩进的搜索方法。
数学上的黄金分割法 ¶
方便起见,我们只看下单峰函数,上单峰函数雷同。
假设 $f(x)$ 函数是区间 $[a, b]$ 上的一个下单峰函数,其极值的位置是 $t$ 。 就是说, $t$ 左边是单调递减的,右边是单调递增的 。
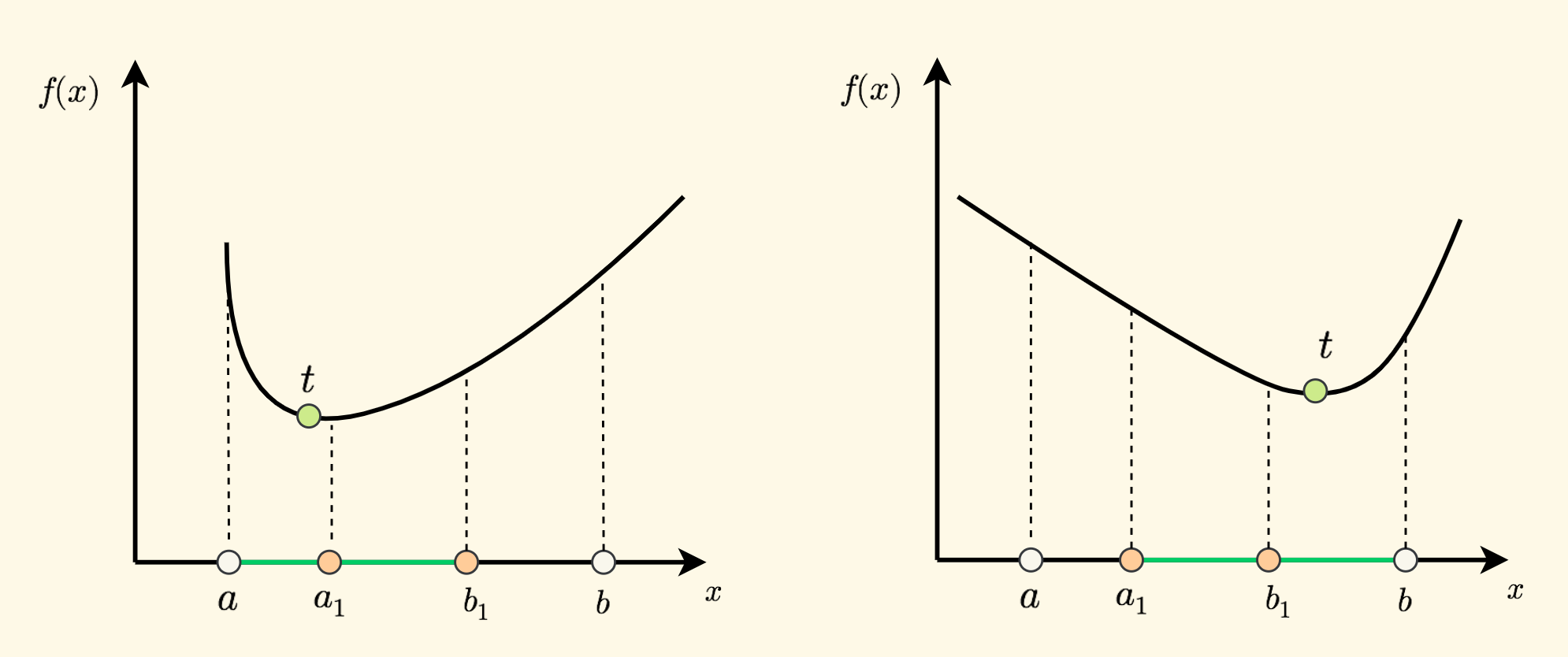
如果我们往区间上放置两个点 $a_1$ 和 $b_1$ ,对区间进行分割,这时候,只有两种情况:
- 如果 $f(a_1) < f(b_1)$ ,则必然 $t$ 在区间 $[a, b_1]$ 内,就是下图中左边的情况。
- 如果 $f(a_1) >= f(b_1)$ ,则必然 $t$ 在区间 $[a_1, b]$ 内,就是下图中右边的情况。
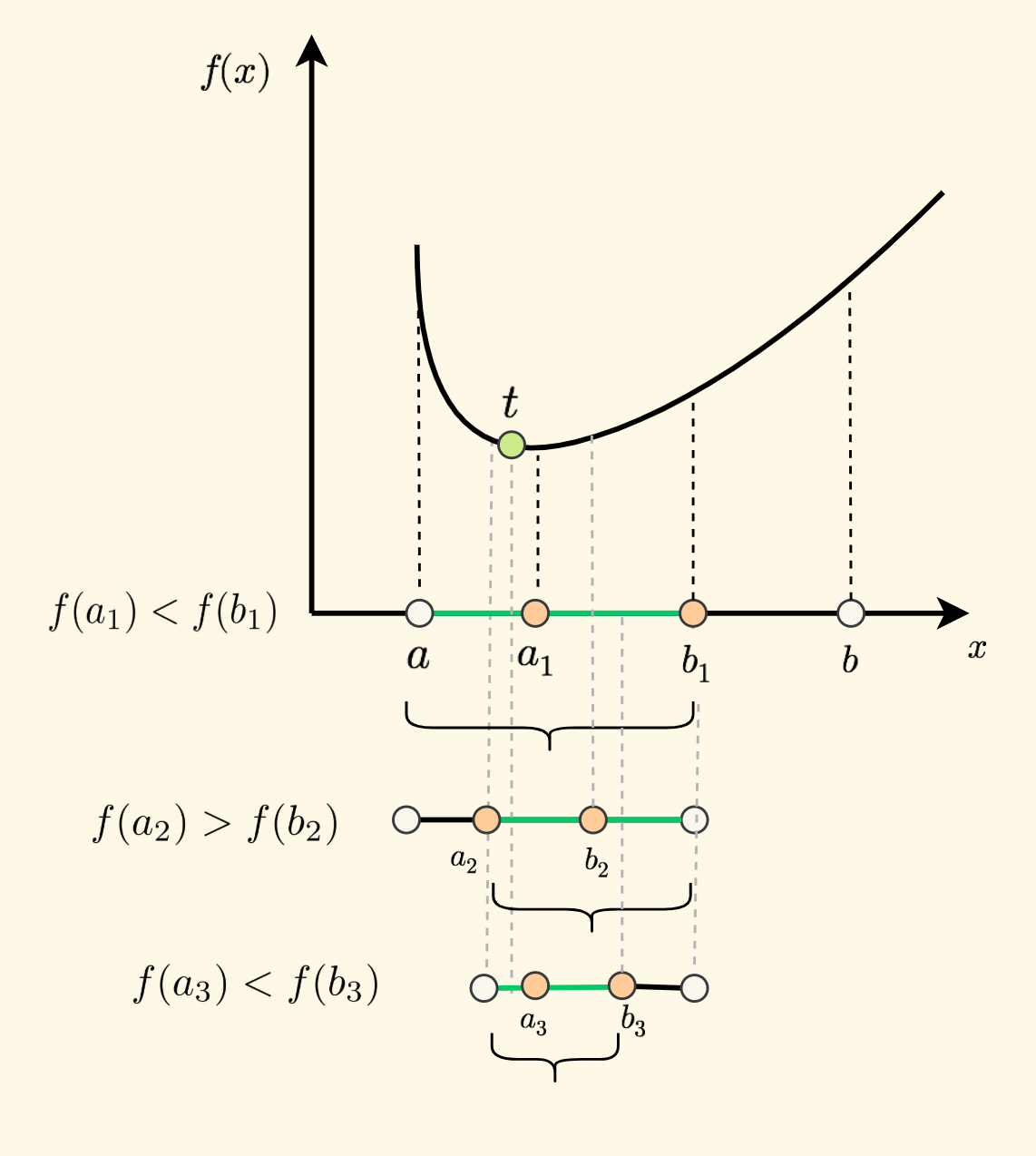
先只考虑上面所说的第一种情况,我们把左边的 $[a, b_1] $ 当做新的区间,代替原来的 $[a, b]$ ,也就是舍弃最右端的区间段; 同理对于上面所说的第二种情况,此时舍弃最左端的区间段。 然后继续比较、舍弃,如此反复进行,区间大小会不断变小,不断逼近 $t$ 。 如下图所示,绿色的线段表示不断缩小的区间:
直到误差达到理想水平,我们即可以获得单峰极值的近似值。
0.618 的由来 ¶
现在要问,区间的大小一次缩小多少比较合适呢?
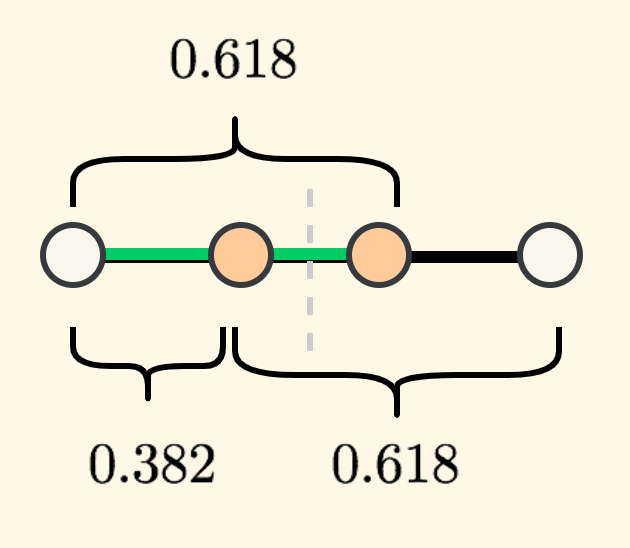
黄金分割法的方法是,每次选择区间的 $0.618$ 处和它的对称点 $0.382$ 处作为一对分割点。
如下图 2.1 所示,左右分割点分别在 $0.382$ 比例处和 $0.618$ 比例处,且两个点关于中轴对称。
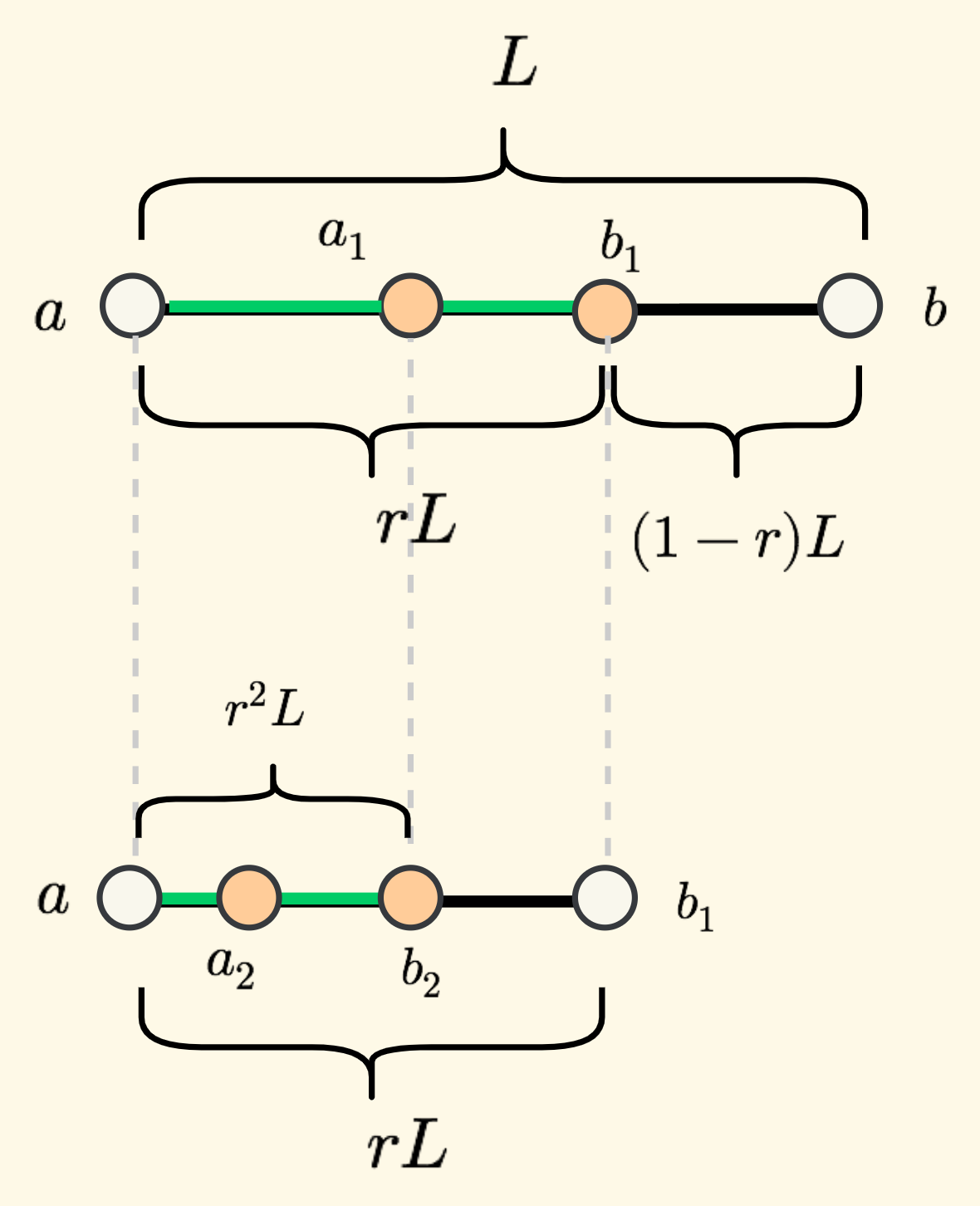
假设原始线段 $ab$ 的长度是 $L$ , 每次缩短的比例是小数 $r$ 。具体来说,我们希望的是:
每次的两个分割点是对称的。
事先并不知道极值点在哪里,对于不对称的分割点,会出现一侧区间大,一侧区间小的情况,如果极值不断落入大的区间, 会恶化迭代的速度。
在下面图 2.2 中的上图中,对称意味着: 线段 $aa_1$ 的长度和线段 $b_1b$ 一样,即 $(1-r)L$ 。
分割点可以复用。
在下面的图 2.2 中,第一次的分割点 $a_1$ 复用 为第二次的分割点 $b_2$ 。
最好上一次的分割点也可以用作下一次迭代的分割点,这样避免重复计算,每次只需要计算一个分割点的函数值。
则下面的线段 $ab_2$ 和上面中的线段 $aa_1$ 一样长,即 $r^2L = (1-r)L$。
解方程 $r^2 + r = 1$ 得 $r = \frac {\sqrt{5} \ -\ 1} {2}$ ,约等于 $0.618$ 。
复杂度分析 ¶
假设总共需要迭代 $k$ 次,区间才可以缩小到单位长度,假设总共的区间长度是 $n$ 个单位长度, 则有 $ n * (0.618) ^ k = 1$ 。假设 $c = 1 / 0.618$ ,则有 $ k = log_{c}{n}$ 。
根据 换底公式 可以知道:
\[log_{c} {n} = \frac {log_{2} {n}} {log_{2}{c}} = C * log_{2}{n}\]也就是说时间复杂度是 $log{n}$ 。
计算机中的三分法求单峰 ¶
在计算机编程上,可以用同样的方式对单峰数组求极值。 不过,不像数学中 $0.618$ 是连续区间的分割点,离散的数组上,使用 三分法。
下面仍然以下单峰数组为例,上单峰数组雷同。
下图是一个算法过程的示意图,其中红色框内的是每次缩减后的区间段,绿色的元素是分割点:
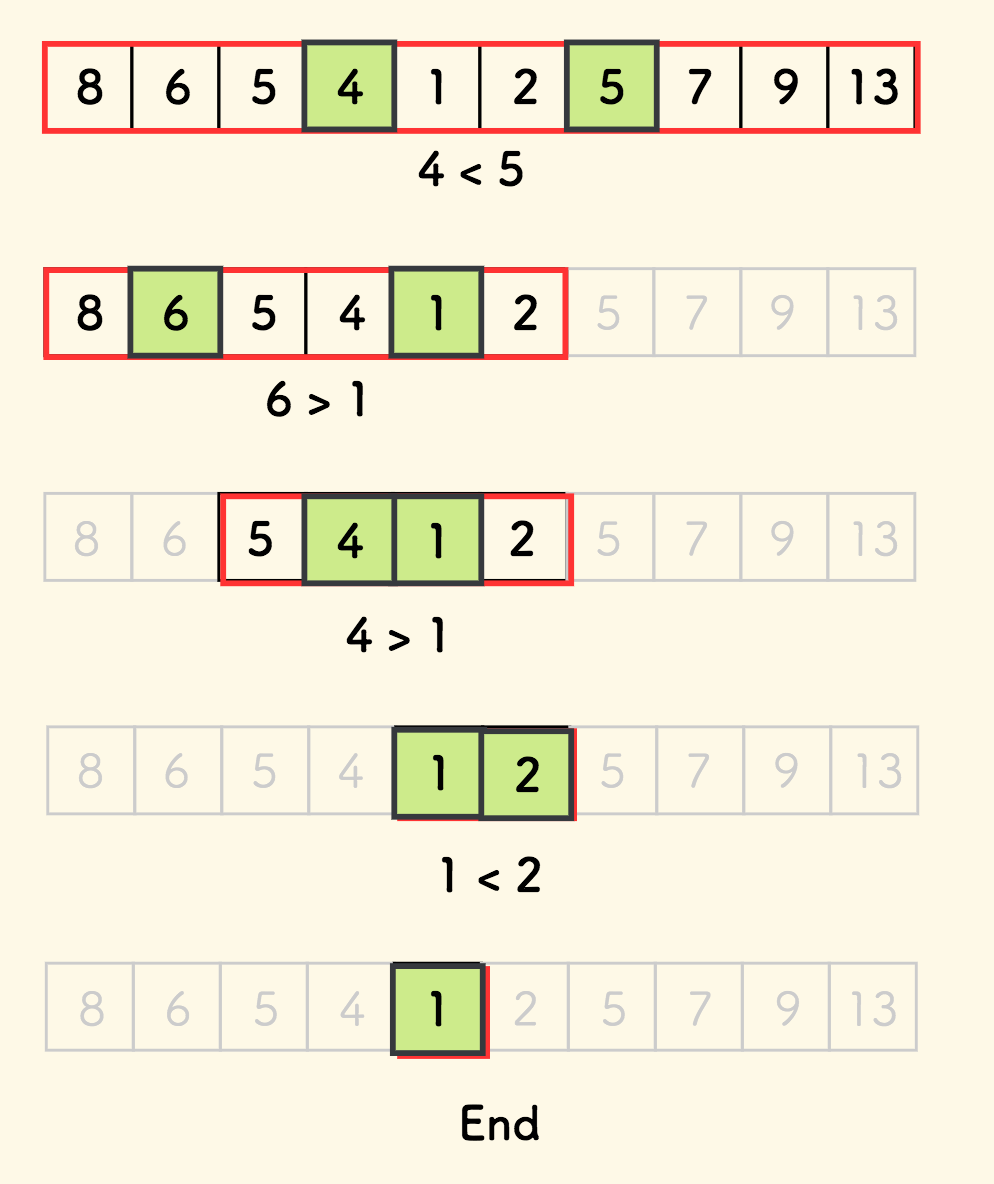
此算法只对存在单峰的数组有效。
算法过程:
- 步骤 1:初始化查找范围为整个数组,即低位 $low = 0$ ,高位 $high = n - 1$ ,$n$ 是数组的大小。
步骤 2:选择分割点:
- 计算整个范围的三分之一大小:$delta = (high - low) / 3$ 。
- 左分割点是 $partition\text{_}left = low + delta$ 。
- 右分割点与左分割点对称,是 $partition\text{_}left = high - delta$ 。
步骤 3:按以下情况进行比较,然后回到步骤 2 继续迭代。
如果左分割点的值严格小于右分割点的值,则舍弃右侧区间段,即 $high$ 缩小为 $partition\text{_}right - 1$ 。
这里同样舍弃了 $partition\text{_}right$ 位置上的值,因为此数据肯定不是单峰。
同理对于右分割点的值严格小于左分割点的情况, $ low = partition\text{_}left + 1$ 。
如果两个分割点的值相等,则两个点都不是极值,两端都舍弃。
- 步骤 4:直到 $low < high$ 不再满足,即 $low$ 和 $high$ 相等,终止迭代,此时已收敛到一个元素上,即峰值的位置。
复杂度分析 ¶
和黄金分割法一样,要把查找范围收缩到 $1$,迭代次数 $k$ 满足 $n * (1/3) ^ k = 1$ , 则时间复杂度为 $O(log_{3} {n})$ ,由 换底公式 可换算到 $O(log_{2} {n})$ 。
非递归实现的空间复杂度是 $O(1)$ 。
C 语言实现 ¶
C 语言的三分法查找数组内的单峰
// 给出大小为 n 的数组 a 的单峰的下标位置。
int TernarySearchPeak(int a[], int n) {
int low = 0;
int high = n - 1;
int delta = 0;
int partition_left = 0;
int partition_right = 0;
while (low < high) {
delta = (high - low) / 3;
partition_left = low + delta;
partition_right = high - delta;
if (a[partition_left] < a[partition_right]) {
high = partition_right - 1;
} else if (a[partition_left] > a[partition_right]) {
low = partition_left + 1;
} else {
low = partition_left + 1;
high = partition_right - 1;
}
}
return low;
}
(完)
