二分查找算法 是一种在 有序数组 中查找给定元素的搜索算法。
算法过程 ¶
二分查找的过程如下图所示:
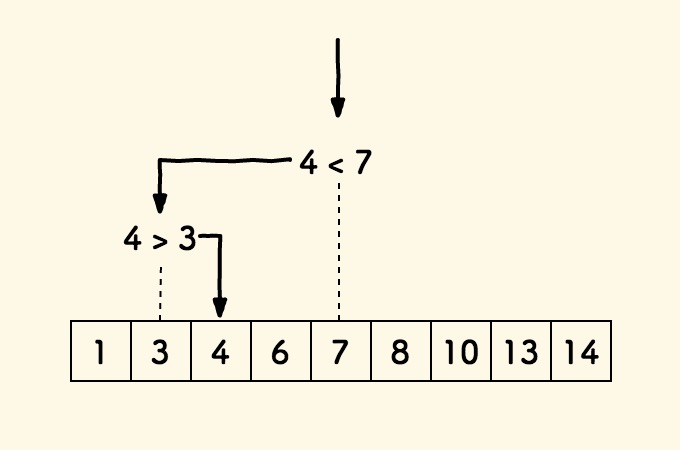
具体的查找过程:
- 步骤 1 :初始化查找范围为整个有序数组,即低位 $low$ 为 $0$ , 高位 $high$ 为数组的大小 $n$ 。
- 步骤 2 :比较中间位置 $mid = (low + high) / 2$ 的元素和目标元素的大小关系:
如果目标元素较小,则降低高位,即 $high = mid - 1$ 。
这缩小了一半的查找范围,重复查找,回到步骤 2 。
如果目标元素较大,则增大低位,即 $low = mid + 1$ 。
这缩小了一半的查找范围,重复查找,回到步骤 2 。
如果正好相等,查找完成,结束整个查找。
- 步骤 3 :直到查找范围无法继续缩小下去,即当 $low <= high$ 不再成立时,未查找到。
具体的算法过程如下图所示,图中的红色框是每次的查找范围,由 $low$ 开始,到 $high$ 结束。 每次查找范围都会缩减一半。
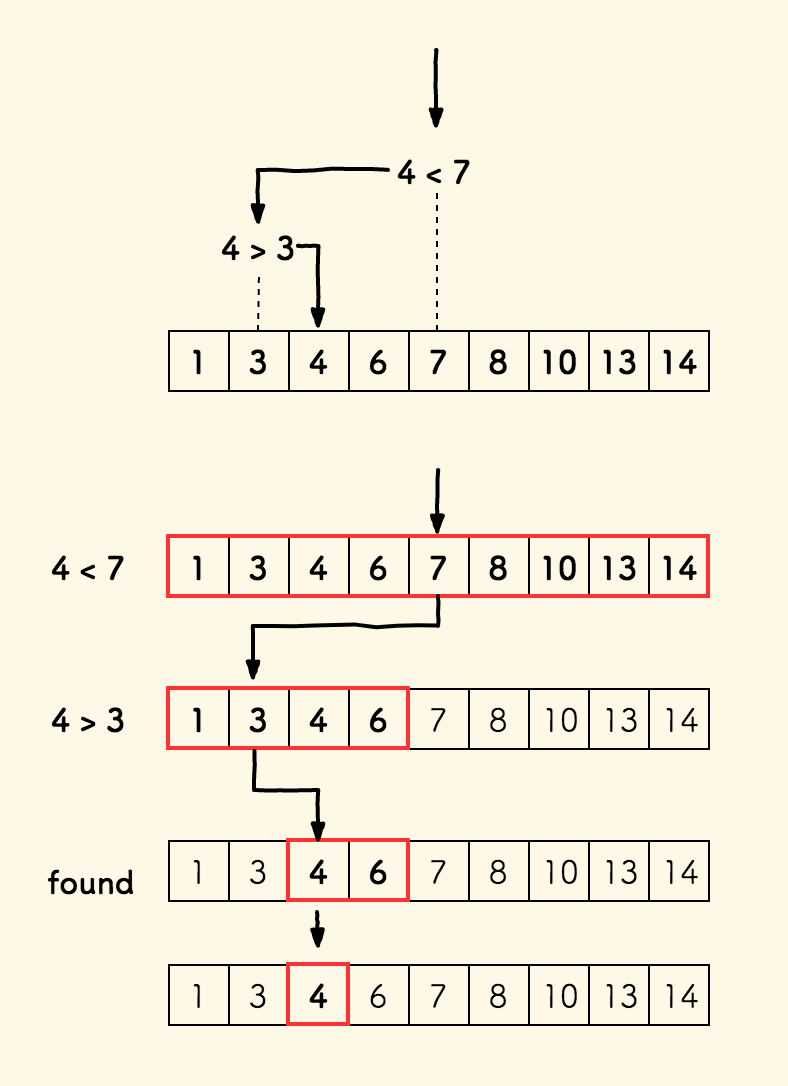
复杂度分析 ¶
假设总共需要迭代 $k$ 次才可以找到目标。
因为每次查找,范围即缩小为原来的一半,最终要缩小为 $1$ 才可以,即 $n * (1/2) ^ k = 1$ , 得到 $ k = \log {n}$ 。 即二分查找的时间复杂度是 $\log{n}$ 。
非递归实现的空间复杂度是 $O(1)$ 。
C 语言实现 ¶
C 语言的二分查找算法实现
// 从大小为 n 的数组 a 中查找元素 target.
// 返回 target 的位置;如果找不到,返回 -1.
int BinarySearch(int a[], int n, int target) {
int low = 0;
int high = n - 1;
int mid = 0;
while (low <= high) {
mid = (low + high) / 2;
if (a[mid] < target) {
low = mid + 1;
} else if (a[mid] > target) {
high = mid - 1;
} else {
return mid;
}
}
return -1; // 未找到
}
数学上的二分法 ¶
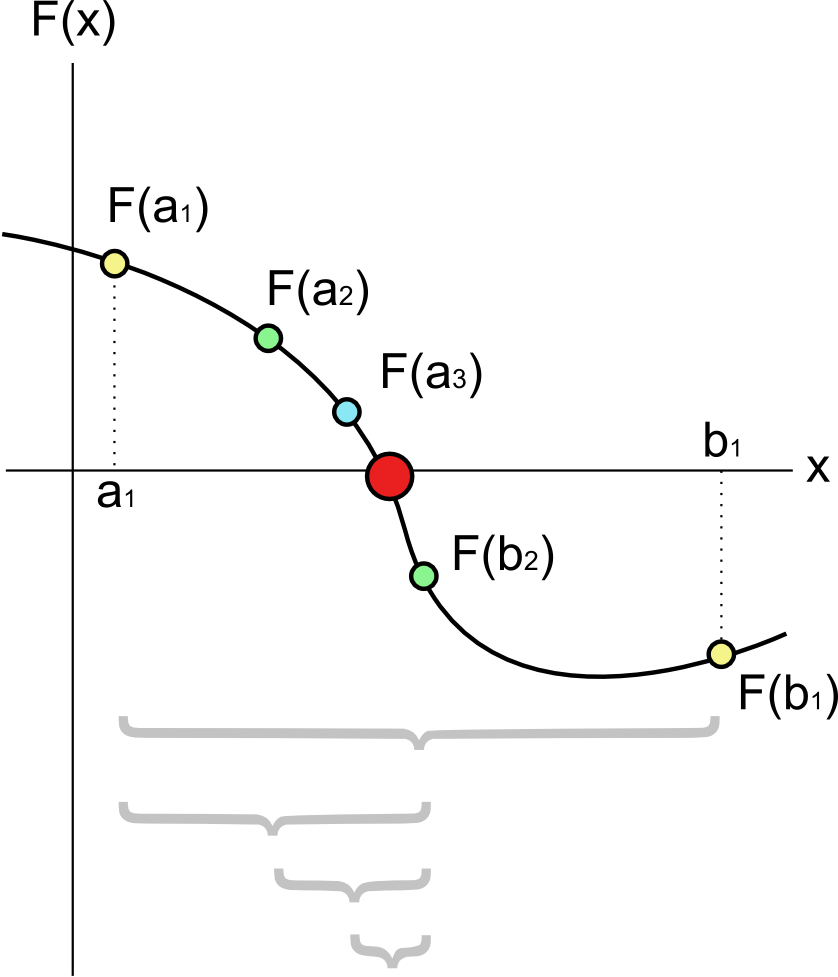
二分法在数学上可以用来求 单调函数 的近似根,和计算机算法中的二分法类似:
- 先找出跨零值的区间 $[a, b]$ ,使得 $f(a)$ 和 $f(b)$ 异号,则这个区间内必然包含函数的根。
- 求该函数的中点 $m = \frac {a+b} {2}$ 。
- 如果 $f(m)$ 和 $f(a)$ 正负号相同,则取 $[m, b]$ 为新的区间,反之则取 $[a, m]$ 。
- 重复第 2、3 两步,直到理想精度为止,即 $(\frac {f(b) - f(a)} {2} < e$ 时终止( $e$ 是理想误差) 。
延伸:
(完)
