本文记录几个常见的数组上原地操作的问题,包括:
以上的问题,虽然简单常见、老生常谈,但是其背后的思想值得总结。
将说明,解决此类问题的思路方法,其实可以统一地化归为「分拣」的思想。
原地反转数组 ¶
原地反转数组是是最为经典的原地操作问题,解决方法都很熟悉。
不断交换左右元素,直到左右迭代变量相遇即可。
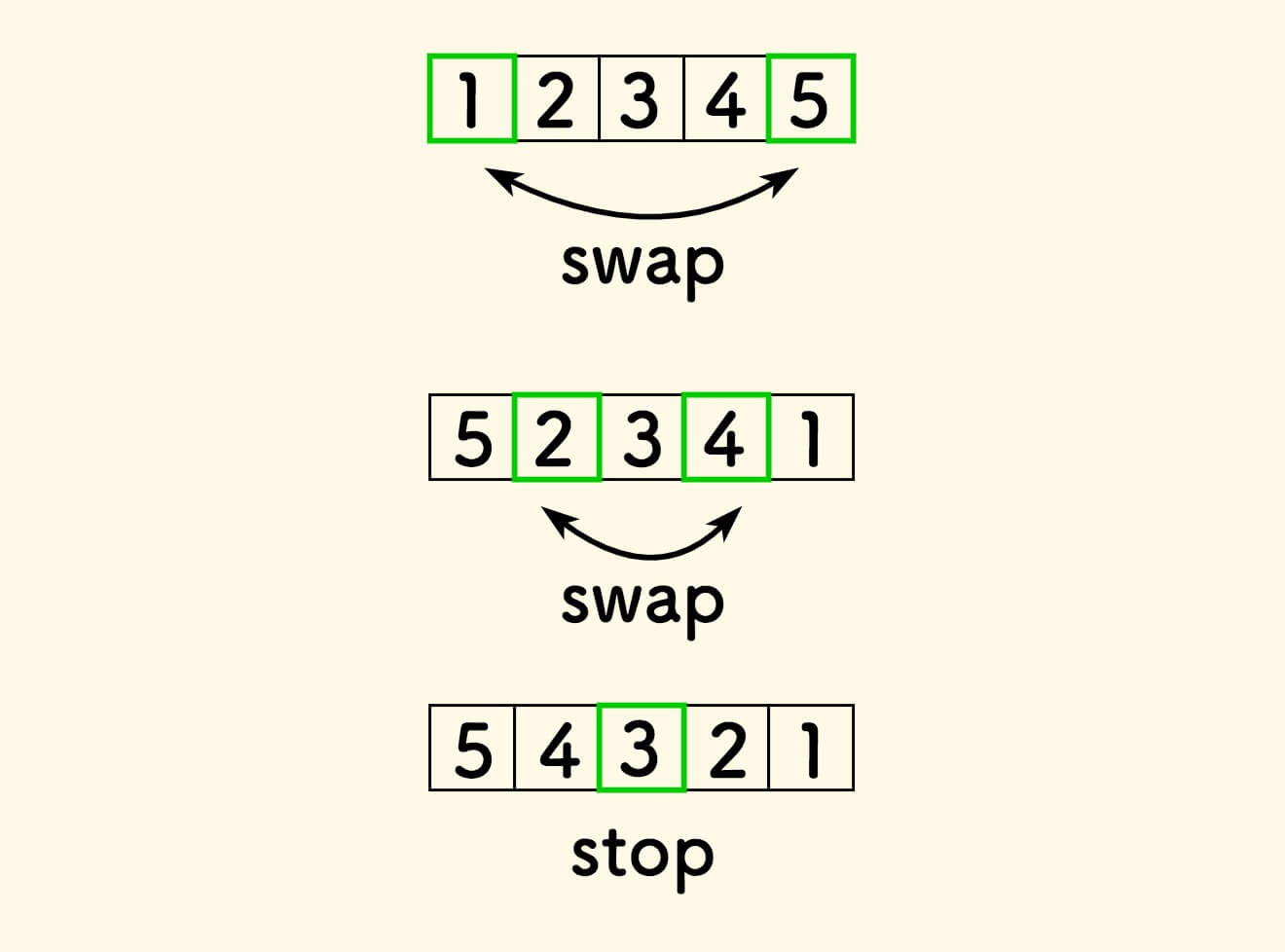
原地反转数组 - C 语言实现 (1)
void Swap(int arr[], int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
// 原地反转数组
void ReverseInplace(int arr[], int n) {
int left = 0;
int right = n - 1;
while (left < right) {
Swap(arr, left, right);
left++;
right--;
}
}
原地反转数组 - C 语言实现 (2)
// 原地反转数组
void ReverseInplace(int arr[], int n) {
for (int i = 0; i < n / 2; i++) Swap(arr, i, n - 1 - i);
}
经典的原地反转算法,是基于原地交换的。
也可以理解为: 数据分为左右两边, 把左边的拣到右边,右边的拣到左边 。
这个思路在原地反转这个简单问题上,了无深意,不妨继续看后续问题。
原地删除数组元素 ¶
问题:从数组中原地删除所有值为 k 的元素,返回删除后的数组的大小。
例如,从数组 [1,3,4,5,3] 中删除 3,为 [1,4,5] ,长度为 3 。
不妨,把不等于k 的元素叫做好元素,等于 k 的元素叫做坏元素。
第一种思路
把数组分为两边,左边是结果集合。
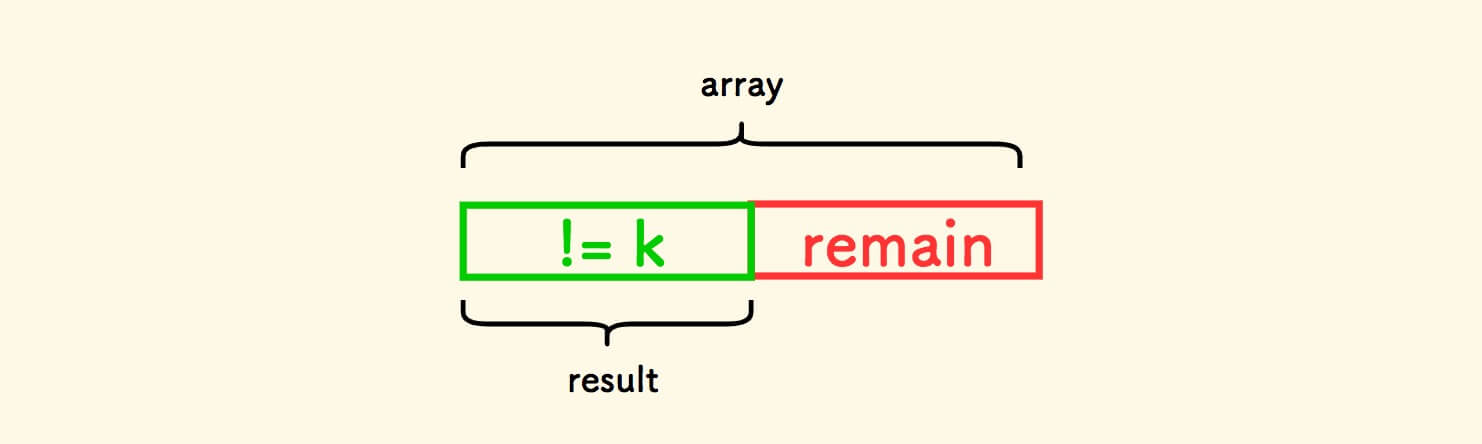
思路是, 把好元素拣到左边去,并计数拣了多少个 。
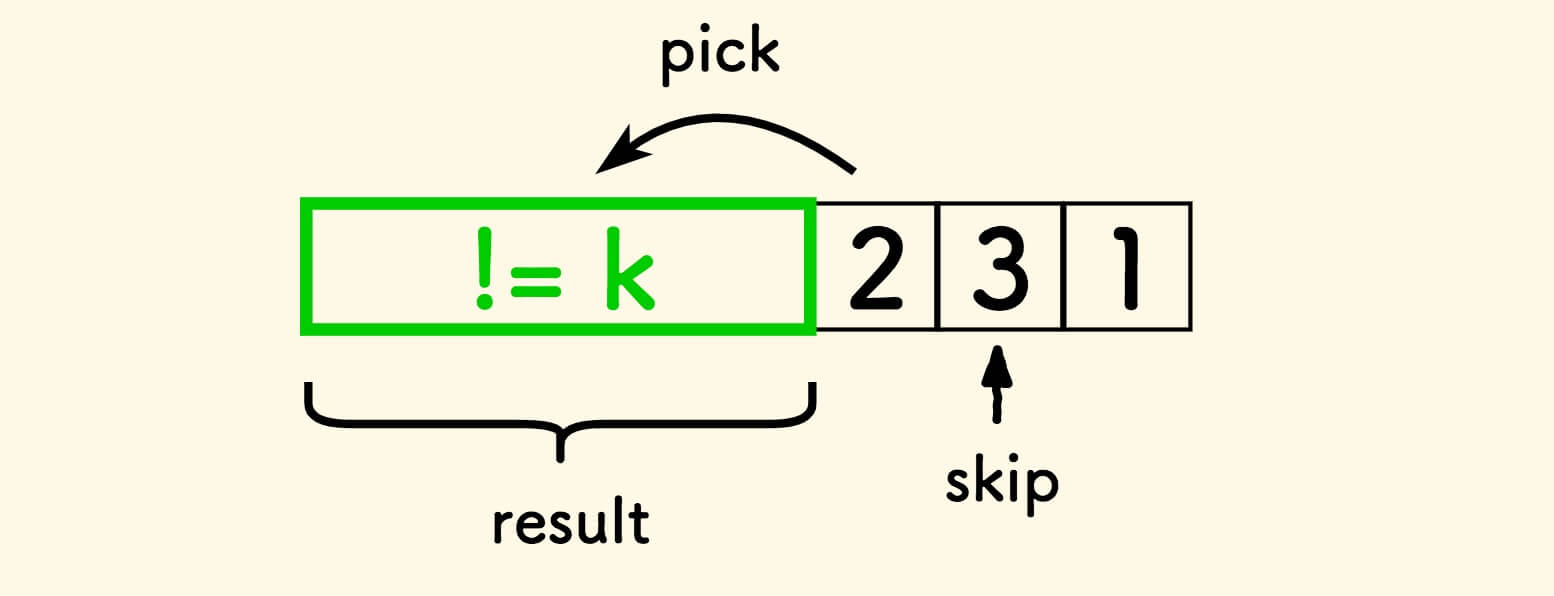
最开始,结果集是空的,不断地把好元素添加到这个结果集即可, 遇到坏元素则忽略。
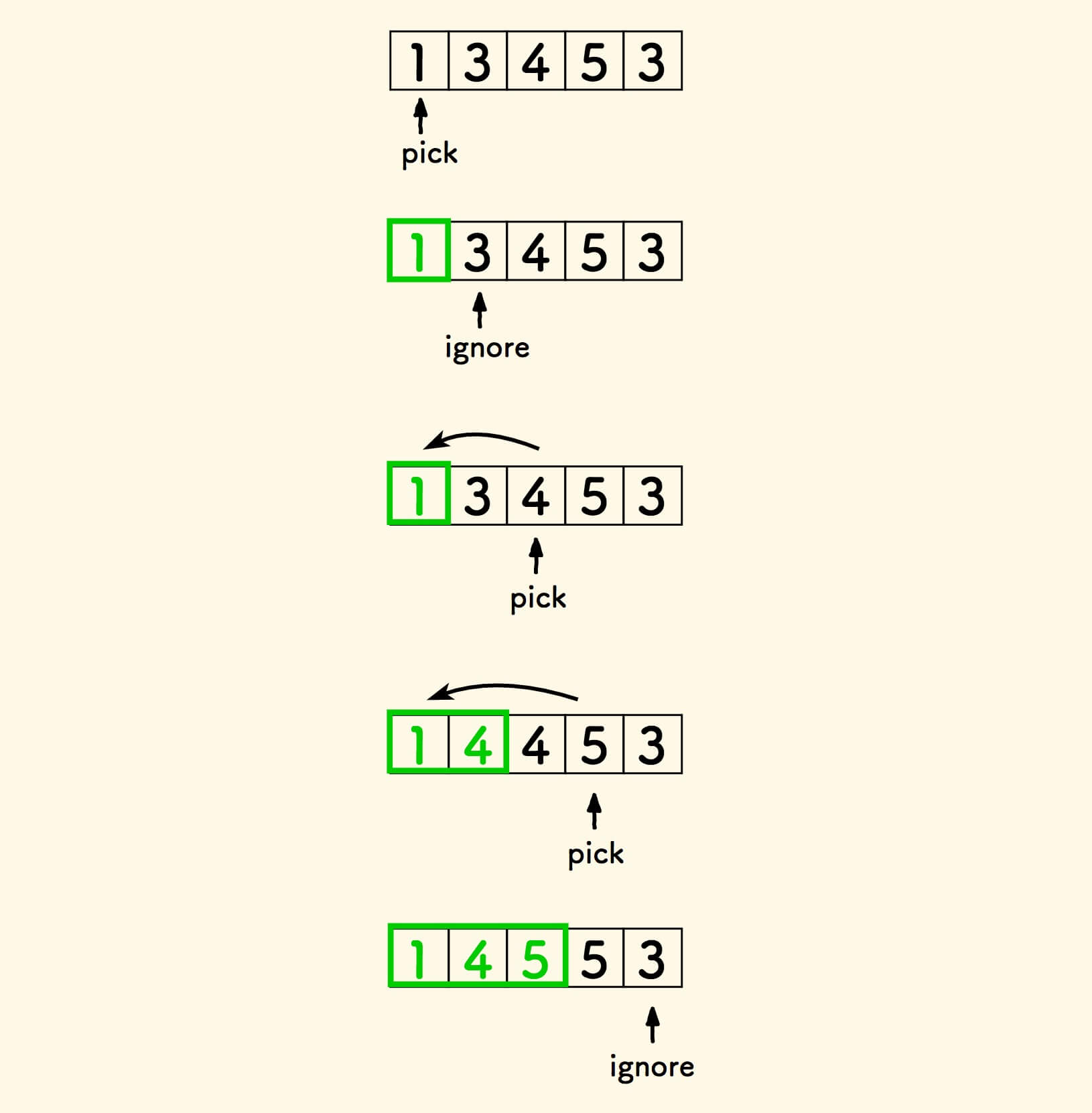
原地删除数组元素 - C 语言实现 (1)
// 从长度为 n 的数组中原地删除给定元素 k
// 思路:不断地把非 k 的元素拣到左边来
int RemoveInplace(int arr[], int n, int k) {
int count = 0;
int i = 0;
while (i < n) {
if (arr[i] != k) {
// 拣到左边来,计数++
arr[count] = arr[i];
count++;
} // 否则忽略
i++;
}
return count;
}
第二种思路
可以把坏元素拣到右边去吗?
拣到哪里去呢?会不会覆盖到其它元素?
一个思路是,和尾巴元素交换,就不会丢失数据了。
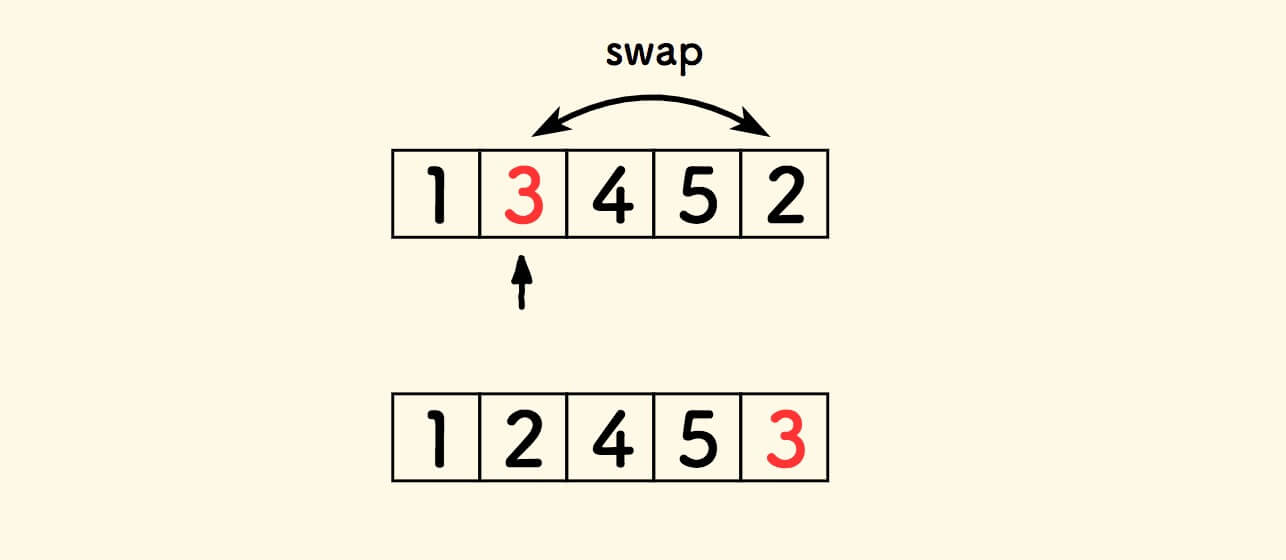
或者看成: 把坏元素拣到右边,把尾巴元素拣到它的槽位上 。
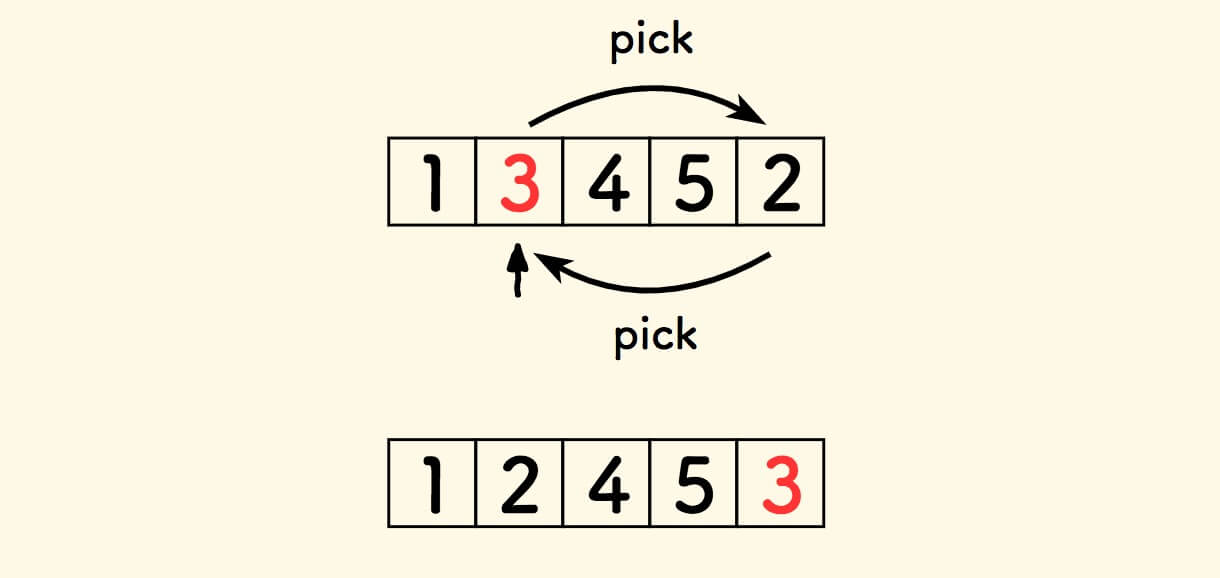
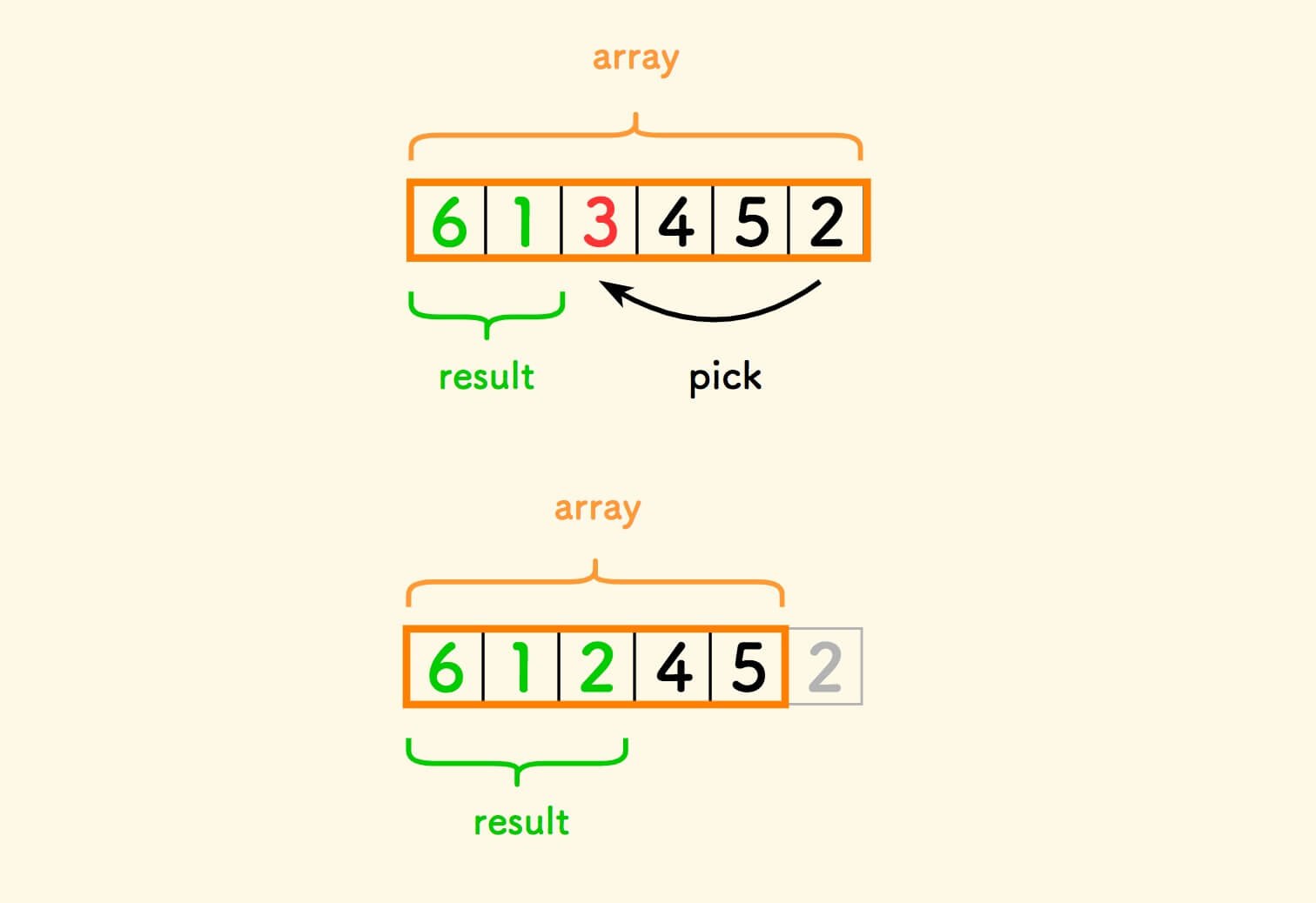
不过,其实 只需要一次 pick 。
为了移除坏元素 ,我们并不需要把它拣走,只需要把尾巴元素拣过来覆盖它就好了。
同步地,数组的大小减一。
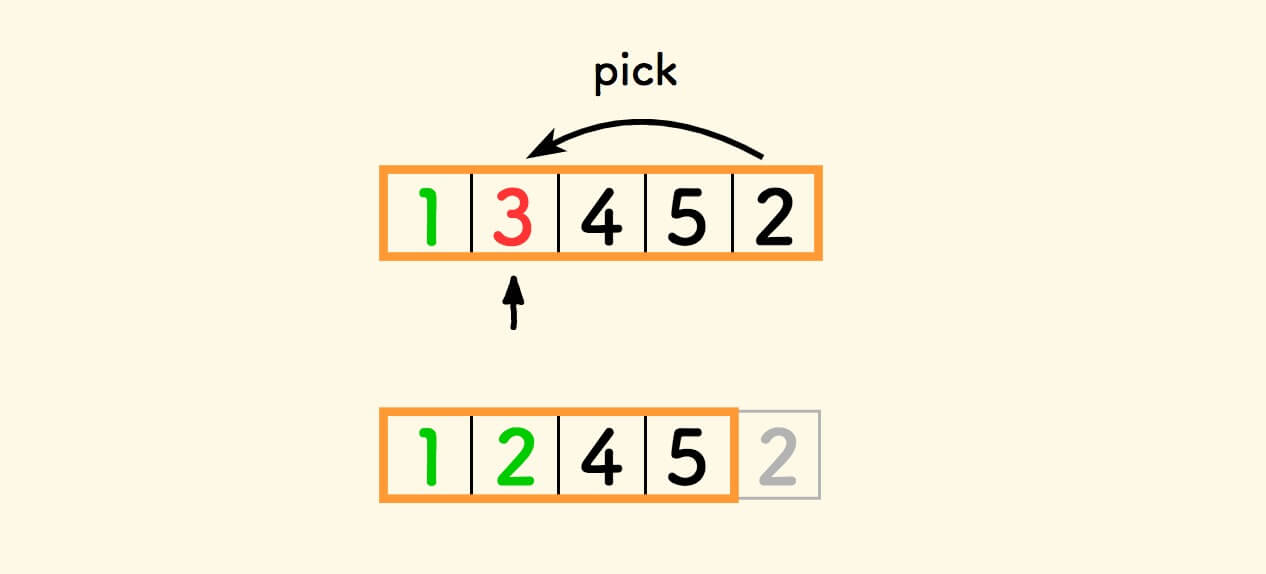
现在有思路了:
遇到坏元素 ,就把尾巴元素拣过来覆盖它 。
如果拣过来的元素也是坏的? 那就再覆盖一次。
直到拣过来的是一个好元素 ,才放过这个槽位,继续前进。
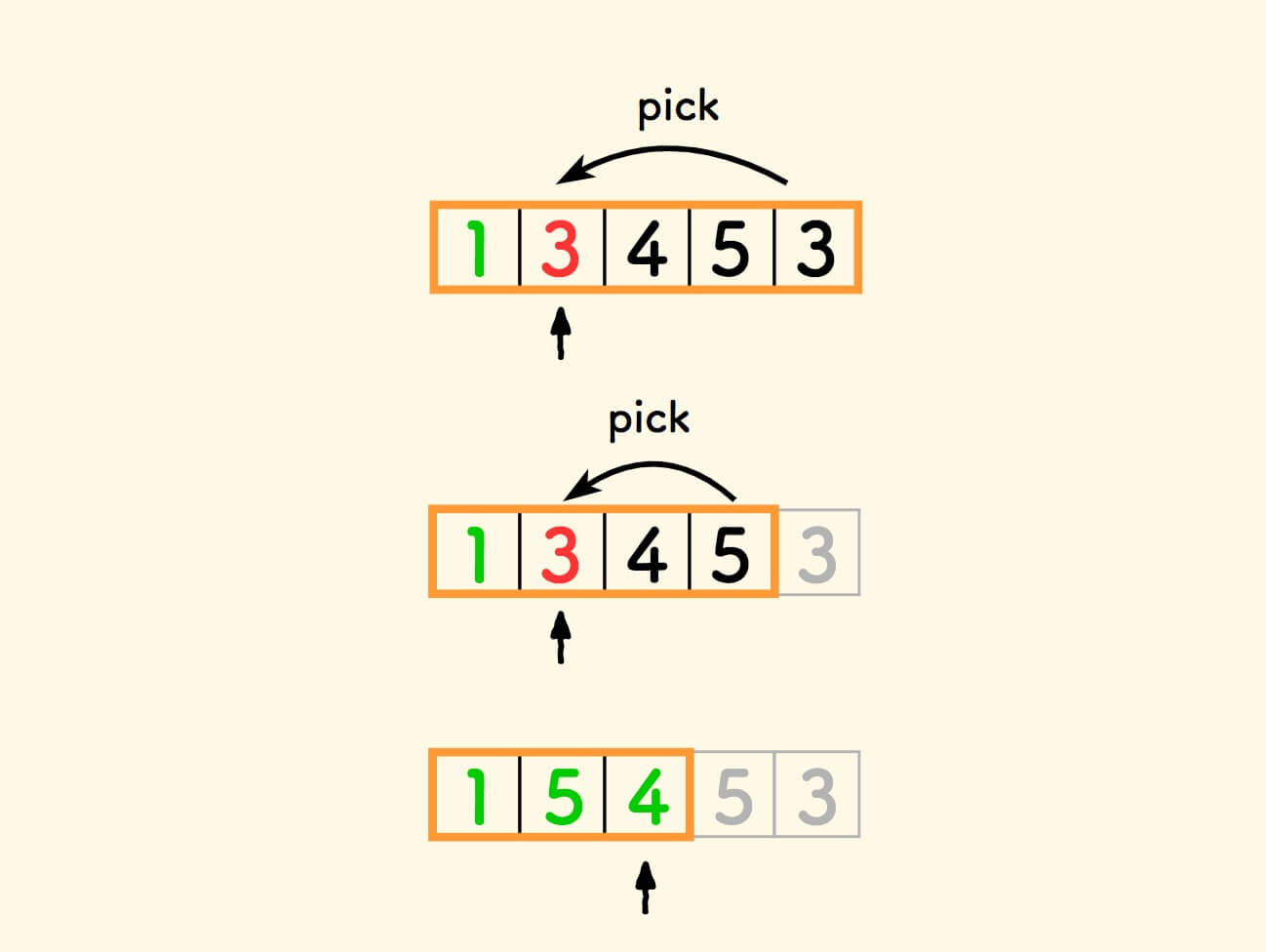
总结下这个思路:
- 结果集仍然必须放左边。
- 遇到好元素,就扩大结果集。
- 遇到坏元素,不断把尾巴拣过来,同步缩小整个数组。
- 当结果集的大小和整个数组的大小一样时,算法终止。
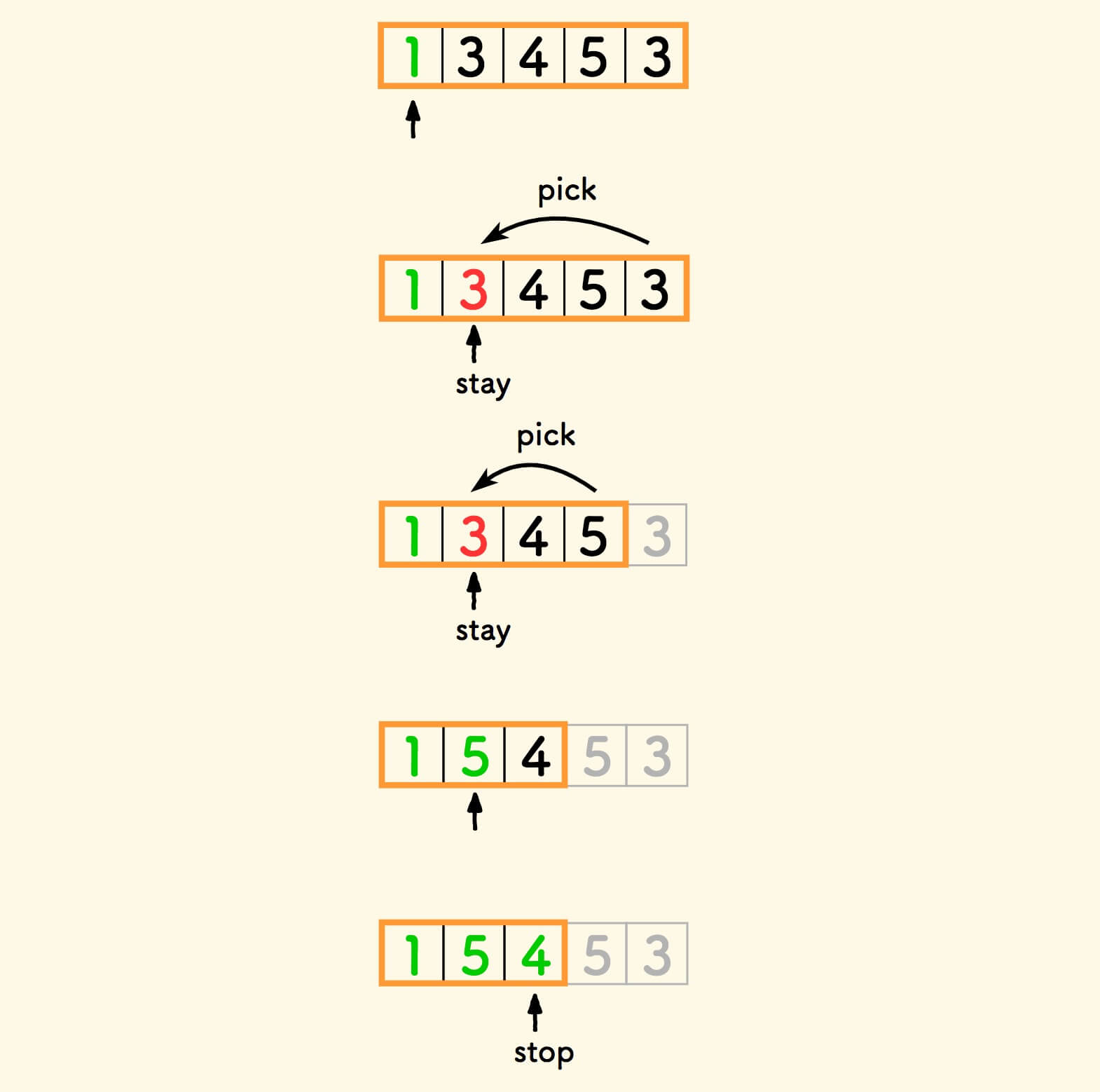
最终,第二种思路的完整删除过程如下:
原地删除数组元素 - C 语言实现 (2)
// 从长度为 n 的数组中原地删除给定元素 k
// 不断把尾巴元素拣过来覆盖 k 元素
int RemoveInplace(int arr[], int n, int k) {
int i = 0;
while (i < n) {
if (arr[i] == k) {
arr[i] = arr[n - 1];
n--;
} else {
i++;
}
}
return n;
}
第三种思路
和第二种思路比较像,也是左右开弓。
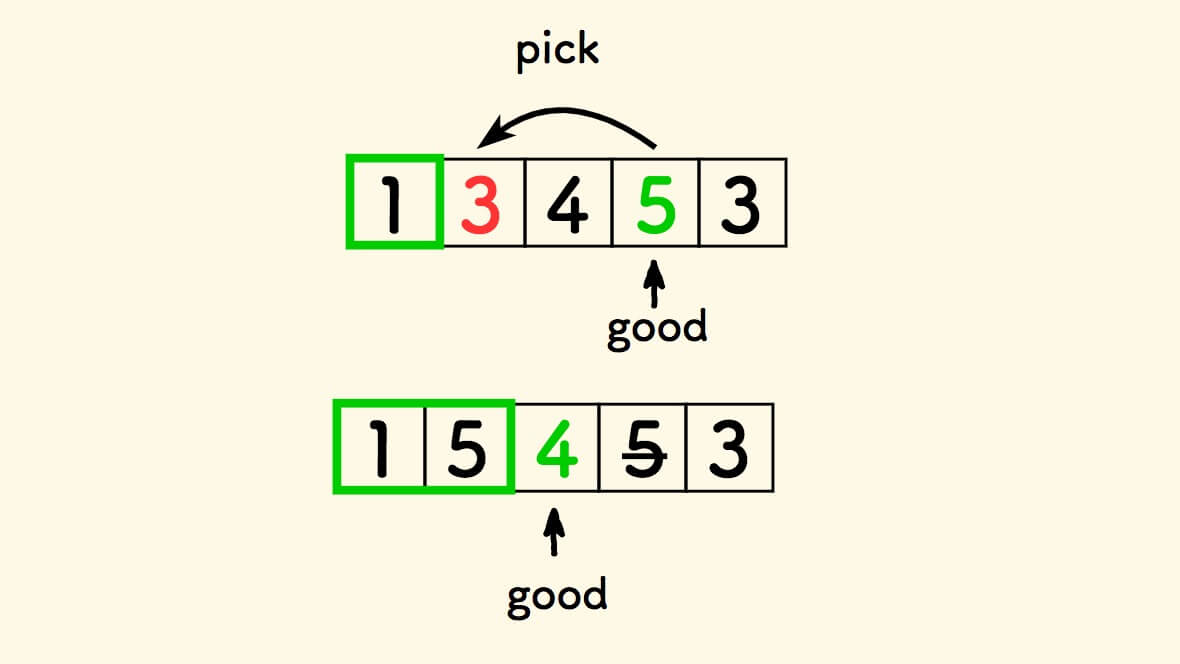
每次遭遇一个坏元素,就从右边找一个好元素拣进来替换 。
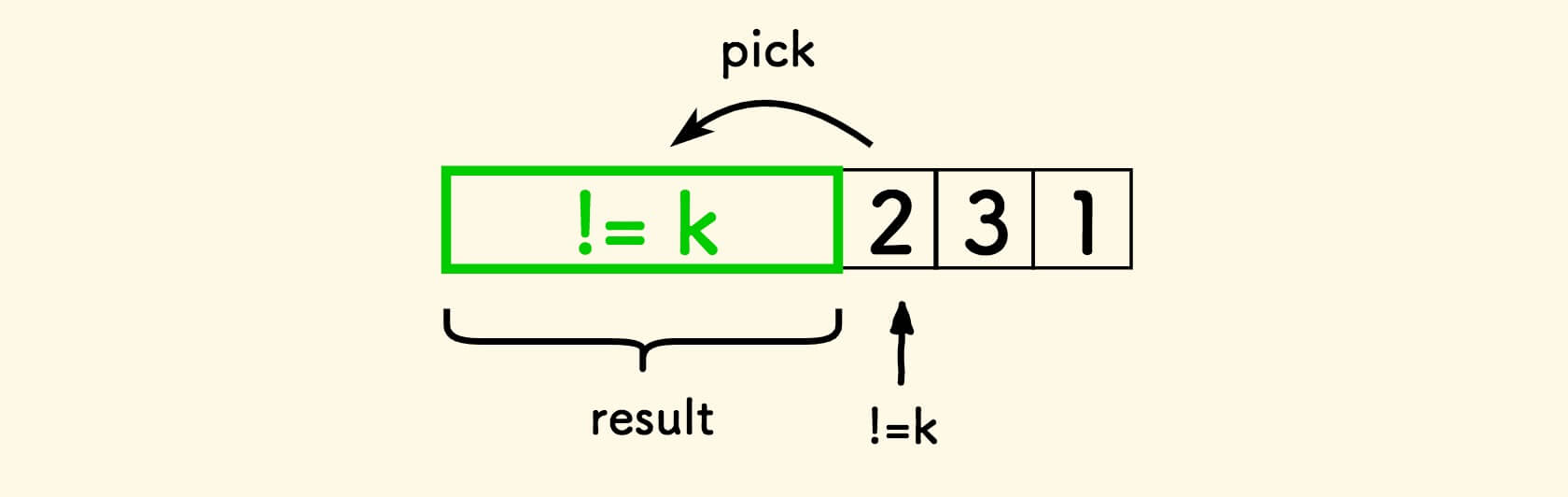
不同点在于,第二种思路每次都拣当前尾巴元素,此思路是每次都要拣一个好元素。
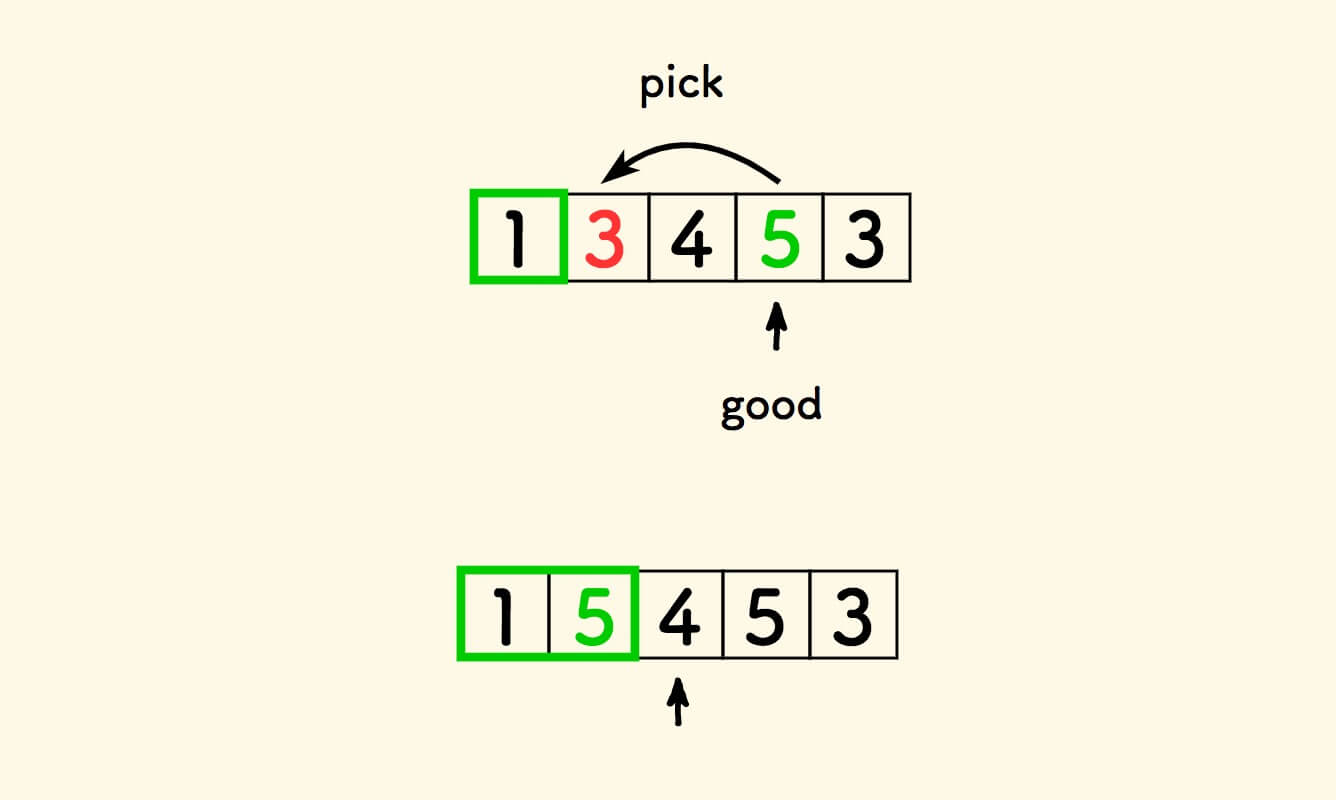
用来替换的好元素, 是从右边找到的第一个没有用过的好元素 。
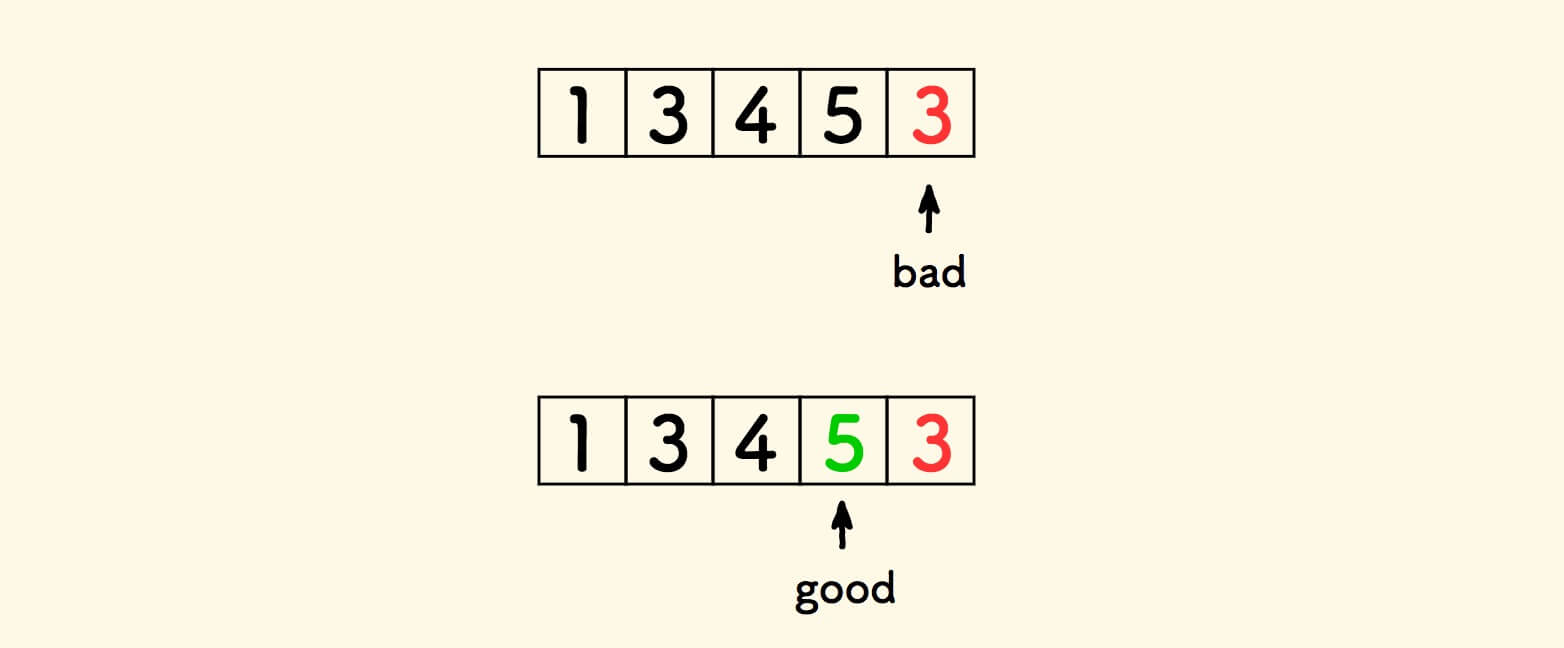
当一个好元素被拣走用过,它就不能再被使用了,不然会出现数据重复。
总结下这个思路:
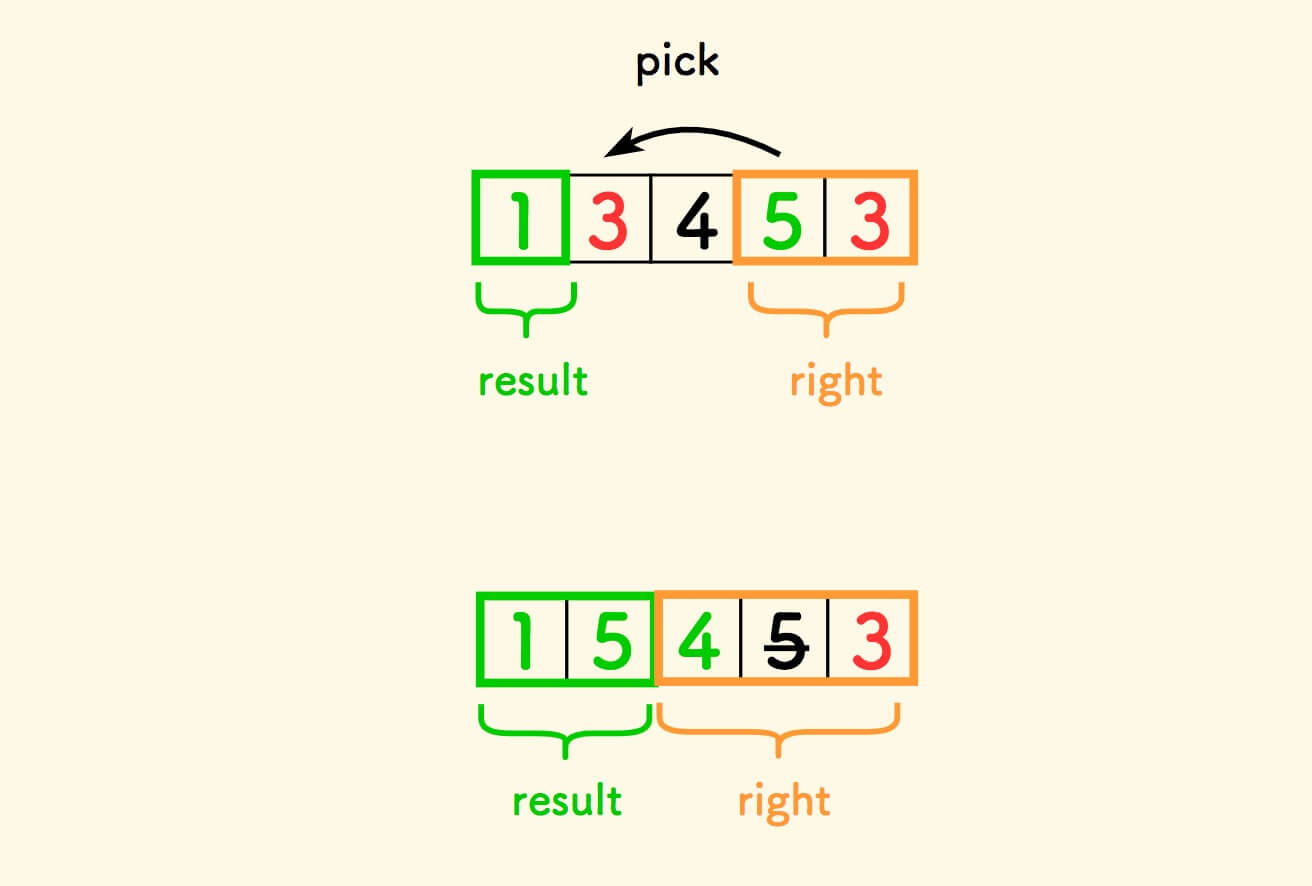
- 结果集仍然必须放在左边。
- 遇到好元素,就扩大结果集。
- 遇到坏元素,就从右边集合拣一个好元素过来。
- 两个集合相交时,终止算法。
具体地,采用 left 和 right 从两边遍历:
- 先等右边
right准备好,找到一个好元素。 然后看左边:
- 遇到好元素,直接放入结果集。
遭遇坏元素,则把右边的好元素拣过来。
此时右边需要重新寻找新的好元素,
right--。- 同步计数
left++。
- 重复以上,当
left越过right时,结束算法。
下面是这种算法的整体执行过程:
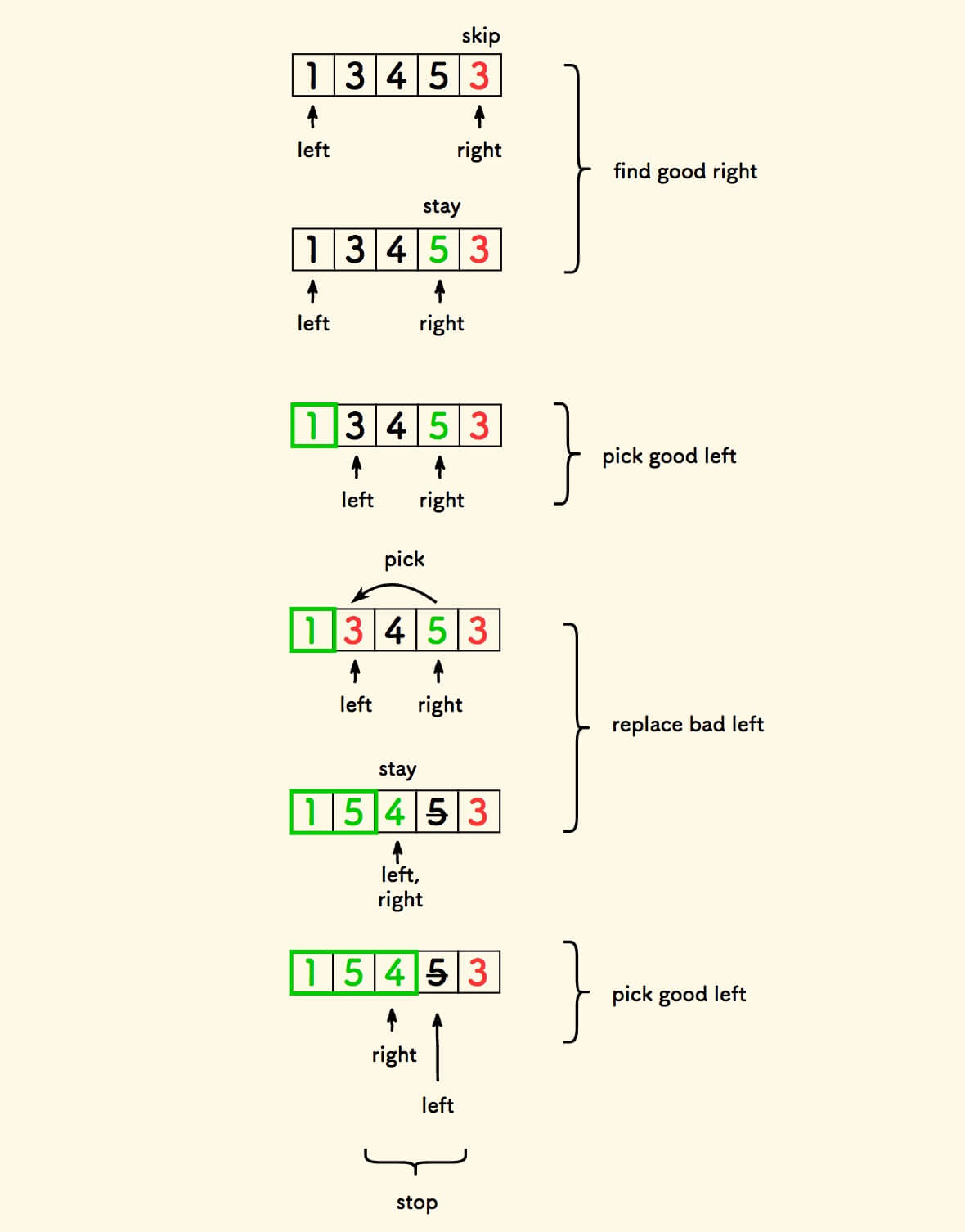
right 每次稳定的位置,是未知的好元素的最右位置 。
left 是已知的好元素的计数 。
当 left > right 时 ,意味着所有好元素都已知,因此可以终止算法。
原地删除数组元素 - C 语言实现 (3)
// 从长度为 n 的数组中原地删除给定元素 k
// 从左到右,遇到 k 就从右边找一个非 k 的元素拣过来覆盖
int RemoveInplace(int arr[], int n, int k) {
int left = 0;
int right = n - 1;
while (left <= right) {
// 右侧先准备好,找到一个非 k 的位置
if (arr[right] == k) {
right--;
continue;
}
// 然后 left 才行动
if (arr[left] == k) {
// 遇到 k ,把右侧的非 k 元素拣过来覆盖
arr[left] = arr[right];
// 这个 right 已经用过,不再利用
right--;
}
left++;
}
return left;
}
小结
三种思路,思想一致: 确定结果集,拣好元素进来 ,只是实施方式不同。
- 第一种思路:从左向右,只拣好的,忽略坏的。
- 第二种思路:从左向右拣好的,遇到坏的,把尾巴拣过来。
- 第三种思路:两边都拣好的,左边遇到坏的,就从右边拣一个好的过来。
三种思路中, 只有第一个思路的方法是保顺序的 。
三种思路下的算法时间复杂度都是 $O(n)$ 。
不过,如果只计算数据拷贝次数:
- 第一种思路,拷贝次数 严格等于 好元素的个数。
- 第二种思路,拷贝次数 严格等于 坏元素的个数。
- 第三种思路,拷贝次数 不超过 坏元素的个数。
当数据拷贝成本较高时:
- 如果
k的在数组中个数不多,第三种思路最上算。 - 否则,如果
k在数组中大量存在,第一种思路上算。
延伸
如何把一个数组中的零移动到数组的右边呢?要求保序。
例如:[0,1,0,3,5] 变成 [1,3,5,0,0] 。
此时则采用第一种思路,因为它保序。
移动零问题 - C 语言实现
// 把值等于 k 的元素移动到数组右边
// 其他元素的顺序要不变
void MoveKRight(int a[], int n, int k) {
int count = 0; // Count !=k elements
int j = 0;
while (j < n) {
if (a[j] != k) {
a[count] = a[j];
count++;
}
j++;
}
// 剩余的刷 k
while (count < n) a[count++] = k;
}
原地分割数组-两份 ¶
原地分割,也可以叫原地切割、原地分类 等, 是 快速排序算法 的一种实现环节。
问题:给定一个数组和一个元素 k ,把不大于 k 的元素放左边,大于 k 的元素放右边。
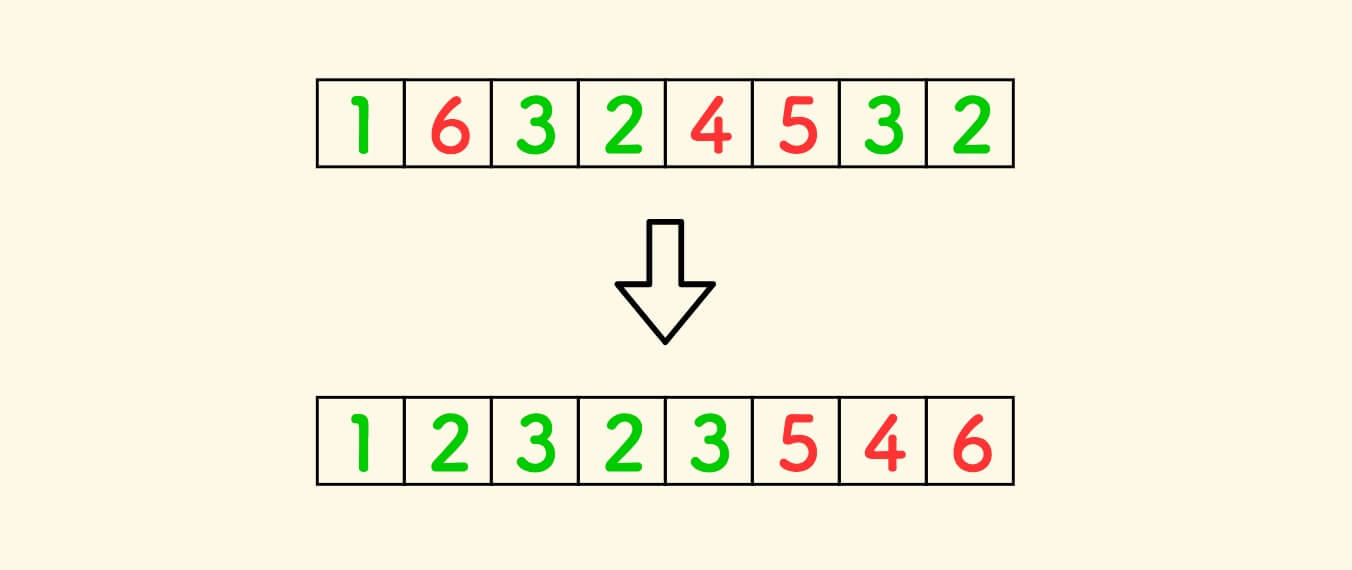
例如,数组 [1,6,3,2,4,5,3,2] 按 k=3 切分的一个结果可以是 [1,2,3,2,3,5,4,6] 。
不妨把元素染成两个颜色,绿色的元素都不大于 k,红色都大于 k 。
目标就是把绿色的放左边,红色放右边。
假设左边的结果集是 L ,右边的是 R 。
需要考虑的是,如何把元素拣到两个集合中去。
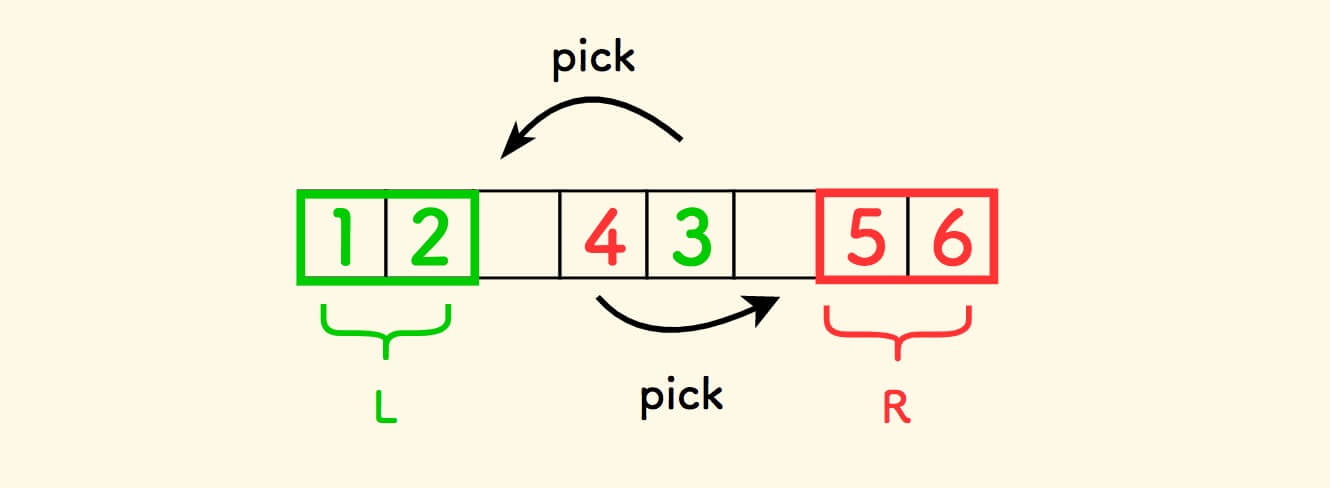
一种方式是:
L只吸收它旁边的绿色元素:
如果它右边是红色元素,则拣给
R。为了不丢失原先
R左邻的元素,需要采用交换,把它安置在L的右边。
如果交换过来的仍然是一个红色元素,
L是不可以拣走的。而是交给
R再拣一次,直到绿色出现。
特殊地,如果红色元素就在
R的左边,就不必和自身交换了,直接吸收即可。
当 L 和 R 两个集合相交时,终止算法。
- 两个集合各自拣自己的。
L遇到不适合自己的,丢给R。R处理完后,主动权再交给L。
按照这个办法,整个的分割过程如下图所示:

原地分割数组(两份)- C 语言实现
// 原地分割数组,使得 <= k 的数在左边, > k 的在右边
// 返回左边的数据多少。
int PartitionInplace(int arr[], int n, int k) {
int left = 0; // 左边集合的上界
int right = n - 1; // 右边集合的下界
while (left <= right) {
if (arr[left] <= k) {
left++;
} else {
if (left != right) Swap(arr, left, right);
right--;
}
}
return left;
}
显然,时间复杂度是 $O(n)$ 。
思路和 原地删除数组元素 的思路完全类似,只是此时不再丢弃元素,而是采用交换保留了数据。
当然,也可以设计一种镜像的分拣策略,R 优先吸收身边的红色元素,遇到绿色原色则交给 L 处理。
如果数组中的红色元素有 m 个,那么会交换 m 次。
当数据拷贝成本较高时:
- 红色的元素少,则采用当前所说的策略,交换红色元素。
- 否则,则采用后面的镜像策略更上算,交换绿色元素。
原地分割数组-三份 ¶
上面的 原地分割数组(两份) 部分并没有把 k 排到中间。
三份分割的问题:
问题:给定一个数组和一个元素 k ,把小于 k 的元素放左边,大于 k 的元素放右边, 等于 k 的放中间。
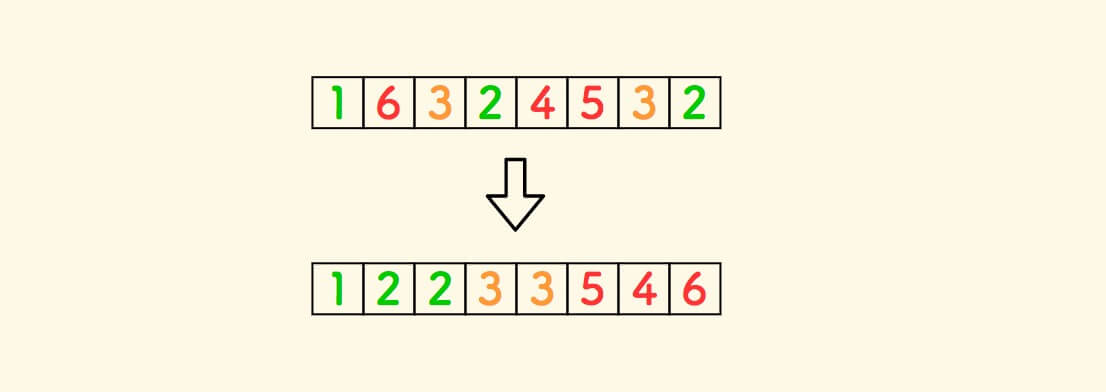
例如,数组 [1,6,3,2,4,5,3,2] 按 k=3 切分的一个结果可以是 [1,2,2,3,3,5,4,6] 。
这个问题也叫做 荷兰国旗问题 , 对应的 leetcode 题目 - 颜色分类 。
同样,不妨把元素染成三种颜色:
- 绿色的元素都小于
k - 黄色的元素都等于
k - 红色的元素都大于
k
目标就是把绿色的放左边,红色放右边,黄色的放中间。
受 原地分割数组(两份) 部分的思路启发,一个简单的思路是:
- 先把数组分成两份,不超过
k的放左边,大于k的放右边。 - 然后对左边的部分再分成两份,小于
k的放左边,等于k的放中间。
此思路的代码从略。
下面讨论一次循环的办法。
假设左边的元素集合是 L ,右边的是 R 。
把中间的元素,绿色元素分拣给 L、红色元素分拣给 R,剩下的都是黄色元素 。
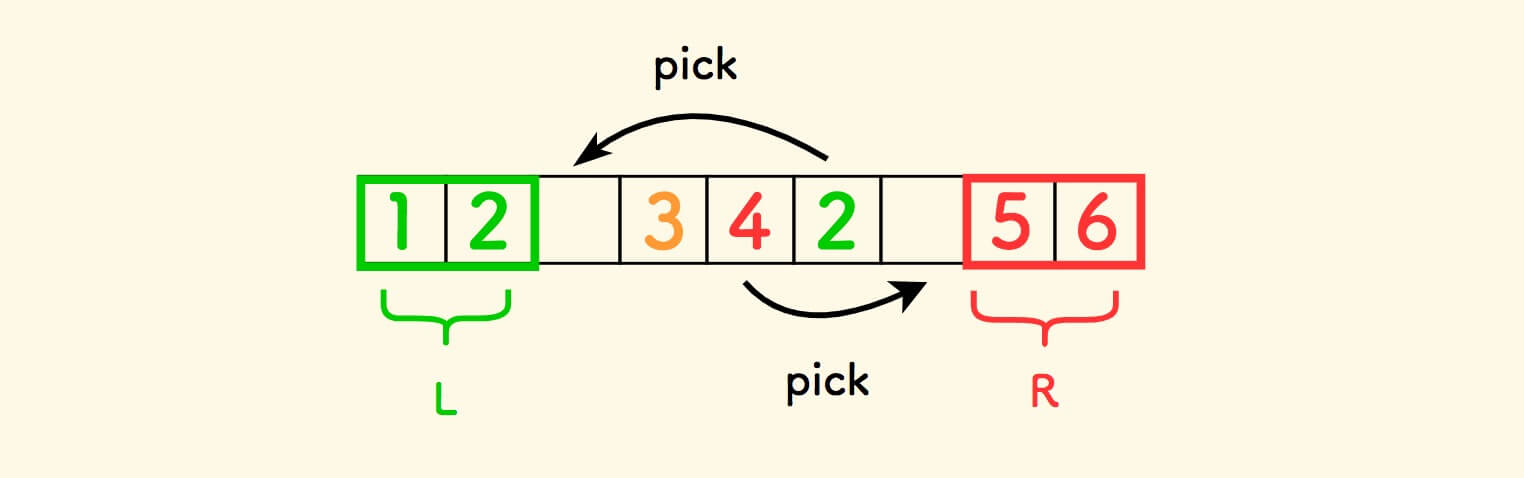
在分拣过程中的任何一个状态中,两头的颜色都是已知的,中间的颜色则是未知的。
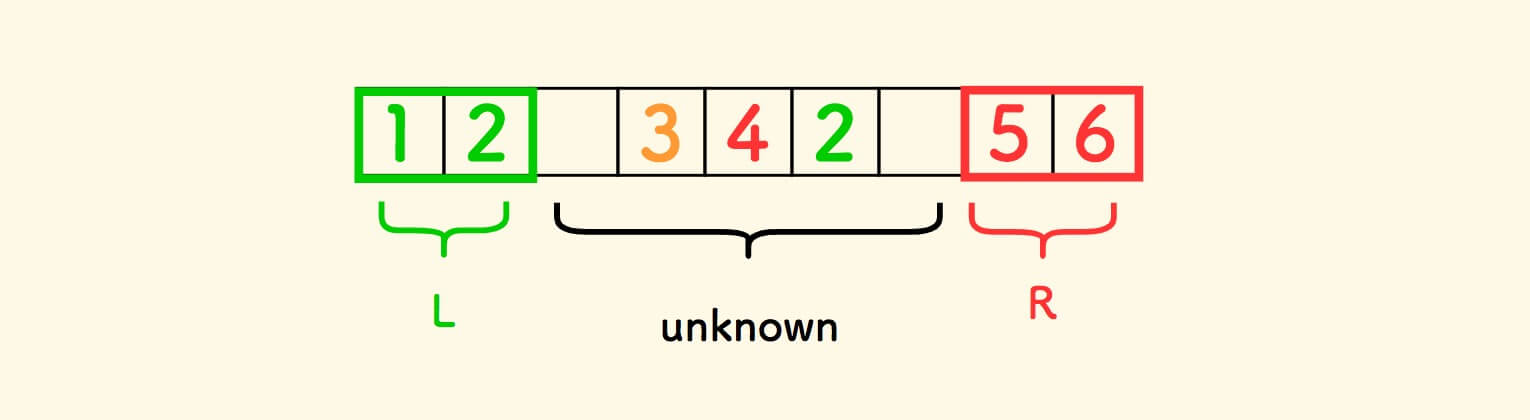
所以,在中间的区间上,取一个变量 i 从左到右 检查元素的颜色:
如果是红色的,则拣给右边的
R。为了不丢失数据,仍然采用交换的方法,把
R左边的元素和当前元素互换位置。
此时,
R向左扩展。右边的元素,还没有检查过其颜色。 从右边换过来的元素,颜色是未知的。
所以
i不动,需要下一轮再检查一次当前位置的颜色。如果是绿色的,则拣给左边的
L。
把
L右边的元素和当前元素互换位置,L向右扩展。左边的元素,已经被
i检查过颜色。 从左边换过来的元素,颜色是已知的。所以
i后移一位,向前继续检查。如果是黄色,跳过。 我们只分拣红色和绿色。
特殊地,如果交换的两元素是同一位置,直接拿走,不必交换。
总结来说:
- 红色的给右边,绿色的给左边,黄色不关心。
- 换过来没见过的元素,要再检查一次颜色,否则直接前进。
当所有的元素的颜色都被检查过,终止算法。
确切的,是指 i 越过 R 的左界时,算法结束。
原地分割三份和 原地分割两份 的算法思想是非常相似的。
下面是一个完整的算法过程:

原地分割数组(三份)- C 语言实现
// 原地分割数组,使得 < k 的数在左边, > k 的在右边, == k 的在中间。
void PartitionInplace(int arr[], int n, int k) {
int left = 0; // 左边集合的上界
int right = n - 1; // 右边集合的下界
int i = 0; // 中间元素的迭代变量
while (i <= right) {
if (arr[i] < k) {
if (i != left) Swap(arr, left, i);
left++;
i++;
} else if (arr[i] > k) {
if (i != right) Swap(arr, right, i);
right--;
} else {
i++;
}
}
}
每个元素被检查且只被检查一次颜色,所以,时间复杂度是 $O(n)$ 。
如果数组中的红绿元素共 m 个,最多发生 m 次交换。
下图是一种交换次数发生最多的情况(最差情况):
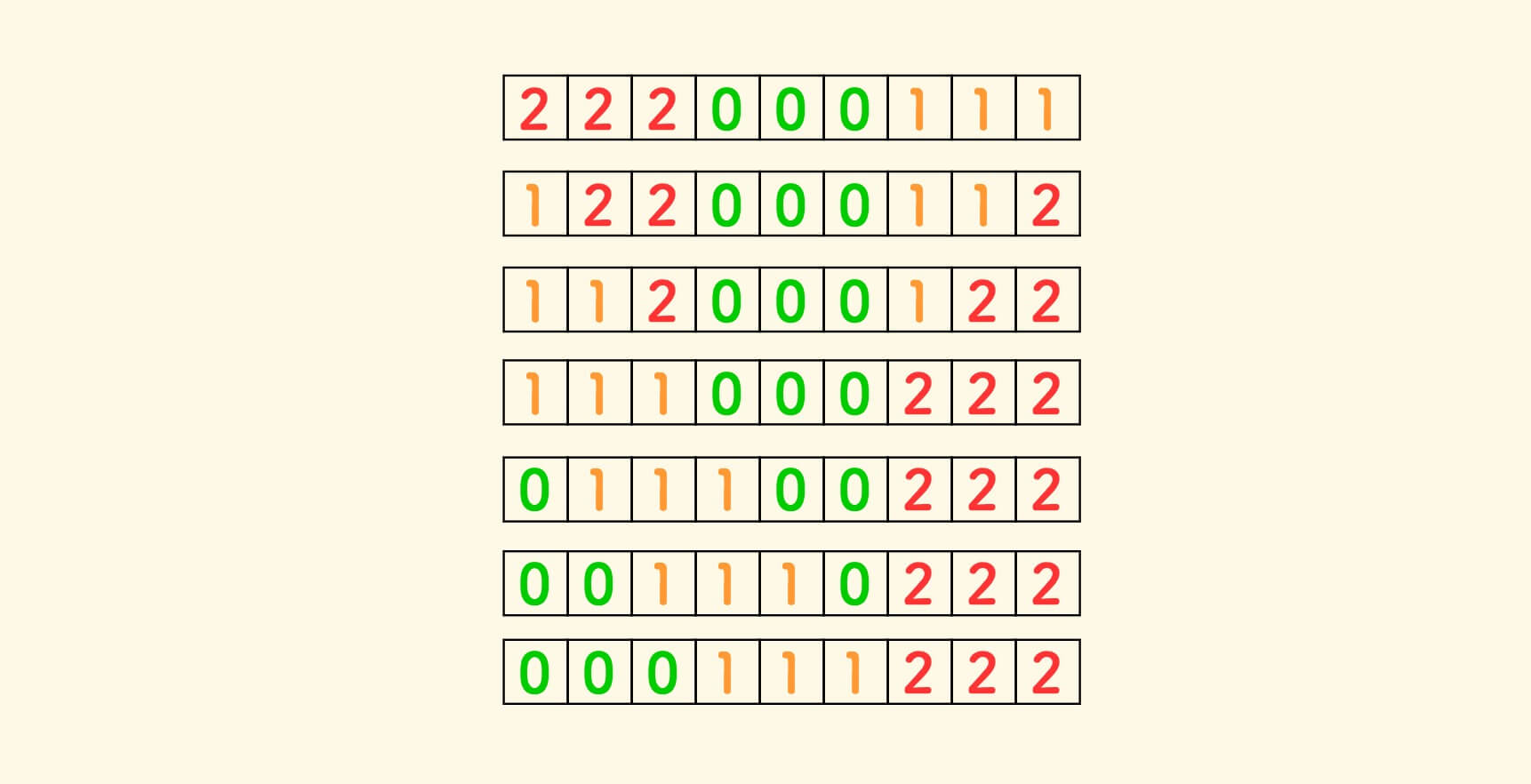
原地分割的稳定性
原地分割当然是不保序的。
此外,通过示例即可发现: 原地分割是不稳定的 。
稳定性是指,值相同的元素在操作前后的相对顺序应该不变。
原地分割有两种交换: 向左交换 和 向右交换。
两种交换都打破了稳定性。
向左交换破坏稳定性的一个示例:
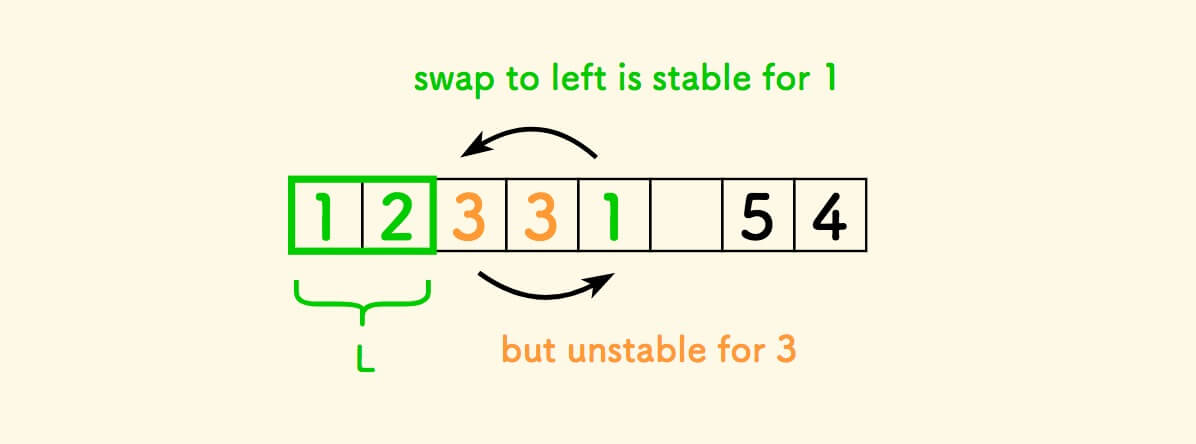
向右交换破坏稳定性的一个示例:
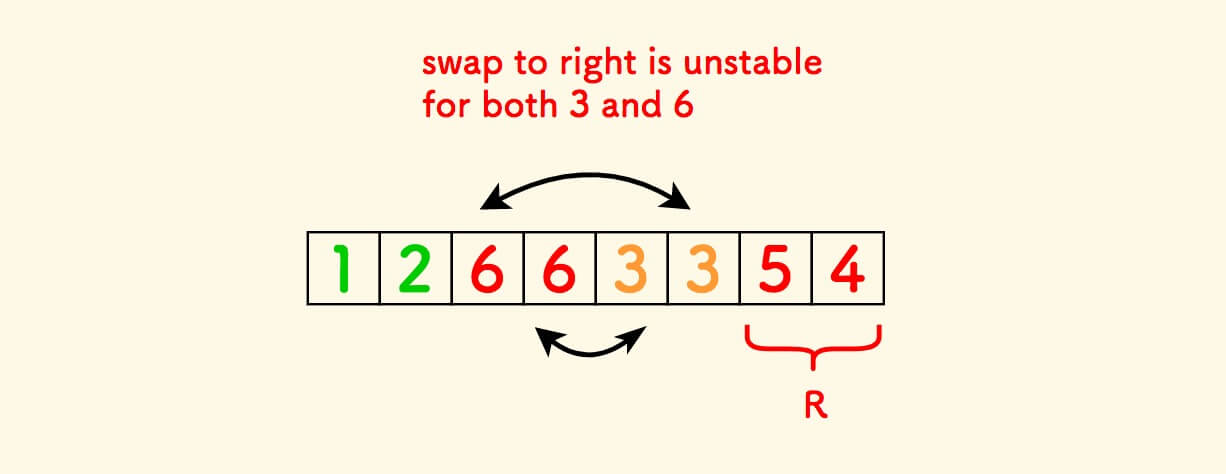
结语 ¶
本文分析的几个数组原地操作的问题,其思路可以化归为「分拣」的思想:
确定集合,设计分拣方式 。
(完)
相关阅读:
本文原始链接地址: https://writings.sh/post/algorithm-inplace-operations-on-array





