排序算法 - 快速排序和归并排序

本文记录两个经典的基于比较的排序算法：

快速排序
归并排序

笔记目的，行文从简。

以下，只讲从小到大排序。

快速排序 ¶

算法思路：

选一个元素当做基准值，把数组原地分割两份：
不大于它的在左边，大于它的在右边。
对左右两边，递归执行以上步骤，直到当前要分割的部分只有一个元素。

原地分割

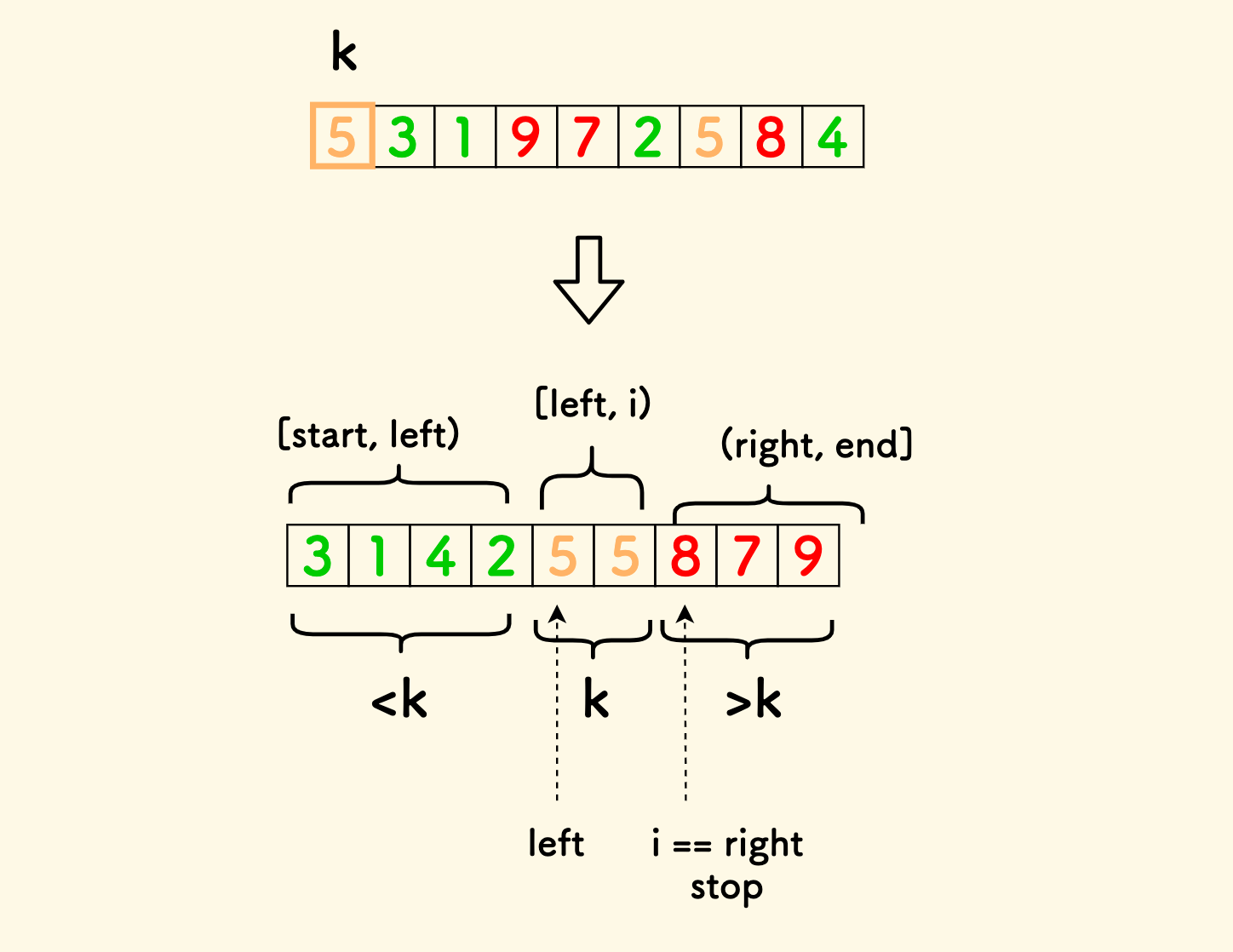
以数组 [5,3,1,9,7,2,5,8,4] 为例，选择第一个元素为基准元素。

原地分割后，小于基准值的放左边，大于基准值的放右边。

Partition 过程的关键点在于闹清楚边界的定义：

left 指针，保证 left 左边（不包括 left）永远小于基准值
right 指针，保证 right 右边（不包括 right）永远大于基准值
i 指针，保证 i 左边 (不包括 i ）永远不大于基准值, 也就是中间这个部分是等于基准值的

原地分割算法详细参考：原地分割 - 三份，其时间复杂度是 $O(n)$ 。

快速排序 - 原地分割 - C 语言实现

void Swap(int a[], int i, int j) {
    int tmp = a[i];
    a[i] = a[j];
    a[j] = tmp;
}

// 分割函数，选取第一个为基准元素
// 把 start 到 end 内的元素，小于基准元素的放在左边，大于的放在右边
// 返回基准值的最右下标
int Partition(int a[], int start, int end) {
    int k = a[start];
    int left = start;  // [start, left) 上保持 < k
    int right = end;   // (right, end] 上保持 > k
    int i = start; // i 是迭代变量, [left, i) 上是已知的 == p 的, 可能为空区间

    while (i <= right) {
        if (a[i] < k) {
            Swap(a, i, left);
            // i 左侧的都已经检查过, 所以都可以 ++
            left++;
            i++;
        } else if (a[i] > k) {
            Swap(a, i, right);
            // 换过来的 right 目前在 i 位置, i 不能移动，要检查一下这个值
            // 换过去后，right 处已经检查, 所以可以直接 right--
            right--;
        } else {
            i++;
        }
    }
    // 返回返回基准值的最右下标
    return i - 1;
}

原地分割函数返回最靠右的基准值的位置。

快速排序过程

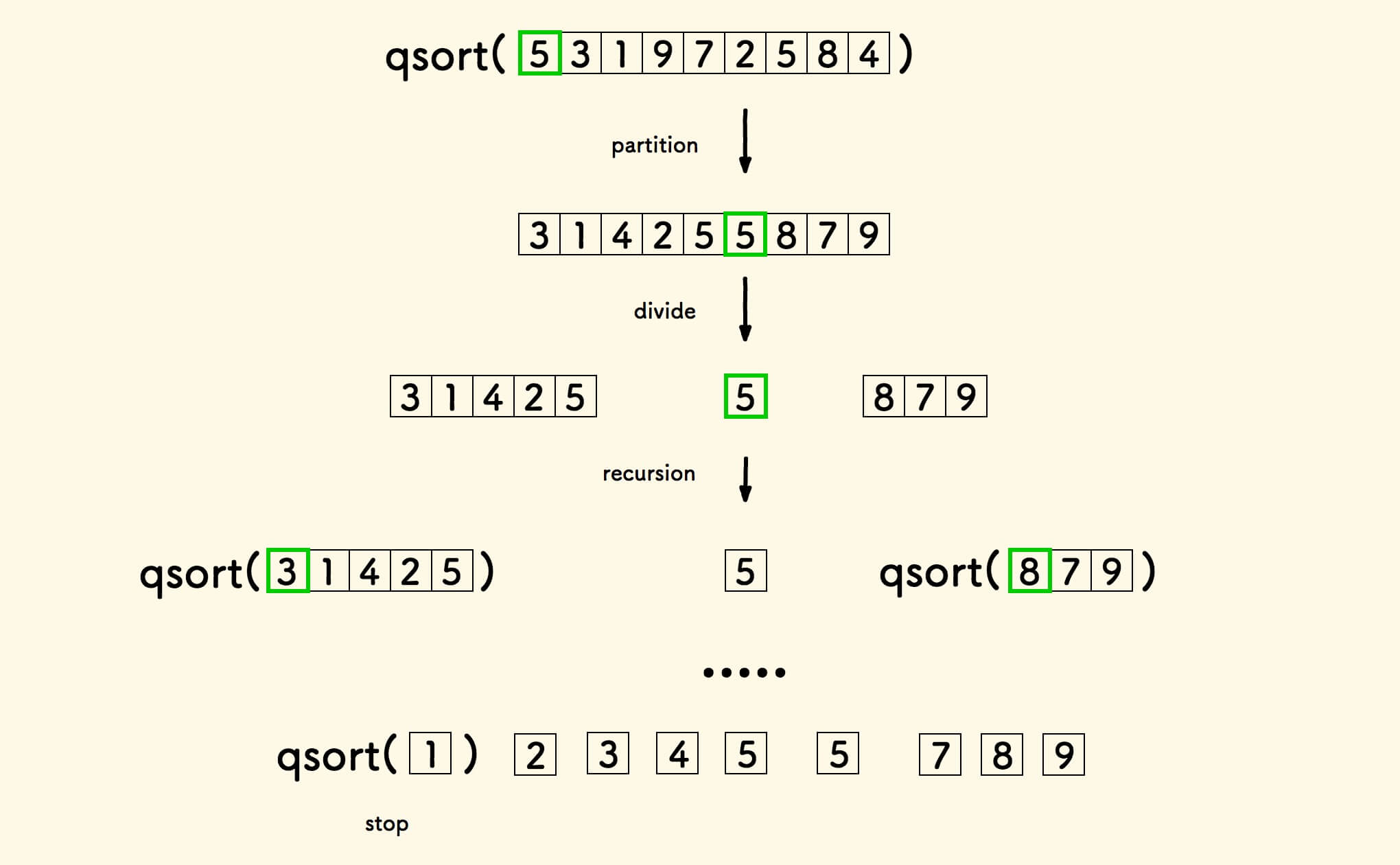
快排实际上是递归的原地分割。

选择基准值，原地分割。
分割的两边，递归分割。
当前数组只有一个元素时，停止递归。

快速排序 - 递归版本 - C 语言实现

// 快速排序 - 递归实现
void QuickSort(int a[], int start, int end) {
    if (start >= end) return;
    int p = Partition(a, start, end);
    QuickSort(a, start, p - 1);
    QuickSort(a, p + 1, end);
}

递归深度是 $\log{n}$ ，平均时间复杂度是 $n\log{n}$ 。

空间复杂度相关于递归深度，是 $\log{n}$ 。

当数组原本是有序时，一直选择第一个元素作为基准的话，快排时间退化为 $O(n^2)$ 。

因此，可以采用选择随机位置的办法，降低退化的风险。

递归的写法，如果快排退化，不仅时间变差，且递归深度退化成为线性，存在调用栈溢出风险。

若随机选择基准，会有效降低快排退化概率，调用栈深度是对数级别的，就会非常有限。

此外，因为原地分割是不稳定的，所以，快排是不稳定的排序算法。

快排的非递归实现

采用一个栈来维护分割函数的调用信息。

类似深度优先遍历的循环写法。

深度优先 - 先序遍历 - 循环实现范式 - 伪代码

stack.push(root)

while !stack.empty()
    node = stack.pop()

    handle(node)

    for child in node.children()
        stack.push(child)

快速排序 - 循环版本 - C 语言实现

// 快速排序 - 循环版本
void QuickSort(int a[], int n) {
    // 保存 start, end
    int stack[2 * n];
    int top = 0;  // 栈顶

    // 初始元素入栈
    stack[top++] = 0;
    stack[top++] = n - 1;

    while (top != 0) {
        // 出栈
        int end = stack[--top];
        int start = stack[--top];

        if (start >= end) continue;

        // 分割
        int p = Partition(a, start, end);

        // 左边、右边分别入栈
        stack[top++] = start;
        stack[top++] = p - 1;

        stack[top++] = p + 1;
        stack[top++] = end;
    }
}

归并排序 ¶

快速排序的过程是递归的原地分割，归并排序的过程则是递归的合并。

合并两个有序数组

如何合并两个有序数组，使得合并之后的数组仍然是有序的？

例如，合并 a=[1,2,5] 和 b=[2,3,6,7] 的结果是 [1,2,2,3,5,6,7] 。

思路比较简单。

新建一个数组，它可以容纳这两个数组。
从两个数组分别取出一个数，把其中小的拿出来放到新数组里，另一个大的数不拿出来。
重复第二步，至少有一个数组会被取完。
把剩下的那个数组中的数全部拷贝到新数组。

合并两个有序数组 - C 语言实现

// 合并两个从小到大有序数组 a 和 b 到 c，使得 c 也是有序的
void MergeSortedArrays(int a[], int m, int b[], int n,
                       int c[]) {
    int i = 0;
    int j = 0;
    int k = 0;

    while (i < m && j < n) {
        if (a[i] <= b[j])
            c[k++] = a[i++];
        else
            c[k++] = b[j++];
    }
    while (i < m) c[k++] = a[i++];
    while (j < n) c[k++] = b[j++];
}

显然，其时间复杂度是 $O(m + n)$ ，空间复杂度是 $O(m + n)$ 。

为方便下面编写归并排序，该函数变形如下。

归并排序 - 合并两个有序数组 - C 语言实现

// 合并两个有序数组
void MergeSortedArrays(int a[], int start1, int end1,
                       int b[], int start2, int end2,
                       int c[], int start3) {
    int i = start1;
    int j = start2;
    int k = start3;

    while (i <= end1 && j <= end2) {
        if (a[i] <= b[j])
            c[k++] = a[i++];
        else
            c[k++] = b[j++];
    }
    while (i <= end1) c[k++] = a[i++];
    while (j <= end2) c[k++] = b[j++];
}

归并排序过程

归并排序就是递归的合并有序数组。

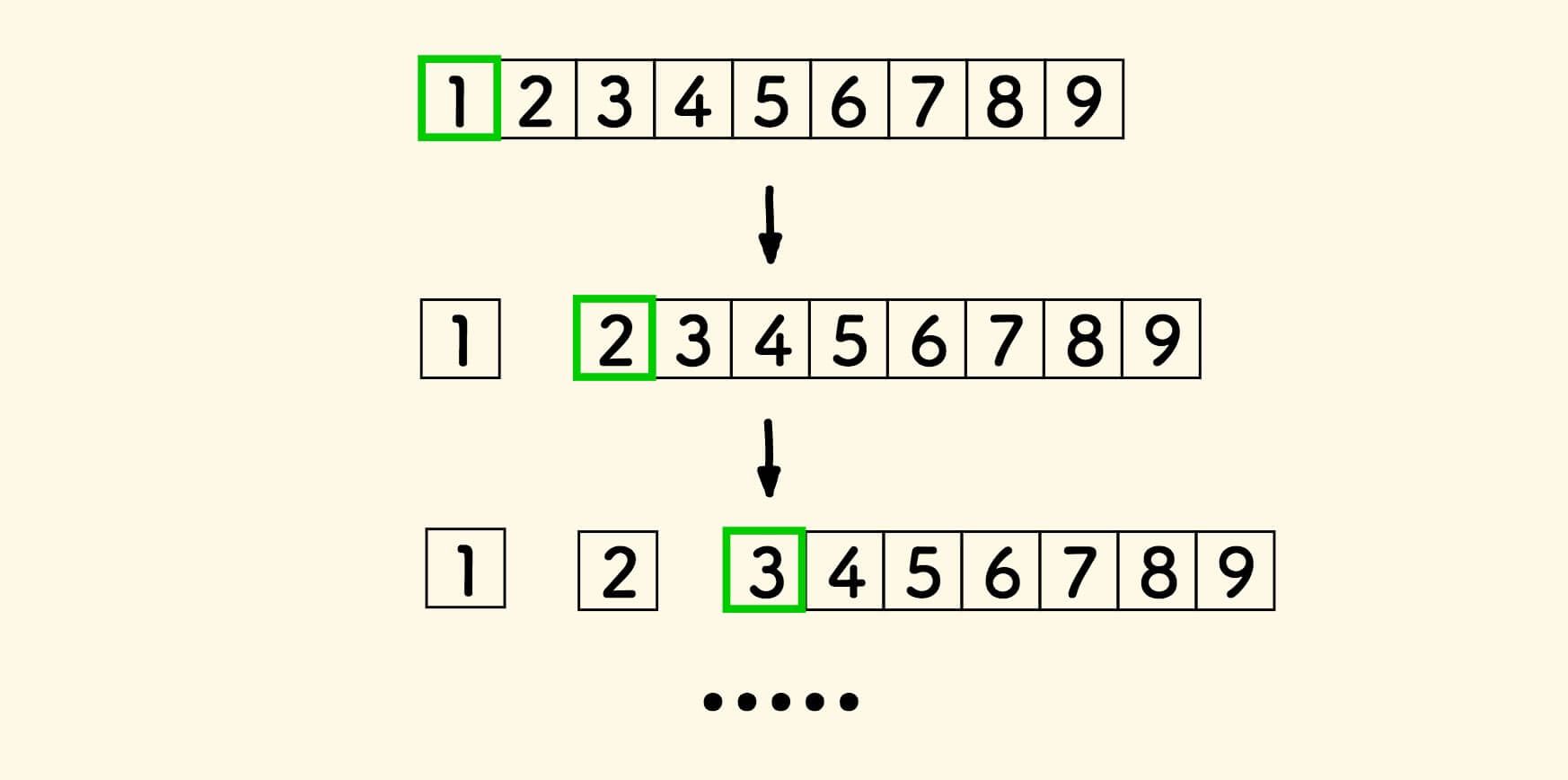
不断二分数组，直到每个子数组只有一个元素。
相邻的子数组归并成大一些的子数组。
重复归并过程，即得到整个有序数组。

总的来说，就是先分后合。

归并排序 - 递归版本 - C 语言实现

// 递归合并过程
void Merge(int a[], int tmp[], int start, int end) {
    if (start >= end) return;

    // 左边
    int start1 = start;
    int end1 = start + (end - start) / 2;

    // 右边
    int start2 = end1 + 1;
    int end2 = end;

    // 归并两边
    Merge(a, tmp, start1, end1);
    Merge(a, tmp, start2, end2);

    // 合并到 tmp
    MergeSortedArrays(a, start1, end1,
                      a, start2, end2, tmp, start);

    // 拷贝 tmp => a
    for (int i = start; i <= end; i++) a[i] = tmp[i];
}

// 归并排序：输入数组和大小
void MergeSort(int a[], int n) {
    int tmp[n];
    Merge(a, tmp, 0, n - 1);
}

归并排序 - 递归版本 - C++ 语言实现

// 合并两个有序数组 a 和 b 的一部分到第三个数组 c
void _MergeTwoSortedArrays(const std::vector<int>& a, int start1, int end1,
                           const std::vector<int>& b, int start2, int end2,
                           std::vector<int>& c, int start3) {
    int i = start1;
    int j = start2;
    int k = start3;
    while (i <= end1 && j <= end2) {
        if (a[i] <= b[j])
            c[k++] = a[i++];
        else
            c[k++] = b[j++];
    }
    while (i <= end1) c[k++] = a[i++];
    while (j <= end2) c[k++] = b[j++];
}

// 递归合并过程
void _MergeSort(std::vector<int>& a, std::vector<int>& tmp, int start,
                int end) {
    if (start >= end) return;

    int start1 = start;
    int end1 = (start + end) >> 1;

    int start2 = end1 + 1;
    int end2 = end;

    _MergeSort(a, tmp, start1, end1);
    _MergeSort(a, tmp, start2, end2);

    // 合并到 tmp
    _MergeTwoSortedArrays(a, start1, end1, a, start2, end2, tmp, start);

    // 拷贝 tmp 到 a
    for (int i = start; i <= end; i++) a[i] = tmp[i];
}

void MergeSort(std::vector<int>& a) {
    std::vector<int> tmp(a.size());
    _MergeSort(a, tmp, 0, a.size() - 1);
}

递归深度是 $\log{n}$ ，每一次归并时间复杂度是 $O(\log{n})$ 。

归并排序的最好、最坏时间复杂度都是 $O(\log{n})$ 。

归并过程依赖临时数组，因此空间复杂度是 $O(n)$。

需要再次注意的是，归并排序是依赖一个大小为 n 的临时空间的。

相比快排而言，归并排序的时间复杂度没有退化情况，而且是稳定排序。

归并排序的非递归实现

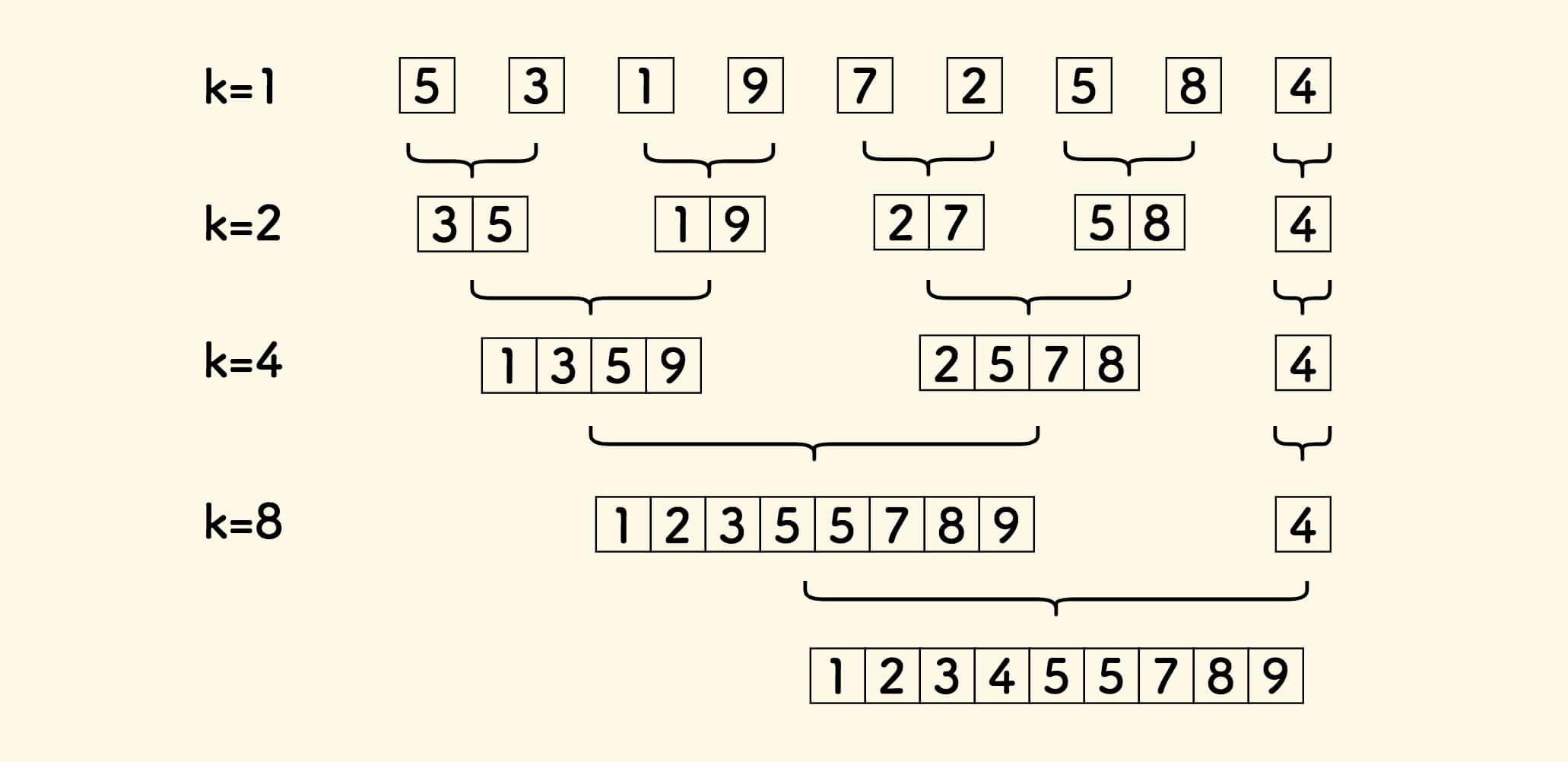
数组切成多个片段，每个片段有 $k$ 个元素。
注意最末尾容许不足 $k$ 个元素。
每两个相邻的片段进行归并，算作一轮归并。
一轮归并完成后，下一次切分，此时每个片段有 $2k$ 个元素。
如上，反复执行。

简而言之，每次合并的段的长度不断倍增。

归并排序 - 非递归版本 - C 语言实现

// 归并排序循环版
void MergeSort(int a[], int n) {
    int tmp[n];
    for (int i = 0; i < n; i++) tmp[i] = 0;

    // k=1 每1个归并一次..
    // k=2 每2个归并一次..
    // k=4 每4个归并一次..
    // k=8 每8个归并一次..
    for (int k = 1; k < n; k *= 2) {
        // 两两 k=1 归并 [0,0]+[1,1], [2,2]+[3,3] ..
        // 两两 k=2 归并 [0,1]+[2,3], [4,5]+[6,7] ..
        // 两两 k=4 归并 [0,3]+[4,7], [8,11]+[12,15] ..
        for (int start = 0; start < n; start += 2 * k) {
            int start1 = start;
            int end1 = start + k - 1;
            if (end1 > n - 1) end1 = n - 1;

            int start2 = end1 + 1;
            int end2 = start2 + k - 1;
            if (end2 > n - 1) end2 = n - 1;

            // 合并
            MergeSortedArrays(a, start1, end1,
                              a, start2, end2, tmp, start);
            // 拷贝
            for (int i = start1; i <= end2; i++) a[i] = tmp[i];
        }
    }
}

归并排序 - 非递归版本 - C++ 语言实现

// 合并有序数组 a 和 b 的两个 range 到 c 的 start3 位置
void Merge(const vector<int>& a, int start1, int end1, const vector<int>& b,
           int start2, int end2, vector<int>& c, int start) {
    while (start1 <= end1 && start2 <= end2) {
        if (a[start1] <= b[start2])
            c[start++] = a[start1++];
        else
            c[start++] = b[start2++];
    }
    while (start1 <= end1) c[start++] = a[start1++];
    while (start2 <= end2) c[start++] = b[start2++];
}

void MergeSort(vector<int>& a) {
    int n = a.size();
    vector<int> tmp(n, 0);

    // 每 k 个元素一归并, 不断翻倍 k
    //
    // [   k 个  ]   +  [   k 个   ]
    // start         |
    // start1   end1 | start2   end2
    //
    for (int k = 1; k < n; k *= 2) {
        for (int start = 0; start < n; start += 2 * k) {
            int start1 = start;
            int end1 = std::min(start1 + k - 1, n - 1);  // 不要越界
                                                         //
            int start2 = end1 + 1;
            int end2 = std::min(start2 + k - 1, n - 1);  // 不要越界

            int end = end2;

            // 合并
            Merge(a, start1, end1, a, start2, end2, tmp, start);

            // 拷贝到原数组
            for (int i = start; i <= end; i++) a[i] = tmp[i];
        }
    }
}

最后值得一提的是：

归并排序是稳定的，也就是保序的。
归并排序的归并过程，是顺序进行的，因此经常用在外部排序中。

（完）