最长回文子序列问题（两种方法）

本文记录最长回文子序列问题的两种解决方法，包括：

最长公共子序列法
动态规划法
延伸 - 输出所有最长回文子序列

问题 ¶

从给定的字符串 s 中找到最长的回文子序列的长度。

例如 s="ababbdab" 的最长回文子序列是 "babbab" ，长度是 6 。

leetcode 题目 - 最长回文串序列

和最长回文子串不同的是，回文子序列不要求连续。

最长公共子序列方法 ¶

字符串反转后和原字符串的最长公共子序列就是最长回文子序列。

最长公共子序列的求解可以采用动态规划法，其时间复杂度是 $O(n^2)$ 。

最长回文子序列 - 最长公共子序列方法 - C 语言实现

#define MAX(a, b) (a) > (b) ? (a) : (b)

// 返回两个字符串 a 和 b 的最长公共子序列的长度
// 例如 "abcbcde" 和 "acabdef" 的最长公共子序列是 "acbde" ，长度为 5
int LongestCommonSubsequence(char *a, int a_length, char *b, int b_length) {
    int table[a_length][b_length];
    int max = 0;

    for (int i = 0; i < a_length; i++) {
        for (int j = 0; j < b_length; j++) {
            if (a[i] == b[j]) {
                if (i >= 1 && j >= 1)
                    table[i][j] = table[i - 1][j - 1] + 1;
                else
                    table[i][j] = 1;
            } else {
                if (i >= 1 && j >= 1)
                    table[i][j] = MAX(table[i - 1][j], table[i][j - 1]);
                else if (i <= 0 && j >= 1)
                    table[i][j] = table[i][j - 1];
                else if (i >= 1 && j <= 0)
                    table[i][j] = table[i - 1][j];
                else
                    table[i][j] = 0;
            }

            if (max < table[i][j]) max = table[i][j];
        }
    }
    return max;
}

// 返回给定字符串 s 的最长公共子序列的长度
int LongestPalindromicSubsequence(char *s) {
    int n = strlen(s);
    if (n <= 0) return 0;
    char r[n];
    for (int i = 0; i < n; i++) r[i] = s[n - 1 - i];
    return LongestCommonSubsequence(s, n, r, n);
}

动态规划方法 ¶

采用动态规划方法。

假设二维数组 dp[i][j] 记录子串 i..j 内的最长回文序列长度。

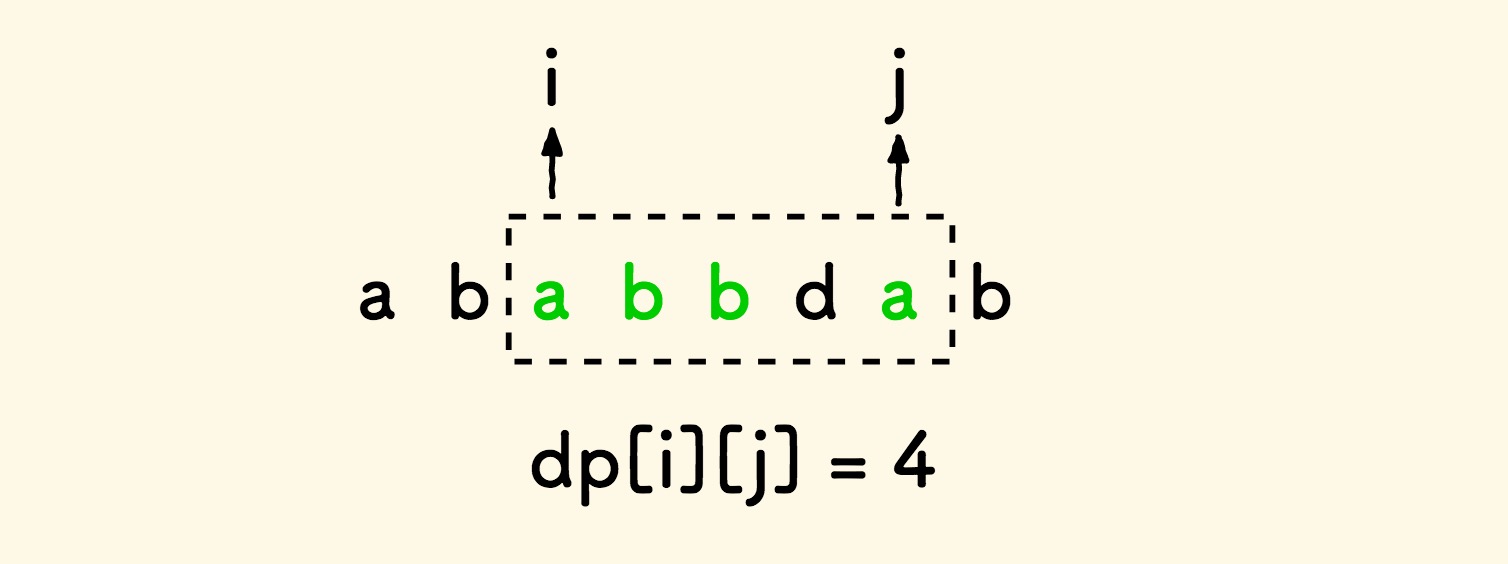
显然，任何一个子串的最长回文序列长度至少是 1，即可初始化所有的 dp[i][j] = 1 。

考虑 dp 数组的递推关系。

如果子串的两边字符相等，那么去掉这俩字符后的子串的最长回文子序列长度比原来少了 2 。

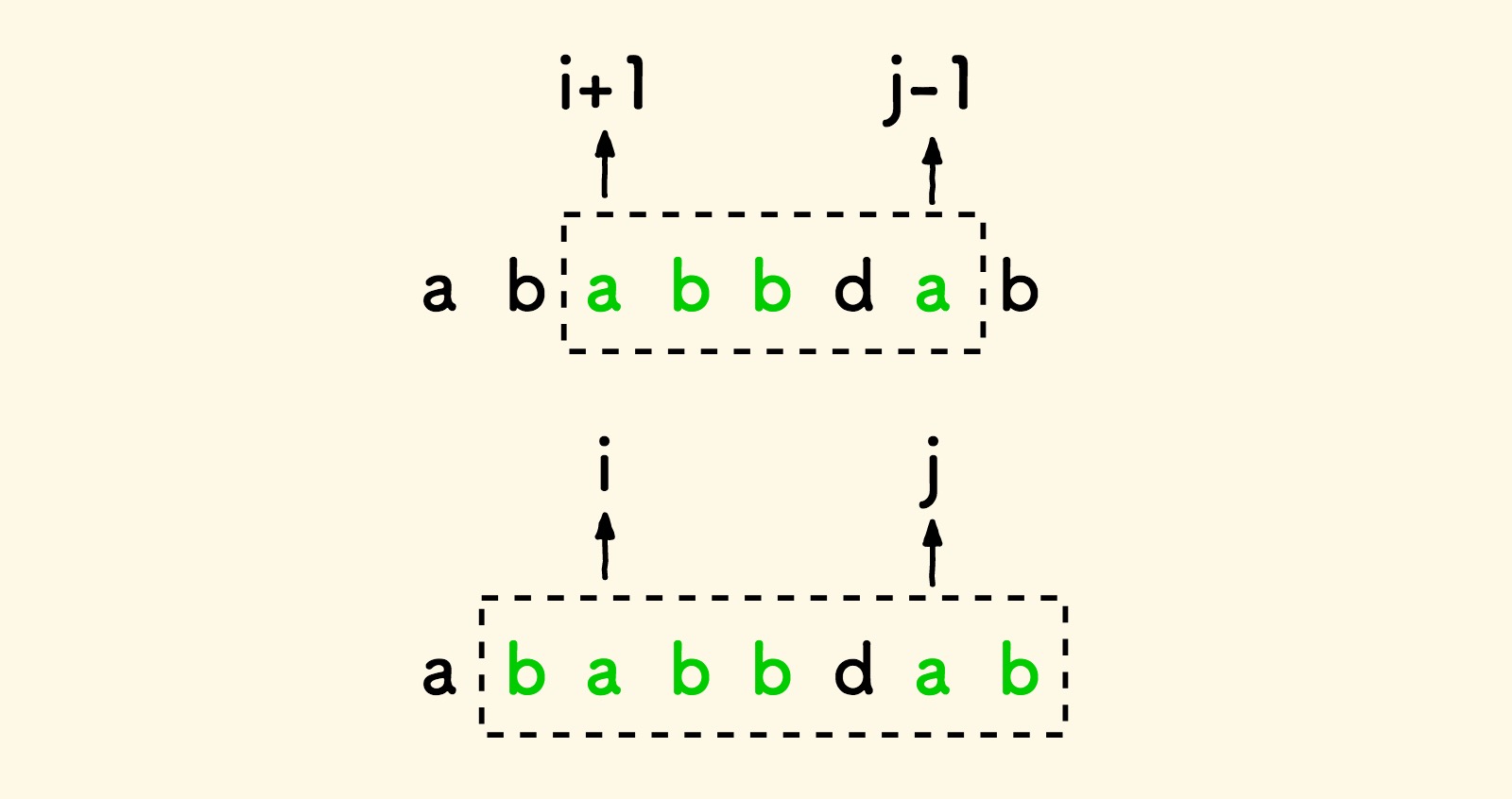
即当 s[i] == s[j] 时，dp[i][j] = dp[i+1][j-1] + 2 。

如果两边字符不相等，最长回文序列要么全落在去掉右边界字符后的左子串内，要么全落在去掉左边界字符后的右子串内。

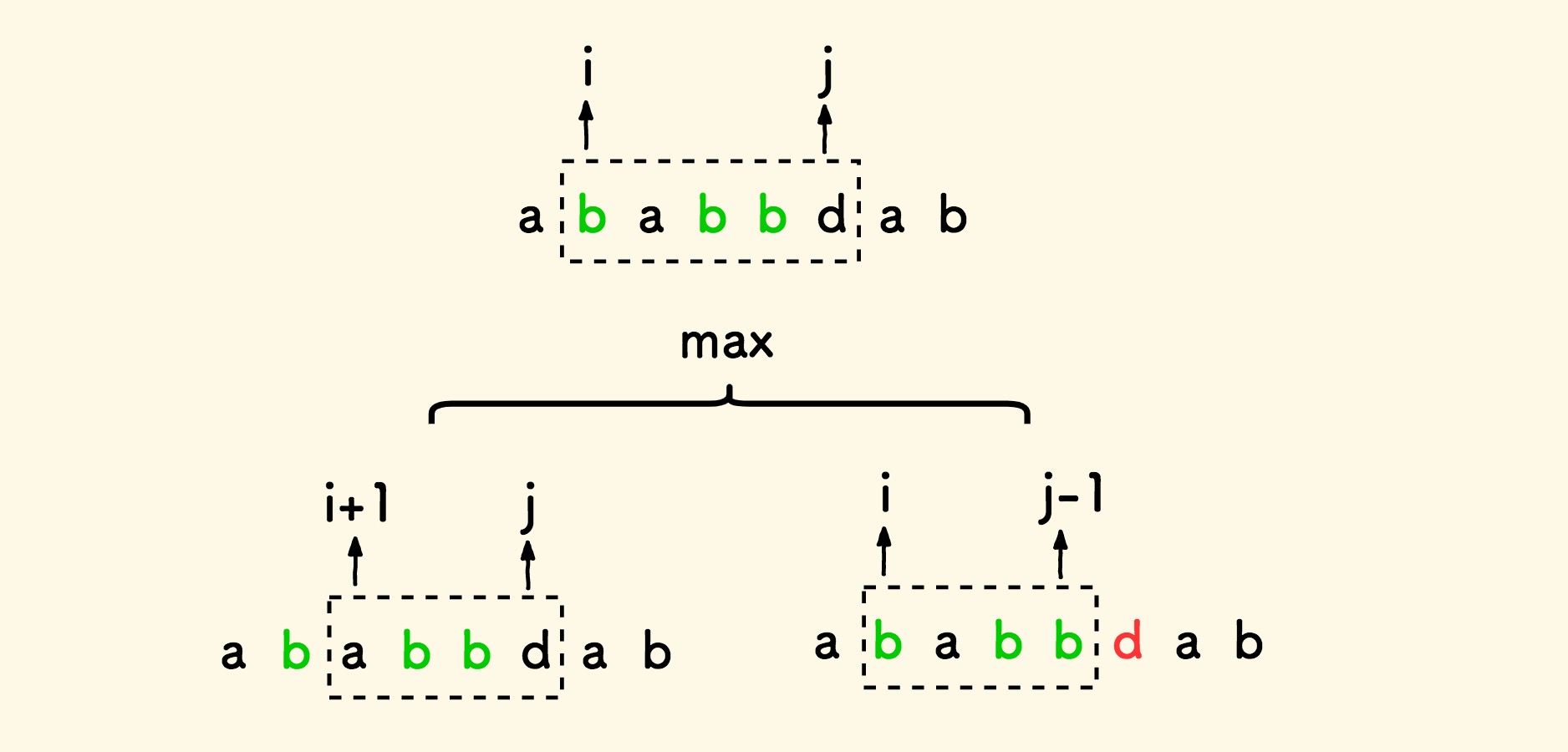
此时 dp[i][j] = max(dp[i+1][j], dp[i][j-1]) 。

上面的两种递推关系，对于子串起始位置的变量 i 的利用逻辑是：先知道 i+1 时候的情况，才能知道 i 时候的情况。所以应倒序迭代变量 i ，同样的道理，应正序迭代变量 j 。

需要注意处理边界情况：

对于第一种递推情况，要考虑子串 i+1..j-1 的有效性，即 i+1 <= j-1 。
反之，子串 i..j 最多有两个字符，又考虑到其两头字符相等，所以整个子串回文。最长回文子序列取其长度即可。
对于第二种递推情况，利用的两个左右子串必然是有效的。
因为此时子串 i..j 的两头字符不相等，所以必然其长度至少为 2 。
所以 i+1 <= j 和 i <= j-1 都成立。
不过，仍需要注意 i+1 和 j-1 的边界。

最后，要求的结果即 dp[0][n-1] ，其中 n 是字符串长度。

本方法的时间复杂度，显然是 $O(n^2)$ 。

最长回文子序列 - 动态规划方法 - C 语言实现

#define max(a, b) (a) > (b) ? (a) : (b)

// 返回给定字符串 s 的最长公共子序列的长度
int LongestPalindromicSubsequence(char *s) {
    int n = strlen(s);
    if (n <= 0) return 0;

    // dp[i][j] 表示子串 i..j 内的最长回文序列长度
    int dp[n][n];

    for (int i = n - 1; i >= 0; i--) {
        for (int j = i; j < n; j++) {
            // 初始化，至少为 1
            dp[i][j] = 1;
            if (s[i] == s[j]) {
                // 第一种情况，两边字符相等 回文序列长度 += 2
                // 注意子串i+1..j-1 的有效性
                if (i + 1 <= j - 1)
                    dp[i][j] = dp[i + 1][j - 1] + 2;
                else {
                    // 即 j-i <= 1 ，此时 i..j 至多有 2 个字符
                    // 两个字符相等时，自身回文，取其长度
                    dp[i][j] = j - i + 1;
                }
            } else {
                // 第一种情况，两边字符不等 回文序列长度取左右之大
                // 此时必然 j > i
                // 所以，一定有 j >= i+1  或者 i-1 <= j，也就是子串一定有效
                // 仍需要注意 i+1 和 j-1 的越界处理
                if (i + 1 < n) dp[i][j] = max(dp[i][j], dp[i + 1][j]);
                if (j - 1 >= 0) dp[i][j] = max(dp[i][j], dp[i][j - 1]);
            }
        }
    }

    return dp[0][n - 1];
}

最后，用一个表格图示来更好地理解其规划过程。

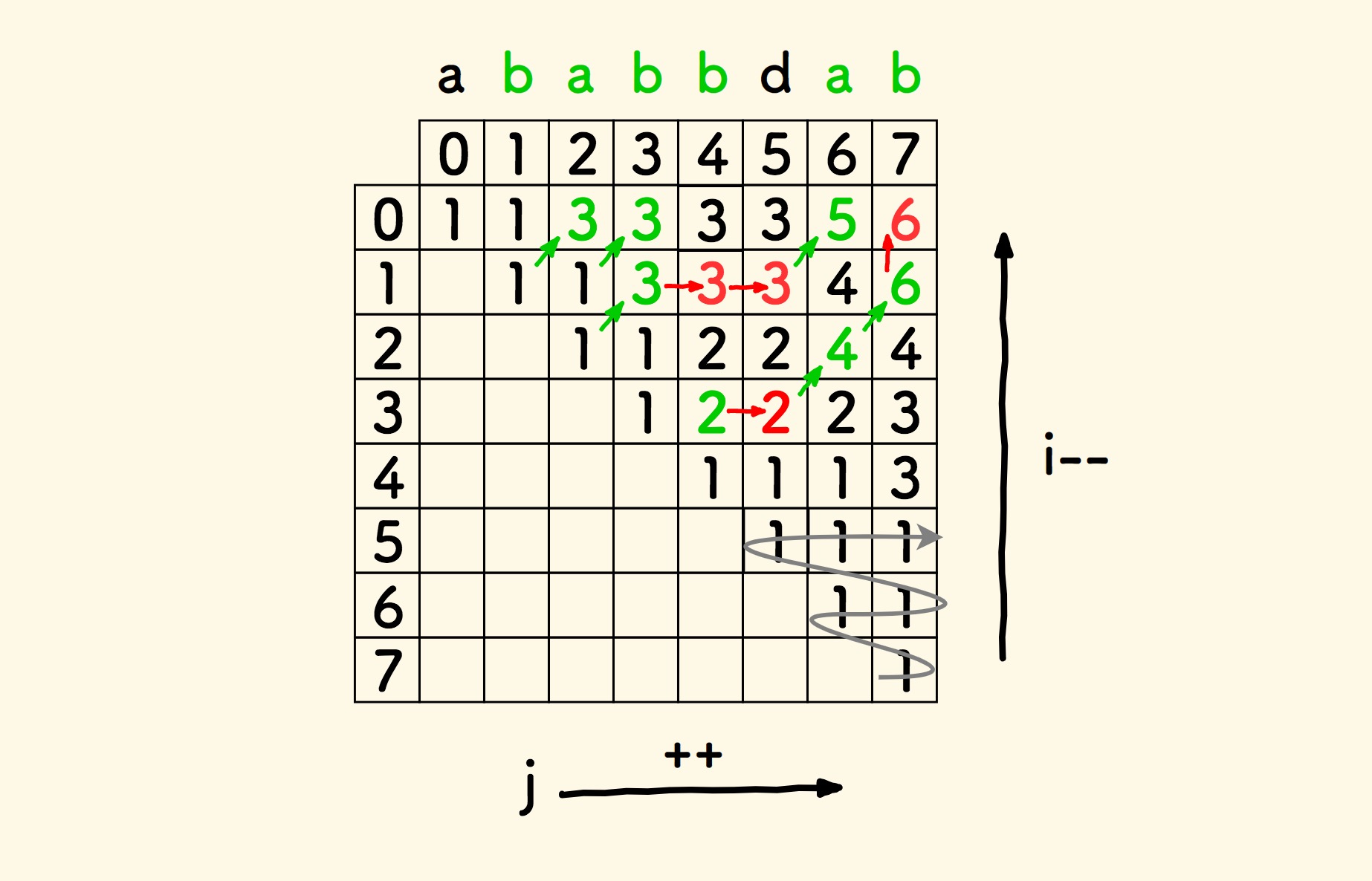
上面的表格填表过程：

初始化所有方格写 1 。
自对角线右下角开始，自下而上、自左而右，按箭头方向根据递推关系填表。
1. 如果 i 和 j 处字符相同，则填写左下角数字 + 2 （图中绿色）。
2. 否则，填写左边和下边两个方格中较大的数字（图中红色）。

延伸 - 输出所有最长回文子序列 ¶

进一步的，如何打印输出所有的最长回文子序列呢？

以 s="abbcca" 为例，它的最长回文子序列长度是 4 ，分别是 "abba" 和 "acca" 。

基于上面所说的动态规划法，其 dp 数组的表格如下：

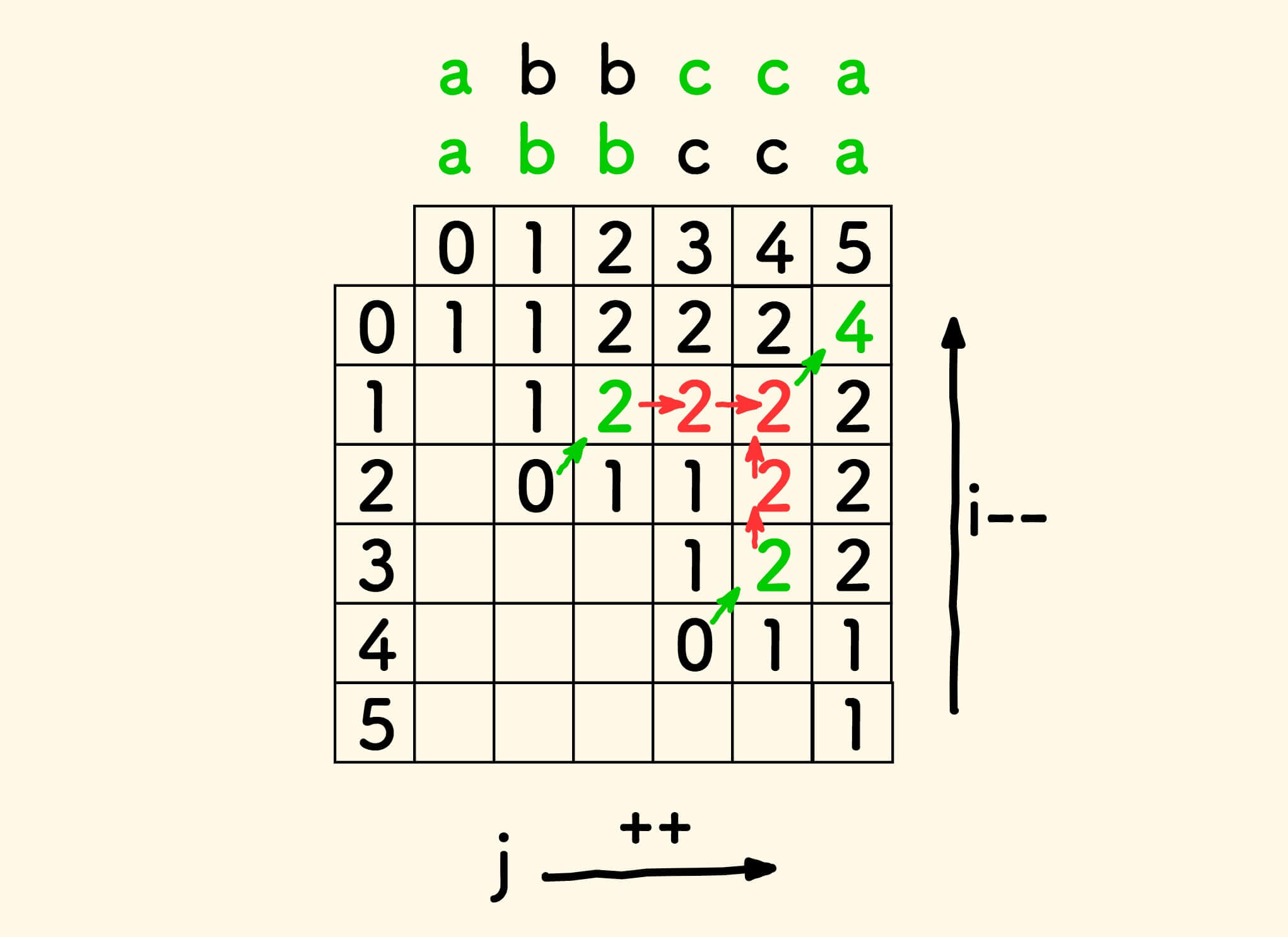
可以看到，一共有两条路径到达右上角的顶点 4 ，其中绿色的字符构成了回文串的一半。

那么，我们需要找到所有到达右上角顶点的路径，然后把绿色的字符打印出来。

构造一个路径数组，path[i][j] 记录当前表格 dp[i][j] 是如何计算而来：

FROM_INIT=0 表示当前表格是初始化而来。
FROM_LEFT=1 表示当前表格是拷贝左边表格的数字而来。
FROM_BOTTOM=2 表示当前表格是拷贝下方表格的数字而来。
FROM_LEFT_BOTTOM=4 表示当前表格是由左下方表格的数字 + 2 而来。

一个细节是，一个表格可能可由多种方式而来，比如，如果左边的数字和下方的数字一样大，此时取或 FROM_LEFT | FROM_BOTTOM ，因此枚举值采用的是 2 的幂次。

动态规划过程中，同步填充 path 数组，如下图所示：

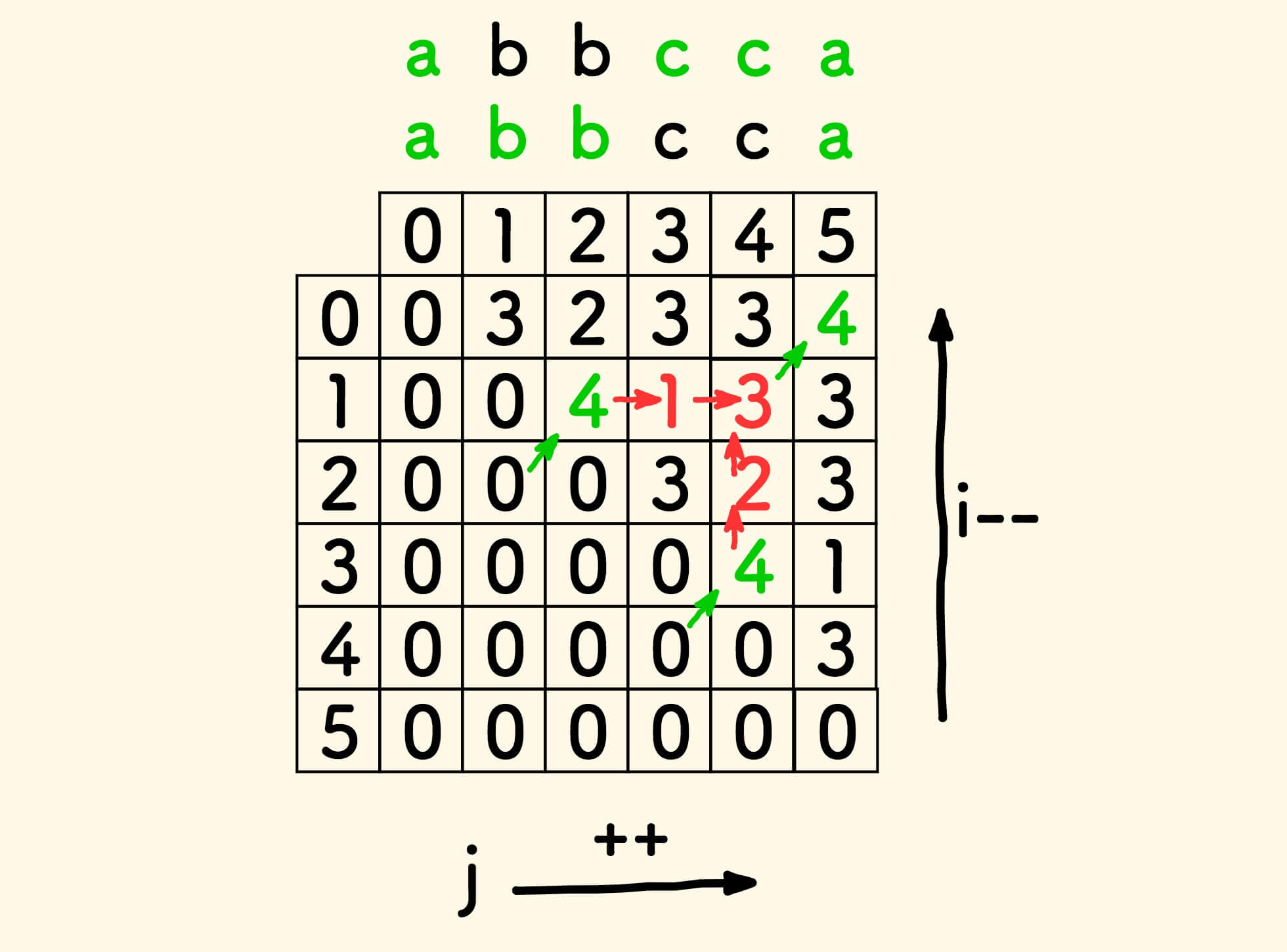
可以看到，上方的 path 表格中，但凡包含 FROM_LEFT_BOTTOM 因素的方格，都被染成了绿色，也就是要输出的字符。

最长回文子序列 - 打印所有 - 填充 path 数组 - C 语言实现

#define FROM_INIT 0         // 0
#define FROM_LEFT 1         // 0b001
#define FROM_BOTTOM 2       // 0b010
#define FROM_LEFT_BOTTOM 4  // 0b100

// 计算长度为 n 的字符串 s 的最长公共子序列的长度
// 填充给定的 dp 数组 和 path 数组。
void ProcessLongestPalindromicSubsequence(char *s, int n, int dp[n][n],
                                          int path[n][n]) {
    for (int i = n - 1; i >= 0; i--) {
        for (int j = i; j < n; j++) {
            dp[i][j] = 1;

            if (s[i] == s[j]) {
                // 优先判断 FROM_LEFT_BOTTOM
                if (i + 1 <= j - 1) {
                    dp[i][j] = dp[i + 1][j - 1] + 2;
                } else {
                    dp[i][j] = j - i + 1;
                }
                if (j != i) path[i][j] = FROM_LEFT_BOTTOM;
            } else {
                if (i + 1 < n) dp[i][j] = max(dp[i][j], dp[i + 1][j]);
                if (j - 1 >= 0) dp[i][j] = max(dp[i][j], dp[i][j - 1]);
            }

            // 无论前面进入的哪个分支，
            // 都可以以「或」的方式补上左方 或 右方来源的可能。
            if (i + 1 < n && dp[i][j] == dp[i + 1][j] && i != j) {
                path[i][j] |= FROM_BOTTOM;
            }
            if (j - 1 >= 0 && dp[i][j] == dp[i][j - 1] && i != j) {
                path[i][j] |= FROM_LEFT;
            }
        }
    }
}

现在的办法是，从右上角开始，根据当前表格的来源，逐步反向遍历路径。

因为目标路径不止一条，所以，采用深度优先遍历的办法。

具体的遍历方法是：

当 path[i][j] & FROM_LEFT_BOTTOM ，则进入左下方表格。
当 path[i][j] & FROM_LEFT ，则进入左方表格。
当 path[i][j] & FROM_BOTTOM ，则进入下方表格。
上面三种分支，可能同时存在。

遍历中的处理过程中：

如果遇到绿色字符，就收集起来。
如果遇到 INIT 表格，意味着收集结束：
1. 把收集到的字符打印出来。
2. 如果 INIT 处是单个字符，那么也是回文序列的一部分，也打印出来，它是回文中心。
3. 由于绿色字符是由于两边字符相等，导致回文序列扩充的情况，所以其左边的镜像字符也需要打印。
  即把收集到的绿色字符，逆序打印一下。
  回文序列正反打印都一样，左边的后打印，右边的先打印，都无妨。

下面分别是 s="abbcca" ，s="ababbdab" 的 DFS 深度遍历情况的示意图：

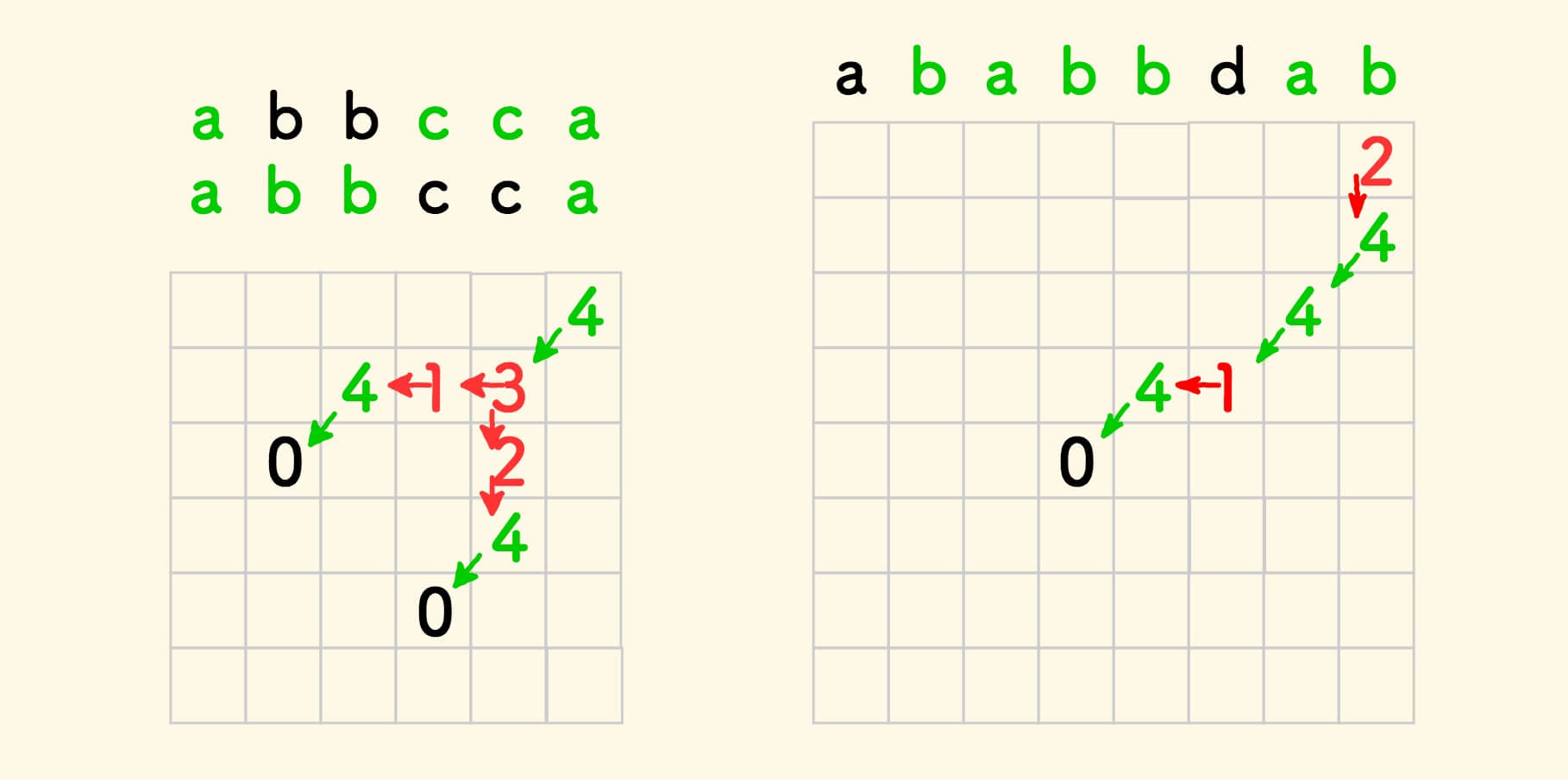
最长回文子序列 - 打印所有 - DFS 遍历打印 - C 语言实现

// DFS 深度优先遍历 path 数组
// 输入的 i,j 是当前的方格位置
// depth 是当前迭代的深度，初始顶级节点depth=1
// parents 是所有父节点需要打印的字符
void DFS(char *s, int n, int path[n][n], int i, int j, int depth,
         char parents[depth]) {
    if (path[i][j] & FROM_LEFT_BOTTOM) {
        // 回文序列得到扩充的情况，需要打印
        // 此时 s[i] == s[j]
        parents[depth] = s[j];
        // 此处只收集了右边字符 s[j]
        // 左边的镜像字符 s[i] 需要晚些打印
    } else if (path[i][j] == FROM_INIT) {
        // 打印的构成
        // abcba => [ab] [c] [ba] 即 parents + 单字符 + 逆序parents
        // 或 abba => [ab] [ba] 即中间无单个字符的打印
        for (int t = 0; t <= depth; t++)  // 正序打印 parents
            if (parents[t] != '\0') printf("%c", parents[t]);

        // 打印 FROM_INIT 处的单个字符
        if (i == j) printf("%c", s[i]);

        for (int t = depth; t >= 0; t--)  // 逆序打印 parents
            if (parents[t] != '\0') printf("%c", parents[t]);

        printf("\n");  // 换行表示找到了一个最长回文序列
    } else {
        parents[depth] = '\0';
    }

    // 向左 DFS
    if (path[i][j] & FROM_LEFT) DFS(s, n, path, i, j - 1, depth + 1, parents);
    // 向下 DFS
    if (path[i][j] & FROM_BOTTOM) DFS(s, n, path, i + 1, j, depth + 1, parents);
    // 向左下 DFS
    if (path[i][j] & FROM_LEFT_BOTTOM)
        DFS(s, n, path, i + 1, j - 1, depth + 1, parents);
}

// 打印给定字符串的所有最长回文子序列。
void PrintAllLongestPalindromicSubsequence(char *s) {
    int n = strlen(s);
    if (n <= 0) return;

    // dp[i][j] 表示子串 i..j 内的最长回文序列长度
    int dp[n][n];
    // path[i][j] 表示 dp[i][j] 的填写是从哪个方格而来
    int path[n][n];

    // 对所有 i, j 进行初始化 0 是必要的：
    // 因为在 DP 过程中，s[i] == s[j] 的边界情况
    // 可以认为是 FROM_LEFT_BOTTOM 的一种，视作 0 + 2 => 2
    // 这要求对 j < i 的 path[i][j] 也要有合理的值 0
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++) path[i][j] = FROM_INIT;

    // 动态规划处理
    ProcessLongestPalindromicSubsequence(s, n, dp, path);

    // dp[0][n-1] 就是最长的回文子序列长度
    int k = dp[0][n - 1];

    // 父节点需要打印的字符，无则是 '\0'
    char parents[k];
    // 当前深度
    int depth = 0;

    //从 i=0, j=n-1 开始 DFS path 数组
    parents[depth++] = '\0';
    DFS(s, n, path, 0, n - 1, depth, parents);
}

（完）

本文中的完整代码 on Github