本文主要记录最长公共子串问题和最长公共子序列问题的动态规划方法。
最长公共子串 ¶
给出两个字符串 a 和 b 的最长连续公共子串的长度。
例如 "abcbcde" 和 "bbcbce" 的最长连续公共子串是 "bcbc" ，长度为 4 。
采用动态规划的思路。
假设字符串 a 和 b 的长度分别是 m 和 n，绘制一张 m x n 的二维表格 table[m][n]。
取字符串 a 和 b 的前缀字符串 a' 和 b' ， 表格位置 i,j 上的数字含义是， 字符串 a' 和 b' 的、以它们尾巴字符结尾的、最长公共子串的长度 。
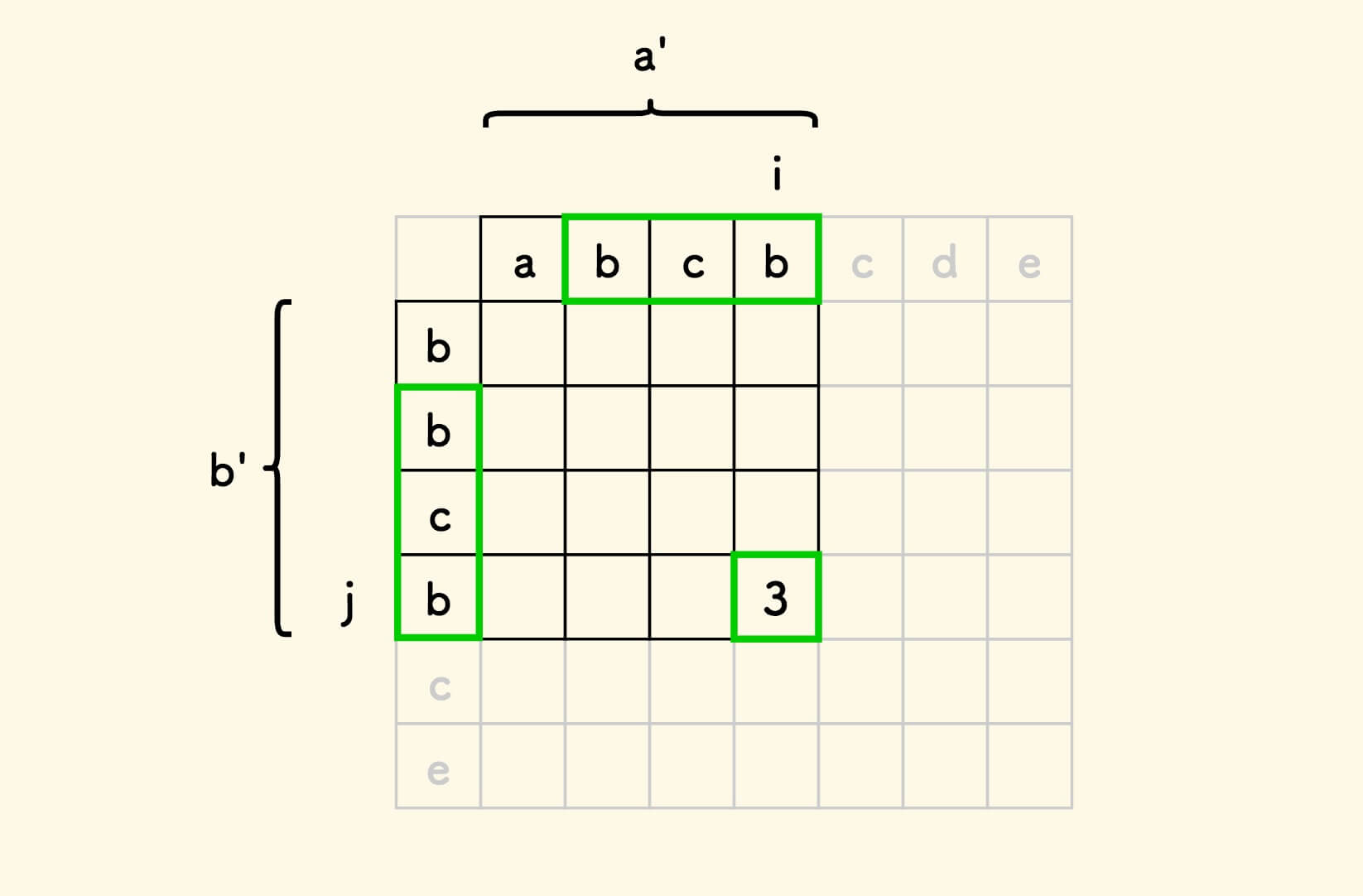
假设，已经知道 i-1, j-1 处的数值，考虑位置 i, j 的数值：
- 如果新的字符
a[i]和b[j]相等，则最长公共子串得到扩展，因此，数值加一。 - 否则，以两个字符为尾巴的最长公共子串不复存在，因此，数值清零。
下图中的左右示例对应着上面的两种情形：
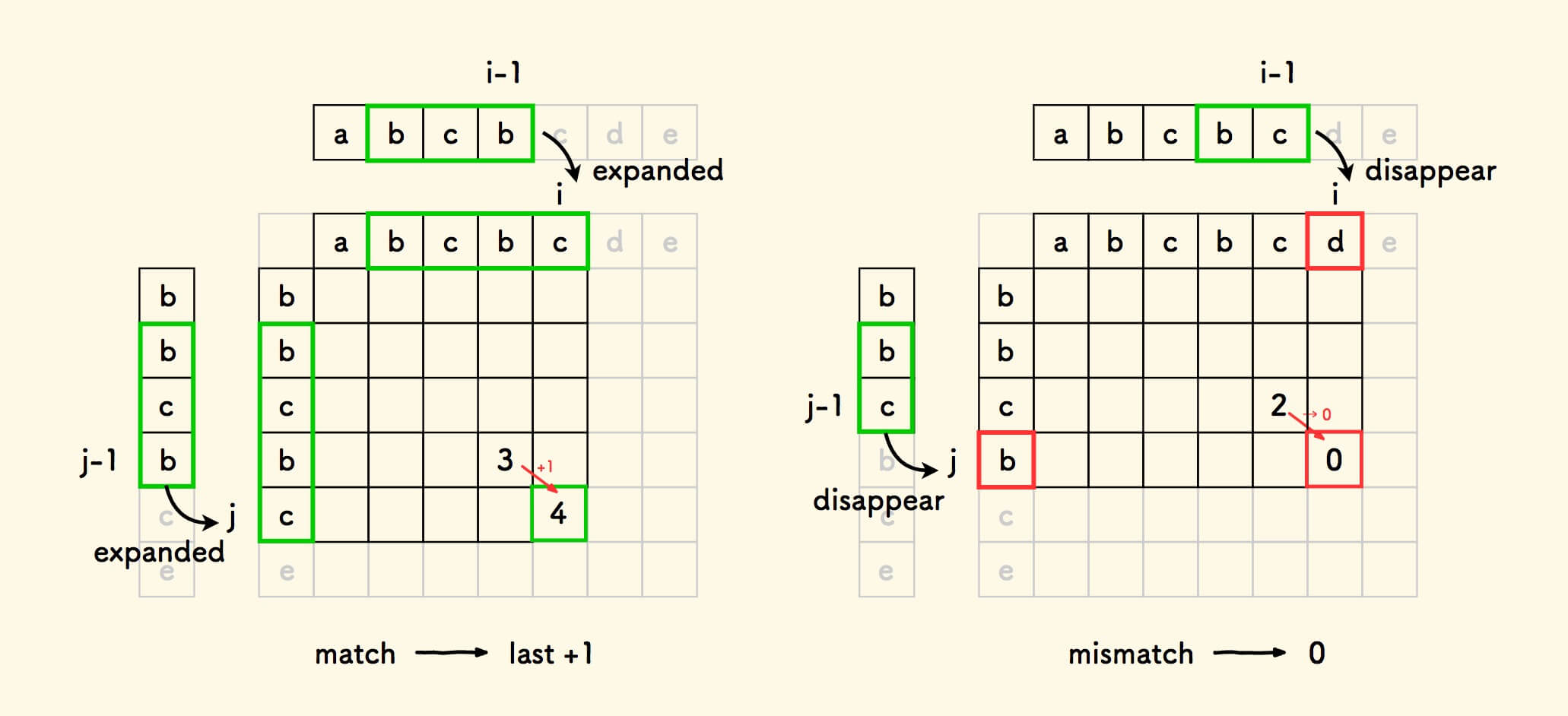
于是得到填表规律：
- 如果当前格子对应的两个字符不同，则写
0。 - 否则，采用斜上方的格子的数值加一。
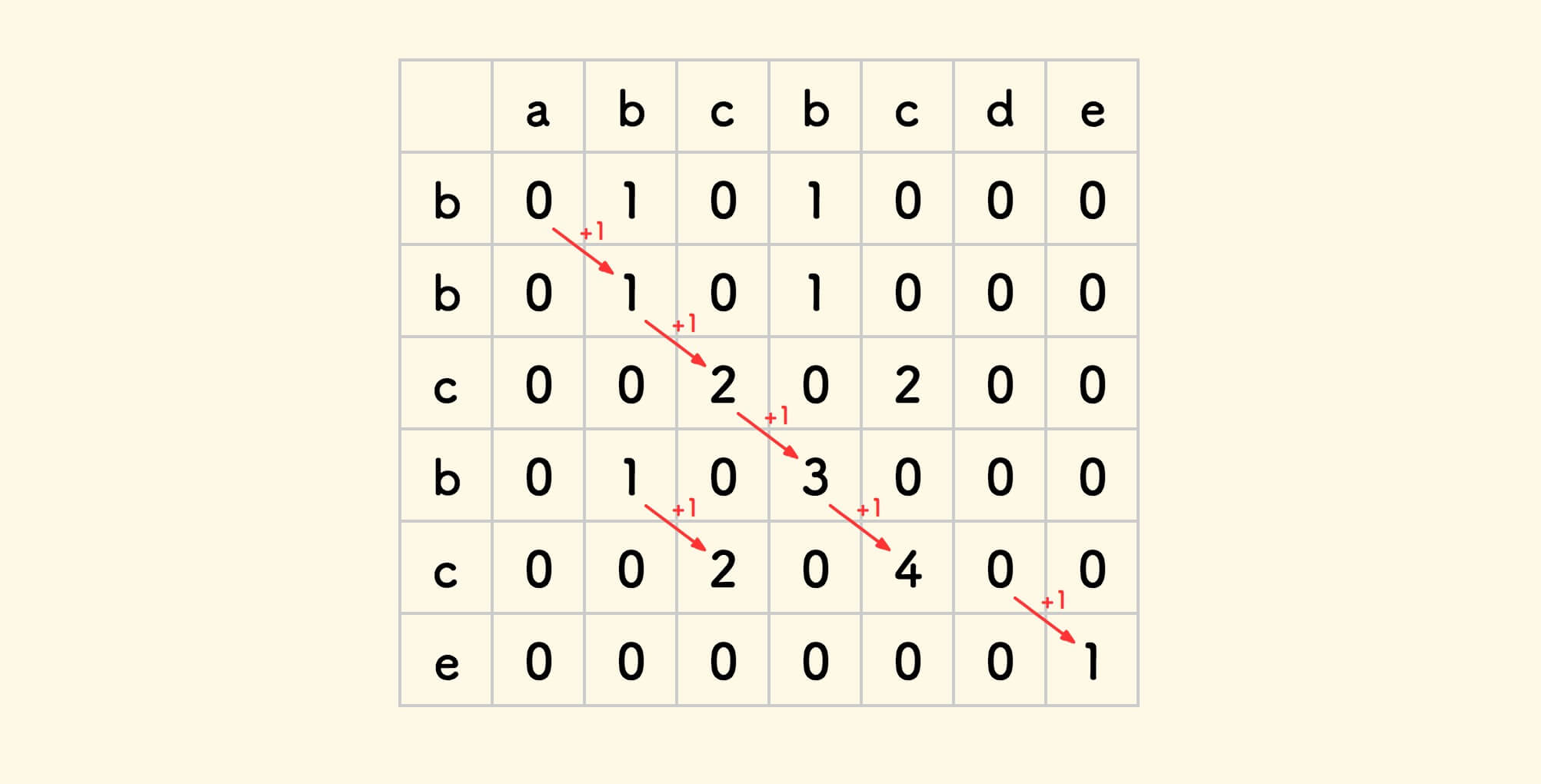
用代码来描述这个填表规则：
- 如果
a[i] != b[j]，则填写table[i][j] = 0 - 否则，填写
table[i][j] = table[i-1][j-1] + 1
表格中的最大值就是最长公共子串的长度。
时间复杂度是 O(mn) 。
最长公共子串长度 - C 语言实现
// 返回字符串 a 和 b 的最长公共子串的长度
// 例如 "abcdbcdef" 和 "bbcbbcdee" 的公共字符串是 "bcde" 长度是 4
int LongestCommonSubstring(char *a, int a_length, char *b, int b_length) {
int table[a_length][b_length];
int max = 0;
for (int i = 0; i < a_length; i++) {
for (int j = 0; j < b_length; j++) {
if (a[i] == b[j]) {
if (i >= 1 && j >= 1)
table[i][j] = table[i - 1][j - 1] + 1;
else
table[i][j] = 1;
} else {
table[i][j] = 0;
}
if (table[i][j] > max) {
max = table[i][j];
}
}
}
return max;
}
最长公共子序列 ¶
给出两个字符串 a 和 b 的最长公共子序列的长度。
和公共子串的不同是，公共子序列不要求连续。
例如 "abcbcde" 和 "acabdef" 的最长公共子序列是 "acbde" ，长度为 5 。
仍然采用动态规划的思路。
如果两个字符串的尾巴位置分别是 i 和 j ， 假设它们的最长公共子序列的长度是函数 f(i, j) ：
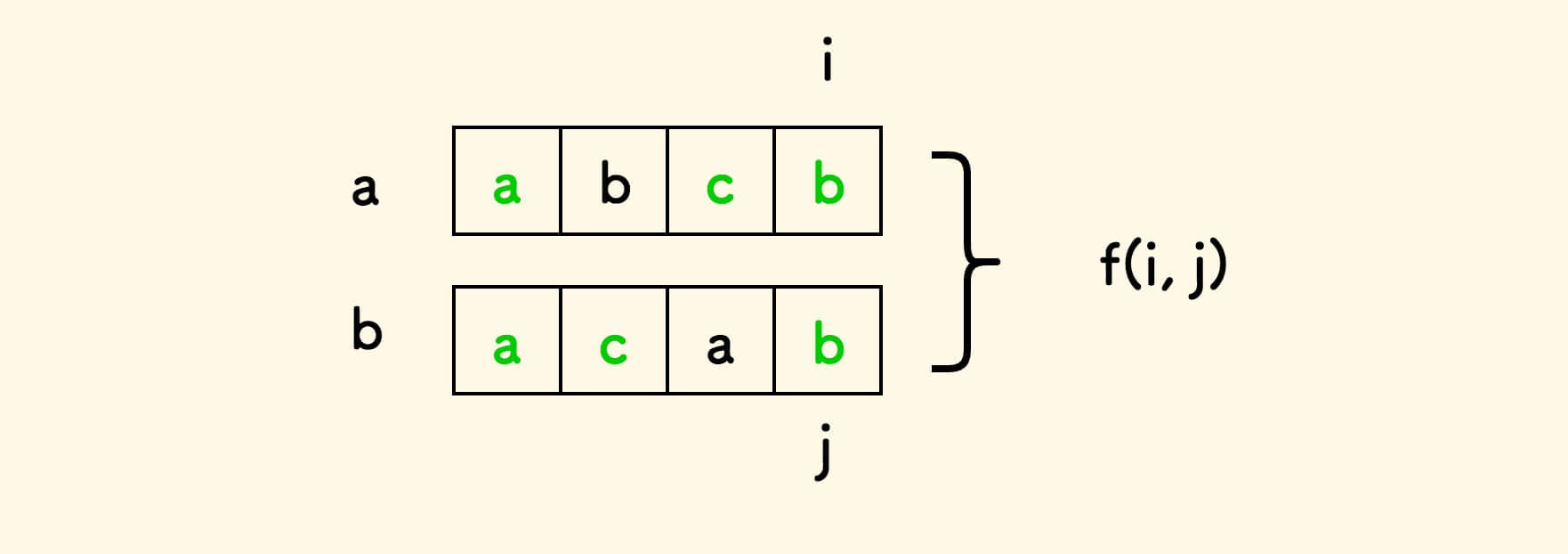
考虑函数的递推关系：
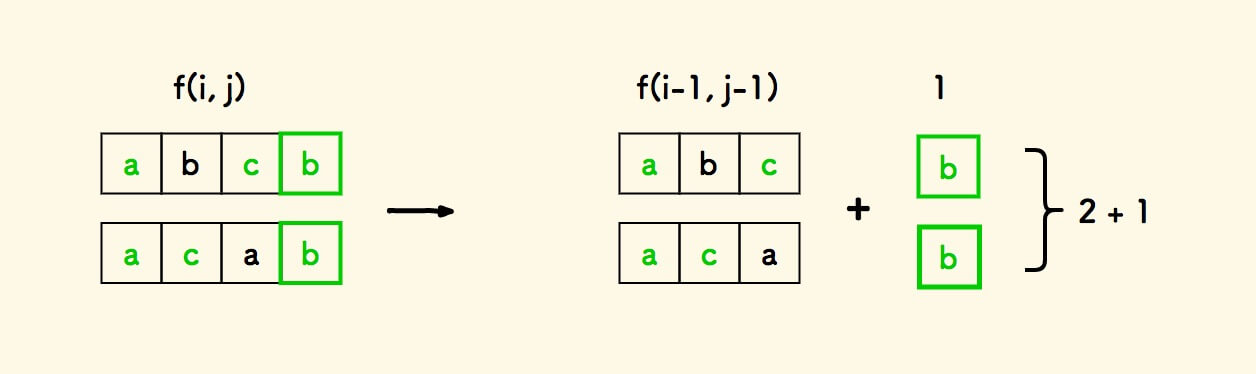
如果两个字符串的尾巴字符相同，易知
f(i,j) = f(i-1,j-1) + 1：
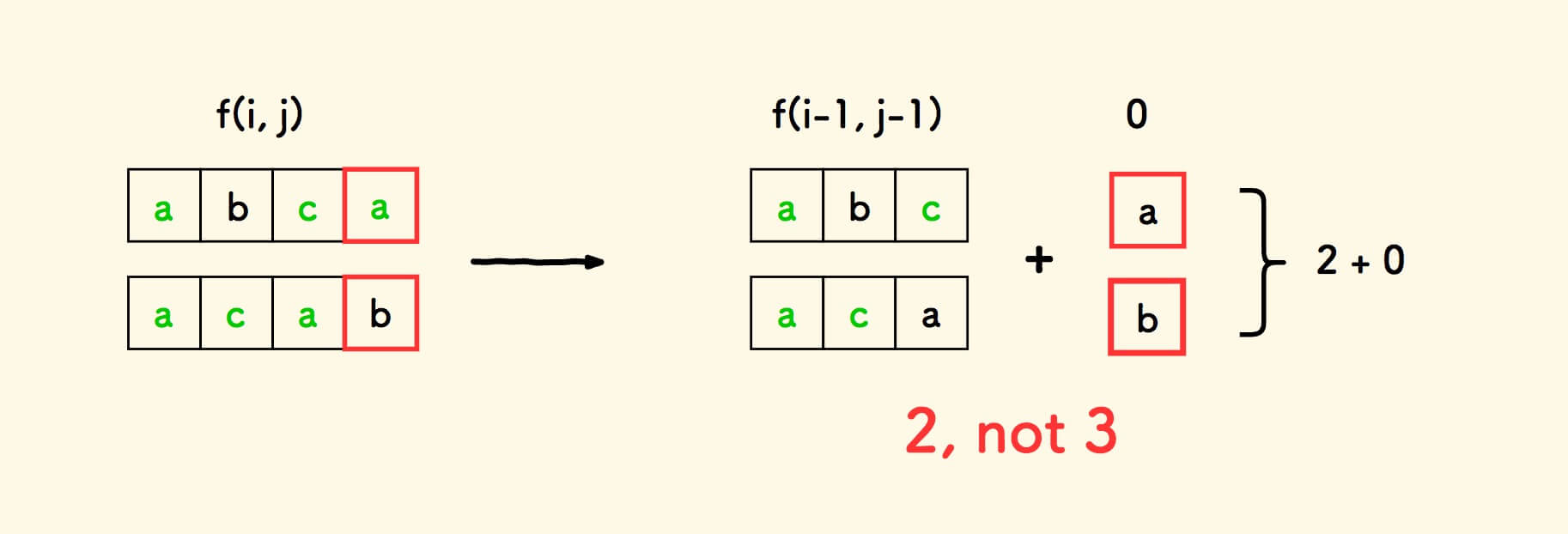
如果尾巴字符不同，上面的递推关系将不再成立。
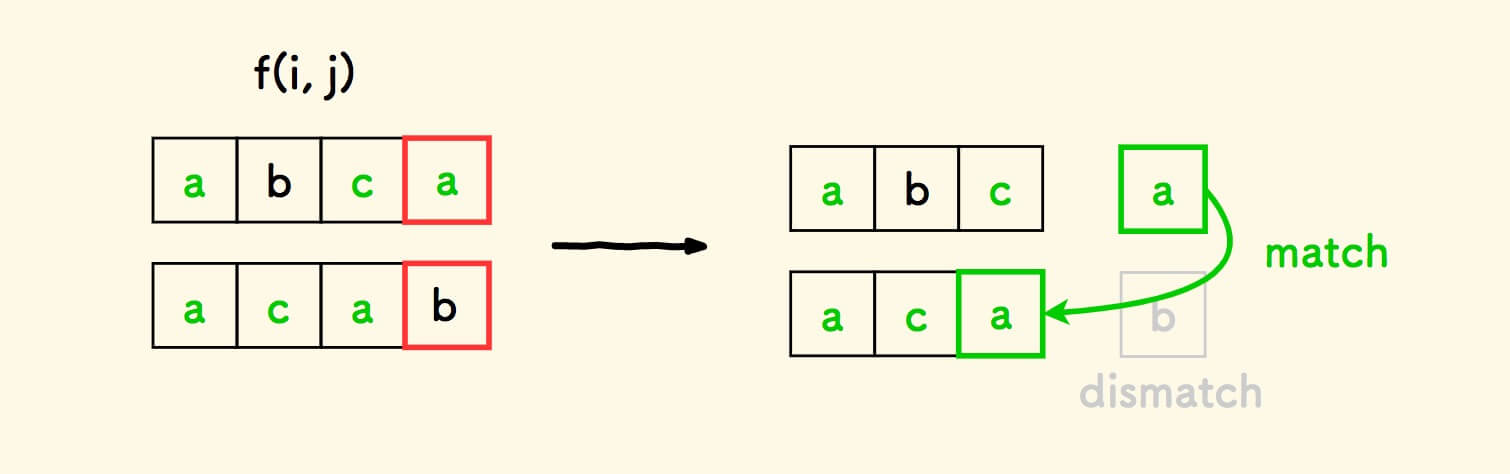
原因在于，虽然尾巴字符不同， 但一个字符串的尾巴字符可能和另一字符串的前面的某个字符相同，导致最长公共子序列得到扩展。
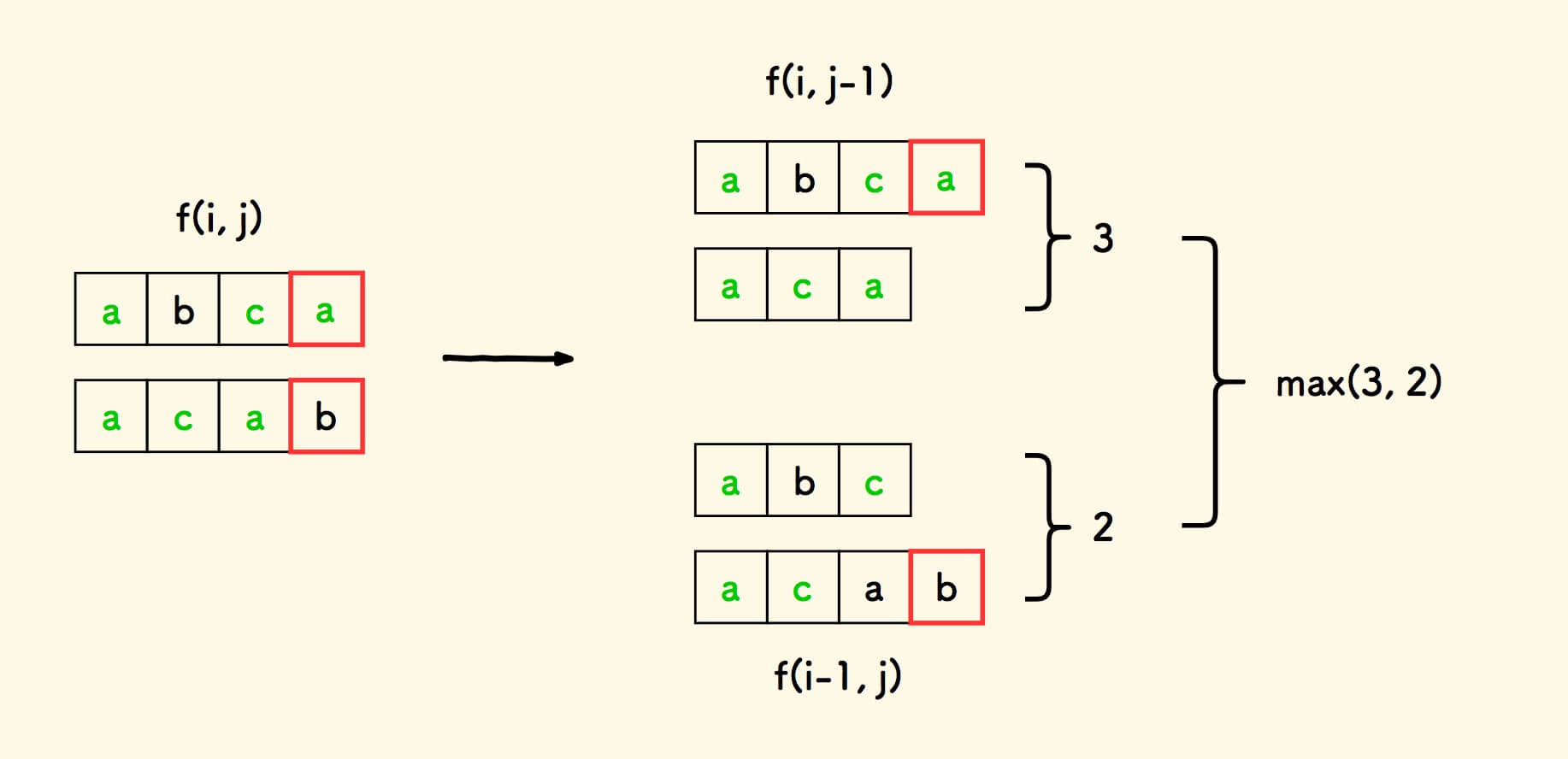
注意，上图中的关系可以进一步表达为：
考虑其一般性，取
f(i-1,j)和f(i,j-1)的最大值：
下面将用填表方式描述动态规划过程。
假设字符串 a 和 b 的长度分别是 m 和 n，绘制一张 m x n 的二维表格 table[m][n]。
取字符串 a 和 b 的前缀字符串 a' 和 b' ，
表格位置 i,j 上的数字含义是 f(i,j) ，即 字符串 a' 和 b' 的最长公共子序列的长度 。
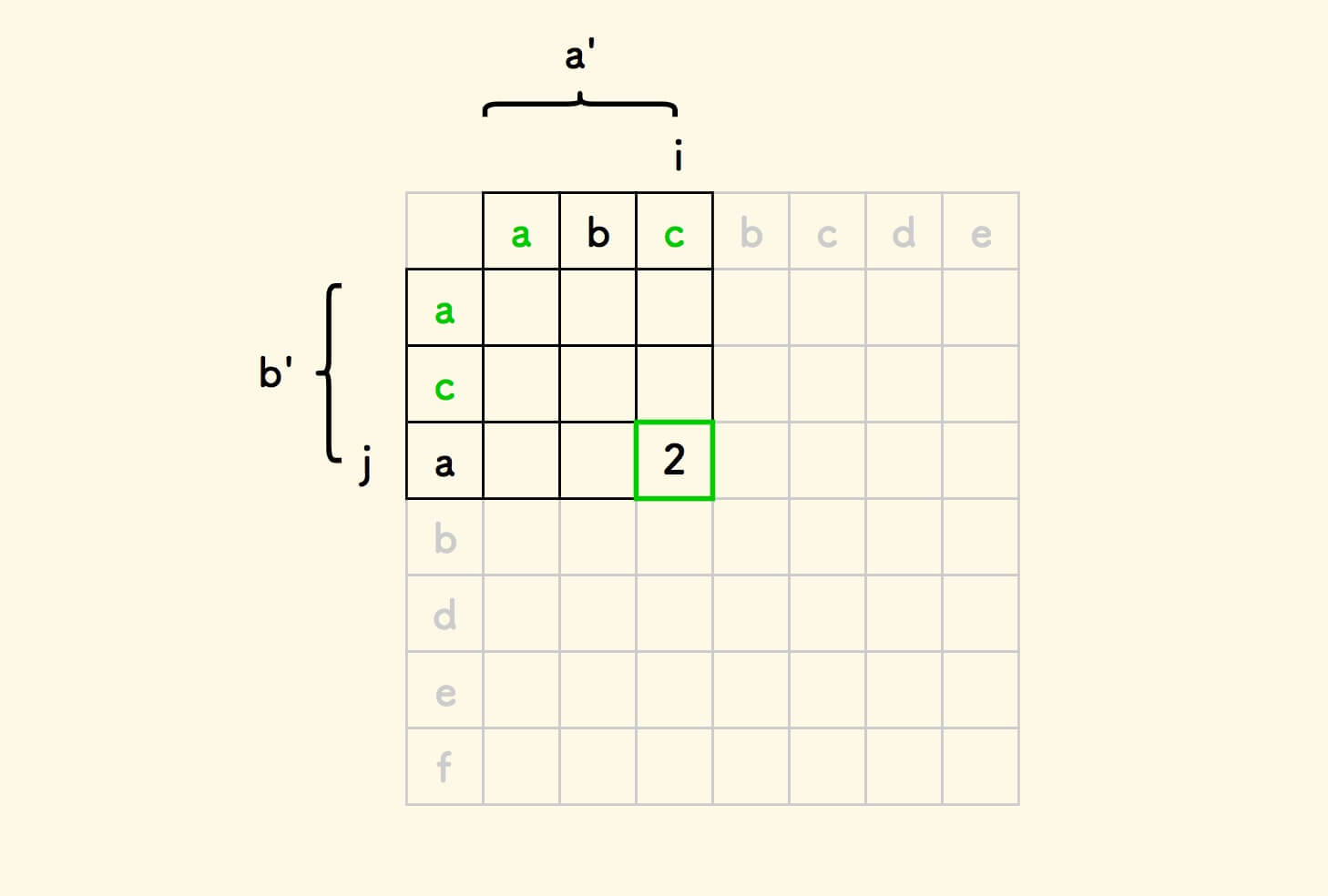
利用已分析的递推关系，表格填写规则如下：
- 如果字符
a[i]和b[j]相同，则最长公共子序列得到扩展，数值加一。 - 否则，采用左边的和上面的方格中的数值的最大值。
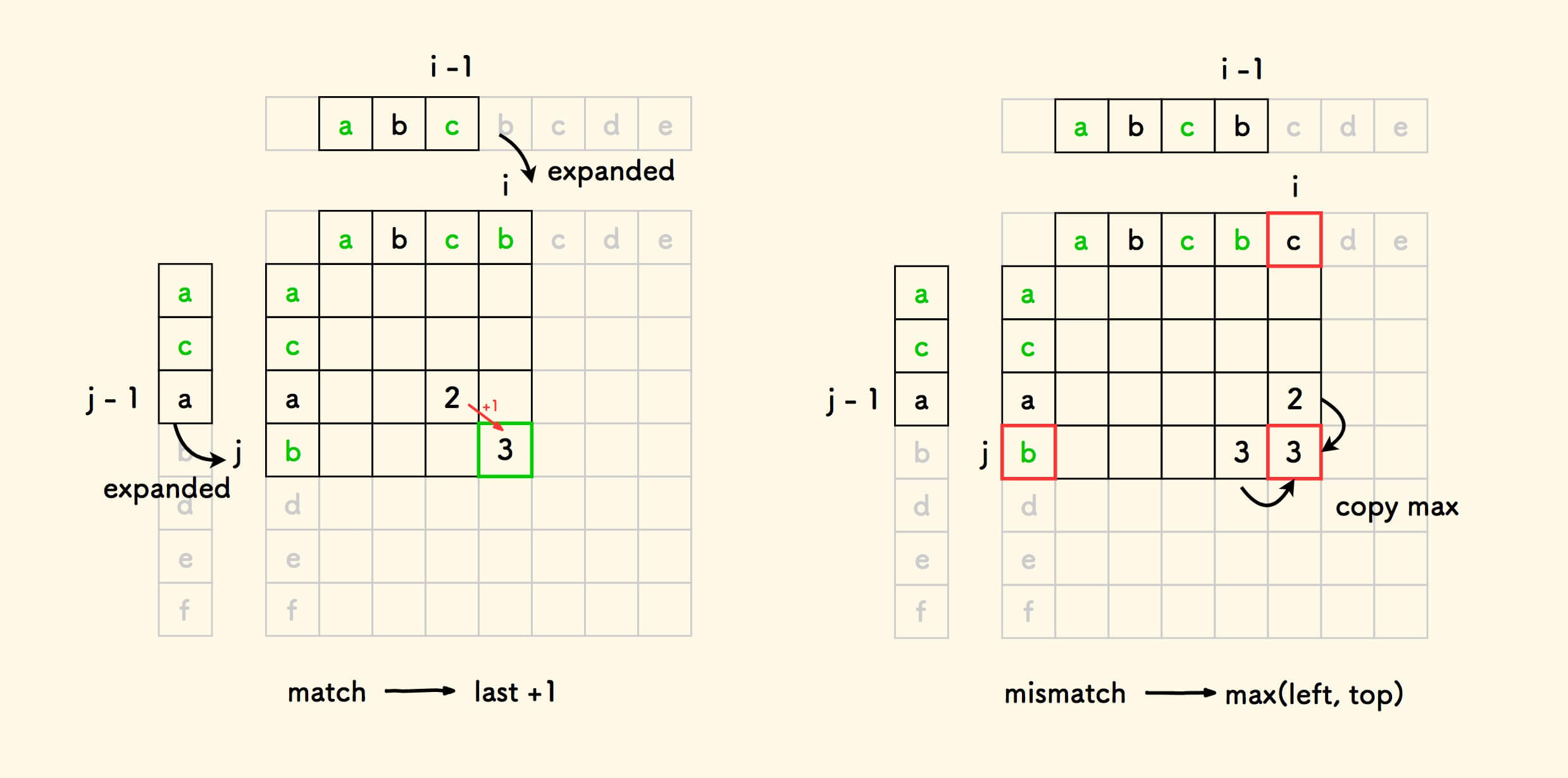
按照此规律，可以示例的两个字符串的填表过程如下：
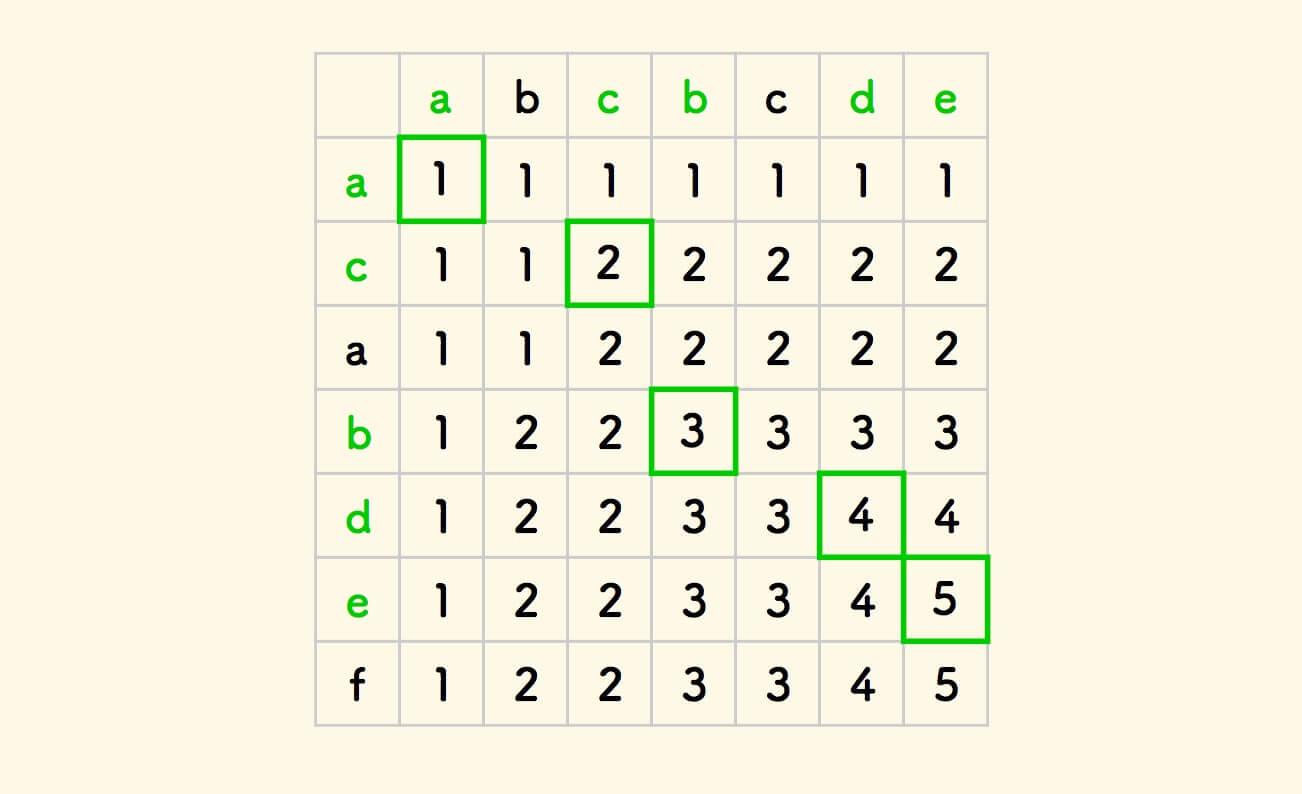
用代码来描述这个填表规则：
- 如果
a[i] == b[j]， 则填写table[i][j] = table[i-1][j-1] + 1 - 否则，填写
table[i][j] = max(table[i-1][j], table[i][j-1])
表格中的最大值就是最长公共子串的长度。
时间复杂度是 O(mn) 。
最长公共子序列长度 - C 语言实现
#define MAX(a, b) (a) > (b) ? (a) : (b)
// 返回两个字符串 a 和 b 的最长公共子序列的长度
// 例如 "abcbcde" 和 "acabdef" 的最长公共子序列是 "acbde" ，长度为 5
int LongestCommonSubsequence(char *a, int a_length, char *b, int b_length) {
int table[a_length][b_length];
int max = 0;
for (int i = 0; i < a_length; i++) {
for (int j = 0; j < b_length; j++) {
if (a[i] == b[j]) {
if (i >= 1 && j >= 1)
table[i][j] = table[i - 1][j - 1] + 1;
else
table[i][j] = 1;
} else {
if (i >= 1 && j >= 1)
table[i][j] = MAX(table[i - 1][j], table[i][j - 1]);
else if (i <= 0 && j >= 1)
table[i][j] = table[i][j - 1];
else if (i >= 1 && j <= 0)
table[i][j] = table[i - 1][j];
else
table[i][j] = 0;
}
if (max < table[i][j]) max = table[i][j];
}
}
return max;
}
（完）
相关阅读：最短编辑距离 - 动态规划方法
