本文记录最短编辑距离问题的动态规划方法,包括:
问题 ¶
将一个字符串 a 编辑为另一个字符串 b ,求需要的最少的编辑步数。
允许三种编辑动作:删除一个字符、替换一个字符 和 插入一个字符。
例如,把字符串 horse 编辑为 ros 的最少编辑步数是 3 :

最短编辑距离 ¶
初始化
采用动态规划方法,假设字符串 a 和 b 的长度分别是 m 和 n 。
建立一个二维数组 dp ,即一个二维表格。
取字符串 a 以位置 i 结尾的前缀 a' ,字符串 b 以位置 j 结尾的前缀 b' 。
表格中数字 dp[i][j] 的含义是: 将字符串 a' 编辑为 b' 的最少编辑步数 。
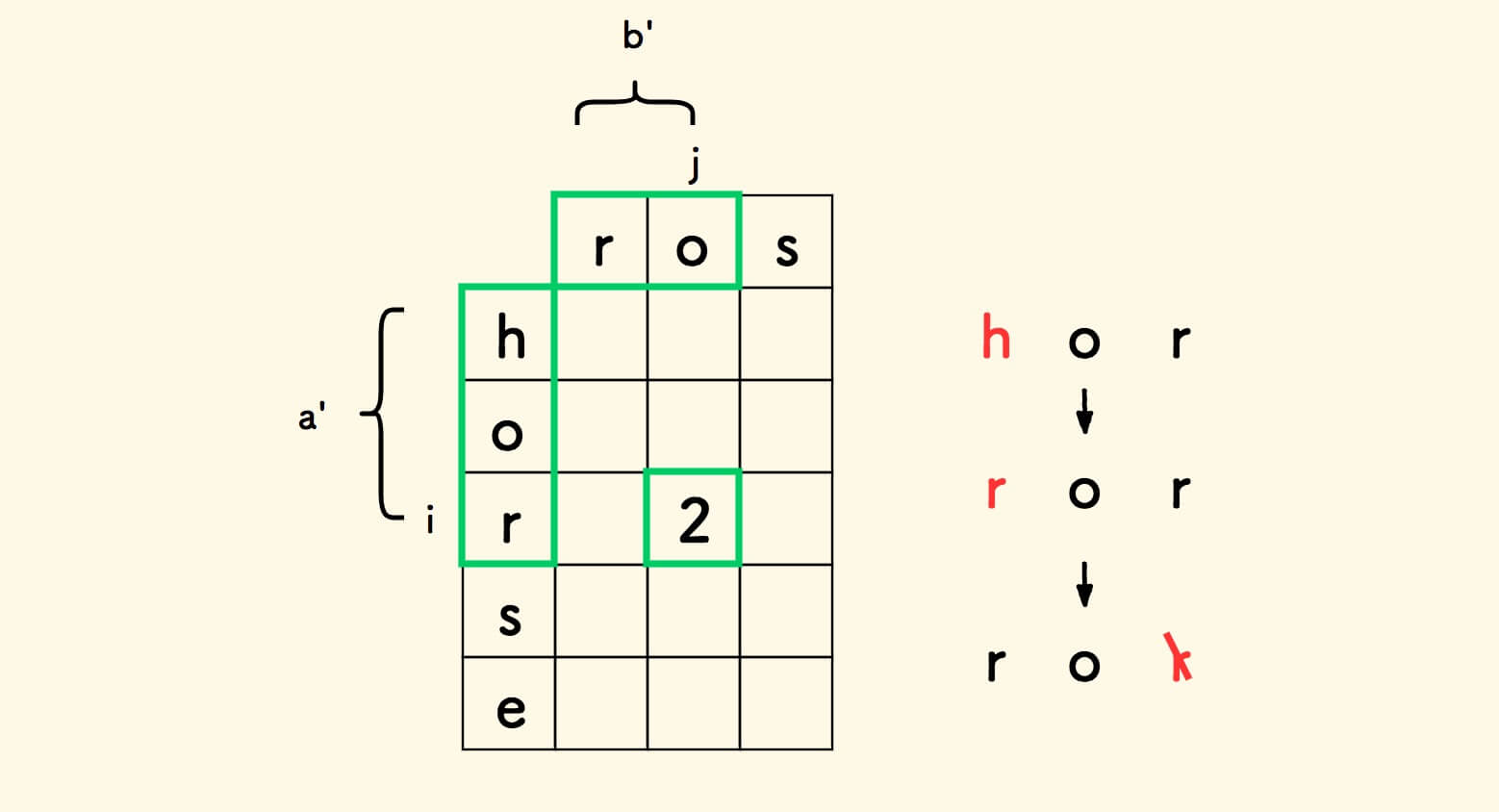
为方便边界处理,在两个字符串的头部插入一个表示空的字符 $ ,稍后将看到这样做的好处 。
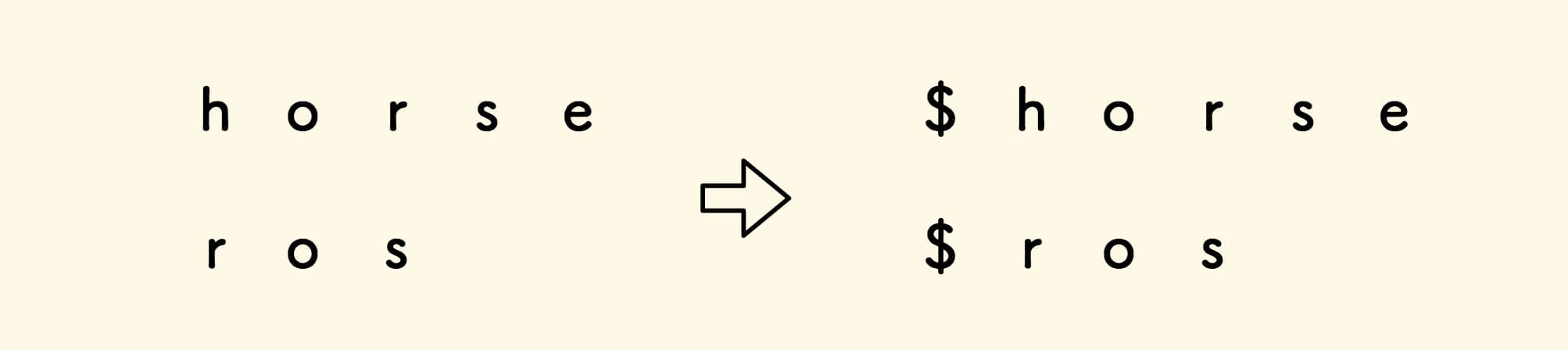
如此一来,表格 dp 的大小就是 (m+1)x(n+1) 。
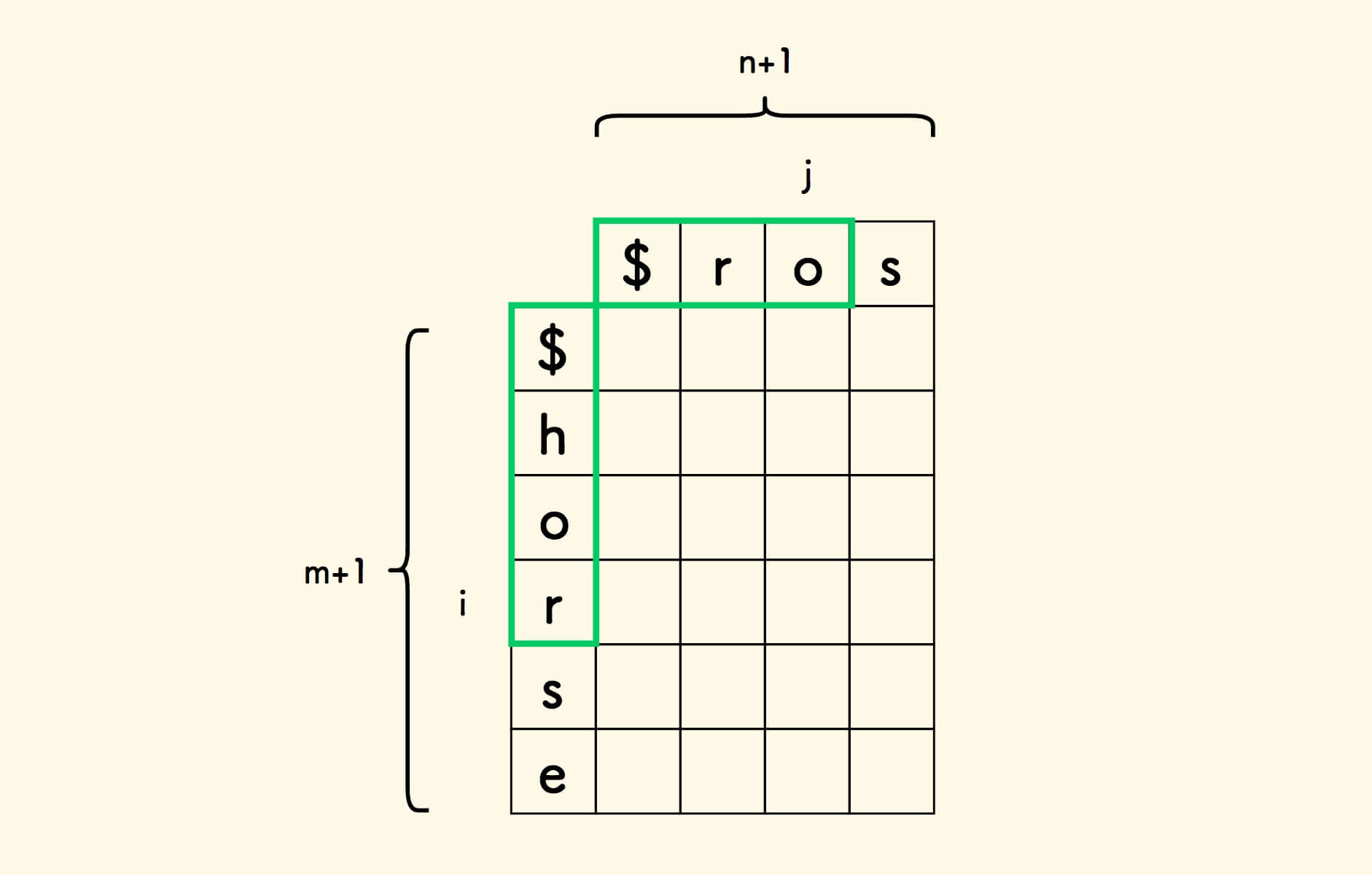
首先考虑表格第一行的值,即如何把单字符的字符串 $ 编辑为任何一个 b 的前缀 b' 。
容易想到,不断执行插入操作,即可。

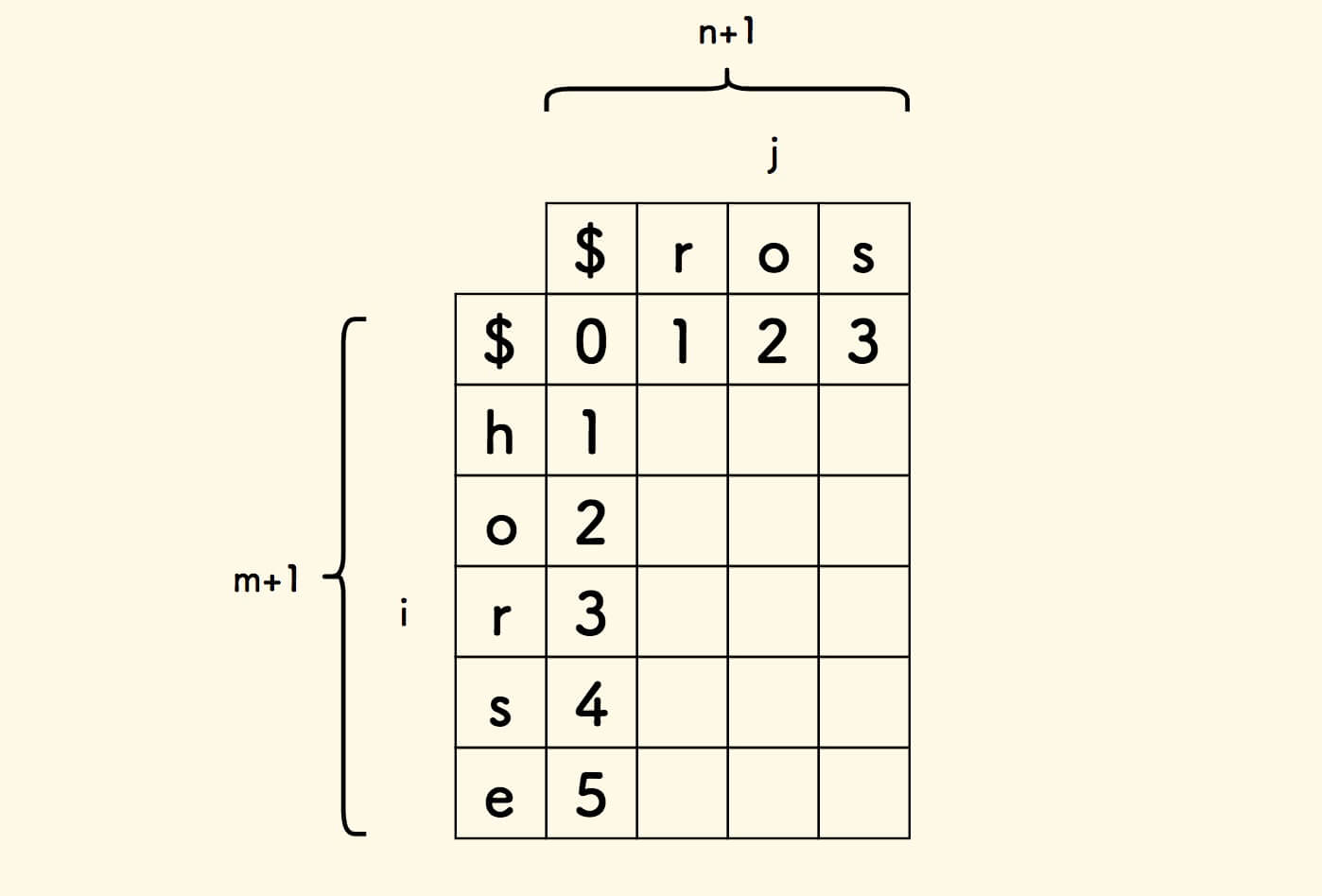
因此,第一行的每一个方格 dp[0][j] 填写 j 。
同样道理,第一列的每一个方格 dp[i][0] 填写 i 。

至此,表格已经初始化完毕,如下图所示。
递推关系
下面考虑如何递推填表。
再次明确,表格 dp[i][j] 的数值, 是原字符串 a 以 i-1 结尾的前缀 a' 编辑到原字符串 b 以 j-1 结尾的前缀 b' 的最小编辑距离。

下面考虑如何填写 dp[i][j] 的值。
考虑将 a' 编辑为 b' 的所有可能情况:
如果已经知道如何把
a'编辑为更短一位的b''的话在此基础上, 直接再插入一个字符即可形成
b'。
上一次形成
b'的过程,最少需要dp[i][j-1]步。可知, 当前表格的值至多是当前表格的左边表格的数值加一 。

此时,插入的字符是
b[j-1]。同样,如果已经知道如何把更短一位的
a''编辑为b'的话那么只需先把
a'删除末尾字符形成a'',再编辑为b'即可。
由
a''编辑到b'的过程,最少需要dp[i-1][j]步。可知, 当前表格的值至多是当前表格的上边表格的数值加一 。

此时,删除的字符是
a[i-1]。如果已经知道如何把更短一位的
a''编辑为更短一位的b''呢?在此基础上,只需要把
a'的尾巴字符替换为b'的尾巴字符即可。
此时,是把字符
a[i-1]替换为b[j-1]。但是,如果两个字符本来就相同,就无需替换了。

由
a''编辑到b''的过程,最少需要dp[i-1][j-1]步。可知:
- 如果尾巴字符相等,那么当前表格拷贝左上方表格的值。
- 否则,至多是左上方表格的数值加一。

综合以上,当前表格的值 dp[i][j] 取它们的最小值。
总结如下:
- 考虑由左面方格的数字加一而来:
left = dp[i][j-1] + 1 - 考虑由上面方格的数字加一而来:
up = dp[i-1][j] + 1 - 考虑由左上方的数字而来:
- 如果尾巴字符相等,那么
left_up = dp[i-1][j-1] - 否则,
left_up = dp[i-1][j-1] + 1
- 如果尾巴字符相等,那么
dp[i][j]取上面三个数的最小值。
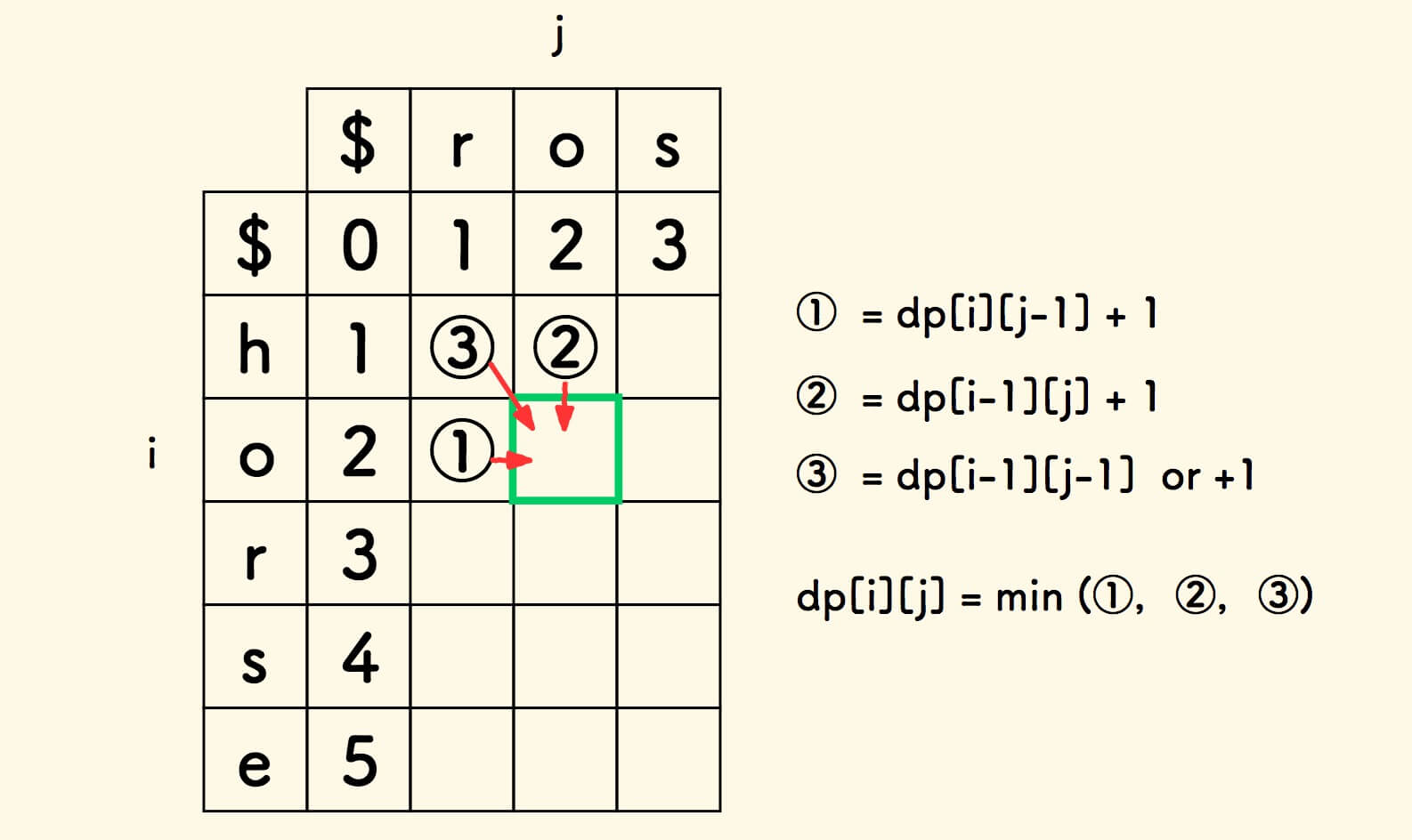
递推过程,会用到左方、上方和左上方表格的数值, 添加一个空字符 使表格的第一行和第一列的得以初始化, 从而避免繁琐的边界处理。
最右下角的方格数值就是将 a 编辑为 b 的最少步数,即 dp[m][n] 就是结果。
下面是对本文中所用例子的填表过程,图中也标出了一种最短的编辑路径。
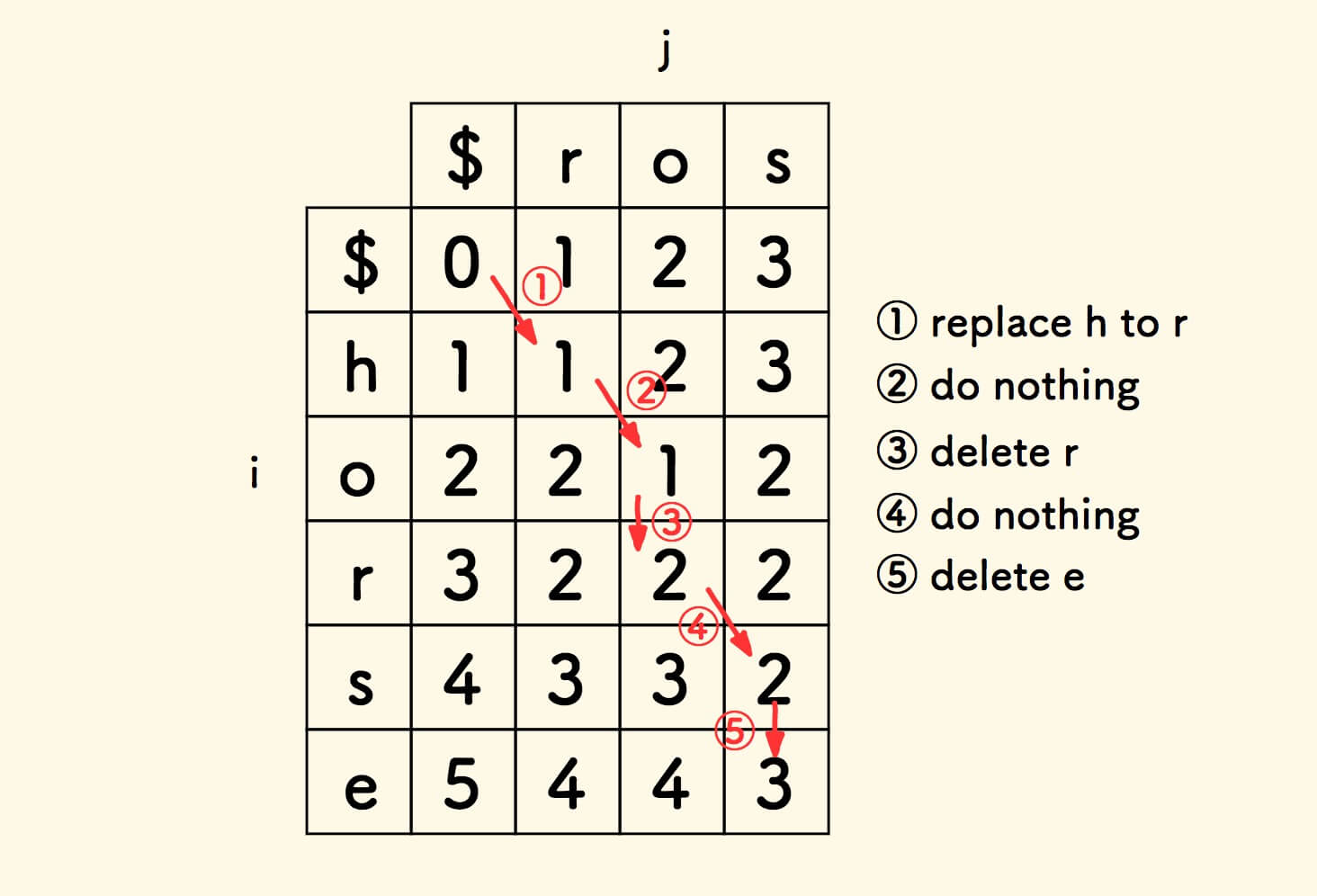
最短编辑距离 - C 语言实现
#define MIN(x, y) ((x) < (y) ? (x) : (y))
// 返回字符串 a 编辑为字符串 b 的最小编辑步数。
int MinEditDistance(char *a, char *b) {
int m = strlen(a);
int n = strlen(b);
// 为处理边界方便,假设对字符串头部插入 $ 符号
// horse => $horse
// ros => $ros
// 如此一来,dp[i][j] 的意思是,a[..i-1] 编辑到 b[..j-1] 的最小编辑距离
int dp[m + 1][n + 1];
// horse => $ 的编辑距离显然是:删除 5 个字符
// 即 dp[i][0] => i
for (int i = 0; i < m + 1; i++) dp[i][0] = i;
// $ => ros 的编辑距离显然是:插入三个字符
// 即 dp[0][j] = j
for (int j = 0; j < n + 1; j++) dp[0][j] = j;
for (int i = 1; i < m + 1; i++) {
for (int j = 1; j < n + 1; j++) {
// 在 a[..i-1] => b[..j-2] 的基础上,再插入一个字符 b[j-1] 得到
// 即表格左方值 + 1 得到
int left = dp[i][j - 1] + 1;
// 在 a[..i-2] => b[..j-1] 的基础上,再删除一个字符 a[i-1] 得到
// 即表格上方值 + 1 得到
int up = dp[i - 1][j] + 1;
// 考虑左上方的数字
int left_up;
if (a[i - 1] == b[j - 1]) {
// 末尾两个字符相等
// a[..i-1] => b[..j-1] 等价于 a[..i-2] => b[..j-2]
left_up = dp[i - 1][j - 1];
} else {
// 否则,需要替换一次
left_up = dp[i - 1][j - 1] + 1;
}
// 取三种方案的最小值
dp[i][j] = MIN(MIN(left, up), left_up);
}
}
return dp[m][n];
}
打印所有最短编辑方式 ¶
左上角出发,每一条通往右下角的路径,就是一种编辑方式。
最短编辑方式可能并不止一种,比如单词 simple 编辑为 example 就有两种最短编辑方式。
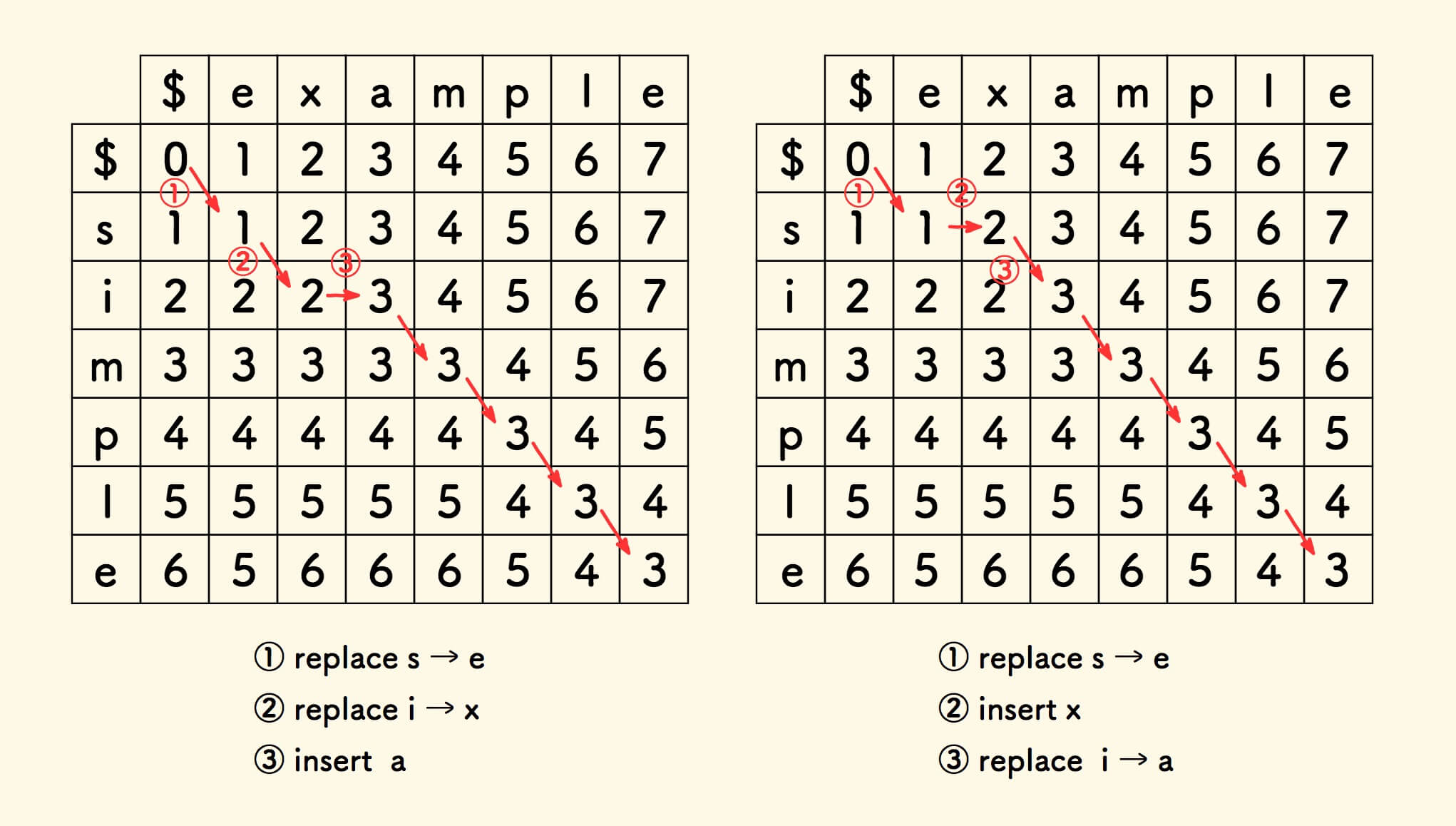
在规划过程中,记住每一个方格的来源,就可以从右下角反向还原整条路径 。
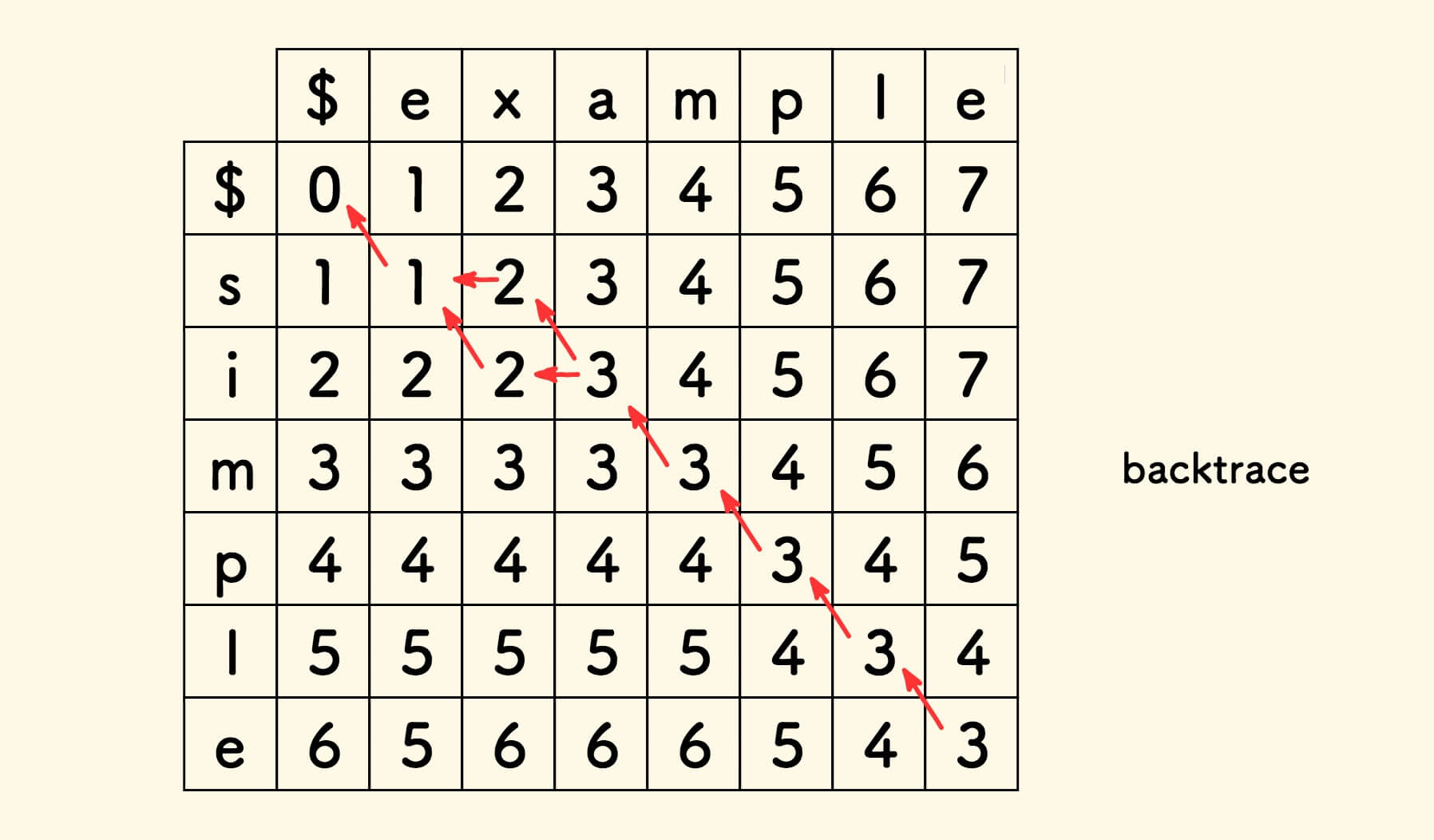
构造一个路径数组, path[i][j] 记录当前表格的来源:
0000表示当前表格是初始化而来。0001表示从左方推导而来,即插入字符。0010表示从上方推导而来,即删除字符。0100表示从左上方加一而来,即替换字符。1000表示从左上方拷贝而来,即无操作。
因为一个方格的数值来源可能有多种, 所以这里采用二进制互不重叠的枚举值。
一个方格的来源是多个此类枚举值的布尔或值 。
动态规划过程中,同步填充 path 数组。
最短编辑距离 - DP 过程同步记录路径数组 - C 语言实现
#define FROM_INIT 0
#define FROM_LEFT 1 // 0b0001
#define FROM_UP 2 // 0b0010
#define FROM_LEFT_UP_REPLACE 4 // 0b0100
#define FROM_LEFT_UP_COPY 8 // 0b1000
int DP(char *a, char *b, int m, int n, int dp[m + 1][n + 1],
int path[m + 1][n + 1]) {
for (int i = 0; i < m + 1; i++) {
dp[i][0] = i;
path[i][0] = FROM_INIT;
}
for (int j = 0; j < n + 1; j++) {
dp[0][j] = j;
path[0][j] = FROM_INIT;
}
for (int i = 1; i < m + 1; i++) {
for (int j = 1; j < n + 1; j++) {
path[i][j] = FROM_INIT; // 初始化 path[i][j]
int left = dp[i][j - 1] + 1;
int up = dp[i - 1][j] + 1;
int left_up;
bool replace = false;
if (a[i - 1] == b[j - 1]) {
left_up = dp[i - 1][j - 1];
replace = false;
} else {
left_up = dp[i - 1][j - 1] + 1;
replace = true;
}
dp[i][j] = MIN(MIN(left, up), left_up);
if (dp[i][j] == left) path[i][j] |= FROM_LEFT;
if (dp[i][j] == up) path[i][j] |= FROM_UP;
if (dp[i][j] == left_up) {
if (replace)
path[i][j] |= FROM_LEFT_UP_REPLACE;
else
path[i][j] |= FROM_LEFT_UP_COPY;
}
}
}
return dp[m][n];
}
要找的路径,不止一条,所以,要进行深度优先遍历。
总之, 按方格来源,自右下角深度优先遍历,不断收集路径上的编辑操作, 直到左上角 。
综合 前面的分析 ,具体的遍历办法是, 考虑当前方格 dp[i][j]:
如果可以从左边方格推导而来
对应编辑操作是,插入字符
b[j-1]。然后向左继续深度遍历。
如果可以从上边方格推导而来
对应编辑操作是,删除字符
a[i-1]。然后向上继续深度遍历。
如果可以从左上方推导而来
如果是拷贝而来,则不收集。
否则,收集,对应编辑操作是,替换字符
a[i-1]到b[j-1]。然后向左上方格继续深度遍历。
直到左上角
dp[1][1]处,进行打印。由于是反向收集,所以要反向打印。
最短编辑距离 - 递归 DFS 打印所有最短编辑方式 - C 语言实现
// 一种编辑操作
typedef struct {
int flag; // 操作方式 1 插入 2 删除 3 替换
char ch1; // 操作的字符 1
char ch2; // 操作的字符 2, 针对替换操作, ch1 替换为 ch2
} Operation;
void PrintOperation(Operation *op) {
if (op == NULL) return;
if (op->flag == 0) return;
if (op->flag == 1) printf("插入 %c\n", op->ch1);
if (op->flag == 2) printf("删除 %c\n", op->ch1);
if (op->flag == 3) printf("替换 %c => %c\n", op->ch1, op->ch2);
}
// DFS 深度优先遍历 path 数组
// 输入的 i,j 是当前的方格位置
// depth 是当前递归深度,初始 depth = 1
// ops 是当前递归深度上的路径,即记录的编辑步骤序列
void DFS(char *a, char *b, int m, int n, int path[m + 1][n + 1], int i, int j,
int depth, Operation ops[depth]) {
Operation *op = &ops[depth - 1]; // 设置当前格的编辑方式
if (path[i][j] & FROM_LEFT) {
// 左边方格,插入一个字符 b[j-1] 而来
op->flag = 1;
op->ch1 = b[j - 1];
// 向左 DFS
DFS(a, b, m, n, path, i, j - 1, depth + 1, ops);
}
if (path[i][j] & FROM_UP) {
// 上面方格,删除一个字符 a[i-1] 而来
op->flag = 2;
op->ch1 = a[i - 1];
// 向上 DFS
DFS(a, b, m, n, path, i - 1, j, depth + 1, ops);
}
if (path[i][j] & FROM_LEFT_UP_COPY || path[i][j] & FROM_LEFT_UP_REPLACE) {
if (path[i][j] & FROM_LEFT_UP_REPLACE) {
// 左上方格,替换 a[i-1] 到 b[j-1] 而来
op->flag = 3;
op->ch1 = a[i - 1];
op->ch2 = b[j - 1];
} else {
// 拷贝而来,无需记录
// 置 0 表示忽略
op->flag = 0;
}
// 向左上 DFS
DFS(a, b, m, n, path, i - 1, j - 1, depth + 1, ops);
}
if (i == 1 && j == 1) {
// 反向打印 ops 序列
for (int k = depth - 1; k >= 0; k--) PrintOperation(&ops[k]);
// 打印结束
printf("已结束一种编辑方式\n");
return;
}
}
// 打印把字符串 a 编辑为 b 的所有最短编辑方式
void PrintMinEditSteps(char *a, char *b) {
int m = strlen(a);
int n = strlen(b);
// DP 数组
int dp[m + 1][n + 1];
// 路径数组
int path[m + 1][n + 1];
// 规划过程,返回最少步数 k
DP(a, b, m, n, dp, path);
// 记录一种最短编辑的操作序列
Operation ops[m + n];
// 记录当且递归深度
int depth = 1;
// 递归打印所有最短编辑的操作方式
printf("编辑 %s 到 %s \n", a, b);
DFS(a, b, m, n, path, m, n, depth, ops);
printf("\n");
}
上面的代码实现的一个示例输出是:
编辑 simple 到 example
替换 s => e
替换 i => x
插入 a
已结束一种编辑方式
替换 s => e
插入 x
替换 i => a
已结束一种编辑方式
结语 ¶
最短编辑距离问题和 最长公共子序列 问题高度相似,是一个经典的动态规划问题。
(完)
相关阅读: 最长公共子串和最长公共子序列
本文原始链接地址: https://writings.sh/post/algorithm-minimum-edit-distance







