二分其实并不简单,可以说 细节是魔鬼。
本文是对二分法的一点总结,内容包括:
二段性的理解 ¶
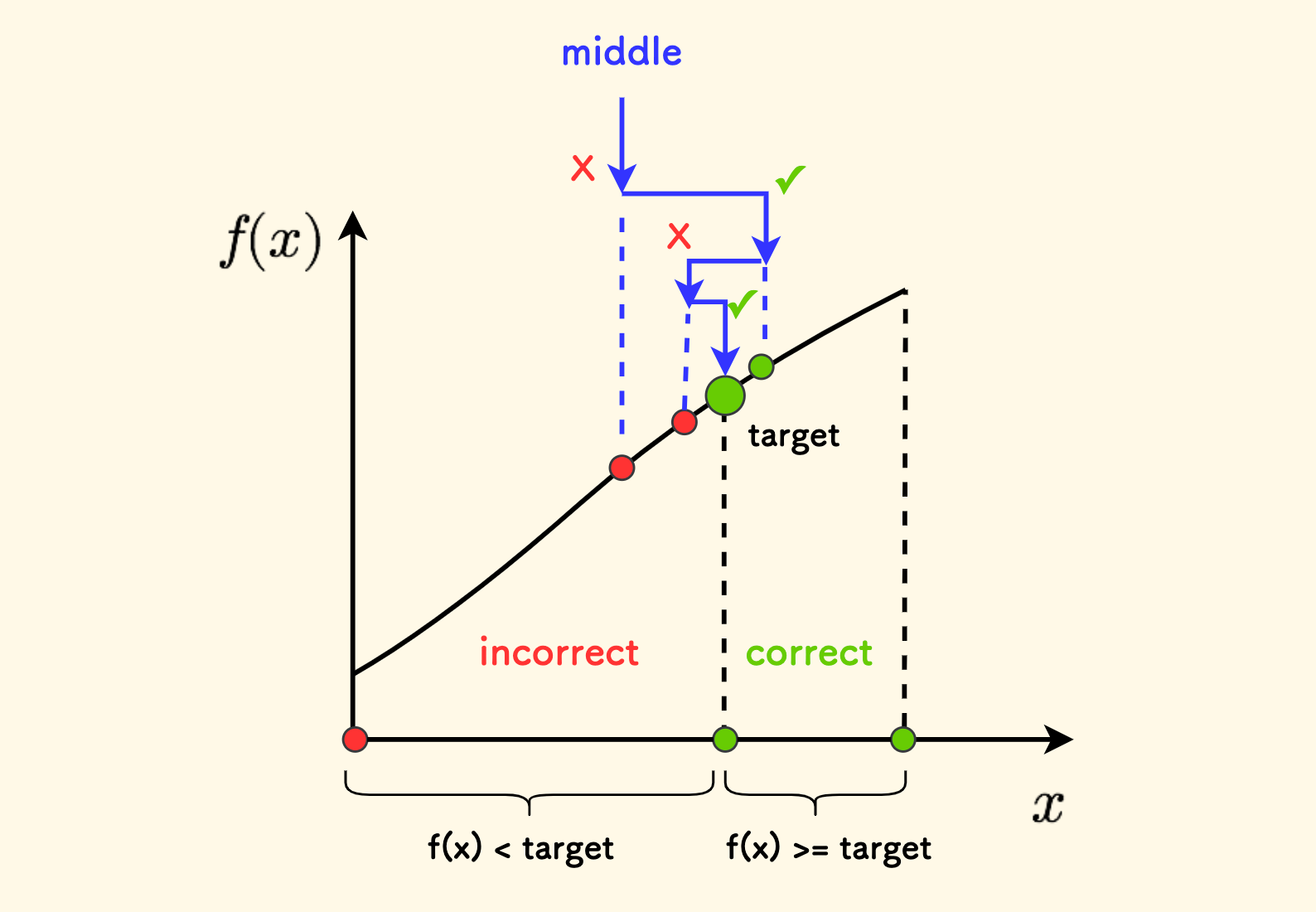
简而言之,对于某个性质,当前的可行区间上,一半满足、一半不满足,就可以二分找分界点。
比方说, 对于一个函数 f(x),参数 x 的域可以分成两段,对一段来说 f(x) 满足一个性质, 另一段来说不满足这个性质,那么就可以用二分法来求解这两段的边界。
单调性是二段性的一种特例:在一个非递减函数中查找目标的左界, 可以用 f(x)>=target 这个条件,把参数域分成两段, 左边的不满足、右边的满足,然后应用二分法。
二分法不要求单调性,更不要求严格的单调性。 本质的理解上,只要有二段性就可以用二分。
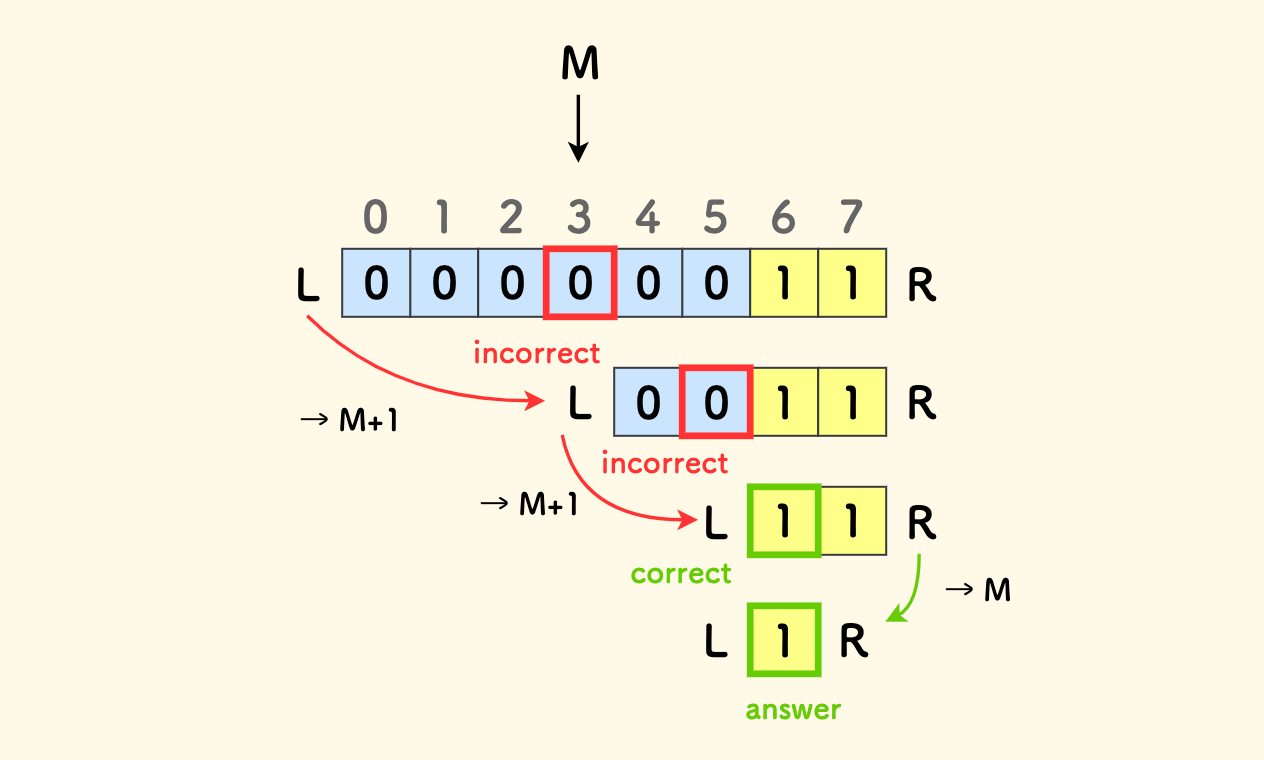
举个例子,假设一个数组的左边全部是 0,右边全部是 1,如何求第一个 1 出现的位置? 也就是找 1 的左界。
这个数组是满足二段性的一个最简单的例子。 下图演示了其求解的二分过程,其规则如下:
- 每次测试中间位置
M处的元素,其中M = (L+R)>>1向下取整。 - 如果测试不正确,则收缩左界:
L ← M+1,可以跨过M,因为它不属于可行解。 - 如果测试正确,则收缩右界:
R ← M,注意M仍在可行解范围内。 - 不断收缩可行解范围,直到
L==R为止,即得到左边界。
从 01 数组中找到第一个 1 的位置 C++ 代码
int FindFirst1(const vector<int>& f) {
int l = 0;
int r = f.size() - 1;
while (l < r) {
int m = (l + r) >> 1;
if (f[m] == 1)
r = m;
else
l = m + 1;
}
return l;
}
大多数时候,可以通过构造一个函数,在整个参数域上表现出二段性。 但是,有时二段性在搜索过程中才呈现。
也就是说,二段性并不要求在整个参数域上划分为两部分。 只要在每一时刻,当前的可行区间可以针对某个性质划分二段, 就可以应用二分法。后面有个例子问题 寻找峰值 会进一步说明这一点。
两套代码模板 ¶
二分代码边界和细节处理很容易出错, 熟悉一种代码模板不失为一种实际的策略。
下面是来自 《算法竞赛进阶指南》 这本书上的两套经典二分代码模板。 假设 f(x) 是非递减函数,初始的可行解是闭区间 [l, r]:
找
f(x) >= target的可行解的左界,即target或其后继:二分中点向下取整,将区间划分为
[l, m]和[m+1, r]两段。int LeftBound(int l, int r, int target) { while (l < r) { int m = (l + r) >> 1; if (f(m) >= target) r = m; else l = m + 1; } return l; }找
f(x) <= target的可行解的右界,即target或其前驱:二分中点向上取整,将区间划分为
[l, m-1]和[m, r]两段。int RightBound(int l, int r, int target) { while (l < r) { int m = (l + r + 1) >> 1; if (f(m) <= target) l = m; else r = m - 1; } return l; }
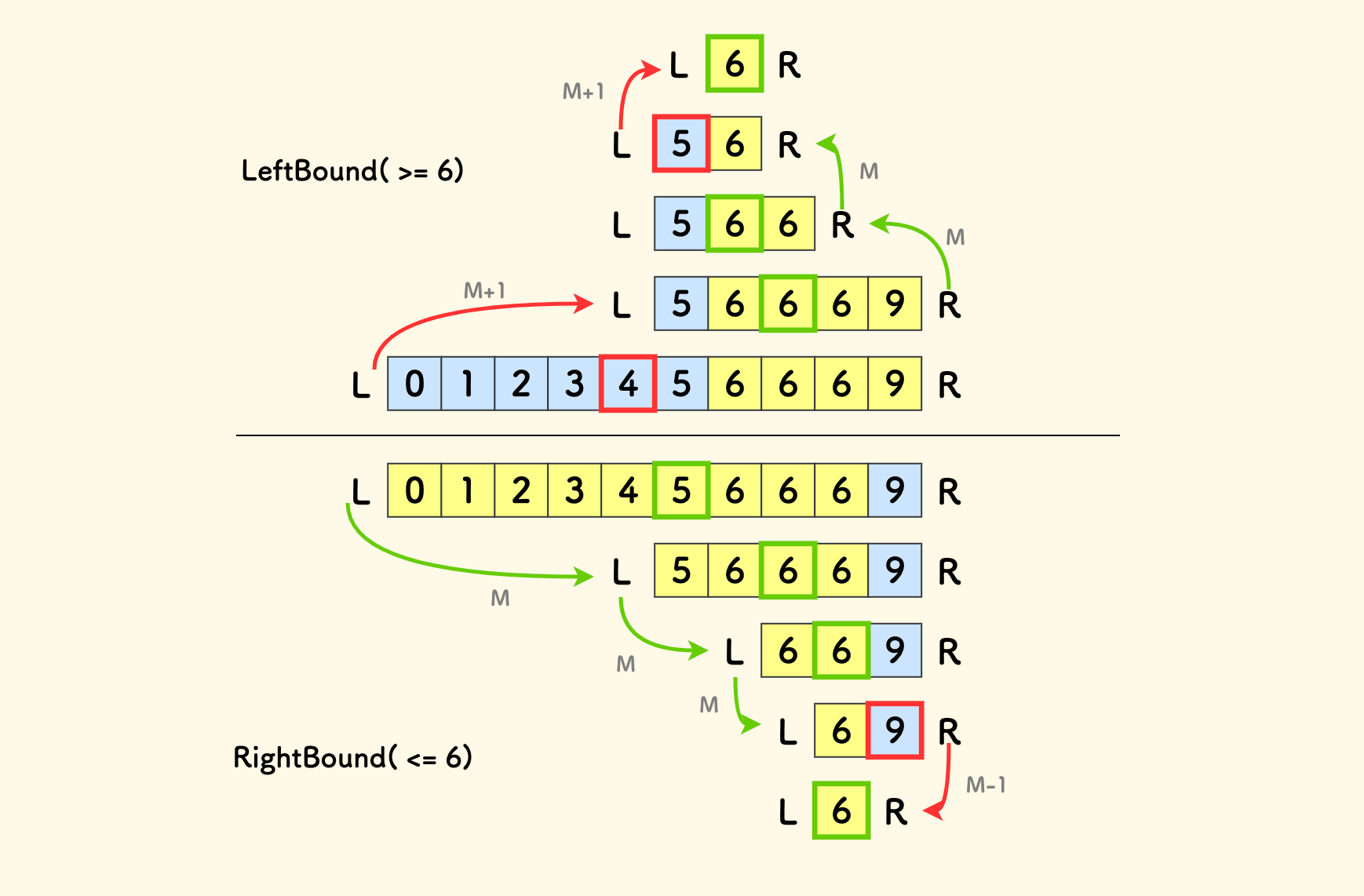
两种模板下,边界相遇点 l 即是最终答案。
下面的图示中,上方的是找左界的过程、下方的是找右界的过程。其中,绿色表示测试正确、红色表示测试错误。 可行区间不断缩小,直到 L 和 R 相遇。
如果取函数 check(x)={ f(x)>=target } 的话,求左界的代码就变成下面的样子。 意思是,找满足判定函数的左界。
while (l < r) {
int m = (l + r) >> 1;
if (check(x)) r = m;
else l = m + 1;
}
类似的,如果取 check(x)={ f(x)<=target },可以用第二个模板来找满足判定函数的右界。
while (l < r) {
int m = (l + r + 1) >> 1;
if (check(x)) l = m;
else r = m - 1;
}
这样就得到了两个更广义的二分模板。 找左界、还是右界,取决于判定函数的设计含义。
理解的关键是,分析每个条件下、可行区间的是哪个,以及中点归属哪个区间。
这两套模板很经典、实用,用顺手了后基本不再怕二分细节了。
很多二分问题,都可以转化为 求左界 或者 求右界 的问题。
接下来,是此模板在几个经典二分问题上的应用:
经典二分找目标 ¶
经典的二分查找确定目标的问题,可以转化为:先求左界,再验证左界的问题。
经典的二分查找可以先转化为找左界模板 - C++ 代码
int ClassicBinarySearch(const vector<int>& f, int target) {
// 先找 >= target 的左界
int l = 0, r = f.size() - 1;
while (l < r) {
int m = (l + r) >> 1;
if (f[m] >= target)
r = m;
else
l = m + 1;
}
// 再具体判断是否真的等于 target
if (f[l] == target) return l;
return -1; // 找不到
}
降序数组二分 ¶
对于降序数组,取巧的办法是:转化为升序。
比如,求非递增函数 f(x) 的不大于目标值的左界:
求非递增数组的不大于目标值的左界 - C++ 代码
int DescendingLeftBound(const vector<int>& f, int target) {
// 求 f(m) <= target 的左界
// 等价于求 INF - f(m) >= INF - target 的左界
auto g = [&](int m) { return INT_MAX - f[m]; };
// g 是升序的
int l = 0, r = f.size() - 1;
while (l < r) {
int m = (l + r) >> 1;
if (g(m) >= INT_MAX - target)
r = m;
else
l = m + 1;
}
return l;
}
但是,如果要在降序数组中求 >=target 的左界呢?就不大好转化了。
不过,关键点仍然是,分析可行区间选取哪个的问题。
当选取中点 m 后:
- 如果
f(m) < target,说明取的 m 太大了,应该收缩右边界,而且中点不是可行解。所以r=m-1。 - 这样,始终划分的方式是
[l,m]和[m-1,r]两个区间,选取第二个模板即可。
// 非递增函数 f(x) 上找 >= target 的左界
while (l < r) {
int m = (l + r + 1) >> 1;
if (f(m) < target) r = m - 1;
else l = m;
}
return l;
例子:求平方根 ¶
给你一个非负整数 x ,计算并返回 x 的 算术平方根 。 由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。
-- 来自 leetcode 69. x 的平方根
首先,设计判定函数,相当于找 m^2 <= x 的右界,为了避免平方溢出,也等价于 m - x/m <= 0 的右界。
求 x 的平方根 - C++ 代码
class Solution {
public:
int mySqrt(int x) {
// 要找 m^2 <= x 的右界
// 等价于找 m - x/m <= 0 的右界
auto f = [&](int m) { return m - x / m; };
int l = 0, r = x;
while (l < r) {
auto m = ((long)l + (long)r + 1) >> 1;
if (f(m) <= 0)
l = m;
else
r = m - 1;
}
return l;
}
};
例子:值等于索引的元素 ¶
给定一个有序整数数组 A,其中元素各不相同,要求确认是否在其中存在一个索引 i 可以使得 A[i] = i 。
-- 来自 《算法概论》 习题 2.17
由于数组中元素各不相同,又都是整数,可以知道:
- 一旦存在某个元素满足
A[i] > i,那么之后的元素必然也满足此条件。 - 一旦存在某个元素满足
A[i] < i,那么之前的元素必然也满足此条件。
构造函数 f(i) = A[i]-i, 它存在二段性:某一刻之后,f(i)>=0 一旦成立,就会一直成立。
问题转化为找 f(i)>=0 的左界,找到后判断下是否 f(l)==l 就可以了。
A[i] = i 是否存在 - C++ 代码
bool CheckAiEqualsI(vector<int>& A) {
auto f = [&](int i) { return A[i] - i; };
int l = 0, r = A.size() - 1;
while (l < r) {
int m = (l + r) >> 1;
if (f(m) >= 0)
r = m;
else
l = m + 1;
}
return A[l] == l;
}
如果想进一步求满足 A[i]=i 的条件的元素的个数呢?
据前面的分析,继续分析二段性:
f(i) >= 1在某一刻成立后,对于更大的i,就会一直成立f(i) <= -1在某一刻成立后,对于更小的i,就会一直成立
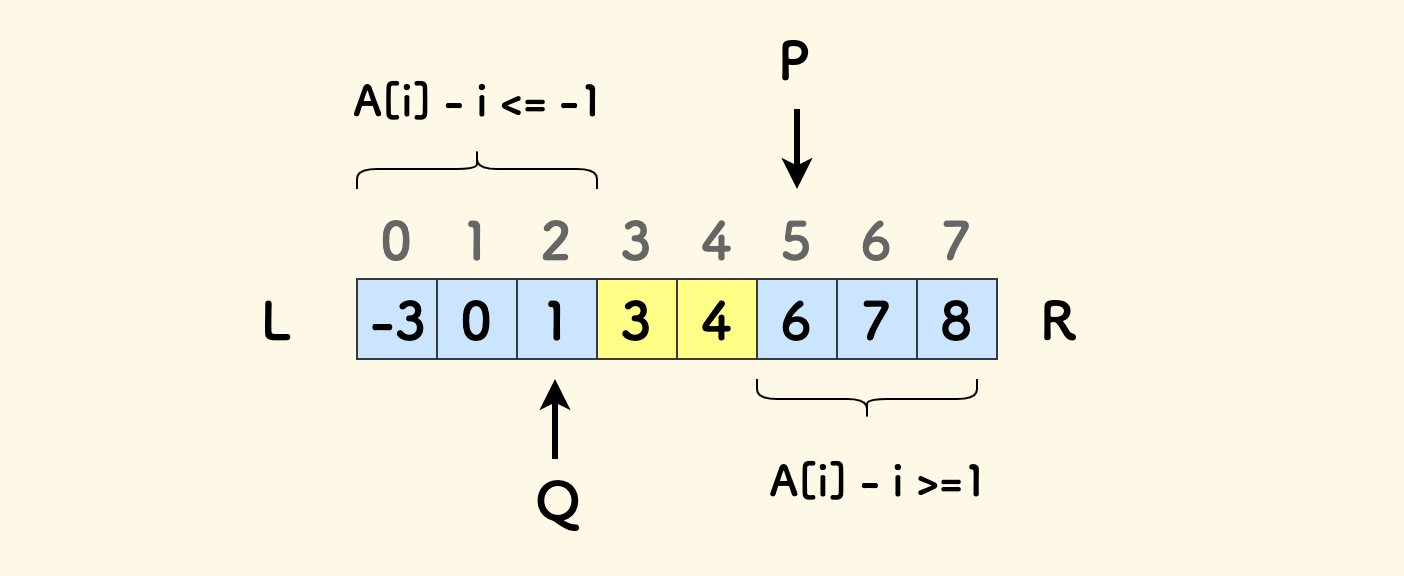
所以,问题转化为:
- 找
f(i) >= 1的左界P和f(i) <= -1的右界Q。 - 答案就是
P和Q之间的元素个数。
A[i] = i 元素的计数 - C++ 代码
int CheckAiEqualsILength(vector<int>& A) {
auto f = [&](int i) { return A[i] - i; };
// 找 f(i) >= 1 的左界
auto find_p = [&]() {
int l = 0, r = A.size() - 1;
while (l < r) {
int m = (l + r) >> 1;
if (f(m) >= 1)
r = m;
else
l = m + 1;
}
return l;
};
// 找 f(i) <= -1 的左界
auto find_q = [&]() {
int l = 0, r = A.size() - 1;
while (l < r) {
int m = (l + r + 1) >> 1;
if (f(m) <= -1)
l = m;
else
r = m - 1;
}
return l;
};
return find_p() - find_q() - 1;
}
例子:寻找峰值 ¶
给你一个长度为
N的整数数组a,找到其中一个峰值元素的位置。 已知数组中元素大小各不相同。 峰值元素严格比相邻元素都大。返回任何一个峰值的位置即可。-- 来自 leetcode 162
考虑当前的可行区间内的一个位置 m:
- 如果
a[m] < a[m+1],也就是在上坡阶段,那么右侧[m+1, r]必有峰,左侧不一定。 - 如果
a[m-1] > a[m],也就是在下坡阶段,那么左侧[l, m-1]必有峰,右侧不一定。
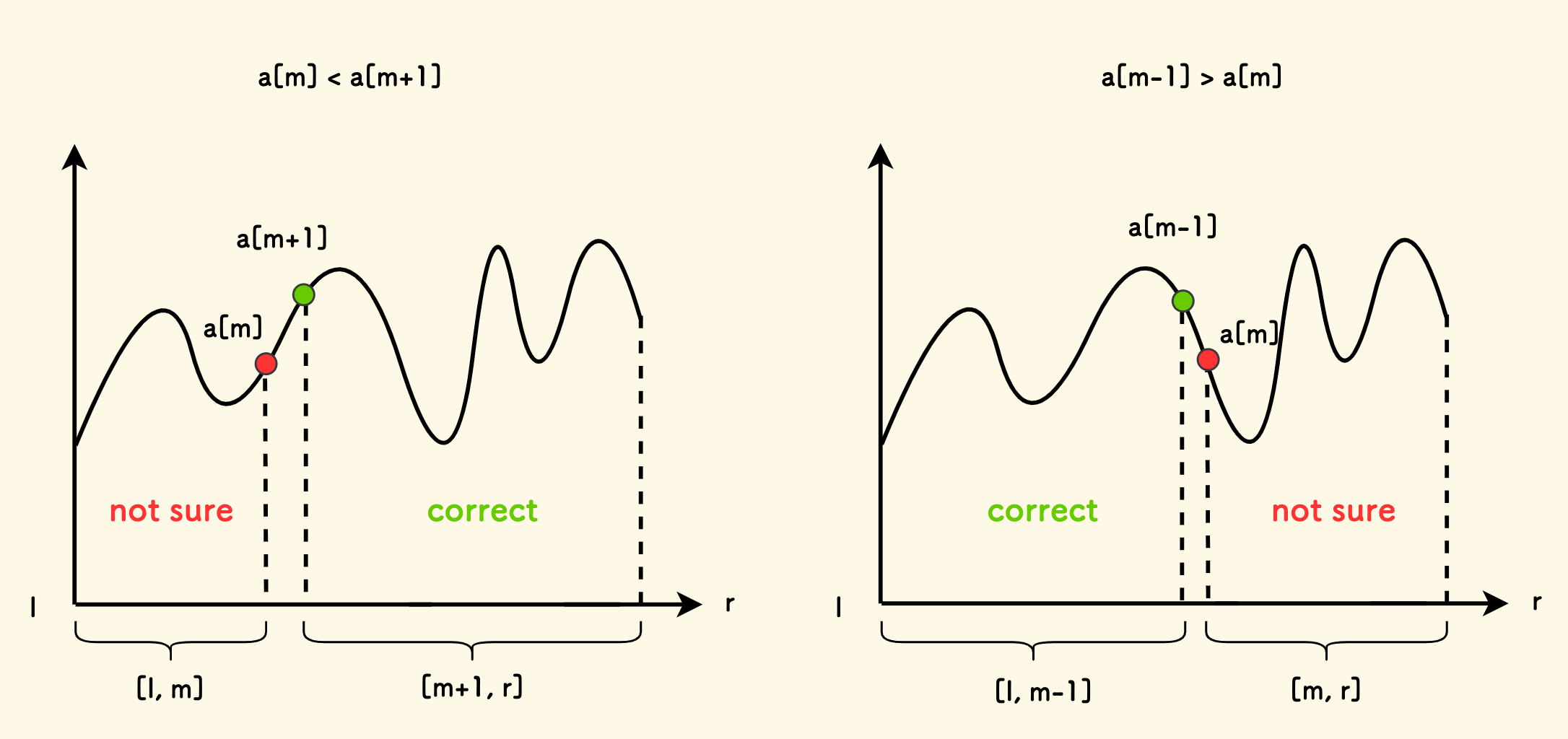
其实不套模板,更容易写出代码:
寻找峰值 - C++ 代码
class Solution {
public:
int findPeakElement(vector<int>& a) {
int l = 0;
int r = a.size() - 1;
while (l < r) {
int m = (l + r) >> 1;
if (m < a.size() - 1 && a[m] < a[m + 1])
// 排除左边, 右侧必有峰
l = m + 1;
else
r = m;
}
return l;
}
};
如果硬是要套模板的话,理解起来反而费劲一点。不过,我们在这里要进一步理解其动态二段性:
check(x) = { !(a[m] < a[m+1]) } // 设计成这样,找其成立的左界
check(x) = { !(a[m-1] > a[m]) } // 或者设计成这样,找其成立的右界
在 [0,N] 整个区间上,判定函数并没有静态的二段性。上坡、下坡的两种情况下,判定函数虽然只有两种返回值, 但划分了好几段,而非各自连续的两段。 在检测点 m 确定后,当前可行区间才可以划分两段,一段一定可行、另一段不确定。
这个问题的特点在于:二段性是动态呈现的。
只要当前的检测点,可以就某个性质将当前可行区间划分两段,就具有二段性。 而不必把整个参数域静态地二分,虽然这种情况占大多数。
二分答案判定 ¶
除了常见的查找元素的场景,二分法的一个重要应用是 枚举答案。
尤其是值域上的二分枚举,给人一种「快而暴力」的感觉。
注意的是,要先确定存在二段性,才可以用二分枚举答案。
大致套路是,设计判定函数,确定答案的上下界,然后二分答案。
// 判定函数
bool check(int m) { ... }
// 确定答案的上下界 l 和 r
int l, r;
// 判定答案,找可行边界
while (l < r) {
int m = (l + r) >> 1;
if (check(m)) r = m;
else l = m + 1;
}
return l;
在 最长回文子串问题 中, 我曾经写过一个 二分枚举的思路。
另外,许多 TopK 系列的问题(比如 有序矩阵找第 k 小的元素、下面的 两个有序数组的 TopK 问题 ) 都可以用 统计计数 + 二分答案 的思路来解决,参考文章 TopK 系列算法问题的总结。
例子:分割数组问题 ¶
给定一个大小为
n的非负整数数组 nums 和一个整数 k ,你需要将这个数组分成 k 个非空的连续子数组。 设计一个算法使得这 k 个子数组各自和的最大值最小。-- 来自 leetcode 410
比如说,数组 [7,2,5,10,8] ,输入 k=2 的情况,最好的分割方式是 [7,2,5] 和 [10,8],此时子数组的和分别是 14 和 18, 最大值是 18,在所有分割情况中最小。
问题可以转化为:
对于一个数字
x,如果满足「分割后各个数组的和」都不超过x的、最小分割数记为cnt,求cnt <= k的最小的x。
所以,先求一个子问题:
给定一个数字
x,满足分割后各个数组的和都不超过x的最小分割数是多少?
只需要不断累加,超过阈值后就计数一次分割,容易写出这个子问题的求解代码:
求满足子数组和不超过给定值的最小分割数 C++
// 给定的 x, 返回分割后各个数组的和都 <= x 所需的最小分割数 k
// 输入的 x 要保证至少为 max(nums)
int count(const vector<int>& nums, int x) {
int c = 1;
int sum = 0;
for (auto num : nums) {
if (sum + num > x) {
sum = 0;
c++;
}
sum += num;
}
return c;
}
对于这个 count 函数,输入的 x 越大,返回的符合要求的分割数越小,也就是非递增的。
将说明的是,对于判定条件 count(x) <= k 具有二段性。
如果存在某个 x0 使得恰好 count(x0) == k ,而且 x0 是其中最小的那个:
- 那么所有大于
x0的数字,相当于和放宽了,所需要的最小分割数肯定不超过k。 - 对于所有小于
x0的数字,相当于和更小了,而x0是使得分割数恰好为k的最小的那个,那么此时所需要的最小分割数肯定超过k。
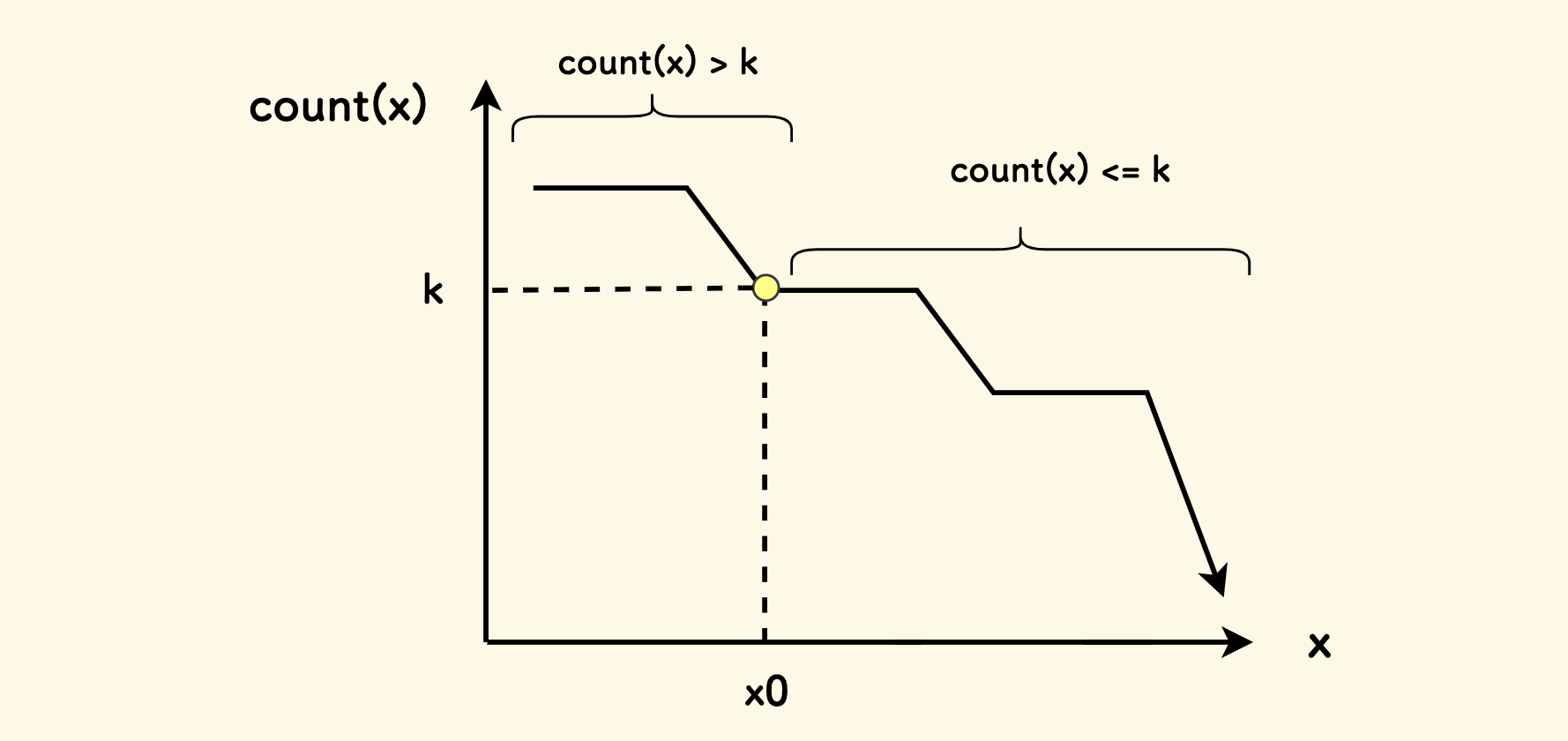
也就是说,count(x) <= k 具有二段性。
因为这个计数函数是降序的,可以构造一个反向的升序函数,套用模板。
auto check = [&](const vector<int>& nums, int x) {
return n - count(nums, x);
};
要找符合条件的最小的和,相当于找符合 count(x) <= k 的左界,也就是找 check(x) >= n-k 的左界。
容易知道,可行解的最大值,是所有元素的和。 可行解的最小值,是数组中的最大值,不然无法分割。这两个作为初始的可行区间。
然后套用找左界的二分模板,枚举答案。时间复杂度是 nlog(Sum - Max)。
分割数组的最大值 - 二分答案 C++
// 二分答案找 满足 count(x) <= k 的左界
int splitArray(vector<int>& nums, int k) {
int n = nums.size();
int r = accumulate(nums.begin(), nums.end(), 0);
int l = *max_element(nums.begin(), nums.end());
// 注意 count 是降序的, 做一个 check 函数来转换为升序
auto check = [&](const vector<int>& nums, int x) {
return n - count(nums, x);
};
// 二分枚举找满足 check(x) >= n - k 的 x 的左界
while (l < r) {
int m = (l + r) >> 1;
if (check(nums, m) >= n - k)
r = m;
else
l = m + 1;
}
return l;
}
例子:寻找两个正序数组的中位数 ¶
这是个很经典的算法问题:
给定两个大小分别为 n 和 m 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数。
-- 来自 leetcode 4
比如说,数组 [1,2,3] 和 [3,6] 的中位数是 3。
再比如说,数组 [1,3] 和 [2,4] 的中位数是 2.5。
这个问题可以推广到「求两个有序数组的第 K 小的元素」,中位数是其一个特例。
经典的做法很巧妙,这里简单讲一下。然后再讲暴力的二分枚举做法。
经典做法
首先,定义一种叫做「分割」的概念。 在数组的两个元素之间,插入一个分割线,把数组分成两段。 这个分割点的位置,以它后一个元素的下标来定义。
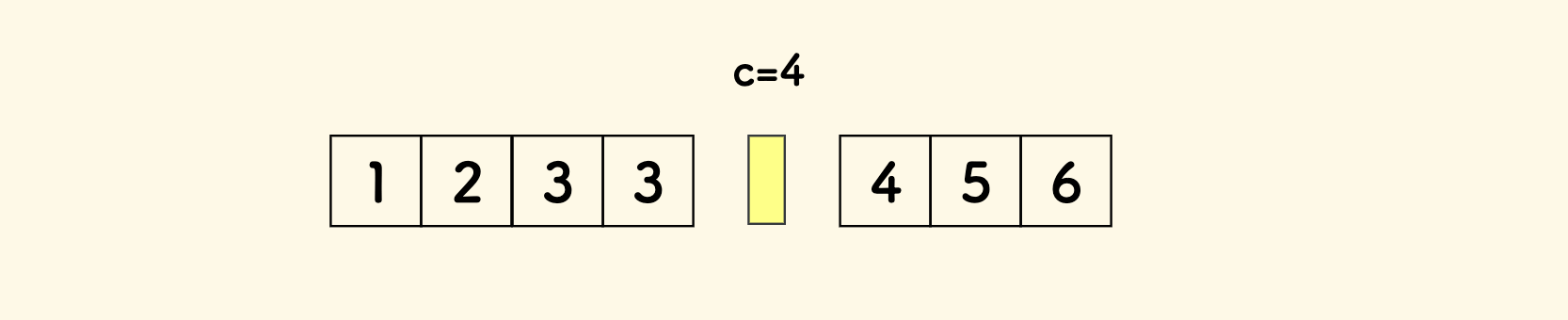
假如第一个数组 nums1 的分割点在 c1 处,它前面有 c1 个元素, 因为总共要找第 k 小, 那么第二个数组的上的分割点就在 c2=k-c1 处。
假设数组 nums1 中分割点左右邻近的元素分别是 L1 和 R1, 数组 nums2 中分割点左右邻近的分别是 L2 和 R2。
两个分割点左边的所有元素,要想成为整体的前 k 个小的话, 左边两段的元素整体上一定要不大于右边两段的元素,也就是说, 必须满足:L1 <= R2 且 L2 <= R1。
一旦这两个条件同时成立,又因为 分割点左边的必然都满足不大于 L,右边的一定满足不小于 R, 所以两个分割点处就是前 k 小的位置。
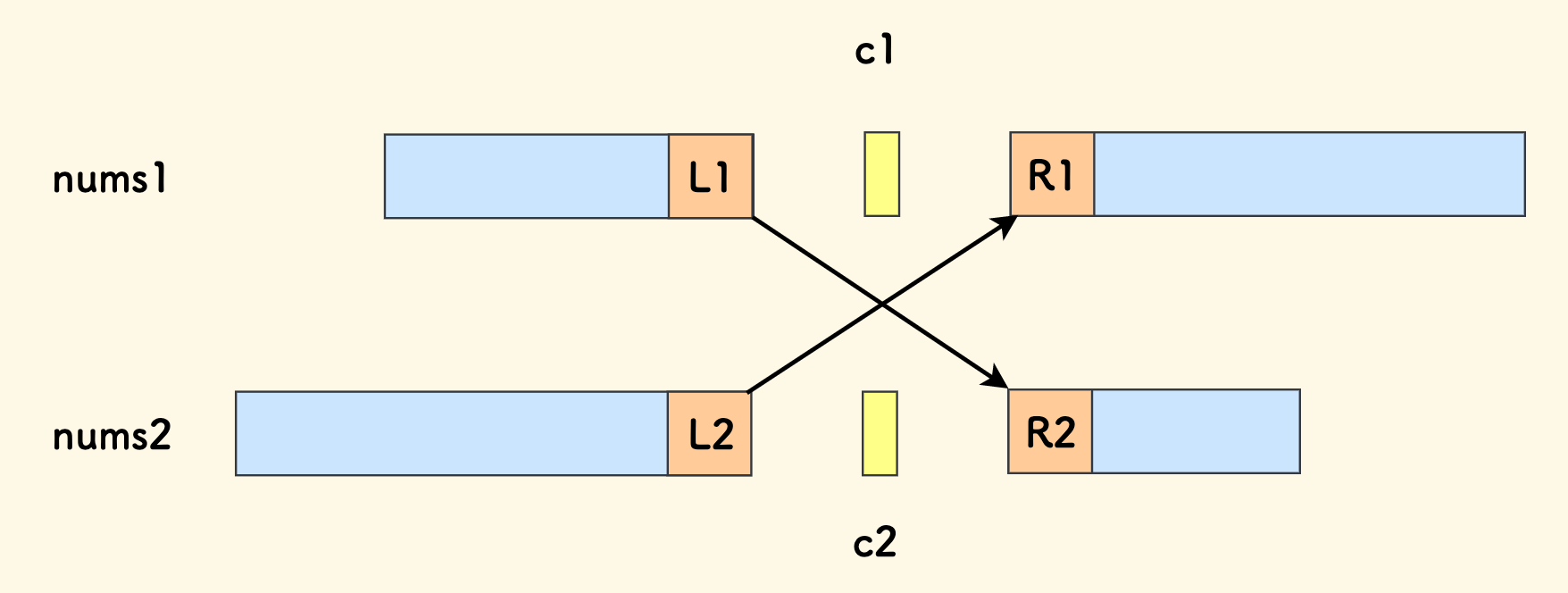
如果不满足呢,就需要调整分割位置,我们以调整 c1 为主:
如果
L1 > R2的话,说明分割点c1太靠右了,则向左移动c1。而且,右侧的位置都不必再考虑, 因为向右滑动
c1分割点的同时,c2分割点会向左滑动,L1进一步增大,而R2进一步缩小,肯定会进一步导致L1 > R2的。所以,可以排除右侧所有的分割点,只需要向左考虑,可行区间减半。

如果
L2 > R1的话,说明分割点c2太靠右了,也就是说c1要向右移动。同样的道理,可以直接排除所有左侧的
c1分割点。
最后,回到中位数的问题上来,我们还要处理总数的奇偶问题。
- 如果总数是奇数,中位数落在最中间的元素上,也就是取
L1和L2之中最大的那个元素。 - 如果总数是偶数,则需要求最中间两个元素的平均值,即
(max(L1, L2) + min(R1, R2))/2.0。
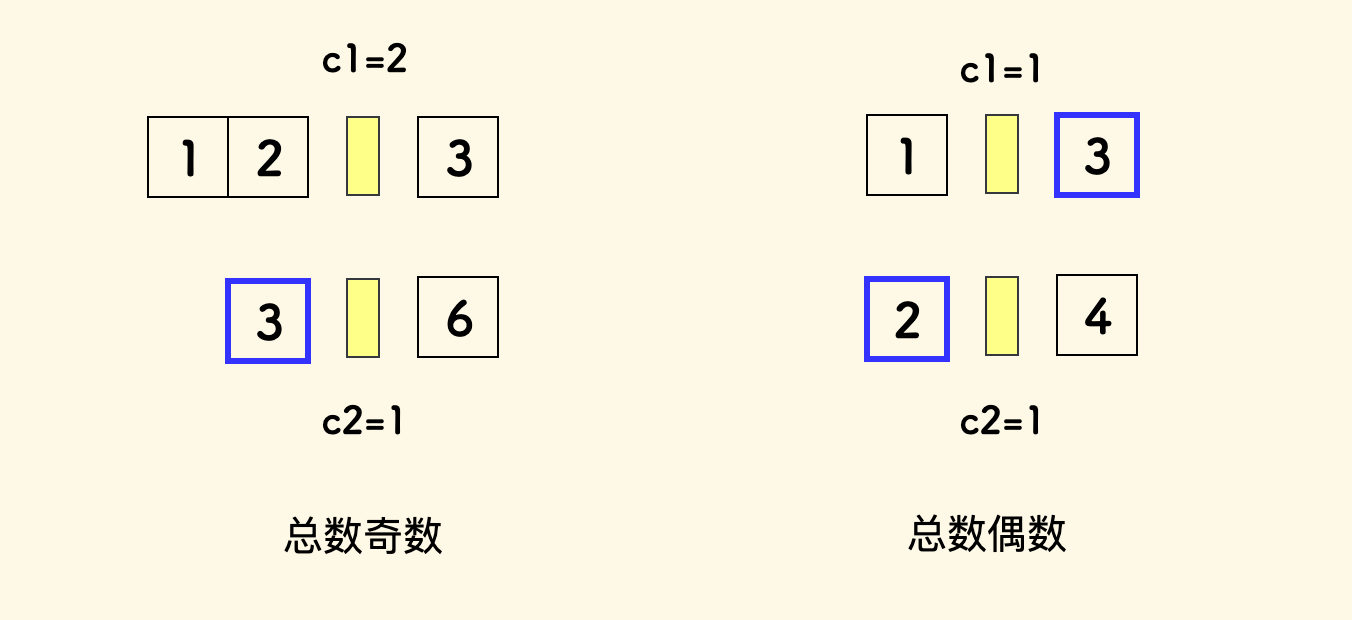
分析下来,可以用二分,伪代码实现如下:
// c1 的分割点的左界 和 右界
int l = 0, r = n;
// 二分
while (l <= r) {
int c1 = (l + r) >> 1;
int c2 = k - c1;
int L1 = nums1[c1-1], R1 = nums1[c1];
int L2 = nums2[c2-1], R2 = nums2[c2];
if (L1 > R2) r = c1 - 1;
else if (L2 > R1) l = c1 + 1;
else break;
}
if ((n + m) % 2) return max(L1, L2);
return (max(L1, L2) + min(R1, R2)) / 2.0;
实际的实现中,还要考虑下边界处理等细节问题,详细代码见下方:
寻找两个有序数组的中位数 - 经典二分做法 - C++ 代码实现 - github
可以知道,时间复杂度是 log(min(m,n))。
这个做法非常巧妙,但是不得不说挺难想的。
下面将看到不那么巧妙,但是更简单暴力的二分枚举做法。
二分枚举做法
二分枚举的做法,仍然是先取一个子问题:
给定一个数字
x,计算两个数组中不超过x的元素的个数。
这个问题是很好做的,因为两个数组都是有序的。 对每个数组而言,只需要找到 <=x 的左界,即可知道不超过 x 的元素数量。
下面的 C++ 实现中,直接采用了 STL 中的 upper_bound 函数,它返回严格大于目标值的第一个位置, 也是用二分实现的。
计算两个数组中不超过给定值的元素数量 - C++ 实现
// 计算两个数组中不大于 x 的元素的数量
// 采用二分法, 查每个数组 <= x 的上界, 再求和
int count(const vector<int>& nums1, const vector<int>& nums2, int x) {
int ans = 0;
if (!nums1.empty() && nums1[0] <= x) {
// upper_bound 返回严格 > x 的第一个元素
ans += (upper_bound(nums1.begin(), nums1.end(), x) - nums1.begin());
}
if (!nums2.empty() && nums2[0] <= x) {
ans += (upper_bound(nums2.begin(), nums2.end(), x) - nums2.begin());
}
return ans;
}
将证明 count(x)>=k 这个条件具有二段性。
假设 x0 是满足 count(x)>=k 的最小的那个 x,那么:
- 对于更大的
x来讲,两个数组中不超过x的元素个数,肯定不少于x0的时候的情况。 - 对于更小的
x来讲,由于x0是满足count(x)>=k的最小的那个x,那么count(x)会肯定小于k。
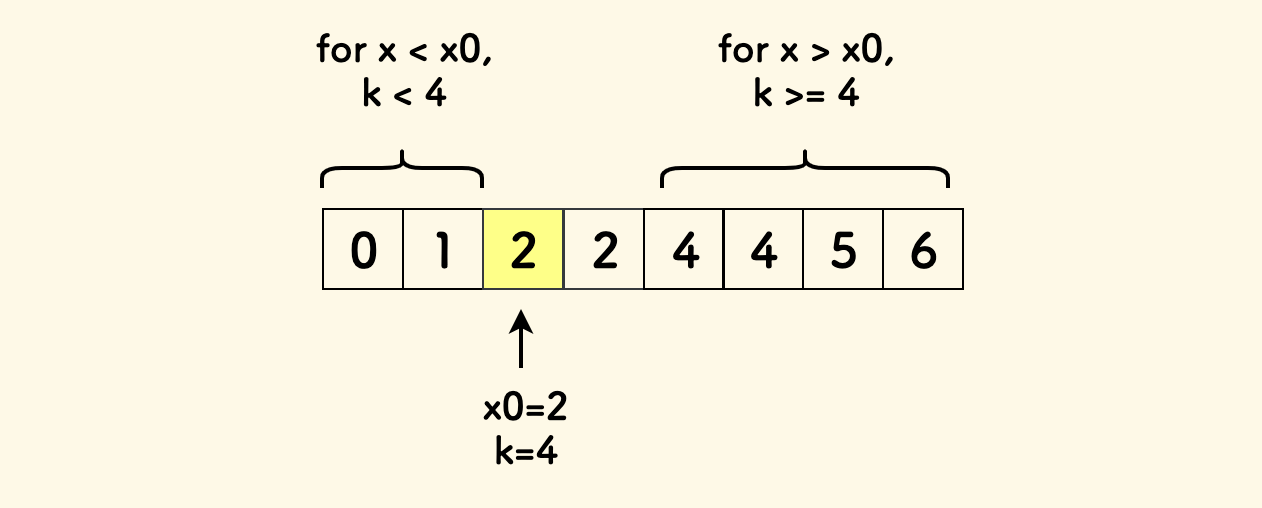
也就是说,count(x) 是一个非递减函数,满足二段性。
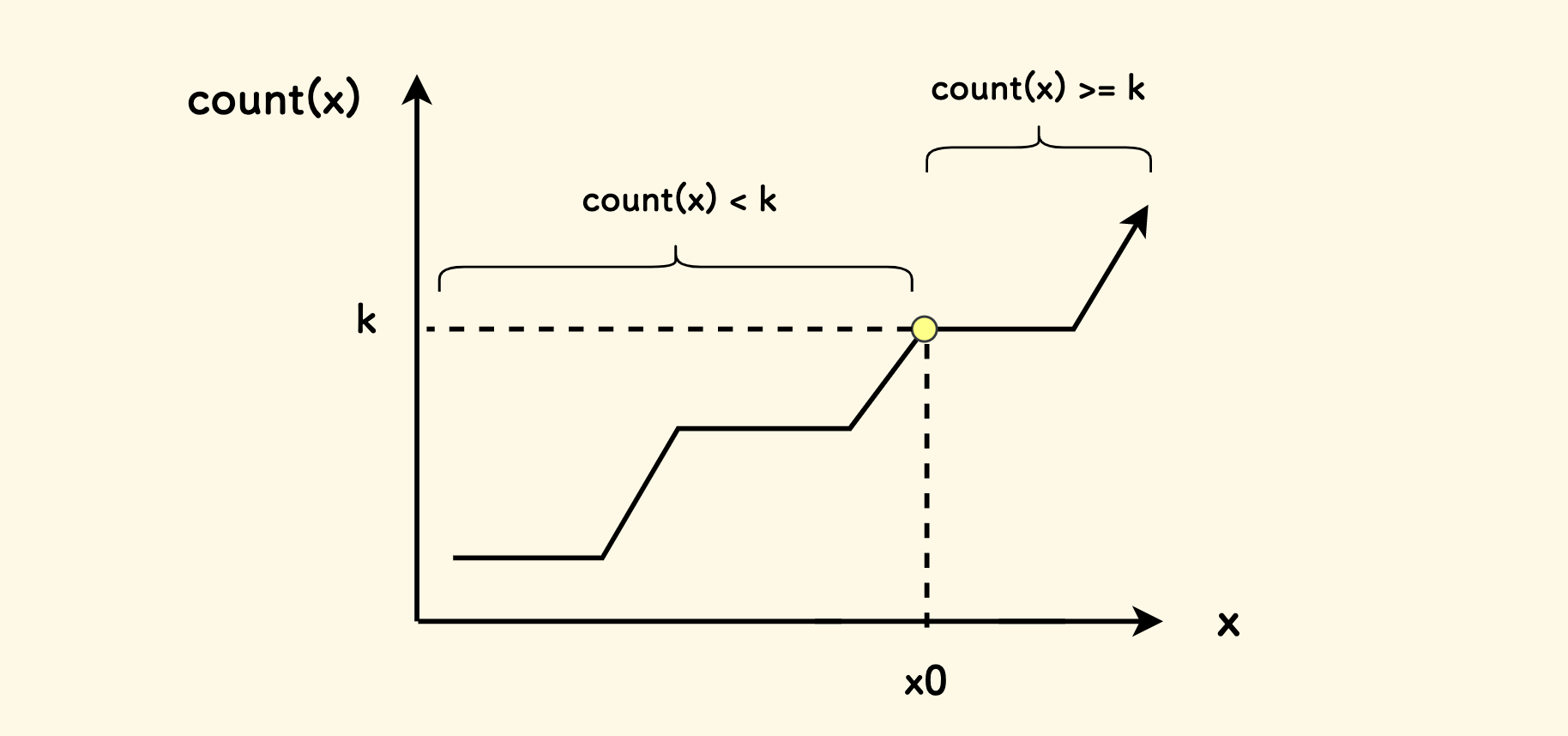
因此,可以使用二分枚举答案。要找第 k 小的数字, 其实就是找满足 count(x) >= k 的 x 的左界。
直接套用前面的模板即可。
不过,读到这里,有的读者可能会有疑问:如何确定 topk 二分的答案一定在两个数组中存在呢? 其实从 count(x) 的函数图像可以知道,所有的拐点都是数组中的元素,而满足二分条件的左界一定在拐点上,所以二分答案一定在两个数组中存在。 子函数 count(x) 本身的设计,就保证了拐点一定是数组中的元素,因为计算数量的这个逻辑, 肯定遇到输入的 x 是数组中元素的时候,函数值才会存在变化。
二分的最大可行解是两个数组的最大元素,最小可行解是两个数组的最小元素。
寻找两个有序数组的 - 二分答案 - C++ 代码
int topk(const vector<int>& nums1, const vector<int>& nums2, int k) {
// 最小 和 最大可行解
int l = std::min(nums1.empty() ? INT_MAX : nums1[0],
nums2.empty() ? INT_MAX : nums2[0]);
int r = std::max(nums1.empty() ? INT_MIN : nums1[nums1.size() - 1],
nums2.empty() ? INT_MIN : nums2[nums2.size() - 1]);
// 二分答案, 求满足 count(mid) >= k 的下界
while (l < r) {
int mid = (l + r) >> 1;
if (count(nums1, nums2, mid) >= k)
r = mid;
else
l = mid + 1;
}
return l;
}
然后,回到求中位数的问题,简单分下奇偶情况即可。
- 总数奇数情况下,就是求第
k=(m+n+1)/2个元素。 - 总数偶数的情况下,先求第
k1=(m+n)/2个 和 第k2=k1+1个元素,然后取其平均值即可。
可以知道,时间复杂度是 log(m+n) * log(Max-Min)。
虽然二分枚举没有直接二分的方法优美,但是它更容易想,简单暴力,也足够快。
例子:路标设置 ¶
在一个长度为
L的公路上,最多允许新增k个路标。现在公路上已经设置了
n个路标,其位置是已知的,由一个严格递增的数组a[n]给出。相邻路标的距离的最大值叫做空旷指数,它越小越好,求这个最小的空旷指数。
-- 来自 洛谷 P3853
和前面的 分割数组问题 有个共同之处:要求「最小的最大值」,这一般是二分答案的提示。 因为你可以拆分一个子问题去假定一个「最大值」,然后看是否满足限制条件,再二分枚举出来的这个「最大值」的左界,也就得到了「最小的最大值」。
所以,仍然是老套路,先构造一个子问题 count(x):
如果最大间隔限定为
x的话,最少需要新增多少个路标?
因为有一些预设的路标,那么先预处理一个差分数组:
路标设置 - 预处理差分数组 - C++ 代码
const int N = 100001;
// 已经设置的路标, 下标从1开始
int a[N];
// 预处理差分数组 diff[i] = a[i]-a[i-1], diff[n+1] = L-a[n]
int diff[N+1];
for (int i = 1; i <= n; i++)
diff[i] = a[i] - a[i - 1];
diff[n + 1] = L - a[n];
那么子问题的求解,就是看每一段 diff 最少需要几个路标,可以直接用除法:
路标设置 - 子问题求解 - C++ 代码
// 如果要求最大间隔是 x 的话, 需要至少设置多少个路标?
// count 具有二段性, 更进一步地, x 越大, 返回值不升
int count(int x) {
int ans = 0;
for (int i = 1; i <= n + 1; i++) {
ans += diff[i] / x;
if (diff[i] > 0 && diff[i] % x == 0) --ans; // 正好整除的情况
}
return ans;
}
很容易看出,如果最大间隔越大,那么必需的最少路标越少,这是个不升的函数,也就具有二段性。
接下来,就可以二分枚举了。为了方便套模板,可以构造一个反方向的函数 f(x),来把单调性转化成不降的:
auto f = [&](int x) { return L - count(x); };
那么,要求满足 count(x) <= k 的左界,也就是要找 f(x) >= L-k 的左界,直接应用第一个模板就可以了。
路标设置 - 二分枚举答案 - C++ 代码
int l = 1, r = L;
while (l < r) {
int m = (l + r) >> 1;
if (f(m) >= L - k) r = m;
else l = m + 1;
}
return l;
结尾语 ¶
- 二分的前提是存在二段性。
- 二段性并不一定是静态呈现的,只要可行区间可就某个性质拆分。
- 二分常用的两种模板:求左界、求右界。
- 二分答案的经验性套路:先构造子问题、分析子问题的单调性或二段性,再判断求左界还是求右界。
- 二分答案的结果一般是子函数的拐点,保证了其存在性。
- 求最大的最小值(或者 最小的最大值)是二分答案的常见提示。
(完)
更新记录:
- 2024/01/04:更新名词「二分判定」为「二分答案」。
- 2024/03/03:添加二分答案问题「路标设置」。
相关文章:TopK 系列算法问题的总结
本文原始链接地址: https://writings.sh/post/binary-search

