TopK 系列算法问题的总结

TopK 问题是求第 K 小或第 K 大的一类问题。

本文是对一系列 TopK 问题的总结，将会看到，其中大多可以用堆/优先级队列或者二分答案的思路来解决。

问题列表：

模型 - 经典 TopK 问题
模型 - TopK 数对和
延伸 - 有序矩阵 TopK 元素
延伸 - 有序矩阵 TopK 数组和
延伸 - TopK 子段和
延伸 - TopK 数对距离

此外，还有一个之前文章已经讨论过的：求两个有序数组的 TopK 问题。

前两个问题，我认为比较经典，可以作为此系列问题的基础模型，后面的几个作为延伸问题，讲解将从简。

模型 - 经典 TopK 问题 ¶

先回顾一下一维数组上的 TopK 问题，是非常经典的算法问题：

求一个无序数组的第 K 大元素。
-- 以 leetcode-215 数组中的第K个最大元素为模板问题展开

解法可以有三种：快速选择、堆置换和二分答案。

快速选择 `O(n)`

类似快排的思路，但是只向一边减治：

每次随机选取一个基准值，原地对数组分类。即著名快排的 partition 过程，也叫荷兰国旗问题。
比较基准值左边的元素个数和 k 的大小，决定向左还是向右递归。
恰好等于 k 个时，即找到了第 k 大。

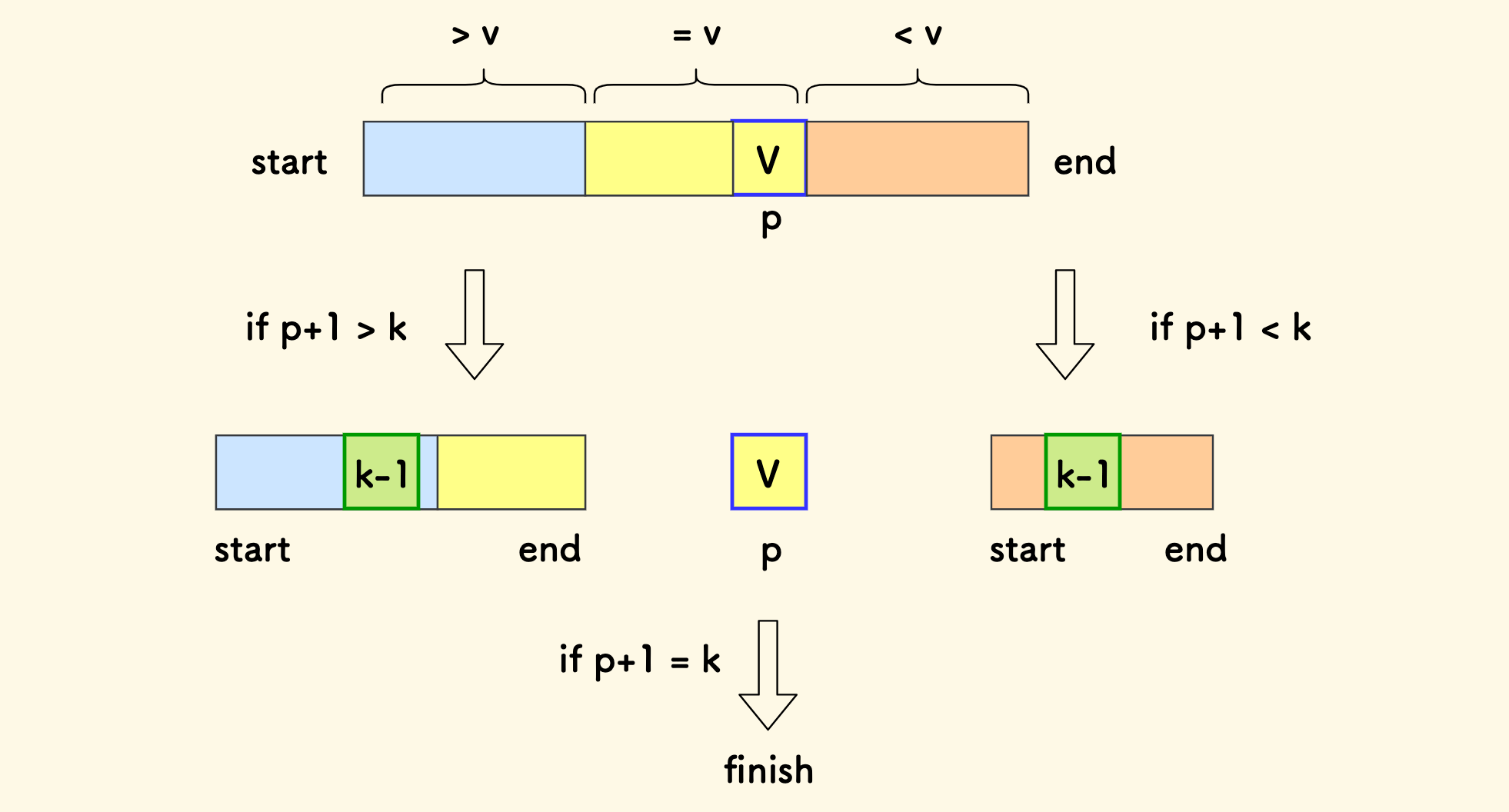
大概的伪代码如下，时间复杂度最好 O(n)，最差 O(n^2)。

int TopK(int a[], int start, int end, int k) {
    // 位置 p 是 <= 基准值的右界坐标
    int p = Partition(a, start, end);
    // p+1 是 <= 基准值的元素个数
    if (p + 1 > k)
        TopK(a, start, p -1, k);
    else if (p + 1 < k)
        TopK(a, p + 1, end, k);
    else
        return a[p];
}

我曾写过一篇的详细的相关文章 TopK 问题 - 快速选择的方法，这里不再展开详细。

但是，快速选择的方法并不如堆置换和二分答案法的应用广泛。此外，和快排一样，在数组原本就有序的情况，存在退化情况。

求无序数组的第 K 大元素 - 快速选择 - C++ 实现 - Github

堆置换 `O(nlogk)`

做一个大小为 k 的小顶堆：

把剩余的元素依次加进堆中。
每次加入一个元素后，都要弹出堆顶最小元素，所谓「置换」。
每次都置换出一个小的，最后总共弹出了 n-k 个更小的，堆中留下的就是前 k 大元素。

堆顶就是这前 k 大之中最小的，也就是第 k 大元素。

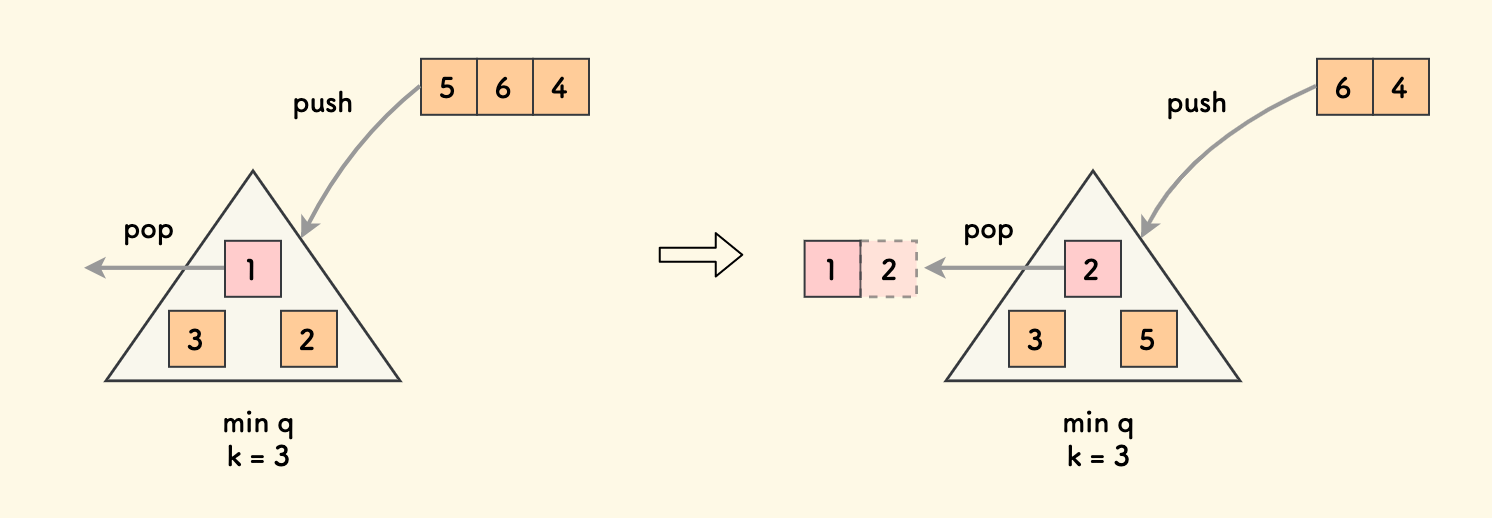
伪代码大概如下，容易知道时间复杂度是 O(nlogk) 。

priority_queue q(a[:k]); // 小顶堆
for (i = k; i < n; i++) { q.push(a[i]); q.pop(); }
return q.top();

我曾写过一篇的详细的相关文章 TopK 问题 - 堆置换的思路，不再展开详细。

从经验来看，堆置换大概是 TopK 问题中最常用的解决思路了。

求无序数组的第 K 大元素 - 小顶堆置换 - C++ 实现 - Github

二分答案 `O(nlog(Max-Min))`

我的前一篇文章，详细说明了二分答案方法。

许多 TopK 问题都可以用暴力的二分枚举猜答案的思路来解决。

先求解一个非常简单的子问题：

计算无序数组中不小于目标值的元素的数目。

容易写出其求解代码，其时间复杂度是 O(n) 的。伪代码如下：

大于 x 的元素计数 - C++ 实现

int count(const vector<int>& nums, int x) {
    int c = 0;
    for (int i = 0; i < nums.size(); i++)
        if (nums[i] >= x) c++;
    return c;
}

对于越大的 x，计数的结果肯定越小。也就是说，count(x) 是非递增函数。

可以证明，条件 count(x) >= k 具有二段性，感兴趣的话可以展开看详细说明：

当 x > x0 时，总会有 count(x) < k。
当 x <= x0 时，总会有 count(x) >= k 。

条件 count(x) >= k 的二段性说明

二段性是说，对于某个条件，当前可行区间可以分成两段，一段满足条件，另一段不满足条件，这样就可以把可行区间减半，达到二分减治的目的。

不妨想象，先把数组从大到小排好顺序，虽然实际上我们并不这么干。

比如说 x0 恰好使得 >=x0 的元素个数为 k。下图中数组是 [7, 6, 6, 4, 4, 2, 1, 1]，取 x0=4，相应的 k=5。注意元素 5 和 3 不在数组中，画出来只是为了展示连续值域上的取值情况：

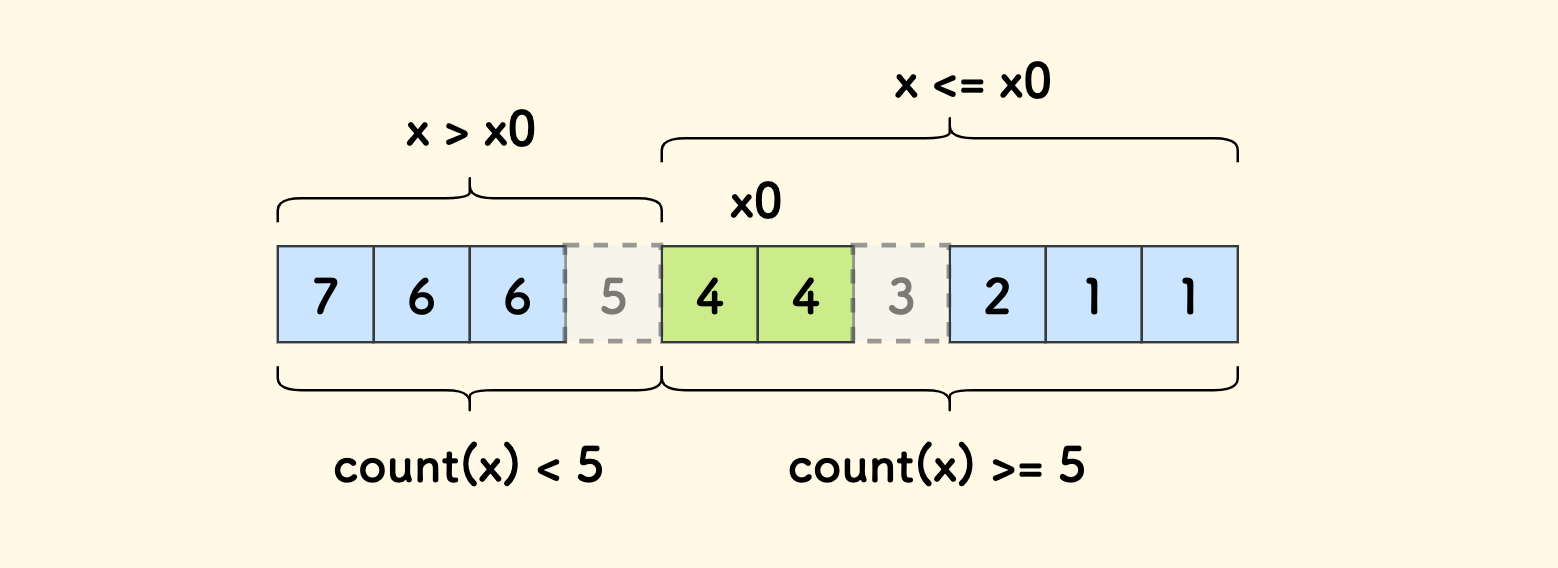
当 x > x0 时，因为计算 count(x) 时不会考虑进去元素 x0，而计算 count(x0) 时会考虑进去 x0，所以严格地会有 count(x) < k。
比如图中最接近 x0 的数字 x=5，函数值为 count(5)=3 < k。
当 x <= x0 时，因为 count 函数计算的是数组内不小于给定数字的元素个数，小于 x0 的数值 x 也有可能不在数组中，如果它恰好介于 x0 和下一个更小的元素之间，其计数结果也会和 x0 的函数值一样。比如图中不止 x0 的函数值为 k，比 x0 小的 3 也会有相同的函数值 count(3)=5。
而对于小于 x0 的且在数组中出现数值，比如图中的元素 2，肯定会有 count(x) > k。
所以总体会有 count(x) >= k。

问题可以进一步转化为：

求 count(x) >= k 的尽量大的数字 x，也就是求满足 count(x) >= k 的 x 的右界。

需要注意的是，count(x) 函数是降序的，选取中点 m 后，如果 count(m) < k 说明选取的中点太大了，要收缩右界到 m-1，可以套用二分模板中的第二套模板。

可行解的最大值是数组的最大元素，最小值是数组的最小元素，它们作为初始的可行区间。

时间复杂度是 nlog(Max-Min) 。

求无序数组的第 k 大元素 - 二分答案法 - C++ 实现

int findKthLargest(vector<int>& nums, int k) {
    int l = *min_element(nums.begin(), nums.end());
    int r = *max_element(nums.begin(), nums.end());

    // 找 >=x 的元素个数不超过 k 的 x 的最大的 x
    // 也就是找满足 count(x) >= k 的 x 的右界
    while (l < r) {
        int m = (l + r + 1) >> 1;
        if (count(nums, m) < k)
            // count 是降序, 说明 m 大了
            // 所以右侧排除, 收缩到 m-1
            // 防止死循环，所以每次取 m = (l+r+1)>>1
            r = m - 1;
        else
            l = m;
    }
    return l;
}

但是，会有一个疑问：二分的结果一定在原数组中吗？感兴趣的话可以展开下面的详细说明。

二分的结果一定在原数组中的说明

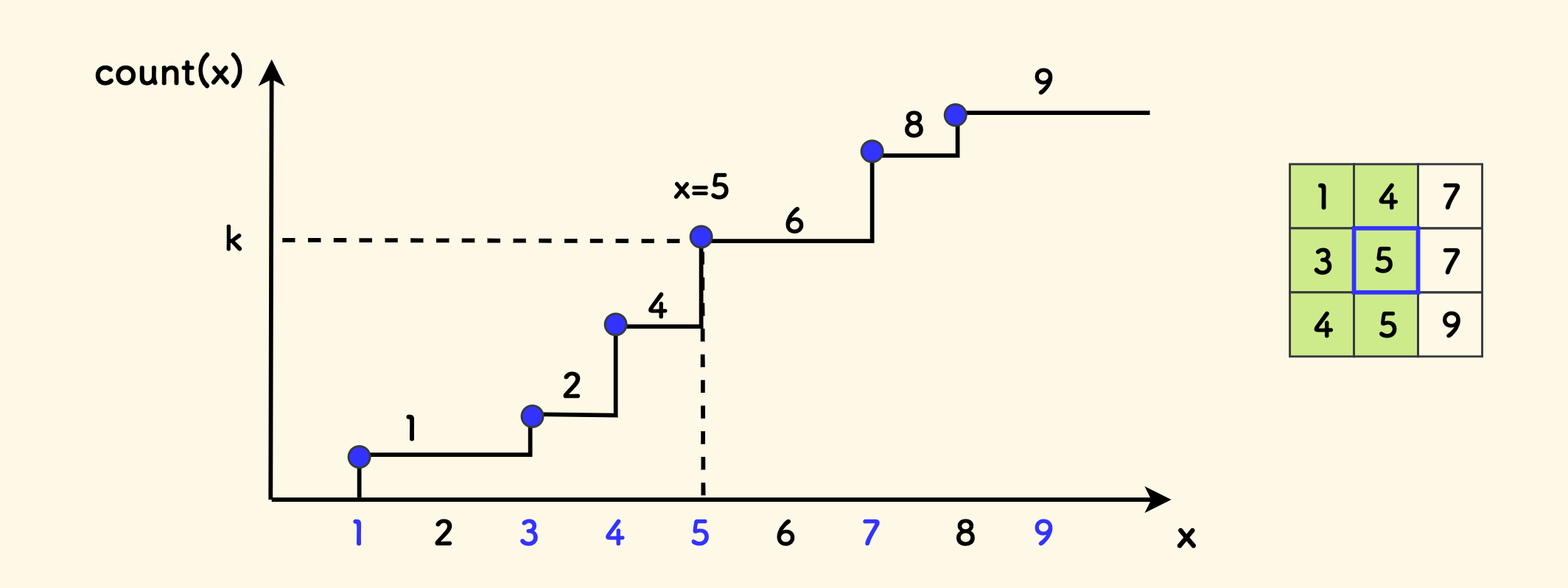
仍以数组 [7, 6, 6, 4, 4, 2, 1, 1] 为例，其 count(x) 的函数图像大概如下图，虽然二分是在 [min, max] 的连续区间上的，但是根据计数函数的构造来看，但是函数的向下拐点全部由数组中的元素构成。

事实上，可以根据计数函数 count 知道，当输入的 x 真正是数组中的值的时候，才会引起函数值的变化。

二分查找的是值域区间 [min, max] 上满足条件 count(x) >= k 的右界，此右界必定是一个向下的拐点。所以 l 肯定在数组中。

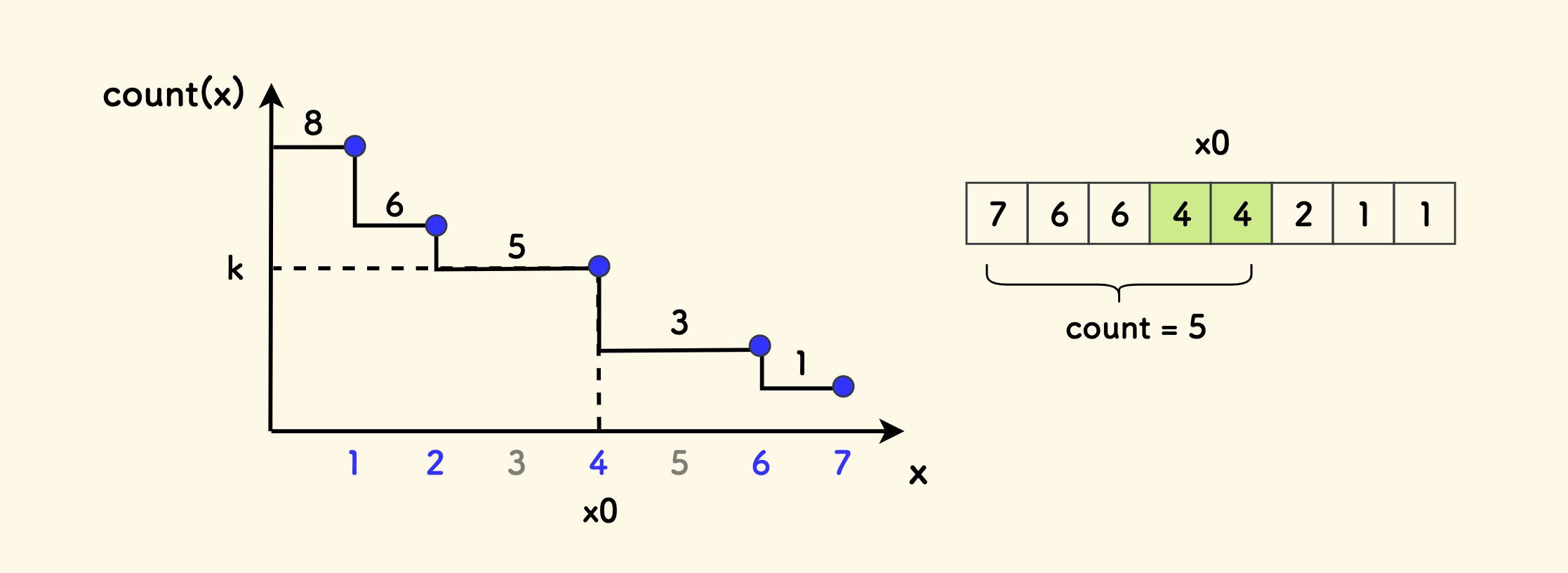
究其本质是因为子函数本身是设计在当前数组上的，函数值因数组元素而变化，最终导致二分结果一定在数组内。

虽然，二分答案的子过程 count 函数并不快，复杂度是 O(n) 的，但是数组的值域跨度毕竟是有限的，在值域上进行 log 级别的二分答案，最终的时间表现也足够快。这也是我经常觉得值域二分有些暴力的原因。

针对经典的 TopK 问题，三种方法正确性上都没问题。leetcode-215 上，后两个方法可以正常提交通过，快速选择的方法由于在数组有序的情况下存在退化、会在一个测试用例上超时。

模型 - TopK 数对和 ¶

给定两个非递减的整数数组 a 和 b, 以及一个整数 k 。从两个数组中各取一个数字组成一个数对（可以重复选取），这两个数字的和叫做一个数对和。求最小的 k 个数对和。
-- 来自 leetcode 373

比如说，两个数组分别是 [2,6,6] 和 [1,4,8,13]，前 k=3 小的数对和依次是 3,6,7。

洛谷上有一道类似的题目 P1631 序列合并是这个题目的一种特例。

解法可以有两种：堆置换和二分答案。

这道题的经典之处在于，其解决思路可以推广到更复杂的 TopK 问题中去。

堆置换之「行头堆」

「行头堆」的名字是我自己起的，我觉得这个名字对于这种类型的堆方法很形象。

如果把所有的数对按下面的方式排列成一个矩阵，可以知道的是：每行的行头的和最小。

如果使用一个小顶堆，因为每行的行头就代表了整行的最小值，所以没必要把所有数对都放到堆里面去，只需在堆中维护各行的行首数对就可以。

弹出堆中最小值后，下一个要考虑的就是它所在行的后继数对，放入堆中。

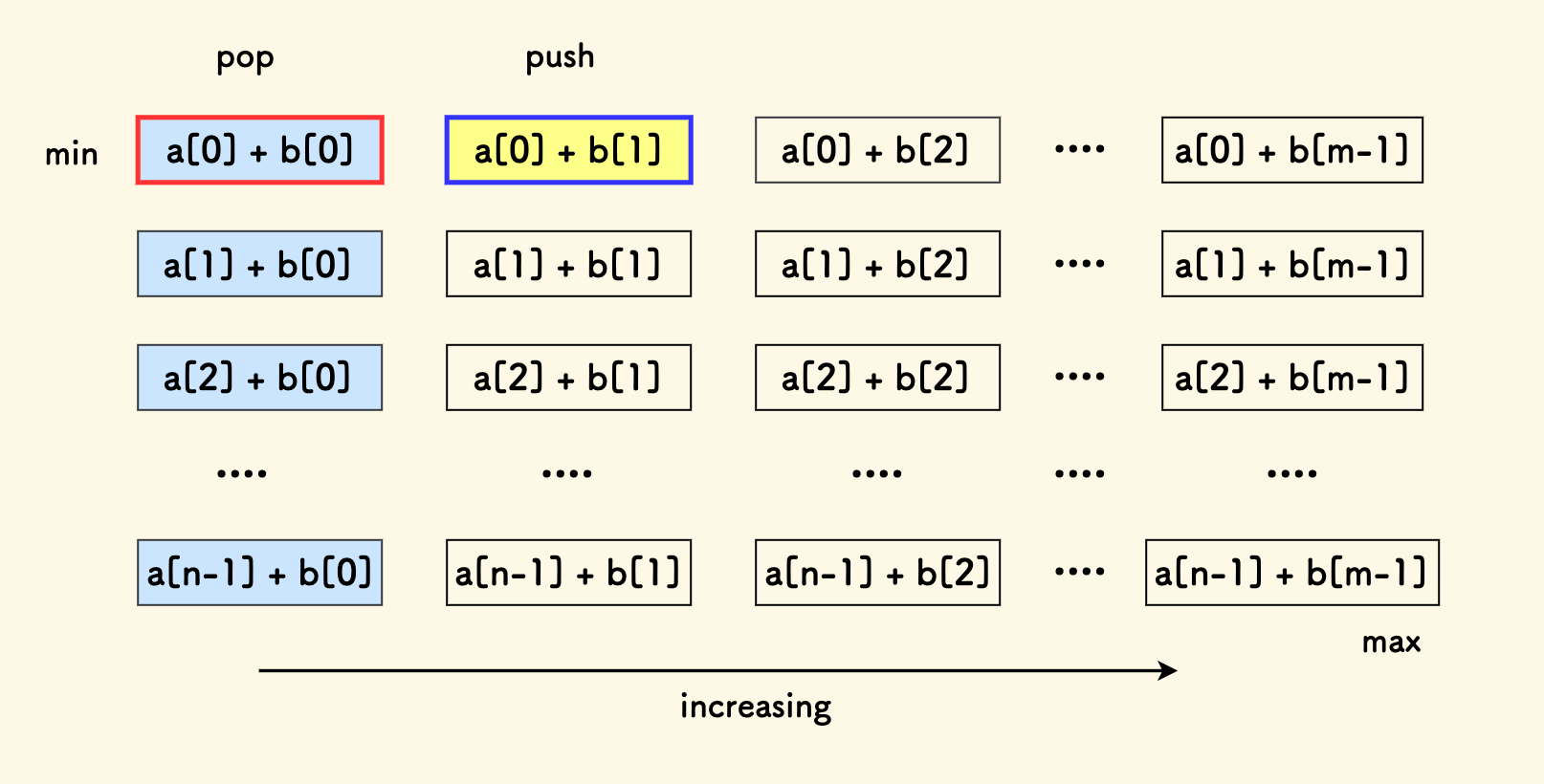
堆置换的逻辑是：

先把每一行的行头加入到小顶堆。
每次弹出堆中最小的堆顶，然后把它所在行的下一个元素加入堆中。
弹出 k 次后即可取得前 k 小的数对和。

大概的伪代码如下，容易知道，时间复杂度是 klog(min(m,n))。

priority_queue q; // 小顶堆
// 放入各个行头 { a[i], b[0] }
for (i = 0; i < n; i++) q.push({i, 0});
// 置换 k 次
ans = [];
while (k--) {
    {i, j} = q.pop();
    ans.push(a[i] + b[j]);
    q.push({i, j + 1});
}

TopK 数对和问题 - 小顶堆置换 - C++ 实现 - Github

这个「行头堆」的思路和一个著名的面试题有点相似，叫做「赛马问题」：

现在有 25 匹马，每匹马的速度是固定的，一共有 5 条赛道，即一场比赛最多 5 匹马参加。需要安排最少多少场比赛才能选出最快的三匹马呢？

赛马问题的网上相关资料很多，可以自行了解。

二分答案解法

二分答案解法的第一步，仍然是构造一个子问题：

找到两个数组中数对和不超过给定值的数对的数量。
也就是说，给定一个数值 x，两个数组中和不超过 x 的元素总共有多少个？

对于数组 a 的每一个元素 a[i] 来说，相当于求另一个数组 b 中不超过 x-a[i] 的元素有多少。又因为两个数组都是有序的，那么一旦先稳定住 a[i]，那么对数组 b 中符合条件的元素进行计数可以直接使用二分。相当于 b 数组中求右界的问题。

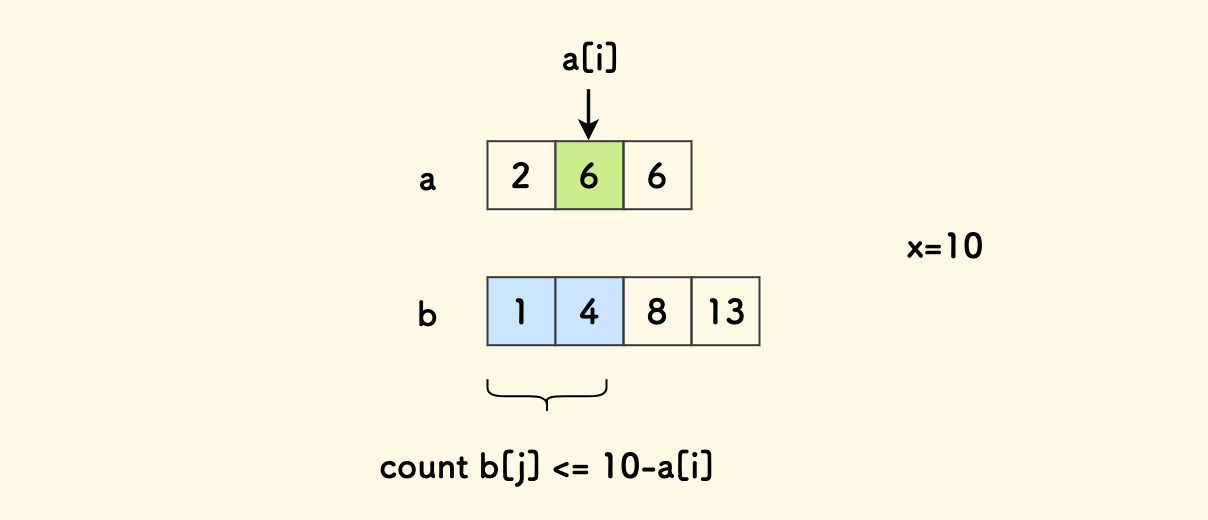
分析到这里，可以写出这个子问题的代码了，其时间复杂度是 nlogm。

TopK 数对和问题 - count 计数函数 - C++ 实现

// 找到两个数组中数对和不超过给定值的数对的数量
// 等效于下面的 findPairs，但是只是计数
ull count(const vector<int>& a, const vector<int>& b, ll val) {
    ull ans = 0;
    // 对 a 中的每一项 x 来说，相当于找 b 中 <= val-x 的右界的问题
    for (auto x : a) {
        int target = val - x;
        // 注意防止全部太大的情况, 此时找不到右界
        if (!(b[0] > target)) {
            int l = 0;
            int r = b.size() - 1;
            while (l < r) {
                int m = (l + r + 1) >> 1;
                if (b[m] <= target) l = m;
                else r = m - 1;
            }
            ans += (ull)l + 1;
        }
    }
    return ans;
}

count(x) 是一个非递减函数，条件 count(x) >= k 具有二段性，具体证明方式和之前的类似，不再展开说明。（虽然这里省略，但是二段性的分析必不可少，有二段性才可以进行二分答案）。

原 TopK 数对和问题，可以转化为：

二分答案找满足 count(x) >= k 的 x 的左界。

可行解的最小值是 a[0]+b[0]，最大值是 a[n-1]+b[m-1]，作为初始可行区间。

二分猜答案即可，伪代码如下，可知其时间复杂度为 (nlogm)log(Max-Min)：

l = a[0] + b[0], r = a[n-1] + b[m-1];

while (l < r) {
    int x = (l + r) >> 1;
    if (count(a, b, x) >= k) r = x;
    else l = x + 1;
}
// l 是第 k 小的数对和

由于题目要求出来前 k 小的数对和，而不只是找到第 k 个，最后还要沿着计数函数 count(x) 的思路，再写个类似的收集函数把答案找出来。

TopK 数对和问题 - 二分答案法 - C++ 实现 - Github

延伸 - 有序矩阵 TopK 元素 ¶

给你一个 n x n 矩阵 matrix ，其中每行和每列元素均按升序排序（非递减顺序），找到矩阵中第 k 小的元素。
-- 来自 leetcode-378

比如，矩阵 [[1,4,7],[2,5,8],[3,6,8]] 的第 k=4 小元素是 4。

这个题目的解法可以有三种：基于「行头堆」的堆置换方法、归并方法和二分答案法。

当然，这三种思路都可以推广到 m x n 矩阵大小的情况，n x n 是其一种特例情况。

「行头堆」的堆置换方法

类似 TopK 数对和问题的思路，因为矩阵本身是有序的，那么行头元素是每行中最小的。

做一个小顶堆，堆中维护当前行的最小元素的位置。堆顶是所有行的当前最小值。每次弹出栈顶后，继续考虑栈顶在其行内的后继元素。

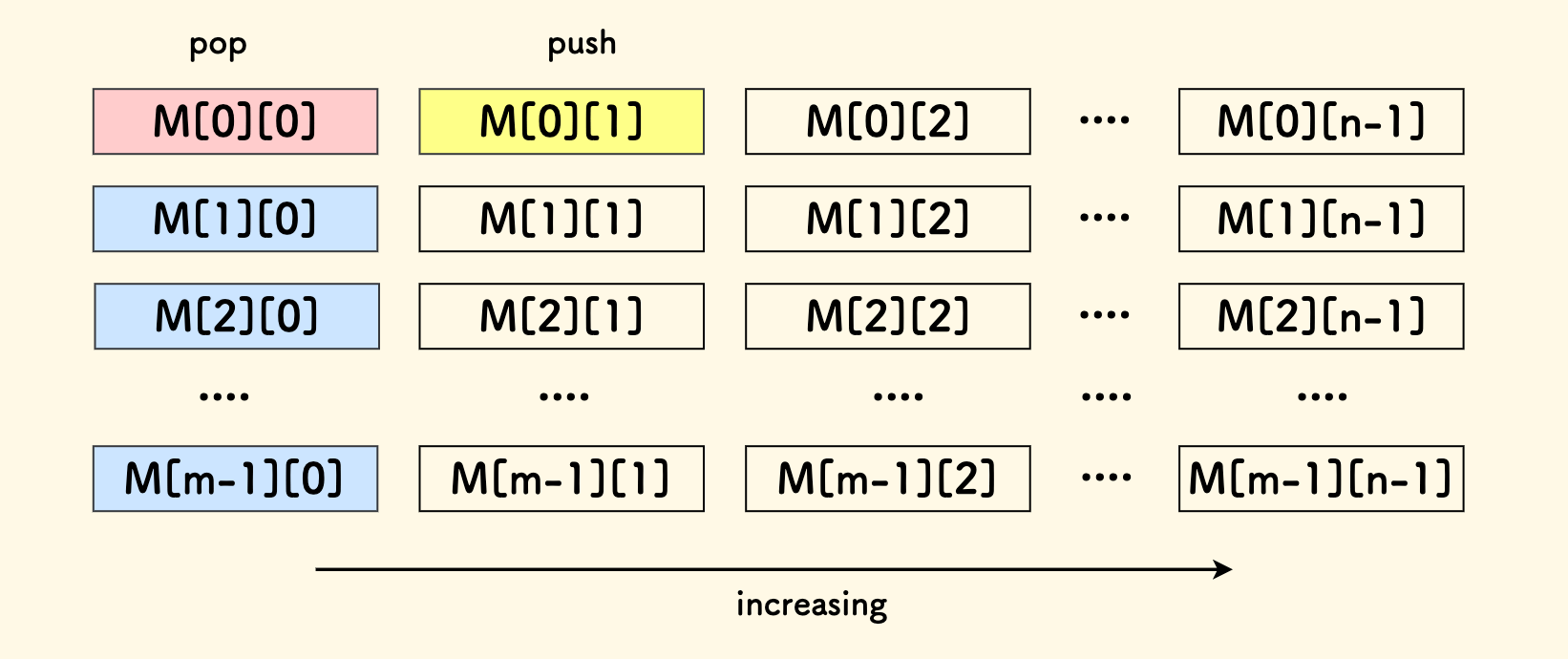
这个思路只利用了矩阵行有序的性质，并没有利用列有序的性质。

代码不再展开讨论，时间复杂度是 klog(min(m,n))。具体实现见下方链接：

有序矩阵 TopK 问题 - 行头堆做法 - C++ 实现 - Github

归并方法

和归并排序几乎完全一样，先不断分治，然后再两两合并。

这个思路不必过多讨论。唯一的细节优化点是，每次合并时，如果元素个数多于 k，可以提前终止合并。

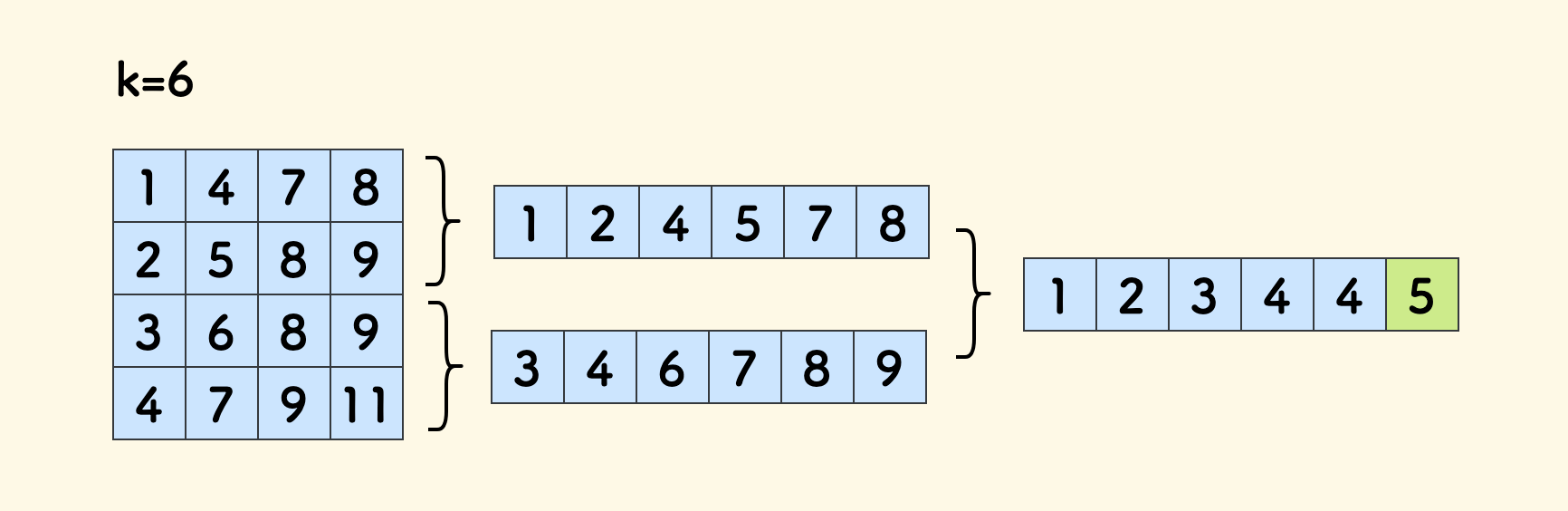
时间复杂度是 nlogm。

同样地，这个思路只利用了矩阵行有序的性质，并没有利用列有序的性质。

有序矩阵 TopK 问题 - 归并方法 - C++ 实现 - Github

二分答案法

这个矩阵的最小值在左上角、最大值在右下角，考虑下进行值域二分答案。

考虑一个子问题：

给定一个数字 x，矩阵中不超过 x 的元素有多少个？

这个子问题和有序矩阵中的搜索问题一样，我曾写过两种思路，一种是 O(m+n) 时间复杂度的方法，另一种是 O(log(mn)) 时间复杂度的方法。由于后一种实现比较复杂，这里直接采用第一种。

从矩阵的右上角出发，因为右上角始终有这样的性质：当前行中最大、当前列中最小。

遇到左边不超过 x 的，当前行左边都更小、不必再看。计数，然后向下走。
否则，就向左走，继续试探。

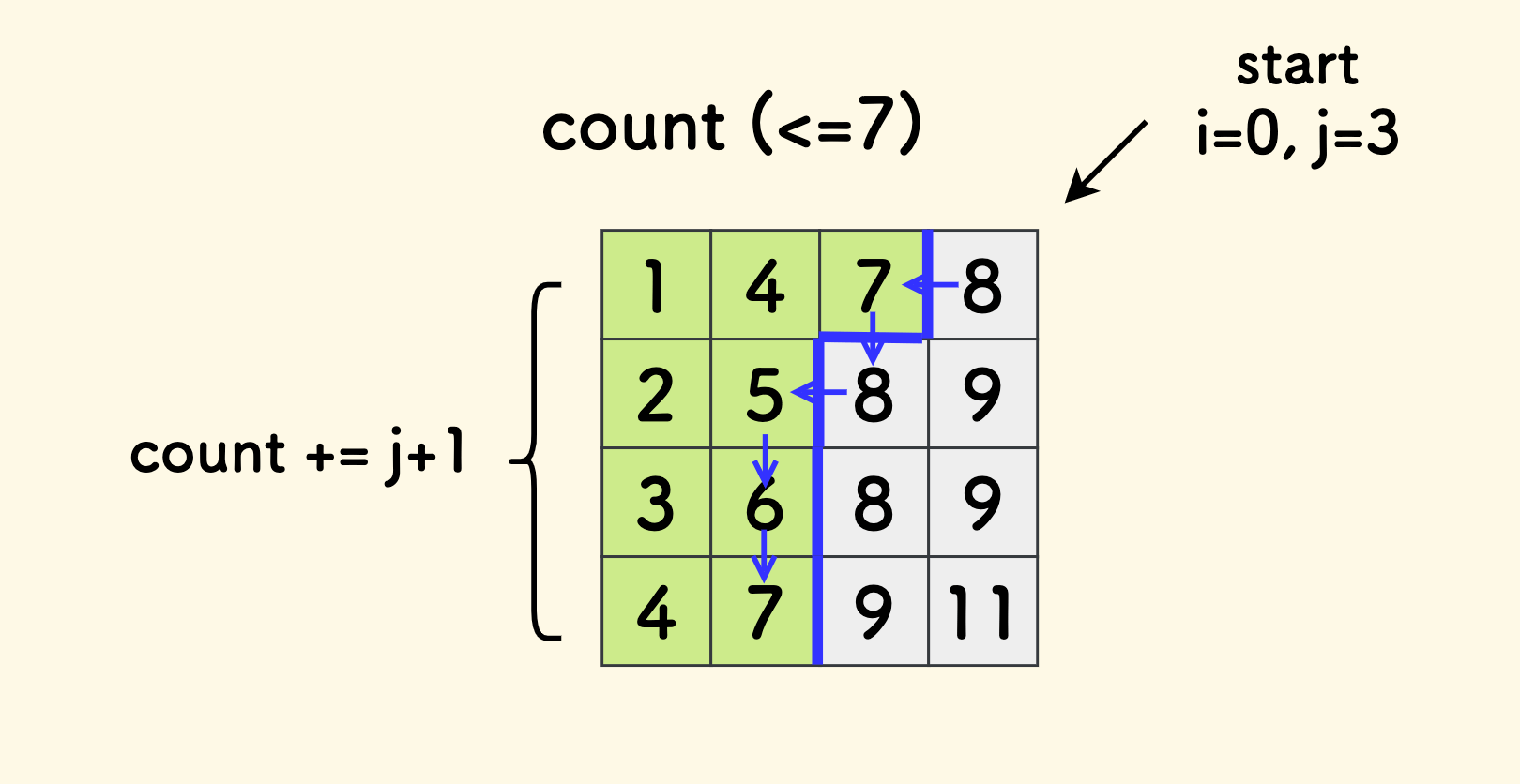
伪代码实现如下，时间复杂度是 O(m+n)：

int i = 0, j = n-1;
int c = 0; // 计数
while (i < m && j >= 0) {
    if (matrix[i][j] <= x) {
        i++;
        c += j - 1;
    } else j--;
}
return c;

然后，可以分析出来函数 count(x) 是非递减函数。条件 count(x)>=k 具有二段性。

原问题可以进一步转化为：二分答案，找 count(x) >= k 的左界。

初始可行区间容易确定，最小值在左上角，最大值在右下角。

伪代码如下，时间复杂度是 (m+n)log(Max-Min)。

int l = matrix[0][0];
int r = matrix[m - 1][n - 1];
while (l < r) {
    int x = (l + r) >> 1;
    if (count(matrix, x) >= k) r = x;
    else l = x + 1;
  }
return l;

这个问题经常会有一个疑问：二分的结果 l 是否一定是矩阵中的元素？其分析和经典 TopK - 二分的结果一定在原数组中吗？一样。

对于计数函数 count 而言，只有输入的数值在矩阵中，才能引起函数值的变化。也就是说，矩阵中的数值都是 count 函数向上递增的拐点。当前的二分查找是在找左界，找的 l 必定是一个拐点，所以 l 肯定在矩阵中。

有序矩阵 TopK 问题 - 二分答案法 - C++ 实现 - Github

延伸 - 有序矩阵 TopK 数组和 ¶

给你一个 m * n 的矩阵 mat，以及一个整数 k ，矩阵中的每一行都以非递减的顺序排列。你可以从每一行中选出 1 个元素形成一个数组。返回所有可能数组中的第 k 个最小数组和。
-- 来自 leetcode-1439

比如说，矩阵 [[1,3,11],[2,4,6]]，第 k=5 小的数组和是 7。

这其实是「两个数组 TopK 数对和」的拓展，可以直接基于它来做。另一种解法是直接二分答案。

基于 TopK 数对和问题 + 归并

前面已经说过两个有序数组的情况，多个有序数组的情况可以两两归并而得。

比如说，现在有三个有序数组，先求前两个数组的前 k 小的数对和，记为数组 temp，它也是有序的。然后，它和第三个数组再求一次前 k 小的数对和，就是最终答案。这是源于加法的结合律。

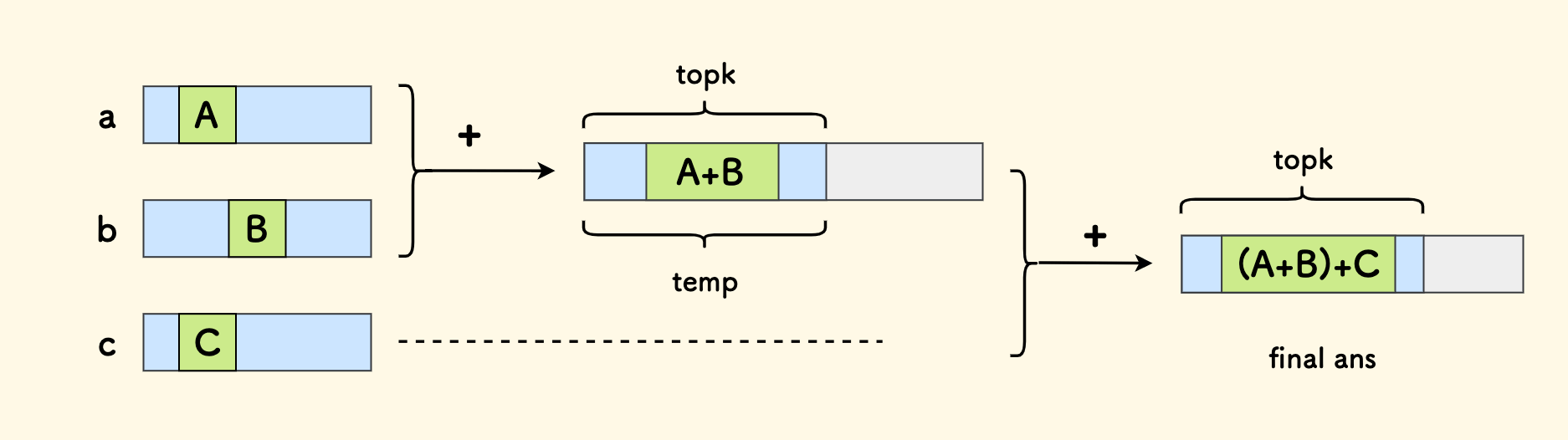
归并的方式，可以有两种：

线性归并：就是滚动式地，每归并一个后，继续归并下一个。
伪代码如下：
```
ans = mat[0];
for (int i = 0; i < m; i++) {
  ans = topkTwo(mat[i], ans, k);
}
```
有序矩阵 TopK 数组和 - 堆置换 + 线性归并 - C++ 实现 - Github

分治归并：类似归并排序的方式，先分治、再两两向上归并。

伪代码如下：

有序矩阵 TopK 数组和 - 分治归并 - 伪代码

int[k] merge(int mat[m][n], int k) {
  // 特判, 终止递归
  if (m == 1) return mat[0];
  if (m == 2) return topkTwo(mat[0], mat[1], k);

  // 二分矩阵，上下两块
  auto mat1, mat2;
  int i = 0;
  for (; i < m / 2; i++) mat1.push(mat[i]);
  for (; i < m; i++) mat2.push(mat[i]);

  // 向上归并
  return topkTwo(merge(mat1, k), merge(mat2, k), k);
}

有序矩阵 TopK 数组和 - 堆置换 + 分治归并 - C++ 实现 - Github

二分答案法 + DFS 计数

这个问题的直接二分答案法没有那么好想。

老规矩是，先构造一个子问题，给定一个数字 s：

计算矩阵中满足 <= s 的数组和的个数。

这个子问题也不是特别好处理，我们继续拆解这个子问题的规模，以方便递归处理。做一个子矩阵上的 dfs 计数函数：

计算矩阵中第 i 行以下的子矩阵中满足 <= s 的数组和的个数。

对于当前以第 i 行为起始行的子矩阵，可以逐个稳定住此行的每个元素，然后把计数问题递归到下一个子矩阵上去。

简而言，思路是：逐列循环，逐行递归。

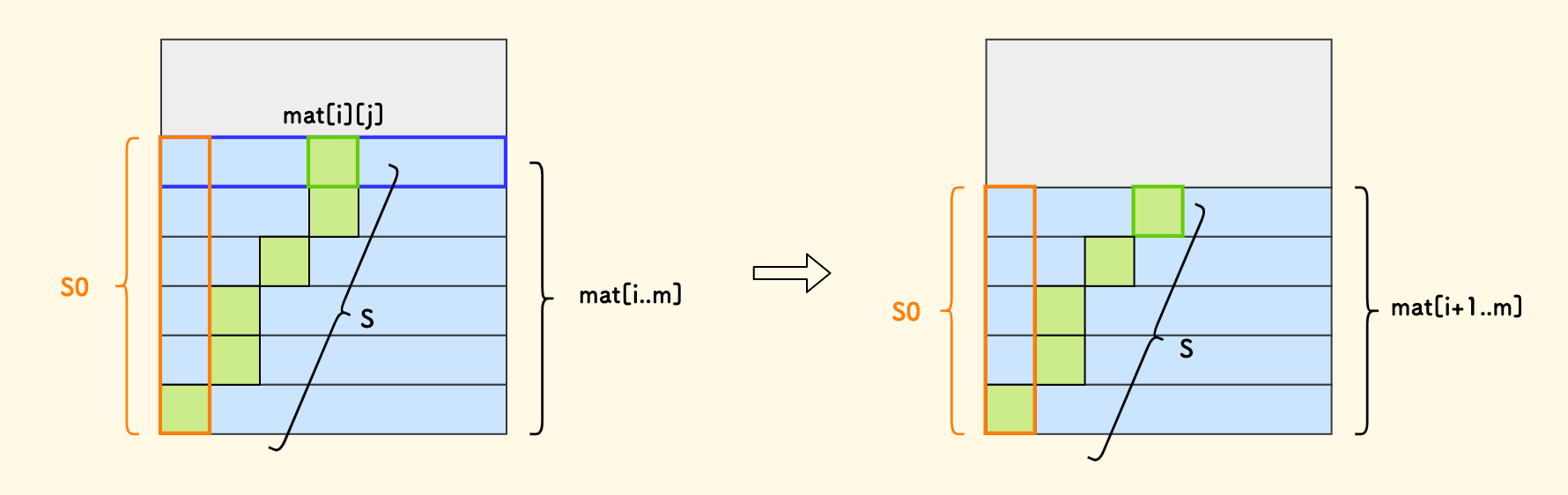
递归的时候：

把每行的第一个元素的和叫做 s0，它一定是所有数组和中最小的。
递归时，s0 应该要减去当前行的第一个元素 mat[i][0]。
递归时，当前的数组和阈值 s 也需要相应的减去当前迭代的元素 mat[i][j]。

另外，注意三种剪枝情况：

s 应不小于 s0。
因为每行是有序的，一旦前面的无法满足 <=s ，后面的也没必要再看了。
计数越过 k 时可以及时终止。

伪代码如下，时间复杂度不作分析。

计数函数 count - C++ 实现

// dfs 函数计算 [i..m] 行的子矩阵中满足 <= s 的数组和的个数
// s 是针对当前子矩阵的数组和的阈值
// s0 是当前子矩阵每行的行头的元素和，也就是所有数组和的最小值
// c 是计数, 递归过程中全局维护, 作为一个引用
void dfs(const vector<vector<int>>& mat, int i, int s, int s0, int k, int& c) {
    if (s < s0 || c >= k) return;  // 提前结束

    if (i >= mat.size()) {  // 越过最后一行，进行计数
        c++;
        return;
    }

    for (int j = 0; j < mat[i].size(); j++) {
        // 提前剪枝: 因为每行是上升的，当前行不满足后，后续也不必要在看
        if (s - mat[i][j] < s0 - mat[i][0]) return;
        // 选择 mat[i][j]，缩小阈值，向下递归
        dfs(mat, i + 1, s - mat[i][j], s0 - mat[i][0], k, c);
        // 提前剪枝: c 在 dfs 函数调用后可能会增加，满足 >=k 后提前退出
        if (c >= k) return;
    }
}

// 计算矩阵中不超过阈值 s 的数组和的个数
int count(const vector<vector<int>>& mat, int s, int s0, int k) {
   int c = 0;
   dfs(mat, 0, s, s0, k, c);
   return c;
}

接下来，可以证明 count(s) 函数是非递减的，条件 count(s)>=k 具有二段性。分析方式和之前类似，不再展开。

问题转化为二分答案找满足 count(s)>=k 的 s 的左界。

二分枚举的初始可行区间 [l,r] 分别是：

l 是矩阵的所有行头元素的和
r 是矩阵的所有行尾元素的和

这个子问题看起来挺慢的，但是在 leetcode 1439 上，这种二分答案的解法比堆的思路跑的还快。

有序矩阵 TopK 数组和 - 二分答案 + DFS 计数 - C++ 实现 - Github

延伸 - TopK 子段和 ¶

返回无序的非负整数数组的第 k 小的子段和。
子段和是指数组中一个非空、且连续的子数组的和。
-- 来自 leetcode 1918

比如说数组 [2,1,4] 中第 4 小的子段和是 4。

因为所有子段和分别是 2,1,4,2+1=3,1+4=5,2+4=6,2+1+4=7，其中第 4 小的是 4。

这个题的解法可以有两种：行头堆的做法和值域二分答案。

行头堆的解法

可以把所有可能的子段列出来，下图中每一个方块中存放的是下标：

采用前面所说的「行头堆」思路，每一行的行头仍然是行内子段和最小的数组，伪代码如下：

priority_queue q;
// 放入各个行头 { start, end, sum }
for (i = 0; i < n; i++) q.push({i, i, nums[i]});
// 置换 k 次
int ans;
while (k--) {
    {i, j, sum} = q.pop();
    ans = sum;
    if (j + 1 < n) q.push({i, j + 1, sum + nums[j + 1]});
}

不过这个做法，在 k 比较大的时候，耗时较长，leetcode 上会显示超时。

所以，下面重点看二分答案法。

二分答案法 + 滑窗

最小的子段和，肯定是数组中最小的元素。

最大的子段和，肯定是整个数组的和。

考虑二分答案法，先考虑一个子问题：

数组 nums 中连续子段和不超过一个给定的数字 x 的连续子数组的数目有多少？

数组元素都是非负的，又是求「连续」子数组，可以考虑滑动窗口来解决。

假设滑动窗口的左侧、右侧的位置分别是 L 和 R：

以右侧为主迭代变量，向右扩展 R++。
如果当前窗口的累积和超过 x，继续向右移动 R 肯定会扩大这个和，所以要收缩左侧 L++。
如果当前窗口内和满足 <=x 的条件，则进行计数。

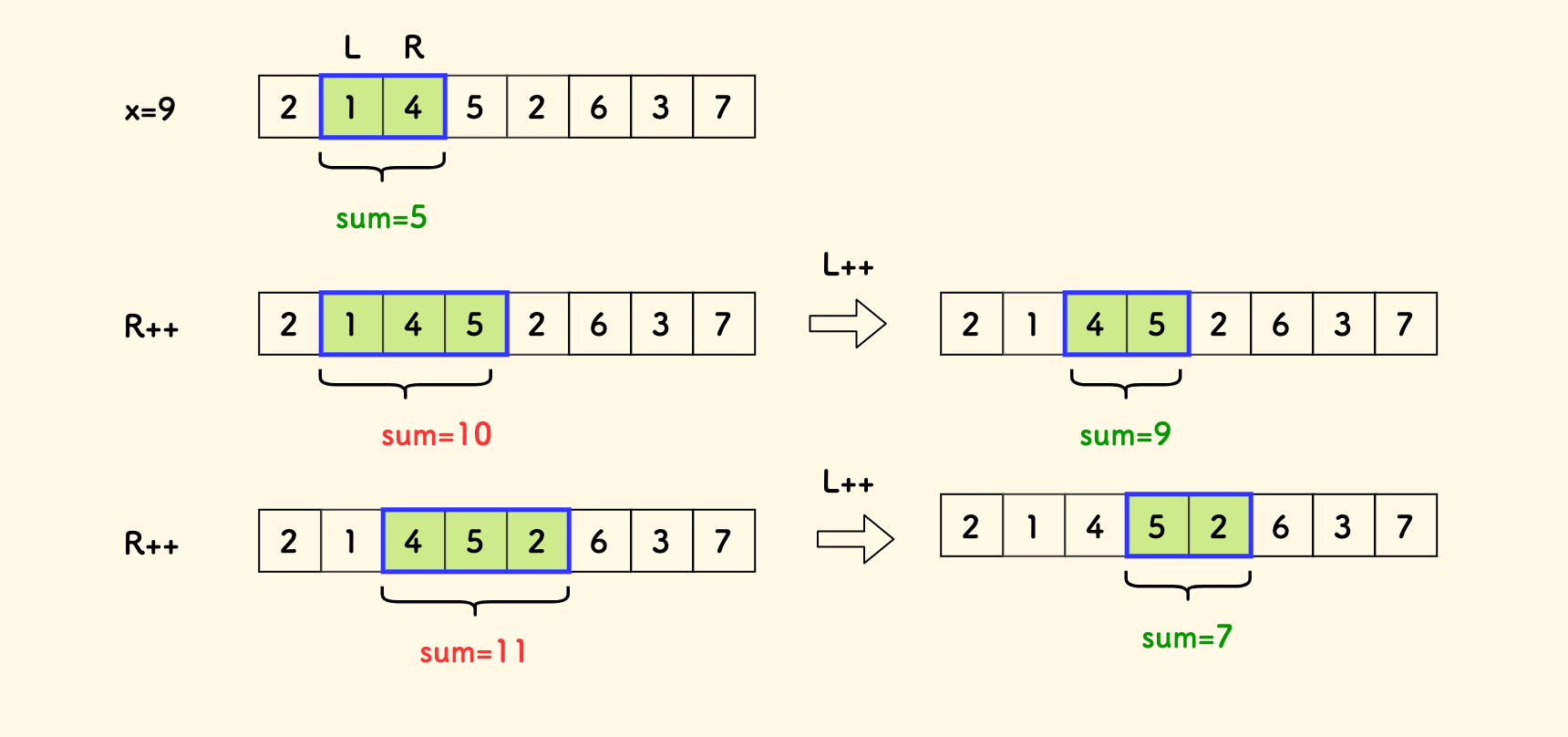
伪代码如下，虽然是两层循环，但是时间复杂度是 O(n)，因为左右界都只会对每个元素至多遍历一次，最多 2n 次。

其中还有一个细节，是计数的时候，要计算窗口内以 R 结尾的子数组数目，而不是计算窗口内所有的子数组数目，防止重复计算，因为 R 会访问每个元素恰好一次。

int count(int nums[n], int x) {
    int ans = 0, L = 0, R = 0, sum = 0;
    while (R < n) {
        // 窗口内和已经超过阈值，左侧收缩
        while (sum > x && L <= R) {
            L++;
            sum -= nums[L];
        }
        // 此时，窗口内和符合 <= x
        // 窗口内的任一子数组都满足条件
        // 以 R 为右界的子数组共 R-L+1 个
        ans += R - L + 1;
        R++;
    }
}

可以推断，count(x) 函数是非递减的函数，输入的 x 越大，符合条件的子数组会越多。

原问题可以转化为：求满足条件 count(x) >= k 的 x 的左界。套用二分模板即可，总体的时间复杂度是 nlog(Sum-Min)

int l = min(nums), R = sum(nums);
while (l < r) {
    int x = (l + r) >> 1;
    if (count(nums, x) >= k) r = x;
    else l = x + 1;
}
return l;

TopK 子段和问题 - 二分答案法 C++ 实现 - Github

延伸 - TopK 数对距离 ¶

从一个非负整数数组中取出两个不同的元素，其差的绝对值定义为这对元素的距离。
求一个给定的数组上第 k 小的数对距离。
-- 来自 leetcode-719

比如数组 [1,3,2,4] 的第 k=3 小的数对距离是 1。

这个问题与 TopK 子段和问题十分相似，而且类似的行头堆的做法，在 leetcode 上也会超时。这里直接介绍二分答案法。

二分答案 + 滑窗

首先，意识到最大的数对距离应该是，全局最大的元素和最小的元素的距离。

最小的距离，应该是最接近的两个元素的距离，所以，在处理之前，不妨先对整个数组正向排序。

考虑一个子问题：

计算有序非负整数数组 nums 中距离不大于给定的数字 x 的距离对的个数。

因为数组已经排好序，元素又都是非负的，可以考虑滑动窗口的做法。

假设窗口的左侧位置是 L，右侧位置是 R，窗口内的元素距离保持不超过阈值 x 。

窗口内元素的距离最大值肯定是：右端减左端，也就是 nums[R] - nums[L]。

滑动窗口的步骤如下：

以右侧为主迭代变量，向右扩展 R++。
如果当前窗口的最大距离已经超过阈值 x，则左测收缩 L++。
因为继续扩展右侧，肯定会造成距离的进一步增大。所以要收缩左端。
如果当前窗口内距离满足 <=x 的条件，则进行计数。

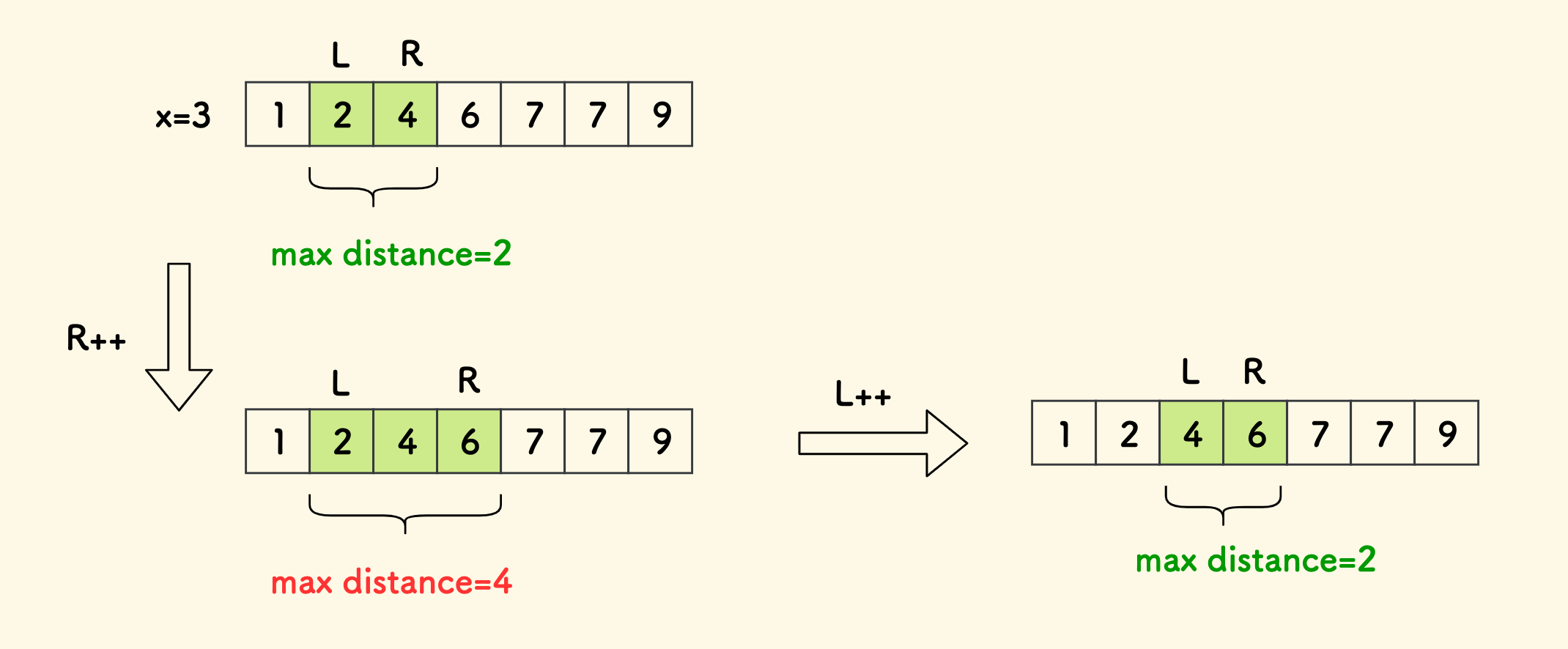
计数的时候，要计算窗口内距离不超过 x 的所有数对的数目。因为 R 会访问数组的每个元素恰好一次，所以只需计算以 R 结尾的距离对的数目，距离对的两个元素不能相同，所以数目为 R-L 个。

伪代码如下，时间复杂度是 O(n) （虽然两层循环，但是左右两个指针每个至多访问每个元素一次。最多 2n 次迭代）。

int L = 0, R = 1;
int c = 0;
while (R < n) {
    while (L < R && nums[R] - nums[L] > x) L++;
    c += R - L;
    R++;
}
return c;

这个计数函数其实也可以用二分来求得。因为数组已经排好序了:

找 z-y <= x 的距离对 (z,y)，就相当于：
对于数组的每个元素 y 找满足 <= y+x 的 z 的右界。

可以线性枚举每个元素，然后二分找右界进行计数。不再展开讨论，时间复杂度 O(nlogn)。

接下来，可以分析出来 count(x) 是一个非递减的函数。输入的数值 x 越大，距离阈值放的越宽，符合条件的数对就越多。可以和之前类似的方式，分析出 count(x) >= k 的二段性。

问题进一步转化为：

找满足条件 count(x) >= k 的最小的 x，也就是找左界。

这个直接套用二分模板就可以了。

初始可行区间的最小值可以直接取 0，最大值是 nums[n-1] - nums[0]，二分枚举的总体时间复杂度是 nlog(Max-Min)。

结尾语 ¶

几个问题中最具代表性的，当属「经典TopK 问题」和「TopK 数对和」。

最具代表性的做法，当属「二分答案枚举」和「行头堆」。

二分答案枚举的方法，看起来非常暴力好用。

这里还有一道二分套二分的做起来细节有点麻烦的问题：2040. 两个有序数组的第 K 小乘积。

（完）

更新记录：

2024/01/04：更新名词「二分判定」为「二分答案」。