CAP 定理是分布式领域中闻名遐迩的一个基石定理, 它表达了一个「鱼和熊掌不可兼得」的遗憾事实: 我们必须从一致性、可用性和分区容忍性中选择两个。 事实上,现实中我们只能从一致性和可用性中选择一个, 因为分区容忍性不可舍弃。 然而,人们对于 CAP 定理的诸多概念和描述都是颇为模糊的, 比如:「分区容忍性」这个 CAP 中最不好理解的性质究竟是什么, 我们常说的一致性和 CAP 定理中的一致性是一回事吗? 大家声称的「高可用」是指什么? 带着这些问题,本文将详细讨论以下内容:
- 从一个例子看为什么 CAP 定理是成立的
- CAP 定理的内容 – 我们要抠概念
- 一致性 – 一致性和一致性的强弱模型、代价。
- 可用性 – 可用性的强弱、高可用和故障转移
- 分区容忍性 – 分区现象和分区容忍性

本文内容非常长,需要读者静心阅读。
从设计一个数据存储系统开始 ¶
首先,我们从一个数据存储系统的设计开始讨论。
我们希望设计一个数据存储系统,它具有以下美好的性质:
- 可用性: 收到请求总会响应。
- 一致性: 两次读请求,总会返回一致的结果。
这两条性质看上去如此简单,却蕴含了人们对分布式系统的无限追求。
对于单节点的系统来说,想要达到这两条性质或许并不难。 我们可以把客户端的请求用队列做线性化处理, 例如下面的图1.1:
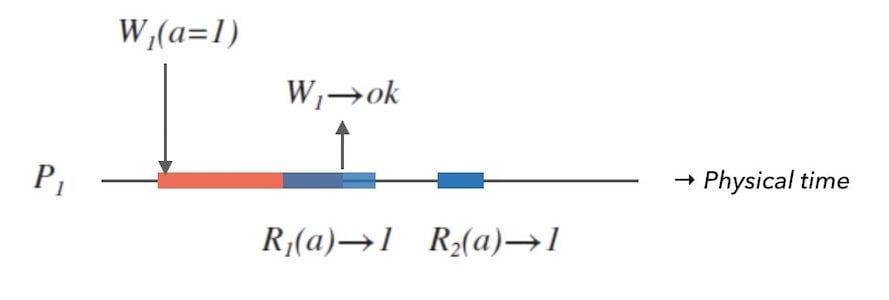
上面的图1.1中,横向黑色实线是物理时间轴, 红色长条是写操作,蓝色长条是读操作。
图中的事件顺序是线性化的,也就是「先收到一定先返回」:
- $W_{1}$ 请求把数据 $a$ 写为 $1$。
- $R_{1}$ 请求读取 $a$ 的值,此时 $W_{1}$ 仍未处理结束。
- $W_{1}$ 执行完成,返回 $ok$。
- 处理 $R_{1}$, 并返回 $1$ 。
- 收到并处理 $R_{2}$ ,返回 $1$ 。
下面图1.2是稍复杂些的单节点系统,包含了「并发读写」和「并发写」的情况。 可以看到,采用线性化方式处理请求的单节点系统是具备一致性的。
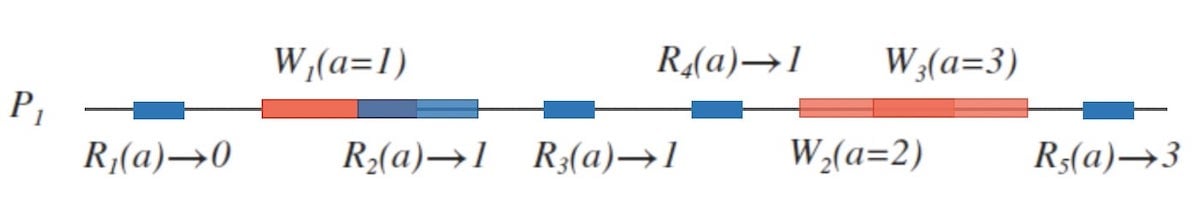
然而,单节点系统有以下问题:
- 服务能力有限。
- 单点风险: 一旦这个节点故障,整个系统将不可用。
更一般地,我们要讨论多节点的分布式系统。 下面的图1.3中是一个由 $P_{1}$ 和 $P_{2}$ 构成的两节点分布式系统。
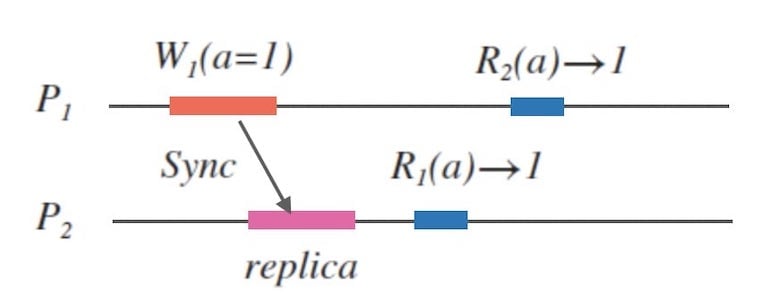
可以注意到,为了 $R_{1}$ 可以在 $W_{1}$ 写入完成后返回正确的查询结果 $1$, 那么 $P_{1}$ 和 $P_{2}$ 之间必然有数据同步。 我们先不论具体的数据同步机制是怎样的, 而是先考虑一个问题:这个网络同步是否可靠?
现实中,网络同步必然有丢包、甚至中断的情况,也就是一定会存在某个时刻, $P_{1}$ 和 $P_{2}$ 是无法网络连通的, 也就是发生了分区现象:
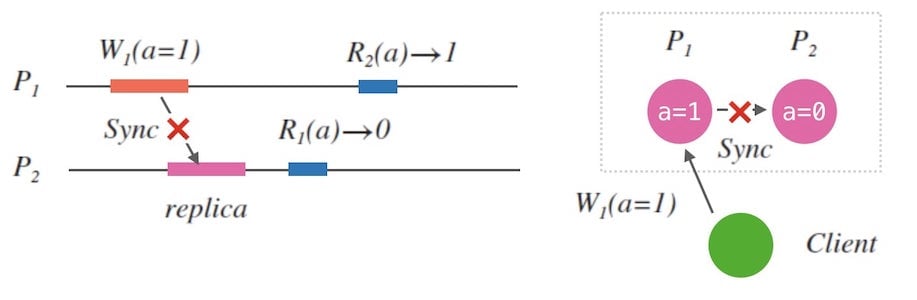
当分区发生时,我们结合下面的图1.5,得出以下结论:
- 如果系统要具有可用性, $R_{1}$ 就必须返回, 由于未同步到副本数据,它只能返回 $0$ , 这和 $R_{2}(a) \rightarrow 1$ 的结果是不一致的。
- 如果 $R_{1}$ 拒绝服务, 即放弃 $P_{2}$ 的可用性, 客户端只能查询另一个节点 $P_{1}$ 拿到一致性的结果。
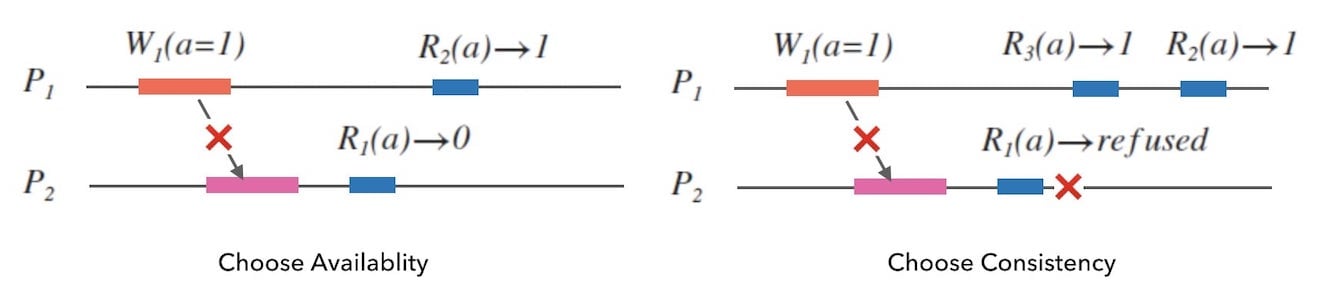
我们似乎认识到,在网络发生分区的情况下,我们必须在可用性和一致性之间做出选择。
读写同一节点,可以避开分区影响吗? ¶
思路延伸一下,如果我们要求客户端的读写请求全部走同一个节点 $P_{1}$ 呢, 这样 $P_{2}$ 是否得到及时同步就不重要了。
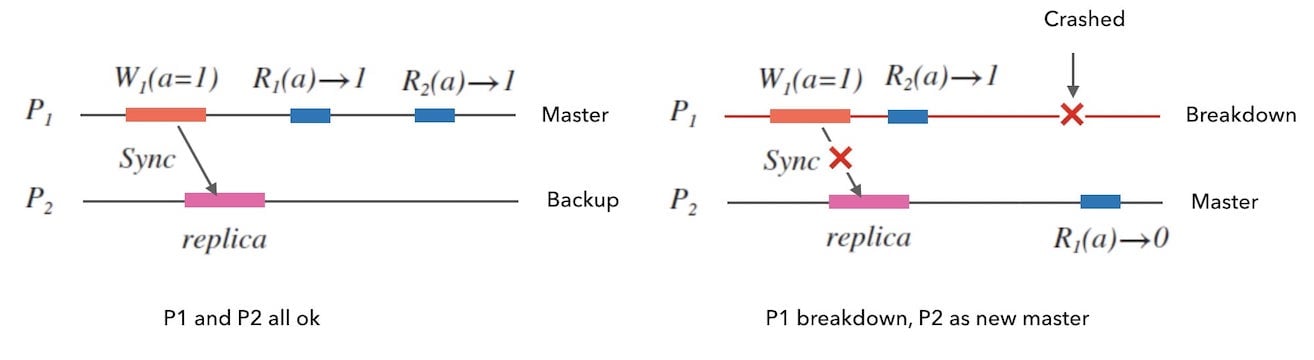
这种情况下, 形成了一种主备结构,$P_{1}$ 叫做主节点, $P_{2}$ 叫做备节点。 只有主节点面向客户端提供服务, 备节点一般不提供服务,只作为数据备份。
貌似这样摆脱了网络分区的影响,但是对于 $P_{1}$ 来讲,面临着和前面讨论的单节点系统完全相同的问题: 服务能力有限、存在单点风险。
即便 $P_{2}$ 可以在 $P_{1}$ 故障后进化成为新的主节点, 来消除单点风险。 但是,网络分区一旦出现, $P_{1}$ 故障前瞬间的写请求仍然不可同步到 $P_{2}$, 就会造成数据丢失以及后续请求的不一致性。
数据同步的两种方式 ¶
我们有说 “节点间必然有数据同步的机制, 不然无法读取到跨节点的写更新”。
数据同步的方式可以分为:
- 同步: 所有节点写入完成后,返回写入成功。
- 异步: 先返回写入成功,再同步到其他节点。
下面的图3.1是两种数据同步方式的示例,紫色长条表示数据备份:
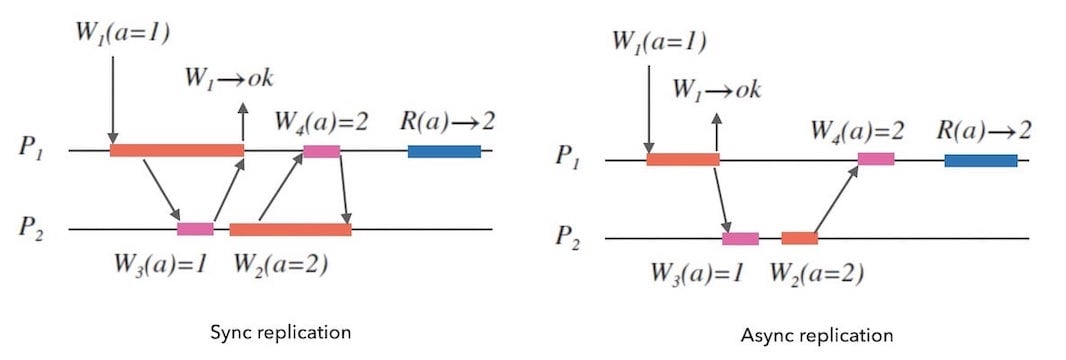
当然,同步和异步的方式并不是绝对的, 我们可以设计出先同步写 $N$ 个节点,回复客户端,再异步写入其他节点的方式。
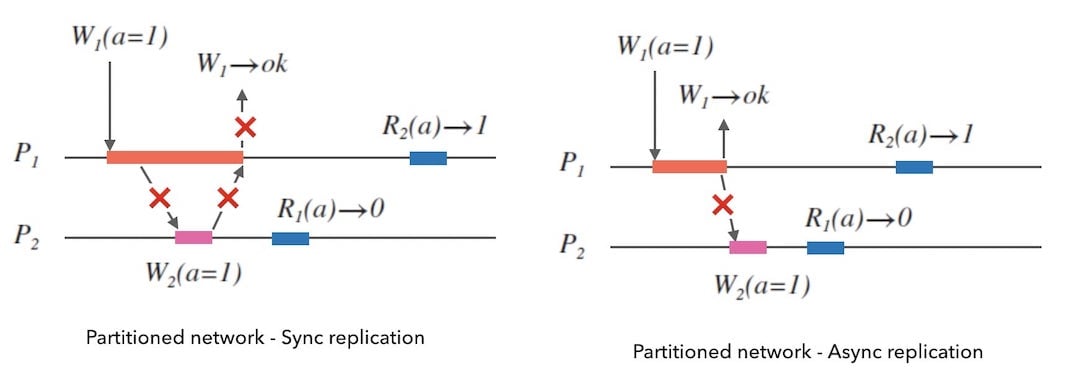
不过,我们稍加分析即可以发现, 网络分区发生的时候,无论同步还是异步的方式,如果不放弃可用性,都不能保证一致性。
CAP 定理 ¶
经过前面的一番讨论之后,所谓「CAP 定理」已经呼之欲出了。
CAP 定理又叫做布鲁斯定理, 该定理源于埃里克·布鲁尔在2000年的分布式计算原理研讨会上提出的一个猜想, 在2002年麻省理工学院的Gilbert和Lynch发表了证明[1],使之成为一个定理:
分布式系统不可能同时保证 一致性(Consistency)、 可用性(Availability) 和 分区容忍性(Partition tolerance)。
这就是所谓「CAP」的名字由来,我们只能在 $C$、$A$、$P$ 中三个性质中选两个。
这个定理也可以表达为: 在网络分区发生的情况下,分布式系统不能同时保证一致性和可用性。 除非是单节点系统, 否则无法同时保证 $CA$。
这个结论在分布式领域已经耳熟能详, 不过, 关于 CAP 定理,需要特别注意搞清楚以下两点:
- CAP 定理范畴下的一致性、可用性、分区的概念都是 非常狭义的 。
- CAP 所说的一致性其实是 线性一致性。
- CAP 所说的可用性其实是非常高的可用性。
- 分区现象在现实网络中不可避免,也就是说,现实中我们只能在 $C$ 和 $A$ 中做选择。
CAP 其实在说 强一致性和高可用性,二者择其一 。
至此,我们或许仍然不能深刻地理解 CAP 定理, 这需要进一步分别讨论这三个性质。
分区容忍性 | Partition tolerance ¶
在前面的讨论中,我们曾多次提到「分区现象」, 正是这个问题导致我们无法同时具备一致性和可用性上。 要了解分区容忍性,就要先了解什么是分区现象。
当两个节点之间的网络不再连通,相当于分成了几块分区,所以叫做分区现象。
下面的图4.1是一个网络分区现象的示意图, 图中出现了三个分区:
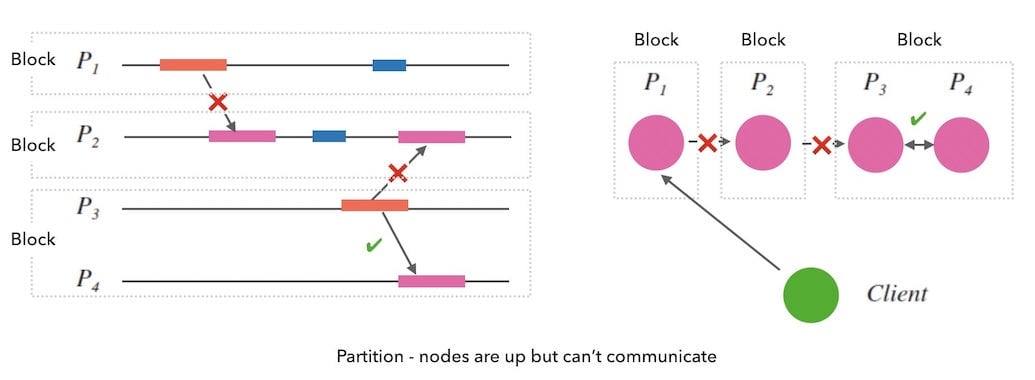
分区所强调的是 节点间的不连通问题,即使每个节点都可以工作 。
简单来说,Partition != Crash。
节点故障一般会造成节点的无响应,导致分区出现, 但是分区的出现不一定代表节点真的故障(宕机)了。
CAP 定理中对分区的定义[1] 同样是相对狭义的 , 比连通性更广义的分区界定是按通信时限的说法:
如果不能在通信时限内达成数据一致,就意味着发生了分区。
例如下面图 4.2 中,数据同步的消息多次重试后,两个节点没有在一定时限内达成数据一致,此时即认为发生了分区。
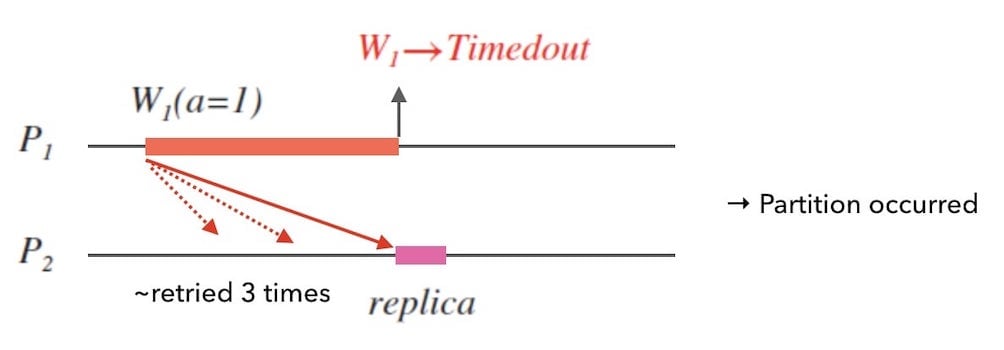
分区现象的概念清楚了后,我们看分区容忍性:
在分布式系统中, 分区容忍性是指即使分区现象发生,系统仍然可以工作的性质。
Continues to function even if there is a “partition”.
换句话说,系统不能在分区发生的时候,选择停机来躲过分区影响的时段。
分区容忍性没有要求分区发生时返回数据的正确性,也没有要求不能回复客户端错误消息, 只有一个约束,就是「不能在分区时停机」。
我们回头看下上面的图 4.2,在分区发生时, $W_{1}$ 最终返回了错误消息 $Timedout$, 即放弃可用性,保证一致性。
现实中的分布式网络,丢包、延迟、中断都是存在的, 所以在实际的系统设计中,分区容忍性是必选的。 也就是说,我们只能在可用性和一致性这两个性质中做选择。
可用性 | Availability ¶
先用最直观地方式理解下其含义:
在分布式系统中,可用性是指每次请求都能获取到非错的响应的性质。
Availability = Reads and writes always succeed.
下面的图 5.1 中, 左边的 $S_{1}$ 具有可用性; 右边的 $S_{2}$ 则不具有可用性。 因为在 $S_{2}$ 中, 由于系统设计的原因,并发写和并发读写导致了带有错误的回复消息。
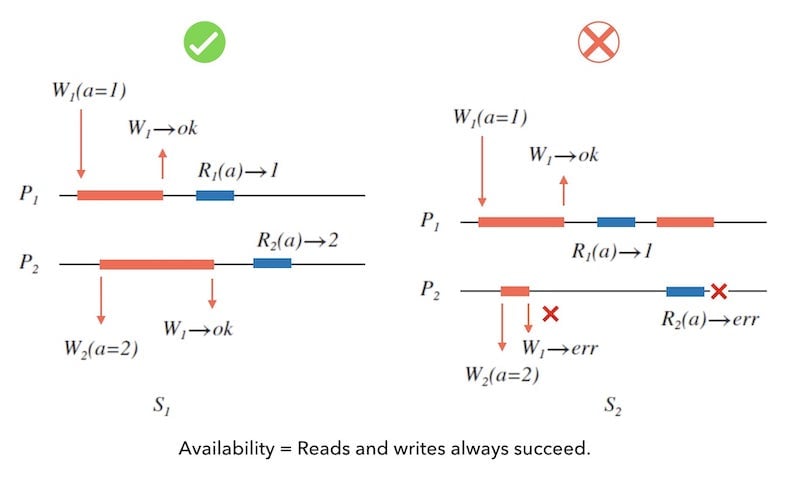
可用性并没有要求读到的数据的正确性,只描述了系统可以总可以非错的工作的能力。
同样,我们看一下,CAP 定理的证明者 Gilbert 和 Lynch 的描述[1]:
Every request received by a non-failing node in the system must result in a response. That is, any algorithm used by the service must eventually terminate.
如果客户端发送一个请求给分布式系统中的一个无故障的节点, 这个节点必须回复请求。 就是,系统所用的任何算法都必须最终结束。
网络分区发生可能持续任意长时间, 如果被请求的节点在一定时间内无法响应, 或者直接简单地响应一个超时或者拒绝服务的错误, 都是不具备可用性的。
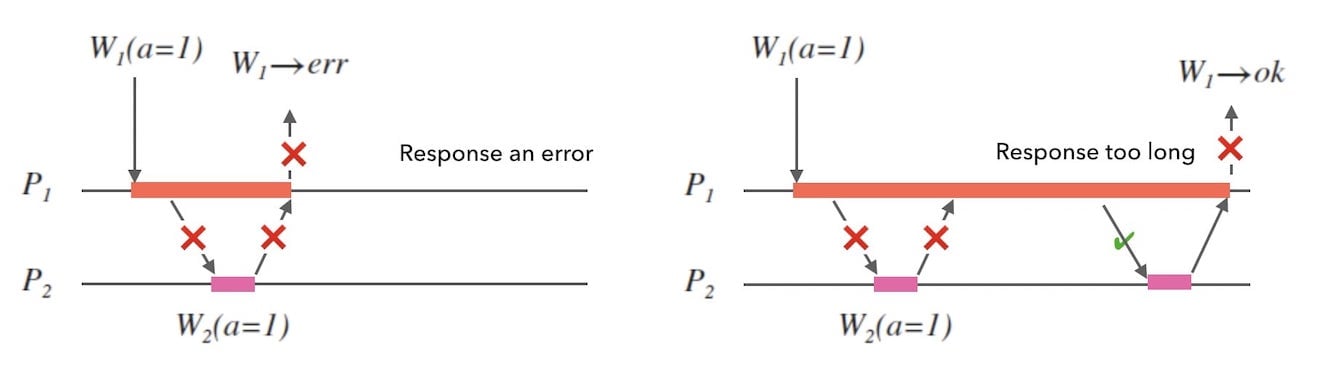
那么,节点故障时,我们是否可以仍然保证可用性?
方法是故障转移: 把故障节点的负载转移给备用节点负责。 下面的图 5.3 演示了主备结构下的故障转移:
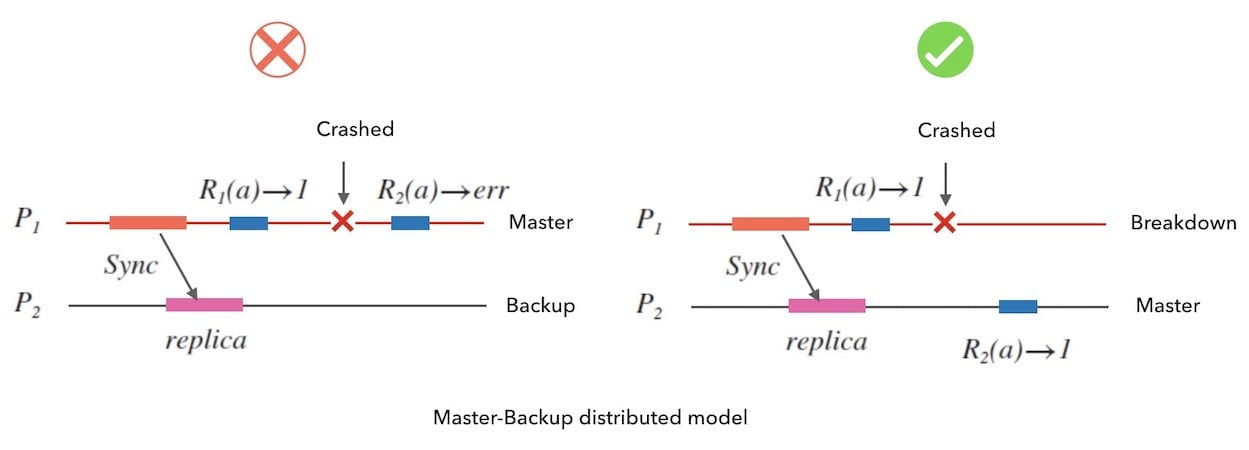
我们注意到,CAP 定理对可用性的定义存在一个 non-failing 的限定语。 也就是说,在 CAP 的范畴下,如果一个系统没有做好故障转移的逻辑, 那么这个系统不具备可用性。
CAP 定理中的可用性的定义,可以说很强,也可以说很弱:
- 很强,是因为要求必须响应 100% 的请求。
- 很弱,是因为并没有要求响应的时限,只需要最终返回。
而通常我们对系统的响应时限是有要求的, 所以说 CAP 定理中的可用性的条件很强, 在 CAP 的理论范畴下,没有「可用性的强弱程度」一说。
综合看来, CAP 定理中对可用性的定义是狭义的。
在实际中,可用性却不是一个非黑即白的简单判定, 和工程上对一致性的概念类似,存在不同可用性高低之分的说法。 我们常说的高可用性 high availability, 一般是指部分节点损失后整个系统仍可以正常工作。 要达成高可用性,就必须做好故障转移。 所以我们也可以说, CAP 定理中的可用性其实是我们所说的高可用性,而且是最高的可用性 。
下面我们列举两种保可用性的方法,都是万变不离其宗地围绕着「故障转移」的思路。
一个方式是通过代理完成故障转移, 这就是工程上熟知的基于代理方式的负载均衡 (负载均衡的主要目的虽然是合理分配负载,但可用性也是其带来的好处之一)。
下面图 5.4 是 一个例子。 当 $P_{1}$ 故障时,代理服务可以发现并暂时把 $P_{1}$ 从代理列表中踢出。 把后续的请求转发到健康的 $P_{2}$ 上去。
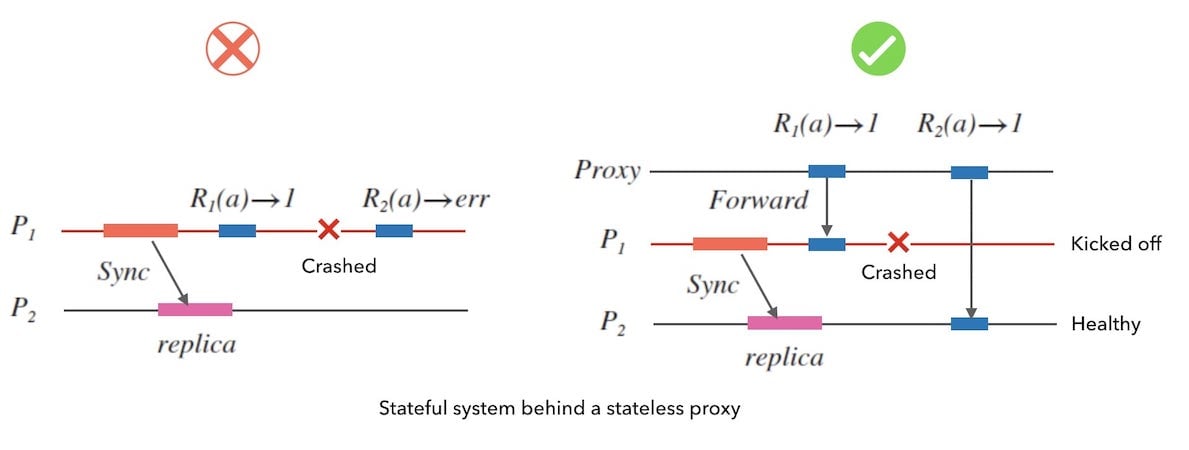
还有一种方式,我们甚至可以 配合客户端完成故障转移。 这就是另外一个工程上常用的负载均衡方案, 叫做「客户端侧的负载均衡」。 下面图5.5是一个例子, 客户端可以通过监测目标系统的服务器健康情况, 来决定向哪一个节点发起请求。
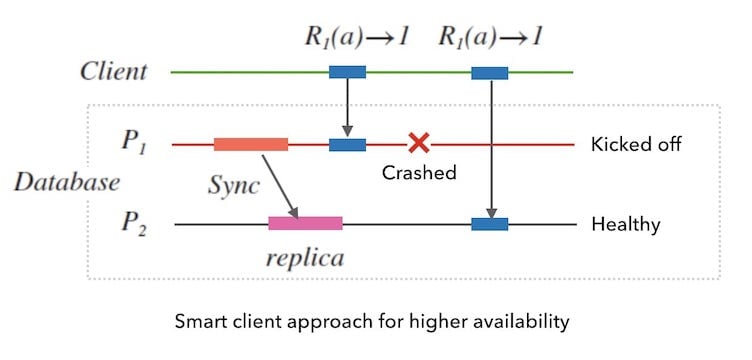
此外,实践中,还可以通过减少人工维护造成的系统宕机、 gracefully-shutdown、添加系统报警等手段来提高系统的可用性。
可用性的度量方式,通常是系统可用时间和总运行时间的比值。 在技术运营上,可用性指标一般是系统运营的核心目标(所谓「 N 个 9 标准」)。
一致性 | Consistency ¶
简单直观地理解是: 分布式系统中多个节点的数据返回始终一致的性质。
Consistency = two reads return the same value.
下面的图6.1中, 我们可以这样讲:左边的 $S_{1}$ 具有一致性, 右边的 $S_{2}$ 则不具有一致性。
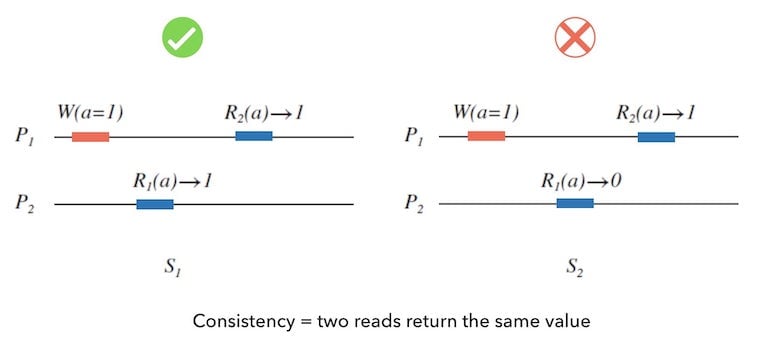
一致性可以理解为「正确性」。
具有一致性的系统,在读写逻辑上并不会给客户端带来「惊讶」。
下面列举的情形,都是不具备一致性的表现:
- 两次读取,分别读到 $R_{1}(a) \rightarrow 1$ 和 $R_{2}(a) \rightarrow 2$ 。
- 在写操作 $W(a=1) \rightarrow ok$ 成功后, 却读到了 $R(a) \rightarrow 2$ 。
- 在写操作 $W(a=1) $ 未完成之前, 却读到了 $R(a) \rightarrow 1$ 。
Gilbert 和 Lynch 对一致性的描述是这样的[1]:
Any read operation that begins after a write operation completes must return that value, or the result of a later write operation.
在一个具有一致性的分布式系统中,一旦一个对任一节点的写入返回成功, 后续对这个系统中其他任意节点的读操作都应该可以返回这个更新的值。
Gilbert 和 Lynch 的话, 换一个简单的理解方式说:
All nodes see the same data at the same time.
所有节点在同一时刻的看到的数据是一样的。
可以看到, CAP 定理中的一致性,要求所有节点都可以看到最新修改的数据。 其实这个要求是非常强的, 我们接下来会讨论一致性的模型, CAP 中的 C 就是强一致性中的线性一致性 。
一致性的分类 ¶
实际中,一致性也不是非黑即白的性质, 而是有强弱之分。 人们对一致性的研究和实践中, 按照强弱程度建立了一致性模型。 一致性按强弱程度可以分为三类:
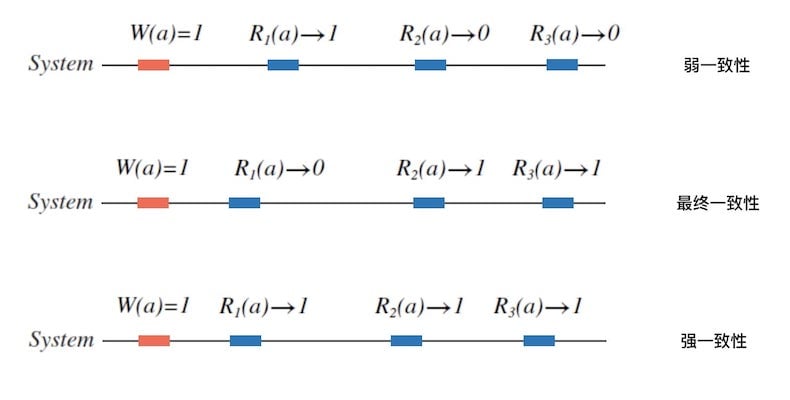
弱一致性
After a write, reads may or may not see it.
向系统写入一个值后,后续的读操作可能读出来,也可能读不出来。
最终一致性
After a write, reads will eventually see it.
向系统写入一个值后,后续立刻的读操作可能读不出来,但是在某个时间段后,读取一定成功。 例如,读写分离的关系型数据库。
强一致性
After a write, reads will always see it.
向系统写入一个值后,后续任意时刻的读取一定成功。
下面的图 6.2 给出了一致性分类的示例:
事件先后和并发 ¶
在进一步讨论这些一致性模型之间,需要先了解全序和偏序关系[2]。
偏序和全序是序理论中常用的两种序关系, 举例来说:
- 自然数之间的大小关系是全序关系,因为所有数字都可以相互比较。
- 集合之间的包含关系则是偏序关系,因为并不是所有集合都有包含关系。
- 复数之间的大小关系就是偏序关系,复数的模之间的关系是全序关系。
简短说: 偏序是部分可比较的序关系,全序是全部可比较的序关系 。 关于全序和偏序更多的信息,可以看这里:逻辑时钟-如何刻画分布式中的事件顺序#全序和偏序。
在分布式系统中, 事件的先后关系通常用「happened before」的关系符, 比如 $W_1 \rightarrow W_2$ 表示 $W_1$ 在 $W_2$ 之前发生。 如果两个事件无法比较先后,我们说两个事件是并发的, 记作 $W_1 \parallel W_2$。
假设节点之间的物理时钟是精确对齐的, 那么我们完全可以根据事件发生的时间戳来判定事件先后关系。 这就是一种全序关系。 然而因为网络延迟的不确定, 时钟精确同步的这种假设是不符合现实情况的。
不同的分布式协调算法,对事件先后的判定逻辑也是不同的。 但是我们一定知道以下先后关系是确定的:
- 节点内的事件先后顺序
- 一次更新的读成功一定发生在写成功之后
观察下面图7.1, 我们可以推导出来一些先后关系和并发关系。
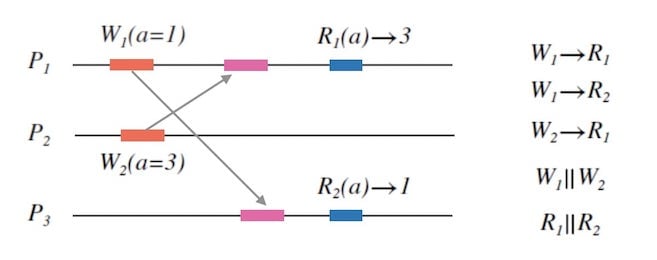
在分布式的事件顺序的理解上,我们一定要清楚的是: 事件的先后关系是具有相对性的。 我们无法在系统中创造一个上帝视角观察到全局情况, 只能通过每个节点对系统的局部感知来推导全局的事件顺序是怎样的, 这取决于我们的一致性协调算法是如何构建的, 而且我们甚至可能无法推导出全序关系, 只能推导出部分事件的偏序关系。 (了解更多可以看 逻辑时钟-如何刻画分布式中的事件顺序#事件先后的相对性)。
一致性模型 ¶
下图8.1中是一种一致性分类 更为精细、严格的一致性模型:

我们接下来详细讨论几个常见的一致性模型, 请注意从事件顺序的角度去观察它们之间的区别:
严格一致性 Strict Consistency
最强的一致性,要求任一节点的任一写入对所有节点立刻可见。
同全局物理时钟一样[2],严格一致性是一致性模型中的可望不可及的灯塔, 现实中,严格一致性是很难实现的, 因为节点间的网络同步的延迟是无法确定的。

图8.2 - 严格一致性的正反例 线性一致性 Linearizability Consistency
也叫做原子一致性 (atomic consistency) 或者 强一致性 (strong consistency),即 CAP 定理中的 C 。 其约束条件如下:
- 任何一次读都能读到某个数据的最近一次写的数据。
- 要求系统中的所有节点看到的事件顺序,都和全局时钟下的顺序一致。
简而言之, 线性一致性要求所有节点达成和物理时钟顺序一致的全序一致 。
我们在本文开头讨论单节点系统时,有提到, 对请求做线性化处理可以对单节点系统实现强一致性。 一个办法就是对请求做队列化,永远是 先到的请求先返回。 在多节点的分布式系统中也是一样的, 线性一致性要求整个系统的请求处理在客户端看来是线性化的。
下面图 8.3 中, 左边的 $S_1$ 是符合线性一致性的,右边的 $S_2$ 则不符合。 我们观察 $S_1$ 可以得出,在外部的客户端的视角上,发给的$S_1$的事件顺序是 $W_{1},W_{2},R_{1},R_{2}$, 回复的事件顺序同样如此, 整个系统的请求处理好像是由单节点来完成的一样, 是线性化的, 这也正是线性一致性的建模出发点。

图8.3 - 线性一致性的正反例 可以观察到,在符合线性一致性的情况下, 事件顺序具有全序关系[2], 并且这个全序和全局物理时间上请求收到的顺序一致。
细心观察图8.3我们可以知道, $S_2$ 和 $S_1$ 的不同点, 在于 $S_2$ 没有按线性化的方式协调并发请求的处理顺序。 但是 $S_2$ 仍然协调了一个全序关系, 它是符合更弱一些的顺序一致性的。
顺序一致性 Sequential consistency
同样是一种强一致性, 由分布式领域的传奇人物 Lamport 于 1979 年提出, 其约束如下:
- 任何一次读都能读到某个数据的最近一次写的数据。 (和线性一致性的第一条一样)
- 所有进程看到事件顺序是合理的,可以达成一致即可,并不要求所有进程看到事件顺序和全局物理时钟上的事件顺序一致。
可以看到,顺序一致性是在线性一致性的基础上有一定的弱化:
- 这点不变:所有节点对事件顺序仍然要达成一致的全序关系[2]。
- 不同在于:这个全序关系不必要和实际全局物理时钟上的事件顺序一致。
简而言之, 顺序一致性要求所有节点达成全序一致 。
下面图8.4中, 左边的 $S_1$ 是符合顺序一致性的, 因为所有节点的视角上看到的事件顺序是一致的。 右边的 $S_2$ 则不符合, 因为 $P_3$ 和 $P_4$ 没有对 $1$ 和 $2$ 的更新顺序达成一致。

图8.4 - 顺序一致性的正反例 和线性一致性相同的点在于: 顺序一致性仍然要求所有节点的视角在全序上一致。 不同的地方在于, 顺序一致性不再要求节点看到的事件顺序一定要是物理时钟上的真实事件顺序, 即 顺序一致性不保证请求处理的先到先回。 比如图8.4中, $S_1$ 中每个节点看到的更新顺序其实是 $2,1$, 这并不符合物理时钟上的真实的顺序 $1,2$。
对于并发请求, 顺序一致性只要求协调出一个所有节点都一致的顺序即可,而不要求这个顺序一定符合物理时间上的真实顺序。
因果一致性 Causal Consistency
因果一致性是一种最终一致性,在顺序一致性的基础上,进一步弱化了约束:
- 不再要求:所有节点看到一致的全序关系。
- 只要求:节点间因果相关的事件顺序要达成一致。
什么是「因果相关」呢? 就是前面我们偏序中所讲的事件先后关系, 并发的事件则因果无关。 对于不同的一致性协调算法, 因果相关取决于具体的算法设计。 同样,无论协调算法如何设计,我们仍然一定有前面那两条因果判断:
- 节点内的事件之间一定有先后顺序
- 一次更新的读成功一定发生在写成功之后
下面的图 8.5 是因果一致性的正反例。 左边的 $S_1$ 是符合因果一致性的, 因为各个节点都可以对因果关系达成一致。我们可以确定,在同一个节点内的事件顺序 $W_2 \rightarrow W_3$, 还可以由通信传播而确定跨节点的事件顺序,例如 $W_3 \rightarrow R_5$ ,因为既然读到了 $a = 3$, 那一定有写 $a = 3$ 发生过。 但是 $W_1$ 和 $W_2$ 是并发写的,无法判断顺序,那么对于 $P_3$ 和 $P_4$ 来说, 结论就是,应该无法判断 $a$ 更新到 $1$ 和 更新到 $2$ 的值这两个的先后顺序。但是应该能判断出来 $a$ 先更新到 $2$ 还是先更新到 $3$ 的顺序, 这两点,$P_3$ 和 $P_4$ 都做到了,所以说 $S_1$ 符合了因果一致性。
而右边的 $S_2$ 则不符合因果一致性。 因为$P_3$ 中先读到了 $3$ 后读到了 $1$, 在 $P_3$ 的视角里 $a$ 先更新到了 $3$ 再更新到了 $1$。 而在 $P_1$ 的视角里 $a$ 先更新到了 $1$ 再更新到了 $3$, 两个节点的因果顺序不一致。

图8.5 - 因果一致性的正反例 在$S_1$ 中,由于$W_1 \parallel W_2$, 所以导致了 $P_3$ 和 $P_4$ 中对 $a=1$ 还是 $a=2$ 没有一致。 我们注意到并发请求是因果无关的,所以 $S_1$ 确实是符合因果一致性的。 因果一致性没有要求对并发进行协调, 因为因果一致性不要求对因果无关的事件的顺序达成一致。
下面的图8.6是另一个不符合因果一致性的反例。 原因在于, $W_1 \rightarrow R_1$ 和 $R_1 \rightarrow W_2$ 可以推导出来 $W_1 \rightarrow W_2$ 。 但是 $P_3$ 的视角上 $a$ 先更新到 $2$ , 再更新到 $1$ , 矛盾。

图8.6 - 因果一致性的反例 关于因果一致性,我认为最重要的一个特征是,因果一致性要求构建的是偏序,不是全序。 著名的向量时钟算法[2],就是一种符合因果一致性协调算法, 算法的核心则是构建偏序关系的向量来描述事件顺序。
现在可以从事件顺序的角度总结下这几个一致性模型:
- 严格一致性: 依赖绝对的全局物理时钟, 无法实现。
- 线性一致性: 要求达成事件顺序的全序一致, 且和物理时钟上的事件顺序一致。
- 顺序一致性: 要求达成事件顺序的全序一致。
- 因果一致性: 要求达成事件顺序的偏序一致,不必协调因果无关事件的顺序。
不同强弱的一致性模型,其实现的难易程度、和带来的代价也是不同的。
一致性的代价 - 响应时长 ¶
回头看下 CAP 定理关于可用性的定义, 其中并没有对响应时限做出约束。 如果一个客户端请求的响应非常非常慢,但是最终得到了响应,在 CAP 的范畴下,这仍然是具有可用性的。
更广义的可用性, 应该是在约定时限的要求下做出响应。 现实中,人们往往是非常关心响应时间的。 我们将看到, 强一致性的代价就是相对高的响应时长。
在理论计算机科学中,除了为人熟知的 CAP 定理之外,还有一个叫做 PACELC 的定理, 这个定理是 CAP 定理的一个扩展定理。
PACELC 定理的命名方式和 CAP 如出一辙,我们来看下这个定理的含义[4]:
当分区(Partition)发生的时候, 必须在可用性(Availability) 和 一致性(Consistency) 中做选择; 否则(Else),当分区不发生时, 必须在响应时长(Latency) 和 一致性(Consistency)中做选择。
前半句的意思,就是CAP定理本身。 后半句则指出了:无分区的情况下,要追求更强的一致性, 就要接受更高的响应时长。
这是个非常酷的结论, 它把可用性的概念广义化到了响应时长。 我们不做理论证明, 而是通过简单的示例分析来解释下为什么会有这样的结论。
在前面的「数据同步的两种方式」章节中, 有提到节点间两种数据同步方式: 同步和异步。 再次回顾图 3.1 中两种节点间数据同步的方式可以显然地看到: 同步的方式对客户端的响应时长更高 。
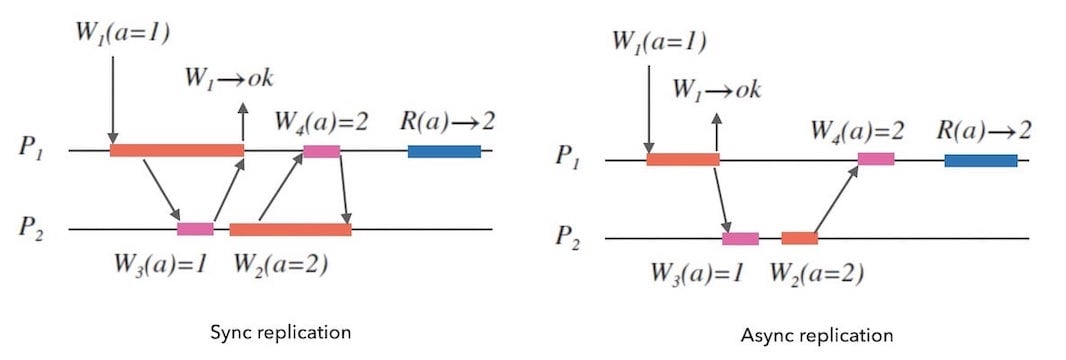
我们接下来可以通过一个小图例来看到, 异步的节点间数据同步方式会降低系统的一致性强度 。
观察下面的图9.1, 左边的 $S_1$ 中写请求会在其他节点完成数据同步后再回复客户端写入完成, 也就是同步方式。 右边的 $S_2$ 中写请求会直接响应客户端,异步地对其他节点进行数据同步。 在左右两个图中, 假如我们在$P_2$未完成数据副本同步之前的这个时间窗内, 从不同的节点分别去读$a$, 在$S_1$ 中会得到一致性的结果, 而在 $S_2$ 则会得到不一致的结果。 也就是异步的数据副本同步方式会降低系统的一致性强度。
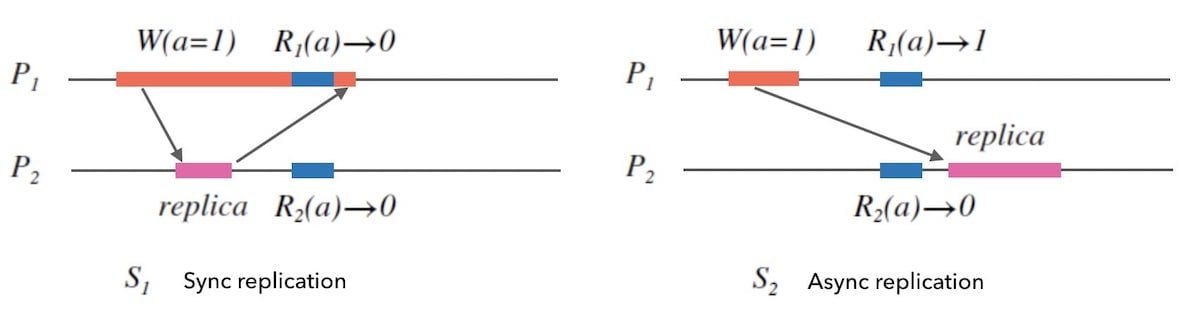
综合来看,我们就可以(不严格地)得到这个结论,要做到更强的一致性,就要接受更高的响应时长。
在论文《A Critique of the CAP Theorem》有总结不同的一致性模型下的读写响应时长和网络延迟 $d$ 之间的关系[3], 其中 $O(d)$ 是一种类似复杂度的表示方法, $O(d)$ 表示请求是网络延迟时长敏感的, $O(1)$ 表示请求是和网络延迟无关的。
| 一致性(consistency) | 写响应时长(write latency) | 读响应时长(read latency) |
| 线性一致性 | $O(d)$ | $O(d)$ |
| 顺序一致性 | $O(d)$ | $O(1)$ |
| 因果一致性 | $O(1)$ | $O(1)$ |
可以通过这个研究小结中看出, 三个常见的一致性模型的读写请求对网络延迟的敏感程度。 也清晰地看到了: 更强地一致性的代价是更高的响应时长。
「CP 或者 AP」 并不是绝对的选择题 ¶
在本文即将结尾的时候, 我们回头再看一下 CAP 定理:
在实际的分布式系统设计中,我们无法同时达成强一致性和高可用性。
CAP 定理是我们在设计一个分布式系统之初时的一个有益参考, 它让我们在设计系统的时候不必浪费时间去寻求理论上都达不成的目标。
CAP 范畴下的一致性和可用性的定义其实是非常狭义的、非常精确的, 它所讨论的是非常极限的情况, CAP 只否定了我们没办法同时达成最强的一致性和最高的可用性。 在实际中,一个分布式系统根本不可能完全放弃 C、或者完全放弃 A, 我们要做的是选择哪个多一点。
选择 C 多一些的情况
为了实现更强的一致性,这个系统可能会在某些情况下拒绝服务、甚至直接关闭节点。 实例中,比较偏好 C 的有 Zookeeper,Hbase,MongoDB 等。
选择 A 多一些的情况
为了实现更高的可用性,这个系统必须做好故障转移,尽可能地响应所有请求,但是有可能返回不一致的结果。 实例中,比较偏好A的是有D ynamo,CouchDB,Riak,Cassandra 等。
没有绝对的选择和放弃,只有更偏好哪个和弱化哪个的说法。
话说, 我们可以做到 CAP 定理下的 CA 吗? – 单节点能 :)
Scaling is hard.
链接 & 脚注 ¶
- Gilbert and Lynch. Brewer’s conjecture and the feasibility of consistent, available, partition-tolerant web services.
- Chao’s blog. 逻辑时钟 - 如何刻画分布式中的事件顺序
- Martin Kleppmann. A Critique of the CAP Theorem
- Daniel J Abadi. Consistency tradeoffs in modern distributed database system design.
– 毕「分布式的CAP定理和一致性模型」
本文原始链接地址: https://writings.sh/post/cap-and-consistency-models





