跳跃表的构造思路和基本操作（跳表 skiplist）

跳跃表 是一种随机化的存放有序元素的数据结构， 对于元素个数为 n 的跳跃表，查找和插入的平均时间复杂度都是 $O(logn)$ ，具有查找快、增删方便、容易实现的优点。

内容目录：

构造思路 ¶

最简单的存储 n 个元素的容器是 数组 和 单链表 。

对于一个有序的数组，采用 二分法 查找一个元素的时间复杂度是 $O(logn)$ ， 但是因为数组存放在连续内存上，插入一个元素则需要移动一批元素。

对于一个有序的单链表，查找一个元素，只能一个一个查看，时间复杂度是 $O(n)$ ，不过，插入一个元素不需要像数组那样移动元素。

那么，是否可以设计一种有序的数据结构，具有 $O(logn)$ 的查找时间、插入元素时也无需移动元素呢？

接下来，将在链表的基础上，加速查找过程，构造出跳跃表。

对一个单链表，做一些冗余，每隔一个节点，搭一条线，指向下下个节点。 另外，给单链表加一个虚拟头节点，它不存储具体数据，只充当链表头。

如此一来，查找一个值，最坏情况下总共需要考察 $ (n/2) + 1$ 个节点。

具体的查找方法是， 从左上角的节点出发，向右考察每个节点，如果右边节点比目标值小， 则继续向右，否则，进入下一层继续，直到最底层。

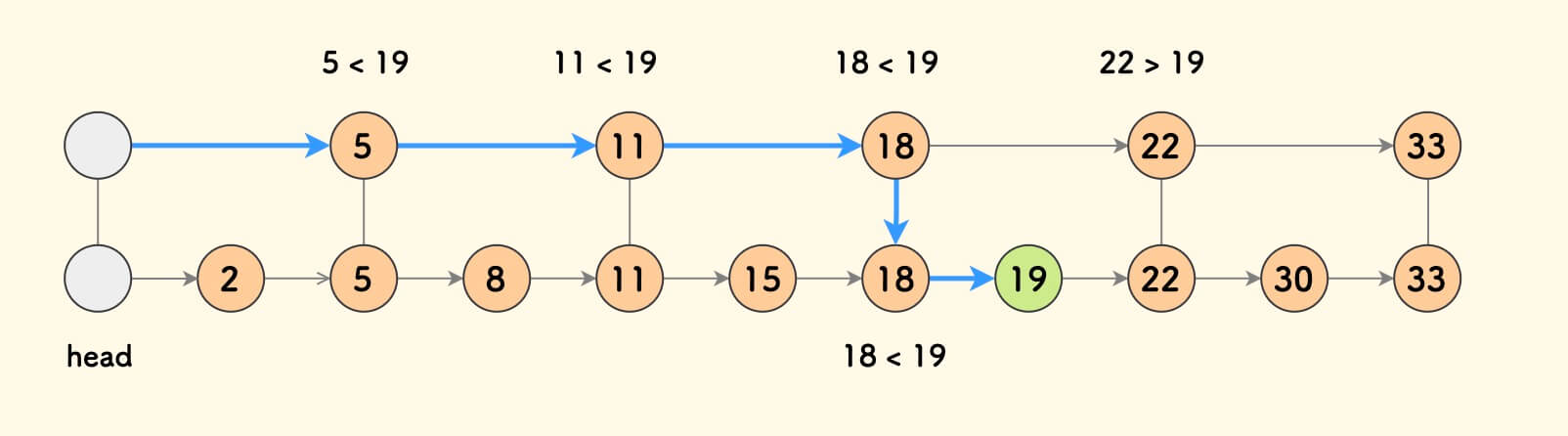
沿着这一思路，再每隔一个节点，搭一条线， 此时，查找一个元素最多需要考察 $(n/4) + 2$ 个节点。

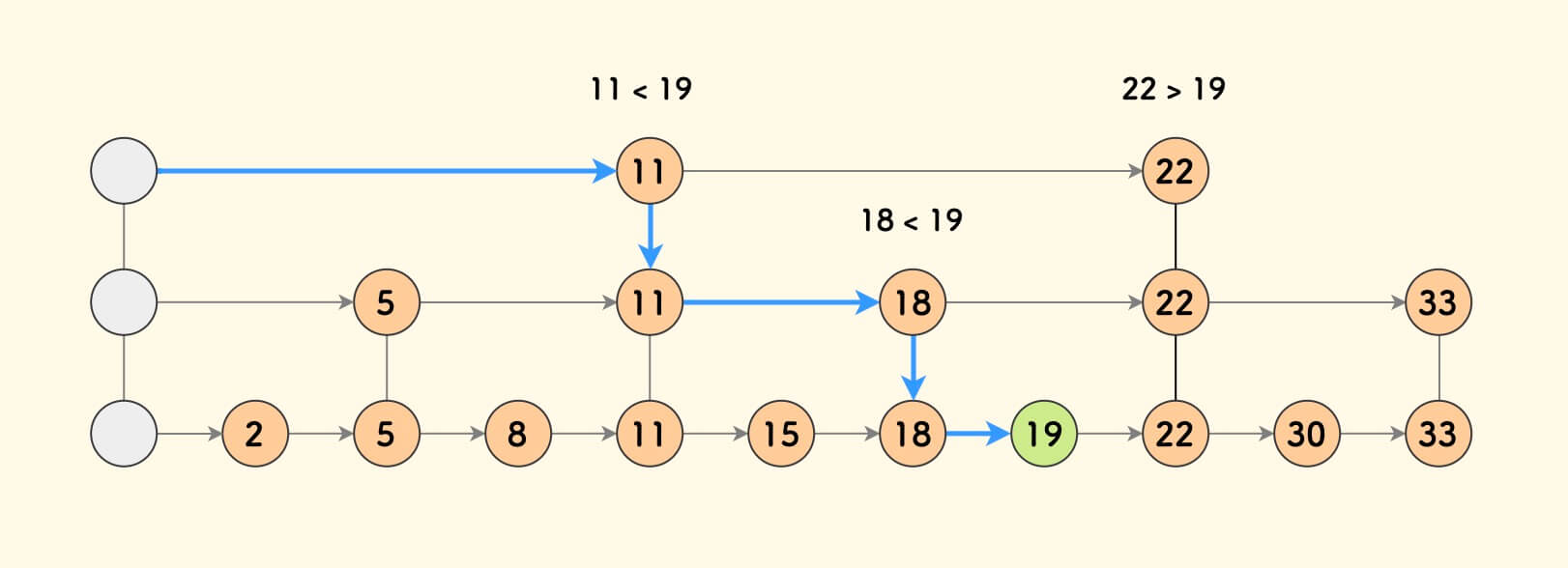
可以推测，盖楼达到 k 层时，查找目标需要考察 $2^{-k} + k$ 个节点。

直到，没有节点可以继续盖楼。

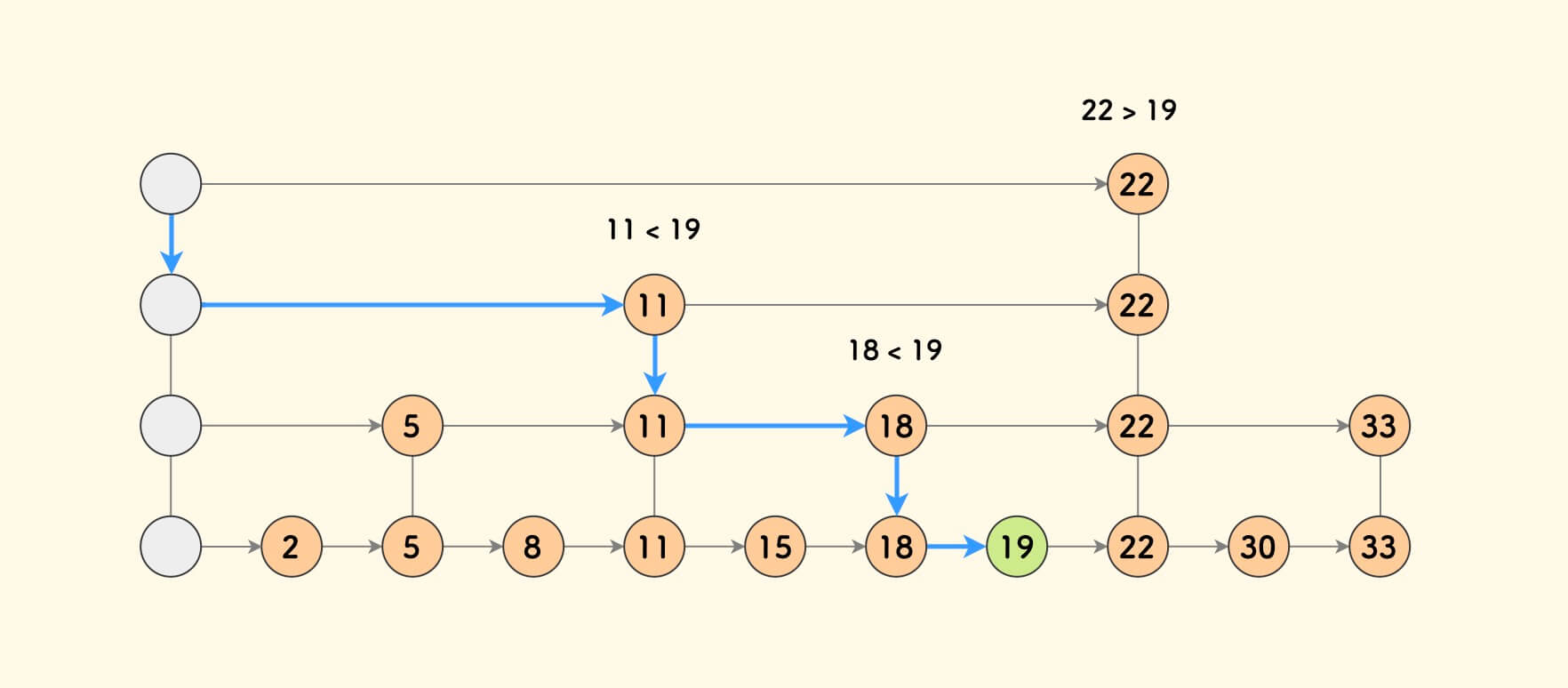
那么，元素个数为 n 的情况下，可以盖多少层楼呢？

和二分查找法过程类似，每盖一层楼，元素个数都缩小为原来的一半， 最终元素个数缩小为 1 才可以，于是有 $n / (2^k) = 1$ ，也就是最多可以盖 $k = logn$ 层楼。

在 $n$ 足够大的时候，考察次数 $2^{-k} + k$ 近似为 $k$ ，即 $logn$ ， 所以在这个思路下，查找的时间复杂度，从 $O(n)$ 降低为了 $O(logn)$ 。

随机化 ¶

然而，上面构造的数据结构太过于呆板，因为它严格要求构造新楼层的时候，每隔一个节点搭一条线。 一旦插入一个新节点，搭线的规则就被打破。而且，稍加思索即知，维护这个规则也是比较繁琐的。

解决的办法，就是稍微放宽结构条件。

不妨，把一个带有 k+1 条搭线的节点，叫做 k 阶节点，从 0 开始。 即下图中的 level 字段，也即 “盖楼” 的高度：

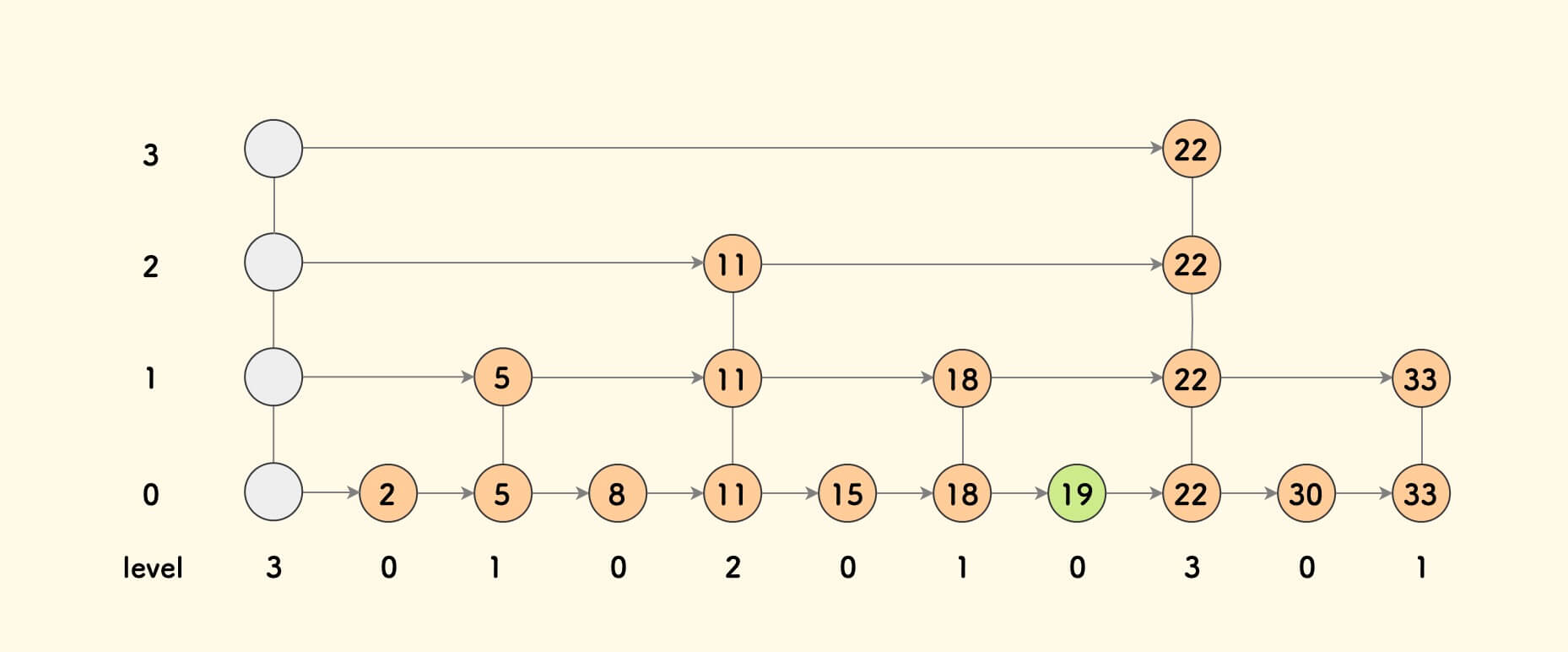
最开始，所有的节点都是 0 阶的。盖好第一层楼后，出现了一半的 1 阶节点，再盖一层楼后， 又出现了四分之一的 2 阶节点…，盖好第 k 层楼后，会有 $1/(2^k)$ 个 k 阶节点。

放宽结构条件的办法就是，按照这个概率分布，让第 k 层楼出现大约 $1/(2^k)$ 个 k 阶节点， 也就是说，插入元素时，新节点成为 k 阶的概率是 $1/(2^k)$ 。

// 生成一个 1 到 MAX_LEVEL 之间的随机层数
int RandLevel() {
    int level = 1;
    // 以概率 P 递增 level
    // 1/2 的概率 level → 1
    // 1/4 的概率 level → 2
    // 1/8 的概率 level → 3
    while ((rand() & 65535) * 1.0 / 65535 < 0.5) level++;
    return level < MAX_LEVEL ? level : MAX_LEVEL;
}

下图是一个示例，它并不严格地符合 “间隔搭线” 的规则。如之前那样， 上层仍然给下层提供了快速通道，加速了查找过程。

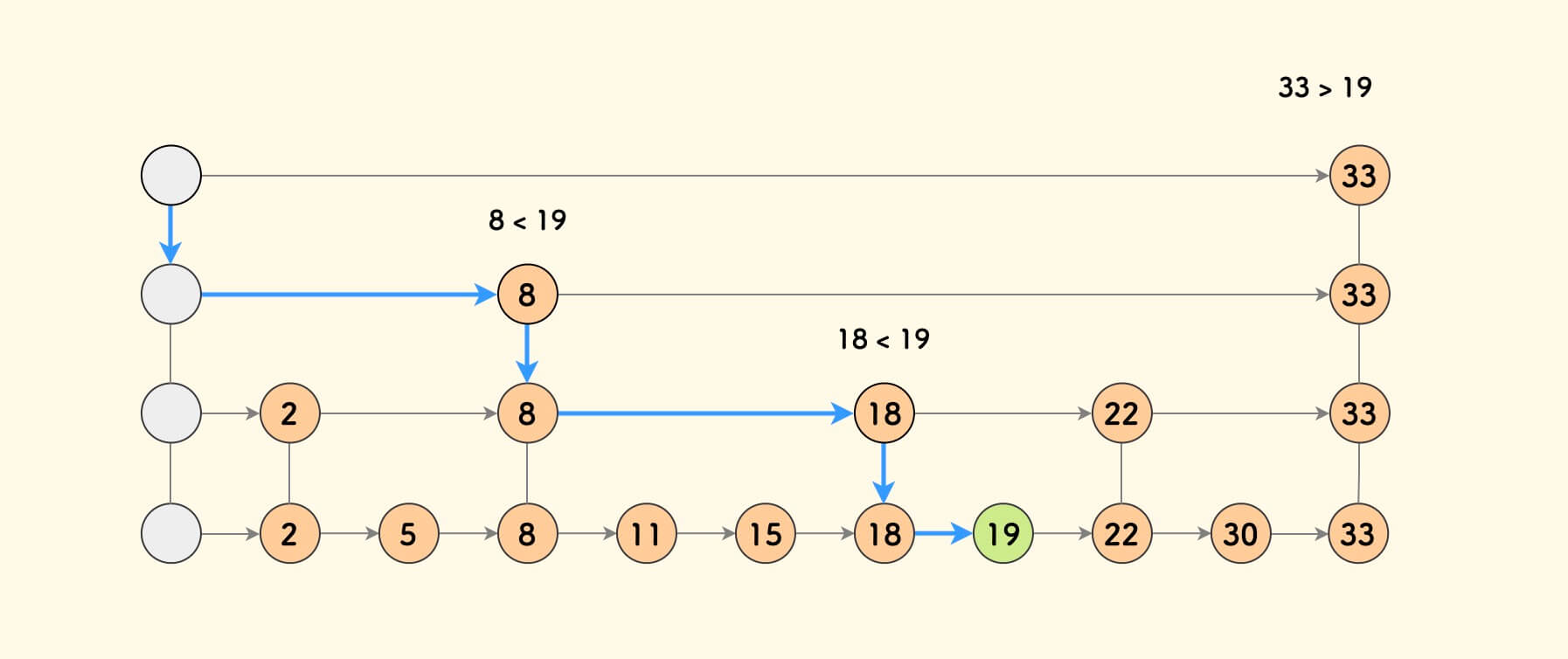
在平均情形下，第 k 层的节点大约有 $n / (2^k)$ 个，且每一层的节点预期分布大致均匀， 相比原来非随机化的情况，查找一个目标的平均时间复杂度并无变化，仍然是 $O(logn)$ 。 插入一个新元素则却变简单了，不必繁琐地维护严格的 “间隔搭线” 的规则。

不过， 跳跃表并不提供对最坏情形的性能保证，因为并不能排除非常小的概率下会生成一个极不平衡的跳跃表。 那时，查找一个元素的时间将退化为 $O(n)$ 。

至此，跳跃表的构造思路即结束。

接口实现 ¶

以下所有接口的实现都将基于以下数据结构：

typedef struct _Node {
    int v;                           // 节点数据
    int level;                       // 节点的总层数
    struct _Node *nexts[MAX_LEVEL];  // 前进数组, 元素索引: 0~level
} Node;

typedef struct {
    int n;       // 节点数
    int level;   // 最大层度
    Node *head;  // 头节点 非数据节点 且 层数最高
} Skiplist;

其中:

• 头节点 head 是一个虚拟头节点，不存储数据；并且它的阶始终和最高阶节点对齐。
• 每个节点都有一个前进数组 nexts 来存储在每一层上的后驱节点的地址。

查找元素

前面 已多次提及查找过程：

从跳跃表的左上角节点，向右考察，直到遇到一个不比目标值小的节点，则向下一层继续，直到最底层。 判断最底层当前节点的下一个节点是否是目标值即可。

bool Has(Skiplist *sl, int v) {
    Node *n = sl->head;
    // 自上层向下
    for (int i = sl->level; i >= 0; i--) {
        // 向右比较大小
        while (n->nexts[i] != NULL && n->nexts[i]->v < v)
            n = n->nexts[i];
    }
    n = n->nexts[0];
    return n != NULL && n->v == v;
}

插入元素

向一个跳跃表中插入元素可以分为三步：

1. 找到各层的插入位置 。

   和单链表一样，要插入一个元素，需要找到前驱节点。跳跃表是多层链表， 那么需要找到各层的前驱节点。

   下图中，要插入一个新元素 20 ，其中数组 last[k] 表示找到的第 k 阶上的前驱节点。

   找的方法和查找过程一样，只需要记住每一层可以向右考察到的最后一个节点即可。

   

2. 决定新节点的阶 。

   用上面提到的 随机函数 RandLevel 决定它的阶。 如果得到比整个跳跃表还要高的阶，需要把头节点的阶增高，与之对齐。 以便任何节点都可以从左上角的头节点出发找到。

   由于 last 数组的含义是各层的插入位置，而且，接下来将要把头节点在新增高的这些层上指向新节点， 于是把头节点 head 记为 last 数组在这些层上的值。

   下图中，假如生成了一个大的阶 4 ，那么跳跃表的阶将会增高到 4， 并设置 last[4] = head 。

   

3. 各层执行插入动作 。

   仍然和单链表一样，插入一个新节点的过程，就是把新节点和前驱、后驱节点分别搭线。 只不过跳跃表是在多层上进行。

   在每一层，前驱节点 last[k] 指向新节点，新节点指向 last[k] 原来的后驱节点。

   

代码实现如下：

void Put(Skiplist *sl, int v) {
    // 第一步 找到各层插入位置

    // last[i] 表示第 i 层的插入位置的前驱节点
    Node *last[MAX_LEVEL];
    Node *n = sl->head;

    for (int i = sl->level - 1; i >= 0; i--) {
        while (n->nexts[i] != NULL && n->nexts[i]->v < v)
            n = n->nexts[i];
        last[i] = n;
    }

    // 第二步 决定新节点的阶
    int level = RandLevel();  // 新节点的层数

    if (level > sl->level) {
        // 新节点的层数比原来的都大
        // 需要补充 last 数组高位，将把 head 指向此节点
        for (int i = sl->level; i < level; i++) last[i] = sl->head;
        sl->level = level;
    }

    // 第三步，各层执行插入
    Node *node = NewNode(v, level);
    for (int i = 0; i < level; i++) {
        node->nexts[i] = last[i]->nexts[i];
        last[i]->nexts[i] = node;
    }

    sl->n++;
}

删除元素

同样地，从一个跳跃表中删除元素可以也可以分为三步：

1. 找到各层的前驱节点和要删除的节点 。

   从单链表中删除一个元素，需找到前驱节点。跳跃表是多层链表，也需找到各层的前驱节点。

   和前面一样，last 数组来存放各层的前驱节点。 查找元素的过程，即可记录 last 数组。

   同时查找结束后，亦可判断要删除的元素是否存在于表中。

   下图以删除元素 22 为例：

   

2. 各层执行删除 。

   仍然与单链表是类似。在各层上，前驱节点直接指向要删除的节点的后驱节点。 最终释放要删除的节点的内存即可。

   不过，并非 last 数组的每一项都是待删除节点的前驱节点， 在删除时需要注意过滤。

   以删除 22 为例，具体的删除动作就是，如果 last[k] 的后驱是 22， 则将 last[k] 的后驱指向 22 的后驱。

   

3. 抹去删除节点后可能残留的孤零的高阶 。

   如果删除的元素是一个高阶节点，可能让跳跃表的头节点残留下孤零零的高阶。

   这一步是可选的，即使不清理也无大碍。

   以删除高阶节点 33 为例，删除 33 后，头节点的阶可以由 4 降为 3 。

   

代码实现如下：

bool Pop(Skiplist *sl, int v) {
    // 第一步 找到各层删除位置的前驱节点

    Node *last[MAX_LEVEL];

    Node *n = sl->head;
    for (int i = sl->level - 1; i >= 0; i--) {
        while (n->nexts[i] != NULL && n->nexts[i]->v < v) n = n->nexts[i];
        last[i] = n;
    }

    // 要删除的节点
    n = n->nexts[0];
    if (n == NULL || n->v != v) return false;

    // 第二步，各层执行删除
    for (int i = sl->level - 1; i >= 0; i--) {
        if (last[i]->nexts[i] == n) last[i]->nexts[i] = n->nexts[i];
    }

    // 第三步，去除删除节点后可能造成的无效层次
    while (sl->level > 1 && sl->head->nexts[sl->level - 1] == NULL) {
        sl->level--;
    }
    sl->n--;
    FreeNode(n);
    return true;
}

可以看到，跳跃表的查找、插入和删除，维护了一条有序的链表，三个动作的平均时间复杂度都是 $O(logn)$ 。

完整代码实现

• C 语言版本 - skiplist - github
• C++ 语言版本 - skiplist - github
• Go 语言版本 - skiplist - github

性质和场景 ¶

跳跃表非常适合「有序字典」的场景，而且在这方面相对于红黑树、二叉搜索树等来说更容易理解、实现更简单。 此外，跳跃表非常棒的一点在于，其最底层的链表本身就是有序的， 这也很适合范围查询。

结尾语 ¶

跳跃表是一种多层的有序链表结构，上层为下层提供快速通道，最底层是有序链表。 其元素查找、插入和删除的平均时间复杂度均是 $O(logn)$ ，但作为随机化数据结构，极小概率在最坏情况下性能退化到 $O(n)$。 同时作为一种链表结构，插入和删除元素更方便，不必像数组那样进行批量内存拷贝。

（完）

本文原始链接地址： https://writings.sh/post/data-structure-skiplist