Fractional Cascading

Recently, I learned an interesting and niche algorithm that primarily addresses online query problems on multiple sorted sequences.

Problem ¶

Simply put, given multiple sorted sequences and asked to perform multiple queries, each query involves a number, and the goal is to find its position in each sequence.

A specific problem comes from Luogu P6466:

Given $k$ arrays $L_i$, each of length $n$, containing distinct elements, and strictly increasing, perform $q$ queries. Each query involves a number $x$, and you need to find the non-strict successor of $x$ in each array (the smallest element satisfying $\ge x$), and output the XOR sum of these successor elements.

Note that array indices in this article start from $1$.

Preliminary Discussion ¶

First, the simplest approach is to perform binary search on each array sequentially, resulting in a time complexity of $O(k\log{n})$ for each query. For multiple queries, this approach is relatively time-consuming.

Another approach is to pre-process the data by merging these arrays into one large sorted array. Then, for each element, store an array $C$ of length $k$, where $C_i$ represents the successor position of that element in the original array $L_i$.

This effectively creates a two-dimensional table of size $kn \times k$. During a query, simply perform binary search on the large array and retrieve the $C_i$ array from the matching row.

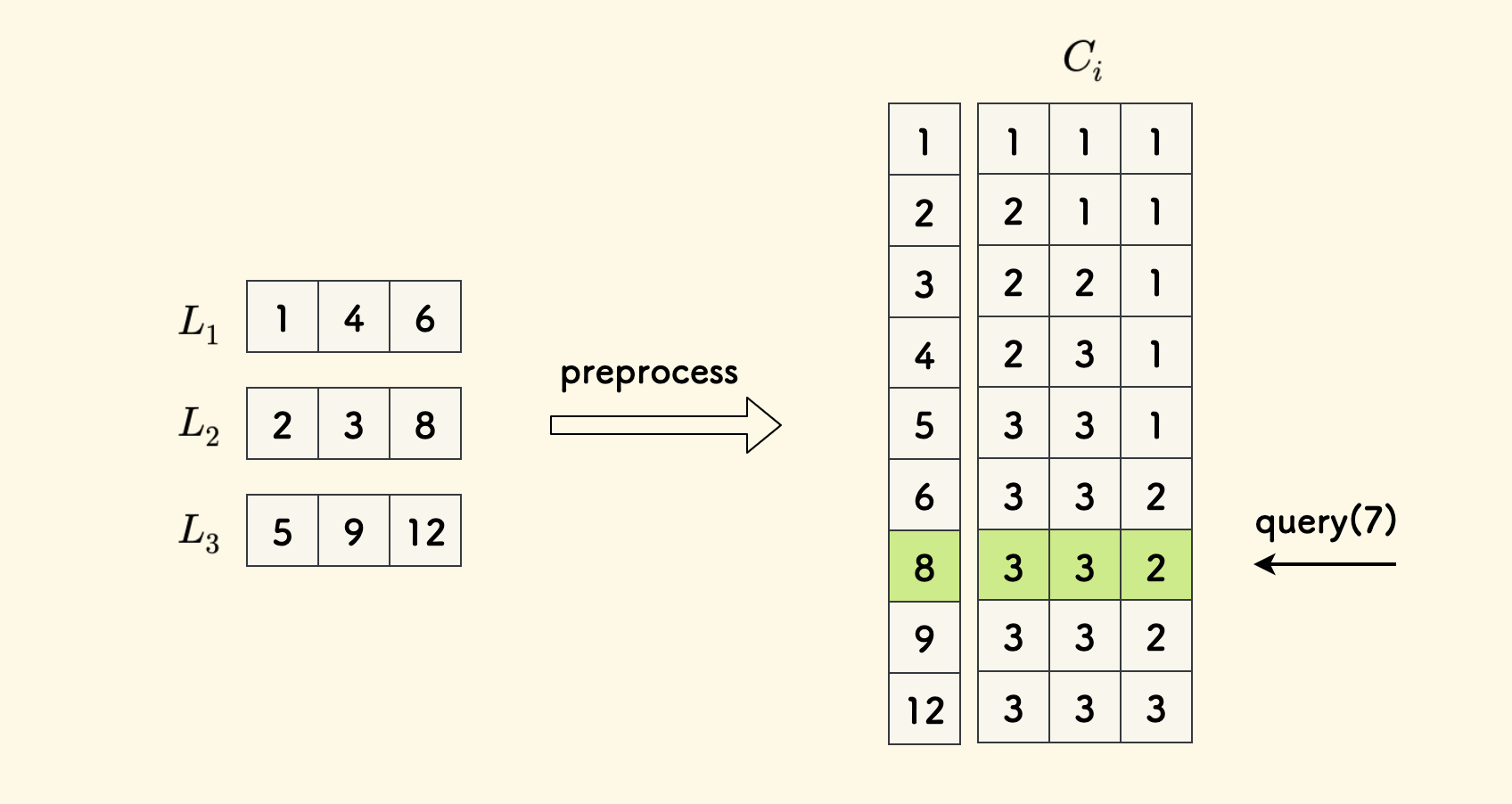
The time complexity for each query in this approach is $O(\log{kn} + k)$, including the binary search time and the time to retrieve the results. However, the space complexity is relatively large, $O(kn\times k)$.

Fractional Cascading ¶

Compared to the previous two methods, the advantage of Fractional Cascading is that it can achieve a time complexity of $O(\log{n} + k)$ and a space complexity of $O(kn)$.

It also involves two phases: pre-processing and online querying.

Pre-processing

The pre-processing step involves constructing $k$ sorted auxiliary arrays $M_i$. First, the last array $M_k$ directly adopts the original array $L_k$. Then, construct from back to front. That is, knowing $M_{i+1}$, construct $M_i$. The specific method is to perform interval sampling on $M_{i+1}$ (taking every other element) and then merge it with $L_i$ to obtain $M_i$.

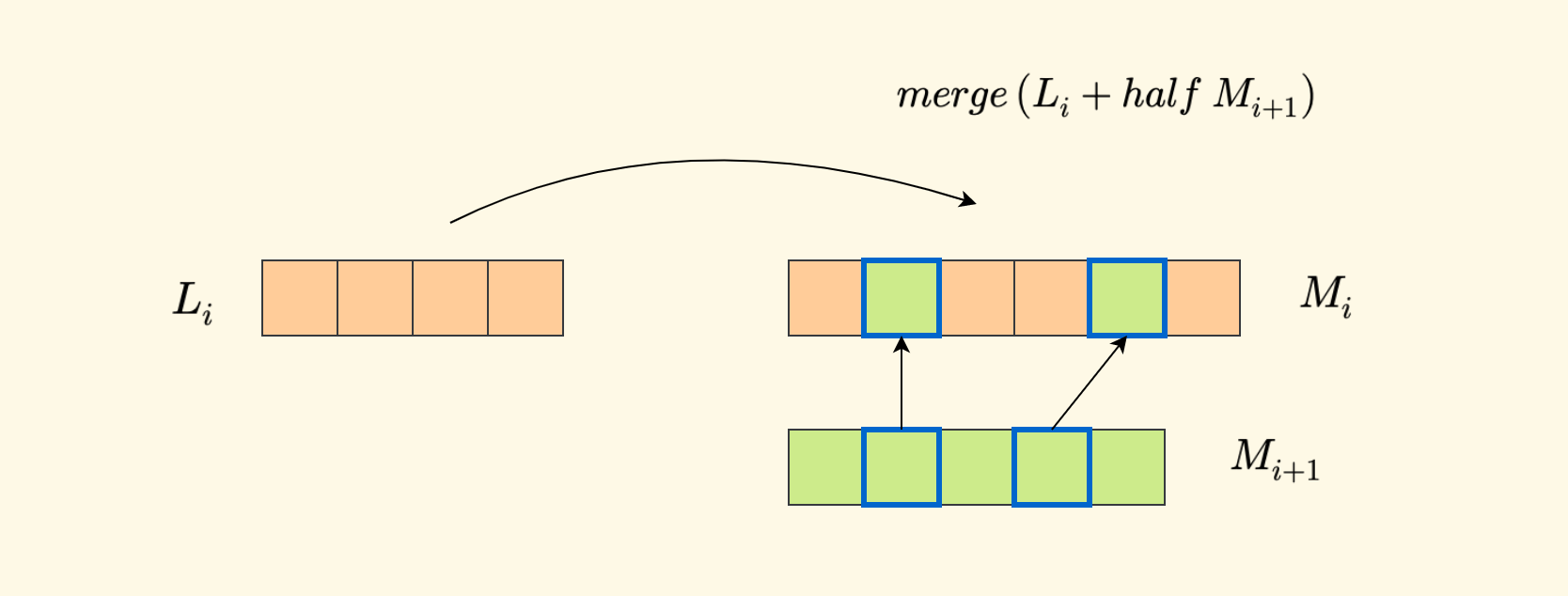
Additionally, for each element in $M_i$, besides recording the element value $x$ itself, also maintain two additional pieces of information $[y,z]$:

$y$ represents the successor position of the value $x$ in $L_i$.
$z$ represents the successor position of the value $x$ in $M_{i+1}$.

This may seem a bit difficult to understand, so let’s look at an example directly.

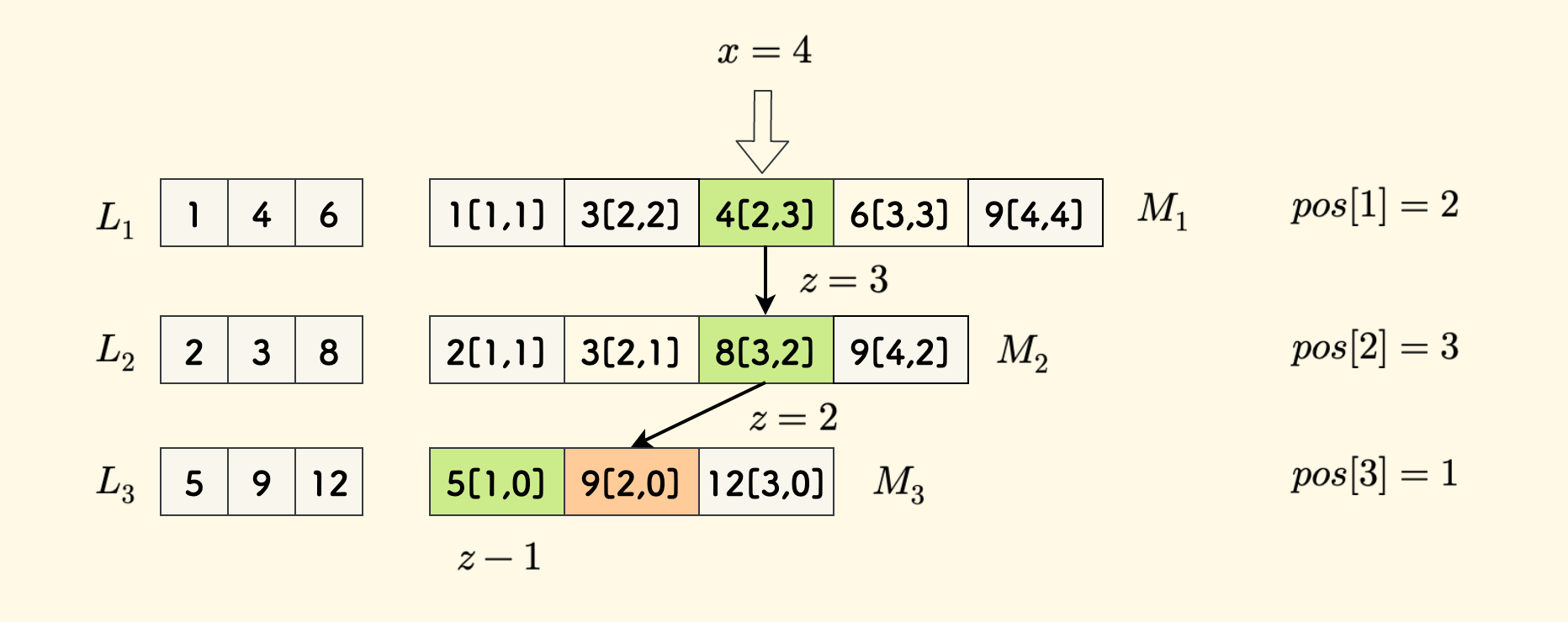
In the figure below, the three fields stored by each element in $M_i$ are expressed in the form $x[y,z]$:

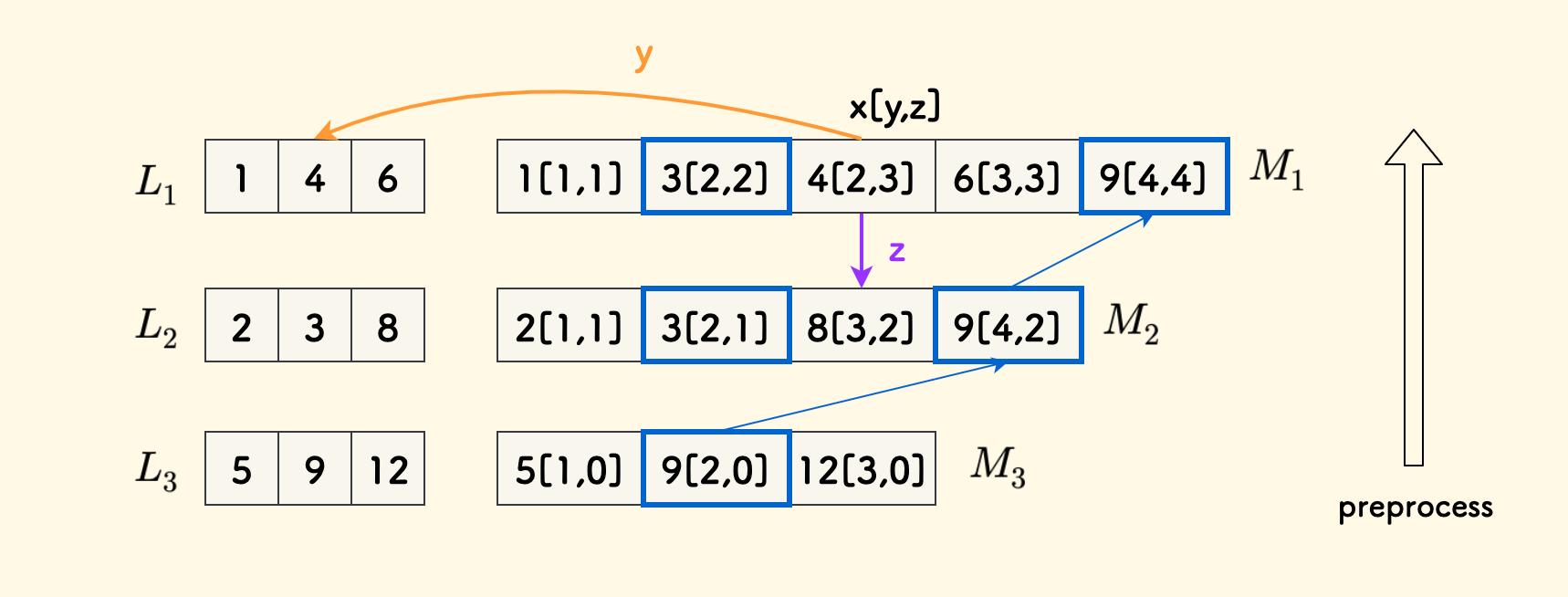
First, construct the final $M_3$ by directly using $L_3$.
Also, the $z$ field in $M_k$ of the last row is meaningless and will not be used.
Then, for the case of $i < k$, starting from position $2$, perform interval sampling on $M_{i+1}$ and merge it with $L_i$. The merging process is the same as merge sort.
Maintain the $y$ and $z$ fields well, which are the successor position of $x$ in $L_i$ and the successor position of $x$ in $M_{i+1}$, respectively.
For example, the $y$ field of $4[2,3]$ in $M_1$ is $2$, pointing to the $2$nd element $4$ in $L_1$. The $z$ field is $3$, pointing to the $3$rd element $8$ in $M_2$.

The $y$ and $z$ fields can be maintained together during the merging process, as can be seen in the code implementation later.

Querying

First, let’s study the properties that constructing these auxiliary arrays can bring.

If the successor of $x$ in $M_i$ is $b[y,z]$, then the successor of $x$ in $M_{i+1}$ is either at position $z$ or at position $z-1$.

The reason is:

First, since $b$ is the successor of $x$, we have $x \le b$.
$b$ points to position $z$ in $M_{i+1}$, so we have $b \le M_{i+1}[z]$. This also indicates that position $z$ is a possible successor (one of them).
Because interval sampling is used, the value $a$ at position $z-2$ in $M_{i+1}$ will also be merged into $M_i$ during the pre-processing phase, so we have $a \lt x$. This must be a strictly less than relationship; otherwise, it contradicts the condition that $b$ is the successor of $x$ in $M_i$.
Combining these observations, in array $M_{i+1}$, $x$ must be located in the interval $(z-2, z]$, which is open on the left and closed on the right. That is, there are only two possible positions for the successor of $x$ in $M_{i+1}$, namely $z-1$ and $z$.

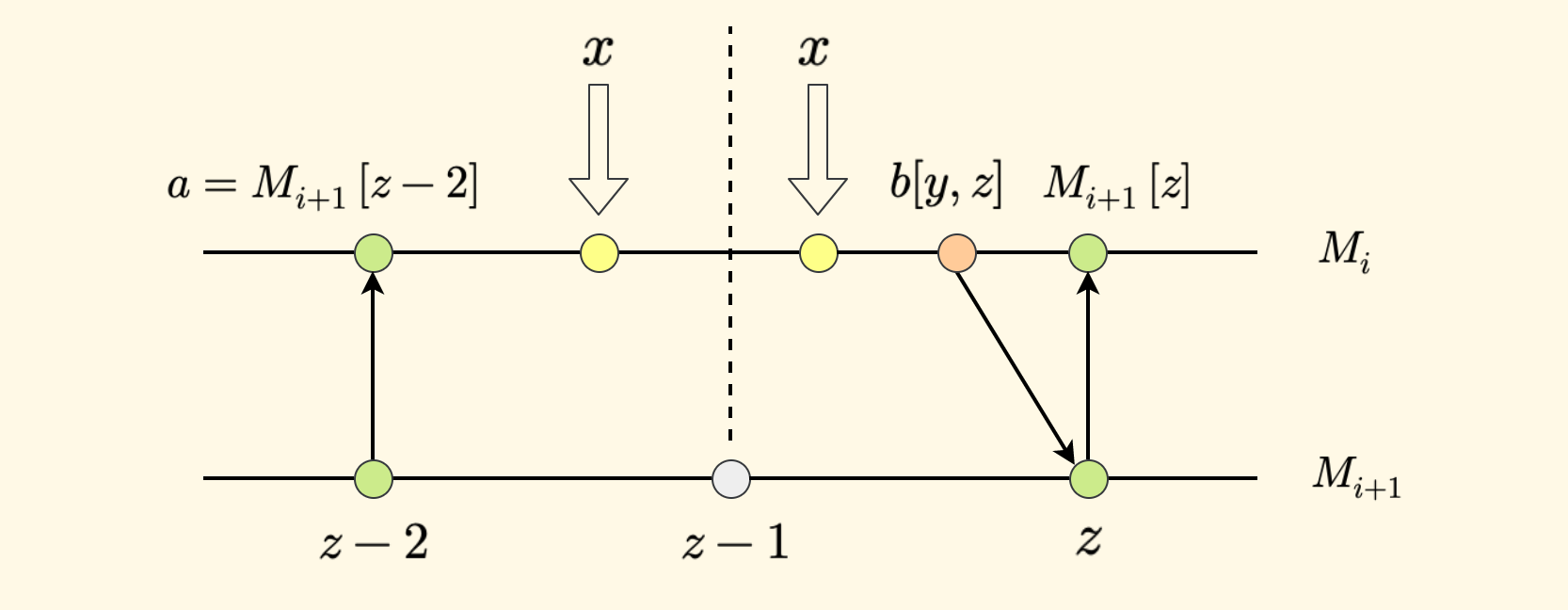
Only need to check these two positions. Specifically, first check the size relationship between the element value at $z-1$ and $x$. If $x \le M_{i+1}[z-1]$ is satisfied, then position $z-1$ is the answer; otherwise, position $z$ is the answer.

After clarifying this point, the steps of the entire query process become simple.

Assume that the array $pos_i$ represents the position of the successor of the input number $x$ in the original array $L_i$:

First, perform binary search on $M_1$ to obtain the successor $x_1[y_1, z_1]$, so $pos[1] = y_1$. Then take $z_1$ into the following steps.
For the case of $i \gt 1$, check the cases at $z-1$ and $z$ to confirm the real successor position $y$. Proceed sequentially.

Take a specific example. In the figure below, the number to be queried is $x=4$:

By binary search in $M_1$, we get the successor $4[2,3]$, so $pos[1] = 2$.
Then taking $z=3$, successively check $3$ and $8$ in $M_2$. At this time, position $z$ is the successor, giving $pos[2]=3$.
Then taking $z=2$, successively check $5$ and $9$ in $M_3$. At this time, position $z-1$ is the successor, giving $pos[3]=1$.

We can manually check the correctness of this answer array.

However, in one case, special handling is required when a successor does not exist.

For example, in the same example, when querying $x=9$, $z=4$ in $M_2$ points to an invalid position. In fact, the successor of $x=9$ does not exist in $L_2$.

In any case, we can check and confirm the validity of the successor during the query.

Complexity ¶

First, look at the size $SZ_i$ of each auxiliary array $M_i$.

The size of the last $M_k$ is $n$, and then half is taken and merged with $L_{k-1}$ to obtain $M_{k-1}$, whose size is $n+n/2$.

Further, the size of $M_{k-2}$ will be $n + SZ_{k-1}/2$, which is $n+n/2+n/4$.

Deriving this way, the size $SZ_i$ of the $M_i$ array will be: $n + n/2 + n/4 + … + n/{2^{k-i}}$, not exceeding $2n$ ^[1].

That is, the size of each $M_i$ array is certainly not more than $2n$.

Therefore, the overall space complexity will be $O(k * 2n)$, which is $O(kn)$, where $k$ is the number of sorted original arrays and $n$ is the size of each array.

Pre-processing is the process of continuously merging $L_i$ and half of $M_{i+1}$ to construct $M_i$. Each merge is linear, and is the same as the merging sub-process in merge sort. A total of $k$ times are performed, so the time complexity is $O(k*(n+2n/2))$, which is $O(kn)$.

During each query, first perform a binary search on $M_1$, and then check downwards in turn. At most two elements are checked in each $M_i$, so the time complexity is $O(\log{n} + k)$.

Code Implementation ¶

With the ideas already sorted out, let’s finally implement the code.

Structure Definition

Assume that $k$ will not exceed the constant $K$, $n$ will not exceed the constant $N$, and define the original array $L_i$.
Each item of the auxiliary array $M_i$ will store three fields $x[y,z]$, which can be defined as a structure V.
The size of each $M_i$ array will not exceed $2n$, so you can directly define the length of the $M$ array as $2*N$.
For each query, use the $ans$ array to record the element value of the successor of the input $x$ in each $L_i$.

Therefore, the structure definition is implemented as follows:

Fractional Cascading - Structure Definition (C++)

const int N = 10001;
const int K = 101;

int L[K][N];  // The original k sorted sequences, starting from index 1

// Each element in the M array is a structure
struct V {
    int x;      // Element value
    int y = 0;  // Position where it appears in L[i]
    int z = 0;  // Position where it appears in M[i+1]
};

V M[K][2 * N];  // The constructed k sequences, starting from index 1
int SZ[K];      // Record the length of M[i]

int ans[K];  // Record the answer in each sequence for one query

Merge Function

Responsible for generating $M_i$ by performing interval sampling on $M_{i+1}$ and merging it with $L_i$. This process is almost identical to the merge function in merge sort ^[2]. There are only two differences (we use $start1$ and $start2$ to represent the scanning pointers of $L_i$ and $M_{i+1}$ respectively):

Since it is interval sampling, the pointer $start2$ of $M_{i+1}$ must increment with a step size of 2.
But a step size of 2 may cause you to miss the real successor.

The second point is very subtle. We know that during the merging process, for the current slot to be considered, either the element of $L_i$ or the element of $M_{i+1}$ is taken, depending on which one is smaller.

When the element in $L_i$ is smaller, the $z$ field to be recorded cannot simply adopt the value of $start2$, because $start2$ goes with a step size of $2$, which may skip the real successor of $L_i[start1]$. For example, the following figure is an example. At this time, it is necessary to check the case of $start2-1$, and select one from $start2-1$ and $start2$ as the value of $z$.

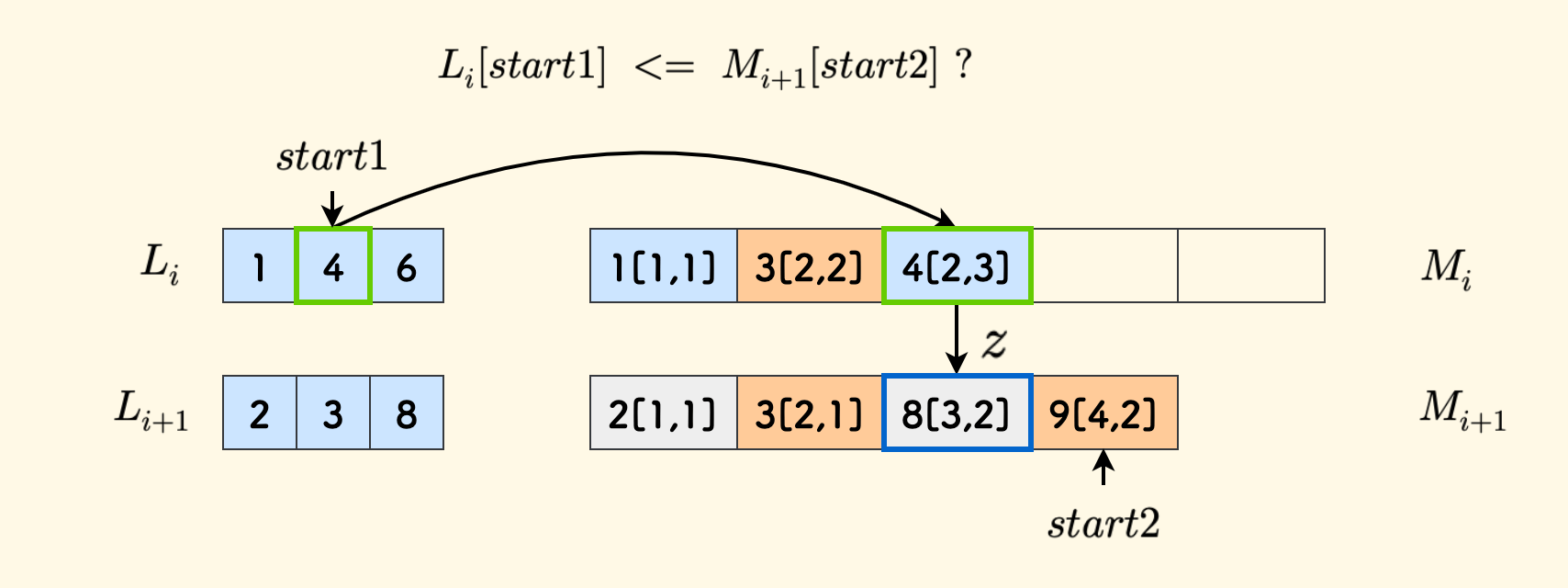
However, when the element in $M_{i+1}$ is smaller, that is, when considering putting $M_{i+1}[start2]$ in this slot, there is no need to deal with this problem, because its successor must be $start2$.

The implementation code of the merge function is as follows:

Fractional Cascading - Merge Function (C++)

// Take samples from M1 every other element, and then merge it with Li into M2
// The start and end of Li are start1, end1; the start and end of M1 are start2, end2
// The start of M2 is start; return start, which is the final size of M2
int merge(int *Li, V *M1, V *M2, int start1, int end1,
                                 int start2, int end2,
                                 int start) {
    auto take1 = [&]() {  // Take the value of Li
        M2[start].x = Li[start1];
        M2[start].y = start1;
        // Note here, to prevent missing the real successor due to the step size of 2 of M1, you need to check
        // whether the start2-1 position is the real successor
        M2[start].z = M1[start2 - 1].x >= Li[start1] ? (start2 - 1)
                                                     : start2;
        start++;
        start1++;
    };
    auto take2 = [&]() {  // Take the value of M1
        M2[start].x = M1[start2].x;
        M2[start].y = start1;
        M2[start].z = start2;
        start++;
        start2 += 2;  // Take samples at intervals
    };
    while (start1 <= end1 && start2 <= end2)
        Li[start1] <= M1[start2].x ? take1() : take2();
    while (start1 <= end1) take1();
    while (start2 <= end2) take2();
    return start;
}

Pre-processing Function

After the idea of the pre-processing process is clear, the implementation is relatively simple:

Fractional Cascading - Pre-processing Function (C++)

void preprocess() {
    memset(M, 0, sizeof(M));
    memset(SZ, 0, sizeof(SZ));

    // M[k] is the L[k] sequence itself
    for (int j = 1; j <= n; j++) {
        M[k][j].x = L[k][j];
        M[k][j].y = j;
    }

    // From back to front, merge half of M[i+1] and L[i] to construct M[i]
    SZ[k] = n;
    for (int i = k - 1; i > 0; --i) {
        // start2: Sample at intervals starting from 2
        // The final size is start2-1
        SZ[i] = merge(L[i], M[i + 1], M[i], 1, n, 2, SZ[i + 1], 1) - 1;
    }
}

Here is a subtle detail: Why start sampling from position 2, instead of directly from position $1$? One benefit is that in this way, when processing the query, when considering the element at position $z-1$, there is no need to consider its validity.

Query Function

The function query(int x) will write the values of the successor elements of $x$ in each array $L_i$ onto $ans[i]$.

First, perform a binary search on $M_1$, which belongs to binary search for the left boundary of $\ge x$ ^[3].

int l = 1, r = SZ[1];
while (l < r) {
   int m = (l + r) >> 1;
   if (M[1][m].x >= x) r = m;
   else l = m + 1;
}

At this time, l is the position of the successor of $x$ in $L_1$. The first round target $v$ is $M[1][l]$:

V *v = &M[1][l]; // Take the pointer

However, always remember to confirm the validity of the successor.

// Pay attention to verifying the validity, there may be no successor
if (v->x >= x) ans[1] = L[1][v->y];

As with the idea analyzed earlier, for the subsequent case of $i>1$, you can just keep finding layer by layer with $z$. For each layer, you only need to confirm two positions, that is, $z-1$ and $z$.

for (int i = 1; i < k; i++) {
    // Examine the z-1 position, pay attention to the case where z exceeds the size of M[i+1]
    if (M[i + 1][v->z - 1].x >= x || v->z > SZ[i + 1])
        v = &M[i + 1][v->z - 1];
    else // Otherwise it is at the z position
        v = &M[i + 1][v->z];
    // But you must pay attention to verifying the validity of the successor
    if (L[i + 1][v->y] >= x) ans[i + 1] = L[i + 1][v->y];
}

Other code specifically related to the Luogu P6466 problem does not need to be explained further. See the complete code implementation: code-snippets - Fractional Cascading Algorithm - P6466.

Concluding Remarks ¶

The Luogu P6466 problem stipulates the conditions that the elements are distinct and each array is strictly increasing, but the fractional cascading algorithm does not require that the original arrays be strictly ordered.

Finally, this algorithm is quite interesting, with excellent time and space complexity. However, the code implementation is not that concise after all~

(End)

Please note that this post is an AI-automatically chinese-to-english translated version of my original blog post: http://writings.sh/post/fractional-cascading.

Original Link： https://writings.sh/post/en/fractional-cascading