一道在矩阵网格中寻找峰值的二分问题

来自 12 月 19 日 leetcode 的每日一题 1901. 寻找峰值 II，挺有趣的二分题，关键在于如何证明。

问题描述：

一个 2D 网格中的「峰值」是指那些 严格大于 其相邻格子 (上、下、左、右) 的元素。
给定一个 m x n 的正整数矩阵 g，任意两个相邻方格的数字都不相同，找出任意一个峰值的位置。
可以假定整个矩阵周边环绕着一圈值为 -1 的格子，也就是说边缘的格子和界外相比总可以算做更大的值。

题目还提示了要用 $O(m\log{n})$ 或 $O(n\log{m})$ 时间复杂度的算法，强烈的二分法暗示。

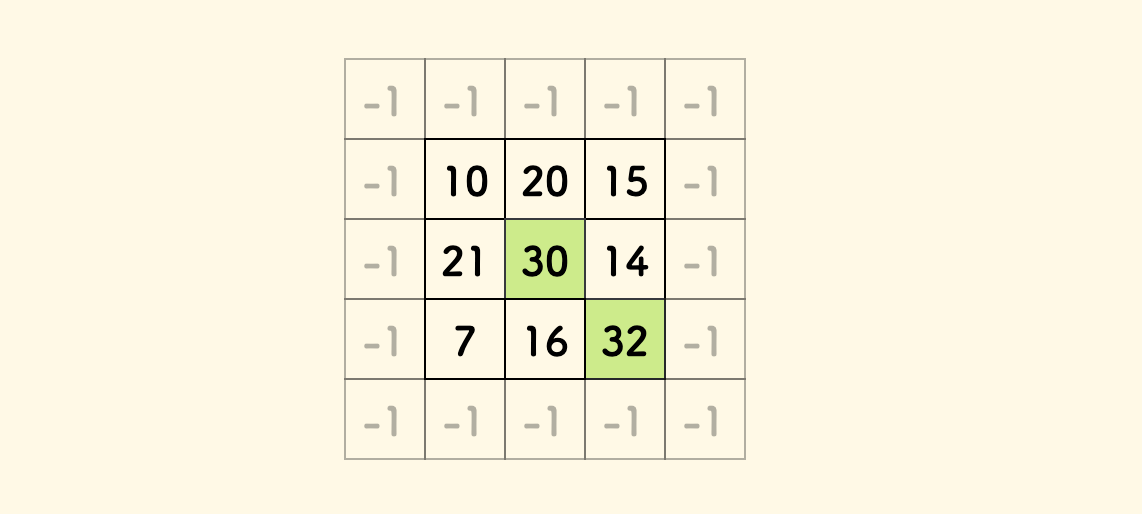
比如说，下面的示例矩阵，可行解是绿色的任何一个方格 [1,1] 和 [2,2] 都可以。

虽然这个题「相邻元素互不相同」、「找到任意一个峰值」、「可以假定界外都是 -1」的这些条件显得非常「刻意」，但是单说解法而言，还是挺巧妙的。

总的思路是，二分枚举可行区间的行，然后找行内最大值进行判定。

大概的伪代码如下，非常简洁：

int l = 0, r = m - 1;
while (l <= r) {
    int i = (l + r) >> 1;
    // 行内最值位置
    int j = max_element(g[i].begin(), g[i].end()) - g[i].begin();
    if (i >= 1 && g[i][j] <= g[i-1][j])
        r = i - 1;
    else if (i+1 < m && g[i][j] <= g[i+1][j])
        l = i + 1;
    else
        return {i, j};
}

关键是，这种二分方式如何是正确的呢？

只说明第一个逻辑分支的情况，另一个分支道理类似。

首先，要时刻注意相邻元素不相等这个性质。

假设当前是第 i 行，行内的最大值是 A = g[i][j]。

现在，遇到其上方的 B = g[i-1][j] 满足 A < B。

假设 B 所在行的最大值是 C, 它下面相邻的是 D，那么肯定有 C >= B > A >= D，也就是 A > D。

C 已经是行内最大了，只需要继续考虑 C 和其上面的 E 的大小关系。

如下图所示，红色的都是行内最值：

             E
        B    C
------- A -- D ----- i

分情况讨论：

如果 E < C, 那么 C 是一个可行解。
如果 E > C, 继续假设 E 所在行的最大值是 F，和刚才一样的推导方式可以知道 F > G （提示：C 是行内最大值，且此时假设的是 E > C)。
此时，F 已经是行内最大，只需要再和它上方的数字进行比较，这样就形成了「套娃逻辑」。
```
             E    F
        B    C    G
------  A -- D ----- i
```
一旦走到第 1 种情况，就会得到一个可行解。
如果不断陷入第 2 种情况，直到边缘第 1 行时会终止，因为题目假设边界外是 -1，即可以确定峰值。

综合来看，此时无论哪种情况，第 i 行的上方必有峰值，可把可行区间折半到 [l, i-1]。

对于第二个逻辑分支的情况，不必再展开讨论。

leetcode 1901. 寻找峰值 II - C++ 实现

（完）