最近新学了一个有意思的冷门算法,主要解决多个有序序列上的在线查询问题。
问题 ¶
简单来说,对多个有序的序列询问多次,每次询问一个数字,给出它在每个序列中的位置。
一个具体的题目,来自 洛谷 P6466:
给定 $k$ 个长度均为 $n$ 的、元素互不重复的、严格递增的数组 $L_i$,询问 $q$ 次。每次询问时输入一个数字 $x$, 要求查出 $x$ 在每个数组中的非严格后继(满足 $\ge x$ 的最小的元素 ),输出这些后继元素的异或和。
注意,本文中的数组下标均从 $1$ 开始。
前置讨论 ¶
首先,最简单的思路是,依次对每个数组二分,每次询问的时间复杂度是 $O(k\log{n})$。对于多次询问的话,这种思路时间上比较吃亏。
另一种思路是,先预处理一下,把这些数组归并成一个大的有序数组,然后其中每一项再存一个长度为 $k$ 的数组 $C$, 其中 $C_i$ 表示这个元素在原数组 $L_i$ 中的后继位置。
实际上就是一个 $kn \times k$ 大小的二维表格,当我们查询时,只需要对大数组二分,然后取出命中的一行的 $C_i$ 数组即可。
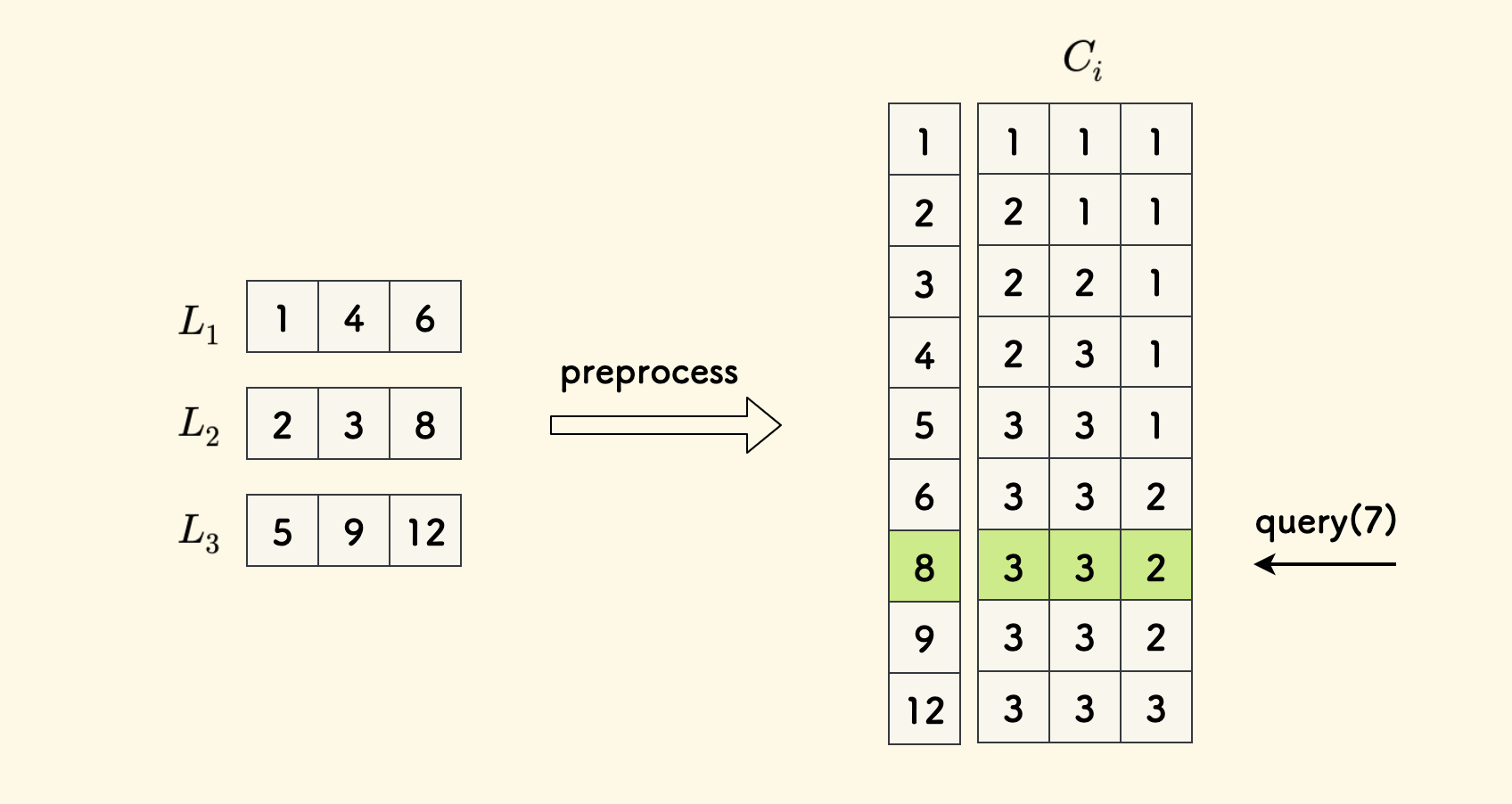
这种做法的每次询问的时间复杂度是 $O(\log{kn} + k)$ ,包括二分的时间和取出结果的时间。但是,空间复杂度是比较大的 $O(kn\times k)$。
分散层叠算法 ¶
相比前面的两种方法来说,分散层叠算法 (Fractional Cascading) 的优秀之处在于,可以做到 $O(\log{n} + k)$ 的时间复杂度 和 $O(kn)$ 的空间复杂度。
同样是分为两个过程:预处理 和 在线查询。
预处理
预处理的过程是,构造 $k$ 个有序的辅助数组 $M_i$。首先,最后一个数组 $M_k$ 直接采用原数组 $L_k$。 然后 从后向前构造,也就是说,知道 $M_{i+1}$ 的情况下,去构造 $M_i$。 具体的方式是,对 $M_{i+1}$ 进行间隔采样(就是每隔一个元素取一个),然后和 $L_i$ 进行归并,得到 $M_i$。
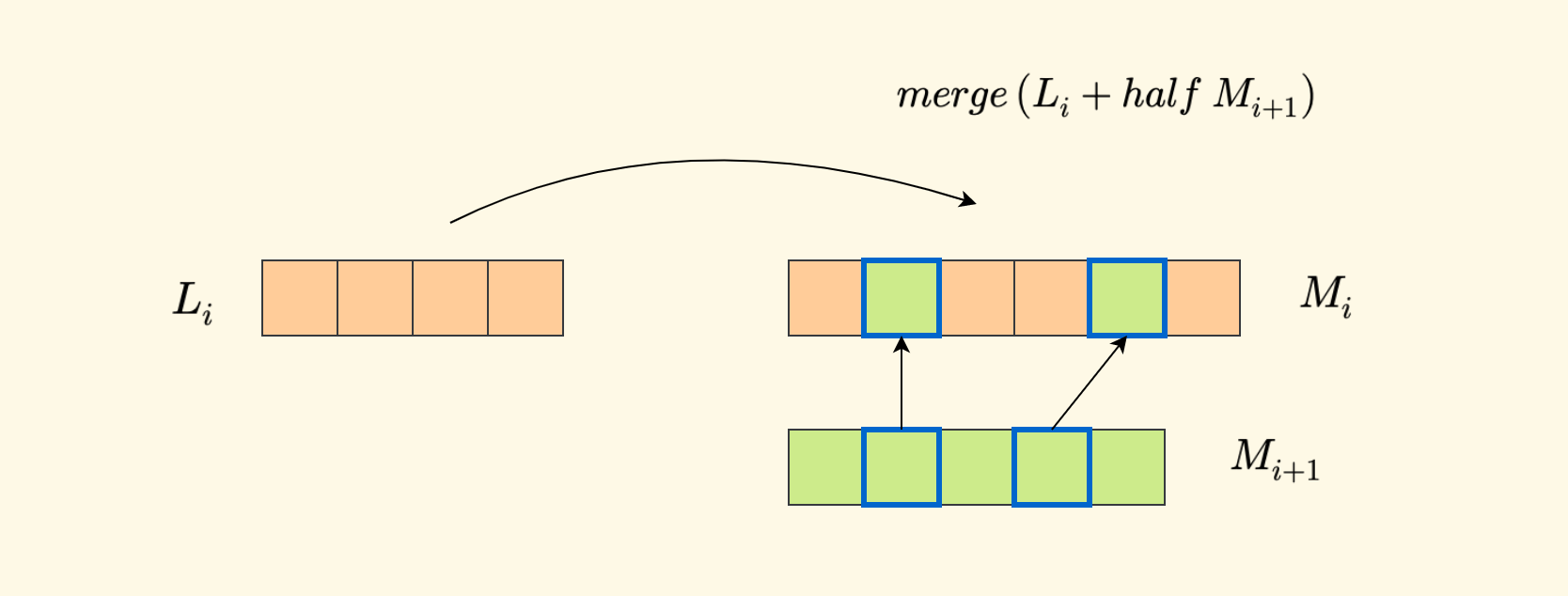
同时,对于 $M_i$ 中的每个元素,除了要记录元素值 $x$ 本身以外,再额外维护两个信息 $[y,z]$:
- $y$ 表示数值 $x$ 在 $L_i$ 中的后继位置。
- $z$ 表示数值 $x$ 在 $M_{i+1}$ 中的后继位置。
看起来有点不好懂,直接来看一个例子。
下图中,$M_i$ 中的每个元素存储的三个字段表达为 $x[y,z]$ 的形式:
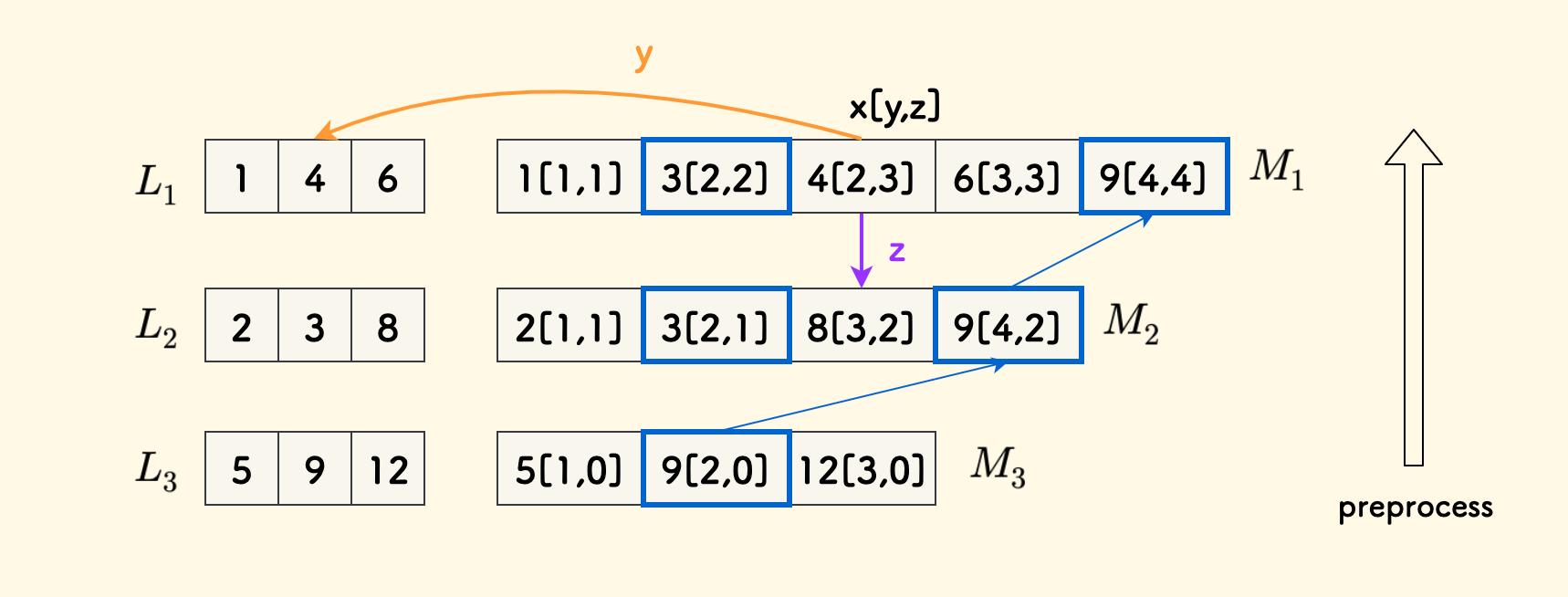
先构造最后的 $M_3$,直接沿用 $L_3$ 即可。
另外,最后一行的 $M_k$ 中的 $z$ 字段是没有意义的,不会用到。
- 然后,对于 $i < k$ 的情况,从位置 $2$ 开始,对 $M_{i+1}$ 间隔采样,再和 $L_i$ 归并,合并过程和归并排序是一样的。
同时维护好 $y$ 和 $z$ 字段,分别是 $x$ 在 $L_i$ 中后继的位置 和 $M_{i+1}$ 中后继的位置。
比如说,$M_1$ 中的 $4[2,3]$ 的 $y$ 字段是 $2$,指向 $L_1$ 中的第 $2$ 个元素 $4$。$z$ 字段是 $3$ 指向 $M_2$ 中的第 $3$ 个元素 $8$。
在归并过程中,可以一并维护 $y$ 和 $z$ 字段,这一点可以在后面的 代码实现 中看到。
询问
先研究一下,构造这些辅助数组可以带来的性质。
如果 $x$ 在 $M_i$ 中的后继是 $b[y,z]$,那么 $x$ 在 $M_{i+1}$ 中的后继要么在 $z$ 处,要么在 $z-1$ 处。
原因在于:
- 首先,$b$ 是 $x$ 的后继,那么肯定有 $x \le b$。
- $b$ 指向 $M_{i+1}$ 中的 $z$ 处,那么肯定有 $b \le M_{i+1}[z]$。同时说明 $z$ 处是可能的后继(之一)。
- 因为采用间隔采样,所以 $M_{i+1}$ 中位置 $z-2$ 处的值 $a$ 也会在预处理阶段归并到 $M_i$ 中去, 那么肯定 $a \lt x$。这里一定是严格小于的关系,否则与 $x$ 在 $M_i$ 中的后继是 $b$ 这个条件矛盾。
- 综合看来,在数组 $M_{i+1}$ 中,$x$ 一定位于区间 $(z-2, z]$ 内,前开后闭。也就是说,$x$ 在 $M_{i+1}$ 中的后继只有两种可能的位置,即 $z-1$ 和 $z$ 。
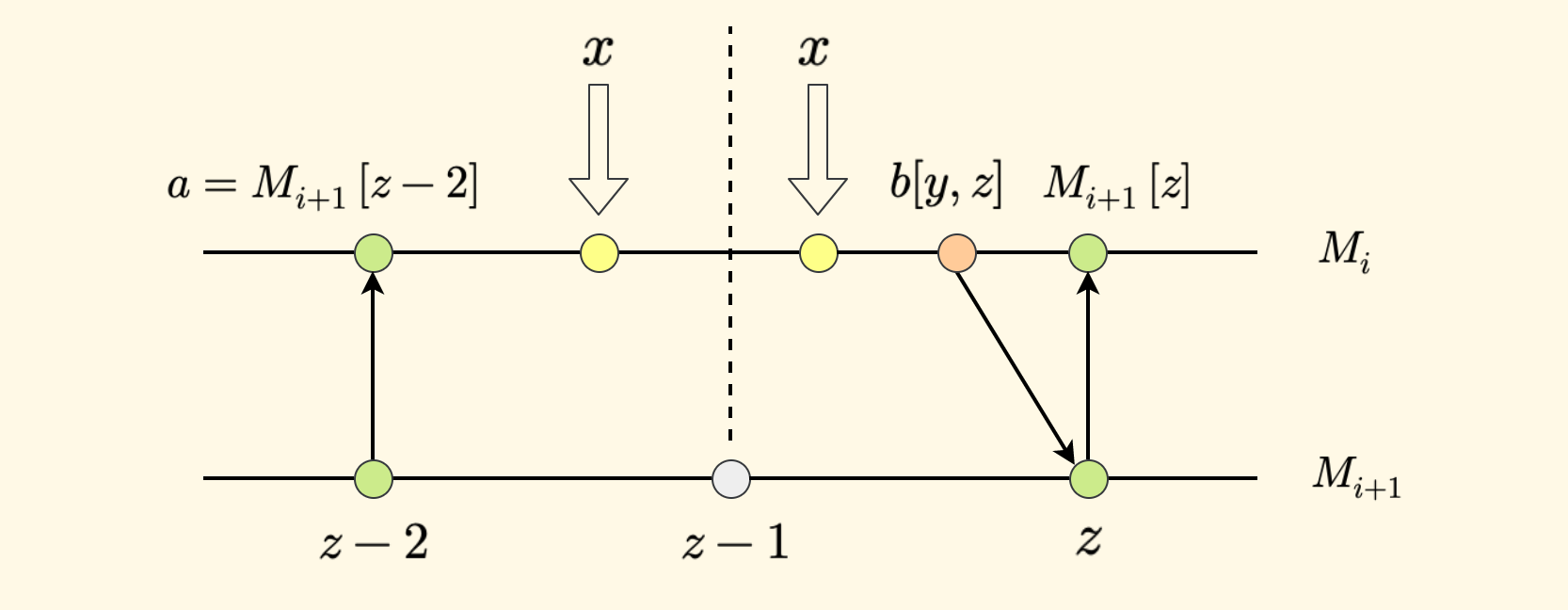
只需要检查下这两个位置,确切地说,先检查一下 $z-1$ 处元素值和 $x$ 的大小关系,如果满足 $x \le M_{i+1}[z-1]$, 那么 $z-1$ 处就是答案,否则 $z$ 处就是答案。
理清了这一点后,整个查询过程的步骤就简单了。
假设数组 $pos_i$ 表示输入的数字 $x$ 在原数组 $L_i$ 中的后继的位置:
- 首先对 $M_1$ 二分,得到后继 $x_1[y_1, z_1]$,即 $pos[1] = y_1$。然后拿着 $z_1$ 进入下面的步骤。
- 对于 $i \gt 1$ 的情况,检查 $z-1$ 和 $z$ 处的情况,确认真正的后继位置 $y$。依次进行下去即可。
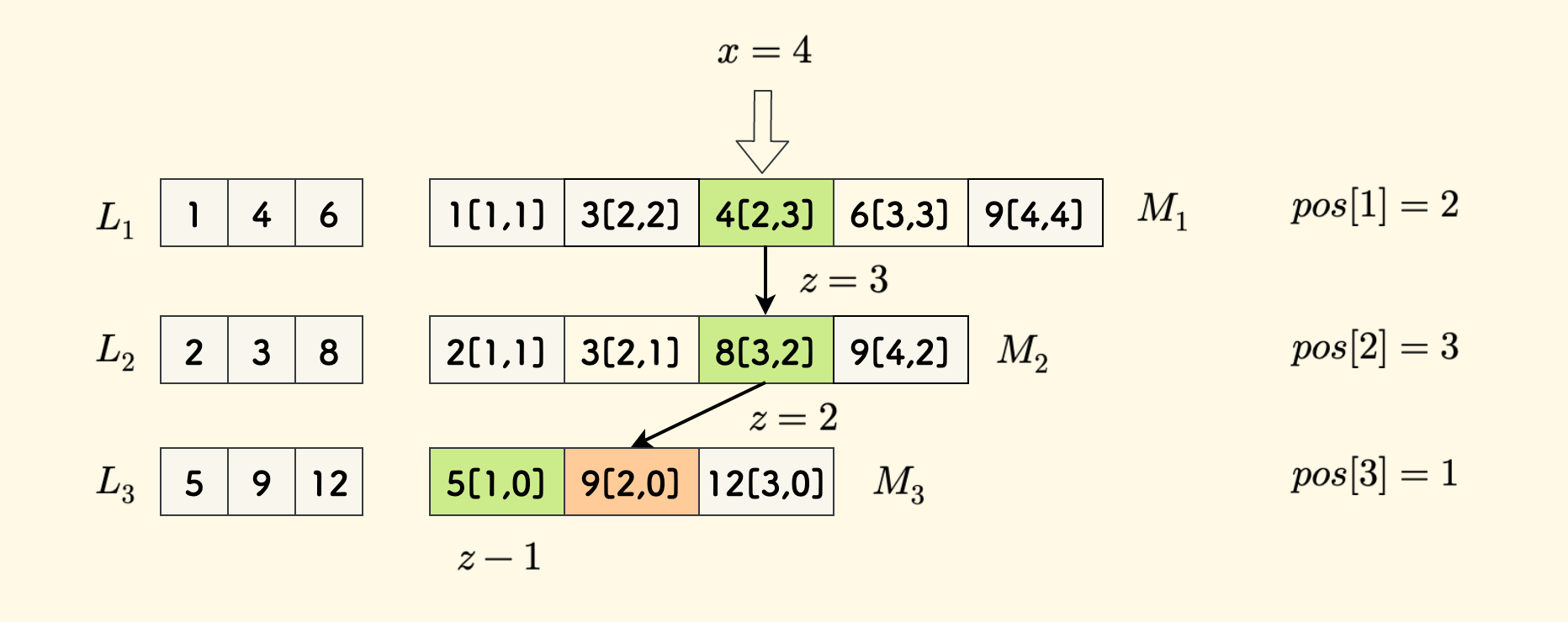
举一个具体的例子,下图中,要查询的是 $x=4$:
- 在 $M_1$ 中二分得到后继 $4[2,3]$,所以 $pos[1] = 2$。
- 然后拿着 $z=3$ 在 $M_2$ 中依次检查 $3$ 和 $8$,此时 $z$ 处就是后继,得到 $pos[2]=3$。
- 然后拿着 $z=2$ 在 $M_3$ 中依次检查 $5$ 和 $9$,此时 $z-1$ 处才是后继,得到 $pos[3]=1$。
我们可以人工检查一下这答案数组的正确性。
不过,有一种情况,当不存在后继时,需要特判处理。
比如说,还是这个例子,查询 $x=9$ 的时候,在 $M_2$ 中 $z=4$ 指向了一个无效位置。事实上,$x=9$ 在 $L_2$ 中不存在后继。
无论如何,我们都可以在查询的时候,检查确认一下后继的合法性。

复杂度 ¶
首先,先看一下每个辅助数组 $M_i$ 的大小 $SZ_i$。
最后一个 $M_k$ 的大小是 $n$,然后取一半和 $L_{k-1}$ 合并,得到 $M_{k-1}$,其大小是 $n+n/2$。
进一步地,$M_{k-2}$ 的大小会是 $n + SZ_{k-1}/2$,也就是 $n+n/2+n/4$。
依次推导下去,$M_i$ 数组的大小 $SZ_i$ 会是:$n + n/2 + n/4 + … + n/{2^{k-i}}$,不超过 $2n$ [1]。
也就是说,每个 $M_i$ 数组的大小肯定不超过 $2n$。
因此,整体的空间复杂度会是 $O(k * 2n)$ ,也就是 $O(kn)$,其中 $k$ 是有序原数组的个数、$n$ 是每个数组的大小。
预处理是不断合并 $L_i$ 和 $M_{i+1}$ 的一半来构造 $M_{i}$ 的过程,每次合并是线性的,和归并排序中的合并子过程是一样的, 共进行 $k$ 次,所以时间复杂度是 $O(k*(n+2n/2))$,也就是 $O(kn)$。
每次询问时,先对 $M_1$ 进行一次二分查找,然后再依次向下检查,每个 $M_i$ 中最多检查两个元素,所以 时间复杂度是 $O(\log{n} + k)$。
代码实现 ¶
思路已经梳理完毕,最后来实现代码。
结构定义
- 假定 $k$ 不会超过常数 $K$,$n$ 不会超过常数 $N$,并定义好原始数组 $L_i$。
- 辅助数组 $M_i$ 的每一项会存储三个字段 $x[y,z]$,可以定义一个结构体
V。 - 每个 $M_i$ 数组的大小不会超过 $2n$,所以可以直接定义 $M$ 数组的长度为 $2*N$。
- 对于每次查询,用 $ans$ 数组来记录输入的 $x$ 在每个 $L_i$ 中的后继的元素值。
因此结构定义的实现如下:
分散层叠算法 - 结构定义 (C++)
const int N = 10001;
const int K = 101;
int L[K][N]; // 原始的 k 个有序序列, 从下标 1 开始
// M 数组中的每个元素是一个结构体
struct V {
int x; // 元素值
int y = 0; // 在 L[i] 中出现的位置
int z = 0; // 在 M[i+1] 中出现的位置
};
V M[K][2 * N]; // 构造的 k 个序列, 从下标 1 开始
int SZ[K]; // 记录 M[i] 的长度
int ans[K]; // 记录一次询问在每个序列中的答案
合并函数
负责把 $M_{i+1}$ 间隔采样后和 $L_i$ 归并后生成 $M_i$, 这个过程和归并排序[2] 中的合并函数几乎完全一样。 不同点只有两处(我们用 $start1$ 和 $start2$ 分别代表 $L_i$ 和 $M_{i+1}$ 的扫描指针):
- 由于是间隔采样,所以 $M_{i+1}$ 的指针 $start2$ 要以步长
2来递进。 - 但是步长
2有可能会导致错过真正的后继。
第二点非常细腻,我们知道在合并过程中,对于当前要考虑的槽位,要么取 $L_i$ 的元素,要么取 $M_{i+1}$ 的元素,这要看哪一方更小。
当 $L_i$ 中的元素更小时,它要记录的 $z$ 字段不能简单的采用 $start2$ 的值,因为 $start2$ 是按步长 $2$ 走的,它可能跳过 $L_i[start1]$ 的真正的后继。 比如下图中就是一个例子。这时候要检查一下 $start2-1$ 的情况,从 $start2-1$ 和 $start2$ 中挑选一个作为 $z$ 的取值。
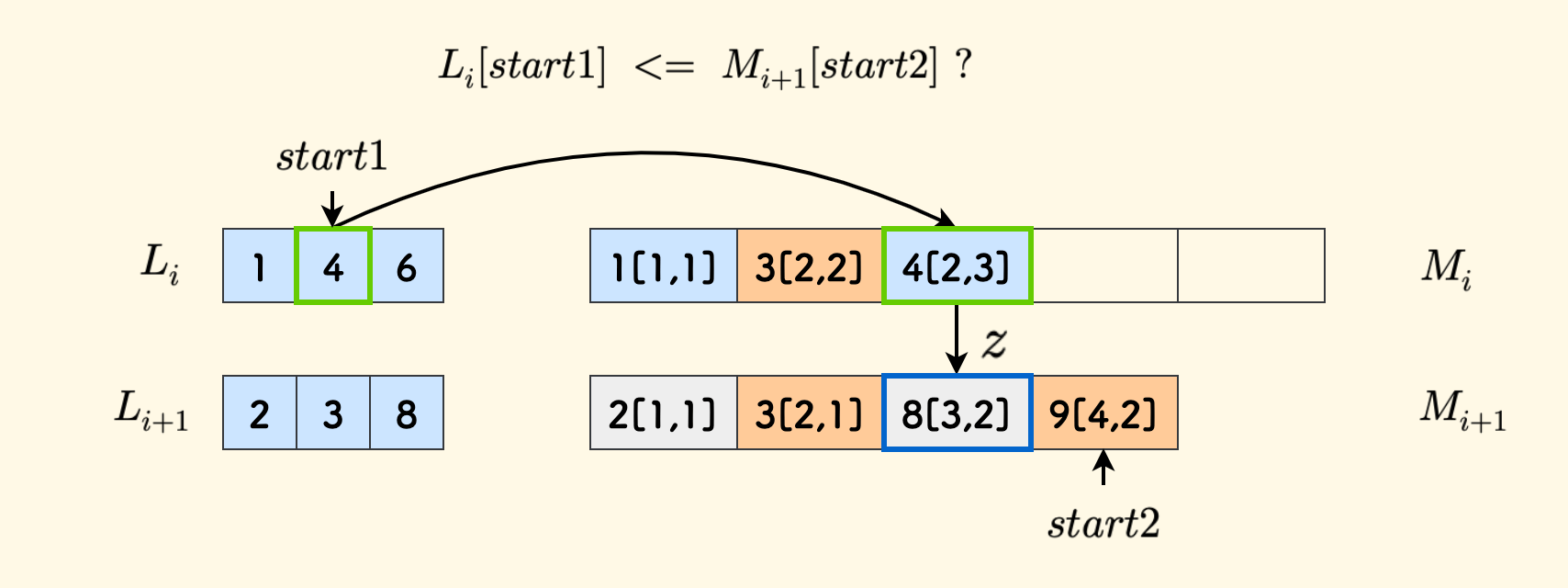
但是当 $M_{i+1}$ 中的元素更小时,就是说考虑这个槽位放入 $M_{i+1}[start2]$ 时,则不必处理这个问题,因为它的后继肯定是 $start2$。
合并函数的实现代码如下:
分散层叠算法 - 合并函数 (C++)
// 把 M1 每隔一个元素取样, 然后和 Li 归并到 M2 中去
// Li 的起始结束是 start1, end1; M1 的起始结束是 start2, end2
// M2 的起始是 start; 返回 start, 即最终 M2 的大小
int merge(int *Li, V *M1, V *M2, int start1, int end1,
int start2, int end2,
int start) {
auto take1 = [&]() { // 取 Li 的数值
M2[start].x = Li[start1];
M2[start].y = start1;
// 注意这里,为了防止 M1 的步长为 2 导致错过真正的后继,需要检验下
// start2-1 位置是否是真的后继
M2[start].z = M1[start2 - 1].x >= Li[start1] ? (start2 - 1)
: start2;
start++;
start1++;
};
auto take2 = [&]() { // 取 M1 的数值
M2[start].x = M1[start2].x;
M2[start].y = start1;
M2[start].z = start2;
start++;
start2 += 2; // 间隔取样
};
while (start1 <= end1 && start2 <= end2)
Li[start1] <= M1[start2].x ? take1() : take2();
while (start1 <= end1) take1();
while (start2 <= end2) take2();
return start;
}
预处理函数
预处理过程的思路清楚后,实现就比较简单了:
分散层叠算法 - 预处理函数 (C++)
void preprocess() {
memset(M, 0, sizeof(M));
memset(SZ, 0, sizeof(SZ));
// M[k] 即 L[k] 序列本身
for (int j = 1; j <= n; j++) {
M[k][j].x = L[k][j];
M[k][j].y = j;
}
// 自后向前, 归并 M[i+1] 的一半和 L[i] 来构造 M[i]
SZ[k] = n;
for (int i = k - 1; i > 0; --i) {
// start2: 从 2 开始间隔采样
// 最终大小是 start2-1
SZ[i] = merge(L[i], M[i + 1], M[i], 1, n, 2, SZ[i + 1], 1) - 1;
}
}
这里有一个细节点:为什么从位置 2 开始采样,而不是直接从位置 $1$ 开始呢? 一个好处是,这样在处理查询时,考虑 $z-1$ 位置上的元素时,就不必考虑其合法性了。
询问函数
函数 query(int x) 会把 $x$ 在每个数组 $L_i$ 中的后继元素的值写在 $ans[i]$ 上。
首先,对 $M_1$ 进行二分查找,属于二分求 $\ge x$ 的左界 [3]。
int l = 1, r = SZ[1];
while (l < r) {
int m = (l + r) >> 1;
if (M[1][m].x >= x) r = m;
else l = m + 1;
}
此时,l 就是 $x$ 在 $L_1$ 中的后继的位置。第一轮的目标 $v$ 就是 $M[1][l]$ 了:
V *v = &M[1][l]; // 取的指针
但是,要时刻注意确认后继的有效性。
// 注意验证合法性, 有可能不存在后继
if (v->x >= x) ans[1] = L[1][v->y];
和前面分析的思路一样,对于后续 $i>1$ 的情况,拿着 $z$ 不断一层一层的找就可以了,对于每一层,都只需确认两个位置,即 $z-1$ 和 $z$ 处。
for (int i = 1; i < k; i++) {
// 考察 z-1 处, 注意 z 超过 M[i+1] 大小的情况
if (M[i + 1][v->z - 1].x >= x || v->z > SZ[i + 1])
v = &M[i + 1][v->z - 1];
else // 否则就是 z 处
v = &M[i + 1][v->z];
// 但是要注意验证后继的合法性
if (L[i + 1][v->y] >= x) ans[i + 1] = L[i + 1][v->y];
}
其他关于 洛谷 P6466 题目具体相关的代码不必再说明, 完整代码实现见:code-snippets - 分散层叠算法 - P6466 。
结尾语 ¶
洛谷 P6466 题目中约定了元素互不重复、每个数组严格递增的条件,但是,分散层叠算法并不要求原数组是严格有序的。
最后,这个算法还挺有意思的,时间复杂度和空间复杂度都很优秀。但是代码实现起来其实也并没有那么简洁~
(完)
