递增的三元子序列

挺有趣的一道题：

给定一个整数数组 nums，判断其中是否存在三元递增子序列。

三元递增子序列是指三个元素，它们的下标关系是 i < j < k，同时满足 nums[i] < nums[j] < nums[k]。

-- leetcode 334. 递增的三元子序列

要求空间复杂度为 $O(1)$、时间复杂度为 $O(n)$。

最开始、我的第一想法是单调栈来做，但是空间复杂度不符合要求。

这实际是在找「长度为 3 的递增子序列」是否存在，和经典的 最长递增子序列 十分相似。

假设当前迭代的元素是 x，定义：

• b 为已发现的长度为 2 的递增子序列的末尾元素的最小值。
• c 为已发现的长度为 1 的递增子序列的末尾元素的最小值，也即 x 左边的最小值。

下图中，a, b 形成了长度为 2 的递增子序列，c 是已经发现的最小值。

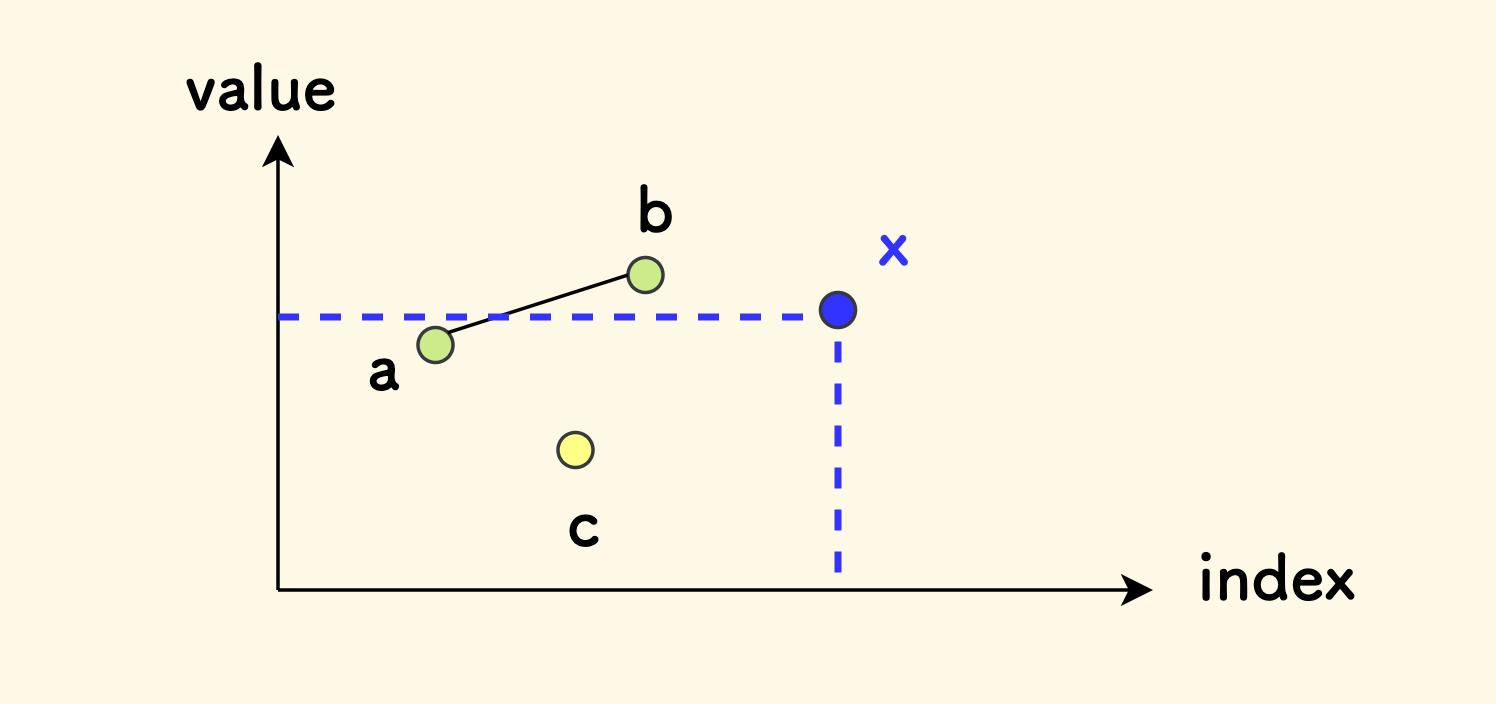
首先，肯定有 b > c，因为 c 是已经发现的最小值, 必定有 c <= a < b。

现在分情况讨论：

1. 如果 x > b，那么已经发现三元递增序列 a < b < x，直接返回 true 即可。
2. 否则，如果 b >= x > c，那么，至少发现了两元递增序列 c < x，那么需要更新 b = x。
3. 最后的情况是，x <= c 的时候，此时只需要更新最小值 c = x。

最开始，设置 b 和 c 都为 INT_MAX 即可。

代码实现如下：

bool increasingTriplet(vector<int>& nums) {
    int b = INT_MAX, c = INT_MAX;
    for (auto x : nums) {
        if (x > b)
            return true;
        else if (x > c) {  // x <= b && x > c
            b = x;
        } else {  // x <= c
            c = x;
        }
    }
    return false;
}

（完）

相关阅读：最长递增子序列（nlogn 二分法、DAG 模型 和 延伸问题）

本文原始链接地址： https://writings.sh/post/increasing-triplet-subsequence