最近重新做了下经典的最长递增子序列问题,我有些新发现要写下来。
这个问题也叫最长上升子序列问题,简称 LIS 问题,描述如下:
在一个数组中找到最长的、元素严格递增的子序列。 并不要求这个序列在原数组中连续,但是其中元素的相对顺序要和在原数组中保持一致。
这个问题的 动态规划解法 是容易理解的,其时间复杂度是 $O(n^2)$。
本文将从更优的、时间复杂度为 $n\log{n}$ 的二分解法出发,对其进行一种分层的 DAG 建模,并讨论一些延伸问题。
本文内容包括:
关于经典 LIS 问题,本博客已经有三篇文章讲了三种方法
- 朴素的
O(n2)DP 解法 - (本文)二分 + 贪心的解法、以及 DAG 模型推广
- 基于朴素 DP 解法 - 进一步优化 DP 转移
二分法求长度 ¶
感性的理解 - 上升尽可能慢
这种方法的感性理解是: 要让序列上升的更慢,才能找到更长的递增子序列 。
做法是:维护一个辅助数组 p,它的每一项 p[i] 的含义是,所有长度为 i+1 的上升子序列的末尾元素中的最小值。
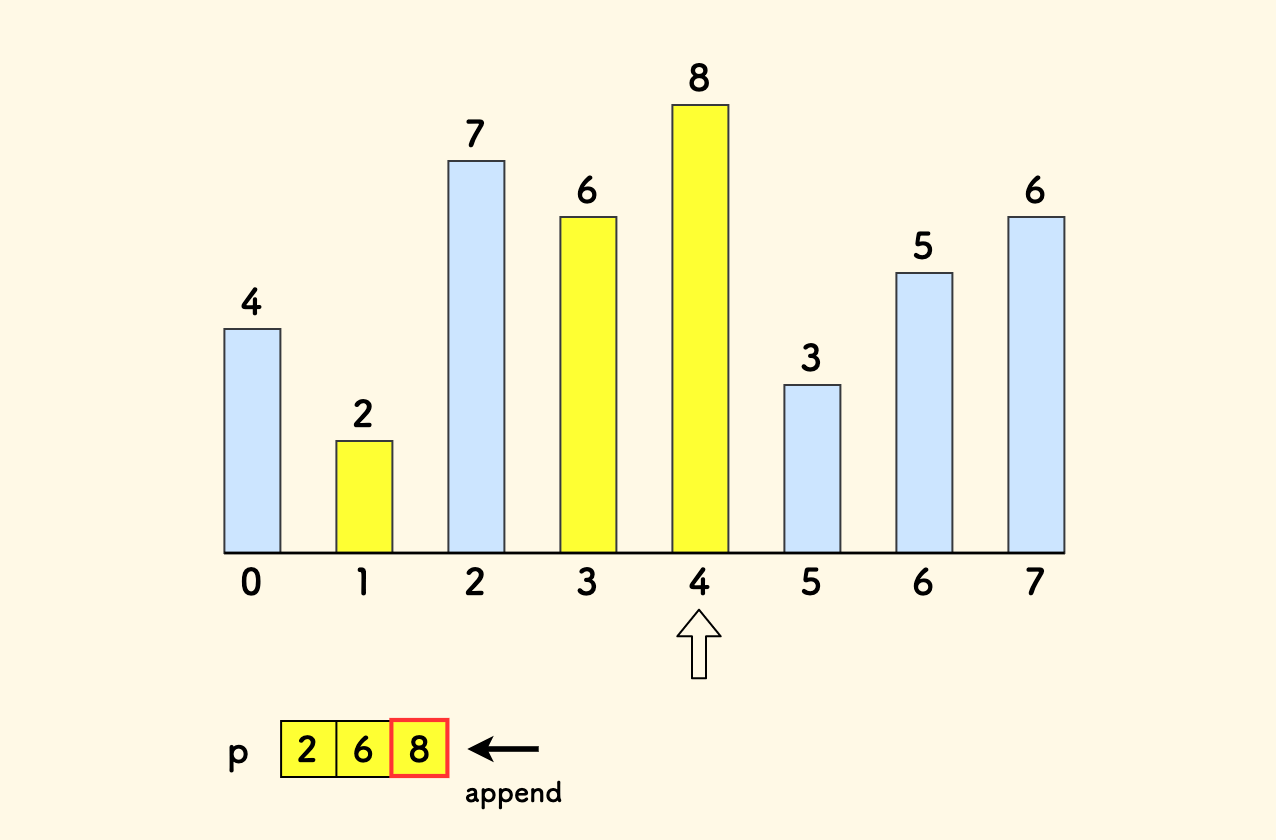
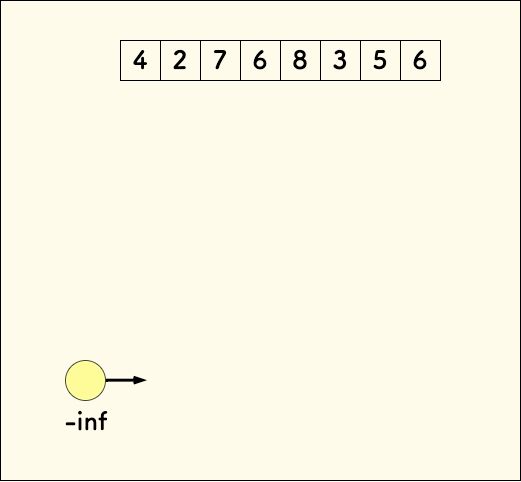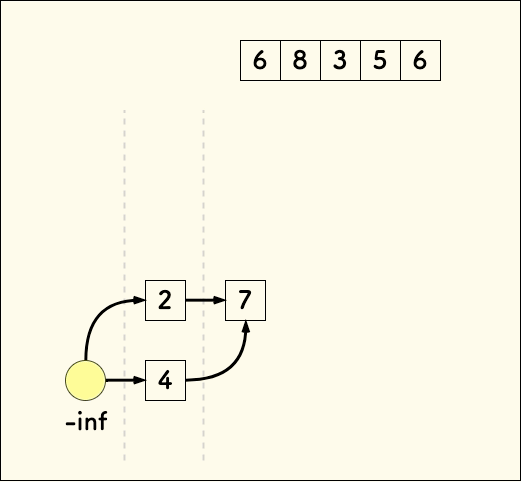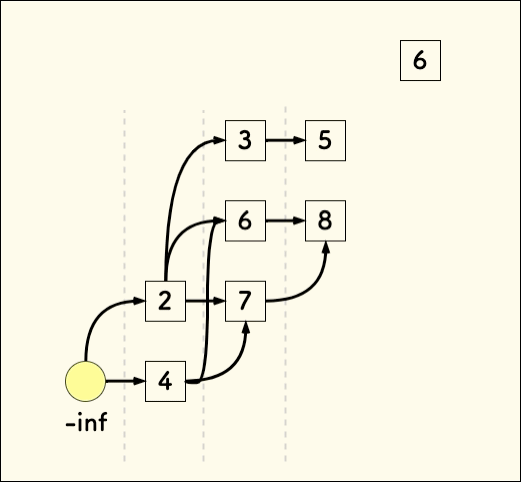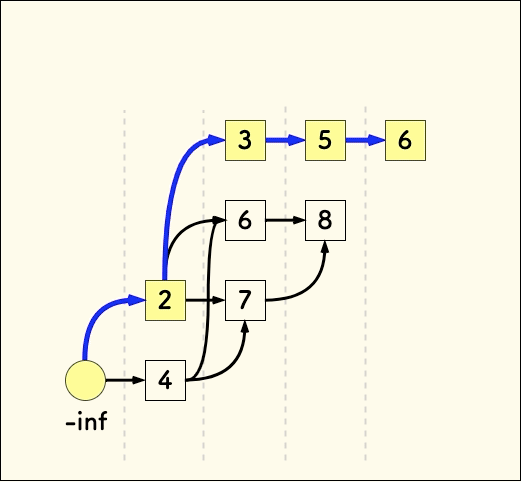
比如下图中,当扫描到第 3 个元素时,目前已知的元素中,长度为 1 的上升序列的末尾元素中最小值的是 2。 长度为 2 的上升序列的末尾元素中的最小的是 6:
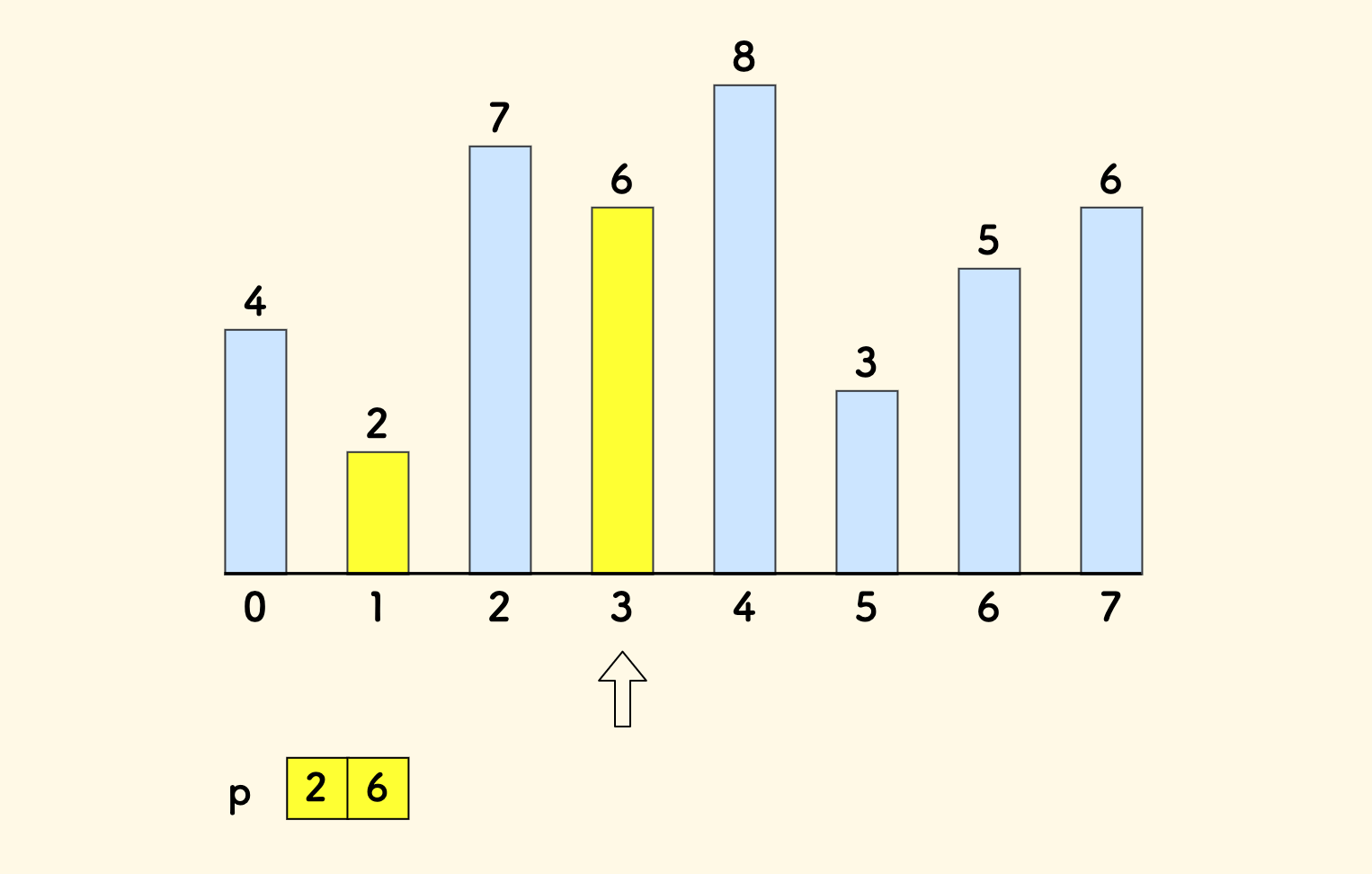
容易知道,数组 p 一定是严格递增的[1]。
为了维护这个辅助数组的性质,在扫描主数组时:
如果遇到一个比
p的尾部元素更大的值,说明形成了一个更长的上升序列。 则把它追加到p的尾部。
如果遇到一个比
p的尾部元素更小的值,说明发现了某个上升子序列的、更小的末尾元素,需要更新它[2]。
因为 p 是有序的,可以二分查找目标位置(lower_bound 查下界)来更新,因此总时间复杂度是 $O(n\log{n})$ 。
最终 p 的长度就是最长递增子序列的长度。
这个算法很简洁,代码实现:
二分求最长递增子序列的长度 - C++ 代码
int lengthOfLIS(vector<int>& nums) {
vector<int> p{nums[0]};
for (int i = 1; i < nums.size(); i++) {
if (auto num = nums[i]; num > p.back())
p.push_back(num);
else {
auto j = lower_bound(p.begin(), p.end(), num);
*j = num;
}
}
return p.size();
}
但是这种「上升地更慢才能更长」的理解有点「感性」。
更严格的理解
回顾朴素的 $O(n^2)$ 复杂度的 DP 实现[4]:
朴素的 $O(n^2)$ DP 的伪代码实现
for (int i = 1; i < n; i++) {
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j])
dp[i] = max(dp[i], dp[j] + 1);
}
ans = max(ans dp[i]);
}
如果 采用值域上定义 DP 的方式, 假设 $dp(x)$ 表示以数值 $x$ 结尾的能形成的 LIS 的长度,转移方程即可写为:
\[dp(x_i) = \max_{j < i, x_j < x_i}{dp(x_j)} + 1\]假如把扫描过的元素的值按照其 $dp$ 值分成桶来组织的话, 如下图所示,蓝色的框中是所有小于 $x_i$ 的决策集合,其中最靠右的桶取胜。
对于要输入的一个不确定的 $x_i$ 来说,可以试想让 $x_i$ 变的更大或更小的时候, 蓝色的决策集合方框的缩放情况。 可以知道,每个桶可以只由桶中的最小值来代表。
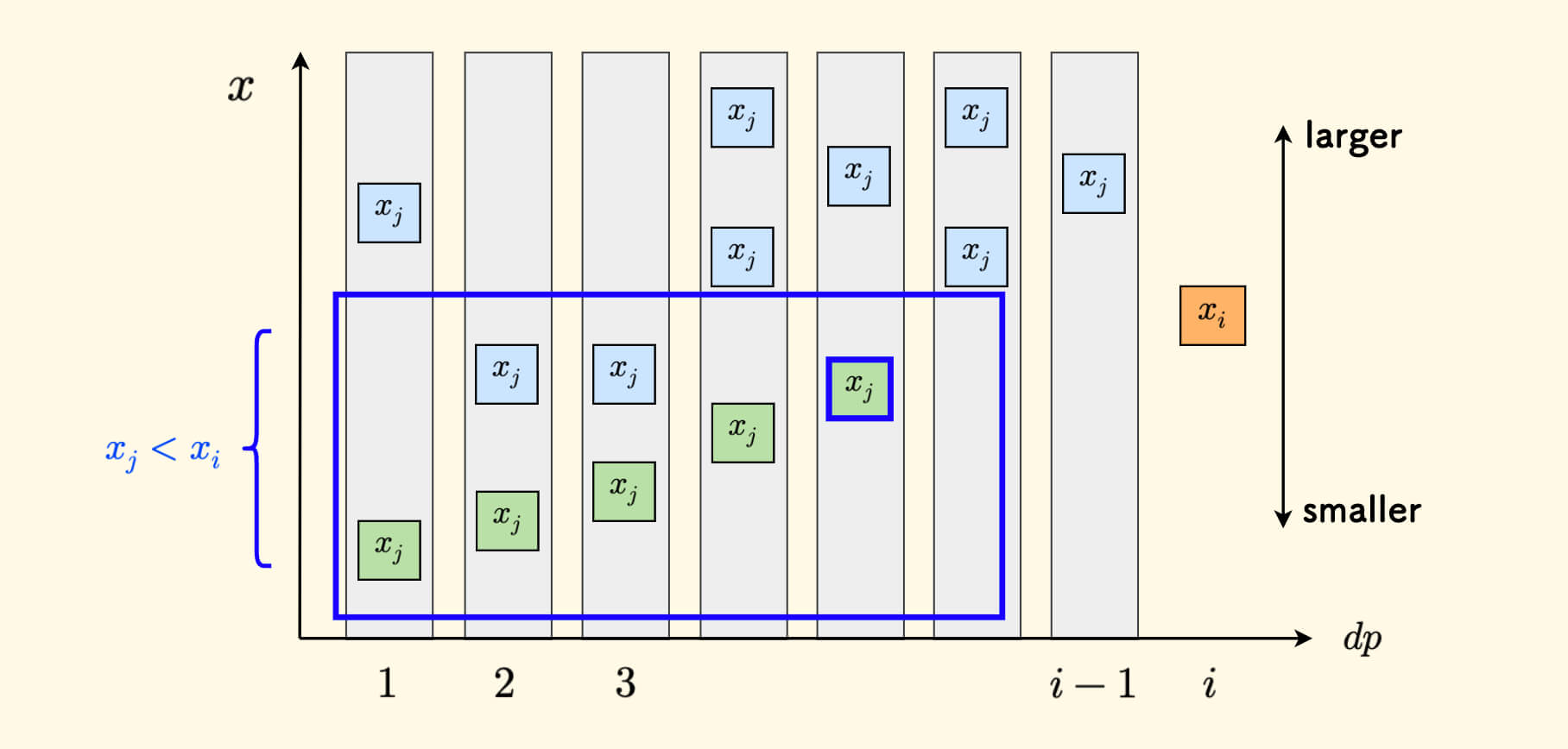
换句话说,对于每个 LIS 长度,仅需要维护结尾元素值最小的那个 $x_j$。
$dp$ 的结果一定是 1~n 范围内的,则可以维护一个数组 p[i] 来表示 LIS 长度是 i+1 的最小的结尾值 $x$。
p 的长度,就是已知的最大的 LIS 长度。
前面已经说过,这种定义下的数组 p 一定是单调递增的[1],所以可以应用二分法来维护它。
这个分桶的思路,后面会引申成为本文要讲的分层 DAG 模型。
形象的动图
最后,给一个形象的动图演示,可以看到: p 数组总是以低趴的姿态存在,这样才可以找到尽可能长的上升序列。
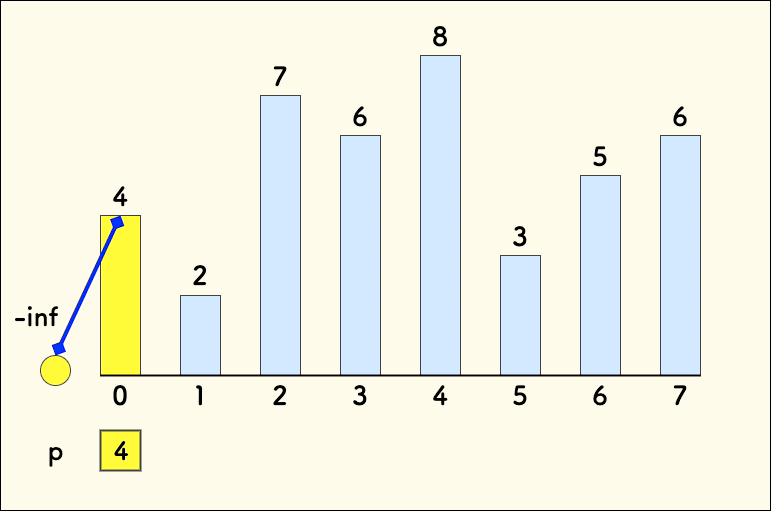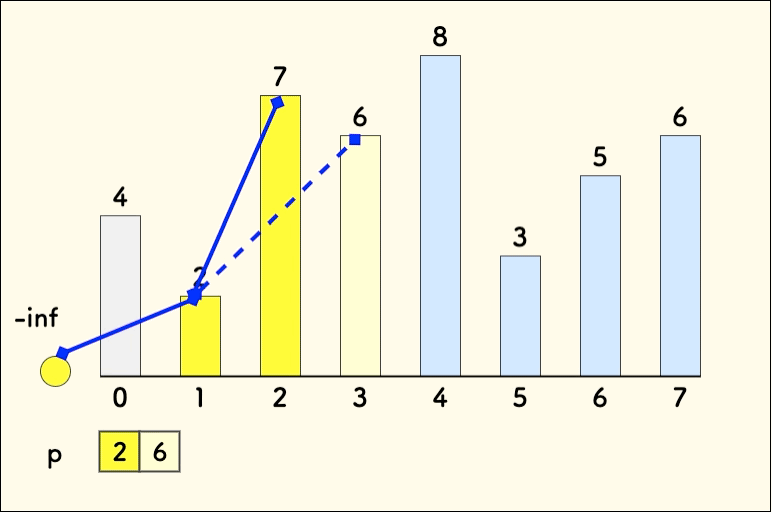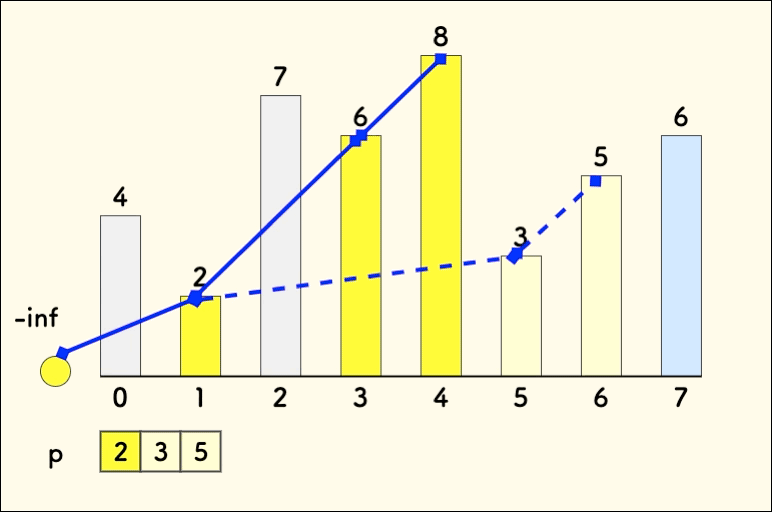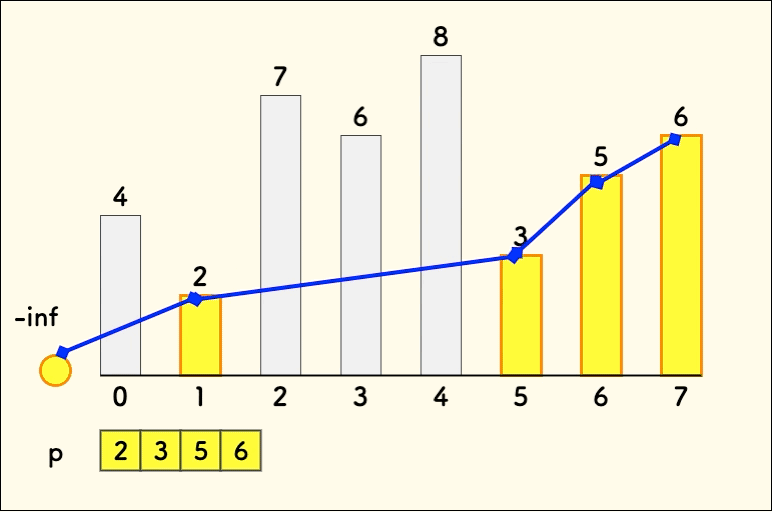
但是注意,辅助数组 p 并不一定存储最长递增序列本身[3]。
只是求「长度」的问题的话,这个简单的算法是够用了。
分层 DAG 建模 ¶
下面将介绍最长递增子序列的一种分层的、 DAG(有向无环图)建模。
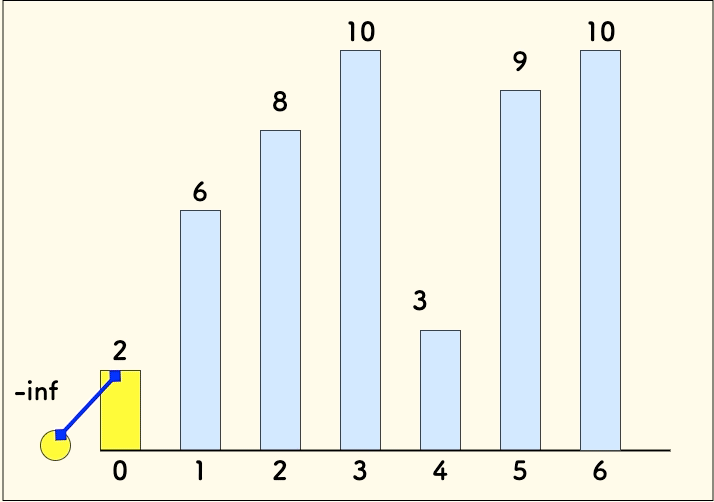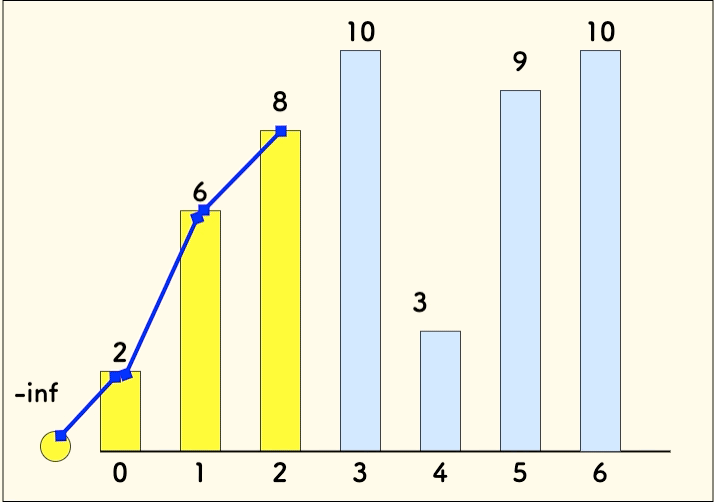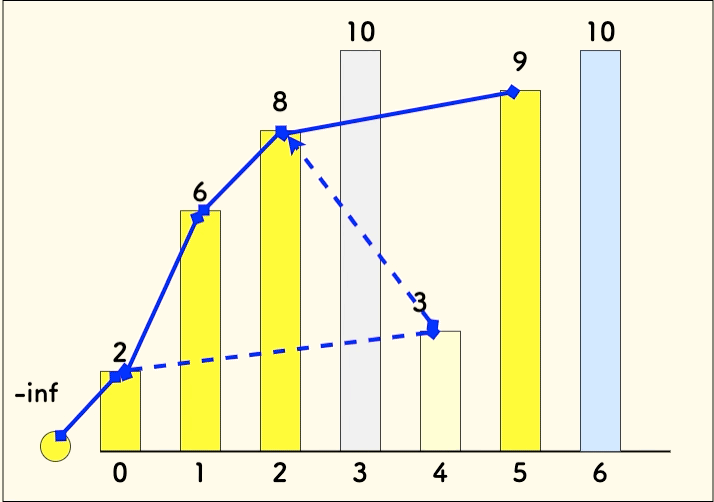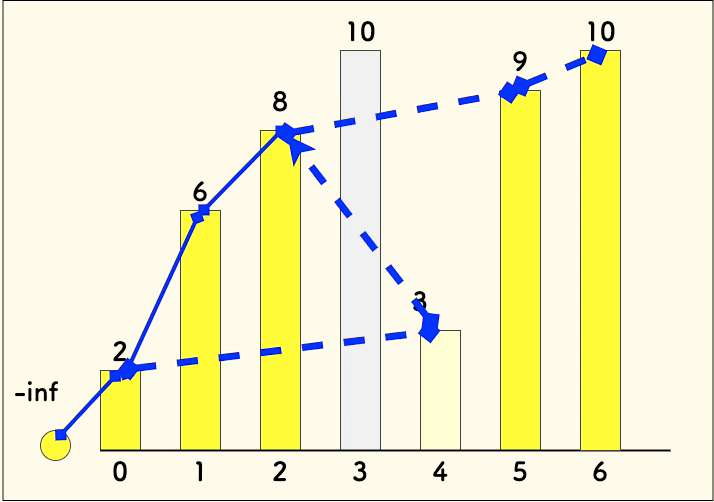
仍以数组 4,2,7,6,8,3,5,6 为例,先加一个无穷小 -inf 为其虚拟头元素。 其作用仅仅是图示上让这个 DAG 看上去更像一棵树。更好理解。
现在,加入第一个元素 4 :
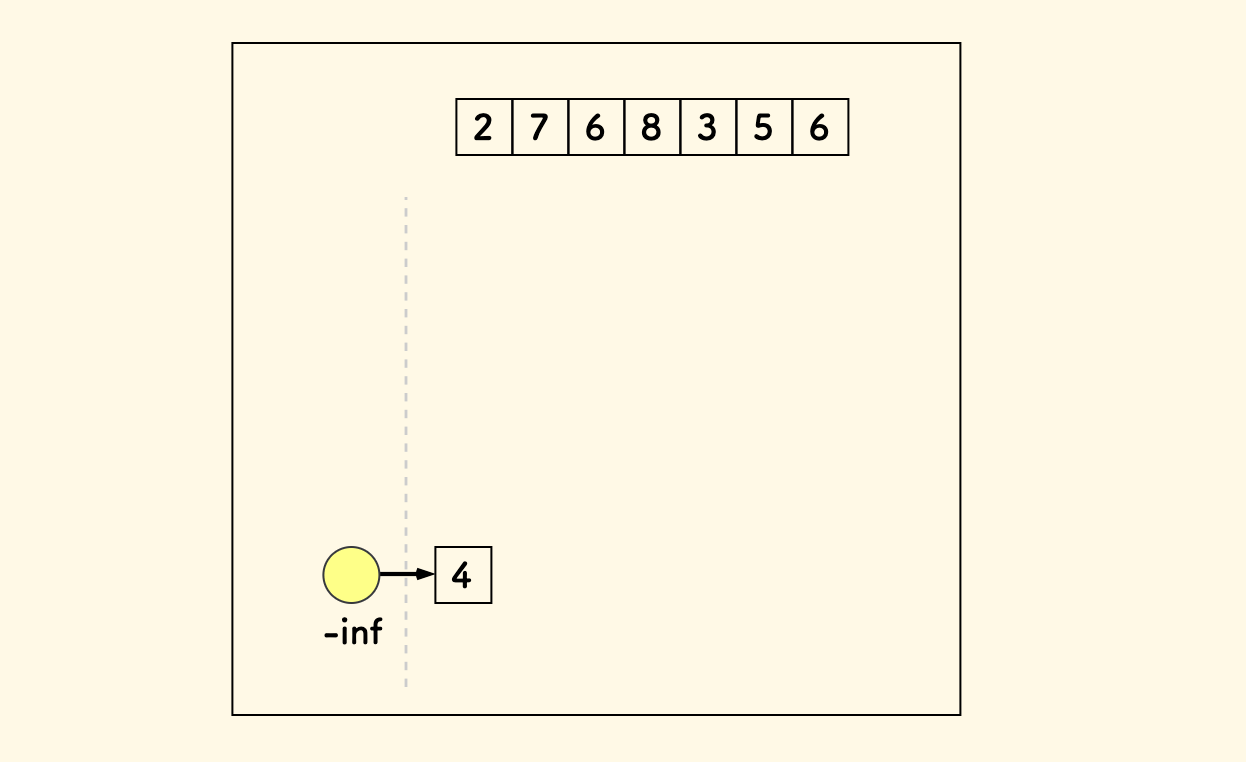
再加入数字 2 ,它无法和前面的 4 形成上升序列,那么写在上面:
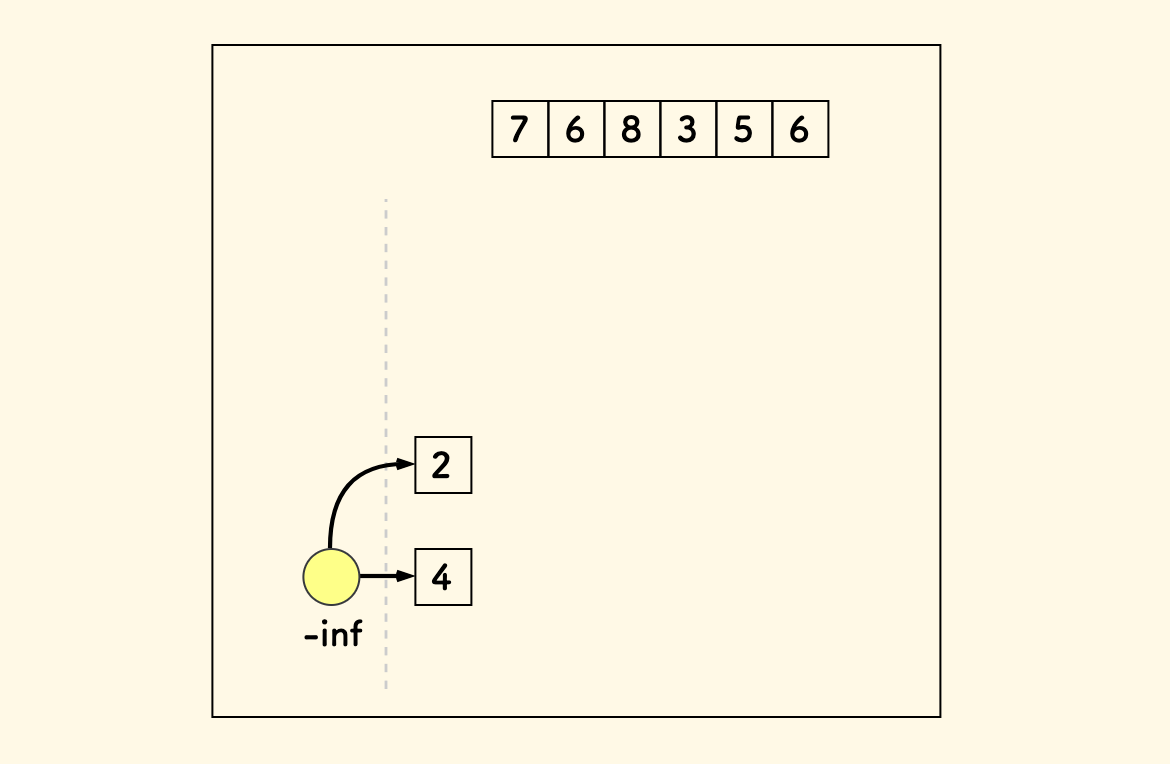
现在,放入数字 7, 它可以跟前面的 2 和 4 分别形成一个上升序列。那么再扩展一层:
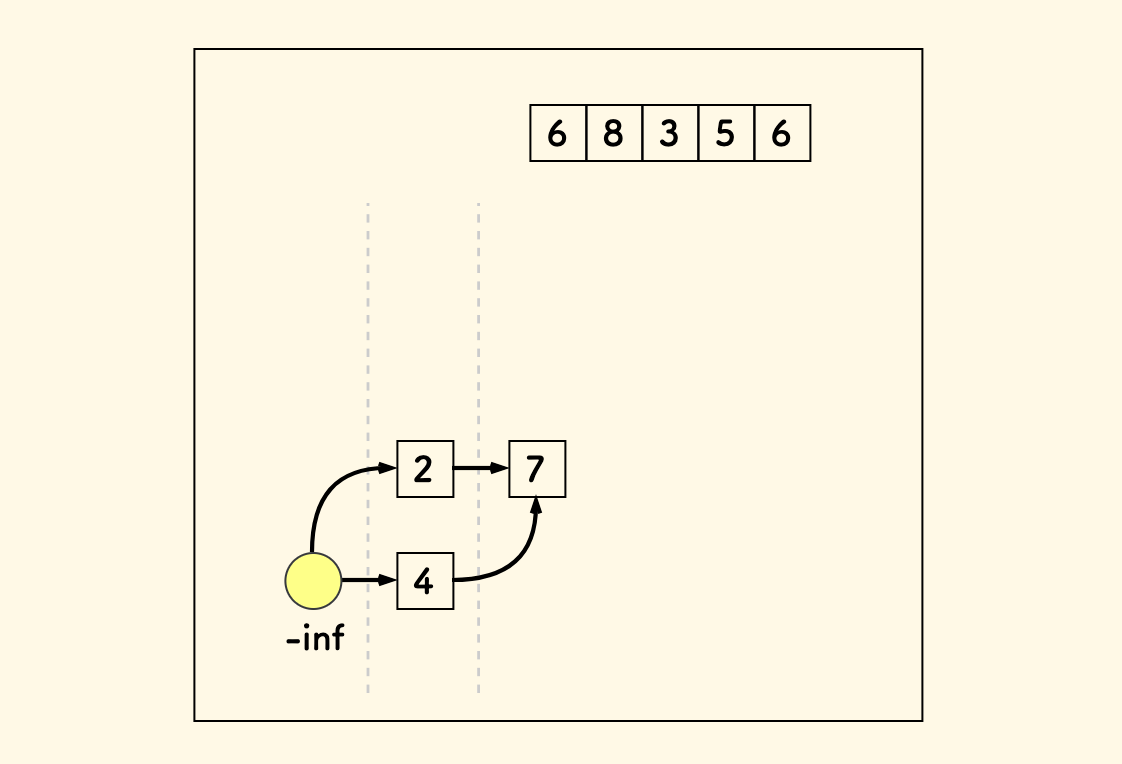
下面放入数字 6,它只可以跟前面的 2 和 4 形成递增关系。
接着放入数字 8,它可以扩展前面所有的序列,形成新的一层:
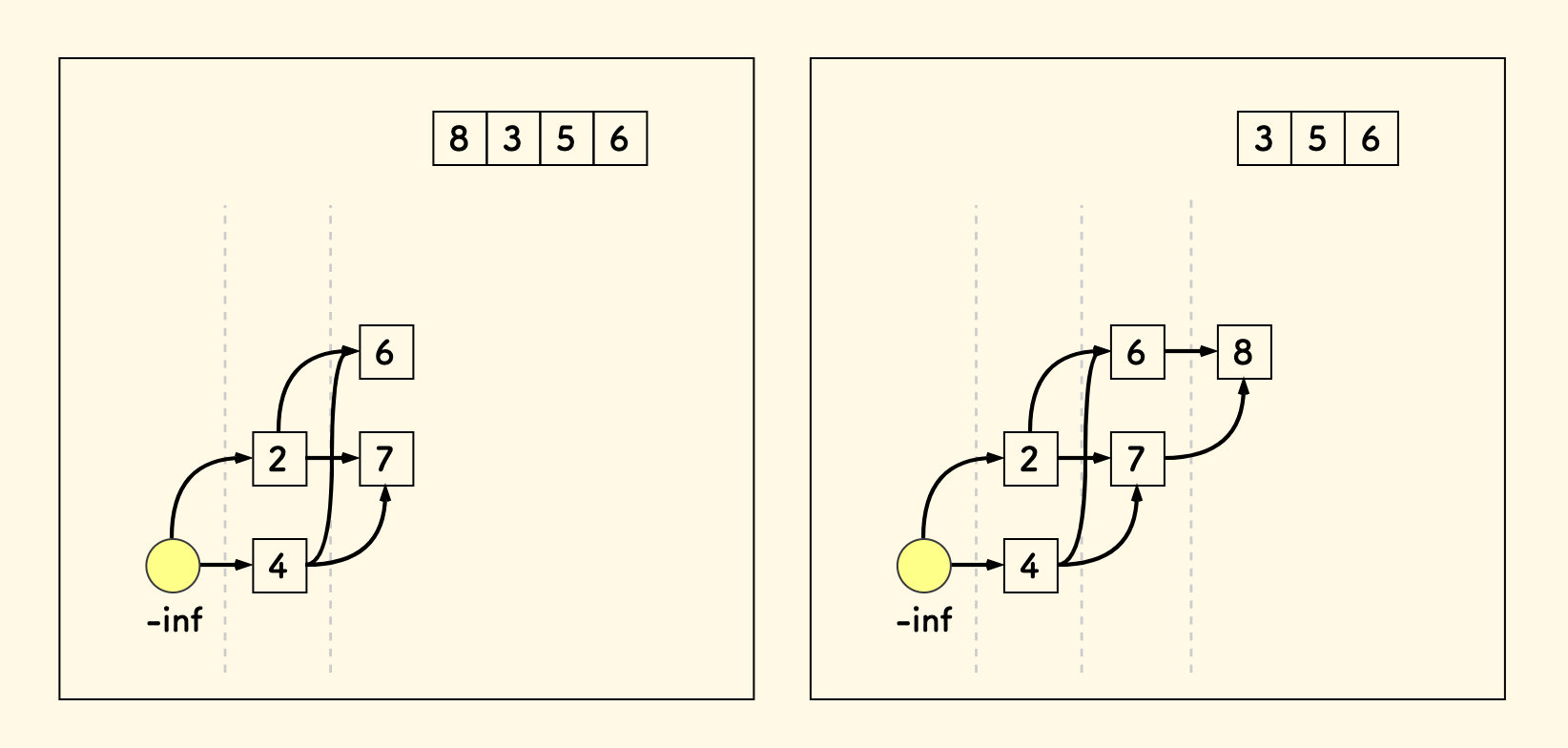
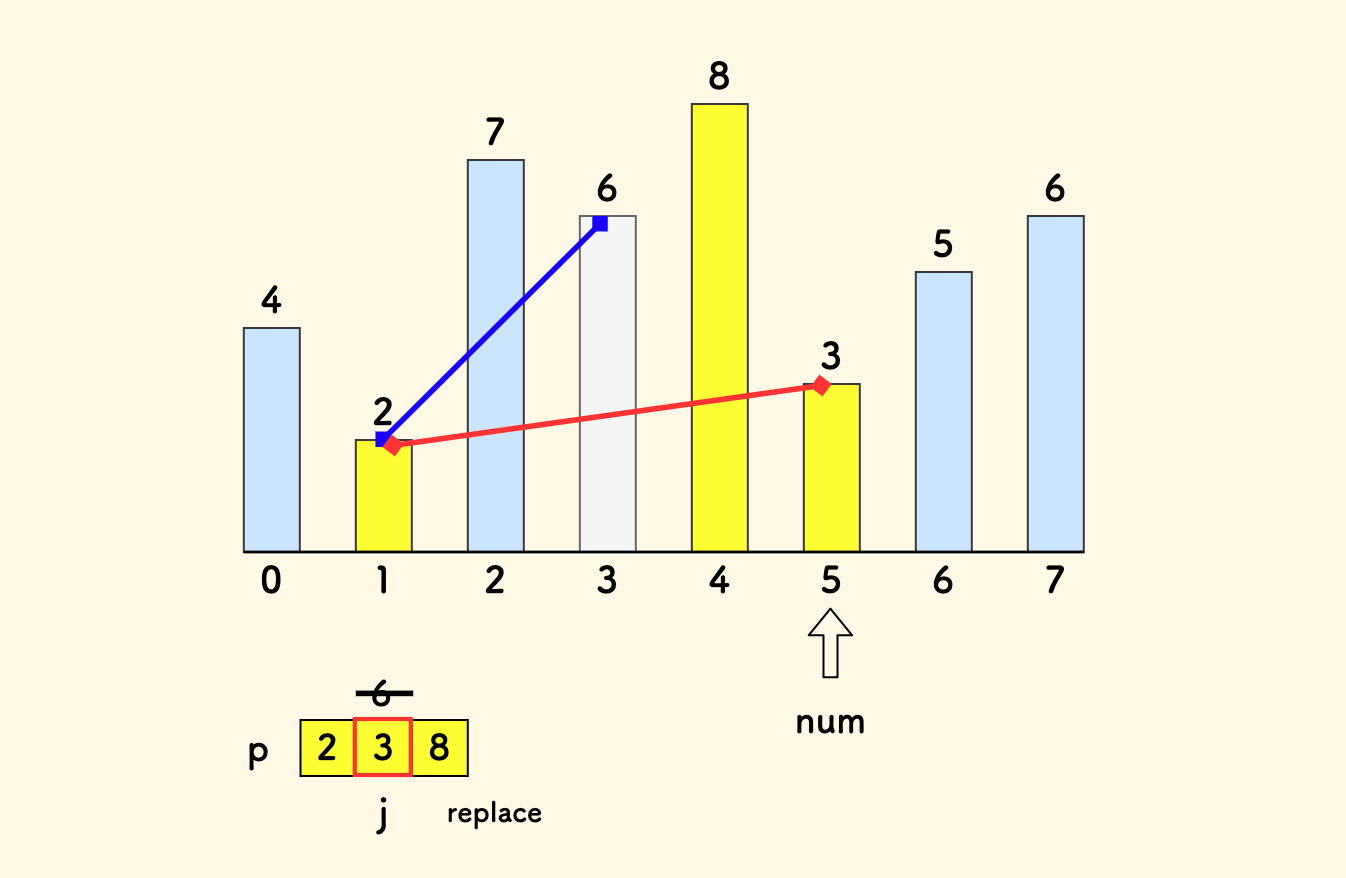
遇到数字 3 时,先找到它该放入的层。
各个层顶部的元素 [2,6,8] 中找到恰好不小于 3 的地方,即 6 的上方。
这个位置左边正好存在比 3 小的元素 2,就可以和之前的序列形成递增关系 。
把 3 放入这一层的顶部,因为找到的是恰好不小于 3 的地方,则 3 就成了这一层新的最小值。 可以看到,每个层中的数字也是有序的。
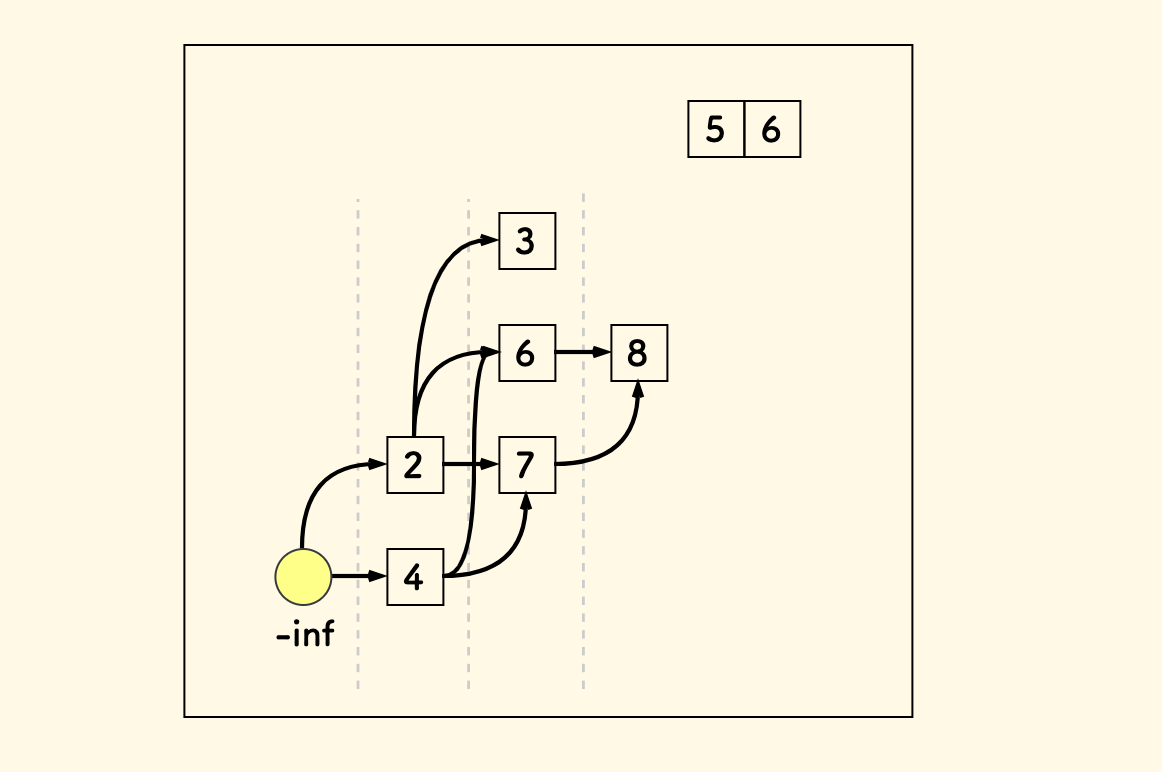
接下来,同样的逻辑,放入 5 到 8 的上方。
最后加入 6,因为它比顶层元素 [2,3,5] 都大,所以扩展一层放入。
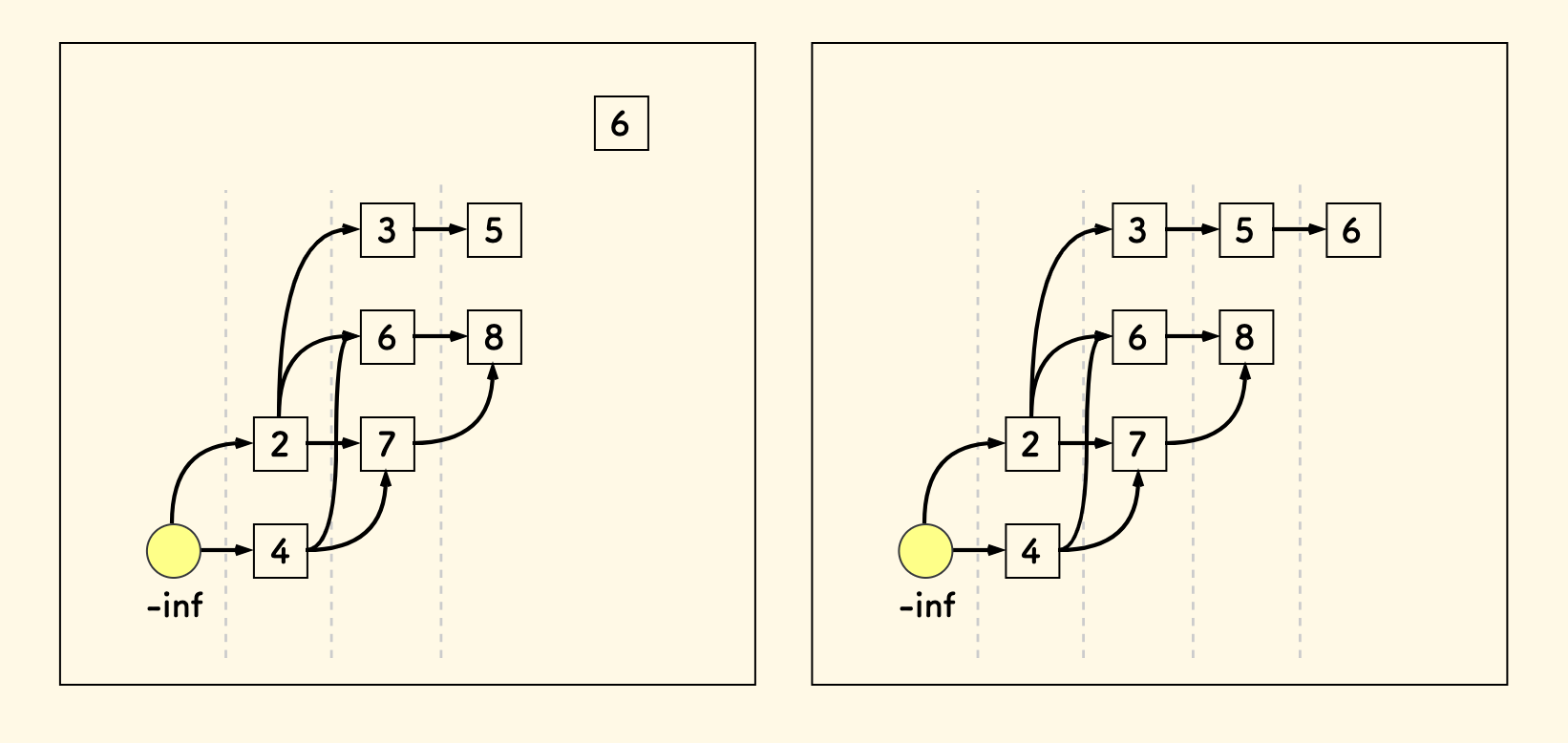
总结下这个图的构建过程:
先确定要放入哪一层。
要保证前面的层中至少有一个值可以和当前元素形成递增关系。 因为每个层的最小值都在顶部,所以 只需要找到恰好不小于顶部元素的层就可以。
如果比所有层的顶部元素都大,那么就新开一层。
放入这一层的顶部。上一层中所有比此元素小的,都作为父节点,连线。
简而言之,从找一个最浅的可以放入的层,放到顶部。
把整个过程的串成一个动图如下:
总结下这个图的性质:
- 求长度时 所说的辅助数组
p其实是在维护各个层的顶部元素。 - 各个层中的元素是有序的,顶部元素最小。
- 每一条路径都是一个上升序列,层数最大的路径对应的上升序列最长。
- 层的数目就是最长上升子序列的长度。
各个层中的元素是有序的,暗示着我们把每一层的元素存在一个数组里,这样方便二分的运用。
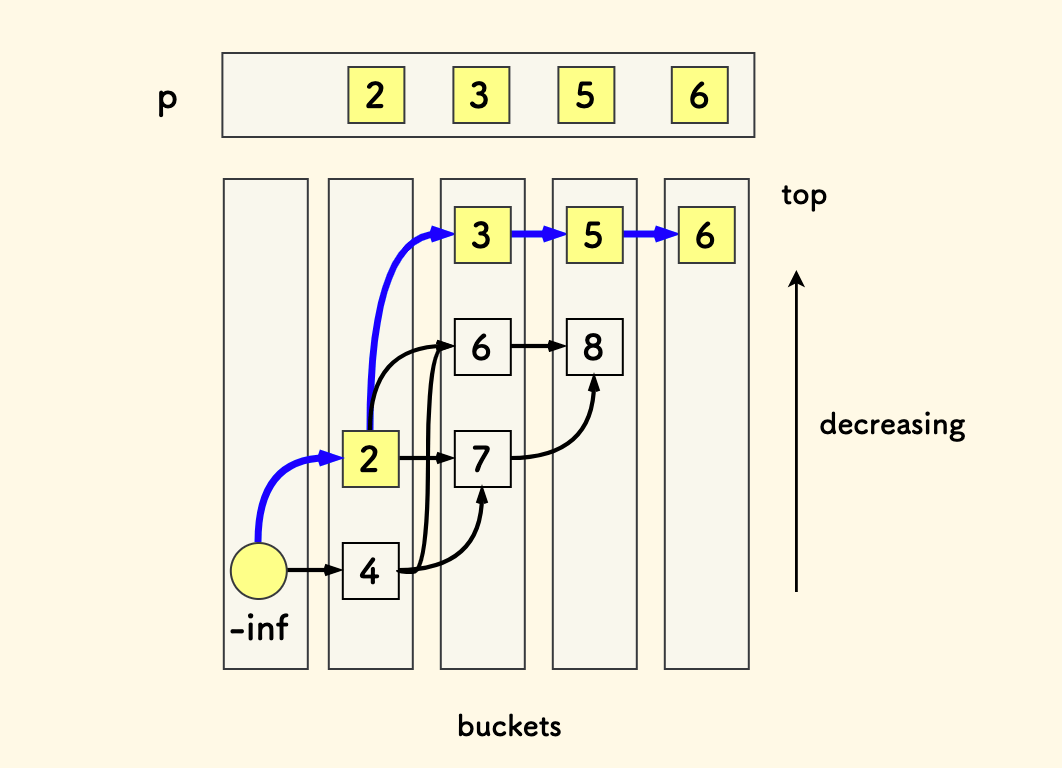
我的建模是这样的,姑且管它叫做一种「分层 DAG 模型」:
- 每一层叫做一个桶,用数组来描述。数组的尾部就是桶的顶部。
- 冗余维护一个辅助数组
p,追踪所有桶的顶部情况。
输出一个最长递增子序列 ¶
首先,最长的路径可能并不止有一条, 比如下面的这个例子,数组是 [8,10,2,9,6,13,1,9,5,12,3,10,16]:
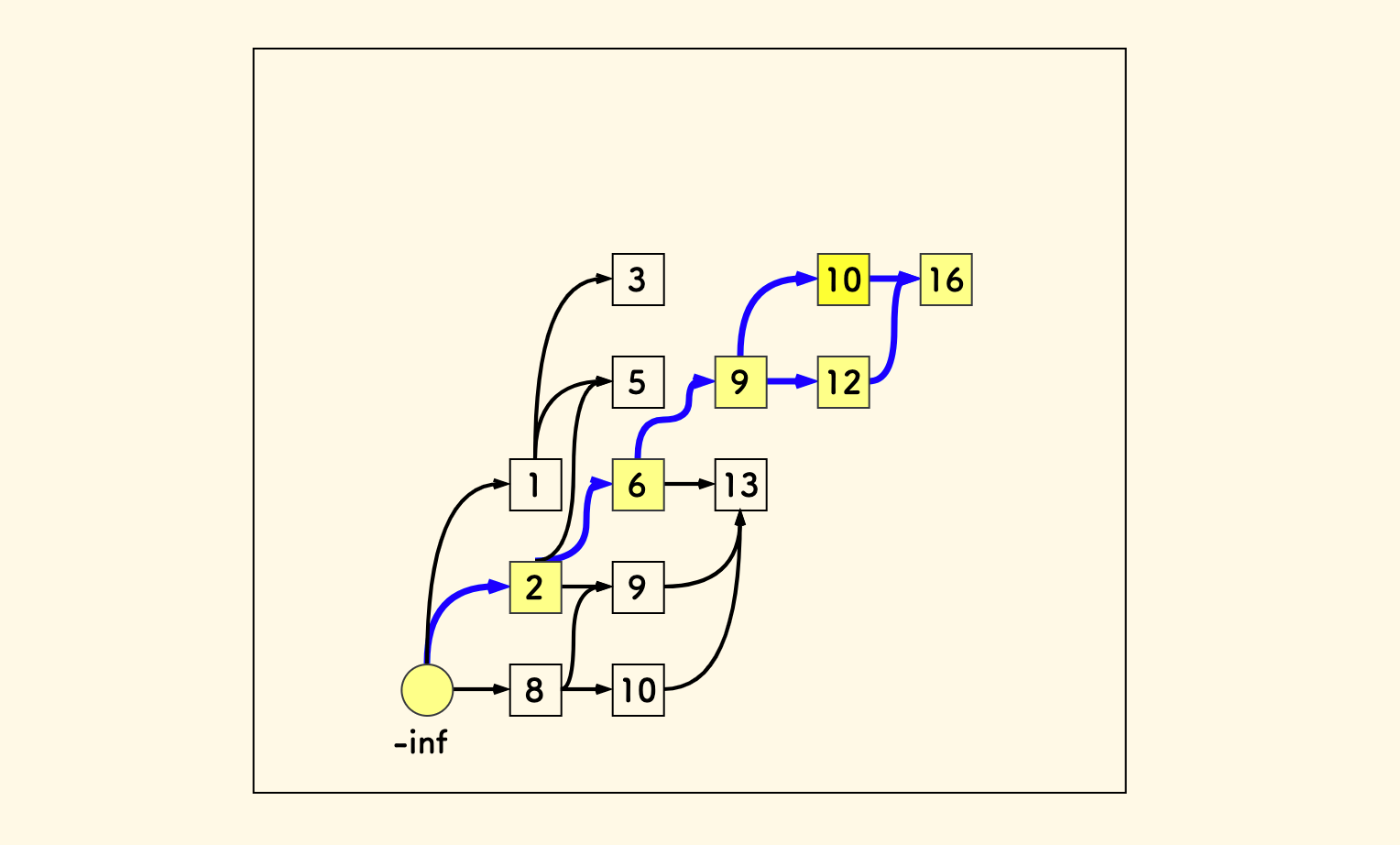
这意味着,要想输出所有的最长递增子序列,就要维护好图中所有的路径。
但是,如果只需要输出一个的话,我们仍可以做到 nlog(n) 的时间复杂度。
这时候,没必要维护所有的路径,每次新加一个元素时,只需要连接上一个桶的顶部作为父节点即可。 这样并不影响找到一个最长的上升序列。 比如下图:

具体的代码实现,不再赘述。
输出一个最长递增子序列 C++ 实现
class Solution {
public:
vector<int> findOneLIS(vector<int>& nums) {
using Node = pair<int, int>; // 槽位, {父节点在桶中的位置、元素值}
using Bucket = vector<Node>; // 桶
vector<Bucket> buckets; // 各个列的桶
vector<int> p; // 辅助数组, 冗余各个桶的尾部元素
// 放入头节点到第一个桶
buckets.push_back({{-1, nums[0]}});
p.push_back(nums[0]);
// 辅助函数, 给第 k 个桶放入一个新元素
auto push = [&](int k, int num) {
// 上个桶的当前尾部节点当做父节点
int j = (k == 0) ? -1 : (buckets[k - 1].size() - 1);
buckets[k].push_back({j, num});
// 更新辅助数组
p[k] = num;
};
for (int i = 1; i < nums.size(); i++) {
if (nums[i] > p[p.size() - 1]) {
// 新建一个空桶, 扩展辅助数组
buckets.push_back({});
p.push_back(0);
// 加入此元素到新桶 (最后一个桶)
push(buckets.size() - 1, nums[i]);
} else {
// 查找合适的桶放入新元素
int k = lower_bound(p.begin(), p.end(), nums[i]) - p.begin();
push(k, nums[i]);
}
}
// 要返回最长的上升子序列,需要从最后一个桶反向找回去
vector<int> ans(buckets.size());
// i 是第 i 个桶,j 父节点在前面一个桶的位置
for (int i = buckets.size() - 1, j = -1; i >= 0; i--) {
auto& b = buckets[i];
auto& [j1, num] = b[j < 0 ? (b.size() - 1) : j];
j = j1;
ans[i] = num;
}
return ans;
}
};
求最长递增子序列的个数 ¶
这个问题的一个延伸问题是,求最长的递增子序列的个数。
从前面做的 DAG 模型来看,这个问题 实际上是在对图中可以到达最后一个桶的路径做计数。
其实这个问题,也没必要维护所有的路径,只需要计数就可以。
原因的关键点在于,每个桶是有序的。
假设我们在构造每个节点的时候,追踪可以到达这个节点的路径数的数量的话,这个过程可以递推。
如下图所示,现在要放入元素 8,到前面一个桶中找到所有比 8 小的绿色节点作为父节点。 那么 8 这个节点处的路径数量,就是前面所有绿色节点对应的路径数量的总和。
由于桶中的元素都是有序的,因此可以二分查找上界位置 loc(upper_bound 函数), 这个位置上的数字恰好严格小于 8。
而绿色节点的计数总和,可以由前面整个桶的总和 sum(n) 减去前缀和 sum(loc-1) 来确定。
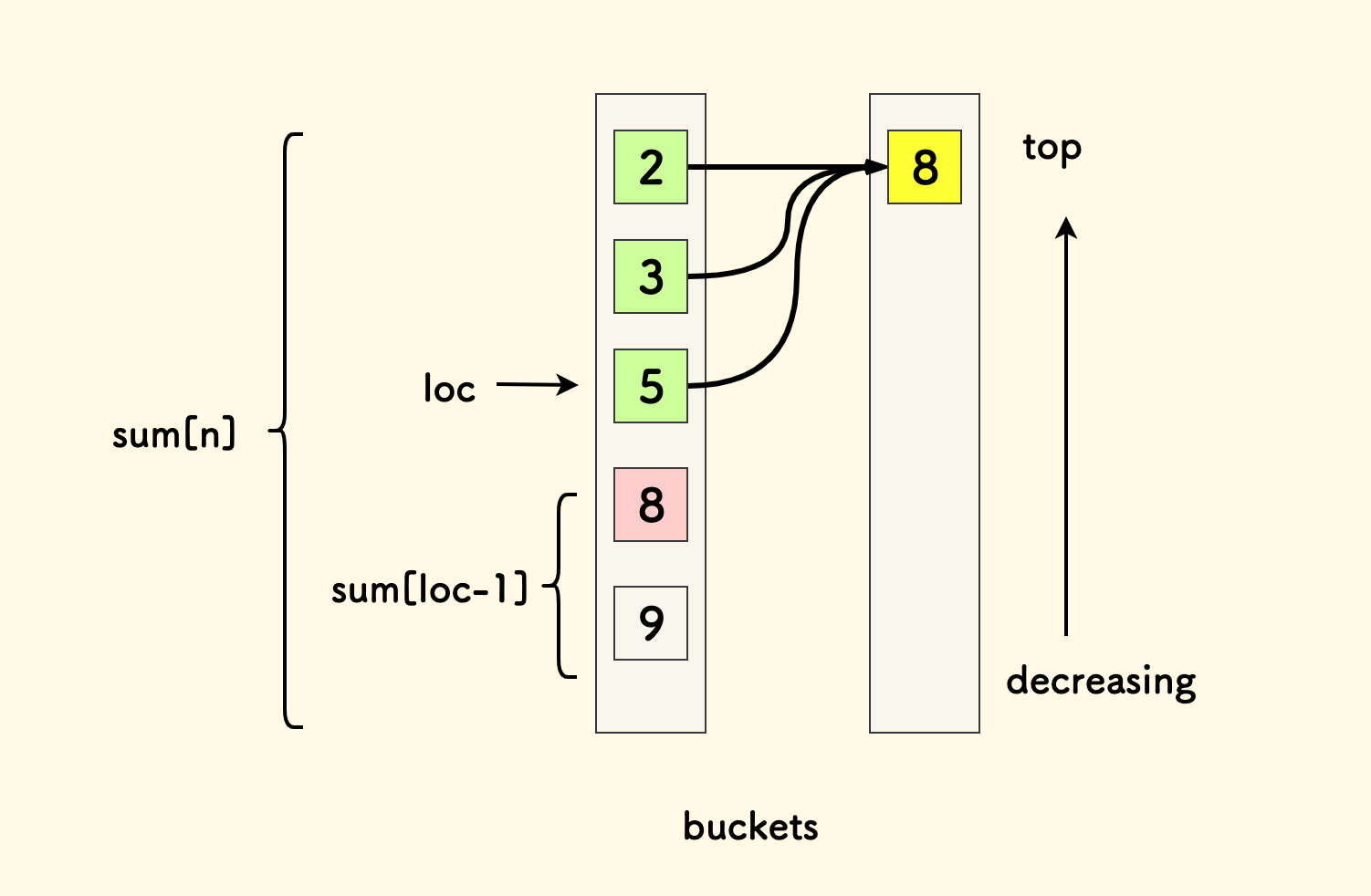
也就是说,我们只需在每个节点维护其在桶内的路径计数的前缀和。
新增一个数字 num 到第 k 个桶时,伪代码是这样的:
push(k, num)
// 上一个桶叫 a、下一个桶叫 b
a, b = buckets[k-1], buckets[k]
// 上一个桶 a 的分界点 loc
loc = upper_bound(a, num)
// 上一个桶的顶部计数总和
count = sum[a][-1] - sum[a][loc-1]
// 新节点的桶 b 在新节点处的前缀和
sum[b].push(sum[b][-1] + count)
最后一个桶中所有的元素的路径计数之和, 其实就是这个桶的顶部位置的前缀和,就是这个问题的最终答案。
这其实是一个在分层 DAG 模型上、结合二分查找、动态规划递推前缀和的过程。 如此看来,其时间复杂度仍然为 nlog(n) 。 前缀和在这里的作用,是 避免了重复求和过程。
其中有一个细节的巧妙点,每次寻找上一个桶的分界点 loc 的过程其实可以渐进式处理。 因为,桶中的元素一定是追加在桶的顶部的,那么下一次进入的元素对应的前一个桶中的 loc 位置, 一定比当前元素的 loc 位置更靠上。也就是说,这一次的 loc 位置可以作为下一次二分查找的起点。 可以维护每个桶当前的 loc 位置,下次二分查找的范围就会更小了。 非常巧妙。
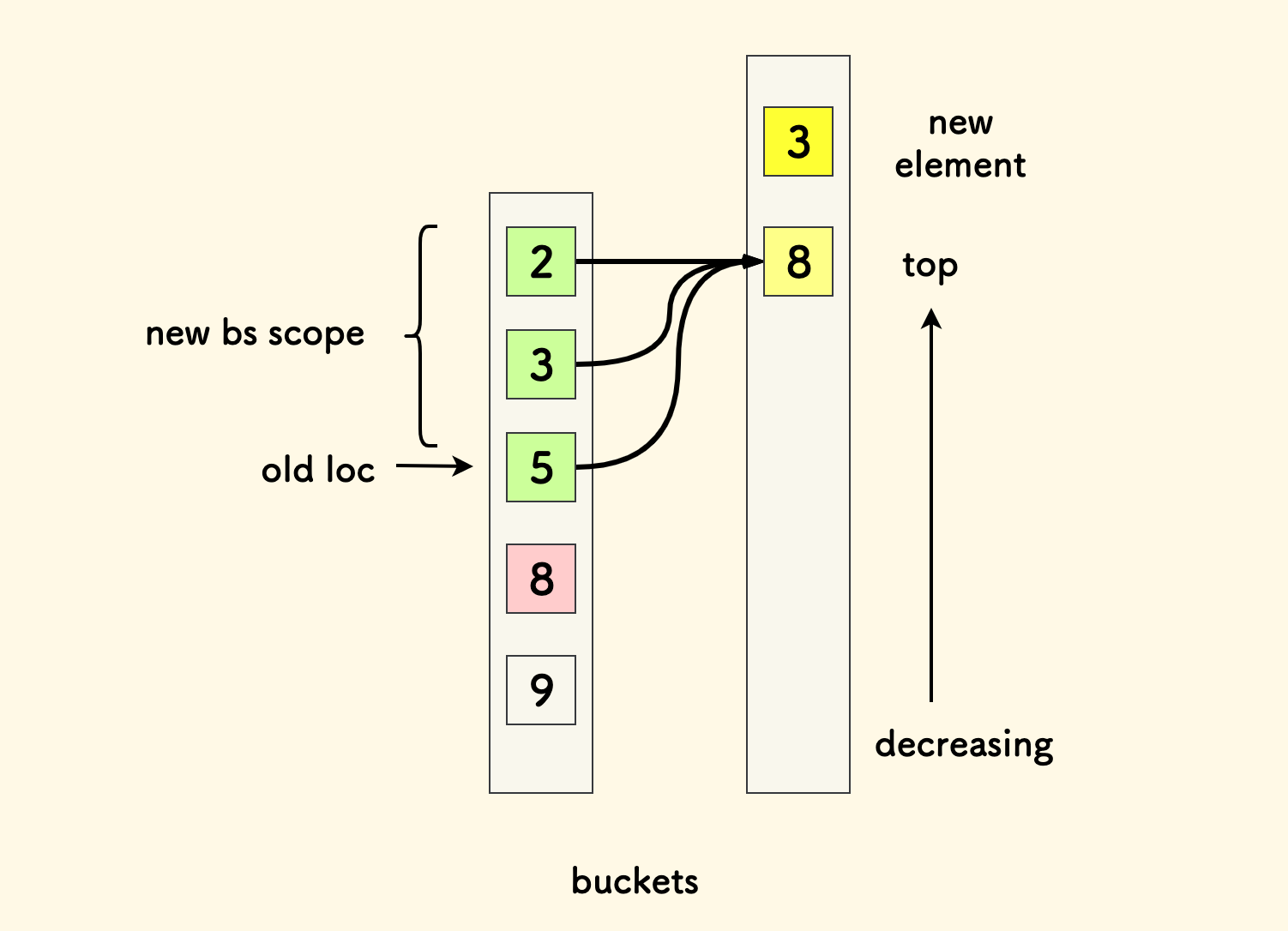
最终的实现代码见下方。相比动态规划的 O(n^2) 的做法,要复杂许多,但是它快,在 leetcode 上的运行时间可以击败 99% 的提交。
求最长递增子序列的个数 C++ 实现
class Solution {
public:
int findNumberOfLIS(vector<int>& nums) {
// 各个列的桶, 每个桶存放元素的值
vector<vector<int>> buckets;
// 每一个桶的二分检索起点, 递进式二分
vector<int> locs;
// 前缀和桶, sums[k][j] 表示第 k 个桶上的 [0..j] 区间上的路径计数的总和
vector<vector<int>> sums;
// 辅助数组, 快照任一时刻各个桶的尾部元素, 辅助主迭代
vector<int> p;
// 放入头节点到第一个桶
buckets.push_back({nums[0]});
locs.push_back(0);
sums.push_back({1});
p.push_back(nums[0]);
// 辅助函数, 给第 k 个桶放入一个新元素
// 并同步计算路径总数, 时间复杂度 log(n)
auto push = [&](int k, int num) {
// 找到上一个桶中严格小于 num 的项,然后把计数累加起来
// 如果是第 0 个桶,count 初始化为 1
int count = 1;
if (k >= 1) {
// 需要注意的是 buckets 数组的尾部才是桶顶
// buckets[k] 都是递减排列的;
// 本次 loc 可以作为下次的二分起点
// 所谓,维护 loc 数组以递进式二分
int k1 = k - 1;
auto& b1 = buckets[k1];
int loc = upper_bound(b1.begin() + locs[k1], b1.end(), num,
greater<int>()) -
b1.begin();
locs[k1] = loc; // 更新上一个桶的检索节点
// 前一个桶的区间 [0..loc] 的 count 总和
// 即区间 [loc, n) 的 (总和 - 前缀和)
auto total = sums[k1][buckets[k1].size() - 1];
// 区间 [0.. loc-1] 的计数和::
// 如果 loc 是 0 , 则相当于区间 [loc, n) 上是求总和
auto sum_before_loc = loc > 0 ? sums[k1][loc - 1] : 0;
count = total - sum_before_loc;
}
buckets[k].push_back(num);
p[k] = num; // 更新辅助数组
// 更新前缀和
auto sum = count;
if (!sums[k].empty()) sum += sums[k][sums[k].size() - 1];
sums[k].push_back(sum);
};
for (int i = 1; i < nums.size(); i++) {
if (nums[i] > p[p.size() - 1]) {
// 扩展桶列表, 扩展辅助数组
buckets.push_back({});
sums.push_back({});
locs.push_back(0); // 初始化其检索起点 0
p.push_back(0);
// 推入此元素到这个新桶
push(buckets.size() - 1, nums[i]);
} else {
// 查找合适的桶放入新元素
int k = lower_bound(p.begin(), p.end(), nums[i]) - p.begin();
push(k, nums[i]);
}
}
// 最长上升序列的个数,就是最后一个桶中所有元素的路径数的总和
const auto& last = sums[sums.size() - 1];
return last[last.size() - 1];
}
};
此外,求 LIS 个数的问题还有其他 nlogn 的方法:
俄罗斯套娃信封问题 ¶
leetcode 354 俄罗斯套娃信封问题 是 LIS 问题在二维上的一个延伸问题:
给你一个二维整数数组 envelopes ,其中 envelopes[i] = [wi, hi] ,表示第 i 个信封的宽度和高度。 当另一个信封的宽度和高度都比这个信封大的时候,这个信封就可以放进另一个信封里,如同俄罗斯套娃一样。 请计算 最多能有多少个 信封能组成一组“俄罗斯套娃”信封(即可以把一个信封放到另一个信封里面)。
一个信封可以装进另一个信封的条件是,宽和高都要严格更大。
如果只有一个维度,其实就是求最长递增子序列长度的问题。
现在有两个维度,要想办法转化到一个维度。
将信封按宽度升序排序就好了。 排序后,宽度是升序的,越靠后的信封宽度越大。那只需要找高度的最长上升子序列就可以了。
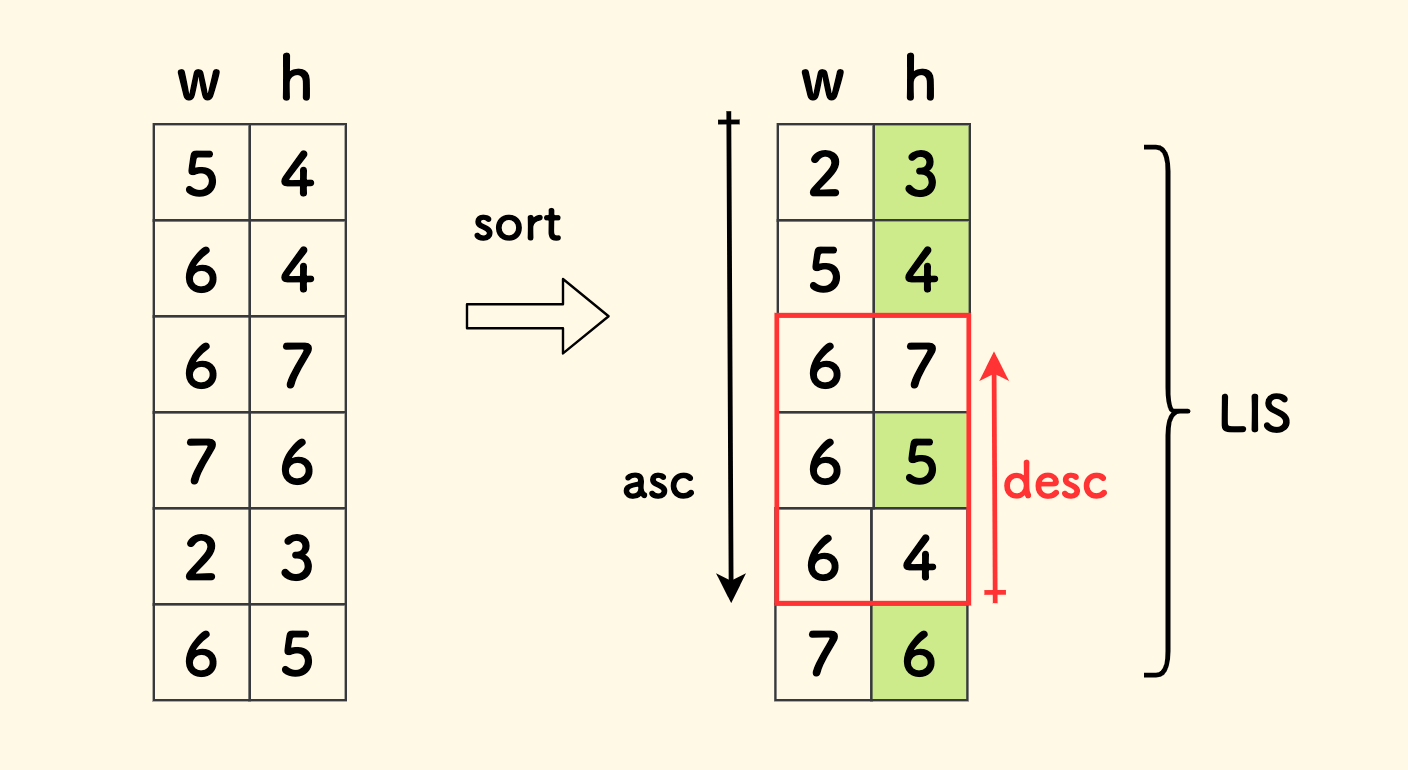
排序中有个细节,却是点睛之笔,如果两个信封宽度相等,要按高度逆序排序 。 无论宽高,当严格大于时,才可以认为装的下。在宽相等的多个信封中,LIS 求解时只能取一个。 此时的局部逆序,则保证了 LIS 序列中最多从中取一个(不一定是其中高度最大的,比如上图的例子)。
总体来说,时间复杂度是 O(nlogn)。
leetcode 上还有一个类似的、三个维度的 LIS 问题: leetcode 堆箱子 。
俄罗斯套娃信封问题 C++ 实现
class Solution {
public:
int maxEnvelopes(vector<vector<int>>& es) {
int n = es.size();
// 先优先按 w 排序
sort(es.begin(), es.end(), [](const auto& a, const auto& b) {
// 如果 w 相同,h 则逆序
// 这里非常巧妙,逆序过来之后,相同的 w 情况下保证 LIS 求解最多取 1 个
return a[0] < b[0] || (a[0] == b[0] && a[1] > b[1]);
});
vector<int> p; // h 升序排列的辅助数组
p.push_back(es[0][1]);
for (int i = 1; i < n; i++) {
auto num = es[i][1];
if (num > p.back())
p.push_back(num);
else {
auto t = lower_bound(p.begin(), p.end(), num);
*t = num;
}
}
return p.size();
}
};
求解非严格递增的最长子序列长度 ¶
如果我们放宽 LIS 问题限制条件, 如何求解一个数组的非严格递增的最长子序列的长度呢?
比如说数组 [2,4,2,7,3,6,3,8,3,5,6] 的最长非严格递增子序列的长度应该是 7。
上面的俄罗斯套娃信封问题,其实给了我们一种思路。
可以把数据看成两个维度:数值 和 它的下标索引。下标是严格递增的,数值的上升意味着和下标同序。 也就是说,如果按值排序,值的上升序列问题可以转换为下标的上升序列问题。
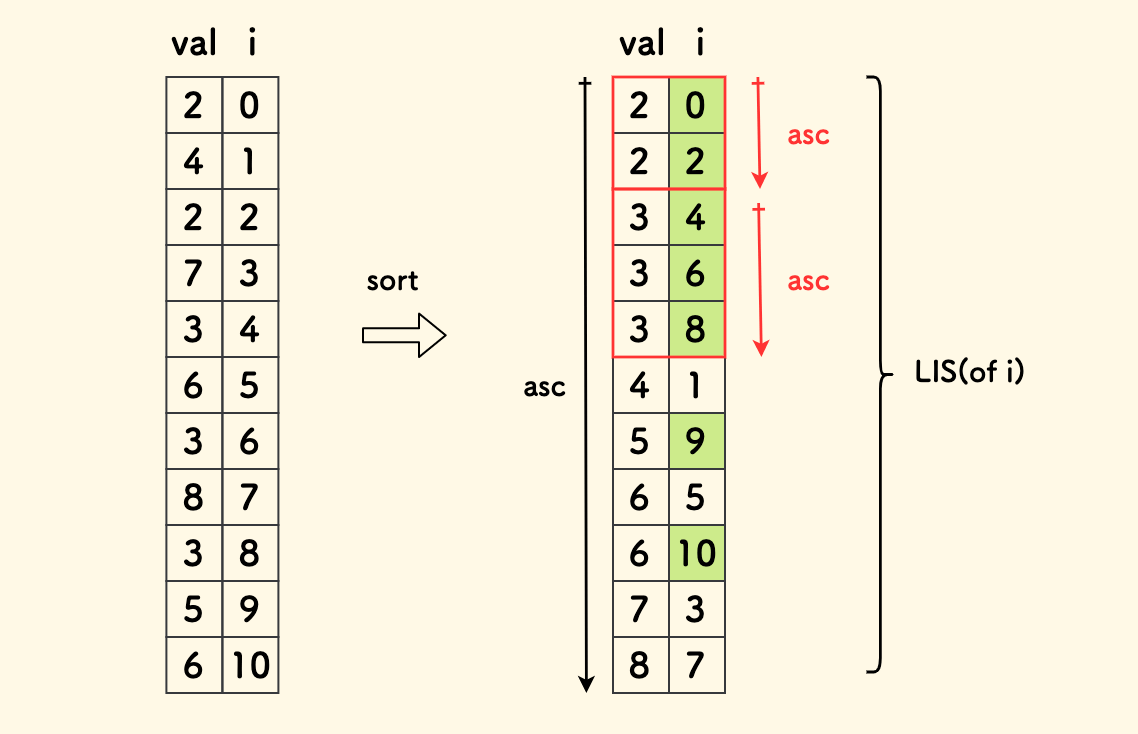
排序的时候,因为现在要求的是「非严格递增」,如果两个数值相等,那么进一步按它们的下标排列。 这样才可以把相等的数字都吸收到最长非严格递增子序列中。
求解最长非严格递增子序列的长度 - C++
class Solution {
public:
// 传统 LIS 问题
int originalLIS(vector<int>& nums) {
vector<int> p{nums[0]};
for (int i = 1; i < nums.size(); i++) {
if (auto num = nums[i]; num > p.back())
p.push_back(num);
else {
auto j = lower_bound(p.begin(), p.end(), num);
*j = num;
}
}
return p.size();
}
// 非严格递增 LIS 问题
int looseLIS(vector<int>& nums) {
// 制作一个下标数组
vector<int> arr;
for (int i = 0; i < nums.size(); i++) arr.push_back(i);
// 按数值排序. 如果数值相等,因为允许非严格递增, 则按下标正序
sort(arr.begin(), arr.end(), [&](const auto& a, const auto& b) {
return nums[a] < nums[b] || (nums[a] == nums[b] && a < b);
});
// 然后求下标数组的最长严格递增序列
return originalLIS(arr);
}
};
求解最长公共子序列 LCS 问题 ¶
最长公共子序列问题是一个经典的算法问题,简称 LCS 问题:
给定两个字符串 text1 和 text2, 求解两个字符串的最长的公共子序列。
子序列内的字符并不要求在原字符串内连续,但是其相对顺序要和在原字符串中保持一致。
例如: "acadfe" 和 "abccadefe" 的最长公共子序列是 "acadfe",长度为 6。
求解 LCS 问题的最经典的方法是 动态规划方法,其时间复杂度是 O(m*n), 其中 m 和 n 分别是两个字符串的长度。
这里将介绍一种 LCS 问题转换到 LIS 问题的思路:
- 找出字符串1 在另一个字符串2 中的字符出现的所有位置。
- 将上面的位置构成的序列逆序,替换掉字符串1 中对应的字符。
- 将这个新构成的位置数组拉平,对其求解 LIS 长度即可。
第二步中,逆序的原因是保证 LIS 求解时一个字符只会被取一次,和俄罗斯套娃信封问题的处理一样。
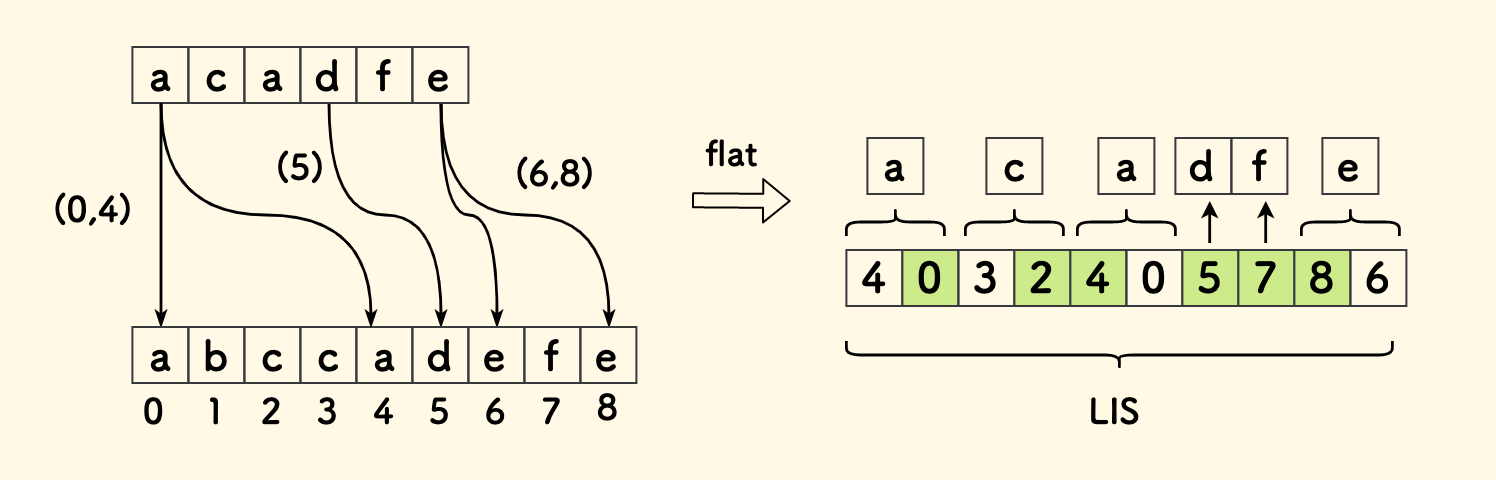
如何理解这个算法呢? 其实它完全等价于前面所说的「俄罗斯套娃信封问题」。 把字符串1 的下标理解为信封的宽度,新构造的数组理解为高度。 最长公共子序列的含义是,其所有字符也在字符串2 中存在,而且相对位置不能变。 比如说下图中的 c 和 a ,相对位置不能变的含义就是,在字符串1 中位置关系是 2>1, 在字符串2中也存在,而且位置关系是 4>2 才行。这样就抽象为套娃信封问题了。
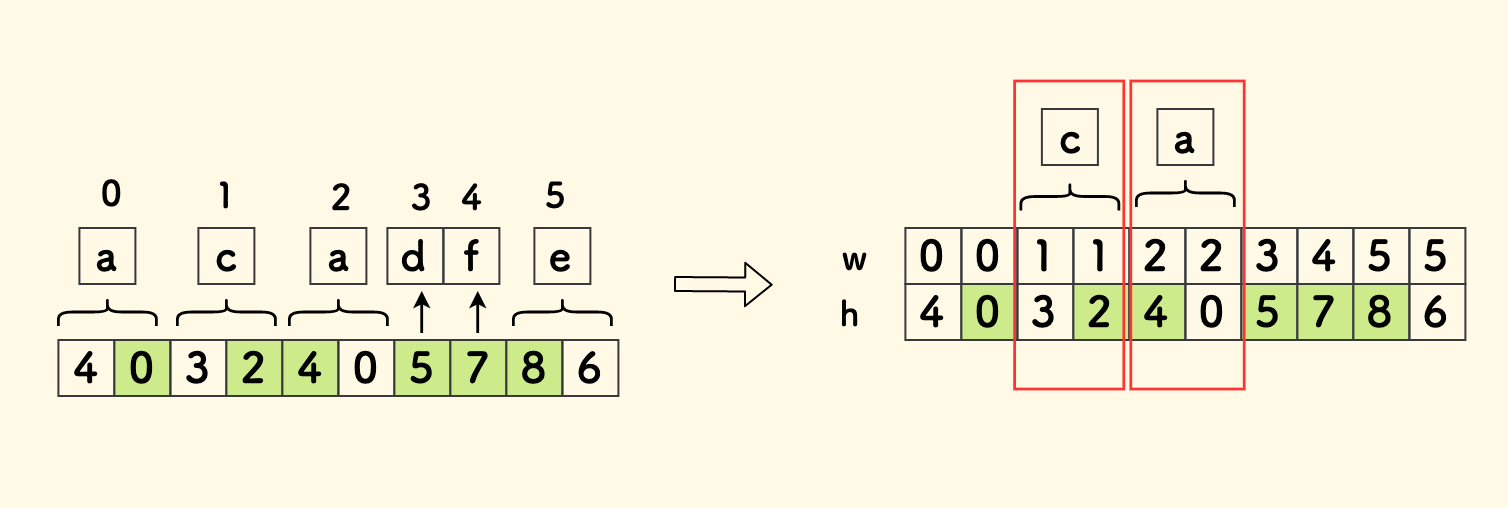
思路非常巧妙,但是注意其时间复杂度存在退化情况,并不总是比动态规划的思路更优。 事实上,如无其他限定,LCS 求解的最优时间复杂度就是 O(m*n) 了。
当新构造的数组很大时,时间会慢于 O(m*n),比如下面的情况,构造的数组会是 m*n 的大小, 最终求解的时间复杂度会是 (m*n)log(m*n) 的。
text1 = "aaaaa..."
text2 = "aaaaa..."
如果我们提前限定两个字符串各自其中的字符都是互不相同的, 假设 n 的值更小的话, 就可以保证构造的数组是大小为 n 的,那么更优的解时间复杂度才可以确保说是 nlog(n) 的。
在 leetcode 上,我试了这个方法是可以通过提交的,但是会比较慢。
求解最长公共子序列长度 - leetcode - 基于 LIS 问题 - C++
class Solution {
public:
int LIS(vector<int>& nums) {
if (nums.size() == 0) return 0;
vector<int> p;
p.push_back(nums[0]);
for (int i = 1; i < nums.size(); i++) {
if (nums[i] > p.back())
p.push_back(nums[i]);
else {
auto t = lower_bound(p.begin(), p.end(), nums[i]);
*t = nums[i];
}
}
return p.size();
}
int longestCommonSubsequence(string text1, string text2) {
int m = text1.size();
int n = text2.size();
if (m > n) return longestCommonSubsequence(text2, text1);
// text2 中每个字符在 text2 中出现的所有位置
unordered_map<char, vector<int>> d;
for (int i = 0; i < n; i++) d[text2[i]].push_back(i);
// 制作一个数组
// 把 text1 中每个字符替换其成在 text2 出现位置的逆序列, 拉平
vector<int> nums;
for (auto ch : text1)
if (d.find(ch) != d.end())
for (int j = d[ch].size() - 1; j >= 0; j--)
nums.push_back(d[ch][j]);
return LIS(nums);
}
};
洛谷上也有这道题 P1439 ,保证了两个数组的元素互不相同。 可以直接应用 LIS 模型,时间复杂度 nlog(n)。
P1439 最长公共子序列 C++
// LIS 问题求解
int LIS(vector<int>& nums) {
vector<int> p{nums[0]};
for (int i = 1; i < nums.size(); i++) {
if (auto num = nums[i]; num > p.back())
p.push_back(num);
else {
auto j = lower_bound(p.begin(), p.end(), num);
*j = num;
}
}
return p.size();
}
int main(void) {
// 处理输入
int n;
cin >> n;
getchar(); // '\n'
int c; // 当前输入
// a[i] 记录数字 i-1 的所在的位置
vector<int> a(n, 0);
for (int i = 0; i < n; i++) {
cin >> c;
a[c - 1] = i;
}
getchar(); // '\n'
// b[i] 记录输入的数字 k, 对应的 k-1 在 a[i] 中的出现的位置
vector<int> b(n, 0);
for (int i = 0; i < n; i++) {
cin >> c;
b[i] = a[c - 1];
}
getchar(); // '\n'
// 公共子序列的长度就是 b 的最长上升序列
cout << LIS(b) << endl;
return 0;
}
有限递增的子序列长度 ¶
在经典的 LIS 问题基础之上,限制序列的相邻元素之差不超过一个给定的数字 k 。
问题来自 leetcode 2407. 最长递增子序列 II:
给你一个整数数组 nums 和一个整数 k 。找到 nums 中满足以下要求的最长子序列:
子序列 严格递增
子序列中相邻元素的差值 不超过 k 。
请你返回满足上述要求的 最长子序列 的长度。 子序列 是从一个数组中删除部分元素后,剩余元素不改变顺序得到的数组。
这个问题挺难的,大部分做法都是做值域上的线段树,将上升序列长度作为线段树节点维护的信息,用 num-k 区间上的长度最值来递推。
但是我总觉得利用值域有限的范围来解决,有点取巧。 遗憾的是,我目前还没有找到 nlog(n) 时间复杂度的基于这个 DAG 模型的解法。
2023/12/25 更新:
- 这个问题的两种 DP 转移优化解法: LIS 问题的 DP 转移优化
欢迎交流。
(完)
脚注:
数组 p 一定是严格递增的详细证明
假设元素
p[i+1]是上升序列s的末尾元素。根据数组
p的定义,在i的情况下,末尾元素s[i] >= p[i]。又因为
s是严格上升序列,所以s[i+1] > s[i]。p[i+1]是s在i+1的情况下的末尾元素,即p[i+1]=s[i+1]。最终,推导出
p[i+1] > p[i],也即p数组是严格递增的。数组 p 遇到更小的元素需要更新的说明
假设当前扫描的元素值是
num, 如果存在某个元素p[j],有p[j] >= num且p数组中j之前的元素都严格小于num, 也就是说j是辅助数组中值 恰好不小于num的那个位置。那么以
p[j]为末尾元素的、长度为j+1的上升序列就遇到了一个更小的末尾元素num, 为了维护p的定义,则需要更新p[j]为num。p 数组并不一定是最长递增序列的一个例子
比如说下面的数组
[2, 6, 8, 10, 3, 9, 10]就是这种情况:
可以看到,最终的
p = [2, 3, 8, 9, 10]并不是有效的上升序列, 背后的[2, 6, 8, 9, 10]才是。因为不止p中的序列在累积,历史存在过的[2,6,8]序列也在累积,而且最终它胜出了。- 朴素的 LIS 动态规划分析
相关阅读:
本文原始链接地址: https://writings.sh/post/longest-increasing-subsequence-revisited