最长连续序列问题（两种方法）

本文记录最长连续序列问题的两种解法。

笔记目的，行文从简。

问题描述 ¶

这是一个经典的算法问题：

给定一个未排序的整数数组 nums ，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。
-- 来自 leetcode 128. 最长连续序列

比如说数组 [100,4,200,1,3,2] 的最长连续序列是 [1,2,3,4]，长度是 4。

注意，要求的序列不要求在原数组中位置连续、也不要求顺序和原数组中一致。

哈希表方法 ¶

要在值域上考虑，分别定义两个函数：

L(x) 表示以值 x 为右端点的能形成的最长的连续序列的长度。
R(x) 表示以值 x 为左端点的能形成的最长的连续序列的长度。

简而言之就是，值域上 x 左右两边已经形成的最长连续序列的长度。

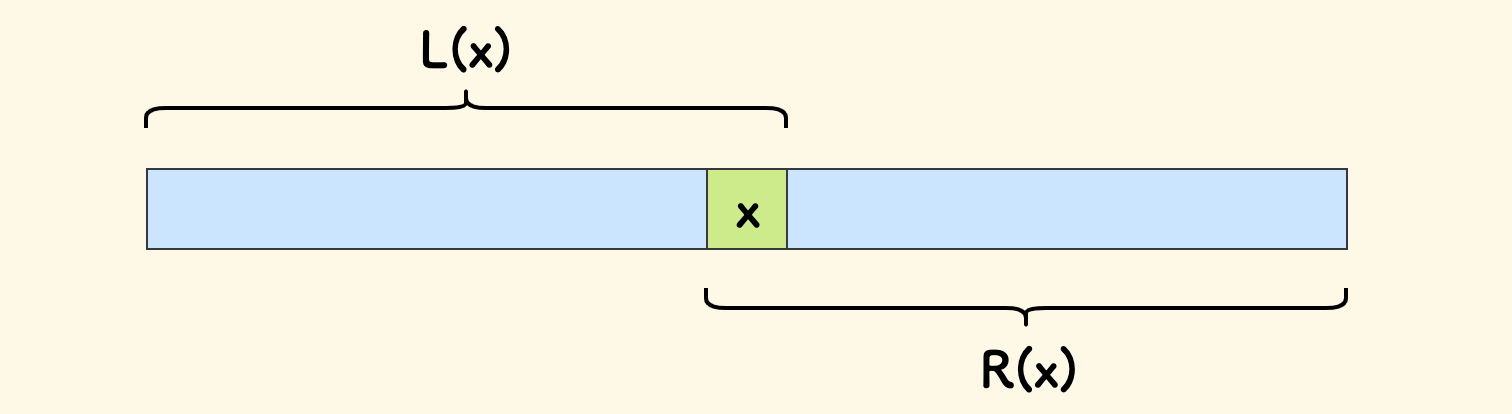
这两个都实现为哈希表。

首先，对于寻找连续序列这个事情，数组中值相同的多个元素，只需考察一次即可。

可以通过 L(x) 和 R(x) 是否有值来避免相同值的多个元素的重复考察。

对于每一个数组中的值 x 来说，它可以连接起来的连续序列如下图所示，即：

找出以 x-1 为右端点的最长连续序列
找出以 x+1 为左端点的最长连续序列
再把中间的 x 带上，三段连起来的连续序列

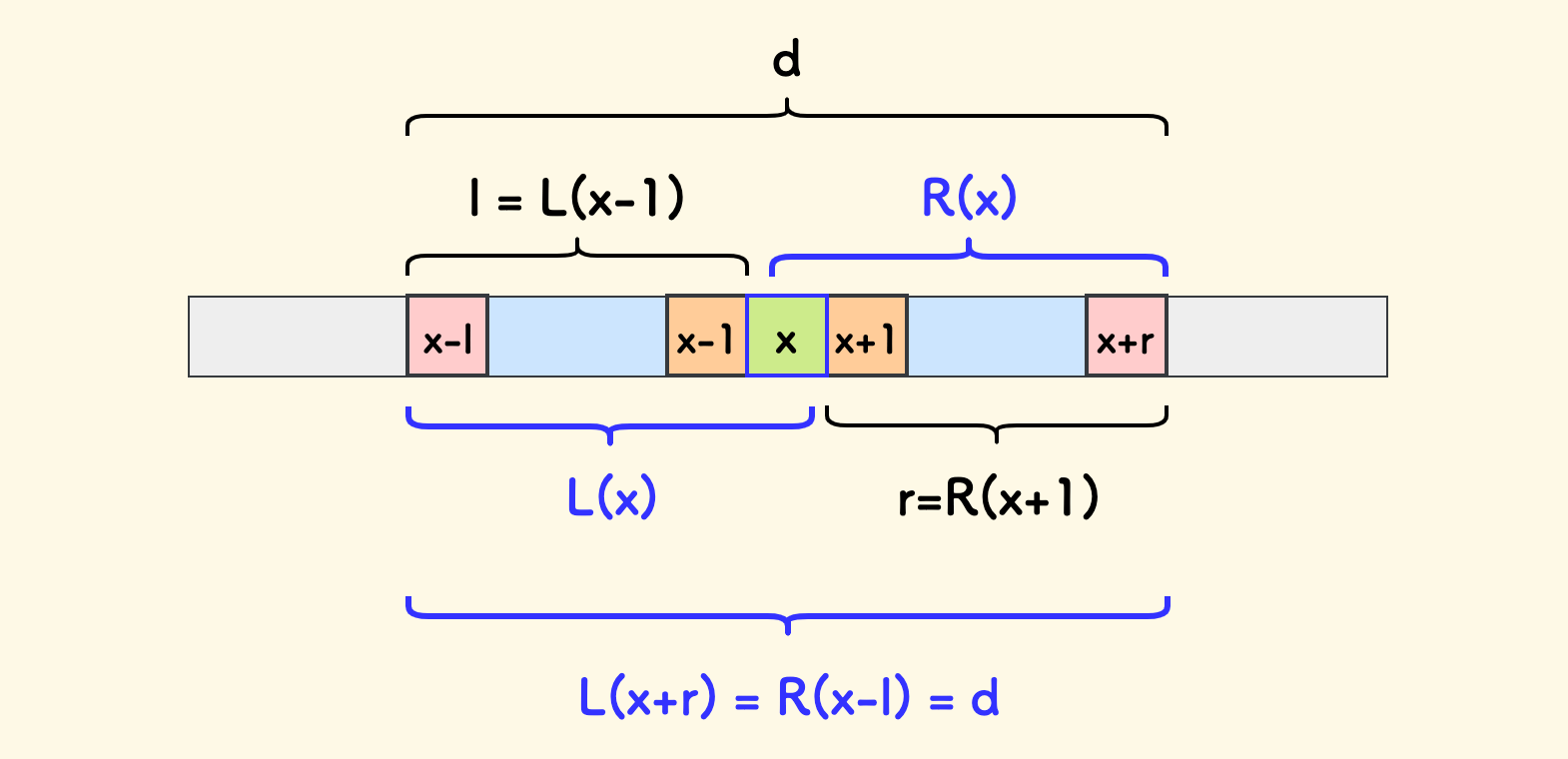
如图所示，形成的新的连续序列的长度 d 是:

l = L(x-1)
r = R(x+1)
d = l + r + 1

追踪所有的 d 之最大者就是答案。

还要维护下以 x 为端点的最长连续序列的长度：

L(x) = l + 1
R(x) = r + 1

不过原来的连续序列中的其他点的函数值也得到了扩展。

但是，我们只需要更新两个端点 x-l 和 x+r （图中红色的方格）。

因为对于后续迭代的一个新的元素值 y 来说：

如果落在当前这个序列里面，那么无需关心，因为对答案无影响。
如果落在当前这个序列外面，无论是更小还是更大的情况，y 有可能恰好是 x-l 或者 x+r 的邻居的话，就会依赖这两个端点的函数值。

总而言之，只有端点的函数值需要更新。

最终代码实现如下，时间复杂度是 $O(n)$：

最长连续序列问题 - 哈希表方法 - C++ 代码

class Solution {
   public:
    int longestConsecutive(vector<int>& nums) {
        unordered_map<int, int> L, R;

        int ans = 0;

        for (auto x : nums) {
            if (L[x] || R[x]) continue;

            // 更新 x 为端点的序列长度
            int l = L[x - 1], r = R[x + 1];
            L[x] = l + 1, R[x] = r + 1;

            int d = l + r + 1;

            // 路过 x 的最长连续序列的长度
            ans = max(ans, d);

            // 两端需要维护, 会影响后续迭代的计算; 中间的不必维护
            L[x + r] = R[x - l] = d;
        }

        return ans;
    }
};

x 的函数值其实也无必要设置

事实上，x 处的函数值都无需设置，本文中代码设置了 L(x) 和 R(x) 的目的仅仅是为了避免重复考察同一个值。

同时，重复计算一个值会出问题，因为依赖的信息可能已经过时，导致 L[x+r] 和 R[x-l] 取得更小的值，最终出错。

你完全可以用一个访问数组 visited[x] 来取代这一做法、同时去掉 L(x) 和 R(x) 的维护也是没问题的。

unordered_map<int, int> visited;

for (auto x : nums) {
    if (visited[x]) continue;

    // 更新 x 为端点的序列长度
    int l = L[x - 1], r = R[x + 1];
    visited[x] = 1;
    // 移除：L[x] = l + 1, R[x] = r + 1;
    // 其他不变
}

更或者，直接允许重复计算。此时，不需要任何访问数组，计算端点函数值时注意取更大者即可，都是可行的方案，只是这样做会更慢一丢。

for (auto x : nums) {
    // 更新 x 为端点的序列长度
    int l = L[x - 1], r = R[x + 1];

    int d = l + r + 1;
    ans = max(ans, d);

    // 两端需要维护, 会影响后续迭代的计算; 中间的不必维护
    if (L[x+r] < d) L[x+r] = d;
    if (R[x-l] < d) R[x-l] = d;
}

哈希表的方法非常巧妙优美，下面并查集的方法则平淡直接一些。

并查集方法 ¶

前置知识：并查集数据结构。

思路很简单：把连续的元素放到同一个集合，最终最大集合的大小就是答案。

因为连续序列是有「传递性」的，就是说，一旦发现一个值 x 可以把两个连续序列 A 和 B 连接起来，那么，A 和 B 中的所有元素都可以算作属于同一个连续序列，也就是可以把它们俩合并起来。

具体来说，扫描数组的每个值 x，分别和 x-1 所在的集合、x+1 所在的集合进行合并即可。

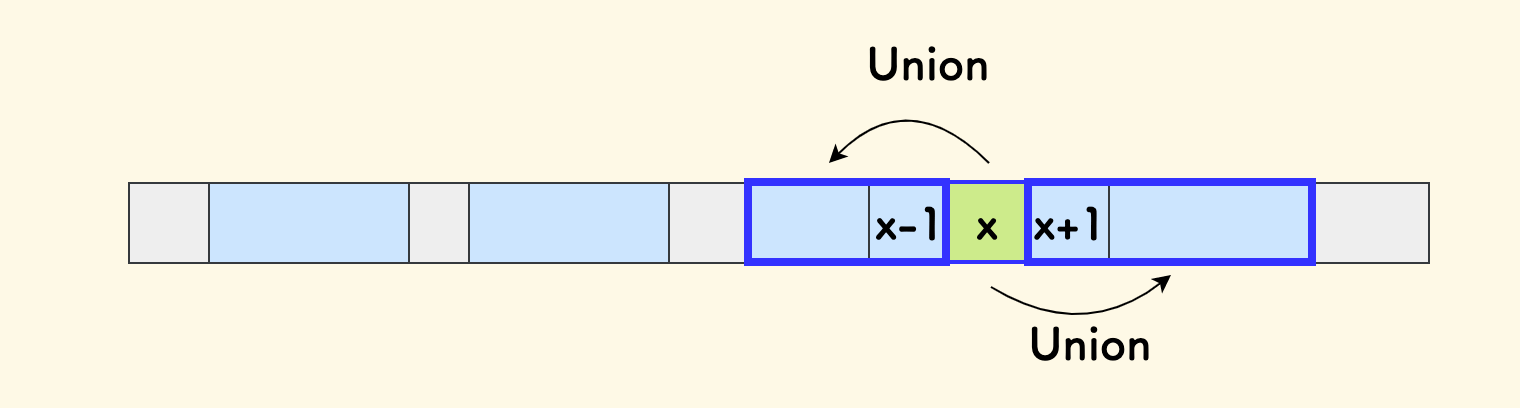
最开始，每一个元素可以算作一个集合。

一个技术细节是，可以用一个哈希表来记录元素值到并查集的节点标号的映射。

最长连续序列问题 - 并查集方法 - C++ 代码

const int N = 1e5 + 1;

struct UF {
    int fa[N], sz[N];  // 父节点数组, 集合大小
    int tot = 0;       // 节点标号指针
    int max_size = 1;

    int find(int x) {
        if (x == fa[x]) return x;
        return fa[x] = find(fa[x]);
    }

    void merge(int a, int b) {
        a = find(a);
        b = find(b);
        if (a == b) return;
        if (sz[a] > sz[b]) {
            fa[b] = a;
            sz[a] += sz[b];
            max_size = max(sz[a], max_size);
        } else {
            fa[a] = b;
            sz[b] += sz[a];
            max_size = max(sz[b], max_size);
        }
    }

    // 添加一个新的节点
    int add() {
        ++tot;
        fa[tot] = tot;
        sz[tot] = 1;
        return tot;
    }
};

class Solution {
   public:
    int longestConsecutive(vector<int>& nums) {
        if (nums.empty()) return 0;

        unordered_map<int, int> m; // 值 到 节点标号的映射
        UF u; // 并查集

        for (auto x : nums) {
            if (m[x]) continue;

            // m[x] 记录值为 x 的节点号
            m[x] = u.add();

            // 合并相邻的节点的集合
            if (m[x - 1]) u.merge(m[x], m[x - 1]);
            if (m[x + 1]) u.merge(m[x], m[x + 1]);
        }
        // 答案就是最大集合的大小
        return u.max_size;
    }
};

（完）

本文原始链接地址： https://writings.sh/post/longest-consecutive-sequence