并查集简记

本文简单总结并查集。

适用场景 ¶

并查集是非常简单的数据结构，代码简短而优美。

适合具有传递性关系的问题，尤其是连通性问题。

结构定义 ¶

并查集是一颗森林，由多颗树组成，每一颗树代表一个集合。

每个集合由树的根节点作为代表元，两个节点在同一个集合中（也就是连通）的话，它们的代表元（也就是根节点）是相同的。

结构的 C++ 定义如下，一般开静态数组来存储即可：

class UnionFind {
    // 父节点数组 pa[i] 表示节点 i 的父节点下标
    std::vector<int> pa;
    // 大小数组 sizes[i] 表示以 i 作为根的集合内的元素个数
    std::vector<int> sizes;
    // 连通分量数量，即互不相连的孤岛数量
    int c;
};

其中：

每个节点用一个数字来表示，也就是下标。
数组 pa 中存放节点的父节点的下标，特殊地，根节点的父节点定义为自身。
数组 sizes 存放树的大小，对于树的根节点才有意义。
连通分量 c 其实就是森林中树的个数（互不相交的集合的个数）。

比如下图中，共有 2 个连通分量，其根分别是 1 和 4，各个节点都指向了其父节点，最终指向所在集合的根：

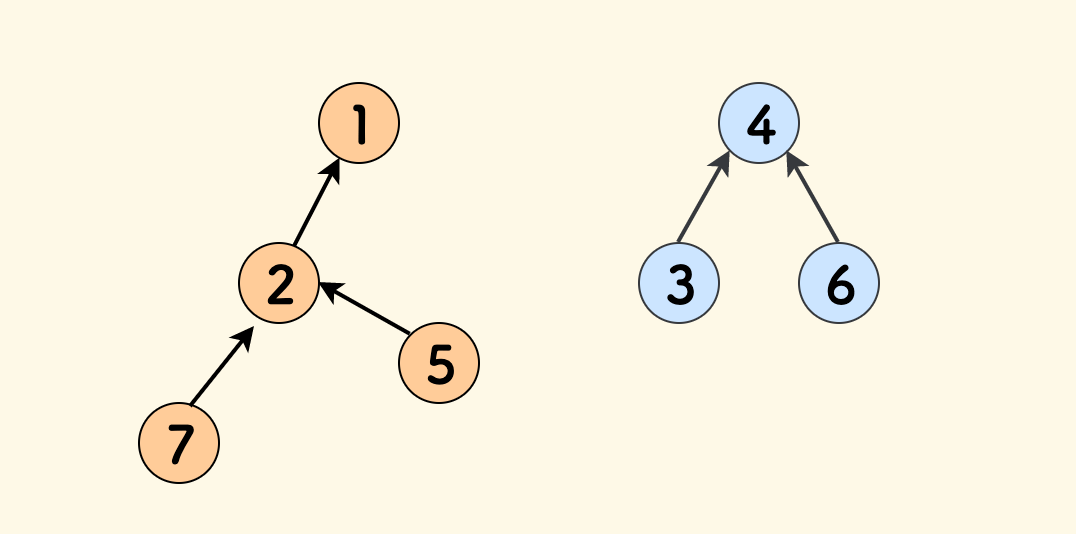
最开始，每个节点都初始化为一颗单独的树，大小均为 1，此时连通分量就是 n：

explicit UnionFind(int n)
    : pa(std::vector<int>(n)), sizes(std::vector<int>(n, 1)), c(n) {
    // 初始化: 自己作为父节点
    for (int i = 0; i < n; i++) pa[i] = i;
}

核心操作只有两个：查询和合并。

find 和路径压缩 ¶

Find 查询操作的函数定义是：

找到节点 x 所在集合的根。

只需递归向上寻找：

x 所在集合的根，就是其父节点所在集合的根。
除非，x 本身就是一个根。

用代码来表示就是：

int Find(int x) {
    if (pa[x] == x) return x; // 根的父节点是本身
    return Find(pa[x]);
}

目前都很好理解，那么，如果一旦找到了 x 的根，可以把 x 直接嫁接到根上，下次找就更快了。

这种把查询结果利用起来，直接拉近节点和根距离的办法，就是所谓的「路径压缩」。

用代码来表示就是：

// 查找一个节点的根节点
int Find(int x) {
    if (pa[x] == x) return x;
    pa[x] = Find(pa[x]); // 重设 x 的父节点到根
    return pa[x];
}

这样，原本向上递归的路径上的所有节点，都会直接嫁接到根下面去，如下图所示，节点 4 向上找根的过程：

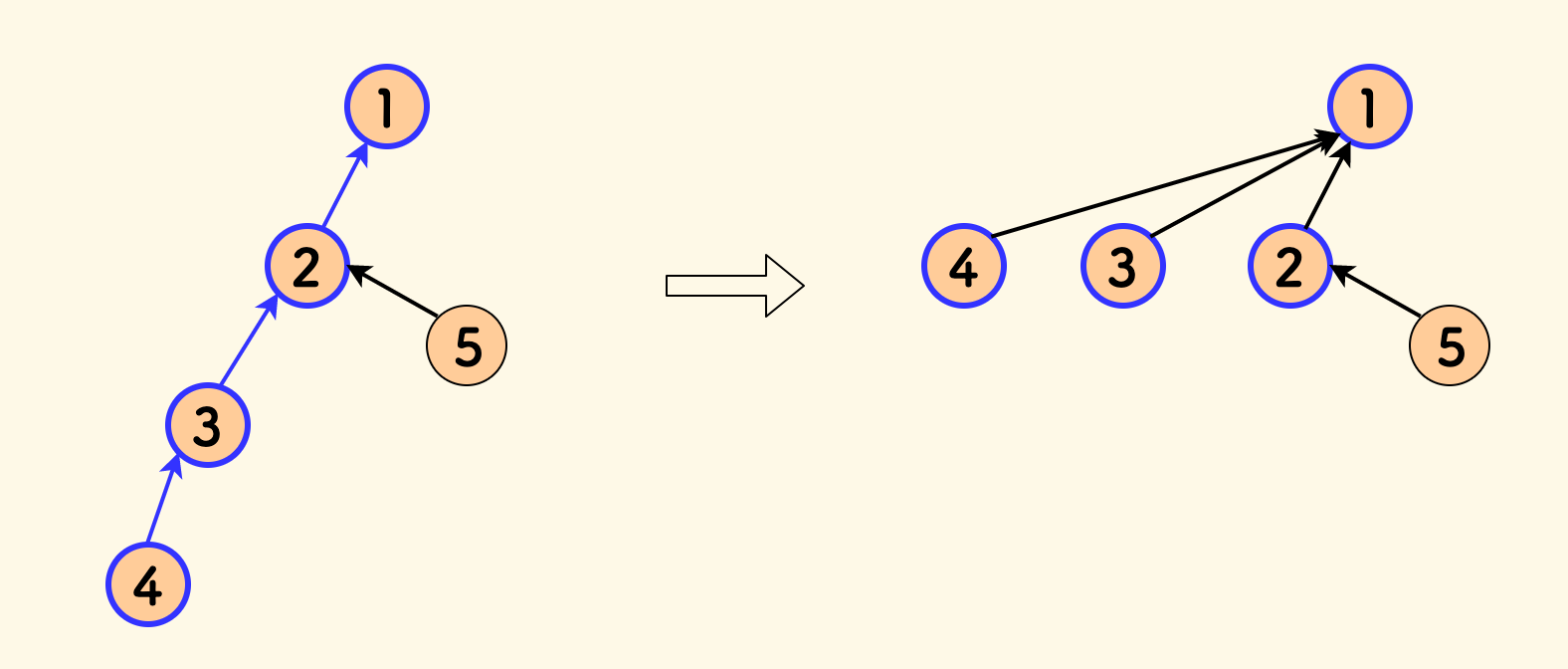
经过路径压缩后，树会变地更扁平，下一次 Find 也会更迅速。

union 和按大小合并 ¶

Union 合并操作的函数定义是：

合并两个节点 a 和 b 所在的集合。

首先，要先分别找出两个节点的集合的根，这只需利用前面所说的 Find 函数。

然后把其中一个根的父节点指向另一个作为其新的父节点，代码会很简洁：

void Union(int a, int b) {
    pa[Find(b)] = Find(a);
}

不过，有的时候，合并后的树会变地不平衡。

其实，谁当新的根无所谓，只要合并后属于同一个集合就可以了。我们只关心连通性。

一种办法是，把更小的树合并到更大的树上去。

下图中，左边的的合并方式明显更好一些，合并后的树会更低。

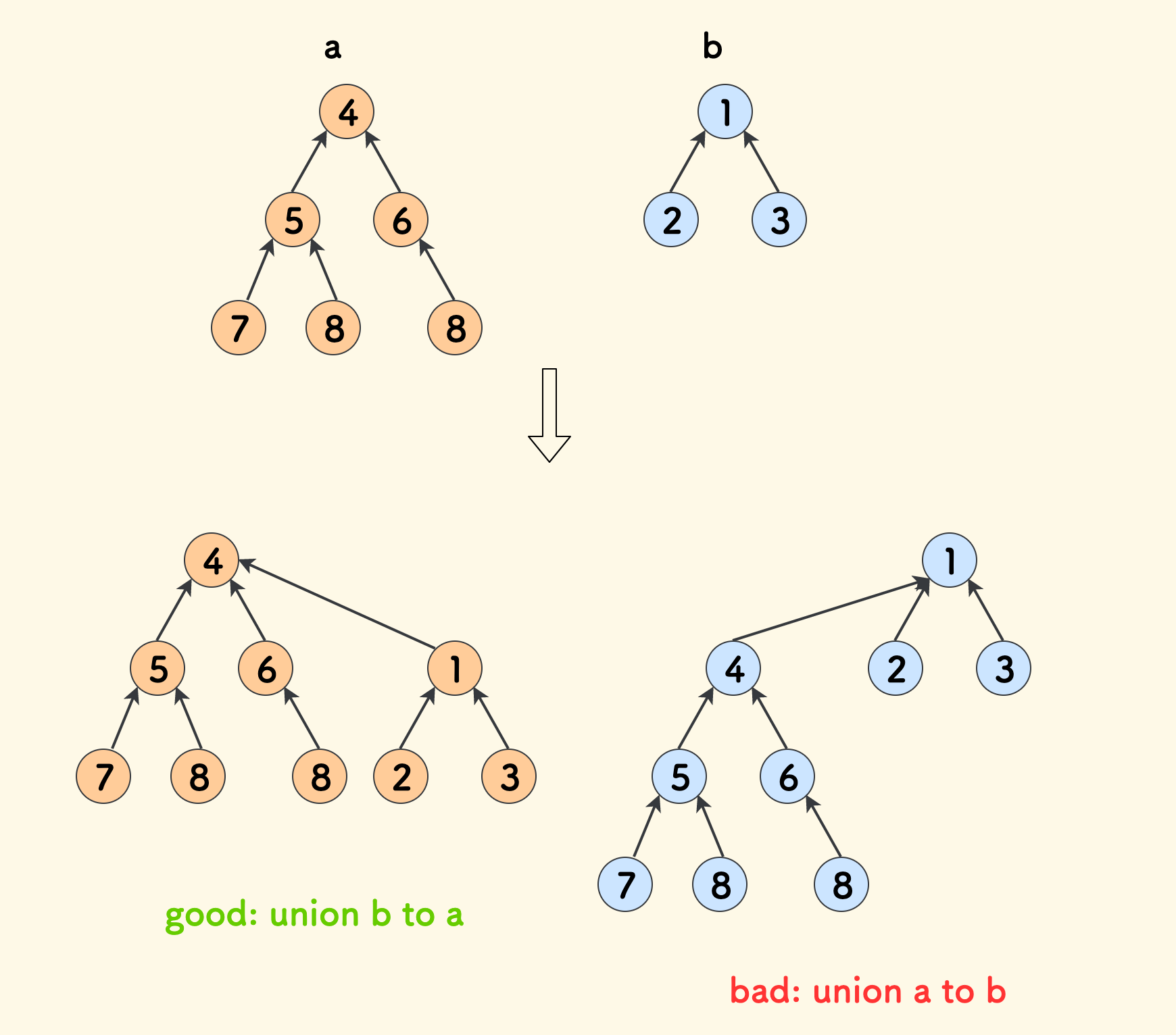
用代码来表示就是：

void Union(int a, int b) {
    a = Find(a), b = Find(b);
    if (a == b) return; // 已经在同一集合
    if (sizes[a] > sizes[b]) { // 把 b 并入 a
        pa[b] = a;
        sizes[a] += sizes[b];
    } else {
        pa[a] = b;
        sizes[b] += sizes[a];
    }
    c--; // 连通分量减一
}

注意，其中也顺便维护了：

树的大小，只需维护新的根的大小
连通分量，每次合并后整体上就会少一个集合

代码模板 ¶

所有的代码见 union-find-cpp - github

岛屿数量问题 ¶

模板题：

给你一个由 "1"（陆地）和 "0"（水）组成的的二维网格，请你计算网格中岛屿的数量。
岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。此外，你可以假设该网格的四条边均被水包围。
-- 来自 leetcode 200. 岛屿数量

示例：

输入：grid = [
  ["1","1","0","0","0"],
  ["1","1","0","0","0"],
  ["0","0","1","0","0"],
  ["0","0","0","1","1"]
]
输出：3

岛屿内的陆地相连，每个岛屿就是一个集合，这是一个求连通分量的问题。

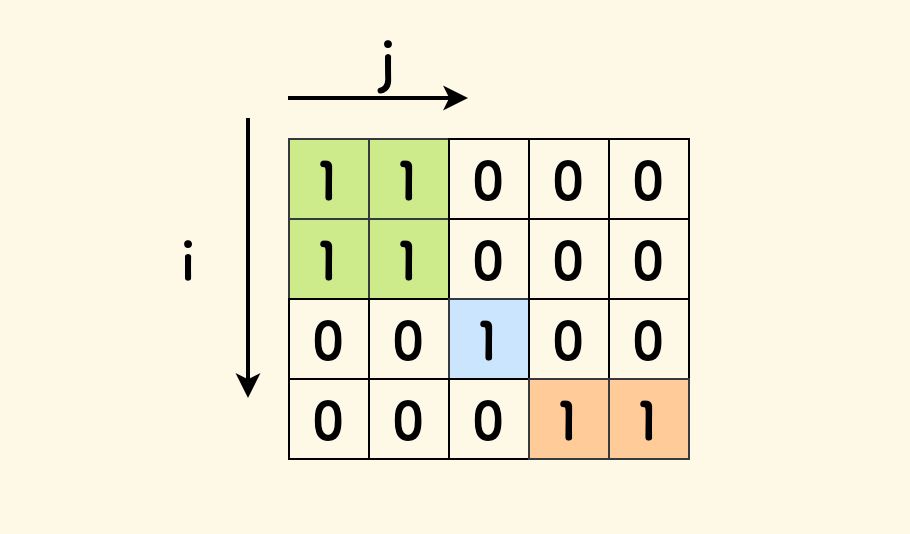
假设输入的方格的大小是 m x n 的，我们通过一个函数来把方格位置 (i,j) 映射到一个数字，以表示并查集中的一个节点标号：

auto f = [=](int i, int j) { return i * n + j; };

也就是 f(i,j) 的值就是代表方格 (i,j) 的节点标号，一共有 m*n 个。

剩下的事情，只需要顺序扫描整个方格，把 1 的格子「合并」到各自归属的集合中去。

由于是自左向右、自上而下扫描，所以只需要合并左边和上边相邻的格子的集合即可。

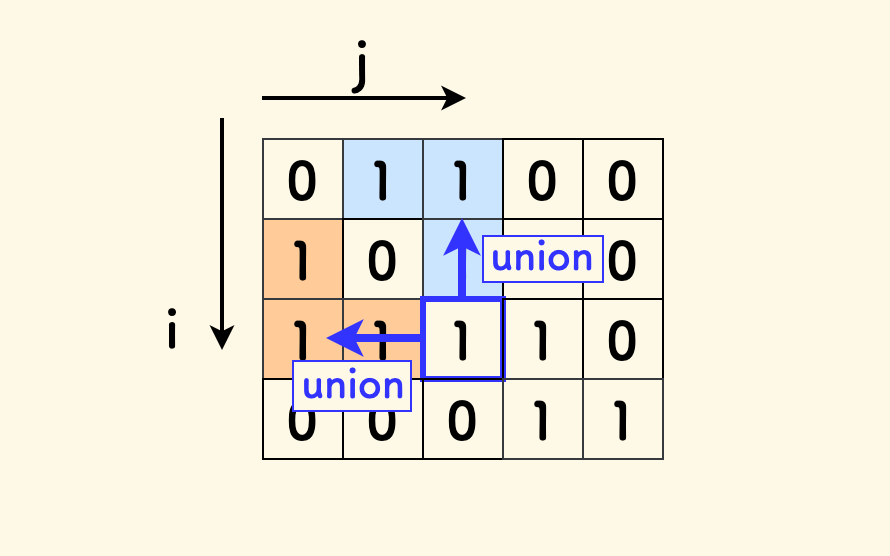
最后，合并完成后，输出连通分量即可。

一个细节是，节点总数量初始化为 m*n 的时候，最后答案要刨除 0 的格子的数量。

岛屿数量 - C++ 代码

// 省略 union-find 代码
class Solution {
   public:
    int numIslands(vector<vector<char>>& g) {
        int m = g.size(), n = g[0].size();

        UnionFind uf(m * n);

        // 映射到节点标号
        auto f = [=](int i, int j) { return i * n + j; };

        int k0 = 0; // 0 的方格数量，最后要剔除

        for (auto i = 0; i < m; i++) {
            for (auto j = 0; j < n; j++) {
                if (g[i][j] == '1') {
                    // 上
                    if (i > 0 && g[i - 1][j] == '1')
                        uf.Union(f(i, j), f(i - 1, j));
                    // 左
                    if (j > 0 && g[i][j - 1] == '1')
                        uf.Union(f(i, j), f(i, j - 1));
                } else
                    k0++;
            }
        }

        return uf.C() - k0; // C() 返回并查集的连通分量
    }
};

（完）

适用场景 ¶

结构定义 ¶

find 和 路径压缩 ¶

union 和 按大小合并 ¶

代码模板 ¶

岛屿数量问题 ¶

find 和路径压缩 ¶

union 和按大小合并 ¶