中位数有一个优美的性质:
一个的数列中到各个元素的距离之和最小的一个数是其中位数。
证明
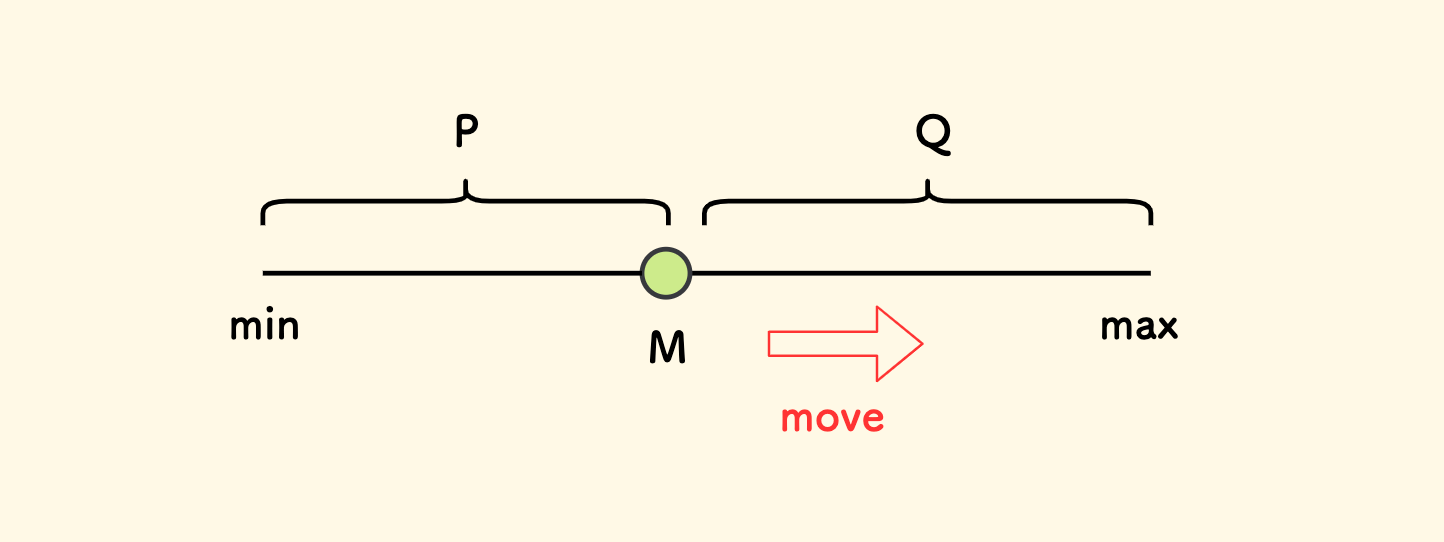
把序列排序,从小到大放在数轴上。然后在上面放置一个数字 $M$。
假设左边小于 $M$ 的元素个数是 $P$,右边大于 $M$ 的元素个数是 $Q$, 此时 $M$ 到各个元素的距离之和是 $S$ 。
- 如果 $P < Q$,那么把 $M$ 向右移动 $1$ 个单位,那么左边的 $P$ 个元素到 $M$ 的距离之和会增大 $P$, 右边的 $Q$ 个元素到中位数的距离之和则会减少 $Q$,综合看,$S$ 总体减少 $Q - P$ 。
- 反之,如果 $P > Q$,类似的操作,$S$ 总体减少 $P - Q$ 。
所以,要想 $S$ 最小,一定要 $P = Q$,即 $M$ 是中位数。
把所有元素变成同一个数的最小代价
leetcode 上有一个问题,利用了这个性质,可以拿来练手: 462. 最小操作次数使数组元素相等 II:
给你一个长度为 $n$ 的整数数组 $nums$ ,返回使所有数组元素相等需要的最小操作数。 在一次操作中,你可以使数组中的一个元素加 1 或者减 1 。
要所有元素都相等,操作的最小代价和就是其中位数到各个元素的距离,所以只要排序求其中位数即可,当然也可以走 topk 来求中位数。
(完)
本文原始链接地址: https://writings.sh/post/median
