单调栈的性质和题目总结

本文总结单调栈的一些个人经验和一些例题。

单调栈是指存放的元素按元素值或者关于某个函数单调递增或递减的栈。

为了维护其单调性质，栈顶压入新元素时，要提前逼迫栈内不满足单调性的元素出栈。

常用模板 ¶

单调栈的结构简单、应用形式非常灵活，没有固定的模式。

常见的代码形式如下（以单调递增栈为例）:

stack<int> s;

for (auto x : a) {
    while (!s.empty() && s.top() > x) {
        // TODO: 一般情况下，计算点在这里
        s.pop();
    }
    s.push(x);
}

每个元素只入栈一次、出栈一次，虽然是两层循环，但是均摊时间复杂度是线性的 $O(N)$。

大多数情况下，用栈的意义在于，先入栈等待，再伺机出栈计算。

所以，一般情况下，单调栈的计算点在元素被逼迫出栈之前。但是并非绝对，后面会有例子。

另外：

单调性并非一定是关于元素值本身的，也可以是关于某个函数的。
栈内存储的也不一定是元素本身，还有一种常见的形式，是存储下标。
一般情况下，单调栈的使用形式是一边入栈、一边出栈计算。但也有例外，比如提前全部入栈进行预处理，然后再出栈计算。

单调栈的性质 ¶

下面的两张图中：

X 是要压入栈的新元素
O 是要被逼迫出栈的元素
E 是历史上已经被逼迫出栈的元素
B 是栈底元素

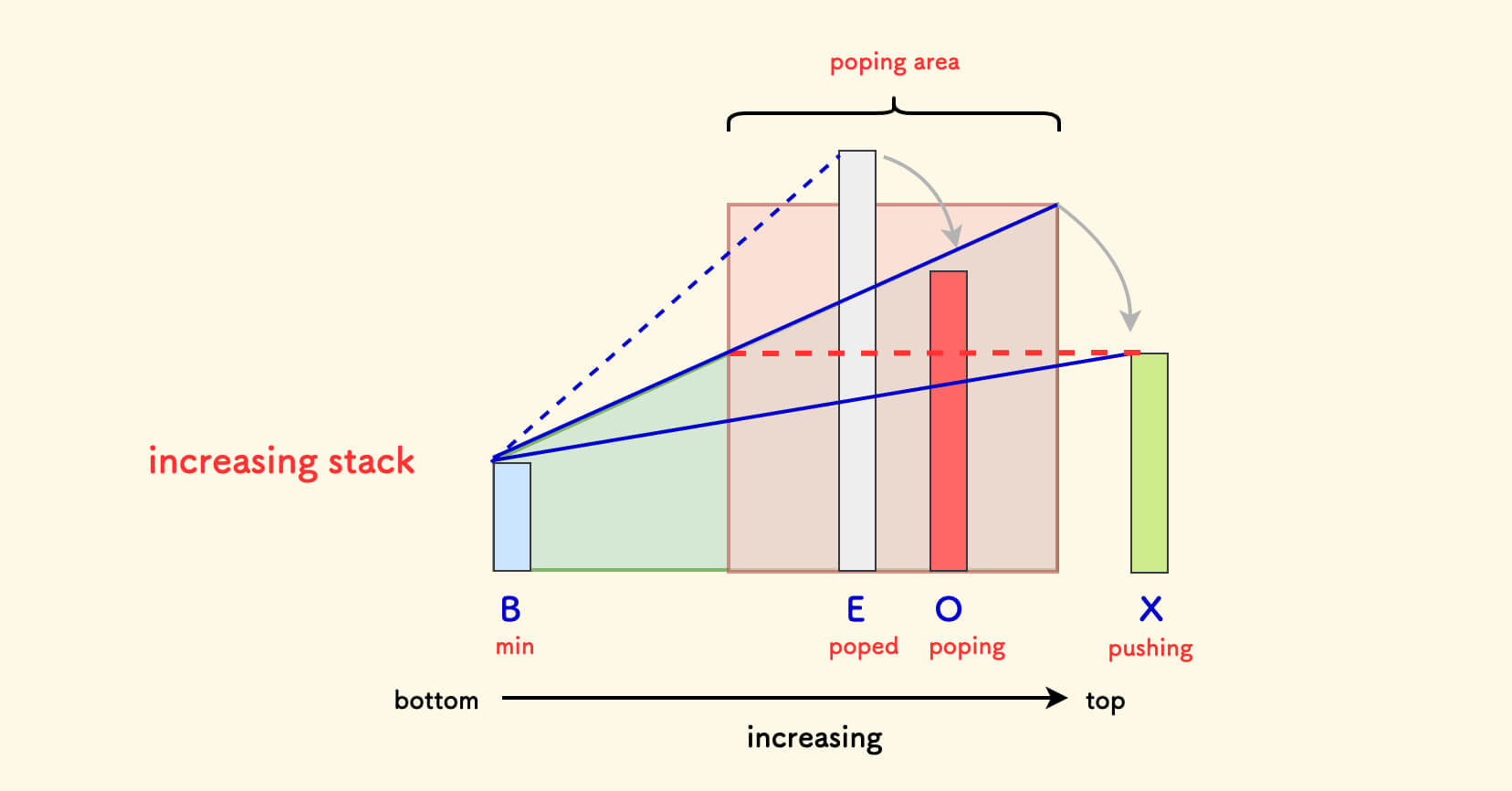
以单调递增栈为例（对应上方图片），可以总结几条性质：

栈底元素 B 是历史最小值。
元素 O 在原数组中下一个更小元素是 X。
X 的局部短板效应： X < O < E。
O 的局部短板效应：在栈内上一个元素和 X 之间的矩形区域中最短。
O 的局部短板效应的解释
图中的 P 是栈内 O 的前面的元素。
1. 由第二点性质可知，O 在右侧到 X 以前的区域中最小。
2. P 右侧到 O 的区域中全部是历史被弹出的元素，都比 O 大。
综合来看，O 是此区域中的短板。

类似地，单调递减栈（对应下方的图片），也可以总结这几条性质：

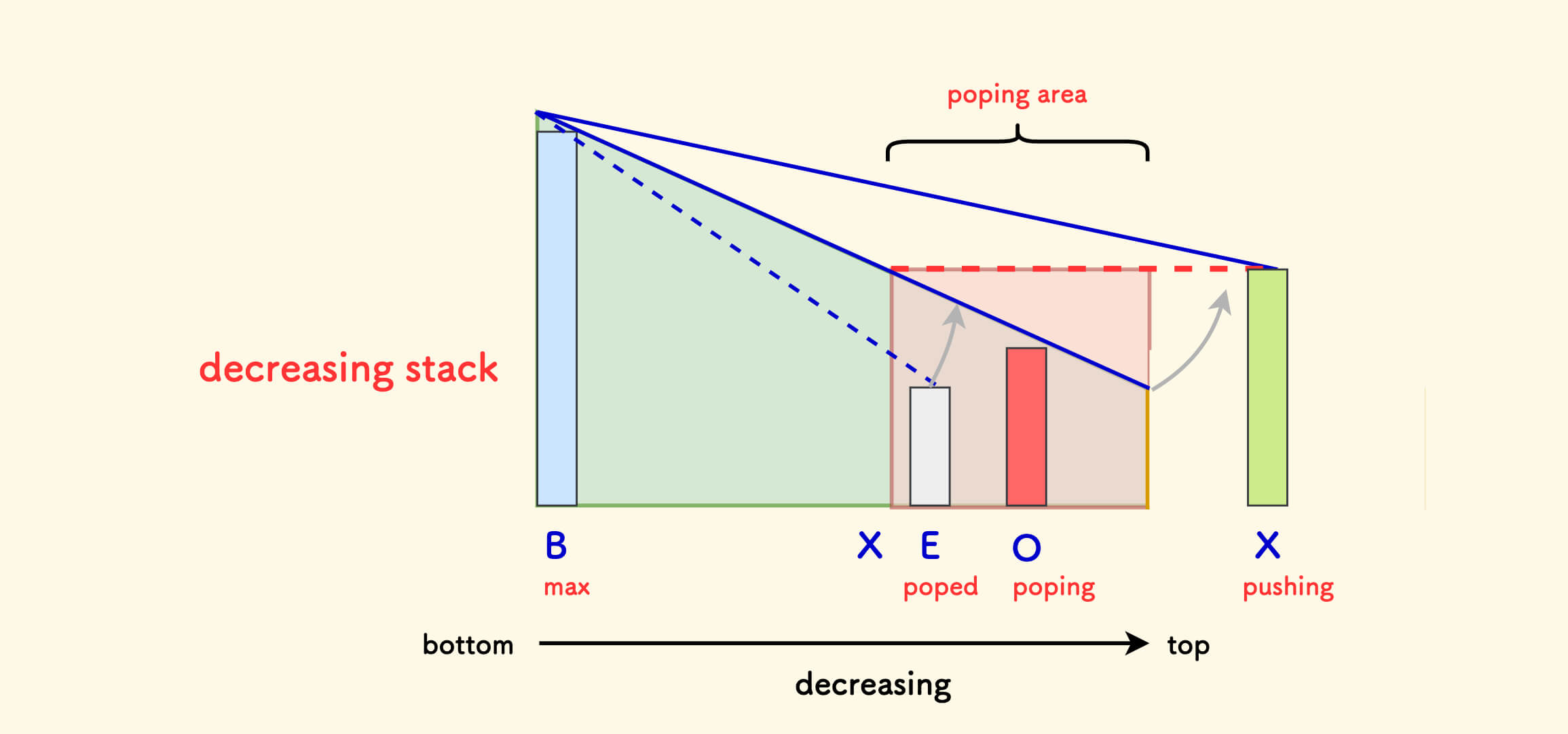
栈底元素 B 是历史最大值。
元素 O 在原数组中下一个更大元素是 X。
这一条性质主要用来解决所谓的「NGE 问题」(Next Greater Element)。
X 的局部长板效应： X > O > E。
O 的局部长板效应：在栈内上一个元素和 X 之间的矩形区域中最大（图略）。

由于计算点一般在元素出栈之时，也就是说，其中的元素 O 的性质需要特别关注。

另外，一个决定到底选用「单调递增栈」还是「单调递减栈」的小技巧是，想一下栈底需要保留的是最大值还是最小值。

接下来的部分，是单调栈的一些有意思的题目。

一些题目 ¶

柱状图中最大的矩形 ¶

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。求在该柱状图中，能够勾勒出来的矩形的最大面积。
-- 来自 leetcode 84

例如，下图中的最大面积是 10。

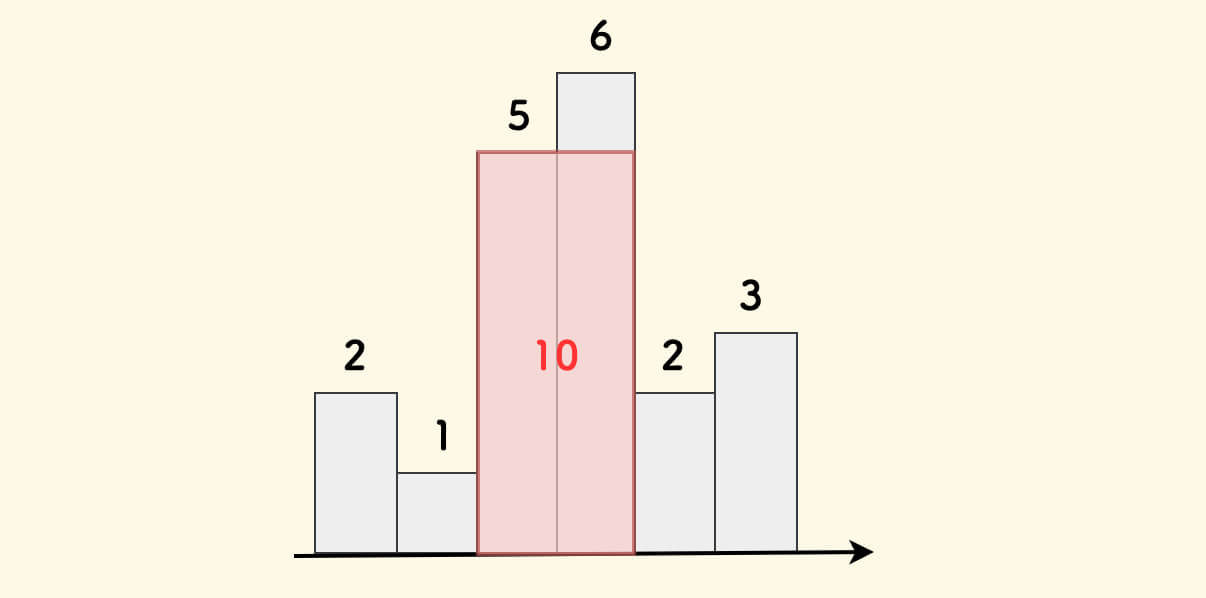
采用一个单调递增栈，存储原数组的下标。

下面的图中：

X 是要压入的柱子。
O 是要被逼迫出栈的柱子。
P 是栈内 O 的前一个柱子。

将利用单调递增栈的第二个局部短板效应 ^[1]。

可以知道的是：

因为 X 是 O 的下一个更小元素，所以 O 和 X 之间的柱子肯定都比 O 高。
P 右侧到 O 左侧的部分都是历史弹出的柱子，都比 O 高。

也就是说，O 是下方的黄色区域中的最短柱子。

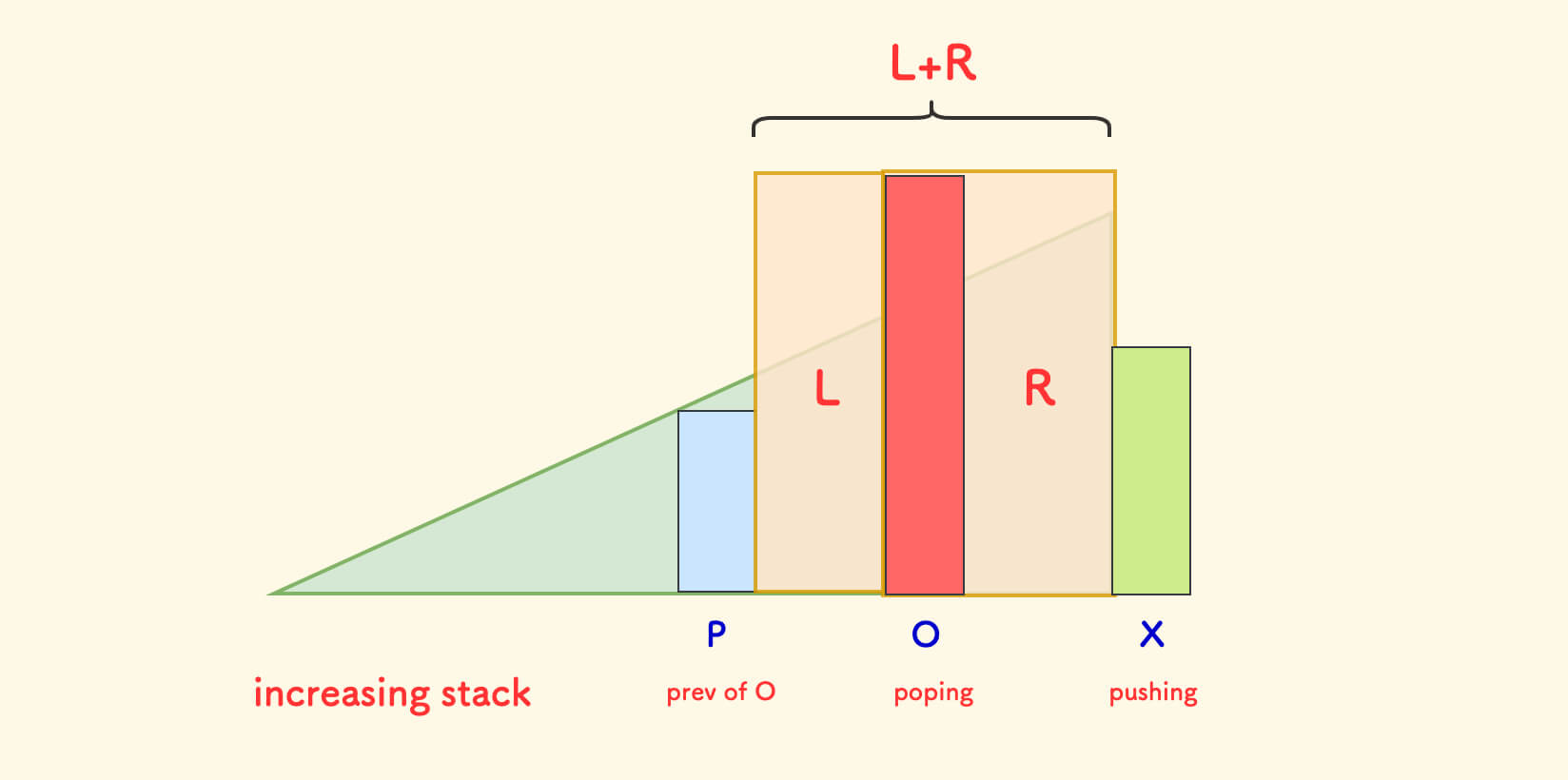
矩形面积取决于短板高度，在弹出一个柱子时，计算以此柱子为短板高度的矩形的面积。

拆成两部分来计算：

右侧矩形 R，包括柱子 O 但不包括柱子 X。
左侧矩形 L，不包括柱子 O，也不包括柱子 P。

因为我们在栈内存储的是原数组中的下标，所以容易计算出 L 和 R 的宽。

最后，追踪最大的矩形面积即是答案。

大概的伪代码如下：

柱状图中最大的矩形的伪代码

stack<int> s; // 存储下标、按柱子高度单调递增栈

for (int i = 0; i < n; i++) {
    while (!s.empty() && heights[s.top()] > heights[i]) {
        auto j = s.top(); s.pop();  // 柱子 O, 计算以此为高度的矩形的面积
        auto R = (i - j) * heights[j];
        auto L = (s.empty() ? j : (j - 1 - s.top())) * heights[j];
        ans = max(ans, R + L);
    }
    s.push(i);
}
// 注意清理栈内剩余元素, 雷同逻辑

完整代码见 leetcode 84. 柱状图中最大的矩形 - C++ 实现 - Github

接雨水 ¶

一道非常出名的面试题：

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。
-- 来自 leetcode 42

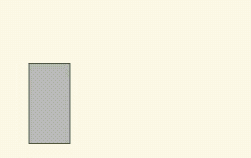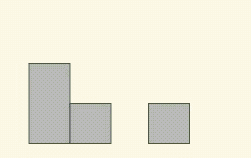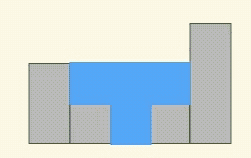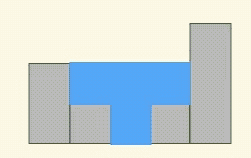
如下图所示，其中蓝色的是雨水。

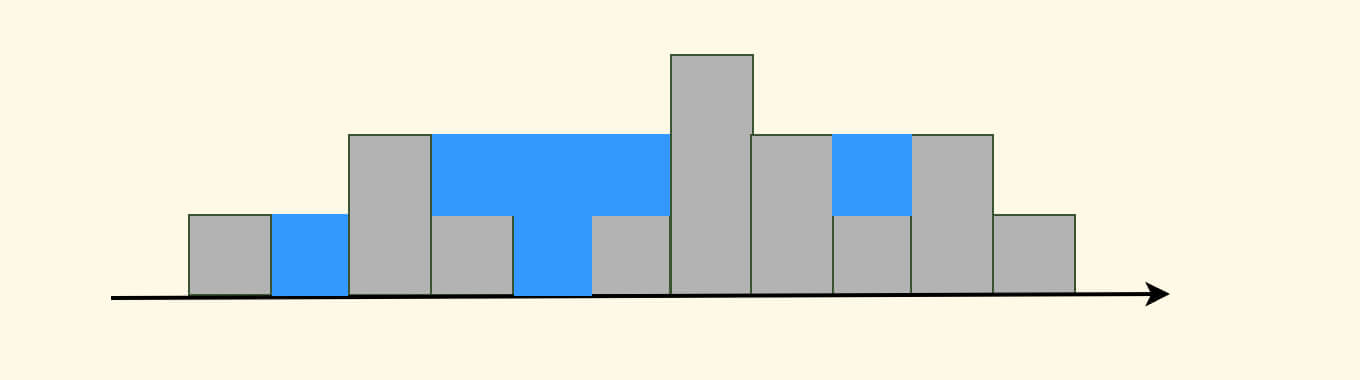
中间的这一块凹槽很有启发意义，可以拆成上下两个矩形，也就是说分两次来接。

思路即是，不断按凹槽为单位来接雨水。

已经出现的柱子，要等待比它更高的柱子出现，才可以形成一个凹槽来接雨水。

那么，历史最高的柱子，要一直等待更高的柱子出现。它适合放在栈底，所以采用一个单调递减栈。

因为计算面积肯定涉及计算宽度，也就是按下标来算，所以栈中存储下标、而不是元素的值。

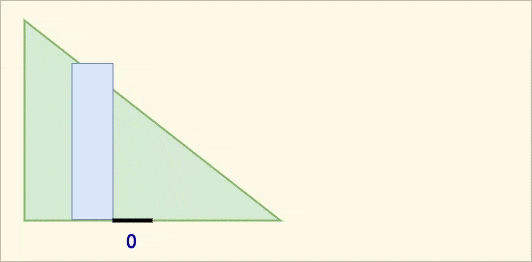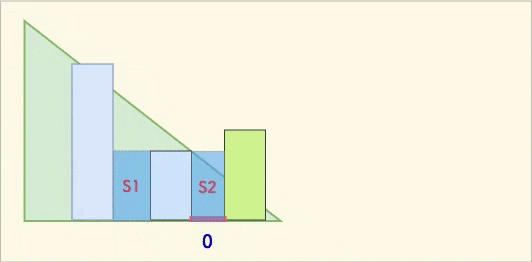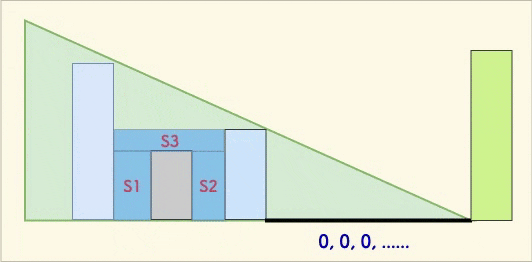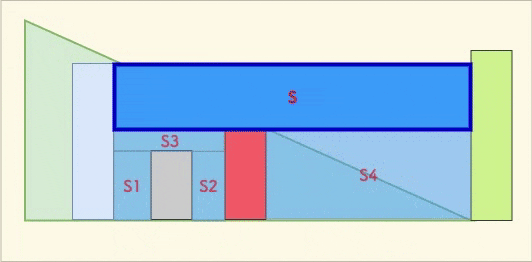
下图中：

X 是正在扫描的柱子，也就是即将压入栈的元素
O 是即将被逼迫出栈的栈内元素
P 是栈内 O 的上一个元素
E 是 O 之前的历史被弹出的元素

从前面的单调栈的性质 ^[2] 的总结来看，可以知道：

X 是 O 的下一个更大元素.
P 一定大于元素 O，因为是单调递减栈.
而且 P 和 O 之间的柱子一定都比 O 小（否则就会在栈内留存了）。

此时可以形成一个新的凹槽 S（如下图所示）。

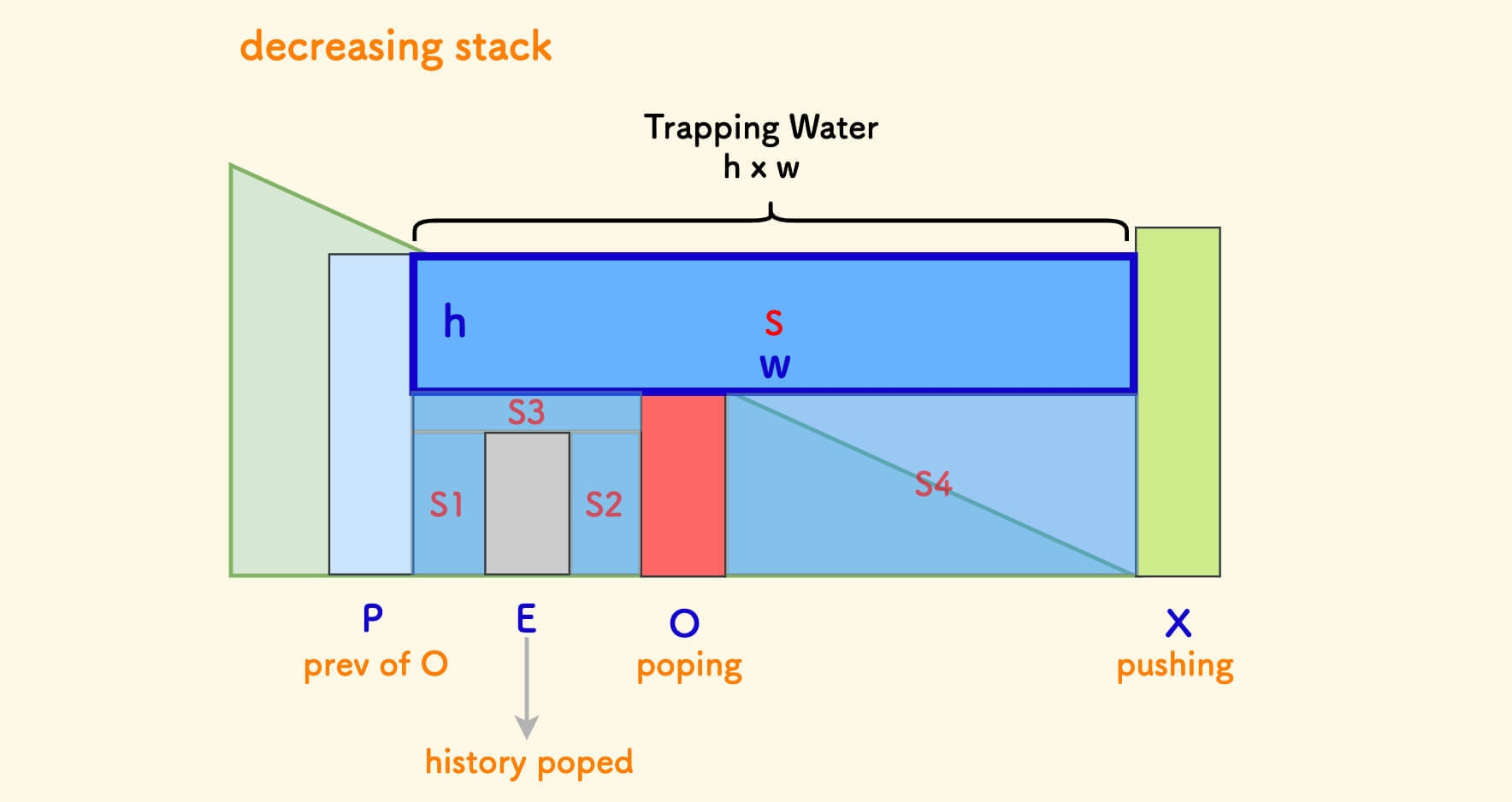
你不必担心图中的其他「凹槽」(即 S1, S2, S3, S4) 的收集问题，因为在历史上，它们都已经被收集过了。

下图是每块面积的一种收集情况的动态演示：

其实我们每次收集的雨水，是以要弹出的柱子为底的凹槽的面积。

当前要收集的只有新的凹槽 S，计算其面积：

高度 h 就是 min(X, P) - O
宽度 w 就是 x - p - 1 （用小写字母表示下标）。

伪代码如下：

接雨水的伪代码

stack<int> s;
int ans = 0;

for (auto i = 0; i < height.size(); i++) {
    while (!s.empty() && height[s.top()] <= height[i]) {
        int bottom = height[s.top()]; s.pop(); // 要出栈的 O
        if (s.empty()) break;
        int left = s.top(); // 左边的 P
        int w = (i - left - 1);
        int h = (min(height[i], height[left]) - bottom);
        ans += h * w;
    }
    s.push(i);
}

完整代码见 leetcode 42. 接雨水 - C++ 实现 - Github

132模式 ¶

这个应该是这几个单调栈题目中最难的一个：

给你一个大小为 n 的整数数组 nums，判断其中是否存在 132 模式的子序列。
132 模式的子序列是指：由三个整数组成，同时满足：
下标满足 i < j < k
元素值满足 nums[i] < nums[k] < nums[j]。
-- 来自 leetcode 456

比如说，数组 [3,1,4,2] 中存在 132 模式的子序列 [1,4,2]，但是 [1,2,3,4] 中就不存在这种子序列。

132 模式中的三个数，大概构成下面的形状：

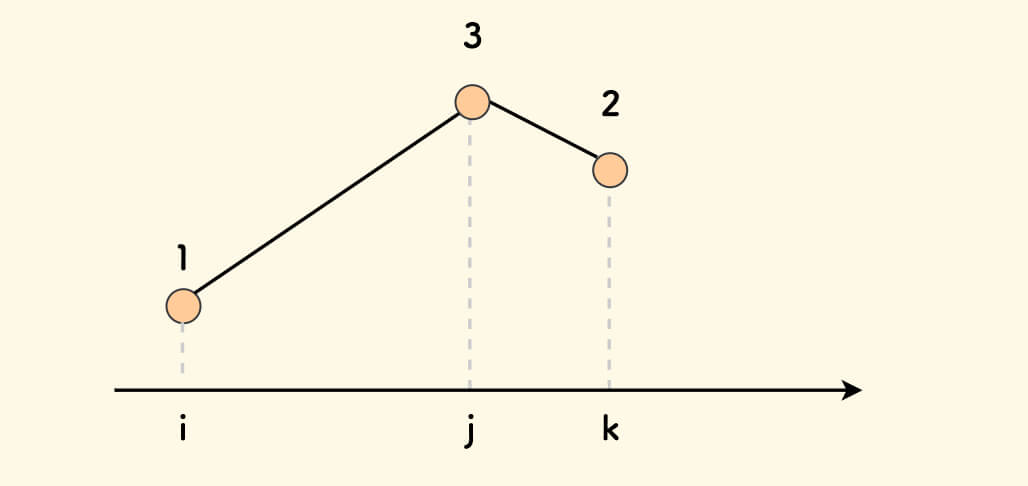
思路是，对于每一对 3 和 2，尝试找 3 左侧的 1 是否存在。

原因在于：

2 和 3 的位置关系是「邻近」的，适合应用单调栈的「下一个更大元素」的场景。
虽然 1 和 3 的位置也是「邻近」的，但是在大小关系上，中间还有个 2。
对每一对满足 2 < 3 的数对，剩下的任务就是在 3 位置左边找一个满足条件的 1 即可。
而这一点只需要在 3 左边找到最小的一个元素来验证即可。

也就是说，对于右边的每一个从左向右的下坡线 L（图中蓝色坡线），在左边的紫色区域内找一个元素是否存在。

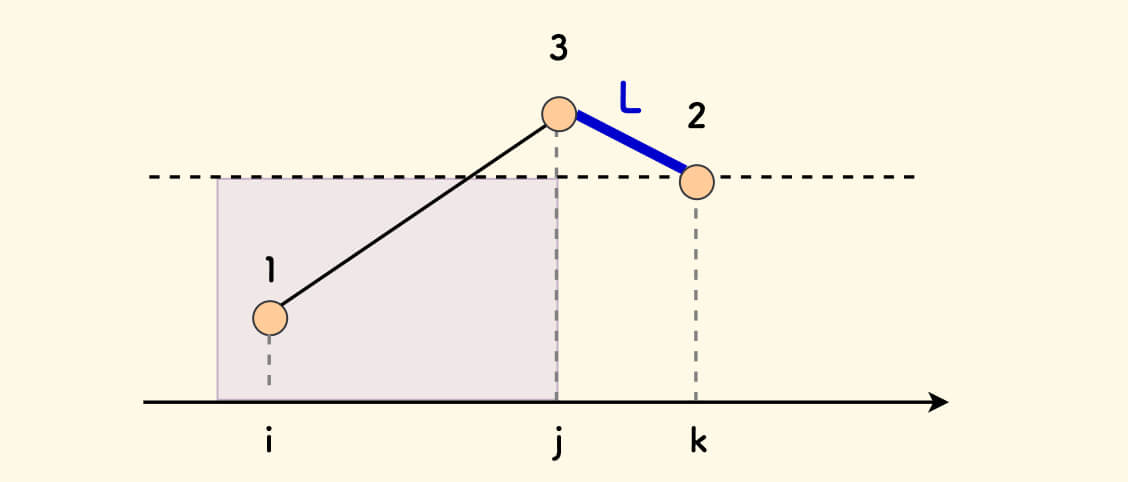
如果已知下图中的 132 符合条件，并且 2 和 3 之间还有一个数字 3'，那么肯定 13'2 也符合条件。也就是说，对于每个 2 只需要找它左边最近的比它大的元素即可，这是典型的单调栈场景。

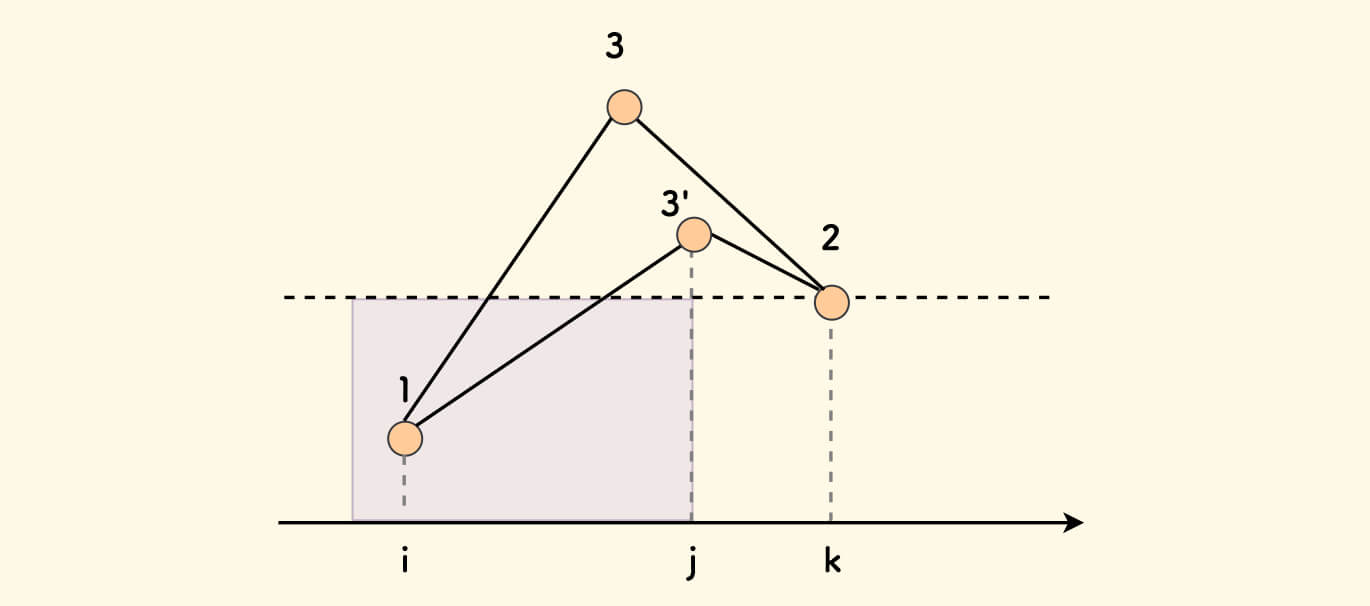
同时，对于每个 2，把它固定来看，左边的 3 越靠近 2，紫色区域就会越大，就越容易找到符合条件的 1。

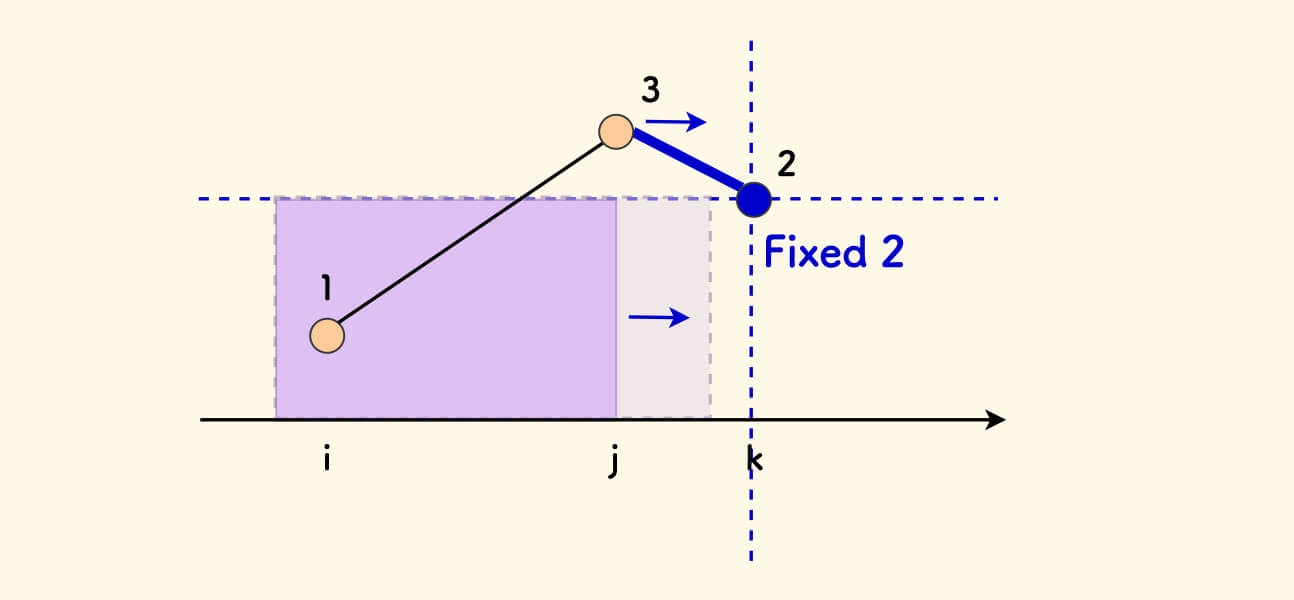
因此，采用一个单调递减栈，从右向左扫描每个元素，作为 3 来逼迫栈内比它小的元素作为 2 出栈。

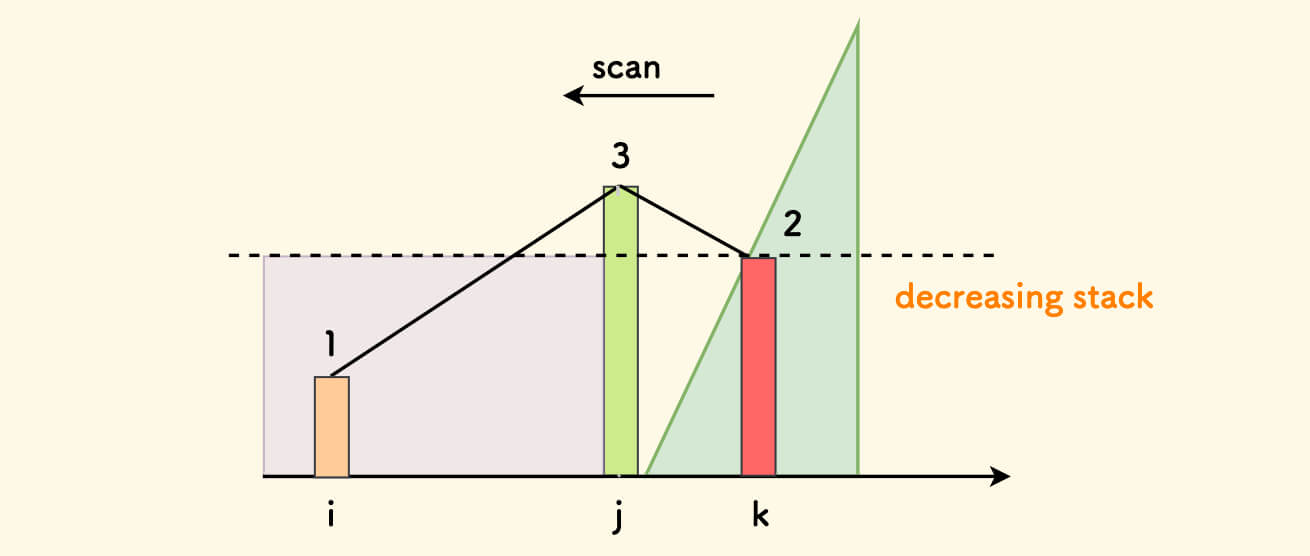
对于如何寻找符合条件的 1，可以提前预处理每个下标 i 左侧的最小值 L[i]，可以在 $O(N)$ 复杂度做到：

// L[i] 表示 i 左边（不包括i）的最小值, 也就是要找的 1
vector<int> L(n, INT_MAX);
for (int i = 1; i < n; i++) L[i] = min(L[i - 1], nums[i - 1]);

另外，逼迫出栈的时候，要弹出的元素 x 不一定满足条件，要分情况讨论。

假设迭代的 3 叫做 nums[i]：

如果 x <= L[i]，也就是不符合条件，直接舍弃。
如果 x == nums[i]，也不符合 132 模式，舍弃。
否则，满足 L[i] < x < nums[i]，就找到了 132 模式。

实现如下：

132 模式的 C++ 实现

stack<int> s; // 单调递减栈，存储元素值

for (int i = n - 1; i >= 1; i--) { // 从右侧向左找
    if (nums[i] > L[i]) { // 必须要能满足: 3 > 1
        while  (!s.empty()) {
            if (s.top() <= L[i]) // 不合法：2 < 1
                s.pop();
            else if (s.top() == nums[i]) // 不合法: 2 == 3
                s.pop();
            else if (s.top() < nums[i])  // 找到了
                return true;
            else  // 无元素可以 pop, break
                break;
        }
        s.push(nums[i]);
    }
}

完整代码见 leetcode 456. 132 模式 - C++ 实现 - Github

最大宽度坡 ¶

给定一个整数数组 A，坡是元组 (i, j)，其中 i < j 且 A[i] <= A[j]。这样的坡的宽度为 j - i。找出 A 中的坡的最大宽度，如果不存在，返回 0。
-- 来自 leetcode 962

题意非常简洁明了，但是其单调栈的运用却与众不同。

首先，从左向右，建立一个单调递减栈，存储下标：

stack<int> s; s.push(0);
for (int i = 1; i < nums.size(); i++)
    if (nums[s.top()] > nums[i]) s.push(i);

这是个只进不出的过程。

将说明：

最大宽度坡的左端点一定在栈内。

利用反证法，假如最大宽度坡的左端点是 b，不在栈内，那么它左侧一定有一个栈内的 c 且满足 c <= b。因为，如果不存在这样的元素 c 的话，就意味着 b 左边的元素都比 b 大，那 b 就会在栈内，矛盾。

那么 c 和最大宽度坡的右端点 a 形成的新的坡线会更宽，导致矛盾。命题得证。

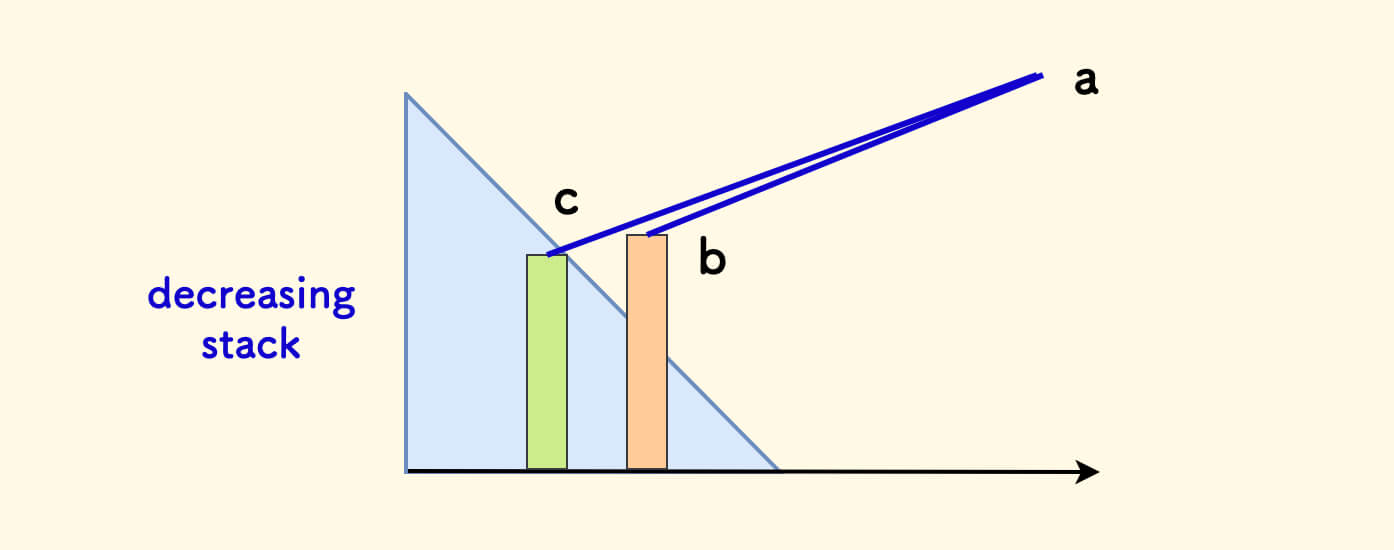
建立完左端点的单调栈后，以右端点为主，来寻找符合条件的左端点：

从右向左寻找右端点，下标用 i 来表示。
与此同时，左端点不断出栈，下标用 j 来表示，取出最大宽度者即为答案。

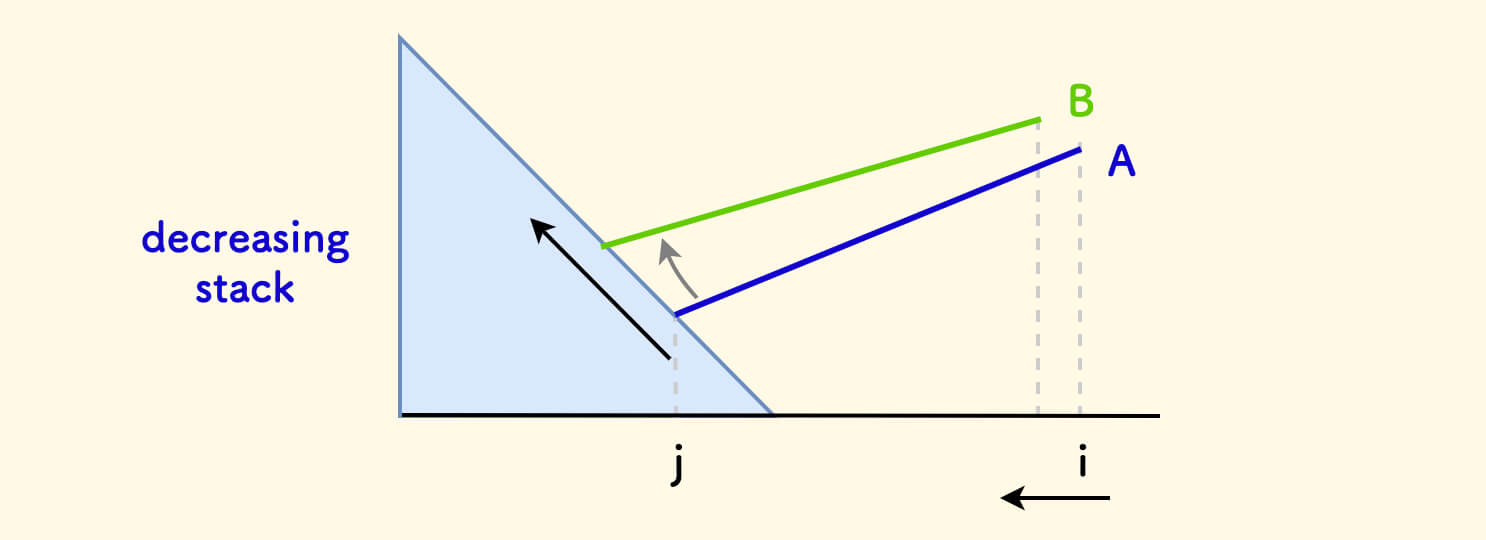
下图中，假设右端点扫描到 i 处时，找到的符合条件的坡线是蓝色的 A，此时左端点是 j。

此时，i 要进一步左移的话，j 只能左移，才有可能找到更宽的坡 B。

也就是说，每次找到一个坡线，都可以直接舍弃左端点，也就是可以直接出栈。

主过程代码如下：

int ans = 0;
for (int i = nums.size() - 1; i >= 0; i--) {
    while (!s.empty() && nums[s.top()] <= nums[i]) {
        ans = std::max(i - s.top(), ans);
        s.pop();
    }
}
return ans;

这道题的特别之处，不像常见的单调栈问题，一边入栈、一边出栈。而是先一股脑的入栈，预处理一波，然后再逐个出栈。

子数组的最小值之和 ¶

这个题我觉得是单调栈里面最好玩的了：

给定一个整数数组 arr，找到 min(b) 的总和，其中 b 的范围为 arr 的每个（连续）子数组。由于答案可能很大，因此返回答案模 10^9 + 7。
-- 来自 leetcode 907

简而言之，题意是把所有子数组的最小值求和。

以数组 [9,6,2,4,5,3,1,7] 为例，下图是其所有子数组的填表结果。

填表的方式是，子数组 [i..j] 的最小值填到方格 [i,j] 中，比如子数组 [2,4,5] 的最小值是 2：

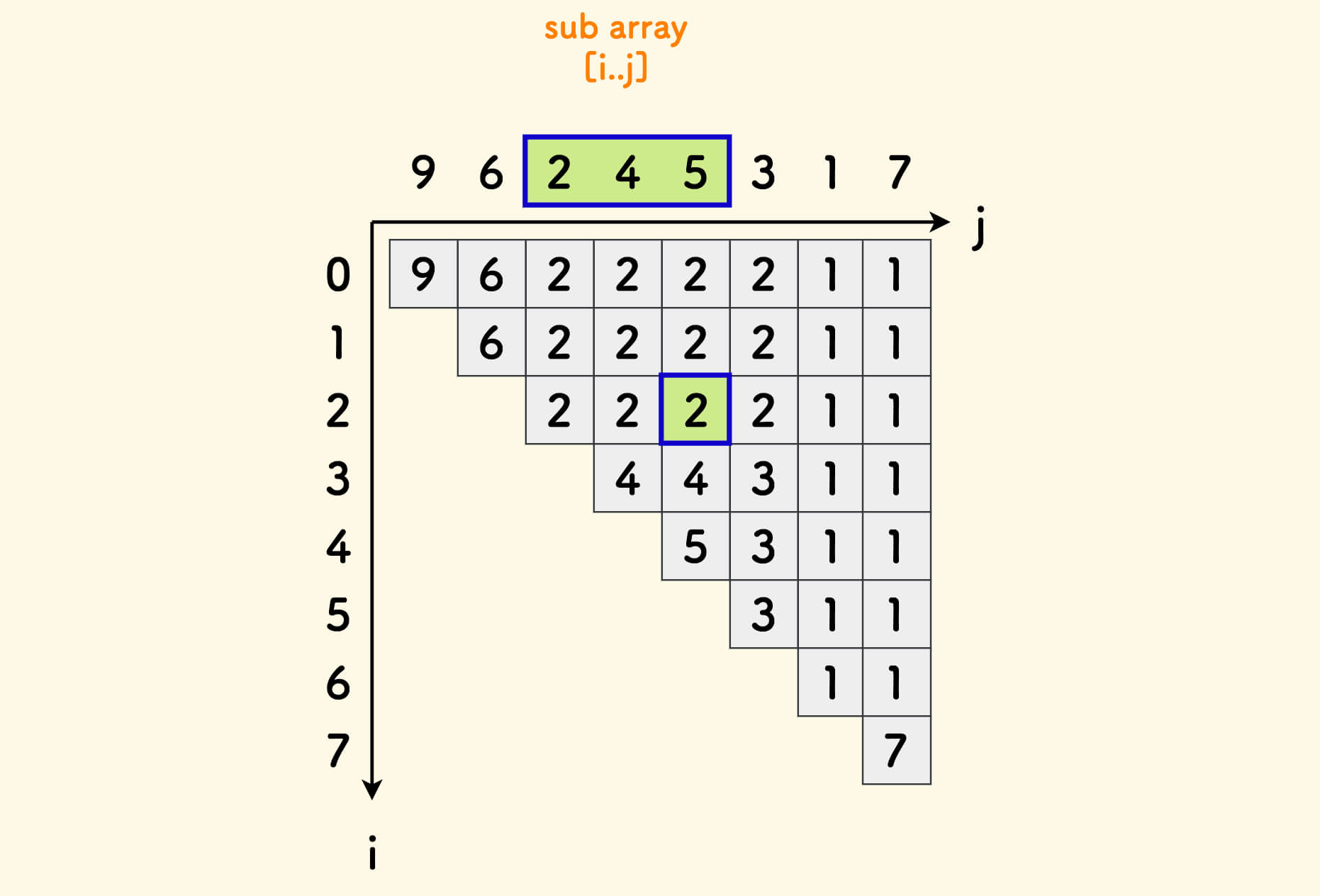
要求的答案，就是这个表格的数字总和。

问题是，如何以 $O(N)$ 的时间复杂度求解这个二维表格数字之和。

秘密是，利用数字重复的规律。

下图把重复的数字染成了同一种颜色，可以很清楚地看到，重复的数字都各自构成了一个矩形！

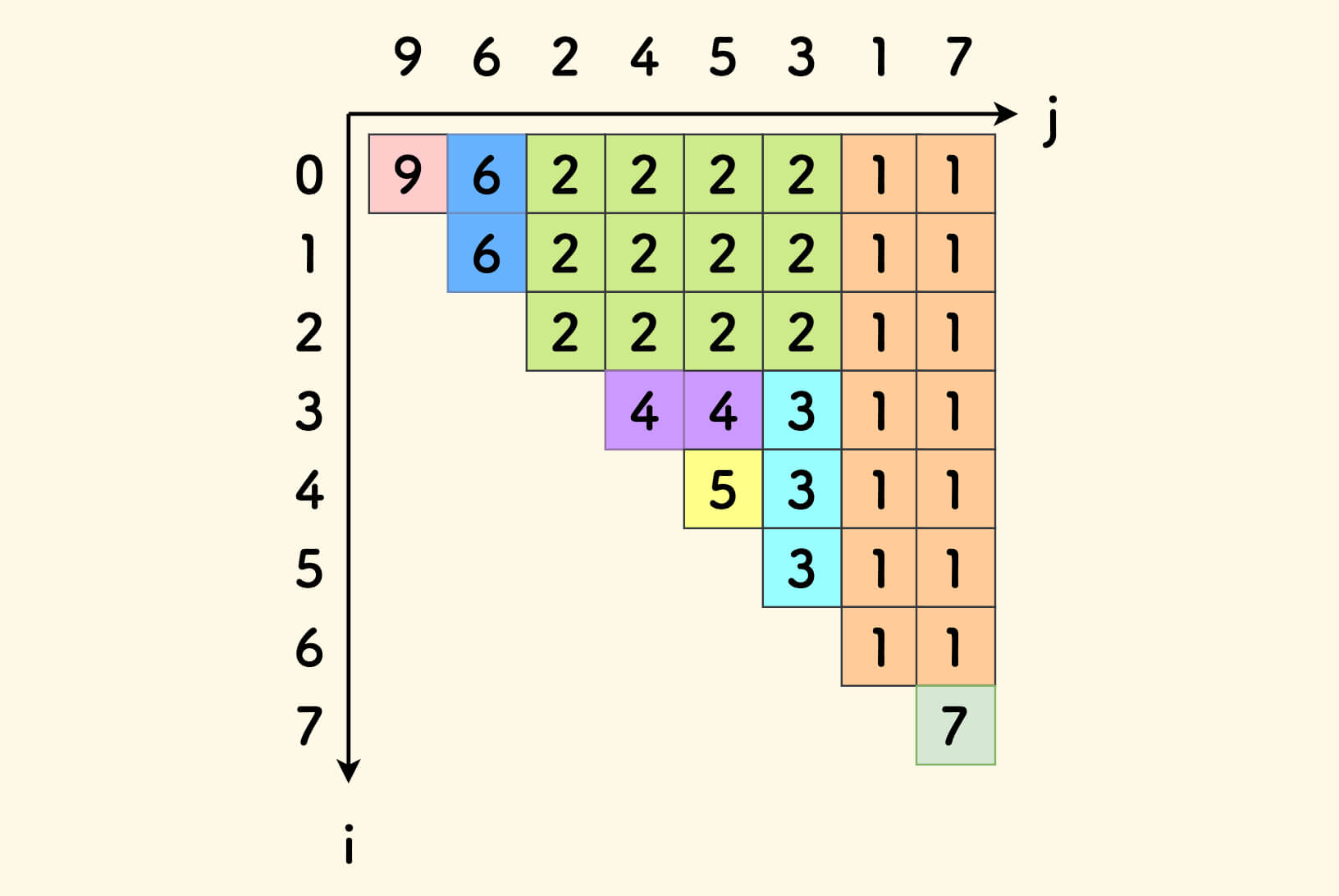
这并非巧合，下图是另一个数组 [3,2,5,7,4,6,1] 的染色情况，也有这种规律：

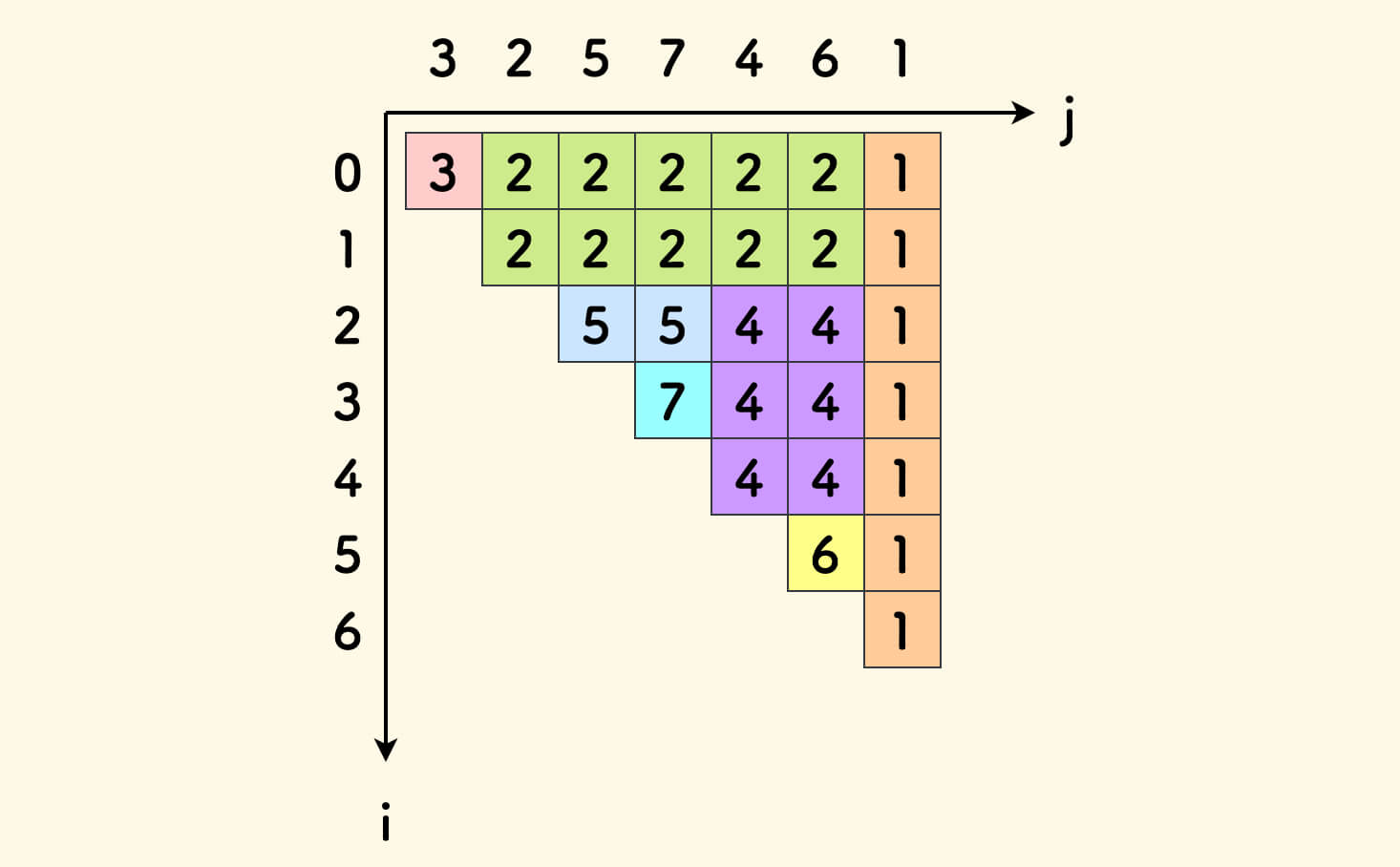
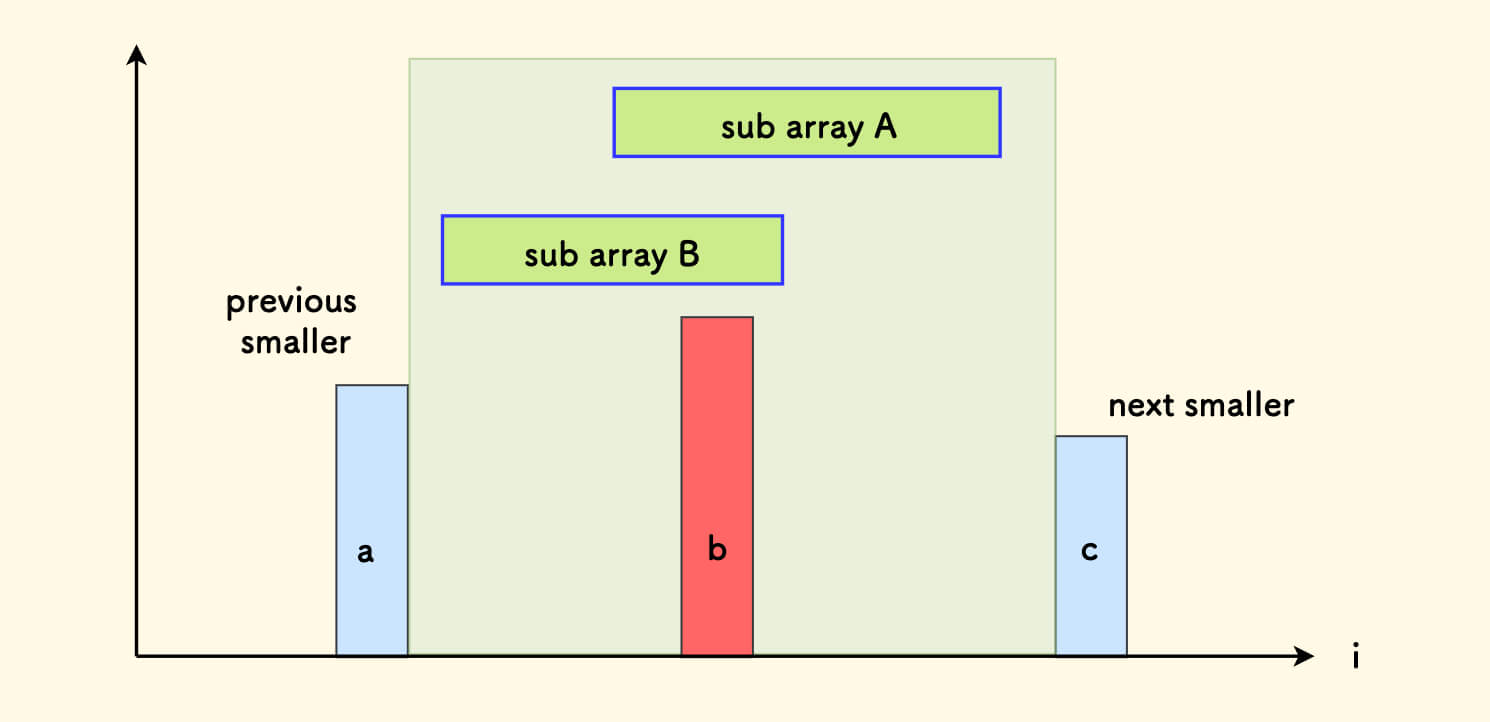
假设元素 b 的下一个更小元素是 c，上一个更小元素是 a，那么它所影响的范围应该是下图中的绿色区域，其中经过 b 的所有子数组的最小值都是 b。

比如说，下图中的子数组 A 和 B，都是经过 b 的，所以它们的最小值都会是 b。

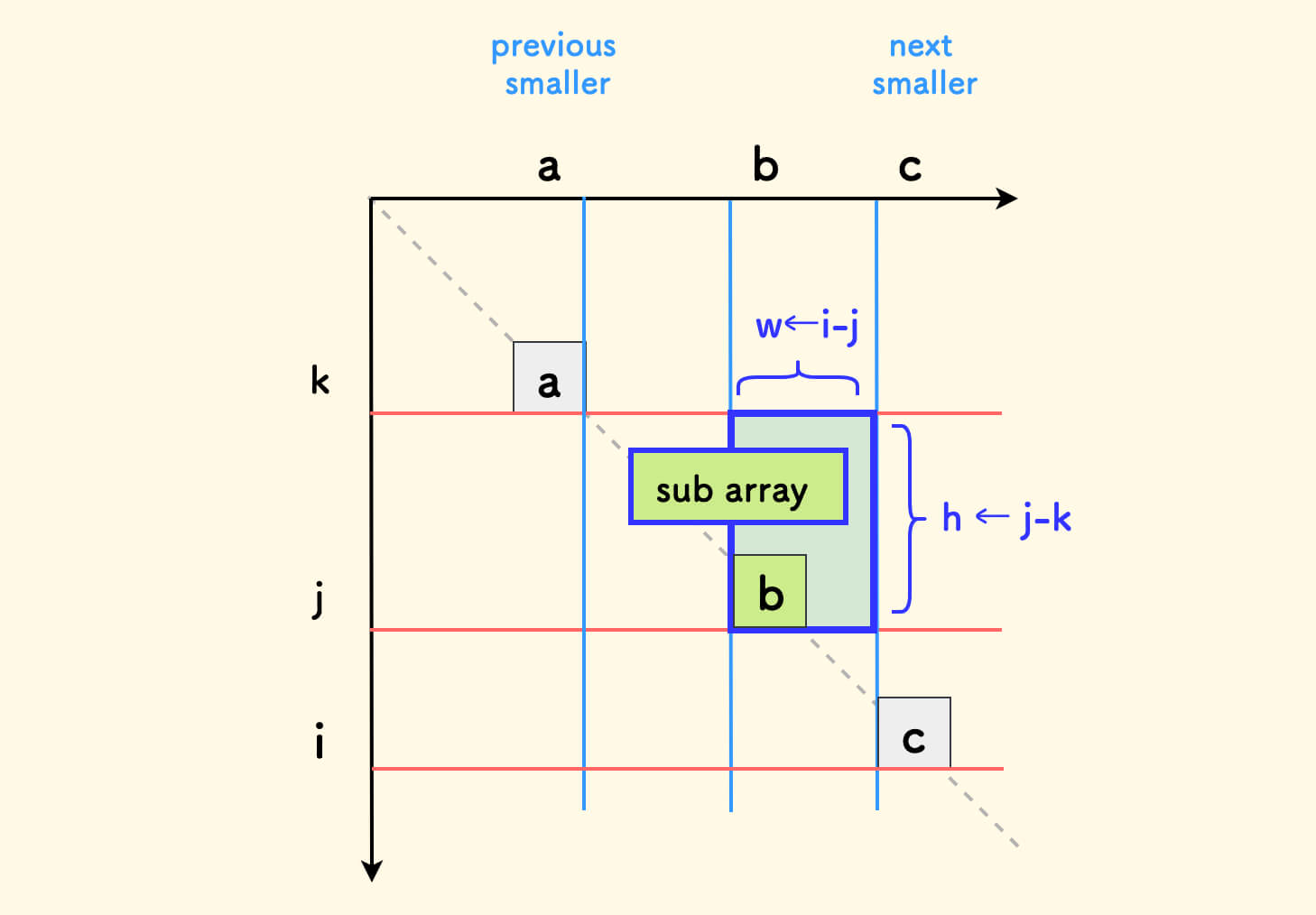
在填表过程中，假设 a,b,c 的下标分别是 k,j,i 的话，如下图所示。

对于 a 和 c 之间经过 b 的子数组而言：

左端点下标范围是 (k, j]
右端点下标范围是 [j, i)
对应的最小值是 b，即要填入的数字是 b

根据填表的方式，可以知道，b 填充的区域是一个矩形，宽是 i-j，高是 j-k。

可以进一步计算其数字总和，贡献给答案即可：

ans += b * (i-j) * (j-k)

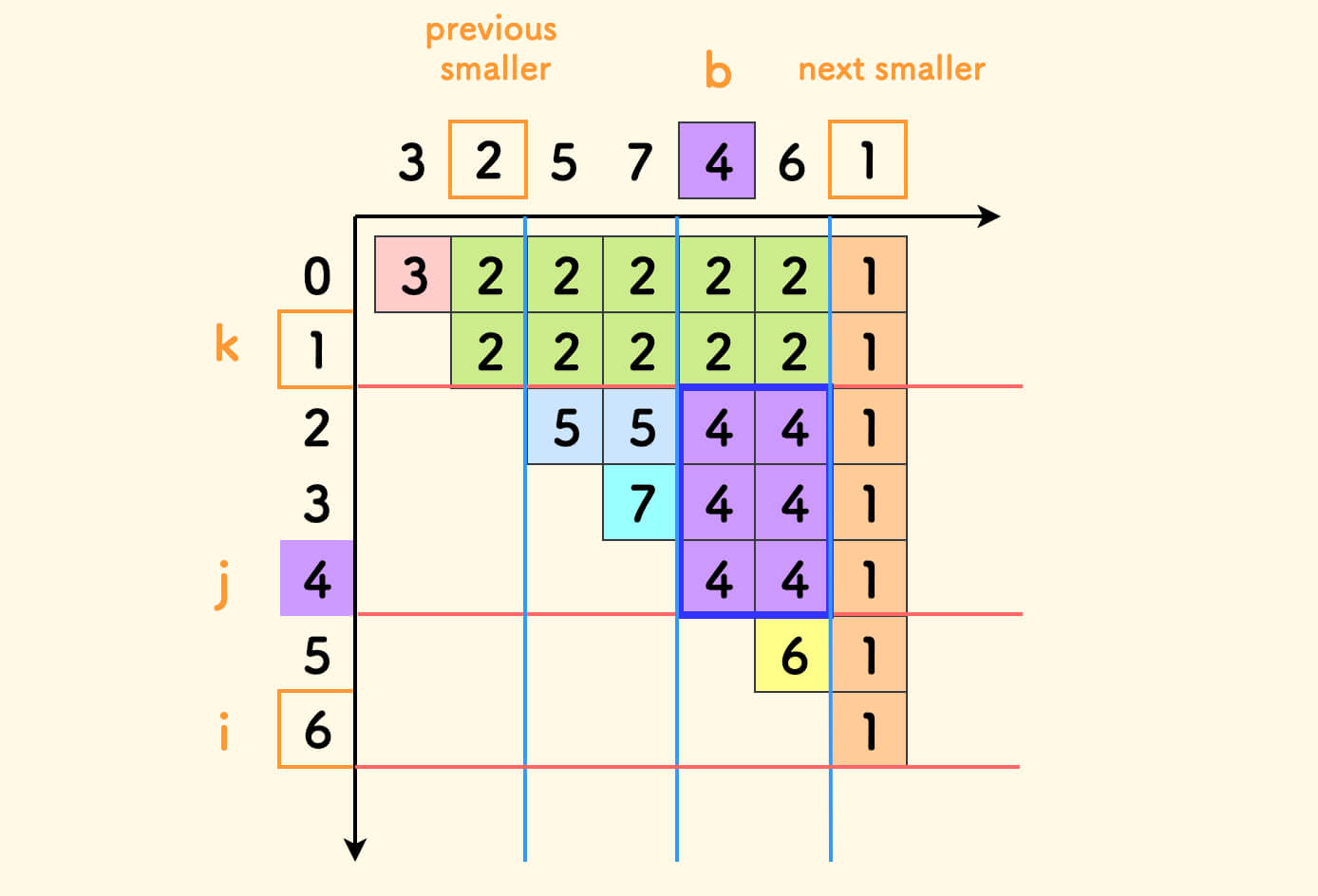
套入前面的具体的例子，下图中 4 填入的区域，就是紫色蓝框矩形：

最后，如何获得一个元素的上一个、下一个更小元素，当然是借助单调栈了，确切的说是一个单调递增栈。

主迭代元素就是 c，它会逼迫栈内更大的元素出栈，以维护单调栈的性质。

每次逼迫出栈时的元素就是上面所说的 b 元素，b 在栈内的前一个元素就是 a。

代码描述这个计算过程如下：

using ll = unsigned long long;
stack<int> s;  // 单调递增栈, 存储下标
ll ans = 0;

auto reduce = [&](int i) { // i 对应元素 c
    // 当前要 pop 的元素, 对应 b
    int j = s.top(); s.pop();

    // j 这个元素重复的宽度 w 和积累的层数 h
    int w = (i - j);
    int h = s.empty() ? (j + 1) : (j - s.top()); // 特判栈空, k 即是 s.top()

    // 加上这个元素积累的总和
    ans += (ll)(w * h) * (ll)arr[j];
};

最后，主迭代过程注意清理栈内剩余的元素，总时间复杂度是 $O(N)$：

int mod = 1000000007;
int n = arr.size();

for (int i = 0; i < n; i++) {
    while (!s.empty() && arr[s.top()] >= arr[i]) reduce(i);
    s.push(i);
}
while (!s.empty()) reduce(n);
return ans % mod;

简单总结 ¶

单调栈非常灵活，没有特别固定的模式。

常见的计算点在逼迫出栈之前。
单调栈中可以存储值本身，也可以存储下标。
常见的形式是，一边入栈、一边出栈。但并非绝对，也有先全部入栈、然后再全部出栈的情况。
单调栈最常见的适用场景：上一个（下一个）最大（最小）元素。
单调栈的局部短板（长板）效应。

我个人觉得单调栈的题还是挺难的，挺考验思维的。

（完）

单调栈的性质 和 题目总结