⟵ 春水煎茶 · 王超的个人博客 算法 | 分类 | 归档 | 订阅 | 关于

单调队列的一点总结

2024 年 1 月 29 日 ·春水煎茶 · 未经允许，不可转载

本文总结单调队列的一些个人经验 和 一些例题。

结构

单调队列是一种双端队列，存放的元素按元素值 或者 关于某个函数单调递增或递减。

只看右半部分的话，单调队列就是一个单调栈，只不过队头是「可收缩的」。

也可以把单调队列理解为一种 滑动窗口 和 单调栈 的组合体。

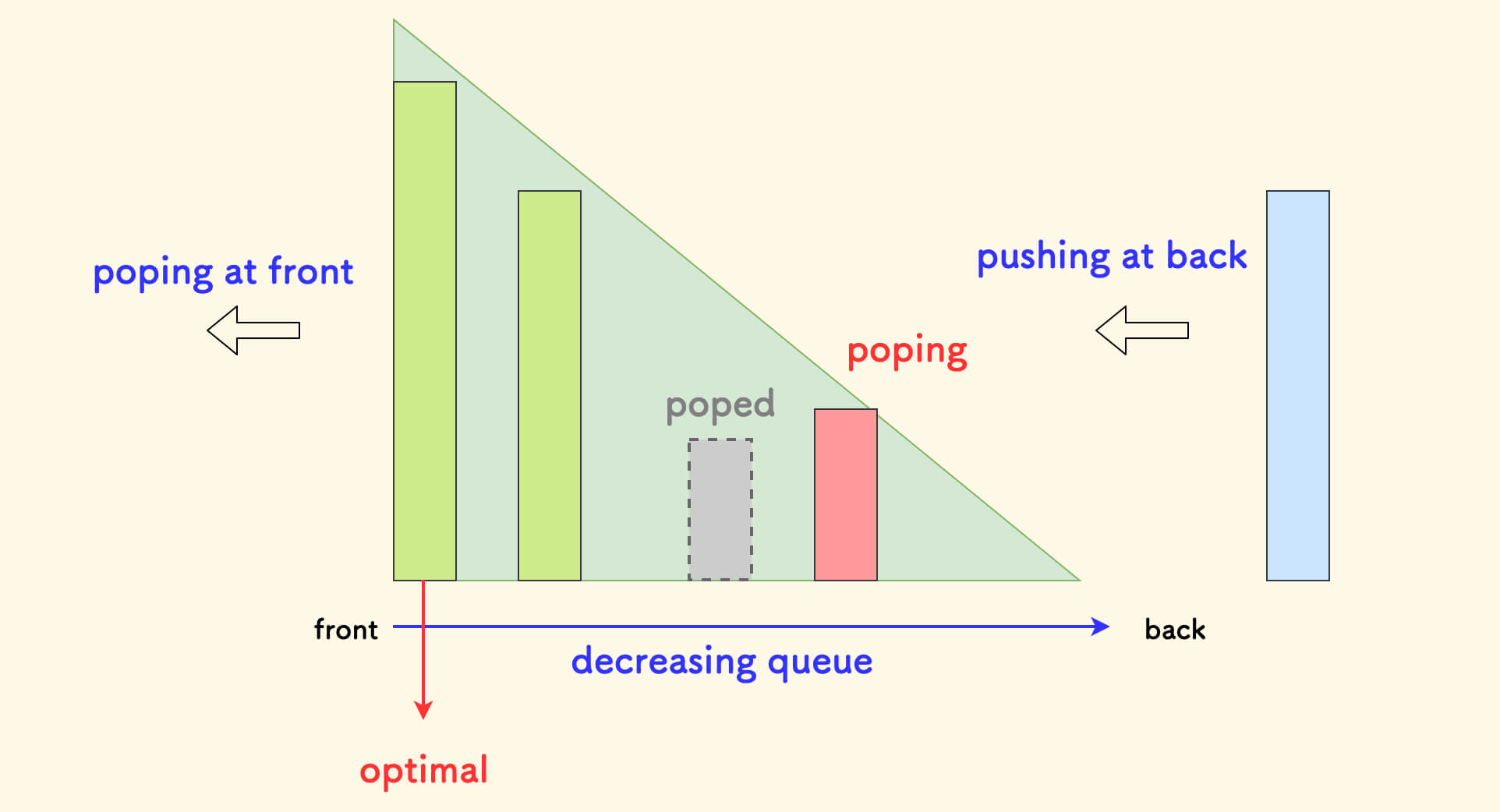
以一个单调递减队列为例，单调队列大概是下图中的样子：

  1. 最优决策点保持在队头。
  2. 队头弹出不合法的元素（单调队列问题常带一个区间限制）。
  3. 队尾和单调栈一样，推入新元素前，先逼迫队中不符合单调性的元素出队。

场景和原理

最经典的场景是，单调队列主要解决滑动窗口最值问题。

更广义的场景是，用来优化一类最优化动态规划转移，主要适用于如下形式的 DP（以求最大值为例）：

\[f(i) = \max_{L(i)\leq j\leq R(i)} { \{ f(j) + a(i) + b(j) \}}\]

其中：

  1. 决策点 $j$ 来自区间 $[L(i),R(i)]$，上下界函数均随 $i$ 单调递增。
  2. $a(i)$ 是仅和 $i$ 有关的函数，$b(j)$ 是仅和 $j$ 有关的函数

因为 $a(i)$ 和 $j$ 无关，所以可以把它移项出来：

\[f(i) = \max_{L(i)\leq j\leq R(i)} { \{ f(j) + b(j) \} } + a(i)\]

区间上下界均单调递增，也就是说，随着 $i$ 的增大，决策区间在右移。

这其实就是一种滑动窗口模型，更特殊地情况下是定长的滑动窗口。

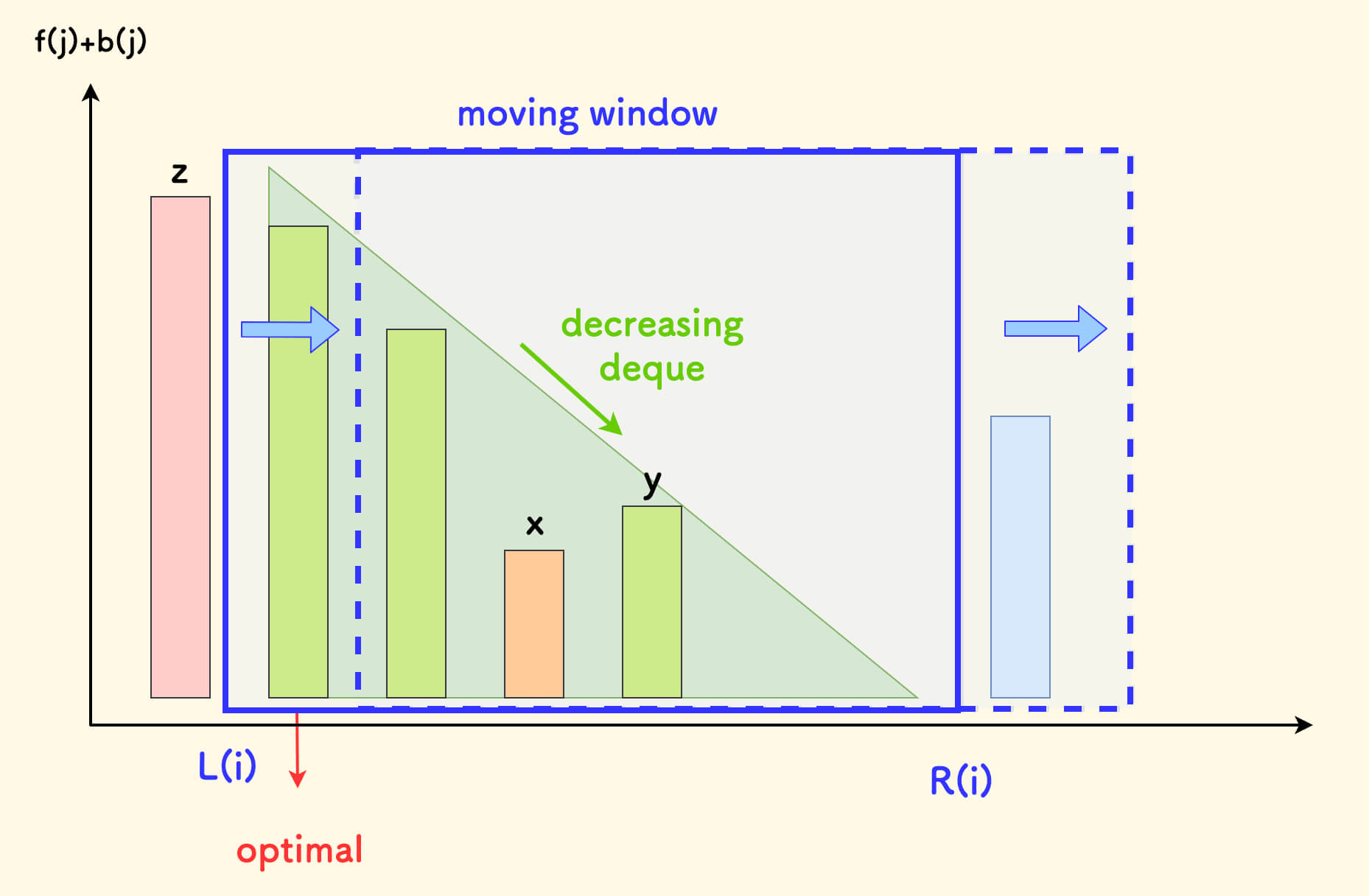
单调队列可以均摊 $O(N)$ 时间复杂度、来维护滑动窗口最值：

  1. 保证队内按 $f(j)+b(j)$ 的值单调递减, 最优决策点保持在队头。

  2. 及时排除非法决策：

    上图中，区间右移时，红色的 z 即成为非法决策，及时出队。

  3. 及时排除不可能成为最优的决策：

    上图中，一旦扫描到决策 y，因为 y 比 x 的决策值更大，而且它在窗口中会比 x 停留地更晚。

    就是说，y 一方面比 x 更优，而且会更晚地离开窗口。

    所以 x 一定永远比不过 y，不再可能成为最优决策，可以排除掉，及时出队。

因为每个元素只入队一次、出队一次，所以均摊是 $O(N)$ 的。

针对常见的情况，对于单调队列的适用场景、更通俗的说法是，DP 转移来自一个滑动的区间（一般是定长的）。

当区间长度恒定为 $k$ 时，方程如下：

\[f(i) = \max_{i-k \leq j\leq i-1} { \{ f(j) + b(j) \} } + a(i)\]

定长滑动窗口最值问题，就是其一种特殊情况：

\[f(i) = \max_{i-k \leq j\leq i-1} { f(j) }\]

常用模板

代码实现上，有三个动作点，实际应用中顺序可能稍有不同：

  1. 维护队尾：保证单调性，及时排除不可能成为最优的决策。

    这一点和单调栈一样，逼迫队内不符合单调性的元素从队尾出队，然后再推入新元素到队尾。

  2. 维护队头：保证队内元素满足某种限制（比如区间的长度），确保决策集的合法性。
  3. 计算点：答案计算过程。

以单调递增队列为例，一般代码模板如下：

deque<int> q;

for (auto x : a) {
    // 维护队尾
    while (!q.empty() && q.back() > x) q.pop_back();
    q.push(x);
    // 维护队头
    while (!q.empty() && !check(q.front())) q.pop_front();
    // TODO: 计算点一般在这里，取队头最优决策来转移 DP
}

此外，队列中可以存元素值本身，常用的形式还有存下标。

一些题目

滑动窗口最大值

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。 你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。 返回 滑动窗口中的最大值 。

-- 来自 leetcode 100

单调队列的模板题，不再赘述，见 场景和原理 部分的通用分析。

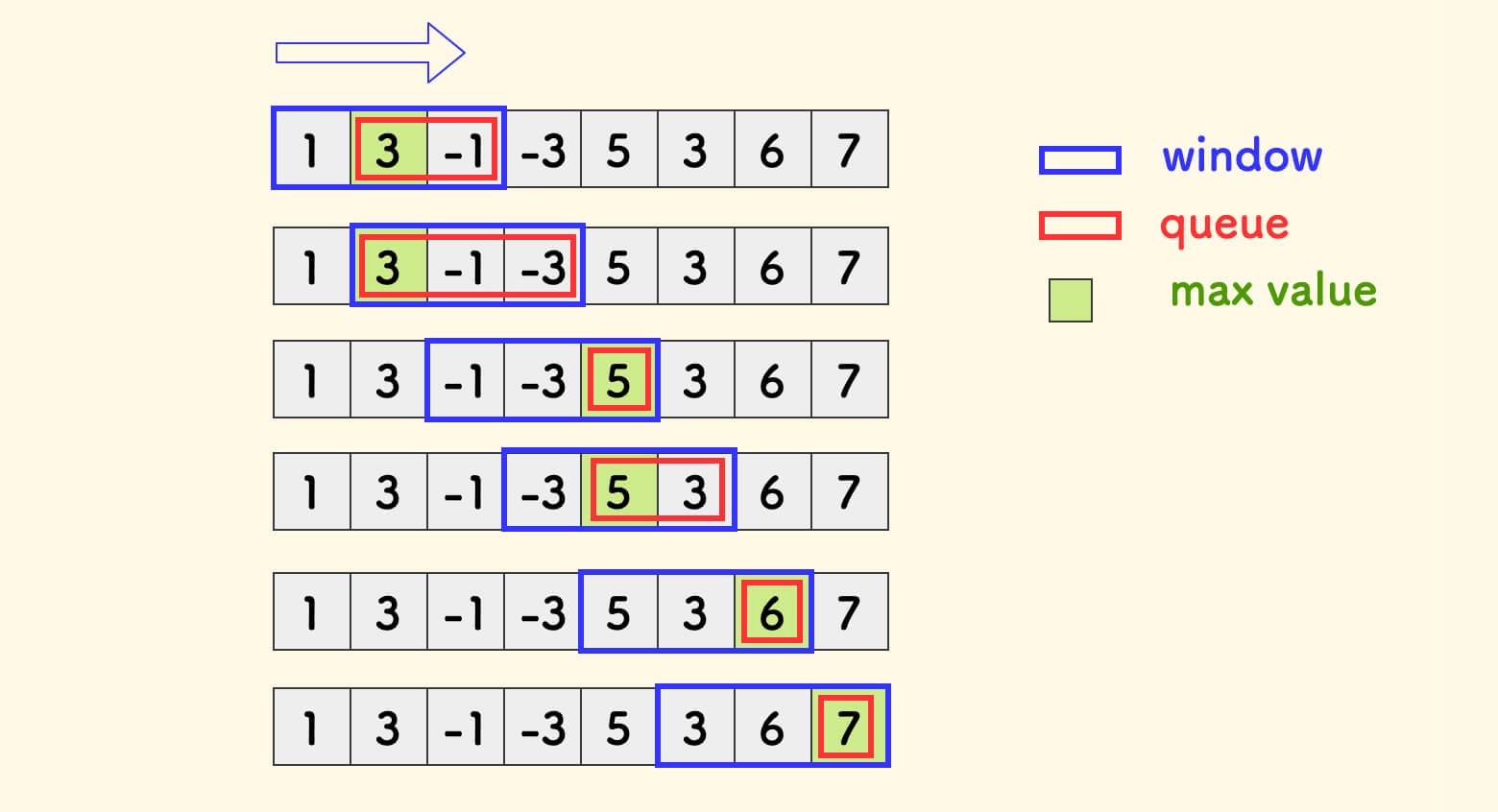
由于求最值，所以采用单调递减队列。

由于要检查窗口长度，所以队列中存储下标。

代码实现如下：

滑动窗口最大值 - C++ 实现
class Solution {
   public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        vector<int> ans;
        deque<int> q;  // 单调递减队列，存储元素下标

        for (int i = 0; i < nums.size(); i++) {
            // 维护队尾
            while (!q.empty() && nums[q.back()] < nums[i]) q.pop_back();
            q.push_back(i);
            // 维护队头
            while (!q.empty() && q.front() + k <= i) q.pop_front();
            // 取队头为最大值
            if (i >= k - 1) ans.push_back(nums[q.front()]);
        }

        return ans;
    }
};
带限制的子序列和

给你一个整数数组 nums 和一个整数 k，请你返回 非空 子序列元素和的最大值，子序列需要满足： 子序列中每两个 相邻 的整数 nums[i] 和 nums[j] ，它们在原数组中的下标 i 和 j 满足 i < j 且 j-i <= k。

数组的子序列定义为：将数组中的若干个数字删除（可以删除 0 个数字），剩下的数字按照原本的顺序排布。

-- 来自 leetcode 1425

简而言之，在数组中找一个（可以不连续的）子序列，满足其中相邻元素距离不超过 k，使得子序和最大。

比如下方图中的数组，限制 k=2 的情况下，最优解是绿色部分：

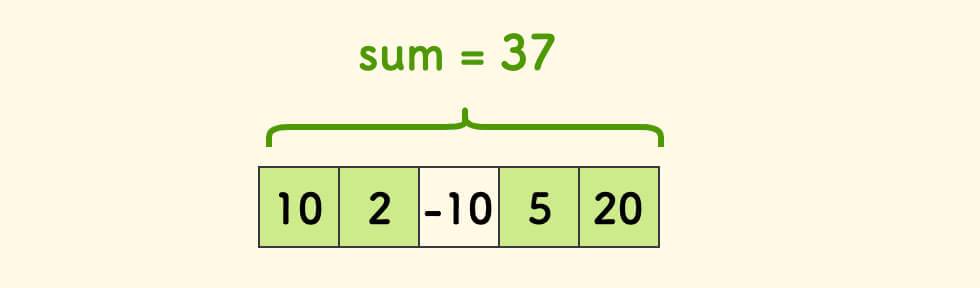
为方便起见，原数组简写作 $a_i$。

从动态规划入手，定义 $f(i)$ 为以 $a_i$ 结尾的带限制的最大子序和。

考虑如何推导 $f(i)$，可分为两种情况（注意 $f(i)$ 的定义，必须选择 $a_i$ 本身）：

  1. 不基于前面的选择，也就是只选择 $a_i$，此时 $f(i) = a_i$。

  2. 基于前面的最优情况，相邻元素的距离不得超过 $k$，所以转移只能来自区间 $[i-k, i-1]$ ：

    \[f(i) = \max_{i-k\leq j \leq i-1} {f(j)} + a_i\]

两种情况取最大者。

从 DP 方程上看，第 2 点是典型的单调队列场景：

  1. 要求最大值，所以采用单调递减队列。
  2. 队列按 $f(i)$ 单调递减。
  3. DP 转移来自一个定长区间，所以单调队列存储下标。

最后，用一个变量 ans 来追踪所有 $f(i)$ 中最大的即为答案。

代码实现如下：

带限制的子序列和 - C++ 实现
class Solution {
   public:
    int constrainedSubsetSum(vector<int>& nums, int k) {
        int n = nums.size();
        int f[n];
        deque<int> q;  // 存储下标, 按 f 单降
        q.push_back(0);

        // f[i] 表示以 a[i] 结尾时的序列的最大和
        f[0] = nums[0];
        int ans = f[0];  // 要求非空序列，所以最开始必须选 a[0]

        for (int i = 1; i < n; i++) {
            // 维护队头合法性
            while (!q.empty() && q.front() + k < i) q.pop_front();

            // 不基于前面的, 只选择 a[i]
            f[i] = nums[i];
            // 基于前面的, 选择 f[j] + a[i], 队头为最优决策点
            if (!q.empty()) f[i] = max(f[i], f[q.front()] + nums[i]);

            ans = max(ans, f[i]);

            // 维护单调递减性质
            while (!q.empty() && f[q.back()] < f[i]) q.pop_back();
            q.push_back(i);
        }
        return ans;
    }
};
跳跃游戏

给你一个下标从 0 开始的整数数组 a 和一个整数 a 。

一开始你在下标 0 处。每一步，你最多可以往前跳 k 步，但你不能跳出数组的边界。也就是说，你可以从下标 i 跳到 [i + 1，min(n - 1, i + k)] 包含 两个端点的任意位置。 你的目标是到达数组最后一个位置（下标为 n - 1），你的 得分 为经过的所有数字之和。

请你返回你能得到的 最大得分。

-- 来自 leetcode 1696

这个题不能用贪心来做，因为有反例： [0,-1,-2,-3,1]，且 k=2 时，最优得分应该是 -1 而不是 -2。

假设 $f(i)$ 表示跳到位置 $i$ 处的最优得分，那么推导其转移来自于定长区间：$[i-k,i-1]$。

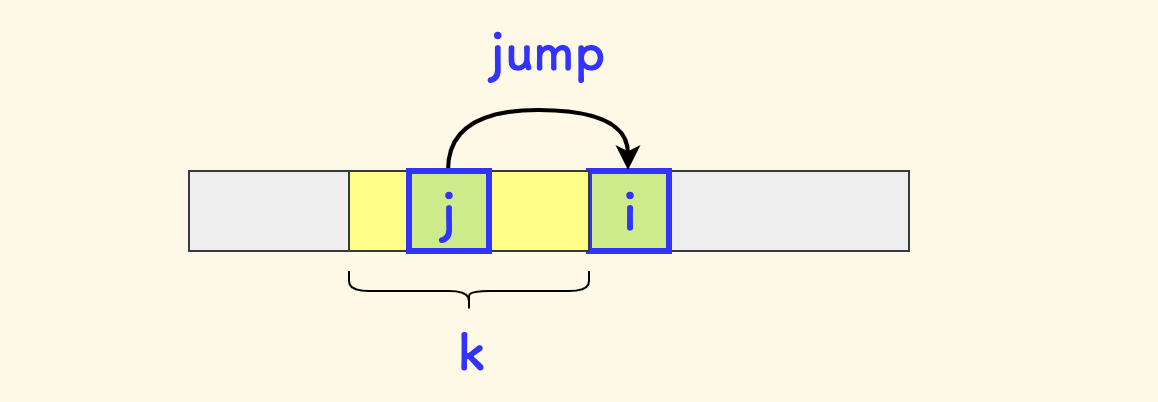
所以 dp 方程如下：

\[f(i) = \max_{i-k \leq j \leq i-1} { \{ f(j) + a_i \} }\]

因为 $a_i$ 和 $j$ 无关，可以移出来，也就是：

\[f(i) = \max_{i-k \leq j \leq i-1} { f(j) } + a_i\]

转移来自定长区间，是典型的 单调队列优化 dp 的场景：

  • 因为求最大值，所以采用单调递减队列，最大值在队头。
  • 存在区间定长限制，则需要存储下标，而不是元素值。
  • 根据 DP 方程，单调队列要按 $f(i)$ 递减。

仍然是三种操作，维护队头、队尾 和 计算点，不过顺序要稍微调，代码实现如下：

跳跃游戏 VI - C++ 代码
class Solution {
   public:
    int maxResult(vector<int>& a, int k) {
        int n = a.size();
        int f[n];      // 跳到 i 处的最高分数是 f[i]
        deque<int> q;  // 按分数递减, 存储下标
        for (int i = 0; i < n; i++) {
            // 维护队头
            while (!q.empty() && q.front() + k < i) q.pop_front();
            // 计算得分
            f[i] = (q.empty() ? 0 : f[q.front()]) + a[i];
            // 维护队尾
            while (!q.empty() && f[q.back()] < f[i]) q.pop_back();
            q.push_back(i);
        }
        return f[n - 1];
    }
};
限制和的最短子数组

给你一个整数数组 nums 和一个整数 k ，找出 nums 中和至少为 k 的 最短非空子数组 ，并返回该子数组的长度。

如果不存在这样的 子数组 ，返回 -1 。

子数组 是数组中 连续 的一部分。

-- 来自 leetcode 862. 和至少为 K 的最短子数组

这个题目稍有不同，不再限制定长窗口，而是限制区间和的下界，然后求最短区间长度。

因为数组可能包含负数，前缀和没有单调性，所以无法采用简单的双指针做滑窗的思路，这个题目的通过率很低。

先求出原数组的前缀和数组 S[i]，这样问题即转化为：

寻找 S 数组中满足 S[i]-S[j] >= k 的两个元素 (i > j)，使得 i-j 尽可能的小。

我们称满足差值限制的下标对 (i,j) 为一组方案，目标就是找到 i-j 最小的最优方案。

主思路是，对于每一个 j，尝试找右侧的 i 来形成一组方案。

下图中，假设 j1 < j2 且 S[j1] >= S[j2]，那么：

如果在右边存在一个 i 可以和 j1 形成一组方案，那么 (i,j2) 会是更优的方案。

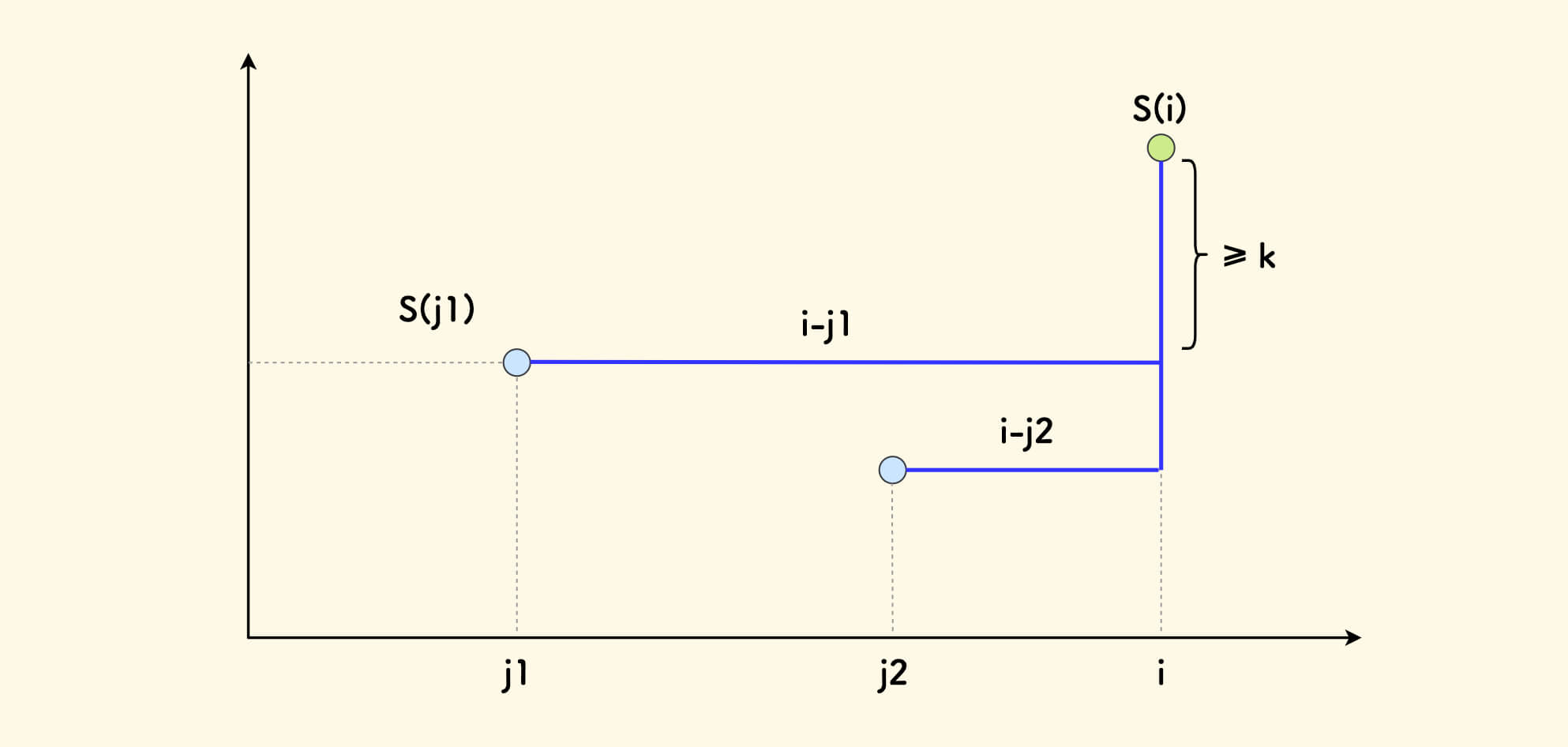
原因是：

  1. 因为 S[j1] >= S[j2] 且 S[i]-S[j1] >= k，那么肯定有 S[i]-S[j2] >= k，也就是 (i,j2) 也能形成一组可行方案。
  2. 而且 j2 在 j1 的右边，更靠近 i，肯定 i-j2 比 i-j1 更小，也即是 (i,j2) 这组方案比 (i,j1) 更优。

简而言之，遇到右侧更小的前缀和，可直接舍弃左边更大的。

另外，从左向右，对于每一个左边的 j，一旦在右侧找到可行方案 (i,j)，那么就不必再向右给它找了，因为要让 i-j 尽可能地短。

综合这两点，可以采用单调队列来求解：

  1. 用单调递增队列存储前缀和 S[i]。
  2. 队头维护：对于队内的每个 j，一旦和当前扫描的 i 形成可行方案，即可出队。
  3. 队尾维护：对于队内的每个 j，如果当前扫描的 i 满足 S[i] <= S[j]，那么可以舍弃 j。 相当于 i 作为一个更优候选者，逼迫 j 出队。同时维护了队列的单调性。

在第 2 点中，出队前记录下 i-j 的值，和答案取最小。

代码实现如下：

至少为 k 的最短子数组 - C++ 实现
class Solution {
   public:
    int shortestSubarray(vector<int>& nums, int k) {
        int n = nums.size();

        // 先求前缀和, 第一项是 0
        vector<long> sums(n + 1, 0);
        for (int i = 1; i < n + 1; i++)
            sums[i] = sums[i - 1] + nums[i - 1];

        // 递增队列, 队列左端留住最小的
        deque<int> q;

        int ans = n + 1;

        for (int i = 0; i < n + 1; i++) {
            // 维护队头：一旦找到一个可行方案，即可出队，并记录给答案
            while (!q.empty() && sums[i] >= sums[q.front()] + k) {
                ans = std::min(ans, i - q.front());
                q.pop_front();
            }
            // 维护队尾：弹出更大的, 留住更小的
            // 队内更大的左侧的 j 已经不可能成为最优方案
            while (!q.empty() && sums[q.back()] >= sums[i])
                q.pop_back();
            q.push_back(i);
        }
        return ans > n ? -1 : ans;
    }
};

这个问题是一种非典型的单调队列的应用，如果用 DP 的方式去思考，应该并不会特别容易。

有趣的是，它的答案计算点是在队头出队之时。

选择数字

给定一行 $n$ 个非负整数 $a_1,…,a_n$。现在你可以选择其中若干个数，但不能有超过 $k$ 个连续的数字被选择。你的任务是使得选出的数字的和最大。

-- 来自 洛谷 P2034 选择数字

从这个问题的描述来看，是一种最优化 DP 问题，转移来自一个定长滑动区间，可以说一眼单调队列。

定义 $f(i)$ 为以前 $i$ 个元素的满足要求的最优答案。

预处理一下，构造前缀和数组 $s(i)$。

当 $i <= k$ 时，是显然的，直接全部选择即可。也就是说，此时的答案就是前缀和 $s(i)$。

当 $i > k$ 时，就无法全部选择了，分为两种情况：

  1. 不选 $a_i$，此时直接沿用上一次的答案，即 $f(i) = f(i-1)$。

  2. 选择 $a_i$，由于不可选择超过 $k$ 个连续的数字，所以，区间 $[i-k,i-1]$ 上必须要排除至少一个数字。

    因为，数列中都是非负整数，所以，肯定只需要排除一个数字。

    此时的 $f(i)$ 的推导可以参考下图，最优决策点 $j$ 来自蓝色的定长区间，它右侧是连续的。

    推导方程是：

    \[f(i) = \max_{i-k \leq j \leq i-1} {\{ f(j-1) + (s(i) - s(j)) \}}\]

    因为 $s(i)$ 和 $j$ 无关，可以进一步变化为：

    \[f(i) = \max_{i-k \leq j \leq i-1} {\{ f(j-1) - s(j) \}} + s(i)\]

    因此，不妨设函数 $g(i) = f(i-1) - s(i)$，一同来维护。

    由于转移来自一个滑动区间，典型的单调队列场景。

    要求的 DP 是最大值，所以采用单调递减队列，按 $g(i)$ 的函数值来递减。

    队头和队尾的细节操作，不再赘述。

两种情况取最大值即可。

最终的 $f(n)$ 即是答案。

P2034 选择数字 - C++
using ll = long long;
const int N = 100005;

ll a[N], f[N], s[N], g[N];
int n, k;

ll solve() {
    // 计算前缀和
    s[0] = 0;
    for (int i = 1; i <= n; i++) s[i] = s[i - 1] + a[i];

    f[0] = 0;
    // g[i] = f[i-1] - s[i]
    g[0] = 0;

    // 维护 [i-k, i-1] 区间上的 g 的单调递减队列, 存储下标
    deque<int> q;

    for (int i = 1; i <= n; i++) {
        // 维护队头
        while (!q.empty() && q.front() + k < i) q.pop_front();
        // 推导 dp
        if (i <= k)  // 前 k 个的答案就是前缀和
            f[i] = s[i];
        else {                // 两种情况
            f[i] = f[i - 1];  // 不选 a[i]
            // 选 a[i],但是要排除 [i-k,i-1] 内的一个 j
            if (!q.empty()) f[i] = max(f[i], g[q.front()] + s[i]);
        }
        // 维护队尾
        g[i] = f[i - 1] - s[i];
        while (!q.empty() && g[q.back()] < g[i]) q.pop_back();
        q.push_back(i);
    }
    return f[n];
}

简单总结

  1. 单调队列在结构上就是一个单调栈加上一个可收缩的队头。
  2. 单调队列的主要使用场景，是优化一类决策区间滑动的 DP 的转移，比如滑动窗口最值问题。
  3. 单调队列的代码三个动作点：维护队尾、维护队头、计算答案，三者的位置顺序视情况而定。

（完）

更新日志:

  • 评论区 liuzimingc 指正 typo：限制和的最短子数组 应该是 i > j 而不是 i < j, 已修改。

相关阅读：

本文原始链接地址： https://writings.sh/post/monotonic-queue

王超 · 2024 年 1 月
原创文章，未经允许，不得转载
微信扫码赞赏
评论 首页 | 归档 | 算法 | 订阅