本文是我实现四叉树 (quadtree) 的一个 C++ 库的开发笔记。
项目的 repo 地址: https://github.com/hit9/quadtree-hpp
四叉树是 2D 平面上划分空间的一种数据结构,它可以更快速的回答「平面上一个位置附近有哪些对象」的问题, 常用于优化碰撞检测。
大概长这个样子,下图中,黑色方格是四叉树管理的对象,整个区域根据某种条件被不断四分。 然后我们可以选中一个矩形区域在这颗树上快速地查询命中的对象有哪些。

四叉树不止可以工作在正方形的区域上,也可以在长方形的区域上:
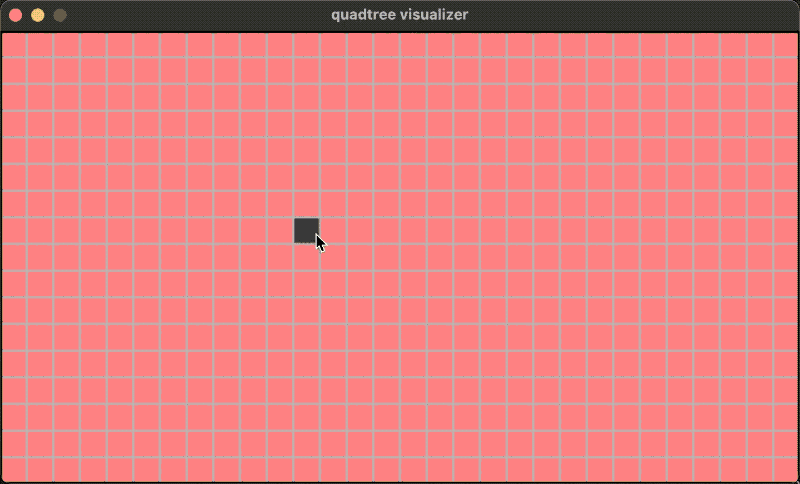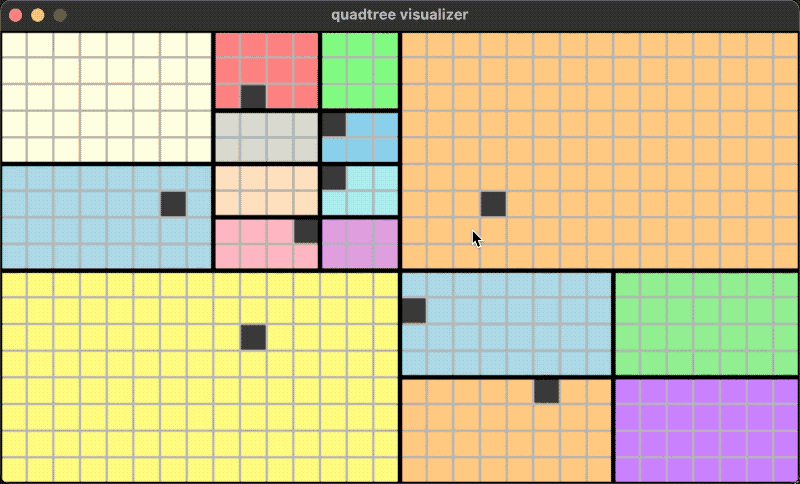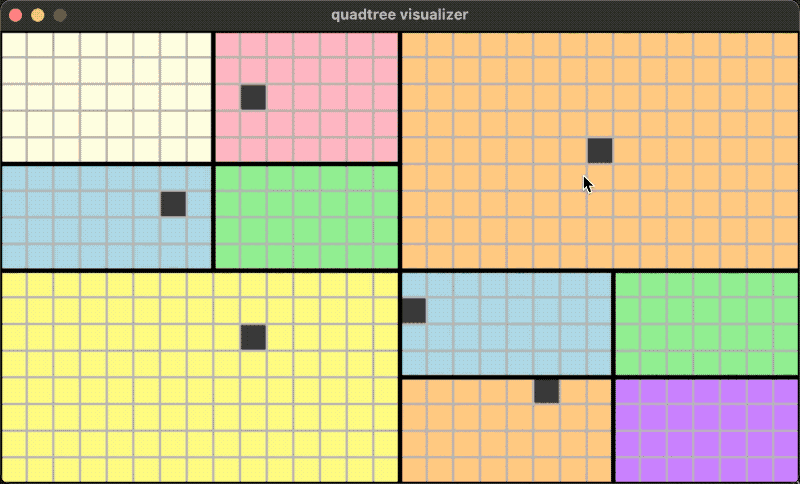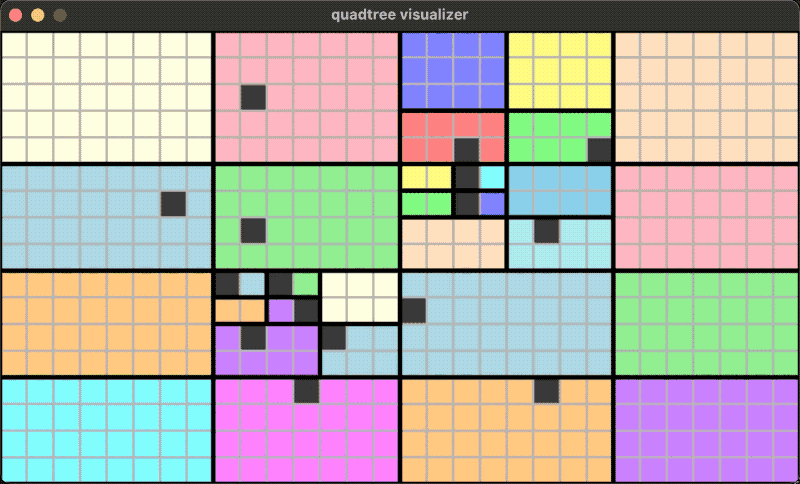
接下来,是对四叉树的实现思路的一些笔记。
分裂 ¶
首先,根节点管辖整张地图,然后,满足条件的情况下,将地图四等分,如果条件仍然满足,则继续下一层的四分,直到叶子节点管辖的区域不再可划分为止。
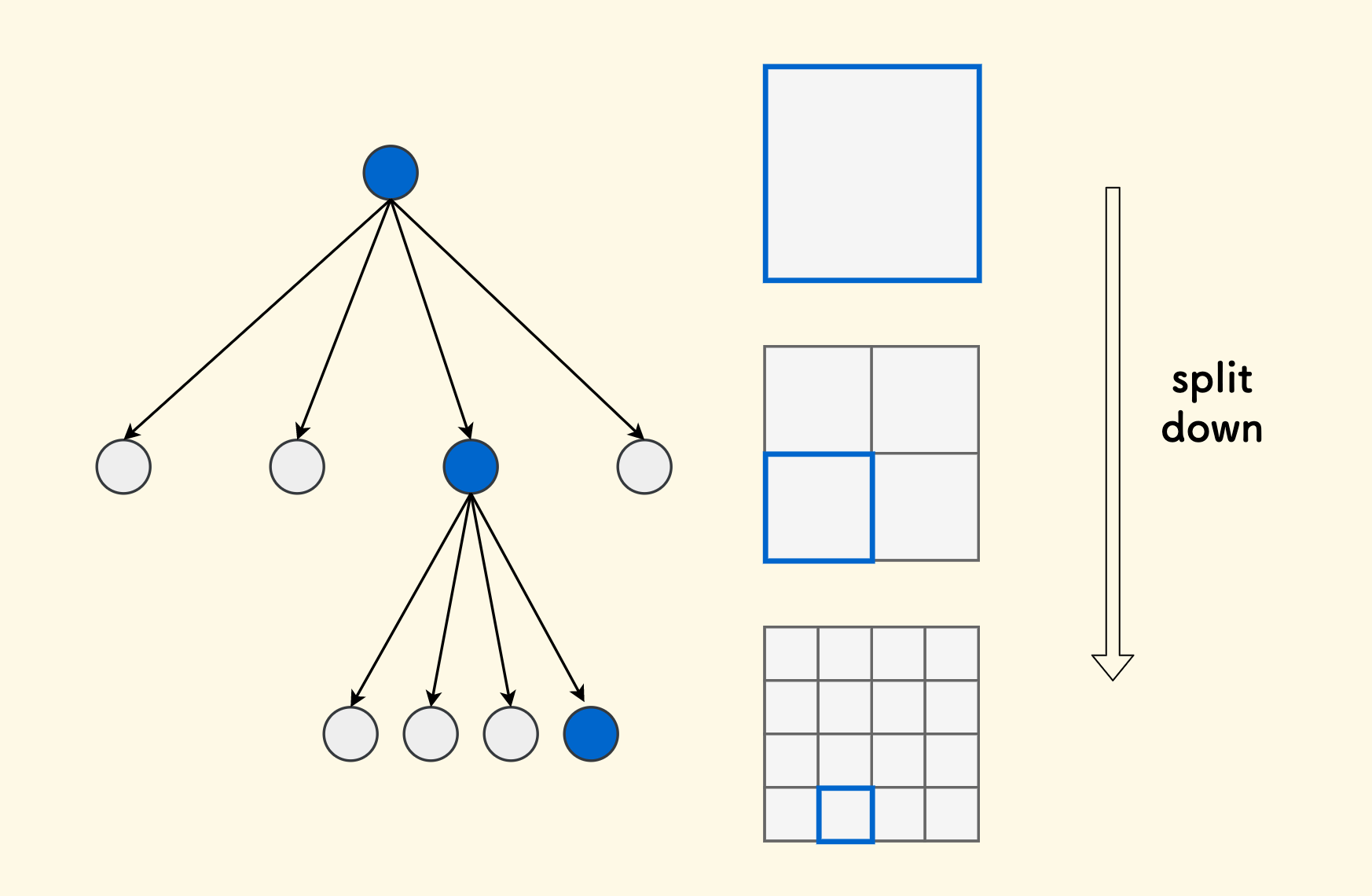
停止分裂的条件可以是,一个矩形内的对象数量不超过某个值,或者一个矩形不要太大 之类的,这个看具体需要。 在 leetcode 上有一个题目 leetcode 427. 建立四叉树,可以拿来练习四叉树的分裂过程, 它的划分条件是,不断四分直到每一个方格内要么全是 $1$、要么全是 $0$。
我设计了一个函数来允许自定义这个条件,比如说下面的四叉树,建立在 $100 \times 100$ 大小的网格地图上,它停止分裂的条件是, 要么叶子节点的矩形小到 $2 \times 2$ 了,要么叶子矩形内的对象数量不超过 $3$ 了。
SplitingStopper ssf = [](int w, int h, int n) {
return (w <= 2 && h <= 2) || (n <= 3);
};
Quadtree<int> tree(100, 100, ssf);
当添加一个对象到一个位置 $(x,y)$ 时,我们要先确定这个位置归属的叶子节点,把对象加到这个叶子节点的管理区内。现在它有可能变地「不稳定」了,所以要测试一下分裂条件, 尝试向下递归分裂,直到不再满足分裂条件。
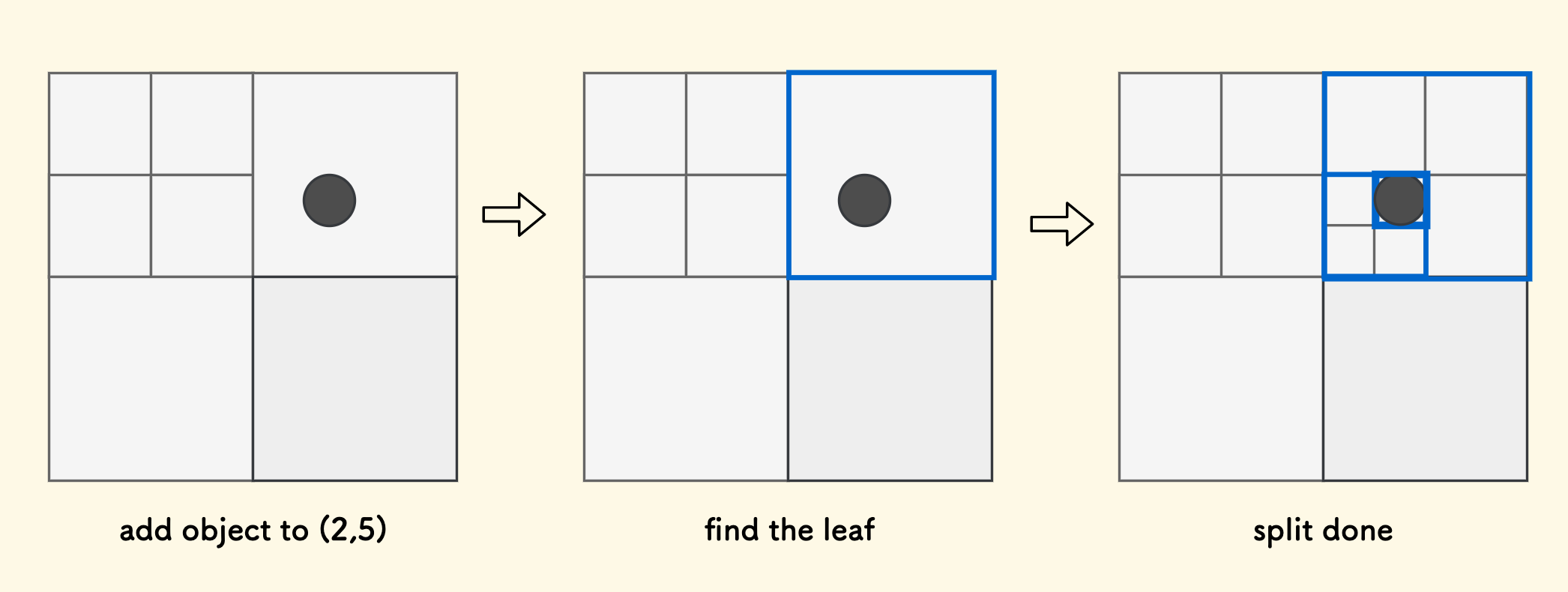
这里留一个线索,如何根据位置坐标,快速定位到其归属的叶子节点呢?后面会讲到,它是一个关键的优化。
合并 ¶
反过来,如果一个非叶子节点不再满足「可分裂」的条件了,也就是说,它原本的划分现在变的太细了,那么可以从叶子节点开始,向上合并回去。
比方说,移除一个对象之后,叶子节点空了,向上来看,叶子节点的父节点内也变地「空旷」了,那么,可以考虑把叶子节点和其兄弟叶子节点,一并释放掉,然后把它们剩余的管辖的对象还给父节点, 这个过程就是合并。
具体来说,要把位于 $(x,y)$ 处的对象从树上移除,先要定位到这个位置归属的叶子节点,然后把它从叶子节点管辖的对象列表中移除。 在此之后,观察下叶子节点的父节点,它可能变地「空旷」了,也就是说它可能自身可以退化成为一个叶子节点,则把其孩子节点都释放掉。如此向上递归,直到不可再合并为止。
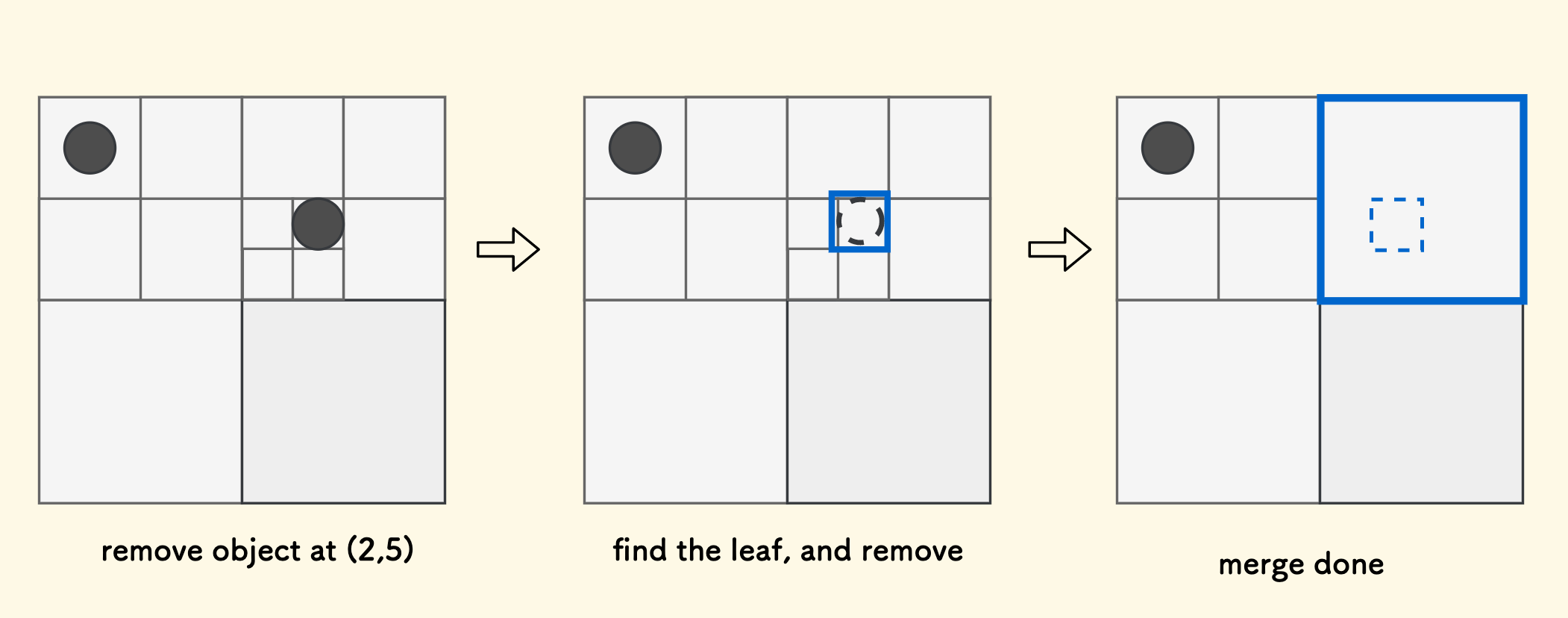
在我的实现中,终止合并的条件,就是终止分裂的相反条件。一个节点不可合并,就是它可以保持在「可以分裂」的状态。仍然由函数 ssf 来指定。
但是,合并也依赖一个操作,怎么快速地根据位置定位到叶子节点呢?后面会讨论到。
在我们实现了「分裂」和「合并」两个能力后,这颗四叉树就有了动态调整的能力了, 添加和移除对象完全不必整颗树重建,而只需要从叶子节点向下或向上地局部调整就可以了。
重新审视终止条件 ¶
但是,我们需要确认一个问题:只有添加对象的时候,才会引起分裂吗?或者另一个对偶问题:只有移除对象的时候,才会引起合并吗?
其实并非如此,关键要看终止分裂条件的 ssf 函数怎么设计的。
举一个例子,我们希望叶子节点在下面的任一情况成立时终止分裂:
- 节点内没有任何管理的对象
- 节点内每一个方格都是对象
这种条件十分适合地图中的固定障碍物的管理(地形、建筑等),四叉树可以把完全空旷的、和完全都是障碍物的地方不重叠地放到不同的叶子中去。
用函数来表达这种策略:
SplitingStopper ssf = [](int w, int h, int n) {
return (n == 0) || (n == w * h);
};
这样可能发生:
- 当添加一个对象时,有可能一个大的矩形正好放满了,引起合并。
- 当移除一个对象时,有可能一个满的大矩形变的不满了,引起分裂。
一个运行的效果如下图:
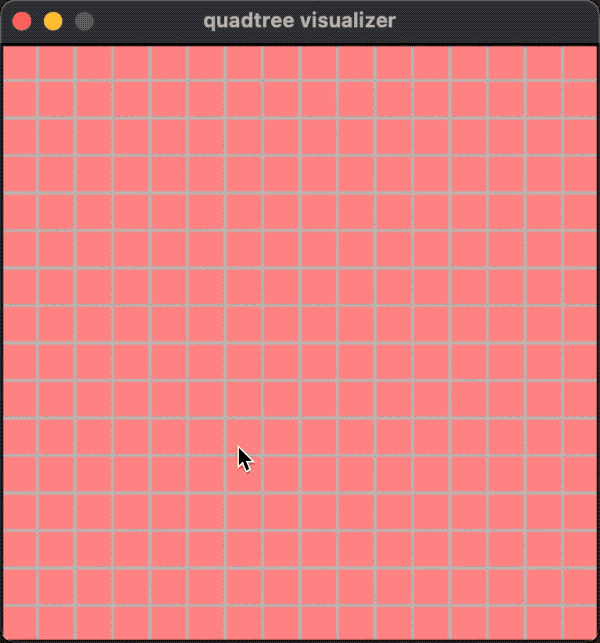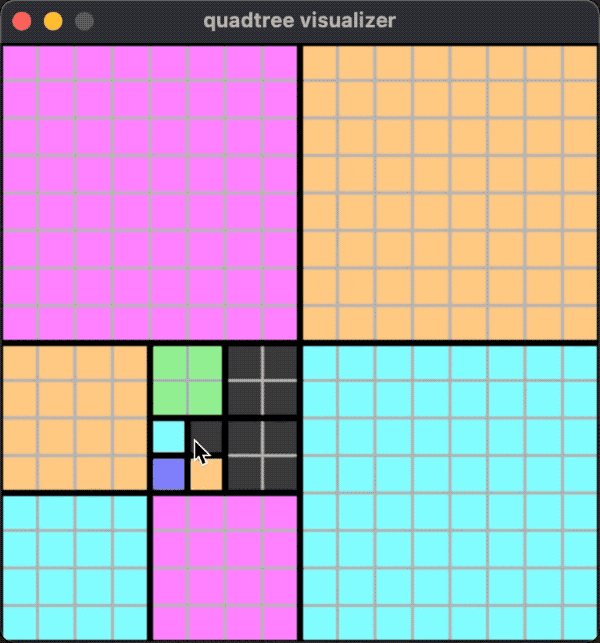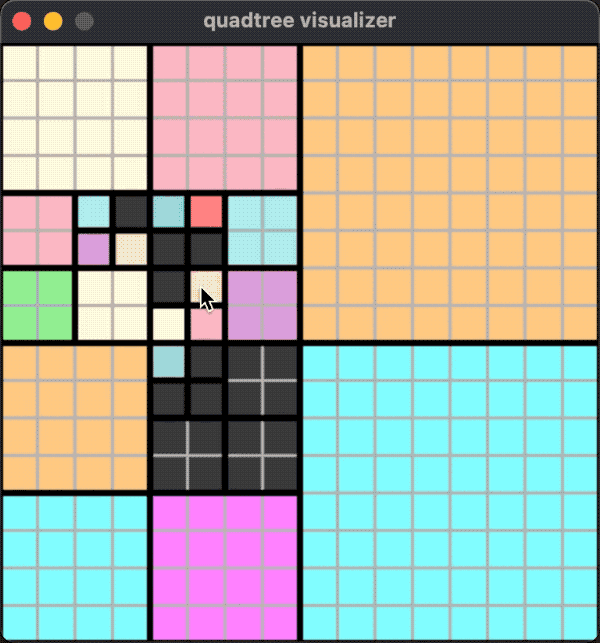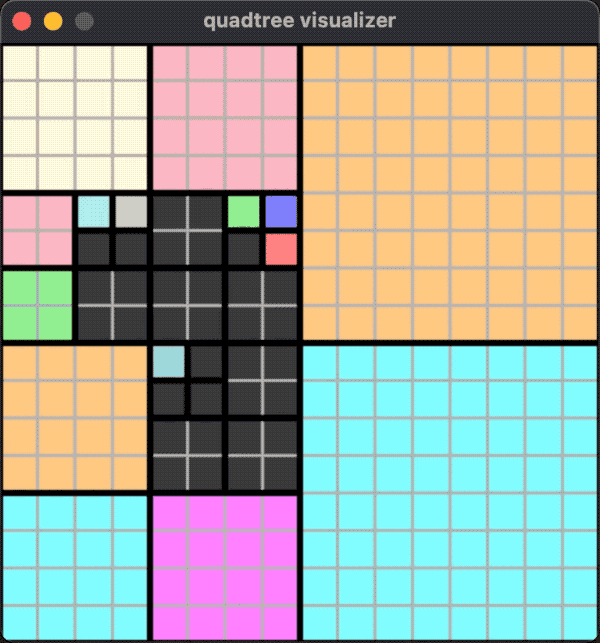
这种情况下,不论是添加还是移除对象,分裂和合并都有可能发生。
但是,我们的设计中,用户定义的条件必须稳定,也就是说保证 分裂和合并的条件不会同时成立,一定是时刻相反的。
在我的实现中,添加或者移除对象时,都会去尝试分裂或者合并,但是 二者最多只发生一个。
// 添加对象时, 先尝试分裂,否则尝试合并
trySplitDown(node) || tryMergeUp(node);
// 移除对象时,先尝试合并,否则尝试分裂
tryMergeUp(node) || trySplitDown(node);
区域查询 ¶
给定一个矩形区域,其左上角是 $(x1,y1)$, 右下角是 $(x2,y2)$,如何查询出来它选中的所有对象呢? 比如说下面的图示中,命中选中的绿色框矩形区域内的对象有 b 和 c,但不包括 a。
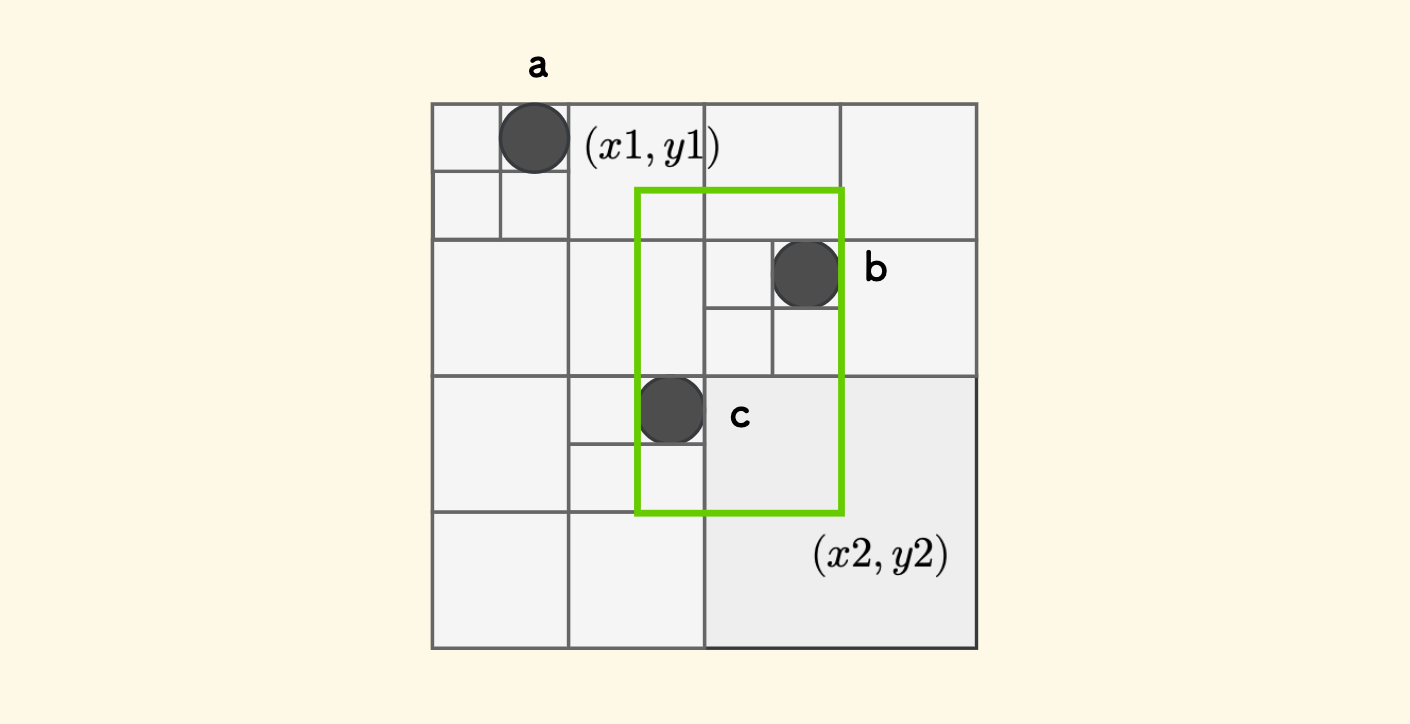
思路也很简单,从根节点开始,不断「判重叠」。 如果当前节点管理的矩形 和 查询区域的矩形存在交叉重叠,那么:
- 如果当前节点是叶子节点,直接收集位于查询区域范围内的对象就可以了。
- 否则,如果当前是非叶子节点,那么向下继续判断其子节点,递归进行下去。
如果没有重叠的话,就不必向下递归了。
整个过程如下图所示:
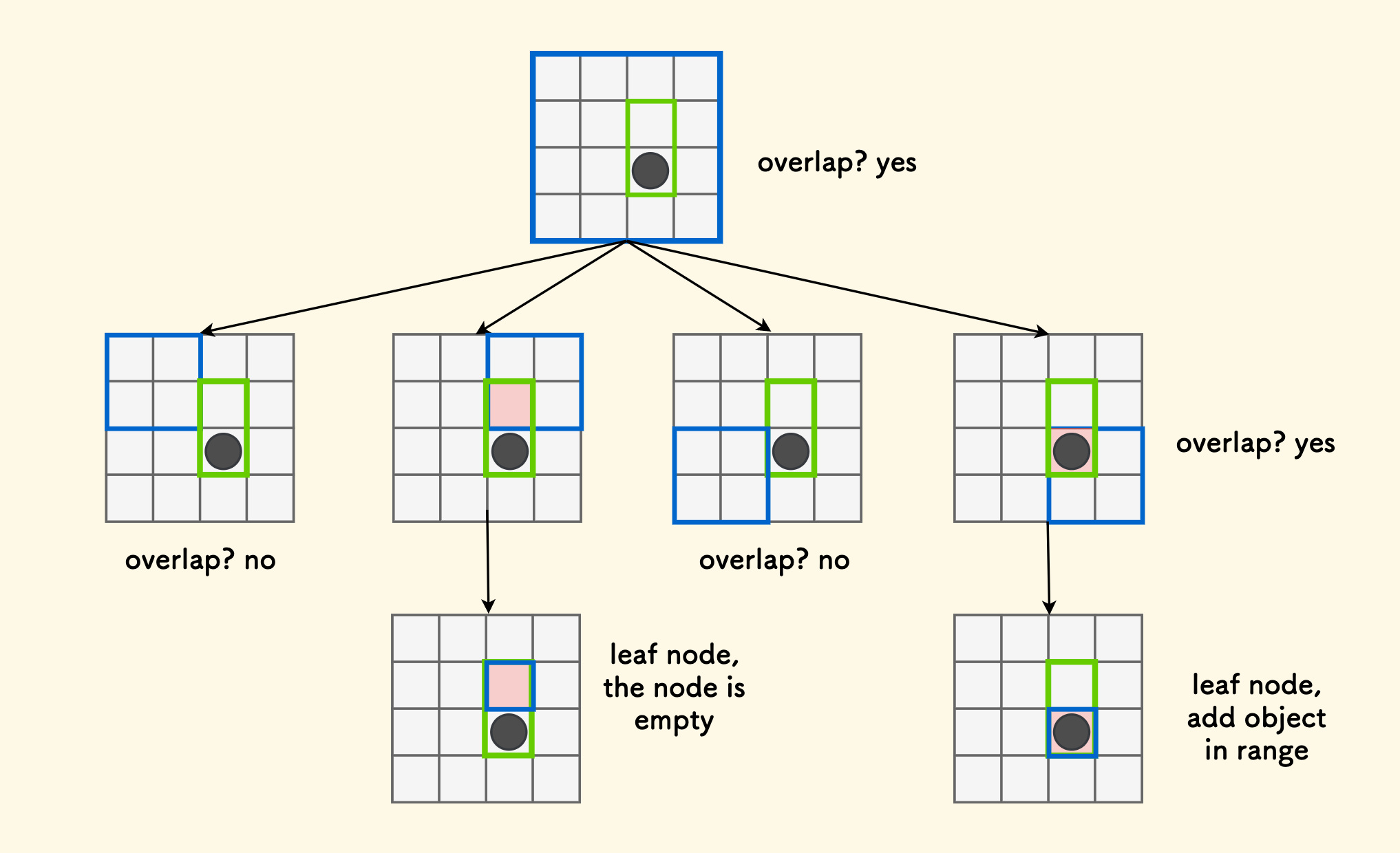
那么,如何判断两个矩形是否存在交叉呢?采用简单的 AABB 算法就可以了,参考另一篇文章 AABB 检测平面矩形重叠,这只需一行代码。
分裂的细节 ¶
先看下分裂的细节过程,假设当前节点管辖的区域,左上角是 $(x1,y1)$,右下角是 $(x2,y2)$,那么:
- 找到 $x$ 轴的中点位置 $x1 + (x2-x1)/2$, 定义为 $x3$
- 找到 $y$ 轴的中点位置 $y1 + (y2-y1)/2$,定义为 $y3$
注意,其中除法是向下取整, 坐标从 $0$ 开始算。
也就是,$x$ 轴和 $y$ 轴都进行二分, 那么,这个中心点的位置在哪里呢?这要分一下奇偶性来看。下面是 $4 \times 4$ 和 $5 \times 5$ 两种规格的示意图:
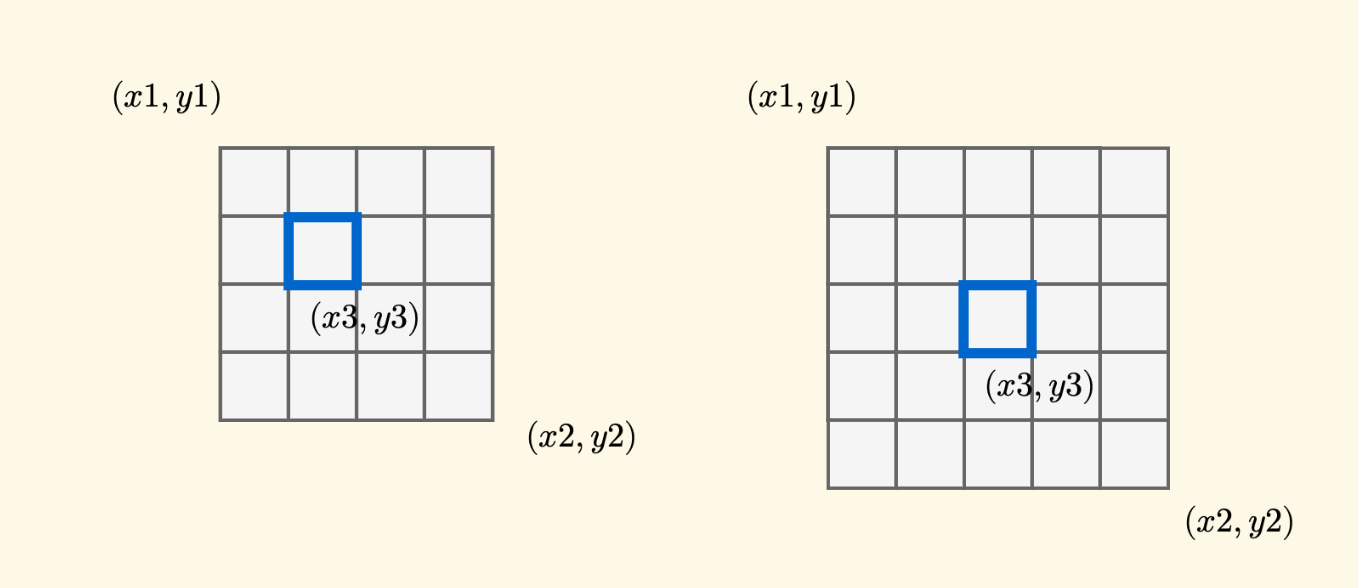
但是,无论奇偶,规律是统一的,中心方格 $(x3,y3)$ 一定位于最中心位置的方格,如果这个地方没有方格,就是其偏左上一点的方格。
由于我们处理的是一个网格化的区域,在分裂后,一个单元格必须归属一个子矩形。
现在可以计算出来四分后的各个子矩形的坐标:
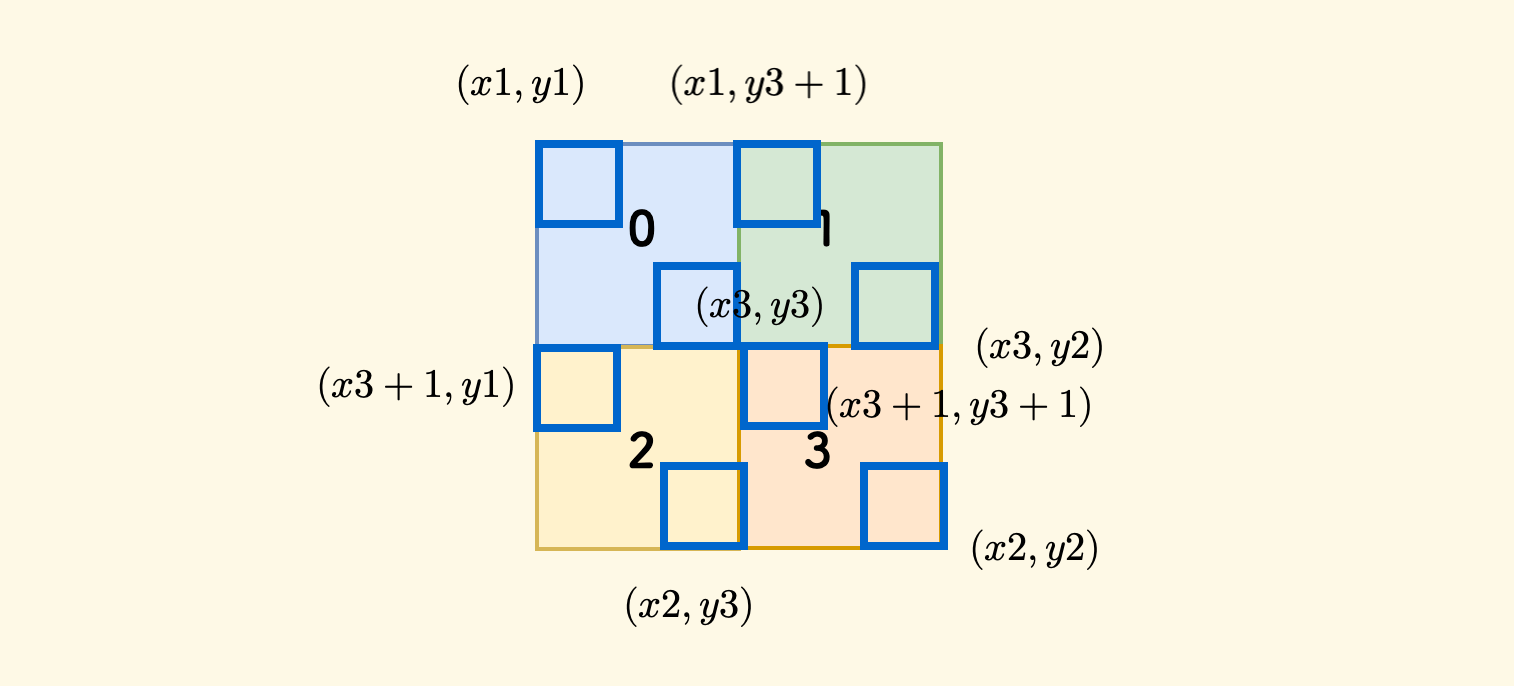
用代码来表示这四个小矩形的坐标和递归过程:
// * 号位置就是 (x3,y3)
// y1 y3 y2
// x1 -+------+------+-
// | 0 | 1 |
// x3 | * | |
// -+------+------+-
// | 2 | 3 |
// | | |
// x2 -+------+------+-
int x3 = x1 + (x2 - x1) / 2, y3 = y1 + (y2 - y1) / 2;
node->children[0] = split(d + 1, x1, y1, x3, y3);
node->children[1] = split(d + 1, x1, y3 + 1, x3);
node->children[2] = split(d + 1, x3 + 1, y1, x2, y3);
node->children[3] = split(d + 1, x3 + 1, y3 + 1, x2, y2);
一个重要的结论 ¶
但是,现在我们要对二分的细节继续优化!稍后即可看到好处。
对于选中的中点 $x3$ 和 $y3$ ,假设当前深度是 $d$,即将分裂的深度是 $d+1$,以 $x$ 轴为例, 我们考虑算式 $2^{d+1}x/h$ 在 $x1$ 和 $x3$ 处的取值是否相等,如果不相等,则 $x3$ 自减一,同理对 $y$ 轴。
uint64_t k = 1 << (d + 1);
if ((k * x3 / h) != (k * x1 / h)) --x3;
if ((k * y3 / w) != (k * y1 / w)) --y3;
通俗的讲,就是(以横向的 $y$ 轴为例):
默认地,选取的中点是给左边的,但是如果我们取的中点和左方的算式值不一致,那么就让中点给右边。
比如说,当 $w=50$ 时,在第 $5$ 轮的时候,会因为这个机制而选择右偏,而不是默认的左偏。
d
0 [0------------------------------------------------------------50]
1 [0--------------------------------24],[25---------------------50]
2 [0----------------12][13----------24]
3 [0--------6][7----12]
4 [0-3][4---6]
5 [4][56]
选用这种二分方式会带来一个好处,就是这样一种结论:
在 $[0,N-1]$ 区间上的 $N$ 个整数,不断如此二分。第 $d$ 轮二分后,整数 $x$ 会落在 $2^{d}x/N$ 个小区间上。
这里 $d$ 是从 $0$ 开始算的,区间的计数也是从 $0$ 开始算的。
这个结论可以快速验证一下,比如说 $N=5$ 的时候,测试下第 $2$ 轮时,$x=2$ 会落在 $2^{2}\times 2/5$ 即 $1$ 号区间上。
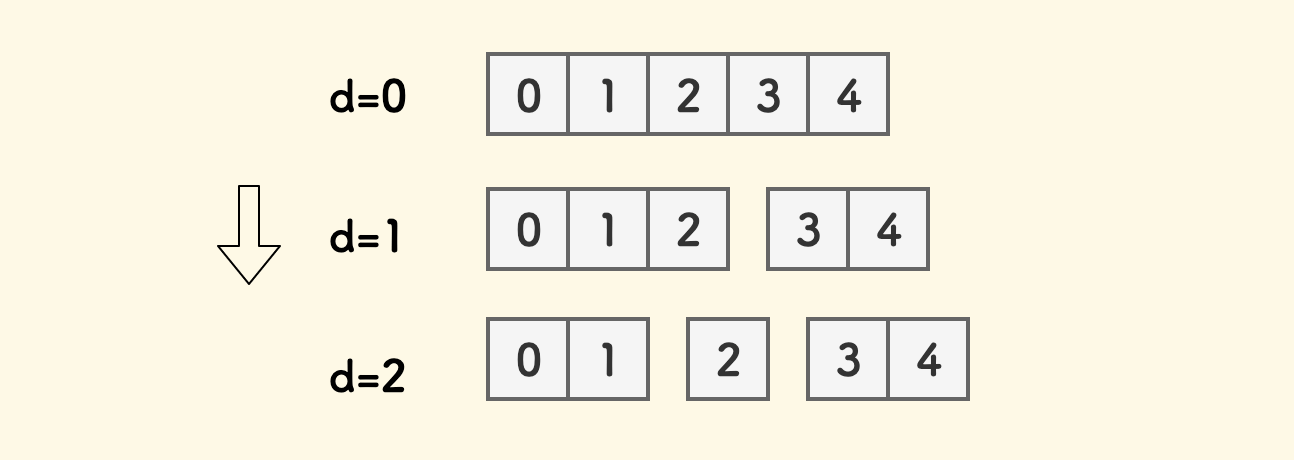
从数学的角度看,第 $d$ 轮的时候,均等划分了 $2^{d}$ 个小区间,每个小区间的长度是 $k=N/2^{d}$,那么整数 $x$ 就会落在第 $x/k$ 个小区间上,也就是 $2^{d}x/N$ 。
但是,在离散的整数区间上的二分,我目前还没有一个严格的证明(欢迎在评论区告诉我!)。但是测试下来它是正确的。
上面说的中点的修正的技巧,其实是在强行把分裂方式对齐到这个结论上。
分裂之前,原本的 $y1$ 和 $y2$ 都是落在第 $q$ 个小区间上;分裂之后呢,因为当前小矩形在 $y$ 轴上二分了, 所以,分裂后假设 $y1$ 落在第 $q1$ 个小区间上,那么 $y2$ 肯定落在 $q1+1$ 个小区间上。 那么中间一定有一个单元格发生了算式值增长的过渡,这个中点附近就是过渡点。那么我们检验一下这个中点, 根据它的实际算式值到底偏向哪一方来决定分裂后这个中点归属哪一方。这样以保证这个结论的正确性。
基于这个结论,我们可以得到二维的类似结论,只需要依次确定每一个轴就可以了。
对于位于第 $d$ 层的节点而言,其管辖区域内的任意一个位置 $(x,y)$,都有:
位置 $(x,y)$ 一定位于 $x$ 轴上第 $(2^{d})x/h$ 个、$y$ 轴上第 $(2^{d})y/w$ 个小矩形内。
这其中,$w$ 和 $h$ 分别是整个区域的宽和高,$d$ 是从 $0$ 开始算,计数也是从 $0$ 开始算。
此外需要注意的是我们的坐标系一直是 $x$ 轴是垂直向下,$y$ 轴是水平向右,左上角 $(0,0)$ 是坐标系原点。
下图是一个 $4 \times 5$ 网格上的示意图,绿色位置是 $(2,2)$,红色框指出了它在每一层节点中位于的小矩形:
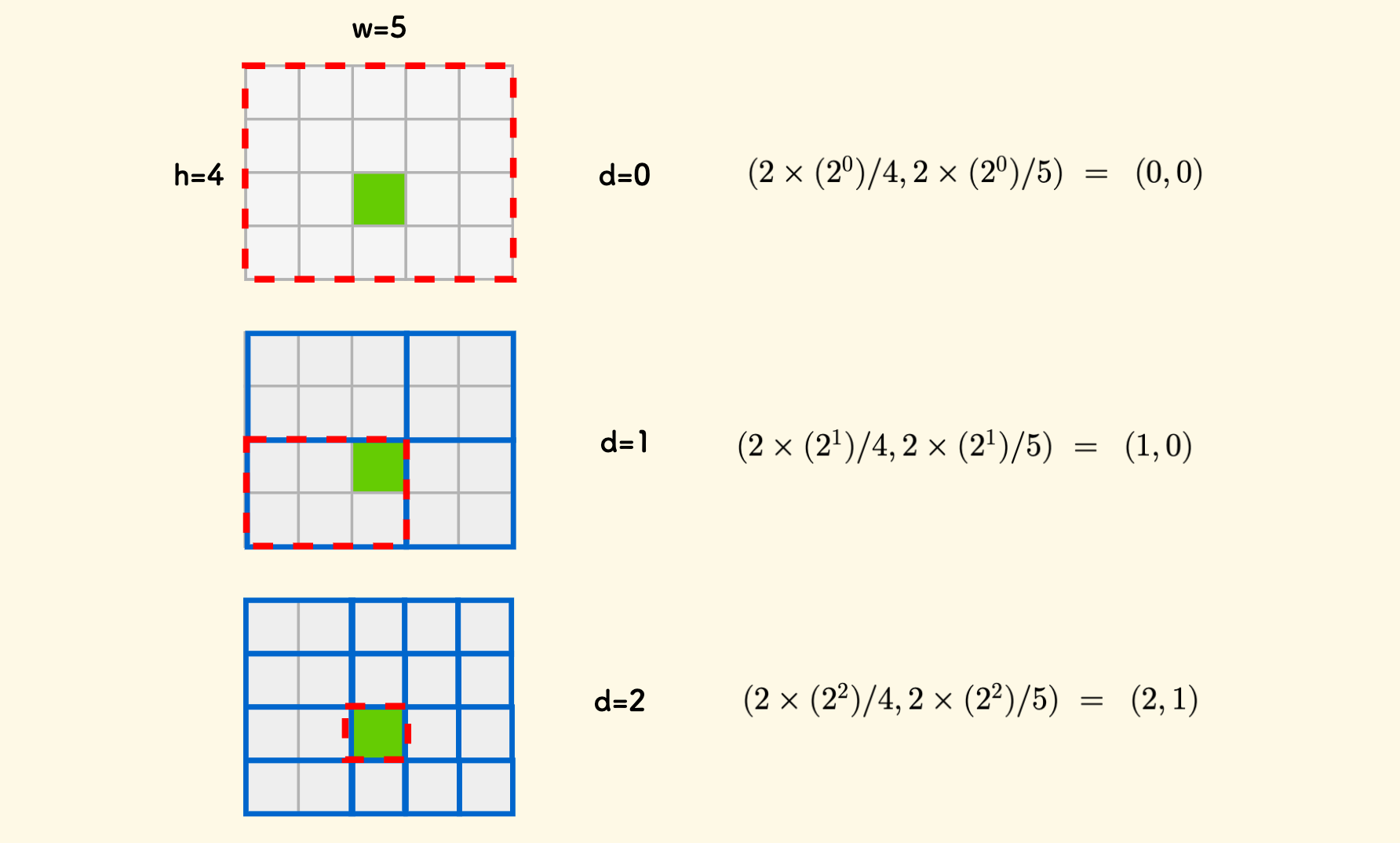
说的通俗一点,就是在每一个轴上,在当前层的分裂粒度下,按这个粒度的小矩形的边长,数到第几个小矩形。
谈到这里,如何快速定位一个位置归属的叶子节点,就呼之欲出了。
快速定位叶子节点 ¶
现在给每个节点设计一个 ID 标号,它由三元组 $(d, 2^{d}x/h, 2^{d}y/w)$ 构成,其中 $d$ 是此节点的深度(第几层)。 可以做一个哈希函数,将这个三元组映射成一个整数。
那么,可以知道的是:
对于节点管辖区域内的任意位置 $(x,y)$,计算出的 ID 都是一致的。
例如下图中,目标位置所在节点的 ID 就是 $(2,2,2)$。
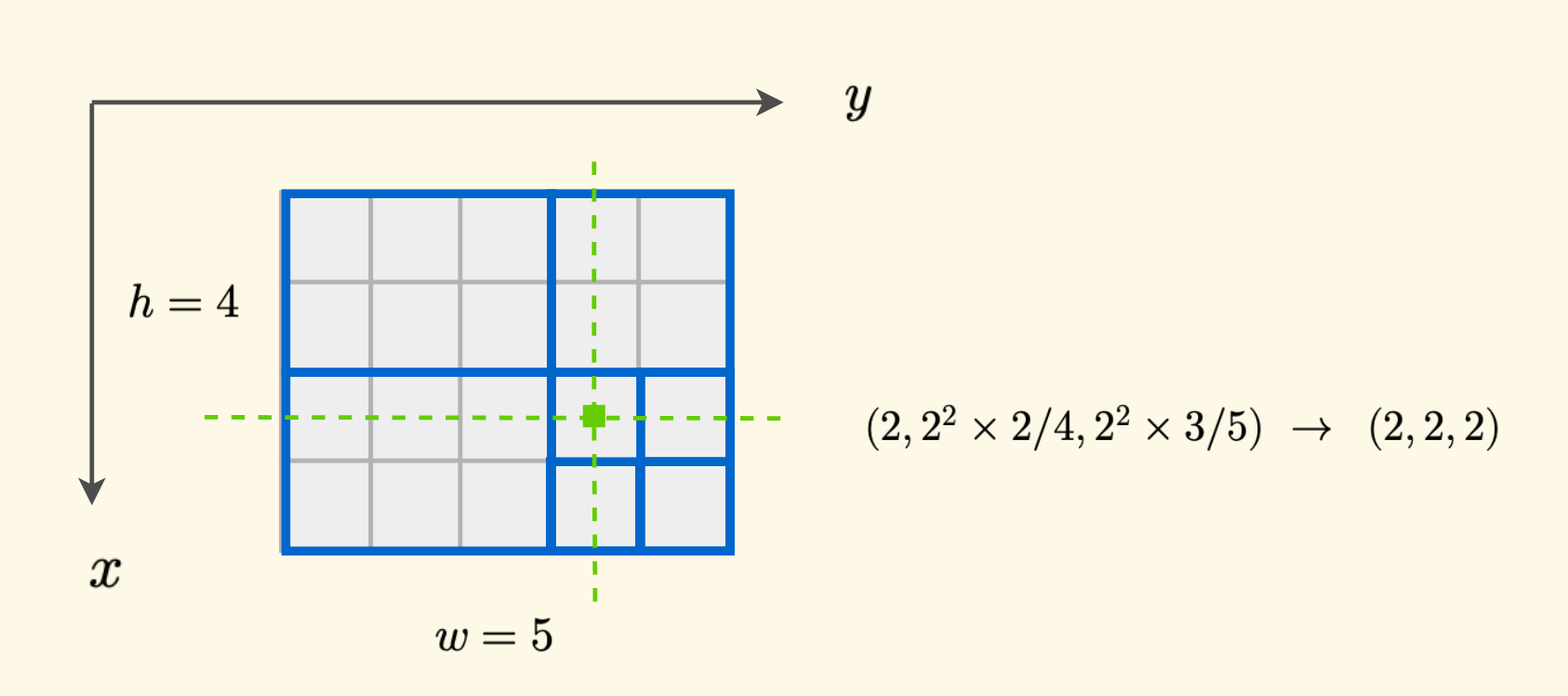
具体的实现中,我采用了一个 uint64 类型来表示节点标号:
- 高 6 位 bit 用来存储节点的深度 $d$
- 中间 29 位 bit 和低位的 29 bit 分别用来存储第二项 和 第三项。
这样,整个区域的宽和高都不可大于 $2^{29}-1$,这已经十分够用了,同时深度不可大于 $29$。
计算 ID 的 C++ 实现,主要是找好位运算的 mask:
uint64_t pack(
uint64_t d, uint64_t x, uint64_t y, uint64_t w, uint64_t h) {
// 0xfc00000000000000 : 高6位全是 1, 其余是0
// 0x3ffffffe0000000 : 高6位全是 0, 接下来29位全是1,其余全是0
// 0x1fffffff : 低29位全是 1,其余全是0
return ((d << 58) & 0xfc00000000000000ULL) |
((((1 << d) * x / h) << 29) & 0x3ffffffe0000000ULL) |
(((1 << d) * y / w) & 0x1fffffffULL);
}
这样,我们可以建立一个哈希表,来存储 ID 到节点指针的映射。
在查找一个位置 $(x,y)$ 所在的叶子节点时,关键在于确定深度 $d$ 。因为 $d$ 十分有限,当然遍历一下也不是不可以。 还可以更快,就是二分猜答案:
- 我们提前维护好整颗树的高度 $maxd$,然后初始的可行域是 $[0, maxd]$,设定 $l=0$ 和 $r=maxd$。
- 然后二分猜 $m = (l+r)/2$,用
pack函数计算出来 ID,如果在哈希表中查不到任何节点,说明猜的太大了,要收缩上界 $r=m-1$。 - 否则,如果哈希表中存在,那么看是不是叶子节点。如果是叶子节点,就已经命中了。如果不是,说明是一个中间的非叶子节点,猜的太小了,要收缩下界 $l=m+1$。
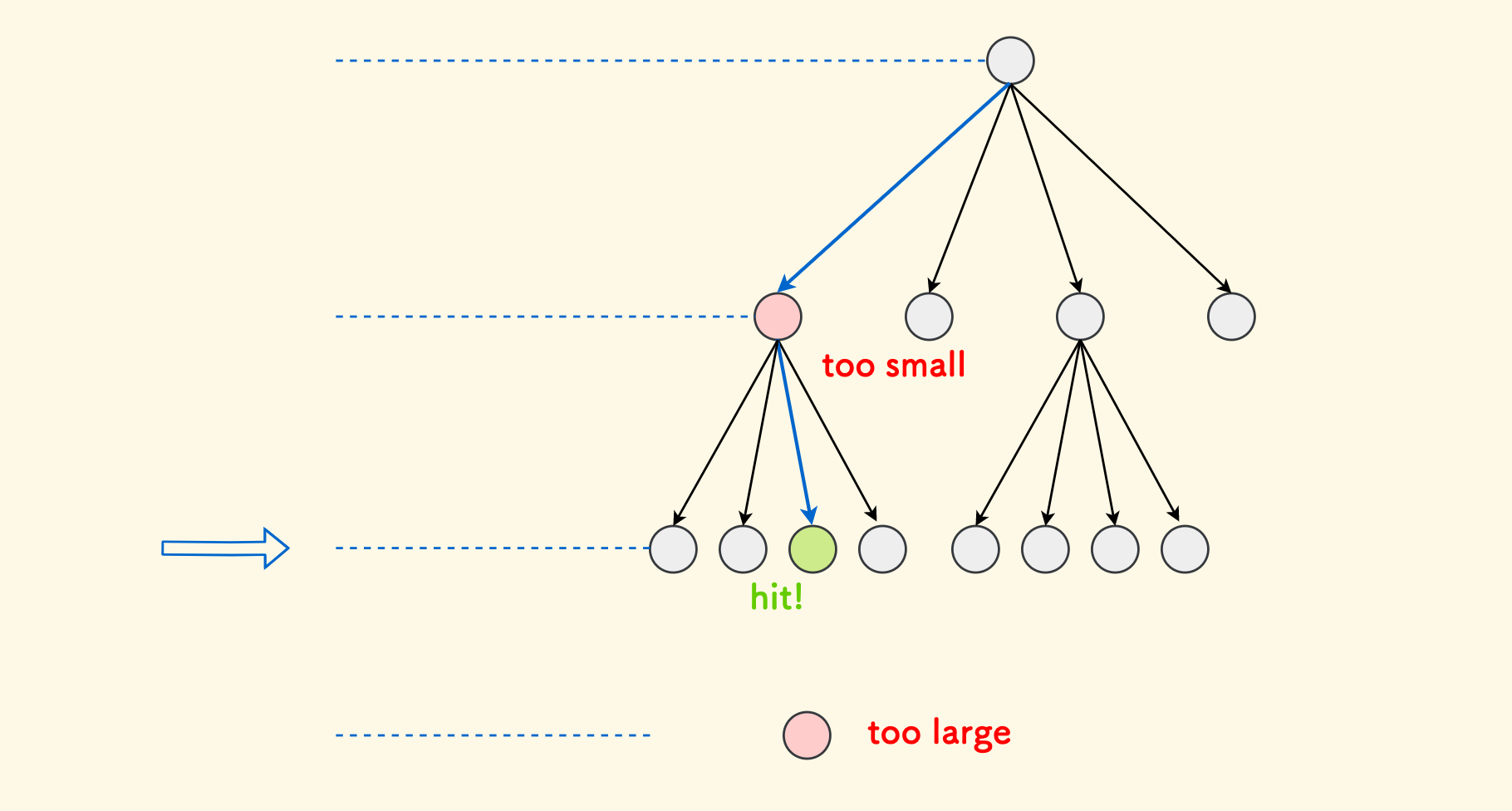
这样,定位一个叶子节点的时间复杂度仅为 $O(\log {maxd})$。
看起来优化不是很明显?毕竟 $maxd$ 的最大值也就是 $29$ 而已。 但是如果我们从根节点一层一层向下搜索的话,要一层一层寻找 $(x,y)$ 所在的节点,要慢的多。
采用这样的一种 ID 标号 和 哈希表 的设计,还有一个好处,要想找到一个节点 node 的父节点,只需要代入上一个深度算一下 pack(d-1, node->x1, node->y1) 就可以找到父节点的标号了。
另外一个细节是,因为维护了最大深度 $maxd$,又支持了动态合并,那么当叶子节点销毁时,$maxd$ 的维护就稍显复杂了,技巧是同时维护每个深度值上的节点个数。 这样,只有最后一个深度为 $maxd$ 的节点销毁时,$maxd$ 才会收缩。
--numDepthTable[node->d];
if (node->d == maxd) {
// 当销毁最后一个最大深度上的叶子节点时,才有必要减小 maxd
// 迭代次数不超过 maxd (<29)
while (numDepthTable[maxd] == 0) --maxd;
}
delete node;
优化区域查询 ¶
此部分是 2024/08/06 日新增的更新。
既然已经有了节点标号机制,那么区域查询可以继续优化一波。
有可能我们每次查询的区域范围并不大,比如说我们只是要查询当前位置附近的一些游戏对象,那么有必要每次从根节点开始向下查找吗?
比如说下面的蓝色查询区域,查询出来的对象被高亮成了绿色。此时我们只需要找到这个红色框出来的节点就可以,从这个红色的节点向下去搜, 而无需从根节点开始。
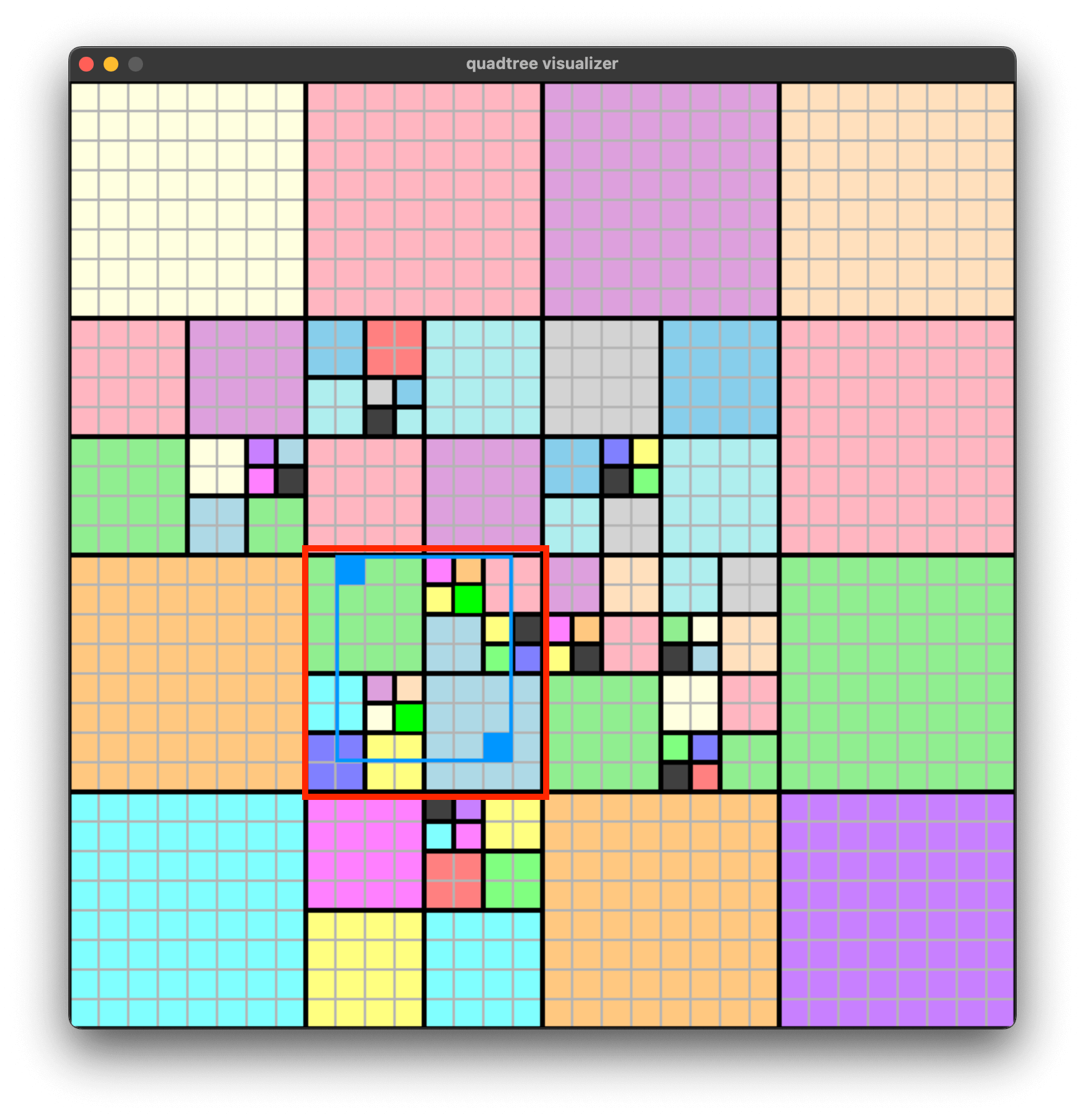
那么,如何先找到这样一个节点呢,实际上是在找 同时包含查询区域左上角和右下角两个点的最小的节点
让我们继续抽象一下这个问题,假设输入的查询区域的左上角是 $a$ 点,右下角是 $b$ 点,同时包含这两个方格的最小的节点是 $Q$, 那么:
- 对于 $Q$,以及它的所有祖先节点,肯定也都同时包含 $a$ 和 $b$ 两个方格。
- 对于 $Q$ 的所有子孙节点,必然不会同时包含 $a$ 和 $b$ 两个方格。
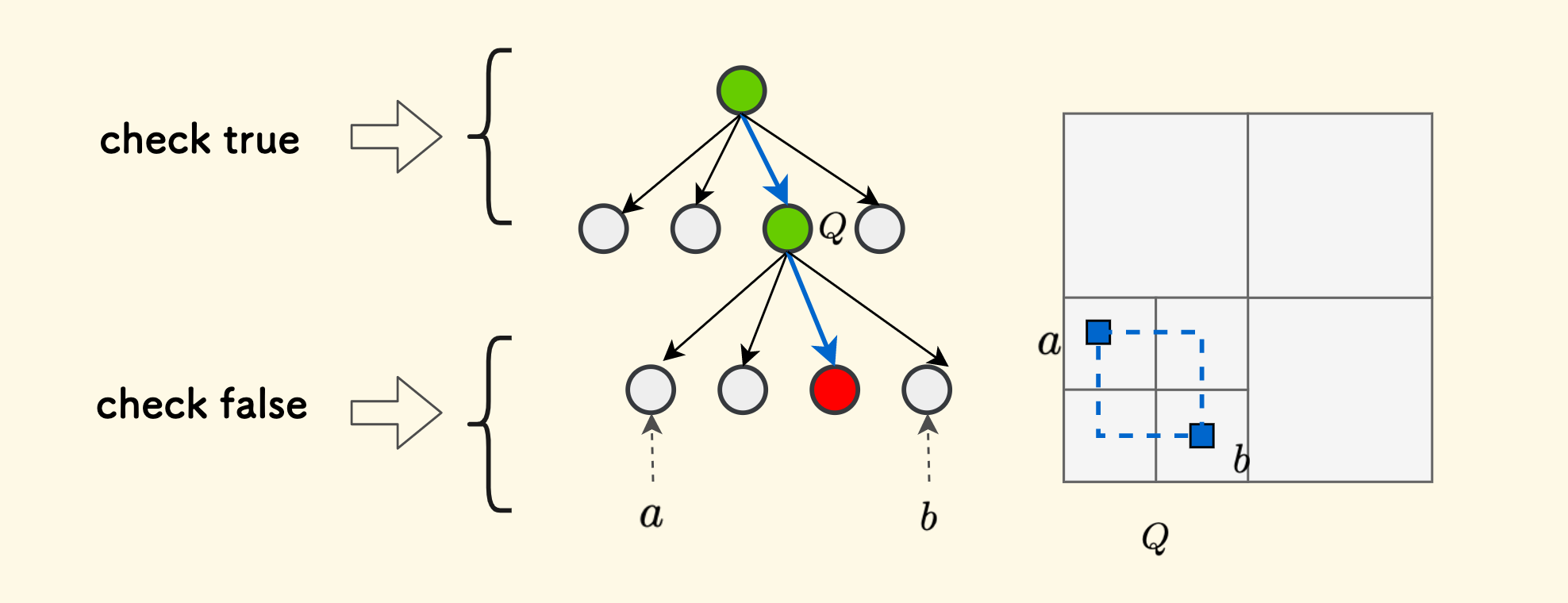
这就具有了二段性,暗示着我们可以进行二分,关键是猜一个深度 $d$。二分答案寻找满足以下条件的上界:
$a$ 和 $b$ 在深度 $d$ 上归属的节点都存在, 且标号一致,亦即是同一个节点.
代码实现大概是:
查找同时包含两个点的最小节点的 C++ 实现
Node* findSmallestNodeCoveringRange(int x1, int y1, int x2, int y2) const {
int l = 0, r = maxd;
Node* node = root;
while (l < r) {
int d = (l + r + 1) >> 1;
auto id1 = pack(d, x1, y1, w, h);
auto id2 = pack(d, x2, y2, w, h);
if (id1 == id2) {
auto it = m.find(id1);
if (it != m.end()) {
// 在深度 d 上,两个点都存在于同一个节点
l = d;
node = it->second;
continue;
}
}
// 否则, 猜的太大了,缩小上界
r = d - 1;
}
return node;
}
这样,对于小区域的范围查询,就减少了层层判断 AABB 重叠检测的次数了。
查询邻居节点 ¶
此部分是 2024/08/06 日新增的更新。
我原本学习四叉树的目的,并非是优化碰撞检测,而是想搞一个基于四叉树的分层 A* 寻路的测试。这其中,就需要用到一个功能,即:
如何寻找一个四叉树叶子节点的邻居叶子节点?
比如说,下面的两幅示意图中,红色的节点是我们要找的黄色节点的邻居,注意我们支持八个方向的邻居(包括斜角):
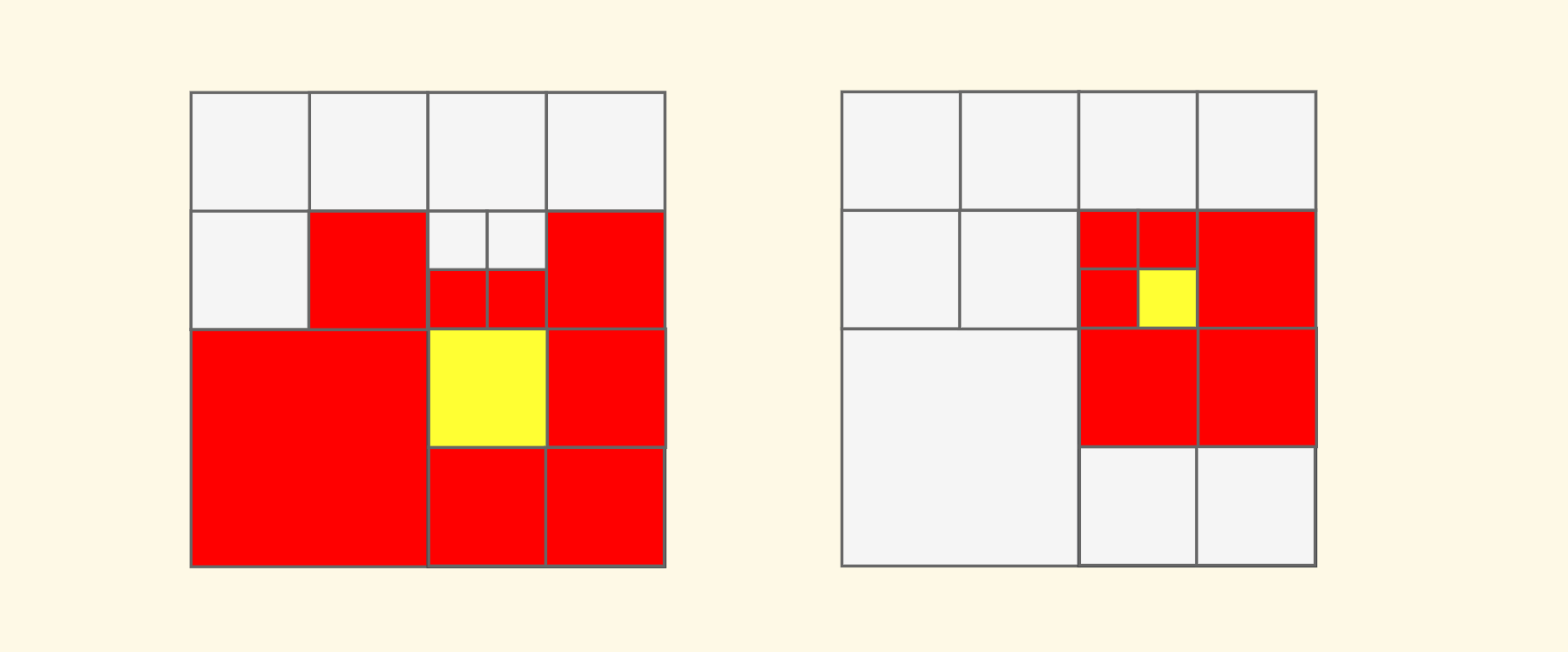
先把问题定义一下,输入的是一个节点 和 一个方向 (可选 8 个枚举值),然后输出在这个方向上的邻居节点。
我们要注意的是,在一个方向上的邻居并不一定只有一个叶子节点、也不一定是其兄弟节点。
首先,斜角方向是最容易处理的,因为在一个斜角方向上肯定只有一个邻居节点。
思路比较简单,找到斜对角最近的那个位置 $p$,然后复用前面讲过的能力,直接定位它所处的叶子节点即可,时间复杂度 $O(\log{Depth})$。
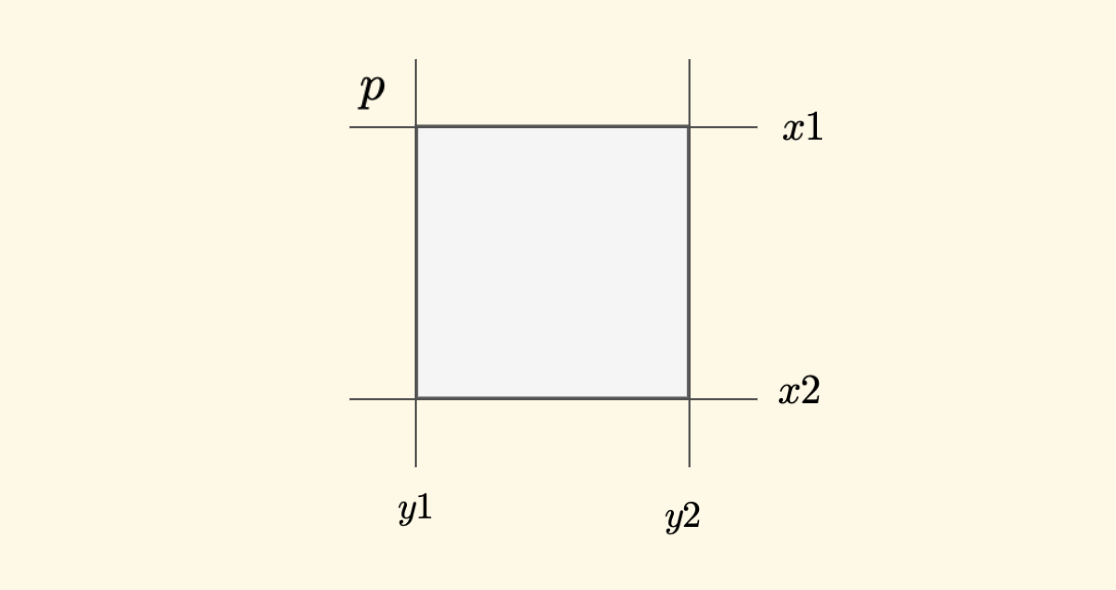
以左上角方向为例,当前节点管辖的小矩形的区域是 $(x1,y1)$ 和 $(x2,y2)$ ,那么,左上的相邻点 $p$ 就是 $(x1-1,y1-1)$, 然后定位此位置归属的叶子节点即可,其他三个斜角方向可以如法炮制。
对于非斜角的方向,稍许复杂一点。这里面有两种情况,以北方向(上方)为例,有可能上面的邻居边长大于或者等于当前节点,也有可能上方是多个小边长的邻居。 下图是这两种情况的示意图,仍然是黄色的表示当前节点,红色的表示邻居节点:
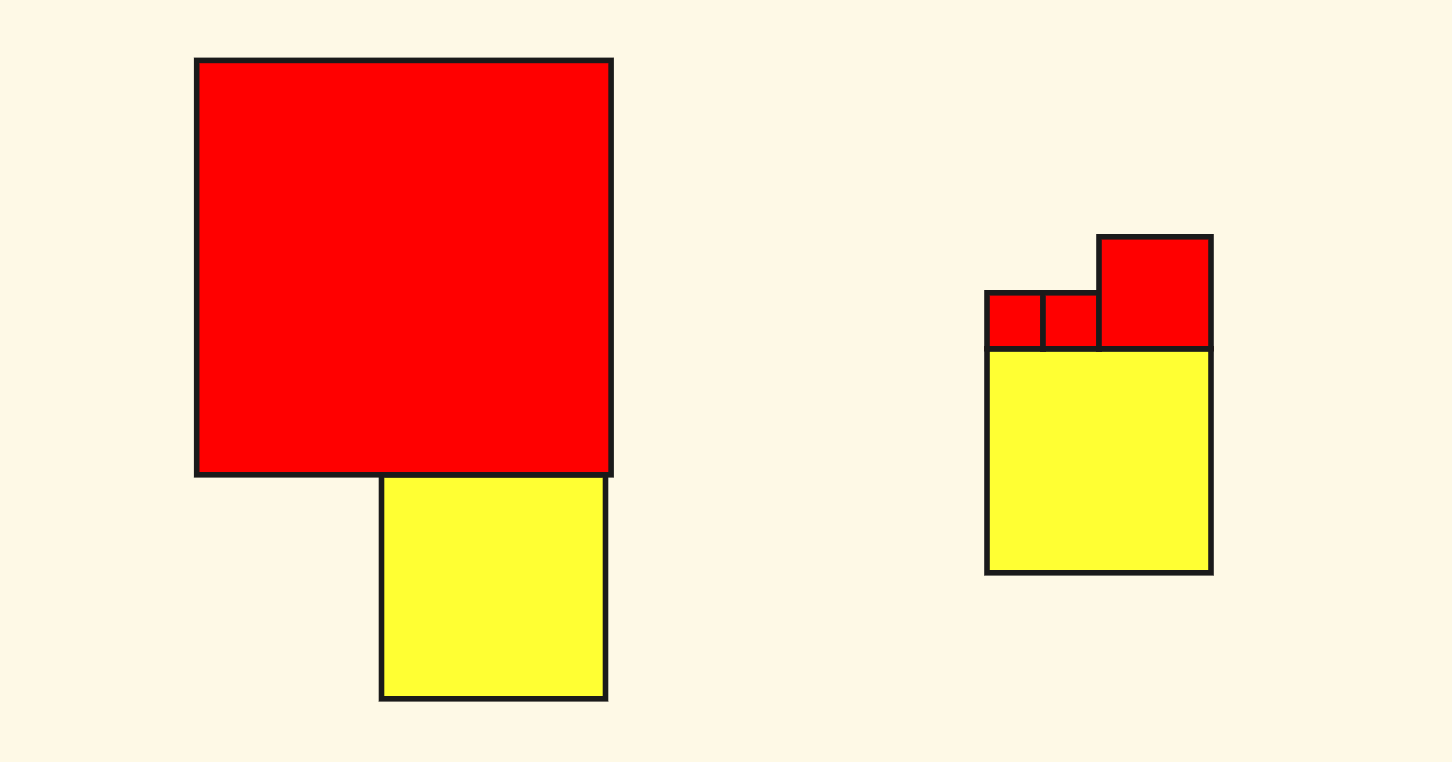
但是,无论那种情况,我们都可以 先去找到上方边长不小于当前节点的邻居节点(它可能不是一个叶子节点),然后再向下递归寻找紧邻着当前节点的叶子节点作为答案。
仍以北方为例,无论如何当前节点的在北边的邻居节点,一定都处于一个边长不小于当前节点的邻居节点中。 也就是说,我们假定,要找的邻居节点,在包含下面蓝色方框的一个大节点中,这个方框的边长不小于当前节点。
- 如果这个蓝色方框存在于一个大的叶子节点中,那么这个叶子节点就是唯一答案。
- 如果这个蓝色方框是一个中间节点,那么从此节点向下递归寻找「南」侧方向的子节点,直到叶子节点,就是所有答案。
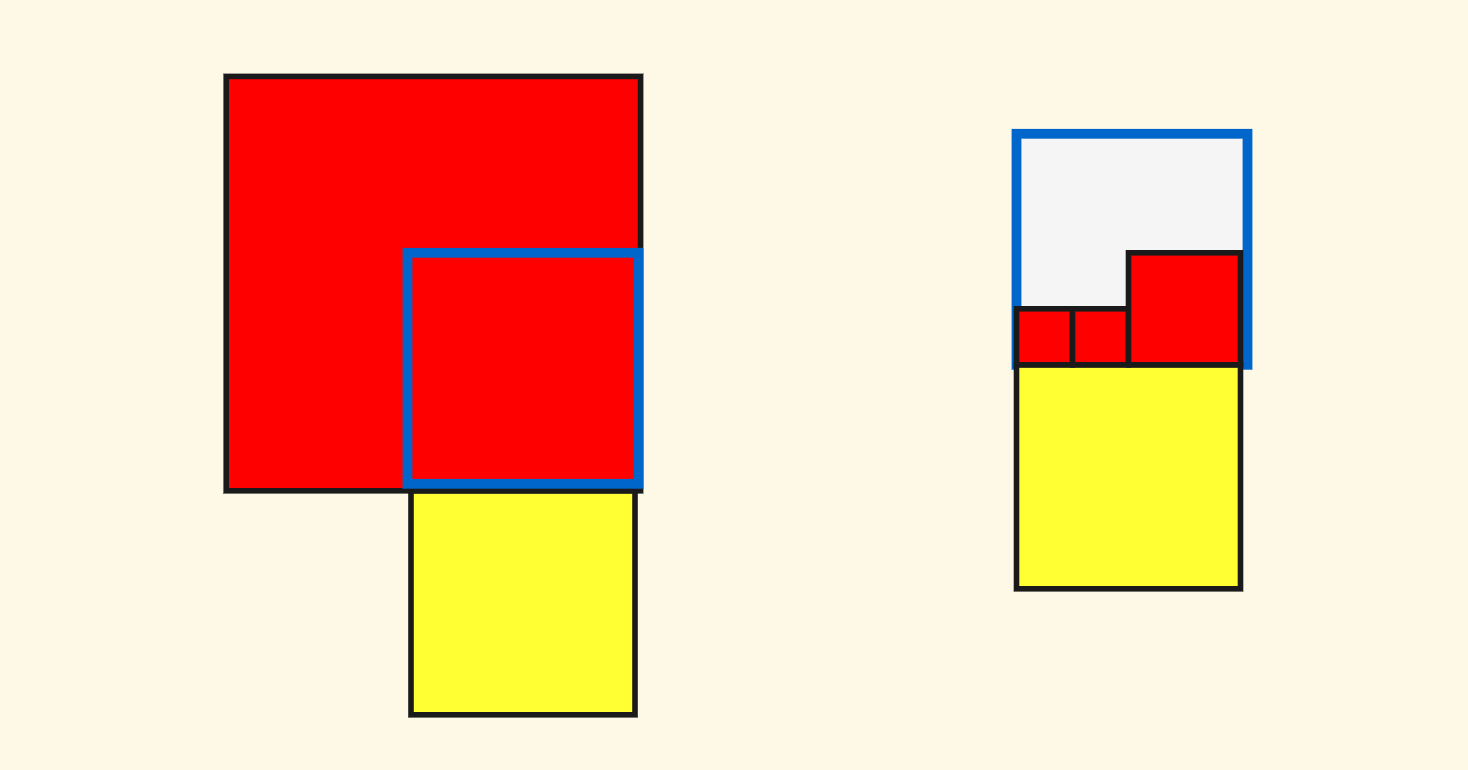
现在可以继续明确一下问题,所谓包含「蓝色方框」的节点是什么?仍然选定两个邻居位置点 $a$ 和 $b$,同时包含此两个位置的节点就是蓝色方框所在的节点!
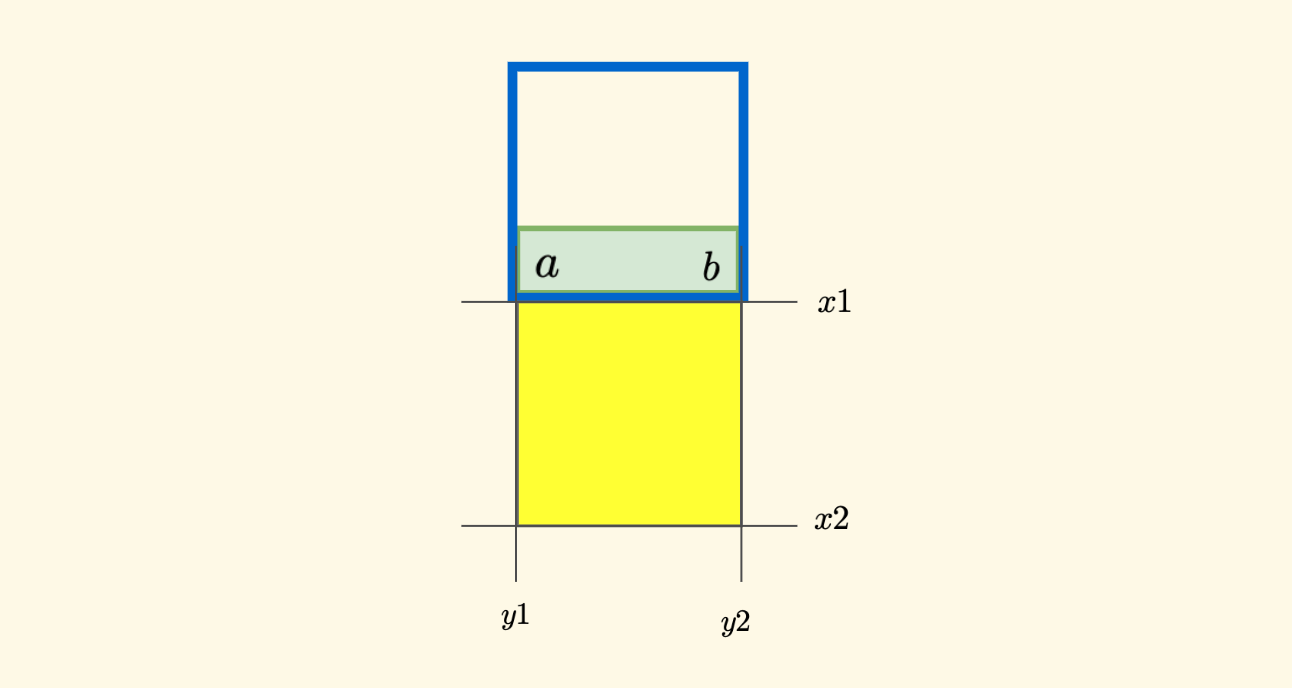
这个 $a$ 和 $b$ 点的选取,和前面所说的 $p$ 点的是类似的,北方的情况下是:$(x1-1,y1)$ 和 $(x1-1,y2)$。如此选取之后,同时包含这两个位置的节点必定边长不小于当前节点。 而如何查找这样的节点呢?可以复用前面所说的 优化区域查询 部分的 findSmallestNodeCoveringRange 函数,时间复杂度是 $O(\log{Depth})$ 。
确定了这个节点之后,如果它就是一个叶子节点,那么查找结束,答案仅此一个。但是如果它不是叶子节点,则要继续向下递归,寻找「南」侧的子孙节点。
这里面有一个细节,就是由于我这个四叉树支持矩形(不一定非要是正方形),也就是说,需要注意的是一个节点内的子节点并非总是有 $4$ 个,可能的子节点布局情况有:
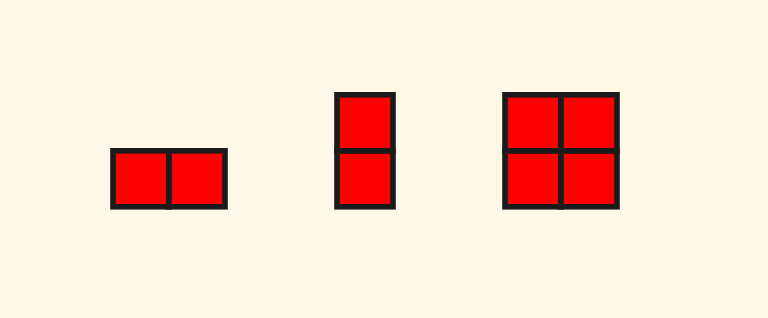
这其中,对于两个节点的情况,需要特殊处理一下。比如说第一种横向两个子节点的情况,对于查询南北向邻居的时候,要全部选取进行递归,而对于查询东西向邻居的时候,只可以选择一个。
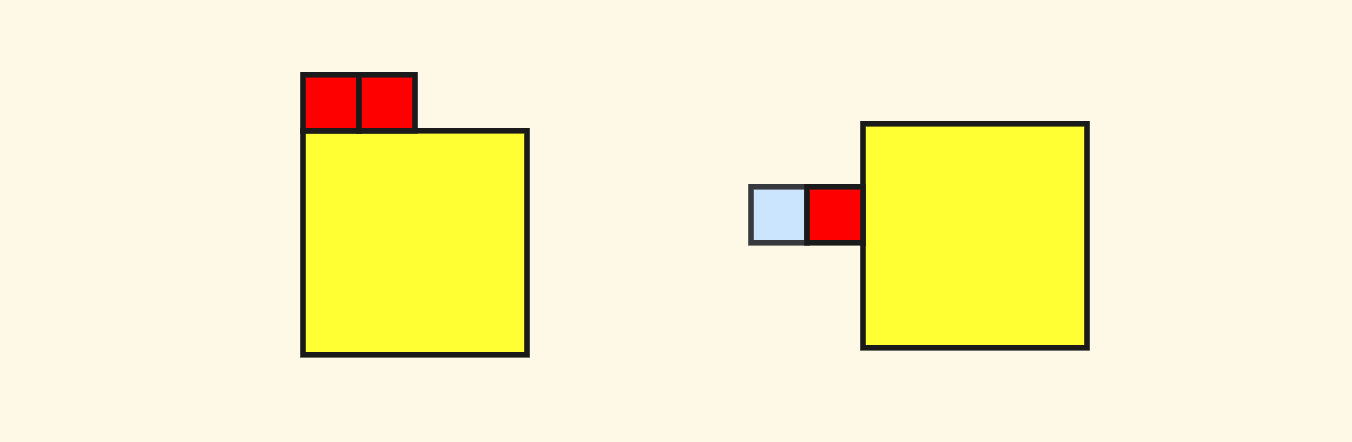
对于 $4$ 个节点的标准子节点布局的情况,会相对简单,比如说查询北向邻居的话,递归的时候只需要选取南边的两个子节点即可:
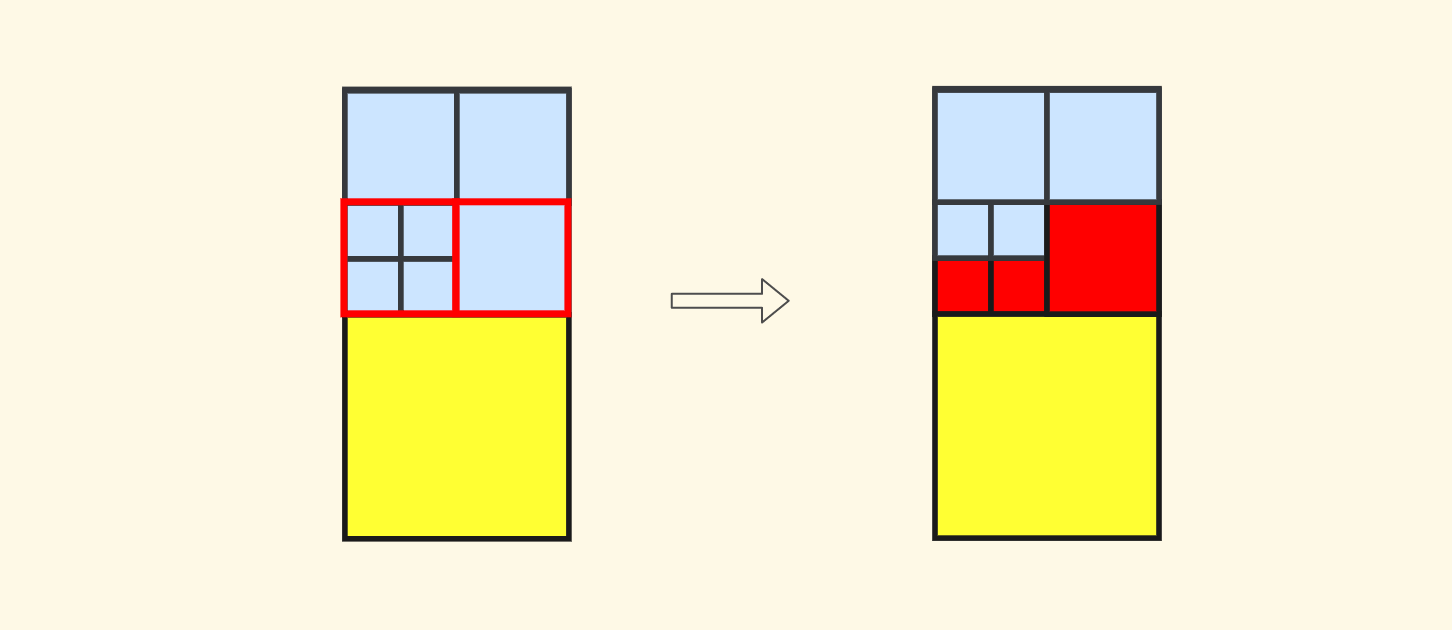
代码不直接在文章中体现了,可以直接看 repo 中的实现,有一些额外的细节。
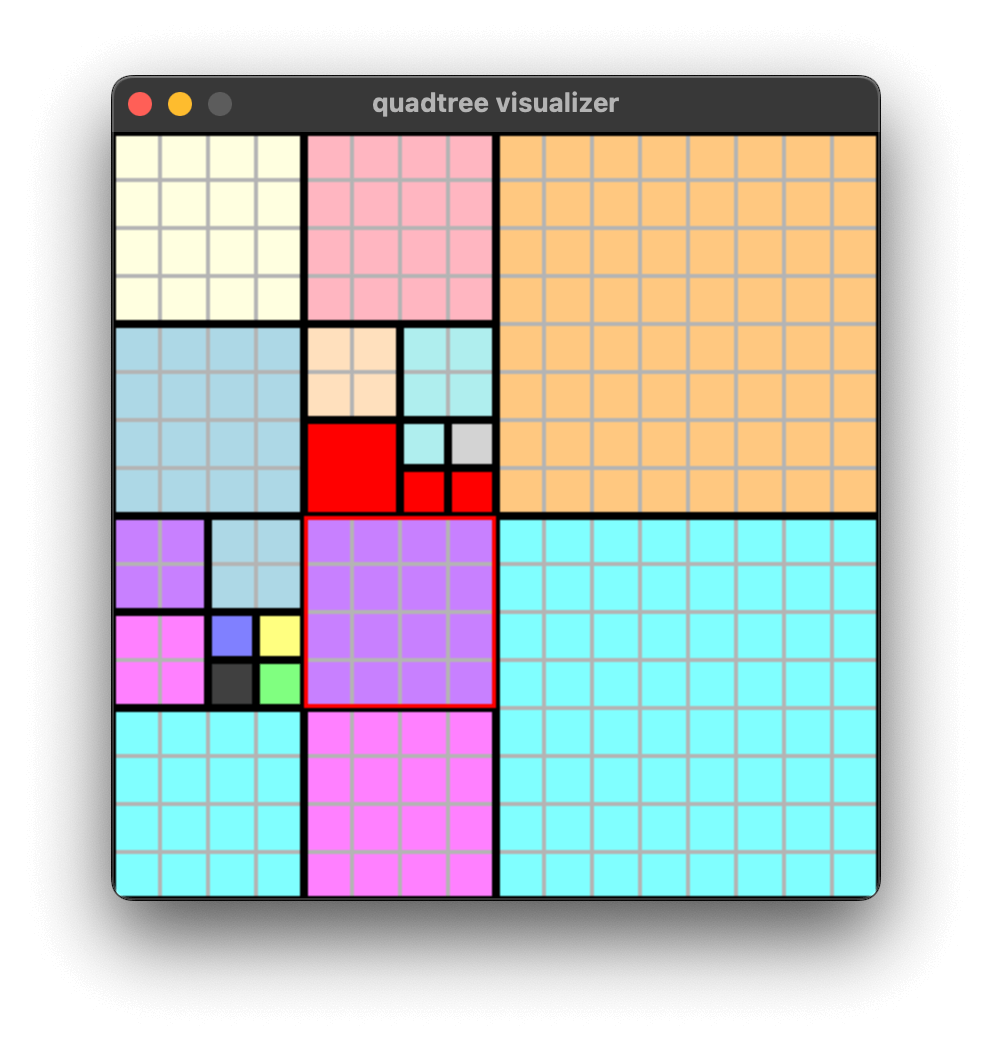
实现效果如下图所示,查询红框节点北方的邻居叶子节点:
结尾 ¶
最后,欢迎给一个小星星!https://github.com/hit9/quadtree-hpp
另外,另外,另外,有一个好玩的 Quadtree Art 的东西,可以瞧瞧:https://www.michaelfogleman.com/static/quads/。

(完)
本文原始链接地址: https://writings.sh/post/quadtree
