本文是对滑动窗口算法的一些总结。
场景和常用代码模板 ¶
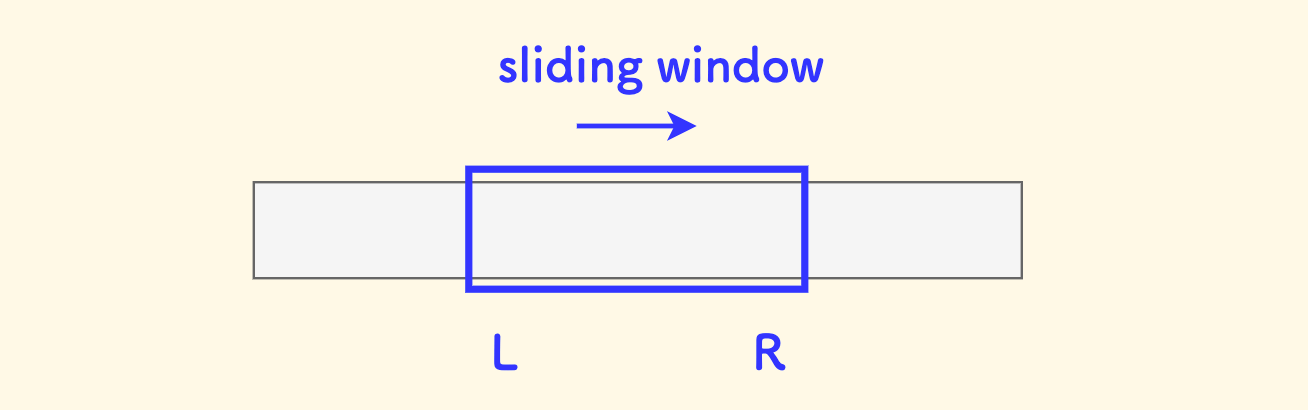
滑动窗口是一种数组上的同向双指针算法,左右两个指针内的连续区间形成一个不断滑动的窗口。
随着右端指针的滑动,左端指针可以及时排除 不合法的 或者 不会成为最优的 决策。
答案的计算一般来自窗口内的元素、窗口的大小等信息。
单调队列 本质上也是一种滑动窗口算法,只不过窗口内的元素关于决策函数高度有序、最优决策点维持在队头。 本文只关注朴素的双指针类型的滑窗、不含单调队列的内容。
我常用的一个代码模板如下:
for (int L = 0, R = 0; R < N; R++) {
// TODO: 维护右端
while (L < R && check()) {
// TODO: 维护左端
L++;
}
// TODO: 计算答案, 此时闭区间 [L,R] 是有效的
}
滑动窗口模板 - Python 版本
L = R = 0
while R < N:
# TODO: 维护右端
while L < R and check():
# TODO: 维护左端
L += 1
# TODO: 计算答案,此时闭区间 [L,R] 是有效的
R += 1
其中:
- 左右指针维护的窗口是一个闭区间
[L,R]。 - 右端驱动滑动、左端伺机收缩。
check函数只是一个占位示例,用来判断窗口左端的收缩条件。- 右端一般是新增类型的维护动作、左端则是撤销类型的维护动作。
- 答案计算点一般在窗口收缩维护完毕后,此时窗口大小是
R-L+1。 - 如果允许空窗口出现,则内层循环的条件
L < R可改为L <= R。 - 虽然是两层循环,但是两个指针都只迭代了一次,如果窗口维护和答案计算的时间复杂度都是 $O(1)$,那么滑窗的时间复杂度是线性的 $O(N)$。
- 实际的题目中,常需要结合数据结构来维护窗口内信息(比如常见的窗口内的元素和、统计元素频次等)。
简单的理解来看,滑窗其实是在枚举区间(包括定长的和不定长的)。 区间左端指针单调右移(不会回溯)是应用滑动窗口算法的前提。
常用的手法是以右端指针来枚举区间。
滑动窗口算法看起来简单,但是非常灵活,有不少巧妙的题目。
可获得的最大点数 ¶
几张卡牌排成一行,每张卡牌都有一个点数,所有点数由整数数组
a给出。每次行动,可以从行的开头或者末尾拿一张卡牌,最终你必须正好拿
k张卡牌。总点数就是拿到手中的所有卡牌的点数之和。
给定数组
a和整数k,返回可以获得的最大总点数。-- 来自 leetcode 1423. 可获得的最大点数
只允许从开头和末尾拿牌,不如转化为:选中一段连续的区间,这个区间内的牌不拿。
问题即转化为:
选出连续的恰好
n-k张牌,使得总点数最小。
比如考虑数组 [1,2,3,4,5,6,1],k=3 时的最优答案是取末尾的 [1,6,5] 三张牌,点数最大。 这就相当于不取连续区间 [1,2,3,4]。
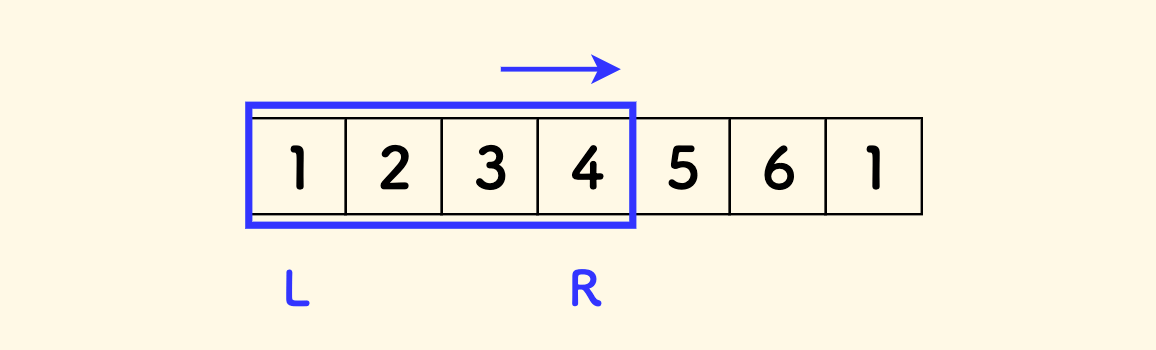
这是一个定长滑窗问题。
考虑转化后的问题,只需要枚举每一段长度为 n-k 的连续区间即可,具体地说,是以右端指针 R 来枚举区间。
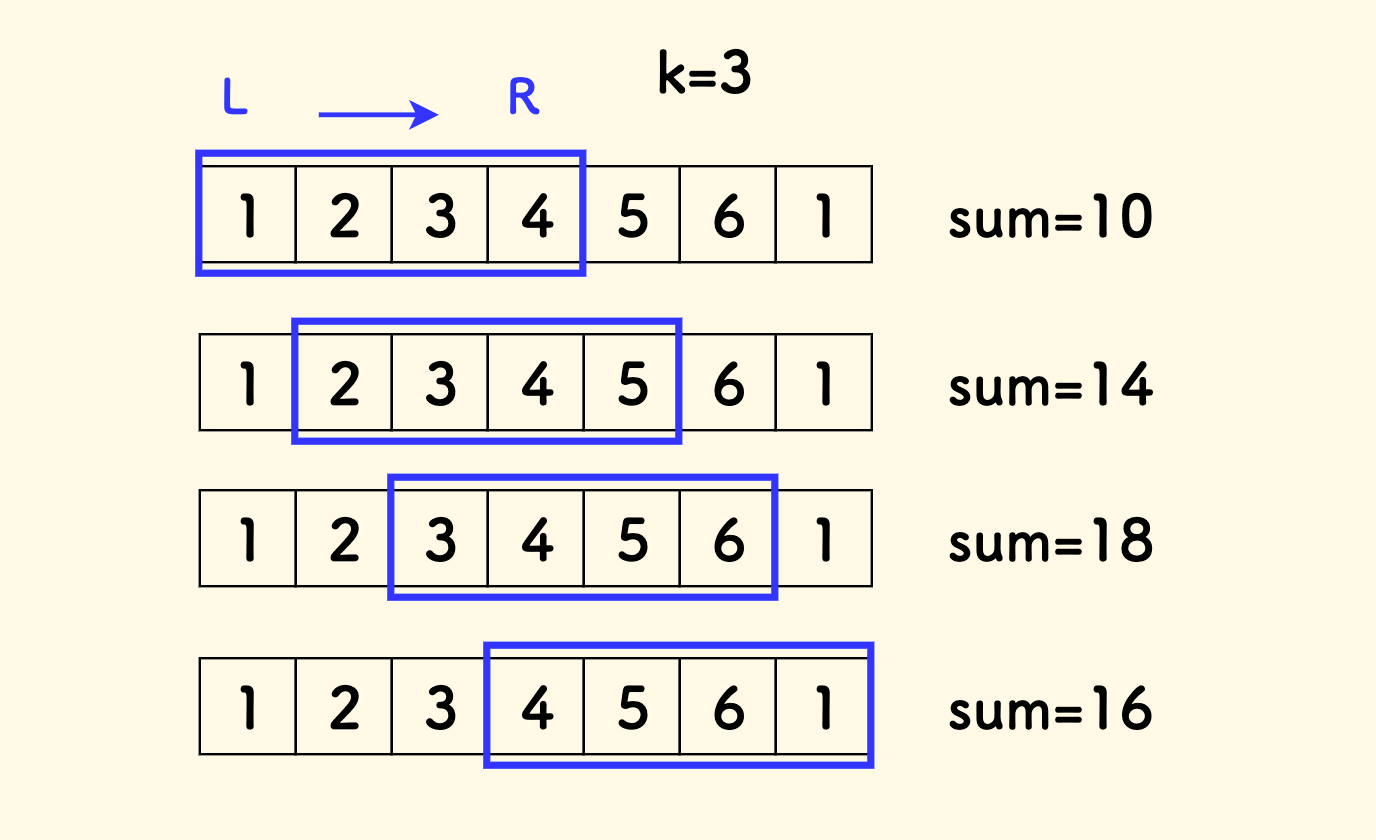
同时,维护窗口内的区间和,找出最小的区间和:
- 右端扩张窗口时,区间和增加
sum += a[R]。 - 左端收缩窗口时,区间和减少
sum -= a[L]。
窗口的维护和区间的计算时间复杂度都是 $O(1)$ 的。
定长窗口的限制条件,就是如果窗口长度超过设定值,就应该收缩左边。
完整实现代码如下:
可获得的最大点数 - C++ 代码
class Solution {
public:
int maxScore(vector<int>& a, int k) {
int n = a.size(), k1 = n - k;
int s = accumulate(a.begin(), a.end(), 0);
int min_sum = s, sum = 0; // sum 维护窗口内区间和
for (int L = 0, R = 0; R < n; R++) {
// 维护右端,区间和增加
sum += a[R];
// 左端收缩条件:窗口长度超过预期
while (R - L + 1 > k1)
sum -= a[L++]; // 同时维护区间和,剔除左端 L 的值
// 此时窗口 [L,R] 的长度保证不大于 k1
// 如果恰好是 k1, 则计算最小区间和
if (R - L + 1 == k1)
min_sum = min(min_sum, sum);
}
return s - min_sum;
}
};
可获得的最大点数 - Python 代码
class Solution:
def maxScore(self, a: List[int], k: int) -> int:
k1 = len(a) - k
S = sum(a)
min_s = S
s = 0
L = R = 0
while R < len(a):
s += a[R]
while R - L + 1 > k1:
s -= a[L]
L += 1
if R - L + 1 == k1:
if min_s > s:
min_s = s
R += 1
return S - min_s
无重复字符的最长子串 ¶
这是个非常高频的题:
给定一个字符串
s,请你找出其中不含有重复字符的 最长子串 的长度。-- 来自 leetcode 3. 无重复字符的最长子串
比如说,"abcabcbb" 的无重复字符的最长子串是 "abc",长度是 3。
找出符合条件的子串,其实也是在枚举区间。
这是一个不定长滑窗问题,限制条件是要求窗口内没有重复字符。
下图演示了滑动的全过程:
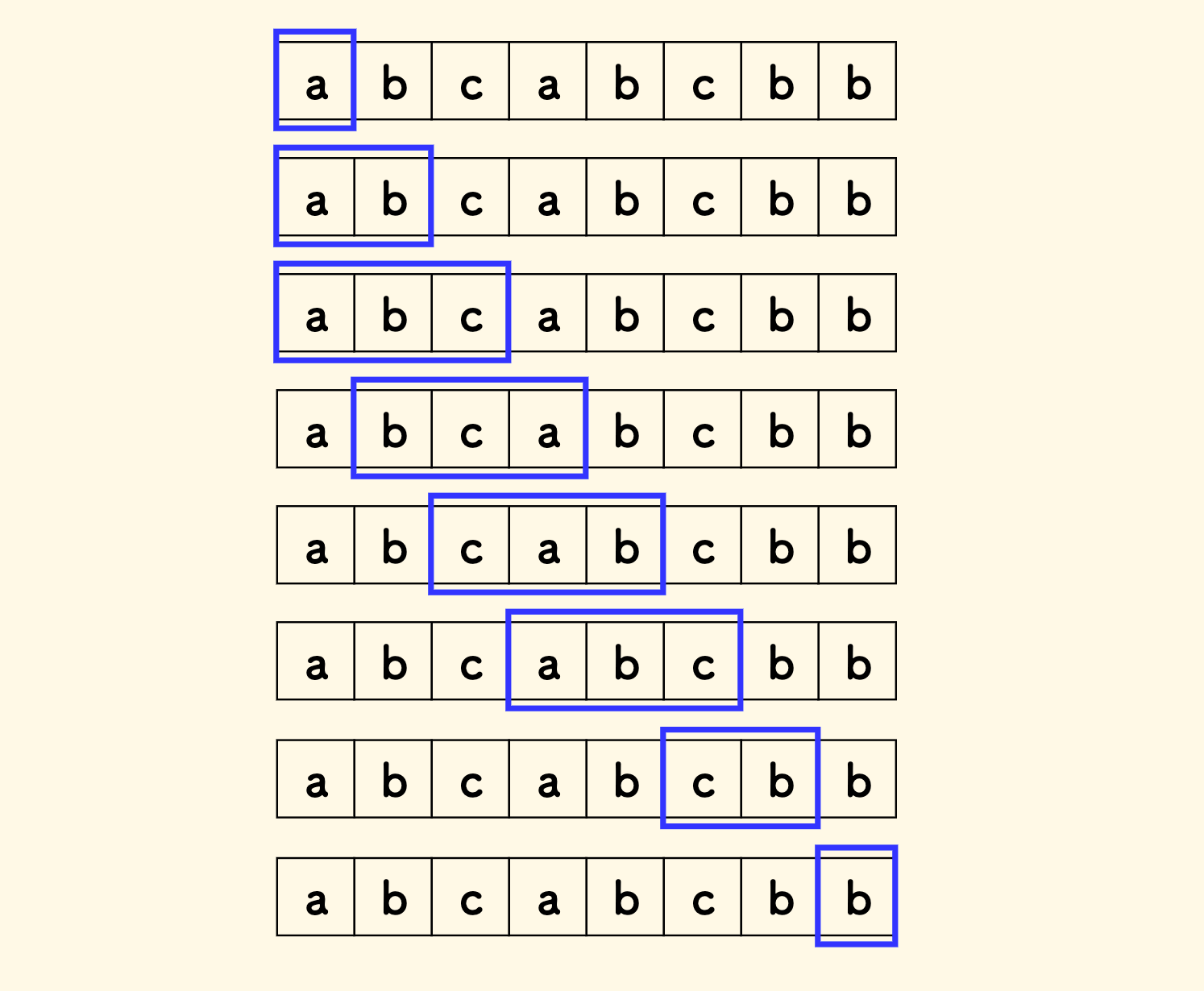
将尝试 维护窗口内的字符种类的个数 c,如果它小于窗口的大小,则说明有重复字符,否则没有。
采用一个哈希表 d 来维护滑窗内的字符出现的频次:
- 当窗口右端扩张时,增加右端字符的出现频次
d[s[R]]++。 - 当窗口左端收缩时,减少左端字符的出现频次
d[s[L]]--。
进一步,可以根据频次来维护窗口内的字符种类的个数:
当窗口右端扩张时,如果右端字符
s[R]的频次恰好为1,说明新增了一种字符:if (++d[s[R]] == 1) c++;当窗口左端收缩时,如果左端字符
s[L]的频次在减少后恰好为0,说明减少了一种字符:if (--d[s[L++]] == 0) c--;
窗口的收缩条件,就是:字符种类小于窗口长度,说明此时包含重复字符,要收缩左端直到窗口内不存在重复字符为止。
答案就是符合条件的最大的窗口长度。
C++ 代码实现如下:
unordered_map<char, int> d;
int c = 0; // 窗口内的元素种数
int ans = 0;
for (int L = 0, R = 0; R < s.size(); R++) {
if (++d[s[R]] == 1) c++;
while (L < R && c < R - L + 1)
if (--d[s[L++]] == 0) c--;
ans = max(ans, R - L + 1);
}
无重复字符的最长子串 - Python 代码
class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
d = defaultdict(int) # 窗口内的元素频次
c = 0 # 窗口内的元素种类
L = R = 0
ans = 0
while R < len(s):
d[s[R]] += 1
if d[s[R]] == 1:
c += 1
while L < R and c < R - L + 1:
d[s[L]] -= 1
if d[s[L]] == 0:
c -= 1
L += 1
ans = max(ans, R - L + 1)
R += 1
return ans
这种统计窗口内元素的出现频次、元素种类的手法,在滑窗问题中很常用。
本题也可以用 dp 来做,感兴趣的可参考代码 无重复字符的最长子串的 dp 实现。
字母异位词问题 ¶
给定两个字符串
s和p,找到s中所有p的 异位词 的子串,返回这些子串的起始索引。不考虑答案输出的顺序。异位词 指由相同字母重排列形成的字符串(包括相同的字符串)。
-- 来自 leetcode 438. 找到字符串中所有字母异位词
比如 s="cbaebabacd",p="abc" 的时候,s 中有两个 p 的异位词,分别是 "cba" 和 "bac",位置分别是 [0,6]。
这个问题仍然是在找子串,也就是在枚举区间。
要求的「异位词」是指两个条件:
- 长度和
p一致。 - 字符的种类和频次和
p完全一致。
只需要枚举具有上述特征的区间,所有符合条件的窗口左端的位置就是答案。
容易知道,这也是一个定长滑窗问题,全过程示例如下:
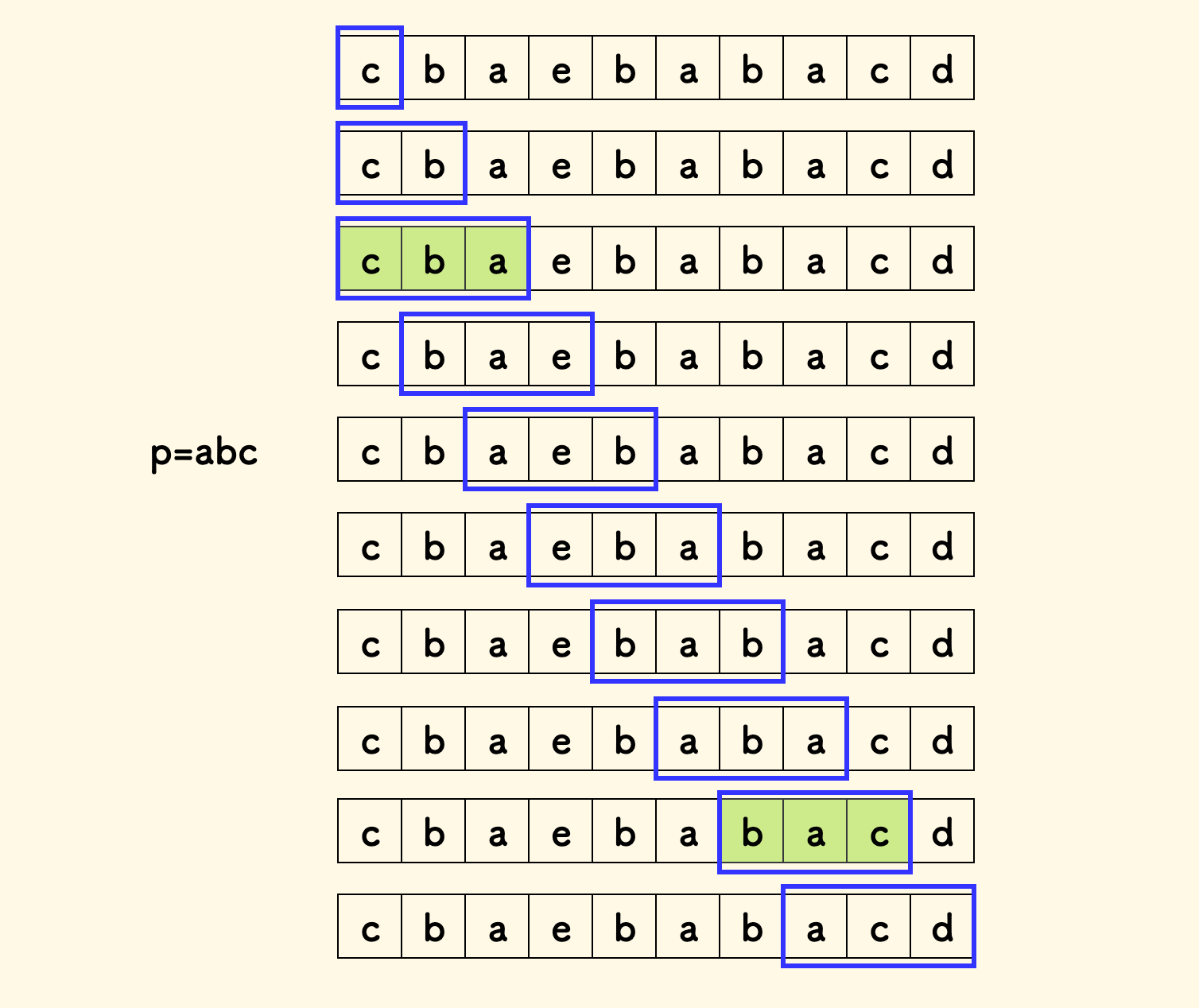
一个问题是,如何快速的判断一个子串是否为 p 的异位词。
直接的办法是,用哈希表追踪窗口内的字符频次,然后再去和 p 的频次哈希表做 $O(N)$ 对比。
但是这样太慢了,会最终导致总的时间复杂度是 $O(N^2)$。
可以复用 前面所说的滑窗频次维护手法 来优化这个检查。
首先,对字符串 p 进行预处理:
- 用哈希表
d来统计每个字符的出现频次。 - 用数字
a来表示p内的字符种类的个数。
容易写出预处理 C++ 代码:
unordered_map<char, int> d;
int a = 0;
for (auto ch : p)
if (++d[ch] == 1) a++;
然后,在枚举每个区间 [L,R] 时:
如果右端遇到
p中的字符,则扣减出现频次,同时维护已抵消的字符种类b:if (--d[s[R]] == 0) b++;左端收缩时,则要撤销这种扣减:
if (++d[s[L++]] == 1) b--;
这里的 b 是窗口内抵消字符串 p 中字符的种类的数目。
这是一种定长滑动窗口,限制条件是窗口的大小。 所以,当窗口大小超过 p 的长度时,需要收缩窗口左端。
for (int L = 0, R = 0; R < s.size(); R++) {
if (--d[s[R]] == 0) b++;
while (L < R && R - L + 1 > p.size()) // 定长限制
if (++d[s[L++]] == 1) b--;
// TODO: 计算答案
}收缩窗口后,如果 b 恰好等于 a 的话,说明找到一个符合条件的区间。
// 收缩窗口后,计算答案
if (a == b) ans.push_back(L);
原因说明:
- 收缩窗口后,窗口的大小是不超过
p的长度的。 对于窗口内的每个字符,只有它在
p中存在、且恰好扣减了d[x]次的时候,b才会进行计数。所以,
p中的每个字符x都至少在窗口中出现了d[x]次。
这一点还可以推导出来,窗口内的字符总数不小于
p的字符总数。
综合这两点,此时,当前窗口的大小一定正好等于 p 的长度,并且各种字符的出现频次完全一致。
总时间复杂度是 $O(N)$,太巧妙了。
最终的代码实现如下:
找到字符串中所有字母异位词 C++ 代码
class Solution {
public:
vector<int> findAnagrams(string s, string p) {
unordered_map<char, int> d; // p 中的各个字符的出现次数
int a = 0; // p 中不同的字符个数
for (auto ch : p)
if (++d[ch] == 1) a++;
int b = 0; // b 是窗口内的扣减了 p 中字符的种类数
vector<int> ans;
for (int L =0, R = 0; R < s.size(); R++) {
// 扣减出现频次, 并且, 如果扣减后是 0 , 则记录一次 b
if (--d[s[R]] == 0) b++;
// 恢复出现频次, 如果恢复前是 0, 则也要恢复 b
while (L < R && R - L + 1 > p.size())
if (++d[s[L++]] == 1) b--;
if (a == b) ans.push_back(L);
}
return ans;
}
};
找到字符串中所有字母异位词 Python 代码
class Solution:
def findAnagrams(self, s: str, p: str) -> List[int]:
d = defaultdict(int) # p 中的各个字符的出现次数
a = 0 # p 中不同的字符个数
for ch in p:
d[ch] += 1
if d[ch] == 1:
a += 1
b = 0 # b 是窗口内的扣减了 p 中字符的种类数
ans = []
L = R = 0
while R < len(s):
# 扣减出现频次,
d[s[R]] -= 1
# 并且, 如果扣减后是 0 , 则记录一次 b
if d[s[R]] == 0:
b += 1
while L < R and R - L + 1 > len(p):
# 恢复出现频次
d[s[L]] += 1
# 如果恢复前是 0, 则也要恢复 b
if d[s[L]] == 1:
b -= 1
L += 1
if a == b:
ans.append(L)
R += 1
return ans
最大连续 1 的个数 ¶
给定一个二进制数组
a和一个非负整数k,如果可以翻转最多k个0,则返回 数组中连续1的最大个数 。-- 来自 leetcode 1004. 最大连续1的个数 III
比如说,数组 [1,1,1,0,0,0,1,1,1,1,0],取 k=2 时的答案是 6,此时翻转的情况如下图所示。
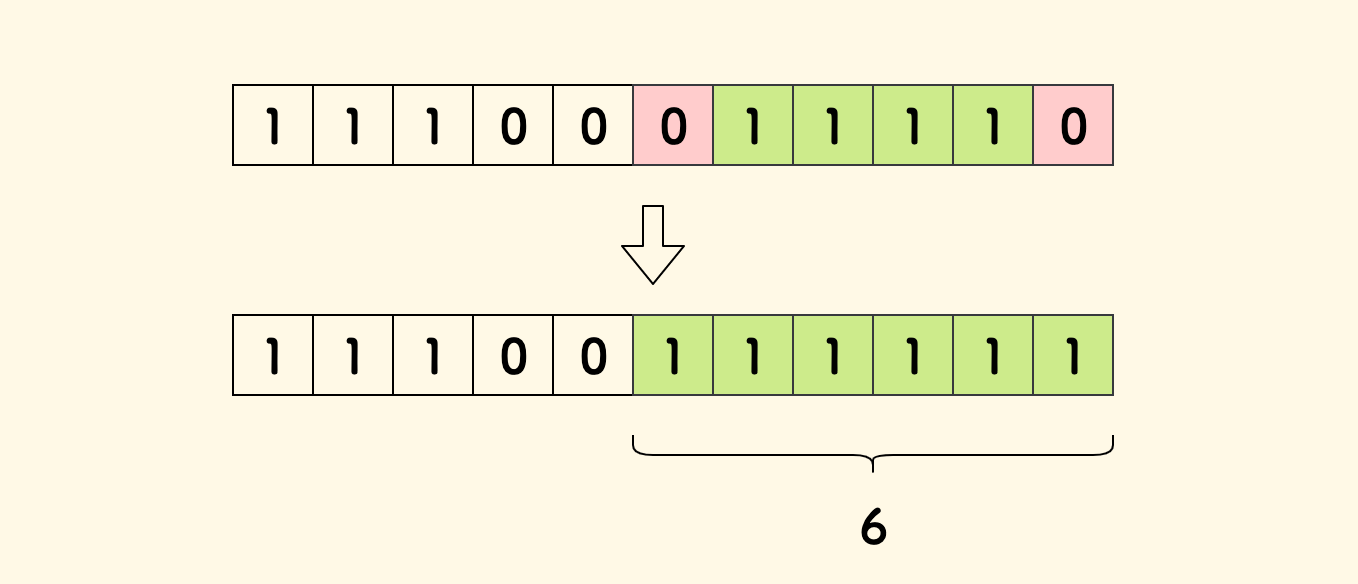
问题的实质是:
要找一段连续的区间,其中
0的数量最多为k个。
所以,仍然是一种枚举区间的问题,而且是一种不定长滑窗。所有符合条件的区间的最大长度,就是答案。
如果当前滑窗内的 0 多于 k 个,左端要收缩,直到不多于 k 个。
左端无需回溯,因为包含过多的 0 的任何一个区间都不会是答案,左端单调右移即可,符合滑窗的场景特征。
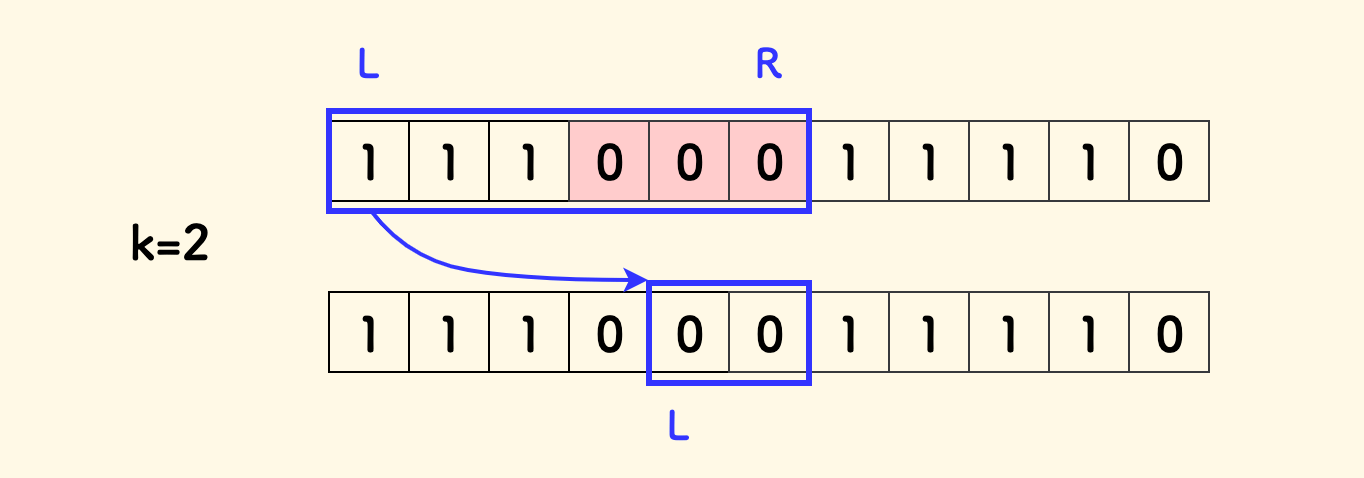
由于 k 有可能是 0,所以要允许空滑窗的出现,也就是说,收缩条件中是 L <= R,而不是 L < R:
while (L <= R && k0 > k) { // k0 是窗内 0 的数量
// TODO: 其他维护逻辑
L++;
}
在滑动过程中,维护窗口内的 0 的计数 k0:
窗口右端扩张时,如果遇到
0,则计数增加:if (a[R] == 0) k0++;窗口左端扩张时,如果是
0,则计数撤销:if (a[L++] == 0) k0--;
每次得到的合法区间,取其长度,所有的长度中最大的就是答案。
最终实现代码如下:
最大连续 1 的个数 - C++ 代码
class Solution {
public:
int longestOnes(vector<int>& a, int k) {
int k0 = 0; // 窗内 0 的个数
int ans = 0;
for (int L = 0, R = 0; R < a.size(); R++) {
if (a[R] == 0) k0++;
while (L <= R && k0 > k) { // 允许空窗
if (a[L++] == 0) k0--;
}
ans = std::max(ans, R - L + 1);
}
return ans;
}
};
最大连续 1 的个数 - Python 代码
class Solution:
def longestOnes(self, nums: List[int], k: int) -> int:
k0 = 0 # 当前 0 的个数
ans = 0
L = R = 0
while R < len(nums):
if nums[R] == 0:
k0 += 1
# L <= R 而不是 L < R,允许空窗口出现,因为 k 可能是 0
# 空窗口的时候,答案恰好是 0
while L <= R and k0 > k:
if nums[L] == 0:
k0 -= 1
L += 1
ans = max(ans, R - L + 1)
R += 1
return ans
最高频元素的频数 ¶
给你一个正整数数组
a和一个整数k。在一步操作中,你可以选择a的一个下标,并将该下标对应元素的值增加1。 执行最多k次操作后,返回数组中最高频元素的最大可能频次 。-- 来自 leetcode 1838. 最高频元素的频数
比如说,数组 [1,2,4],取 k=5 时,答案是 3。
可以对 1 执行三次自增操作、对 2 执行两次自增操作,最终得到数组 [4,4,4],其最高频元素的频次是 3。
首先,可以意识到,元素的频次问题,和原数组中的顺序无关。
将尝试把这个问题转化成为关于「连续区间」的问题,技巧是,先对原数组正序排序。
这样问题转化为;
在
k次操作都完成后,找出一段最长的连续区间,其中元素要都相同。
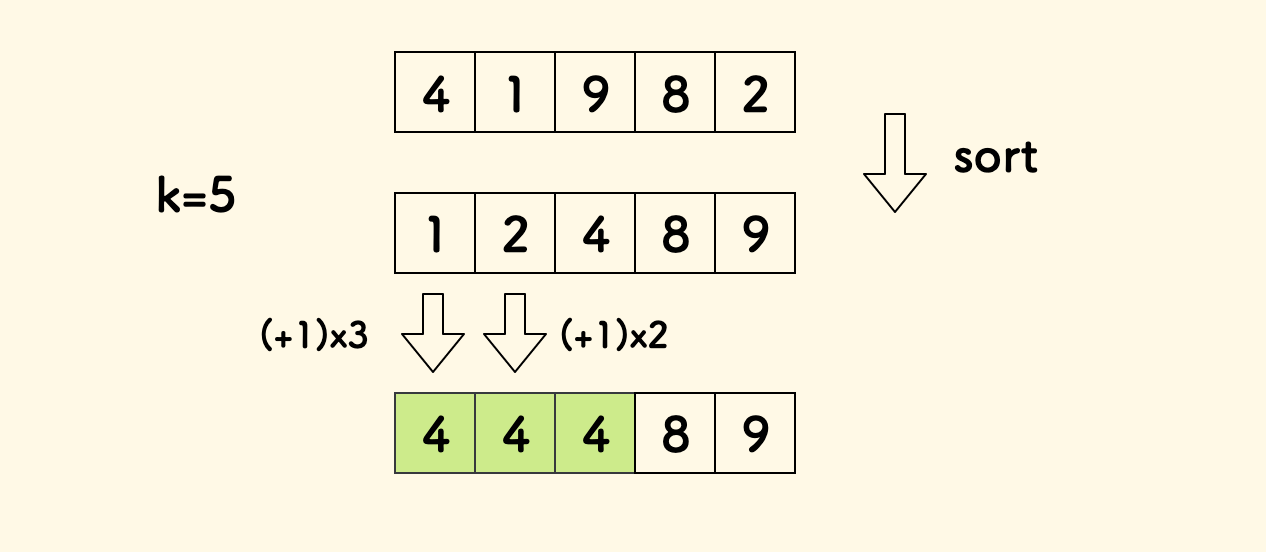
这又成为了一种「枚举区间」的问题。
最终的局面是,会有一个连续的区间,里面元素都一样。那么以此区间的右端点来枚举区间。
又因为只允许自增操作,只能从小到大变,所以,要尝试把区间内的元素都变成右端点的元素。
每次自增操作的步长是 1,变化前后,操作了 k 次的话,区间和就增加了 k。
最终的预期区间和是:
S = (R-L+1) * a[R]
问题即转化为:
在排序后,找到一个连续的区间,它的区间和距离
S的差不超过k。
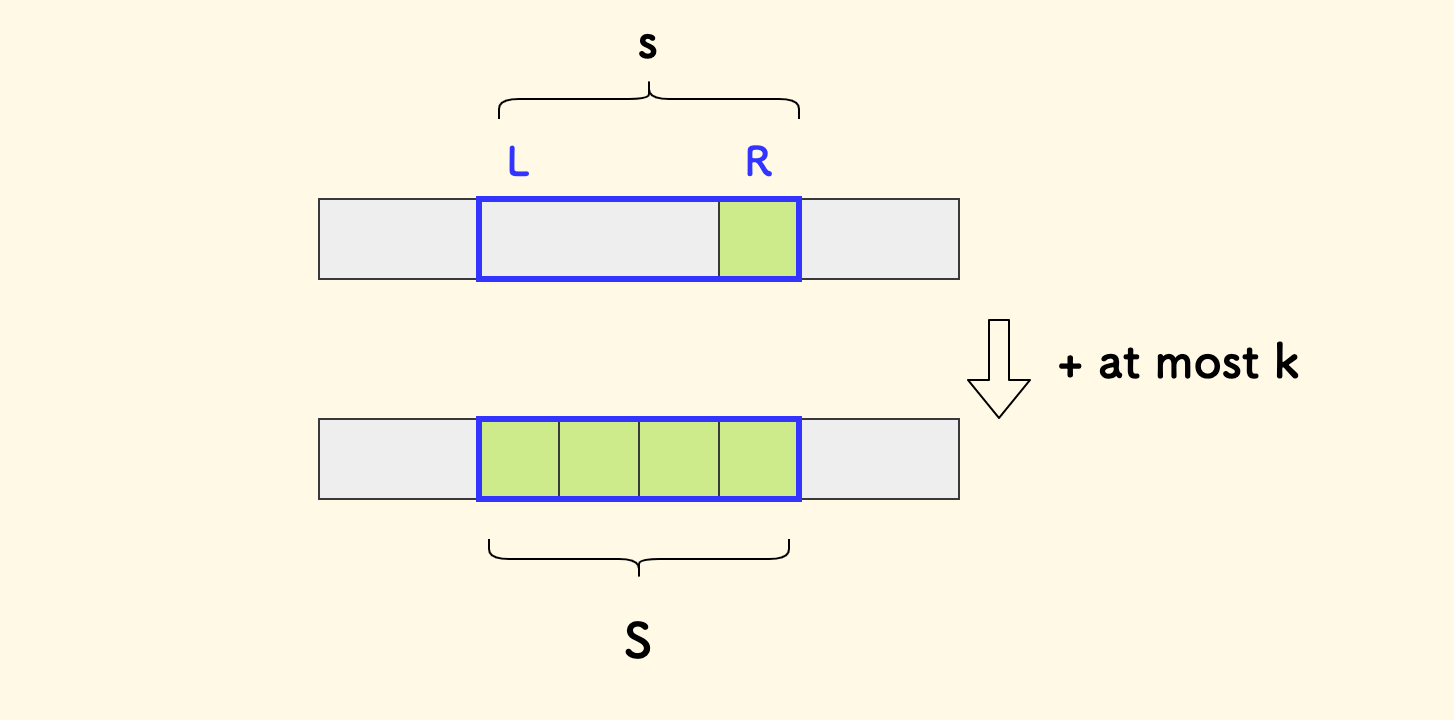
问题的答案则是满足条件的区间的最大的长度。
假设滑动窗口内的区间和是 s,那么要时刻保证 S-s <= k, 也就是,一旦下面的情况发生,左端就要收缩:
(R-L+1) * a[R] - s > k
左端收缩后,后续无需回溯。
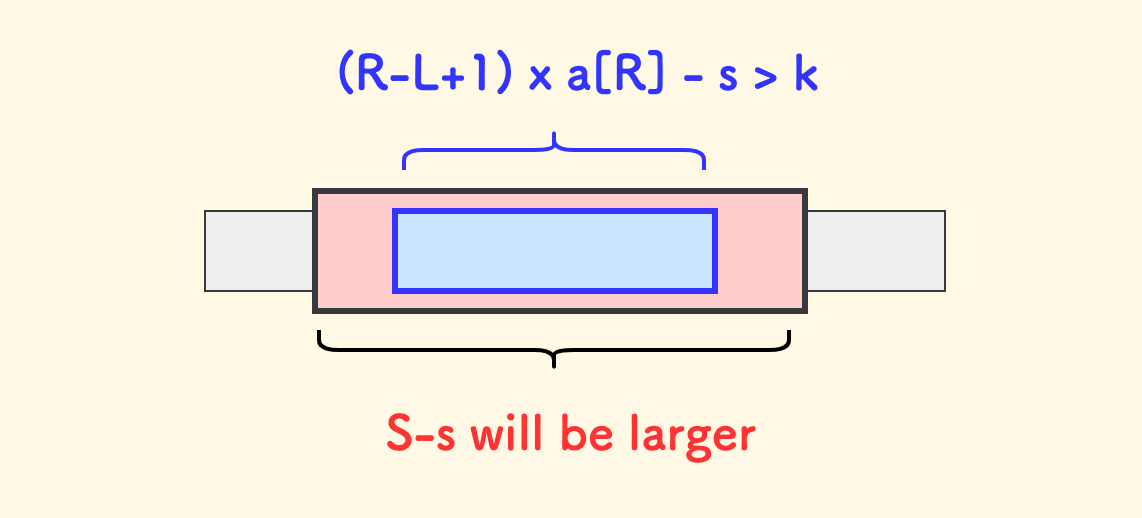
这一点的根本原因在于,数组是正序的正整数数组。如果左端不收缩的话,右端窗口后面补充的元素只会拉大 S-s 的差值。 所以,任何包含这个区间的大区间都不是可行解。
左端收缩的单调性,是应用滑动窗口算法的前提。
在滑动过程中,维护区间和 s 是非常简单的,不再赘述。
最终代码实现如下:
最高频元素的频数 - C++ 代码
using ll = long long;
class Solution {
public:
int maxFrequency(vector<int>& a, int k) {
ll s = 0; // 窗口内实际区间和
int ans = 0;
sort(a.begin(), a.end());
for (int L = 0, R = 0; R < a.size(); R++) {
s += a[R];
// 变更后区间和是 (R-L+1)*a[R],至多变更量是 k
while (L < R && (ll)a[R] * (R - L + 1) > k + s) {
s -= a[L++];
}
ans = max(ans, R - L + 1);
}
return ans;
}
};
最高频元素的频数 - Python 代码
class Solution:
def maxFrequency(self, a: List[int], k: int) -> int:
a.sort()
s = 0 # 窗口内的实际的区间和
ans = 0
L = R = 0
while R < len(a):
s += a[R]
while L < R and a[R] * (R - L + 1) > k + s:
s -= a[L]
L += 1
ans = max(ans, R - L + 1)
R += 1
return ans
最小覆盖子串 ¶
给你一个字符串
s、一个字符串t。返回s中涵盖t所有字符的最小子串。如果不存在、则返回空字符串""。-- 来自 leetcode 76. 最小覆盖子串
比如说,s="ADOBECODEBANC"、t="ABC" 的时候,最优解是 "BANC"。
这个问题和 字母异位词问题 非常相似,解决方法也是类似的。
仍然是一个「枚举区间」的问题,要找的区间的特征是:
- 字符串
t中的每一种字符在区间内的出现频次不少于在t中的出现频次。 - 这个区间要尽可能的短。
将继续采用前面所说的 滑窗内元素频次的统计方法。
首先,用哈希表 d1 统计字符串 t 中的字符频次。
数字 c 负责维护还需要满足的字符种类数目,初始化为 t 中的字符种类数。
unordered_map<char, int> d1;
int c = 0;
for (auto ch : t) {
d1[ch]++;
if (d1[ch] == 1) c++;
}
另外,用哈希表 d2 来统计滑窗内的字符频次。
初始化答案的起始位置 ans_L 和大小 ans_size:
unordered_map<char, int> d2; // 窗口内的字符频次计数
int ans_L = 0, ans_size = 0x3f3f3f3f;
窗口左端收缩的条件是,左端字符 s[L] 的在窗口内的出现次数超过其在 t 中的频次。 此时当前窗口一定不是一个最优解,因为它一定有一个子区间比它更优。
for (int L = 0, R = 0; R < s.size(); R++) {
while (L < R && d2[s[L]] > d1[s[L]]) {
//...
}
}
这个条件也兼容了左端字符在 t 中不存在的特例情况。
当左端字符的频次还没有得到满足时,不可以收缩窗口,否则可能会错过一个可行解。
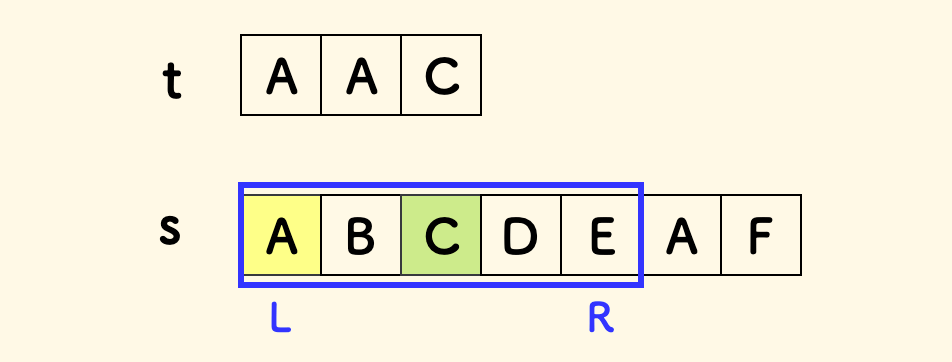
否则,一旦左端字符的频次超过了需求,此时,任何包含这个区间的更大的区间,也都不会是最优解。
下图中,ABCAEA 的频次超过了需求,它有一个子区间 CAEA 比它更优。虽然现在我们还没发现这个最优解,但是完全可以及时断定当前窗口不会是最优。
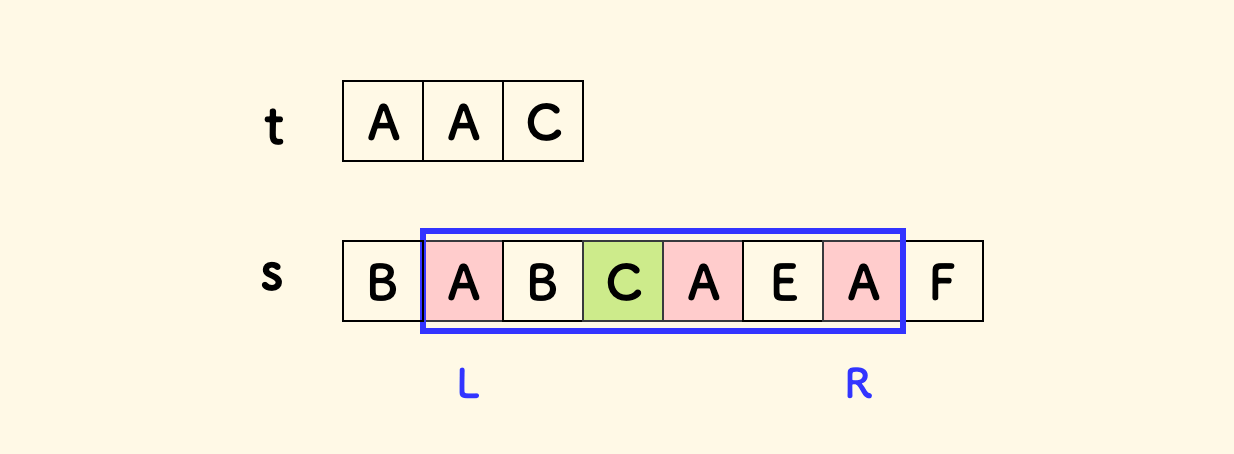
也就是说,窗口左端收缩后,不必回溯,左端指针可以单调右移。符合滑窗的应用前提。
下图是一个左端连续收缩的示意图:

窗口滑动过程中,当右端扩充一个新的字符时:
- 维护窗口内的计数,右端字符在
d2中的计数加一。 - 如果右端字符在
t中存在,且刚好和t中频次一致,那么这一种字符得到满足。
if (++d2[s[R]] == d1[s[R]]) c--;
下图是一个示意图:
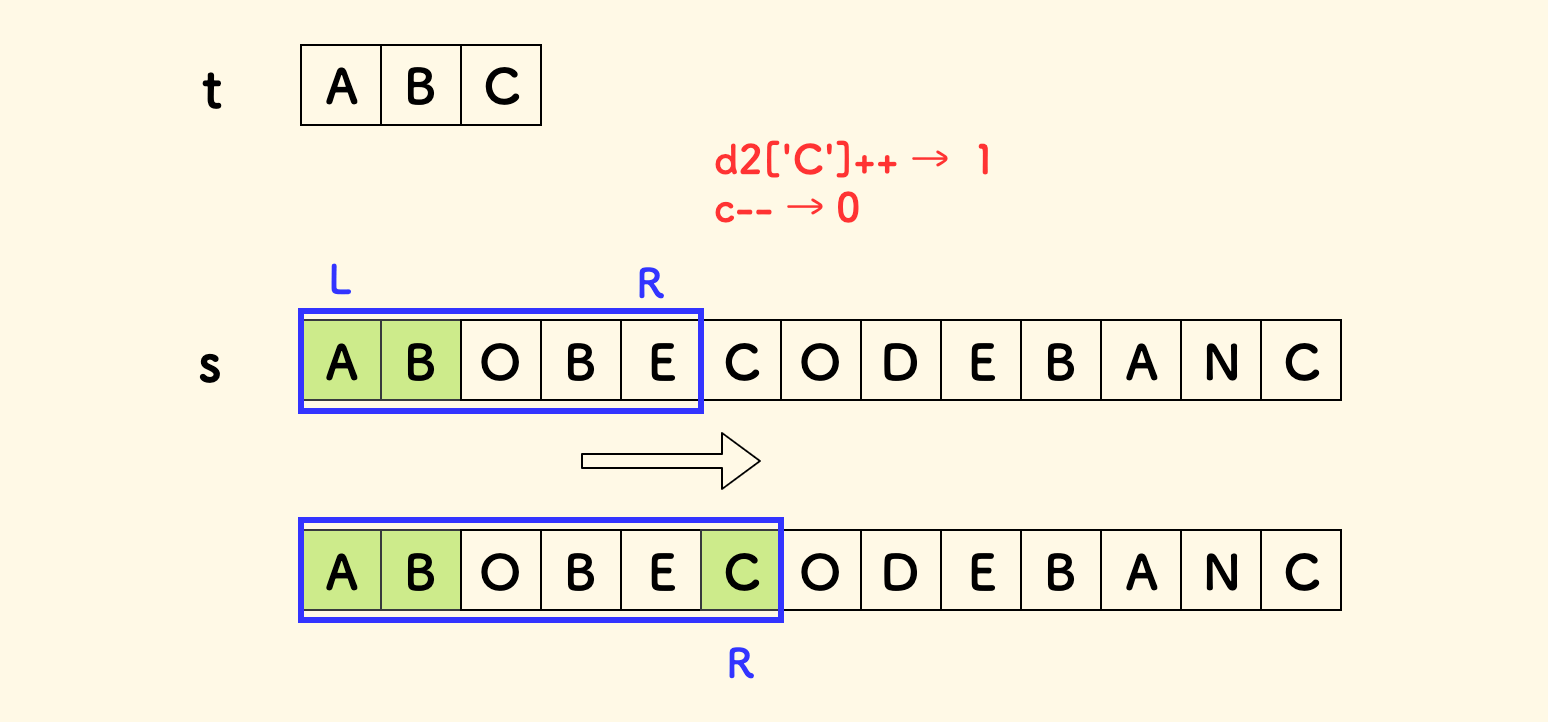
当左端收缩时,只需维护窗口内的左端字符的计数即可:
d2[s[L++]]--;
此时不必维护 c,因为收缩必然终止于 d2[s[L]] == d1[s[L]],并不会造成已满足的字符种类的减少。 自然也不会影响待满足的字符种类数 c。
下图演示了这个情况,收缩左端时,已满足的字符种类数目并不会改变,只是会把超出频次的部分抹掉而已。
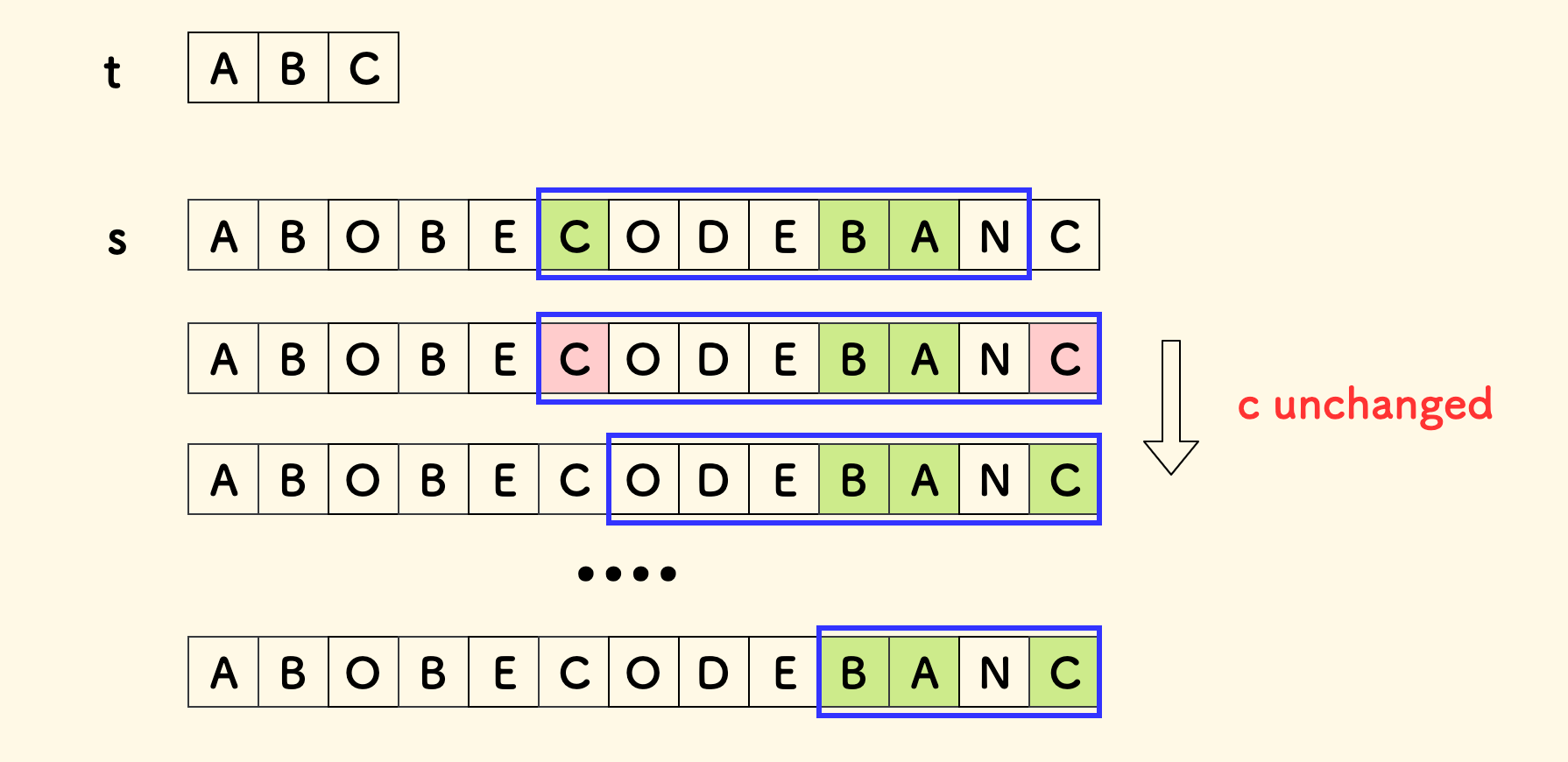
在每次维护完毕窗口后,如果待满足的种数 c 为 0,说明当前窗口满足了 t 的所有字符。
一点点说明
事实上,刚才也已经说明,收缩左端时,已满足的字符种类数目并不会改变。
因此 c 一旦变为 0,后续就一直为 0 了。后面的滑窗过程是在寻找更优的解。
追踪符合条件的最小窗口,就是答案。
完整代码实现如下:
最小覆盖子串 - C++ 代码
class Solution {
public:
string minWindow(string s, string t) {
unordered_map<char, int> d1; // t 内的字符频次计数
// 还需要统计的字符种类, 初始化为 t 中的字符种类
int c = 0;
for (auto ch : t) {
d1[ch]++;
if (d1[ch] == 1) c++;
}
unordered_map<char, int> d2; // 窗口内的字符频次计数
int ans_L = 0, ans_size = 0x3f3f3f3f;
for (int L = 0, R = 0; R < s.size(); R++) {
if (++d2[s[R]] == d1[s[R]]) c--;
while (L < R && d2[s[L]] > d1[s[L]])
d2[s[L++]]--;
if (c == 0 && ans_size > (R - L + 1))
ans_L = L, ans_size = R - L + 1;
}
if (ans_size > s.size()) return "";
return s.substr(ans_L, ans_size);
}
};
最小覆盖子串 - Python 代码
class Solution:
def minWindow(self, s: str, t: str) -> str:
d1 = defaultdict(int) # t 内的字符频次计数
c = 0 # 还需要统计的字符种类, 初始化为 t 中的字符种类
for ch in t:
d1[ch] += 1
if d1[ch] == 1:
c += 1
d2 = defaultdict(int) # 窗口内的字符频次计数
ans_L = 0
ans_size = 0x3F3F3F3F
L = R = 0
while R < len(s):
# 维护右端: 窗口内计数+1
# 并且如果是需要的字符, 则维护需要的种类 c
d2[s[R]] += 1
if d2[s[R]] == d1[s[R]]:
c -= 1
# 维护左端: 左端 L 字符的出现次数超过 t 中的
while L < R and d2[s[L]] > d1[s[L]]:
d2[s[L]] -= 1
L += 1
# 维护答案
if c == 0 and ans_size > R - L + 1:
ans_L, ans_size = L, R - L + 1
R += 1
if ans_size > len(s):
return ""
return s[ans_L : ans_L + ans_size]
K 个不同整数的子数组 ¶
给定一个正整数数组
a和一个整数k,返回a中 「好子数组」 的数目。如果
a的某个子数组中不同整数的个数恰好为k,则称a的这个连续、不一定不同的子数组为 「好子数组 」。-- 来自 leetcode 992. K 个不同整数的子数组
比如说, [1,2,1,2,3],取 k=2 时的好数组有 7 个,分别是:
[1,2]
[2,1]
[1,2]
[2,3]
[1,2,1]
[2,1,2]
[1,2,1,2]
这个问题也是在「枚举区间」。
要找的区间的特征是:区间内的元素种类的数量恰好为 k。
但是,尝试后会发现,以目标区间来套滑窗的话,左端不满足单调右移的性质。
可以拆解为 两个滑窗,也就是寻找两种区间:
- 区间
w1:其中的元素种类个数不多于k,左端指针记为L1。 - 区间
w2:其中的元素种类个数严格少于k,左端指针记为L2。
两个滑窗共享同一个右端指针 R。
将以区间右端点来枚举符合条件的答案。
如下图所示,L1 和 L2 之间的任一个元素,和右端 R 形成的区间中的元素个数都会恰好为 k。 也就是,以当前 R 为右端的目标区间的个数,就是 L1 和 L2 之间的元素个数(不含 L2,包含 L1)。 用代码来表示就是:
ans += L2 - L1;
具体地,在图中,以当前的 R 为右端点的目标区间有 2 个,分别是 [2,1] 和 [1,2,1]。
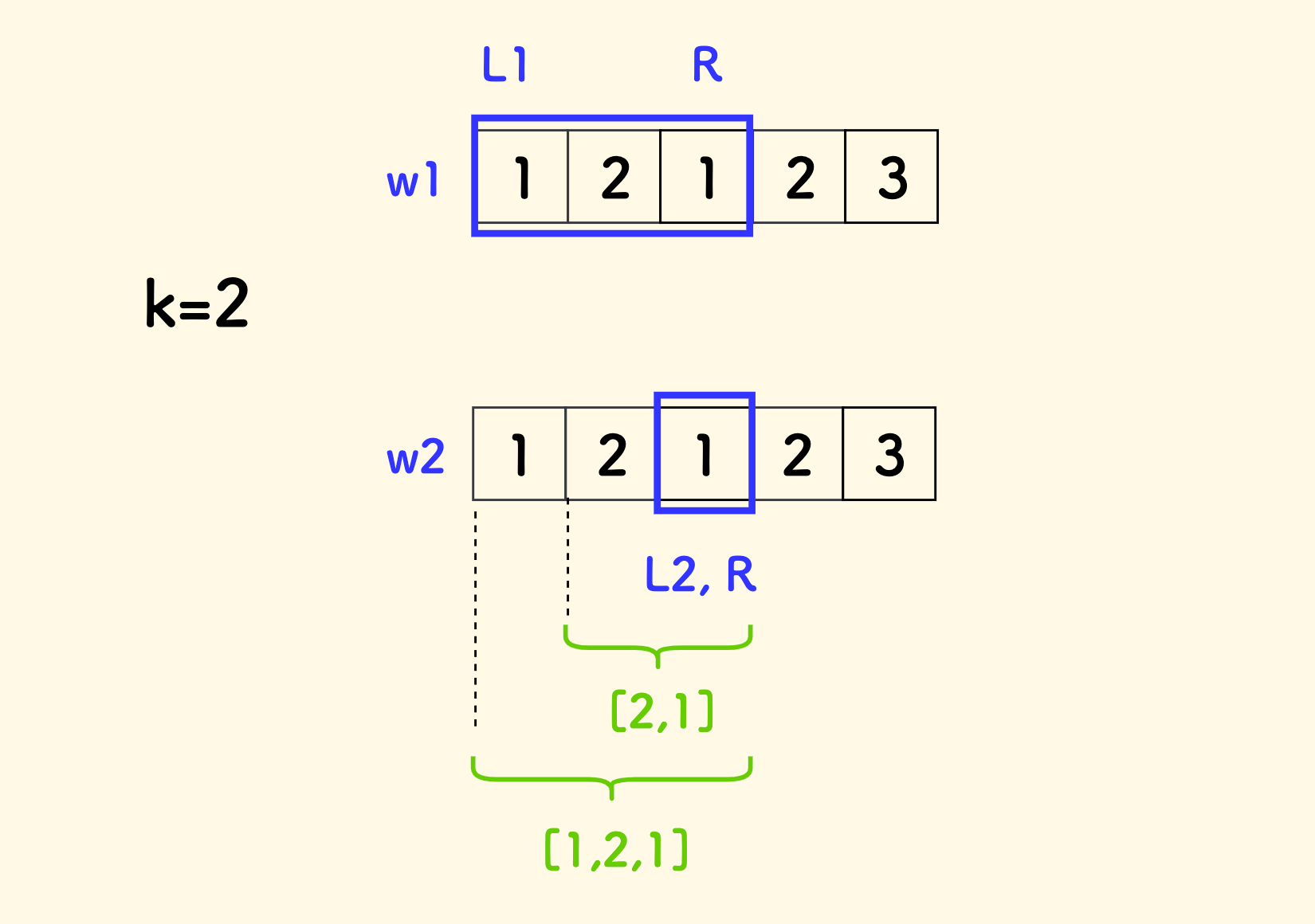
如何维护滑窗内的元素种类,前面多个问题已有所涉及, 以滑窗 w1 为例,用一个哈希表来统计滑窗内的元素频次,数字 c 来统计窗口内的元素种类:
unordered_map<int, int> d1;
int c1 = 0;
当滑窗右端扩张时:
if (++d1[a[R]] == 1) c1++;
当滑窗左端收缩时:
if (--d1[a[L1++]] == 0) c1--;
对于滑窗 w1 来说,窗口收缩的条件很显然:如果窗口内的元素种类数 c1 超过 k,左端即需要收缩。
while (L1 < R && c1 > k) { // w1 的左端收缩条件
...
}
我们需要论证一下 w1 的左端收缩具备单调性。
下图中,k=2 的时候,上面的情况中红色的区间内的元素种类超过 k,不再合法。任何包括此区间的更大的区间,都不会合法。 也就是 w1 的左端一旦收缩,即不必回溯,符合滑窗的应用场景。
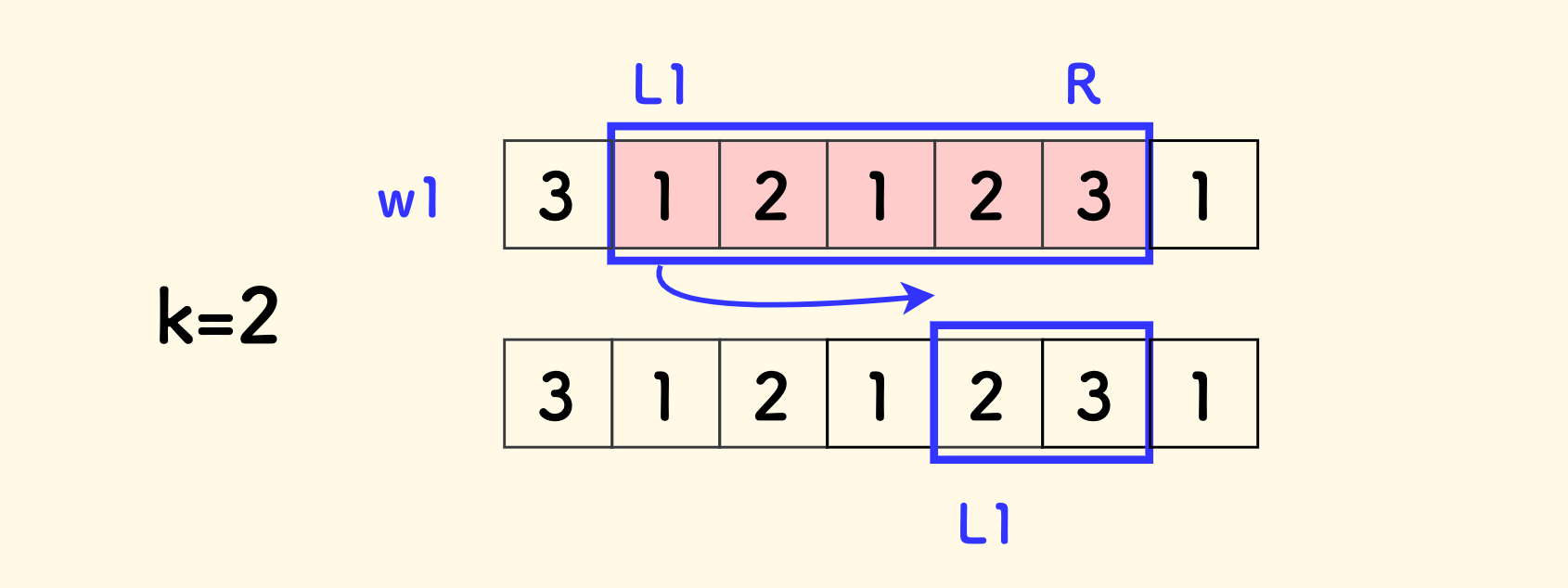
同样的分析,也适用于窗口 w2。
一个细节是,w2 要允许空窗出现。因为空窗中的元素种类数是 0,也是严格小于 k 的。
综合一下,可以得到最终的代码实现:
K 个不同整数的子数组 - C++ 代码
class Solution {
public:
int subarraysWithKDistinct(vector<int>& a, int k) {
// 窗口1: <= k, 窗口2: <k
// 两个窗口之间的个数即是答案
unordered_map<int, int> d1, d2;
int c1 = 0, c2 = 0, ans = 0;
for (int L1 = 0, L2 = 0, R = 0; R < a.size(); R++) {
if (++d1[a[R]] == 1) c1++;
while (L1 < R && c1 > k) {
if (--d1[a[L1++]] == 0) c1--;
}
if (++d2[a[R]] == 1) c2++;
while (L2 <= R && c2 >= k) { // 注意,允许空窗
if (--d2[a[L2++]] == 0) c2--;
}
ans += L2 - L1;
}
return ans;
}
};
K 个不同整数的子数组 - Python 代码
class Solution:
def subarraysWithKDistinct(self, a: List[int], k: int) -> int:
# 窗口1: <= k, 窗口2: <k
# 两个窗口之间的个数即是答案
d1, d2 = defaultdict(int), defaultdict(int)
c1 = c2 = ans = 0
L1 = L2 = R = 0
while R < len(a):
# 维护窗口 w1
d1[a[R]] += 1
if d1[a[R]] == 1:
c1 += 1
while L1 < R and c1 > k:
d1[a[L1]] -= 1
if d1[a[L1]] == 0:
c1 -= 1
L1 += 1
# 维护窗口 w2
d2[a[R]] += 1
if d2[a[R]] == 1:
c2 += 1
while L2 <= R and c2 >= k: # 注意,允许空窗
d2[a[L2]] -= 1
if d2[a[L2]] == 0:
c2 -= 1
L2 += 1
ans += L2 - L1
R += 1
return ans
本题的特色在于,双滑窗,有点意思。
找出最长等值子数组 ¶
如果子数组中所有元素都相等,则认为子数组是一个等值子数组。注意,空数组是等值子数组。
从整数数组
a中删除最多k个元素后,返回可能的最长等值子数组的长度。-- 来自 leetcode 2831. 找出最长等值子数组
比如数组 [1,3,2,3,1,3],k 取 3 的时候,删掉 2 和 1 后得到 [1,3,3,3],最长等值数组是 [3,3,3],长度为 3。
这个问题也是在「枚举区间」,转化一下,其实要找的区间特征是:
区间内由
freq个同一种元素 和 另外k个与之不同的元素构成。window = freq 个同一种元素 + k 个其他元素找这种区间中 最大的
freq就是答案。
比如下图中,目标区间是蓝色的窗口,freq 就是框中的绿色的元素的个数 3。
图中的最后一个元素 3 不能算进来,是因为会打破 k 的限制。

枚举区间的策略是:
- 以右端来枚举区间。
- 追踪窗口内的最高频元素的频次
freq。 - 如果窗口的大小超过
freq+k,则收缩窗口左端。
下图是一个完整的滑动示例,这个例子中的最终答案是 4:
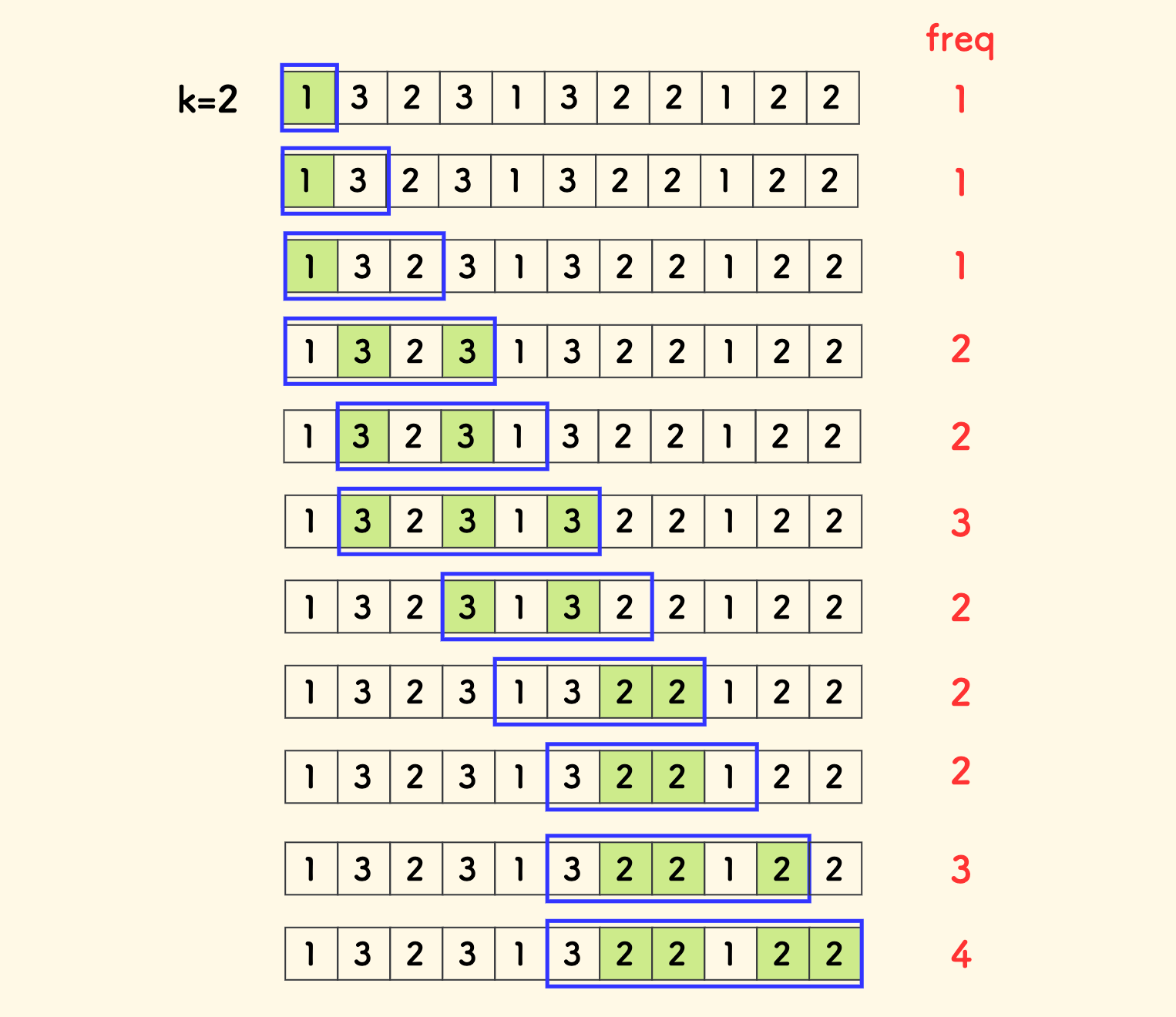
具体地,用一个哈希表 d 来记录窗口内每个元素的频次,再用一个数字 freq 追踪频次最高的元素。
用伪代码来表示就是:
unordered_map<int, int> d;
int freq = 0, ans = 0;
for (int L = 0, R = 0; R < a.size(); R++) {
++d[a[R]];
freq = max(d); // 待定伪代码
while (L < R && freq + k < R - L + 1)
d[a[L++]]--;
ans = max(ans, freq);
}
return ans;注意代码中的高亮的一行,问题在于:动态维护一个哈希表中的最大值,很难做到 $O(1)$。
你可以在这个部分做一遍线性循环来找出最大值, 比如把高亮的一行代码换成下面的,这样是正确性没有问题的,但是提交后会超时。
for (auto x : d) freq = max(freq, x.second);
当然也可以弃用哈希表改用平衡树之类的数据结构,但是最多只能做到 $O(\log{N})$。
解决的技巧,非常简洁而巧妙:放宽窗口的收缩策略。
具体的是说,追踪窗口内历史出现过的最大频次 maxfreq,窗口大小超过 maxfreq+k 时才收缩窗口。
最终答案其实就是 maxfreq,C++ 代码实现如下:
int longestEqualSubarray(vector<int>& a, int k) {
unordered_map<int, int> d;
int maxfreq = 0;
for (int L = 0, R = 0; R < a.size(); R++) {
maxfreq = max(maxfreq, ++d[a[R]]);
while (L < R && maxfreq + k < R - L + 1)
d[a[L++]]--;
}
return maxfreq;
}
找出最长等值子数组 - Python 代码
class Solution:
def longestEqualSubarray(self, a: List[int], k: int) -> int:
d = defaultdict(int)
ans = 0
L = R = 0
while R < len(a):
d[a[R]] += 1
ans = max(ans, d[a[R]])
# 窗口的大小至少为 ans+k
# 后续遇到更高频的, 窗口才会扩张
while L < R and ans + k < R - L + 1:
d[a[L]] -= 1
L += 1
R += 1
return ans
原因在于,正是因为 maxfreq 就是最终答案,那么当历史最大频次降低时,窗口没必要收缩了,因为里面的结果也肯定不是最优解。
下图是一个示例,红色框是改善收缩策略后的窗口情况。可以看到,中间有三个步骤窗口没有像以前那样积极地收缩。因为反正这里面没有最优解。 但是到最后,真正的最优解出现的时候,也就是 maxfreq 最终被再一次拉高的时候,maxfreq 就又开始等同于窗口内的最高频次 freq 的意义了。
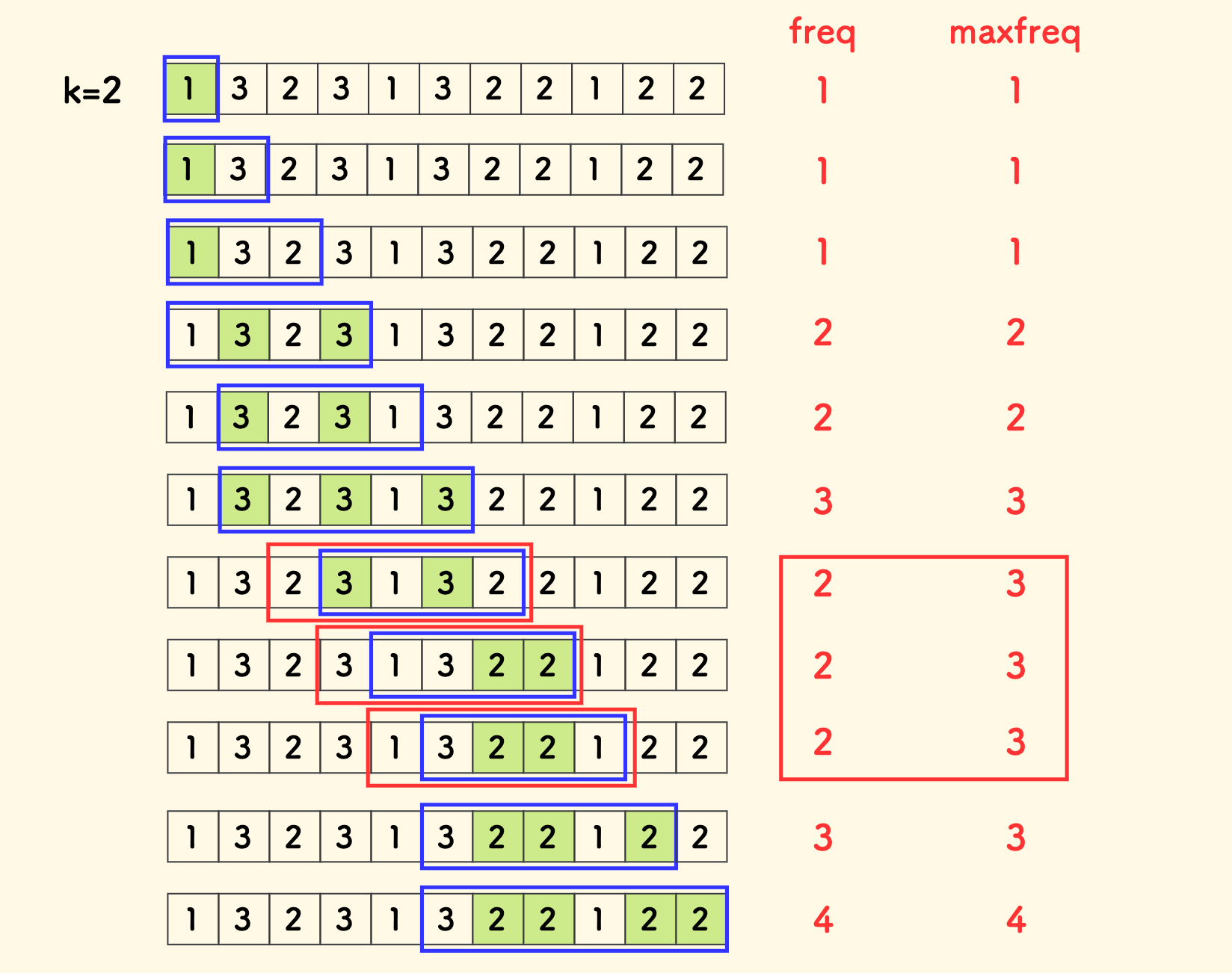
总而言之,maxfreq 在面对更优的解时,意义是等同于 freq 的,否则窗口也不必积极地收缩。
如此一来,总体时间复杂度就是 $O(N)$ 的,非常巧妙 !
简单总结 ¶
- 滑窗的本质,是在枚举区间。
- 常以右端来枚举区间,区间的左端必须单调右移,不可回溯。
- 右端驱动滑动、左端伺机收缩。
- 四个点需要考虑:左端是否单调、左端收缩条件、左端和右端的维护操作、答案计算点。
- 结合哈希表、统计窗内元素种类的手法[跳转]。
- 如果答案本身影响窗口的收缩,可以考虑放宽窗口收缩策略来优化时间复杂度。
(完)
更新历史:
- 2024/02/19: 添加 Python 代码
相关阅读: 单调队列的总结
本文原始链接地址: https://writings.sh/post/sliding-window

