自动机校验浮点数字符串 (DFA & NFA)

有限状态机为何如此有用，其原因之一是它们能识别序列。

最近我在学习正则表达式的构造，期间自己设想了一个问题：

如何识别一个字符串是否是合法的浮点数？

合法的例子：

 '31.25'
 '0.2'
 '.2'
 '1.'
 '-5.28'
 '+1.2'
 '1.0'
 '123'
 '+123'
 '-2'

非法的例子：

 '-.'
 '-'
 '+'
 '-.5'
 '+-1'
 '1.1.1'
 ''
 '.'

解决的思路，当然是用文章开头所说的状态机。

但是解决这个问题的过程中，充满了乐趣，所以写一篇文章。

本文包括两种解法：非确定有限自动机 NFA 的方法和确定有限自动机 DFA 的方法。它们在空间和时间表现上有所不同，但二者在能力上并无高低之分。

需要说明一下：这个问题所举的用例并不完全符合一些编程语言的情况 (比如这个 -.5 在大部分编程语言中是合法的)。而且正负号在一些编程语言中并不直接识别为浮点数字面量，而是作为算术表达式来解析和计算。这些用例只是我自己设定的一套规则。本文主要目的还是分享状态机在识别序列上的应用。

一些铺垫 ¶

首先，NFA 和 DFA 有一些不同点，需要事先说明：

对于确定的输入符号，NFA 可以有多个目标状态，DFA 最多只能有一个。这也是 NFA 叫做非确定自动机、DFA 叫做确定自动机之缘由。

NFA 可以有空边，就是接受一个空符号 ε ，但是 DFA 则不可以。意思是说，在无任何输入的情况下，NFA 中可以沿着空边向前递归跳转。

NFA 的方法 ¶

正则表达式可以等价表示为一个 NFA，也可以进一步转换为等价的 DFA 。

本文中不采用现成的成熟的正则表达式语法，而是采用一种非常简单的正则语法，这有助于理解正则表达式到 NFA 的转化过程。它仅仅支持以下几种规则：

ab 连接两个表达式串
a* 克林闭包，即重复 0 次或多次
a|b 两个表达式取「或」的关系，匹配其中任一即可
a? 即重复 0 次或 1 次
[0-9] 之类的写法，表示范围，它命中一个数字字符
(ab) 括号表示其中的表达式优先结合

那么，识别这种浮点数的正则表达式可以表达为：

((+|-)[0-9])?[0-9]*(([0-9].)|(.[0-9]))?[0-9]*

我们不能用诸如 (+|-)?[0-9]*.?[0-9]* 之类的表达式来匹配，是因为：

+, +. 或者 -. 之类的是非法的案例
. 也是非法的案例

因为正负符号一定要后置一个数字才合法；小数点也一定要相邻一个数字才合法。

所以，这个正则表达式的理解是这样的:

((+|-)[0-9])? 表示符号部分可有可无，而且正负符号必须右侧结合一个数字
[0-9]* 表示小数点前的剩余部分整数
(([0-9].)|(.[0-9]))? 表示小数点部分，而且它必须左侧或者右侧结合一个数字
最后一个 [0-9]* 来匹配小数点后剩下部分的数字串

关键点来了，正则表达式可以表达为 NFA 。具体的表示方法可以看下图：

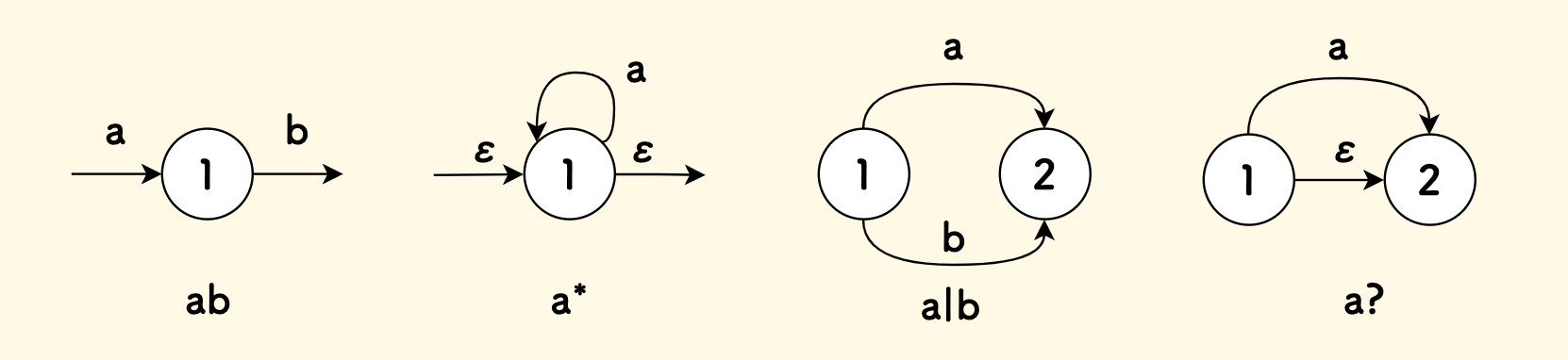
ab 是一种串行连接
a* 是一种循环
a|b 是一种并行连接
a? 其实是 a|b 的一种特例情况，即当 b = ε 时。

根据这种基本规则的表示方法，我们可以把这个正则表达式表示为一个 NFA 状态机：

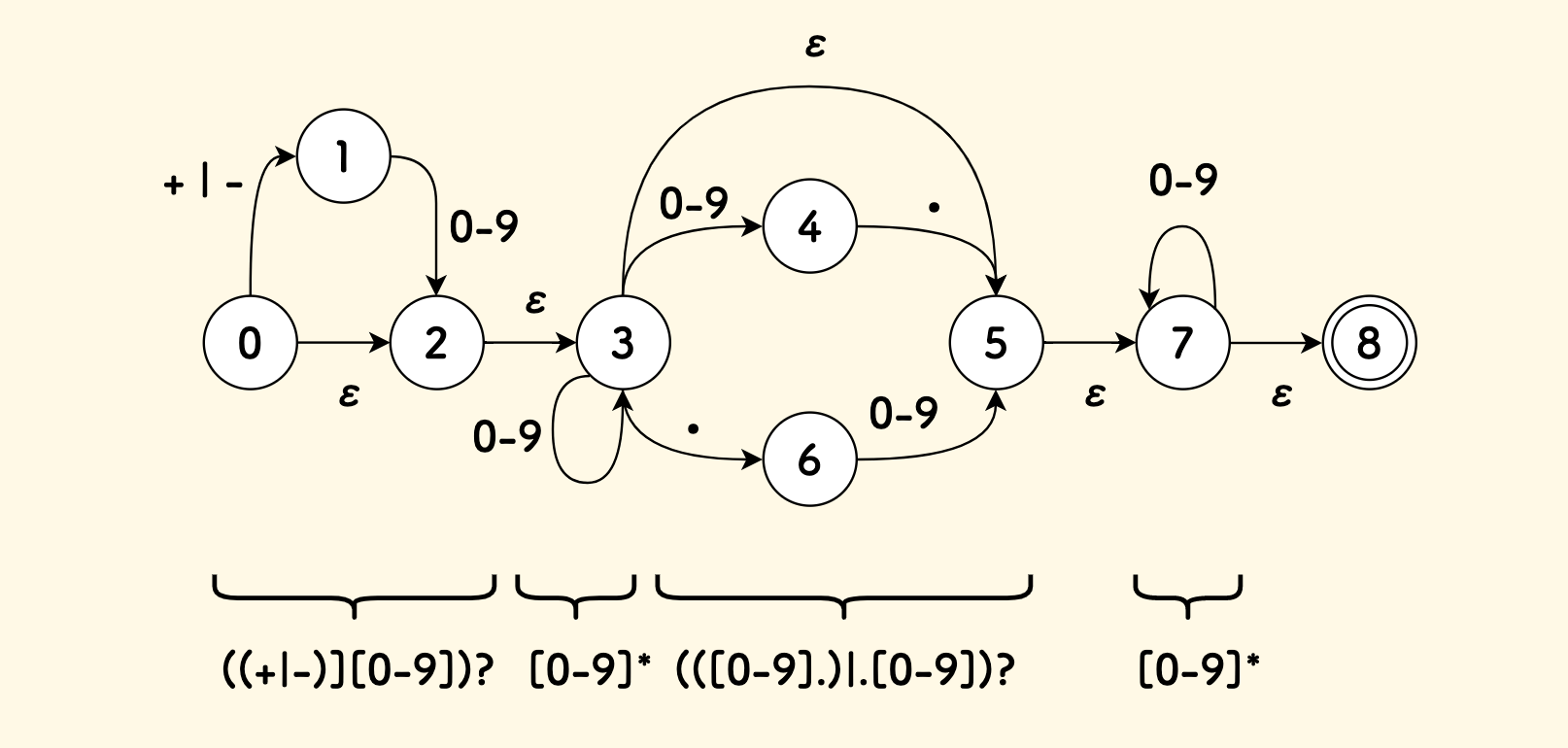
上图中:

有 9 个状态，0 号是起始状态，8 号是终态
可以沿着空边 ε 在无任何输入的情况下递归前跳
3 号状态在相同的输入下，可能会跳转到 {3, 4} 两个状态，所以是一种非确定状态机

字符串输入完毕时，如果可以跳入终态，匹配即成功。

程序实现会有两部分：跳转函数和匹配主函数。

因为每一次跳转，目标状态可能有多个，所以需要检查每一条可能的跳转路径。

最后是代码实现： NFA 识别浮点数 C++ 版本 on Github

DFA 的方法 ¶

NFA 一定可以表达为一个等价的 DFA。

但是转换 NFA 到 DFA 的过程，以及化简 DFA 状态数目的过程，比较复杂。我后面会写一篇关于正则表达式引擎的文章 (已更新: 实现一个简单的正则表达式引擎)。

直接放出来一个匹配这种浮点数的 DFA （实际上它也是最小的）：

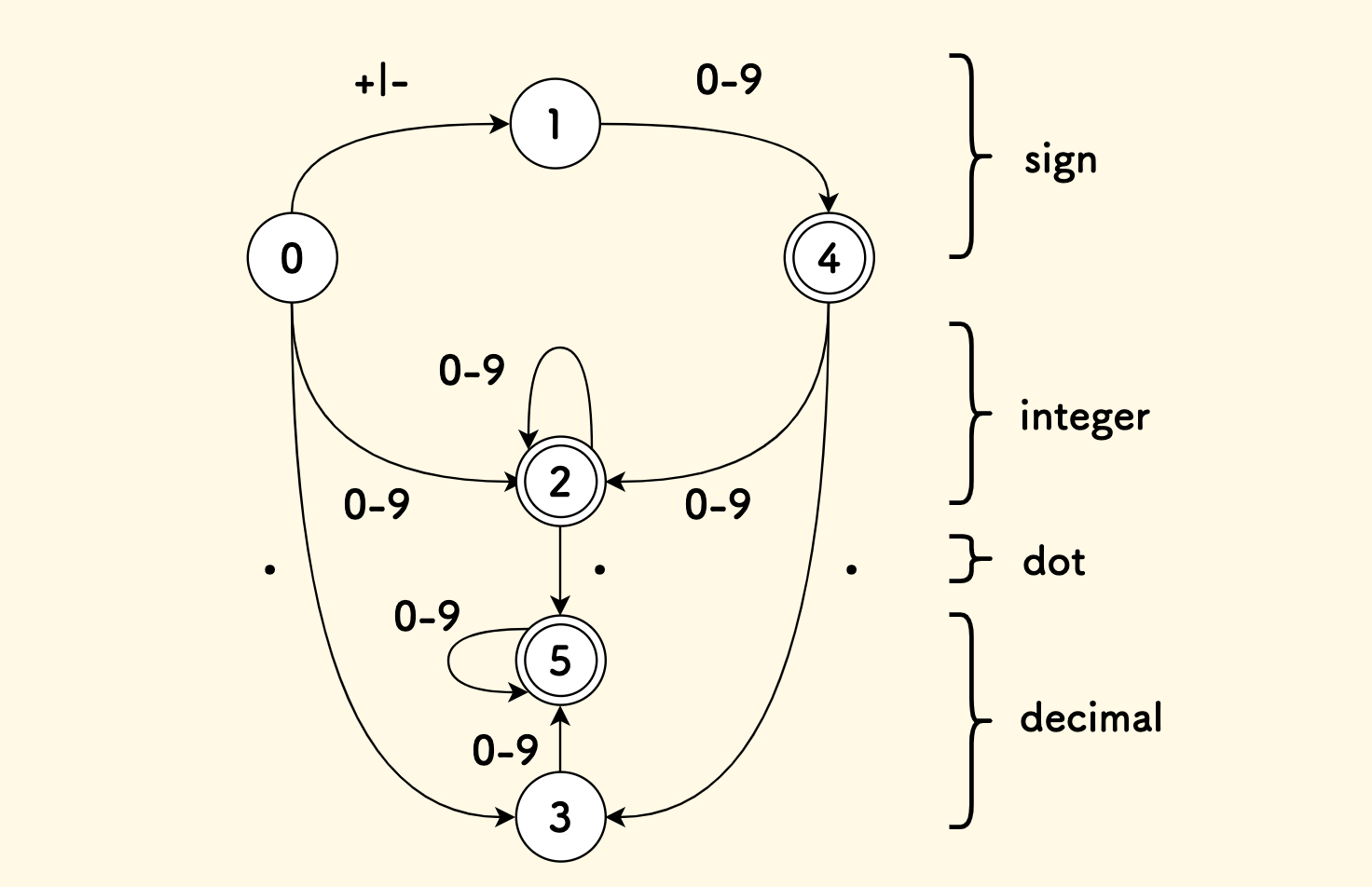
这张图上同时解释了它的含义：

一共有 6 个状态, 其中 0 号状态是起始状态，2, 4, 5 是三个终态
最上面的 sign 部分匹配正负号（并跟随一个数字）
中间 integer 部分匹配剩余的、小数点前面的整数部分
下面 dot 是小数点，它过 3 号状态来右结合一个数字、过 2 号状态来左结合一个数字。
最下面 decimal 部分是匹配小数点后剩余的数字串

对比看起来，和 NFA 部分中的正则表达式的含义是完全一致的。

如果问这个 DFA 是怎么来的？我只能说有两种路子：

硬凑出来，如同配化学方程式一样。
用正则表达式的 NFA 转换到 DFA （所以我可以知道这个 DFA 同时是最小的）

匹配的方法仍然是：字符串输入完毕时，如果可以跳入终态，匹配即成功。

采用 DFA 的方法相对 NFA 的方法有一个好处，就是更快。因为：

DFA 在同一个输入符号下，目标状态是确定唯一的。不像 NFA 需要遍历所有可能的路径。
DFA 不存在空边，不会在跳转函数内级联跳转，简单轻巧。

DFA 匹配的时间复杂度只有 O(n)，其中 n 代表输入字符串的长度。

最后的代码实现： DFA 识别浮点数 C++ 版本 on Github

结尾语 ¶

文章的最后，再来回味一下这句话吧：

有限状态机为何如此有用，其原因之一是它们能识别序列。

不过，有限状态机并不能识别所有类型的序列，正则只是一种能力比较弱的文法。

（完）