本文是有向无环图的 拓扑排序 和 一些相关题目 的笔记。
拓扑排序 ¶
对于一张有向无环图,把它的所有节点输出成一个序列 A,如果对于任何一条从节点 x 到节点 y 的有向边, 都有 x 在序列 A 中的位置会出现在 y 之前,那么 A 就是这个图的一种拓扑排序。
简而言之,就是把所有节点排成一个序列,不违反在图中的方向关系。
下图是一个示例:
- 最开始,没有任何边指向节点
1和2,那么它们肯定出现在排序后的最前面。 - 取下
1和2号节点后,余下的节点中没有指向3号节点的,那么继续取下它。 - 如此继续下去,即可完成拓扑排序。
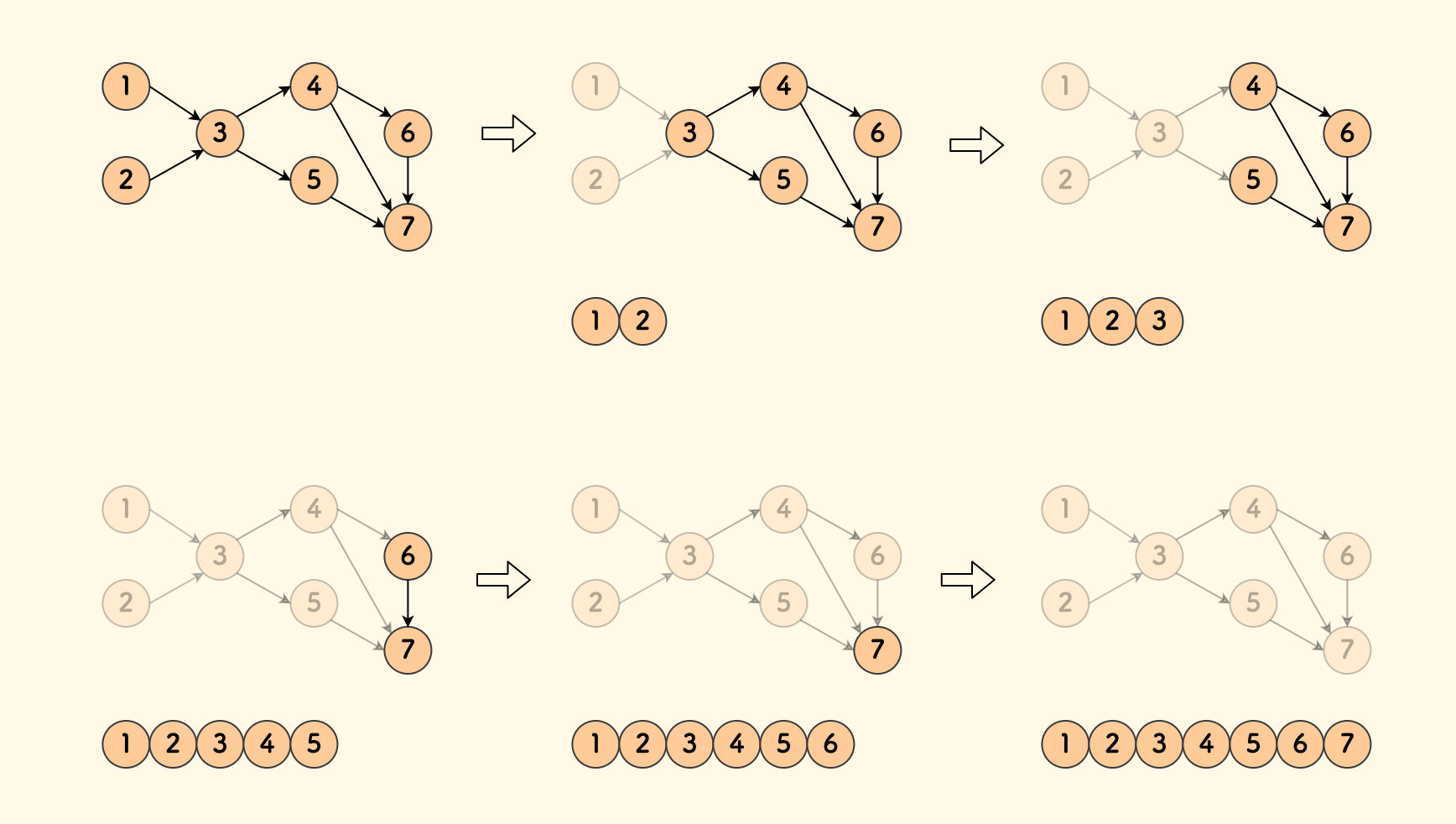
对于一个节点,把指向它的边的个数称为这个节点的 入度,可以总结出来 拓扑排序的核心思路:
- 不断取出入度为
0的节点,加入序列。 - 对于取出的节点、同时把它指向的所有邻居节点的入度减一。
也就是说,拓扑排序将所有节点按照入度递增排列。
从这个例子也可以知道,一个有向无环图的拓扑排序并不唯一。
Unix 系统上有一个命令 tsort 就是做这个事情的。
tsort 命令的示例
tsort 命令的使用方式是,每行输入一个有向边,最后输入 CTRL-D 结束,则会返回一种拓扑序:
$ tsort
1 2
2 3
1 3
3 4
1D
2
3
4
带环的情况
如果图上有环呢?就无法得到完整的拓扑排序,下面是一个带环有向图的示例:
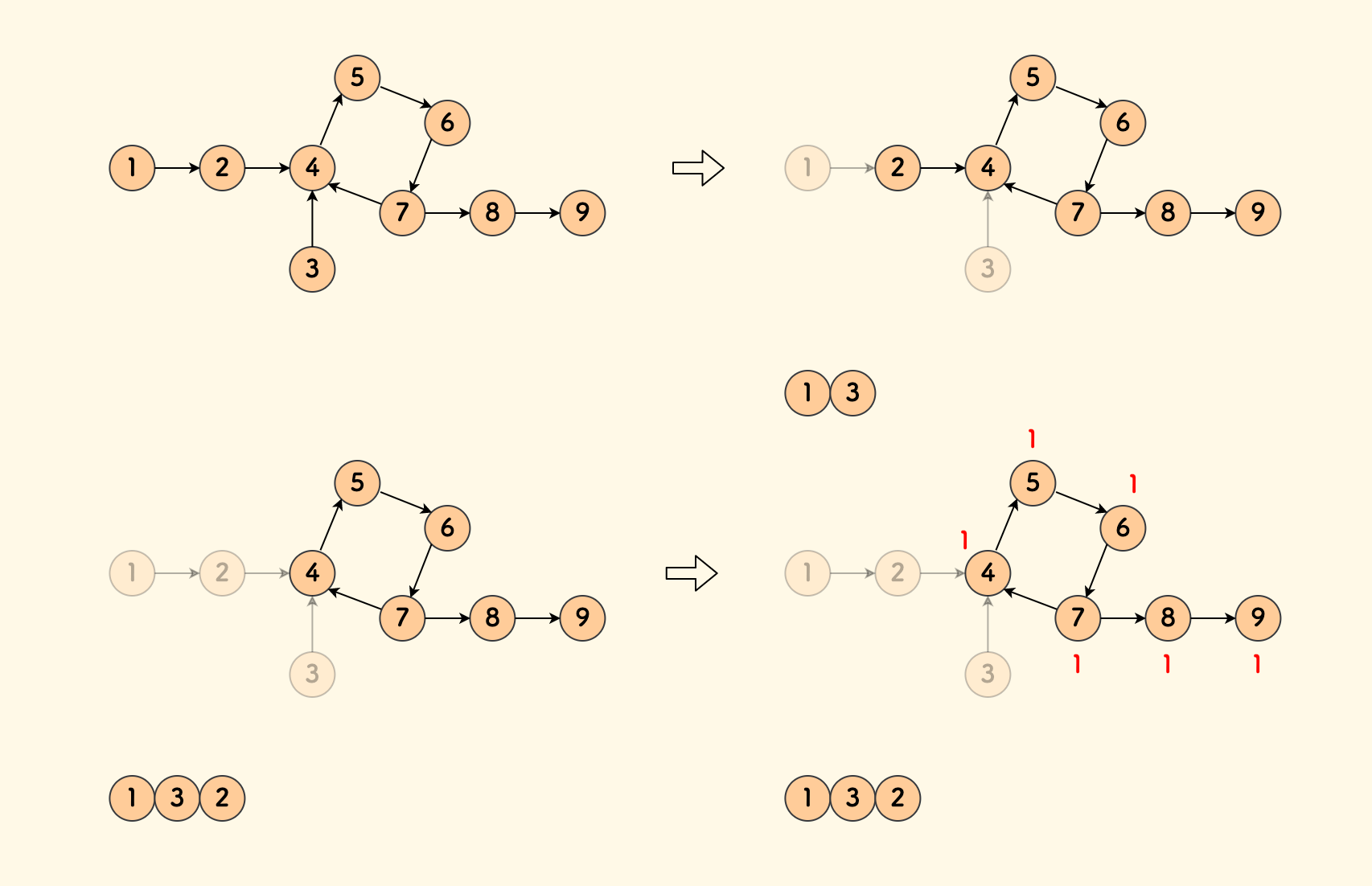
可以看到,有环的情况下,拓扑排序无法取完全部节点。
为什么拓扑排序的规则无法取下环内的节点?
究其原因在于,环上的任一点 x,肯定存在一条节点个数至少为 2 的环形链最终到达自身,比如说 x → a → b ... v → w → x, 要想 x 的入度降低为 0,那么就要依赖取出前置的 w,进而依赖取出前置的 v,逐步推导下去,就会最终依赖回了取出 x 本身,产生逻辑矛盾。
代码模板 ¶
首先,采用 vector 来存图:
vector<vector<int>> edges(n);
for (...) {
// 从节点 x 到 y 存在一条有向边
edges[x].push_back(y);
}
拓扑排序可以采用一个队列来做:
int a[N]; // 拓扑序结果
int deg[N]; // 入度表
void toposort() {
// 初始化入度表
memset(deg, 0, sizeof deg);
for (int x = 1; x <= n; x++)
for (auto y : edges[x]) ++deg[y];
// 入度为 0 的节点初始化入队
queue<int> q;
for (int x = 1; x <= n; x++)
if (deg[x] == 0) q.push(x);
int cnt = 0;
while (!q.empty()) {
auto x = q.front();
q.pop();
a[++cnt] = x;
for (auto y : edges[x])
if (--deg[y] == 0) q.push(y);
}
// 如果 cnt < 节点数,则存在环
}
看上去代码有点长,但是只要抓住核心思路:
不断取出入度为 0 的点、同时扣减邻居节点的入度。
拓扑序也有 DFS 的实现[2],但是我基本不用它。
性质和应用 ¶
判环
如果存在环,那么拓扑排序不会彻底,也就是生成的序列大小一定小于总的节点数目。
对于一些「关系依赖」问题可以抽象为「判环」问题,如果出现环,说明检测到矛盾。
可达性问题
在拓扑序中,可以到达节点
x的点一定出现在它的前面,而x可到达的点一定出现它的后面。 简而言之,祖先一定在其前面、子孙一定在其后面。这个性质对于可达性的判断和统计很重要,往往还会结合拓扑序上的 DP,此时 DP 转移所依赖的方向值得注意。
拓扑序还可以做 DAG 的最短路问题 [1]。
定全序问题
DAG 所描述的其实是一种偏序,就是说并非所有元素都可以比较。 与之对应的关系是「全序」,是说任两个元素都可以有个明确的先后关系,比如实数轴上的所有点。
下图是一个对比,偏序中并非所有元素都可以比较先后,比如图中的
2和3:
这也是拓扑序并不唯一的原因。
偏序是全序的必要但不充分条件。拓扑排序可以帮助确定偏序的合法性,进而如果再满足下面的条件,即可确定唯一全序:
- 只有一个节点的入度是
0,其他节点的入度都是1(进来只有一条路)。 - 只有一个节点的出度是
0,其他节点的出度都是1(出去只有一条路)。
- 只有一个节点的入度是
基环树问题
对于一种特殊的带环图,叫做「内向基环树」,拓扑排序可以剥离出来其中所有的环。
内向基环树的每个节点的出度都恰好为
1,简单说,就是一个环带有多条无环的内向树状链(和一般的树的边方向正好反一下)。 可以看到,所有的边都是指向环内的,所以叫做「内向」嘛。多颗内向基环树可以组成一个带环的有向图,可以用拓扑排序取下树链、留下多个独立的环,即下图中所有蓝色节点组成的环。

还有一种「外向基环树」,其每个节点的入度恰好为
1,边是指向环外的,可以把其所有的边反向,转化到内向基环树。
DAG 最短路 ¶
拓扑排序可以用来求有向无环图上的 单源带边权最短路,而且允许负边权。
求一个有向无环图中,每个边有一个权值,从节点
s出发到达每个节点的最短的边权和。
定义 d(x) 表示到达节点 x 的最短边权和,最开始初始化其中每一项为无穷大。
设置 d(s) = 0。
先对整个图做拓扑排序,然后沿着拓扑序从 s 起正向扫描每个节点 x。
对从 x 出发的每条有向边 (x,y),假设这个边的权值是 w,那么要想到达节点 y,有两种选择,经过 x 或者不经过。
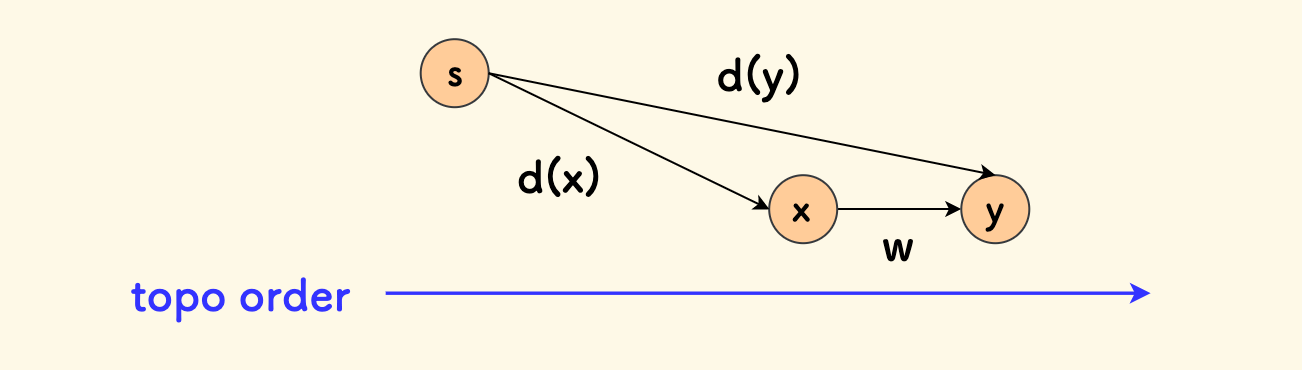
经过 x 到达 y 时,花费的最小代价是 d(x) + w。
不经过 x 时,d(y) 保持不变。
二者取最小值即可:
d(y) = min(d(y), d(x)+w)
因为我们是正向扫描,所以后面的 y 依赖前面 x 的 DP 值进行转移是没问题的。
当然,也可以求 DAG 的最长路问题。
一些题目 ¶
下面是一些题目 和 简单分析。
课程表
leetcode 上拓扑排序的标准模板题:
要学习
n门课程,标号是0~n-1。 在学习一门课程时,必须先修一些前置课程,由数组p给出,其中p[i]=[a, b]的含义是要学习a必须先学习b。 请你判断是否可能完成所有课程的学习?-- 来自 leetcode 207. 课程表
这是个典型的判断循环依赖的问题,也就是判环问题。直接拓扑排序判环即可。
课程表 - C++ 实现
class Solution {
public:
bool canFinish(int n, vector<vector<int>>& p) {
// 存边
vector<vector<int>> edges(n);
vector<int> deg(n, 0); // 入度表
for (auto e : p) {
edges[e[0]].push_back(e[1]);
deg[e[1]]++;
}
// topo sort
queue<int> q;
for (int i = 0; i < n; i++)
if (deg[i] == 0) q.push(i);
int cnt = 0;
while (!q.empty()) {
int x = q.front();
q.pop();
cnt++;
for (auto y : edges[x]) {
if (--deg[y] == 0) q.push(y);
}
}
return cnt == n; // 判环
}
};
排序
给一组形如 $A < B$ 的不等式(只有小于号),要求判断是否可以根据这组关系确定整个数列的顺序。
输入的 $A$ 和 $B$ 都是大写字母。 输出的结果要涵盖三种情况:存在矛盾、无法确定、可以确定,此外应优先判断是否存在矛盾。
-- 来自 洛谷 P1347 排序
多组不等式,可以构成一个有向图,把 x<y 这个关系建立一条边 (x,y)。
首先,判断是否存在矛盾,也就是判环。
而本题目要明确的是更进一步,是否可以确定全序,所以还要进一步判断:
- 是否有且仅有一个节点的入度是
0,其他节点的入度都是1。 - 是否有且仅有一个节点的出度是
0,其他节点的出度都是1。
其他不必再详细分析。
排序 - C++ 实现(省略存图过程)
const int N = 27;
vector<unordered_set<int>> edges; // edges[x] {y} => x < y
int n; // 节点数目
int a[N]; // 拓扑序结果
int deg[N]; // 入度表
// 0 成功, 1 矛盾, 2 无法确定全序
int solve() {
// 入度表
memset(deg, 0, sizeof deg);
for (int x = 1; x <= n; x++)
for (auto y : edges[x]) ++deg[y];
// 同时满足条件矛盾与条件不足, 应该优先输出矛盾, 先看数据有没有矛盾
int flag = 0;
// 特判,没有出度的点应该不多于1个
int c = 0;
for (int x = 1; x <= n; x++) {
if (edges[x].empty())
if (++c > 1) {
flag = 1; // 延迟返回 2
break;
}
}
queue<int> q;
// 加入没有入度的点
for (int x = 1; x <= n; x++)
if (deg[x] == 0) q.push(x);
// 但是, 如果没有入度的点超过 1 个, 说明需要等待继续输入
if (q.size() > 1) flag = 1;
// 没有入度 0 的点一定矛盾
if (q.empty()) return 1;
int cnt = 0;
while (!q.empty()) {
auto x = q.front();
q.pop();
a[++cnt] = x;
int p = 0; // 计算没有入度的点的个数
for (auto y : edges[x]) {
if (--deg[y] == 0) {
// 没有入度的点超过 1 个, 无法定全序
if (++p > 1) flag = 1;
q.push(y);
}
}
}
if (cnt != n) return 1; // 矛盾
if (flag) return 2; // 条件不足
return 0; // 成功
}
去边拆环
给定一个 $n$ 个顶点,$m$ 条边的有向图。你允许从其中去掉最多一条边。
你能够去掉最多一条边就让这个图无环吗?输出 YES 或者 NO.
-- 来自 Codeforces 915.D Almost Acyclic Graph , 洛谷 CF915D
尝试删除一条边,就相当于枚举每个节点,将其入度减一,然后跑拓扑排序判环。
具体的:
- 先跑一次拓扑,如果不存在环,说明已经是 DAG,直接返回 YES。
此时,剩余的入度非
0的点,有可能在环上,也有可能不在环上,如下图所示。此时只好一个一个地进行枚举,依次跑拓扑判环。

细节是,拓扑排序会修改入度表,所以在每次尝试一个节点后,都要注意恢复入度表。
去边拆环 - C++ 实现(省略存图过程)
const int N = 500 + 1;
int n;
vector<vector<int>> edges; // x => {y1, y2, y3...}
queue<int> q; // q 是拓扑队列
vector<int> deg; // 入度表
unordered_set<int> rem; // 待拓扑输出的节点列表
// flag=true 时会操作 rem 集合
// 返回 true 表示无环
bool topo(bool flag) {
int cnt = rem.size();
while (!q.empty()) {
int x = q.front();
q.pop();
cnt--;
if (flag) rem.erase(x);
for (auto y : edges[x])
if (--deg[y] == 0) q.push(y);
}
return cnt == 0;
}
bool solve() {
// 初始化入度表
deg.resize(n + 1);
for (int x = 1; x <= n; x++)
for (auto y : edges[x]) ++deg[y];
// 全部加入剩余列表
for (int x = 1; x <= n; x++) rem.insert(x);
// 把所有入度 0 的入队
for (auto x : rem)
if (deg[x] == 0) q.push(x);
// 先执行一次拓扑
if (topo(true)) return true; // 已经是 DAG
// 找到所有入度 1 的
auto deg1 = deg; // copy
for (auto x : rem) {
if (deg[x] != 1) continue;
deg[x]--; // 删除一个入度, 继续拓扑
q.push(x); // 入度为 0 的入队
if (topo(false)) return true;
deg = deg1; // 恢复入度
}
return false;
}
矩阵中最长递增路径
给定一个 $m \times n$ 整数矩阵
matrix,找出其中 最长递增路径 的长度。对于每个单元格,你可以往 上,下,左, 右四个方向移动。不能 在 对角线 方向上移动或移动到 边界外(即不允许环绕)。
-- 来自 leetcode 329
比如下面的矩阵中,最长路径已经用绿色标出。
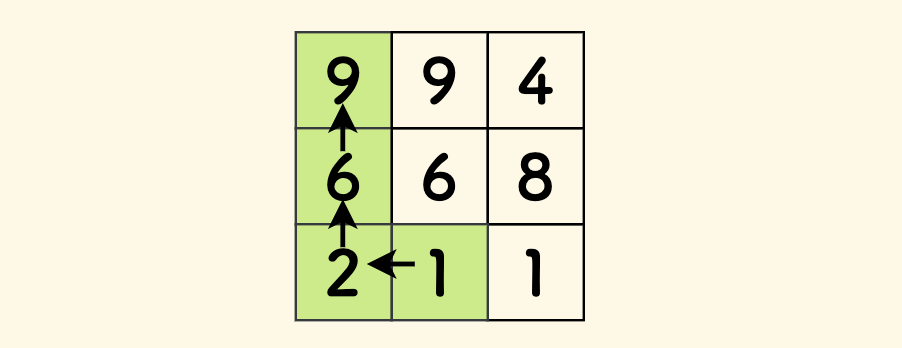
「递增」关系,其实就是 x < y 的小于关系,可以扫描这个矩阵,按照这个小于关系建一张有向图。
扫描的时候,对于每个方格,只需要判断和 左方 和 上方 的邻居方格的关系,无需考虑 下方 和 右方,因为我们是自上而下、自左而右的扫描,这样就避免了重复考察。
如果 x<y,那么加入边 (x,y),否则如果 x>y,就加入边 (y,x),二者相等时不建边。
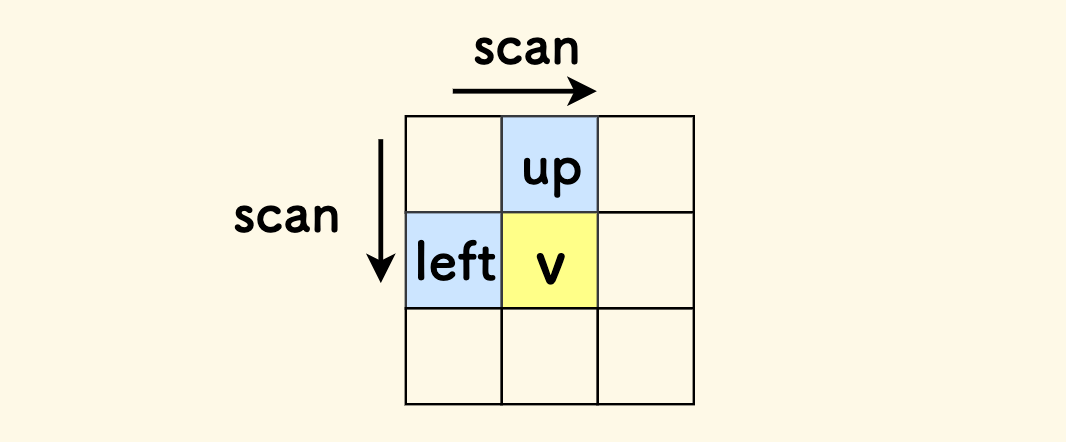
矩阵中最长递增路径 - 建图过程 - C++ 代码
int tot = -1; // 收集节点标号,从0开始
int m = matrix.size(), n = matrix[0].size();
vector<vector<int>> g(m, vector<int>(n, 0)); // g[i][j] -> tot
int N = m * n;
vector<vector<int>> edges(N);
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
g[i][j] = ++tot;
int v = matrix[i][j];
if (i > 0) { // 上边
int up = matrix[i - 1][j];
int x = g[i - 1][j];
if (up < v)
edges[x].push_back(tot);
else if (v < up)
edges[tot].push_back(x);
}
if (j > 0) { // 左边
int left = matrix[i][j - 1];
int x = g[i][j - 1];
if (left < v)
edges[x].push_back(tot);
else if (v < left)
edges[tot].push_back(x);
}
}
}
如此建立的有向图,一定是无环图,因为如果形成环,意味着存在这样一条链: x < y < ... < x,显然是矛盾的。
要求最长的递增路径,就是要求无边权 DAG 的最长路,可以借 拓扑序求最短路 [3] 的思路来做,即 在拓扑序上 DP。
先构造此图的拓扑序 seq:
矩阵中最长递增路径 - 构造拓扑序 - C++ 代码
// 入度表
vector<int> deg(N, 0);
for (int x = 0; x < N; x++)
for (auto y : edges[x]) deg[y]++;
// 拓扑排序
queue<int> q;
vector<int> seq; // 排序后的结果
for (int x = 0; x < N; x++)
if (deg[x] == 0) q.push(x);
while (!q.empty()) {
int x = q.front();
q.pop();
seq.push_back(x);
for (auto y : edges[x])
if (--deg[y] == 0) q.push(y);
}
然后,定义 $f(x)$ 表示 $x$ 开始 (包括自身) 的最长递增路径的长度, 最开始都初始化为 $1$。
倒序扫描拓扑序,对于每一个节点 $x$,考察其指向的邻居节点 $y$ 。 由于是倒序扫描,此时已经知道了 $f(y)$ 的值, 那么从 $x$ 出发的最长递增路径,有两种选择:
- 经过 $y$,此时是 $f(y)+1$
- 不经过 $y$,此时保持原有的 $f(x)$
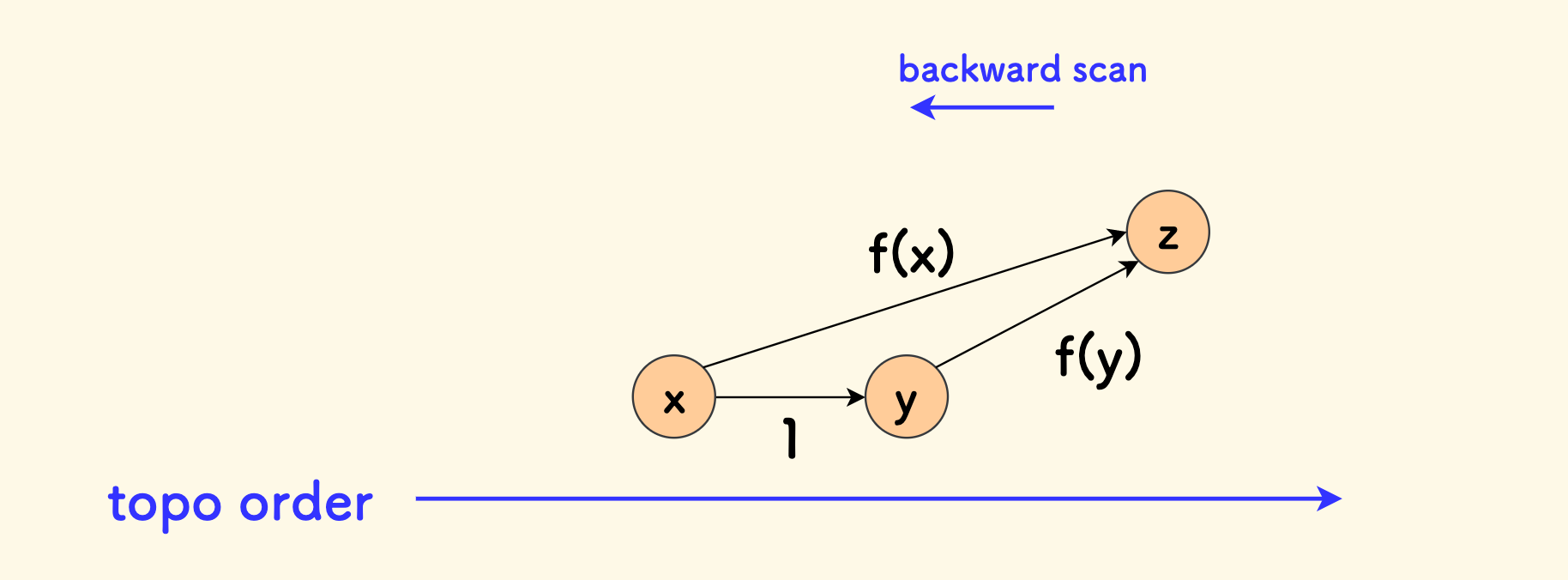
综合来看,取最大值即可:
\[f(x) = \max { \{ f(x), f(y)+1 \}}\]最终答案,就是所有 $f$ 中最大的那个。
矩阵中最长递增路径 - 拓扑序上 DP - C++ 代码
// 从后向前 DP 转移
// f(x) 表示 x 开始(包括x) 的最长递增路径的长度, 最开始都为 1
vector<int> f(N, 1);
for (int j = N - 1; j >= 0; j--) {
auto x = seq[j];
for (auto y : edges[x]) {
f[x] = max(f[x], f[y] + 1);
}
}
// 答案是最终最大的那个 f
return *max_element(f.begin(), f.end());
可达性统计
这是拓扑序的非常经典的一道题:
给定一张 $N$ 个点 $M$ 条边的有向无环图,分别统计从每个点出发能够到达的点的数量。
-- 来自 《算法竞赛进阶指南》· 李煜东, acwing 164. 可达性统计
对这个有向无环图先做一个拓扑排序,那么,对于每一个节点 $x$ 来说,它可以到达的点在拓扑序上的位置一定只会出现在其后面。
对于任何一个 $x$ 可以到达的点 $z$ 来说,必然经过 $x$ 的一个邻居节点 $y$ 来到达。
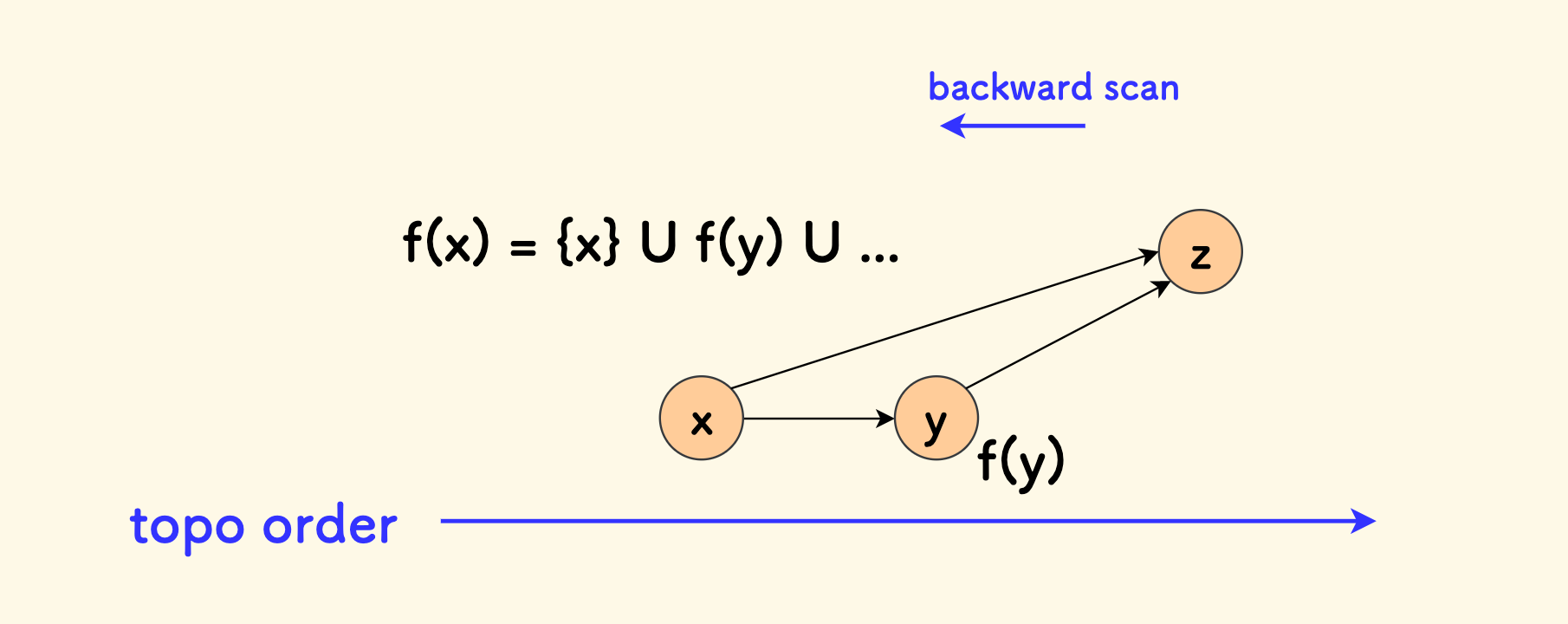
定义 $f(x)$ 为节点 $x$ 可以到达的节点集合,那么:
\[f(x) = \{ x \} \bigcup_{i} f(y_{i})\]因为 $x$ 依赖后序的节点 $y$ 的结果,所以仍然采用倒序扫描拓扑序的办法。
但是,如何统计节点数目呢?不能简单地采用加法求和,因为是集合取并的关系,求和不足以消去重复节点。
这就来到了这个题目最巧妙的地方,采用二进制来解决,在 C++ 中就是 bitset。
定义一个 bitset 的数组 $V[N]$,其中节点 $x$ 可以到达节点 $y$ 表达为 $V[x]$ 的第 $y$ 个比特设置为 $1$。
而集合取并的操作,就是把两个 $V[y_i]$ 和 $V[y_j]$ 进行取或操作,最后再统计每个 $V[x]$ 中的比特为 $1$ 的位数即是答案。
略去拓扑排序的代码,核心统计计数部分实现如下:
可达性统计 - C++ 代码(略去拓扑排序实现、只包含计数统计部分)
const int N = 30000 + 5;
int n;
vector<vector<int>> edges;
int ans[N];
int a[N]; // 拓扑序结果
void solve() {
toposort();
// V[x] 的第 y 位比特表示 x 是否可以到达 y
vector<bitset<N>> V(n + 1, 0);
for (int j = n; j >= 1; j--) { // 倒序
auto x = a[j];
V[x].set(x); // 可以到达自身
for (auto y : edges[x]) V[x] |= V[y]; // 可以到达 y 到达的点
}
// 答案
memset(ans, 0, sizeof ans);
for (int x = 1; x <= n; x++)
ans[x] = V[x].count(); // 计算 1 的位数
}
后面的 最多可删的边数 将再次领略 bitset 统计可达节点数这一技术的威力。
带基环的可达性统计
给定一张 $n$ 个节点(编号从 $0$ 到 $n-1$)的有向图,包含 $n$ 条边。
所有边由数组 $edges$ 给出,其中 $edges[i]$ 表示存在一个有向边从节点 $i$ 指向节点 $edges[i]$。
统计每个节点出发能够到达的点的数量。
-- 来自 leetcode 2876. 有向图访问计数
题目中所说的图,每个节点只有一个出边,一定由多个 内向基环树[4] 构成。
因为可以反证一下,假设这个图是一个有向无环图,那么它就可以做一个完整的拓扑序。在这个拓扑序上,每个节点只有一个出边,是自左向右的方向, 那么最多只能有 $n-1$ 条,多余的一条边必然是反向的,和拓扑序的含义矛盾。
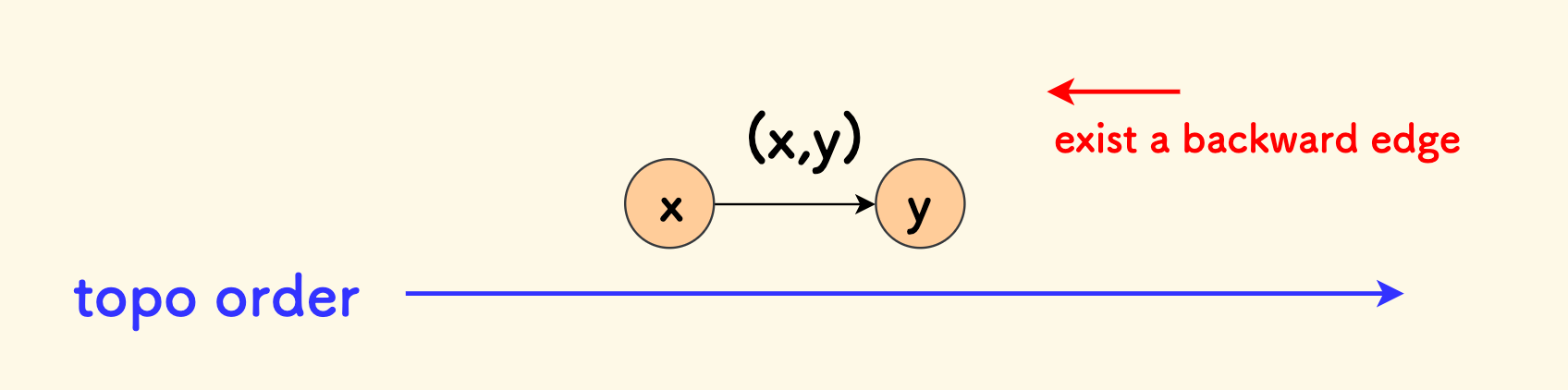
既然存在环,那么环上的任一节点至少有一个出边指向环内,而每个节点的出边恰好为 $1$, 也就是说,每个环没有出边,这就是一个内向基环树构成的有向图。
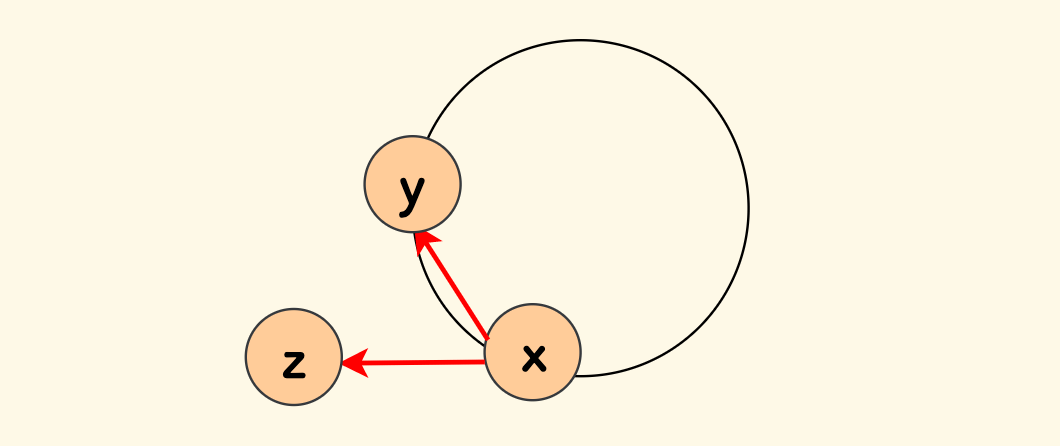
仍然用前面用过的这张图来看,题目中所说的图长这种样子:
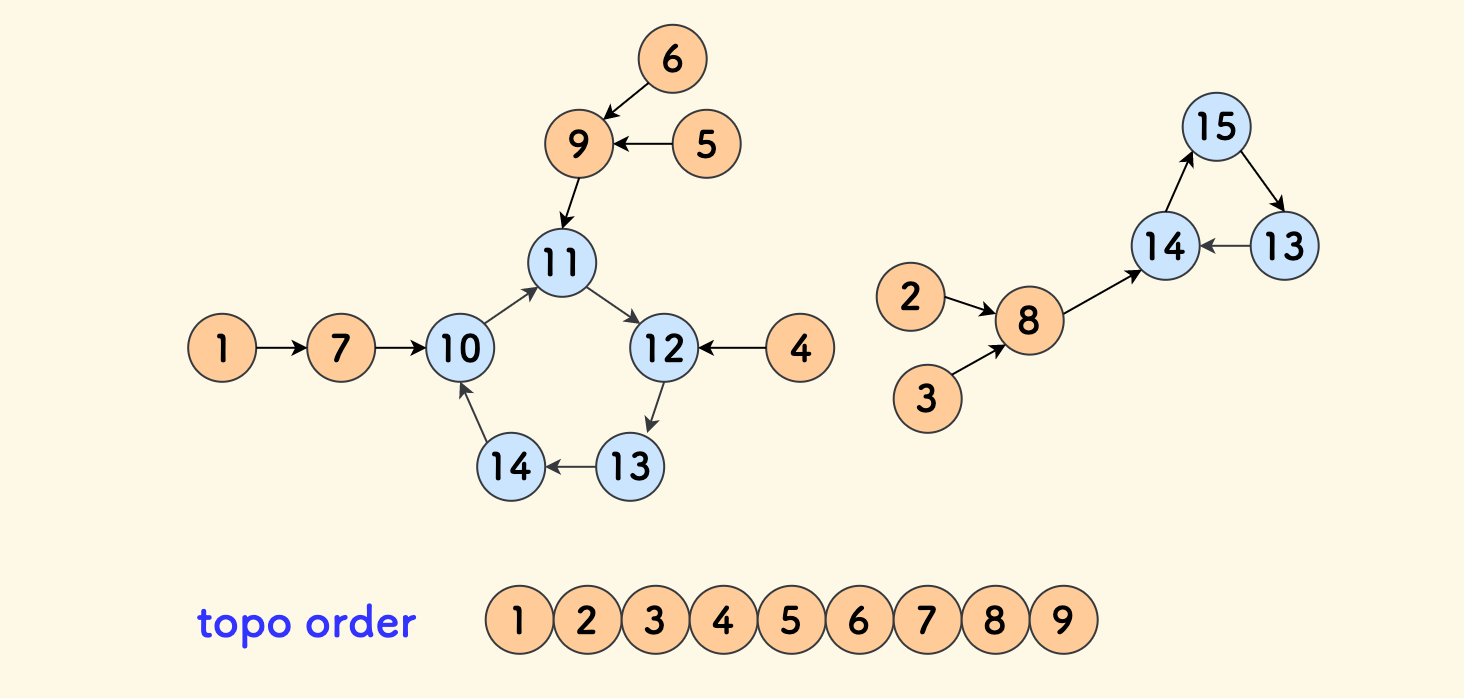
现在的任务是,计算每个节点可到达的节点数量 $f(x)$:
- 对于环上的点来说,答案是其所在环的长度。
- 对于不在环上的节点来说,答案是其连通的环的长度,再加上拓扑序中可到达的节点数目。
先拓扑排序,这样会取出不在环上的、树状链上的黄色节点,留下多个独立的环。
带基环的可达性统计 - 拓扑排序链上部分 - C++ 代码
int n = edges.size();
// 拓扑序
vector<int> deg(n, 0); // 入度表
for (int x = 0; x < n; x++) deg[edges[x]]++;
queue<int> q;
for (int x = 0; x < n; x++)
if (deg[x] == 0) q.push(x);
vector<int> seq; // 链上的拓扑序
while (!q.empty()) {
auto x = q.front();
q.pop();
seq.push_back(x);
auto y = edges[x];
if (--deg[y] == 0) q.push(y);
}
然后,要枚举每个环,来计算其长度。
拓扑序之后,剩余的入度非 0 的点,一定在环上。
另外,对于每个环我们只需要迭代其两次即可,因为同一个环的不同节点的答案是一样的,这可以用一个访问数组来避免重复访问。
求环的长度,只需依次沿着它行走,直到再次遇到出发点。
带基环的可达性统计 - 计算环上的答案 - C++ 代码
vector<int> f(n, 0);
// 先更新环上的答案
for (int x = 0; x < n; x++) {
// 拓扑后环上的点的入度一定非 0
// 每个环只会遍历 2 次 (f[x] 避免重复访问了)
if (!deg[x] || f[x]) continue;
int k = 1;
// 找环的大小
for (int y = edges[x]; y != x; y = edges[y]) k++;
for (int y = x, j = 0; j < k; y = edges[y], j++) f[y] = k;
}
对于不在环上的节点,只需倒序扫描刚才得到的拓扑序,从环上向外更新答案。
对于每个在树链上的节点 $x$ 而言,它可到达的节点有:
- 它自身.
- 节点 $y = edges[x]$ 可以到达的节点,此时不用取并集,因为只有一个出边。
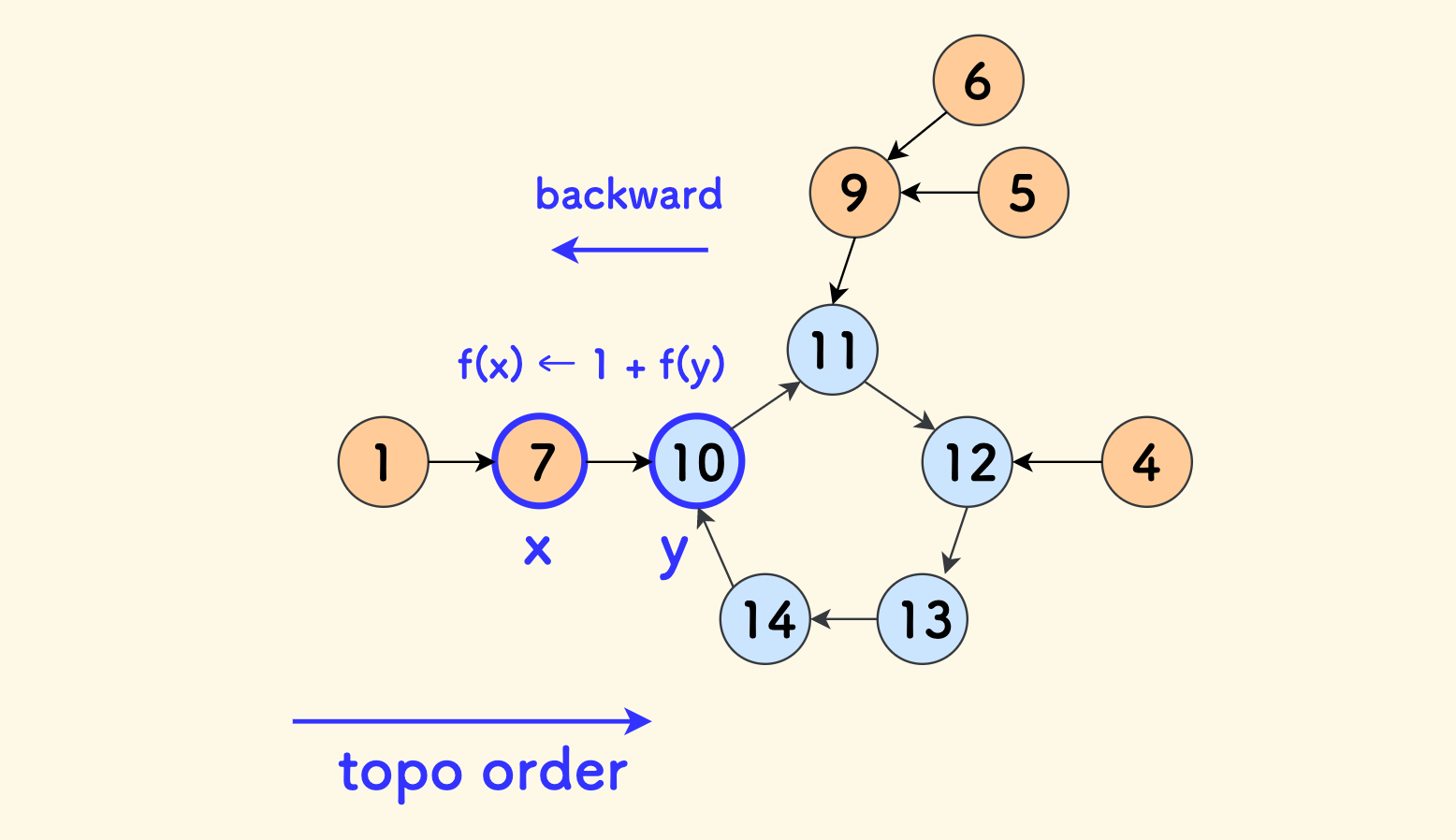
计算 $f(x)$ 的转移方向,在拓扑序上是从后向前的。虽然环上的节点不在拓扑序中,但是并不影响它来初始化链上的答案。
带基环的可达性统计 - 计算链上的答案 - C++ 代码
// 反向拓扑序, 更新链上答案
for (int j = seq.size() - 1; j >= 0; j--) {
auto x = seq[j], y = edges[x];
f[x] = 1 + f[y]; // x 可以到达 y 和 自身
}
最后,重述一下利用到的关键性质:拓扑序可以给内向基环树组成的有向图剥环。
这里还有一道类似的题目 leetcode. 2360 图中的最长环,可以拿来练习。
最多可删的边数
对于一个 $N$ 个点(每个点从 $1$ 到 $N$ 编号),$M$ 条边的有向无环图,想要删除一些边,使得原图任意两点的连通性保持不变,最多可以删除多少条边?
-- 来自 洛谷 P6134 [JSOI2015]. 最小表示
题目保证了给定的是一个有向无环图,那么可以先做一个拓扑排序。
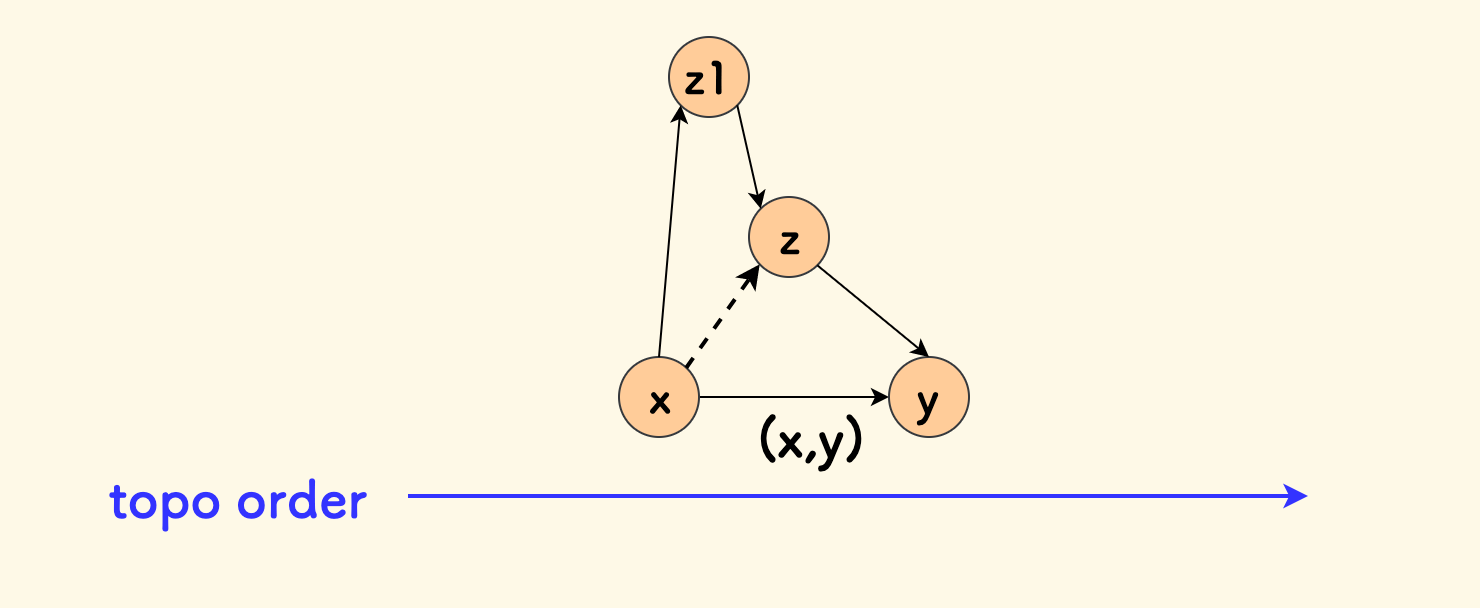
对于任何一条边 (x,y) 来说,如果存在一个点 z 满足:
x可以到达zz可以到达y
那么边 (x,y) 是可以删掉的,而不影响 x 和 y 的连通性。
而且符合此条件的 z,在拓扑序上的位置一定处于 x 和 y 之间。
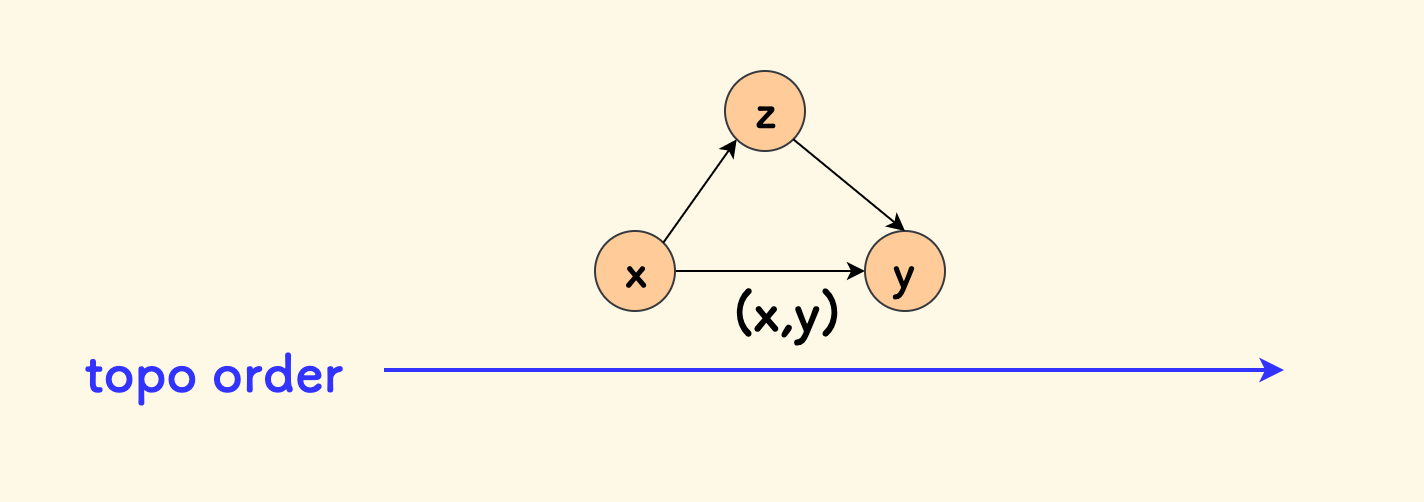
但是,如果边 (x,z) 也被删除了呢?是否可以继续删除 (x,y),会不会删多了呢?
假设,(x,z) 之间也有一个点 z1,导致 (x,z) 被删边。那么显然还是不会影响 x 到 y 的连通性的,因为可以 x → z1 → z → y 的路径来到达。 不影响接下来继续删边 (x,y)。 也就是说,前面的删边操作并不会影响后面的删边。
定义两种集合:
- $from(x)$ 表示可以到达节点 $x$ 的点的集合(不包括自身)。
- $to(x)$ 表示节点 $x$ 可以到达的点的集合(不包括自身)。
那么,枚举每一条边 (x,y),它可以被删掉的条件是下面的这个交集非空:
原问题就转化到了两个子问题,即求解两个集合。
基于前面的问题 可达性统计 的启发,可以仍然采用 bitset 用比特位来表达可达性的办法。
以 $from$ 为例,定义一个 bitset 的数组 from[N],其中 from[y] 的第 x 个比特为 1 表示 y 可以来自 x。
只需要正序扫描拓扑序,对于每一个节点 x,考虑其指向的每个邻居节点 y,那么可以到达 y 的节点有:
x本身x的来源节点集合from[x]
二者取并集即可,也就是:
const int N = 30000 + 1;
bitset<N> from[N]; // 来源集合
for (int j = 1; j <= n; j++) { // 正序转移
int x = seq[j]; // seq 是拓扑序结果
for (auto y : edges[x]) {
from[y][x] = 1; // y 可来自 x
from[y] |= from[x]; // y 可来自 x 的来源
}
}
同样地手法,倒序扫描拓扑序,可以求解 to 数组。
最多可删的边数 - 计算 to 数组 - C++ 代码
bitset<N> to[N]; // 来源集合
// 倒序求可达, 不包含自身
for (int j = n; j >= 1; j--) {
int x = seq[j];
for (auto y : edges[x]) {
to[x][y] = 1; // x 可到达 y
to[x] |= to[y]; // x 可到达 y 的到达
}
}
最后计算答案即可,求交集自然地转化为 bitset 的「与」操作:
for (int x = 1; x <= n; x++) {
for (auto y : edges[x])
ans += (to[x] & from[y]).any();
}
return ans;
简单总结 ¶
- 拓扑排序的主要思路是:不断取出入度为
0的节点,同时扣减其邻居节点的入度。 - 拓扑序的结果并不唯一。
- 主要应用:判环、可达性问题、协助定全序、内向基环树剥环、DAG 最短路(最长路)。
- 拓扑序上 DP 是一种重要应用,注意转移的顺序来确定扫描的方向。
- 借助拓扑序求 来源/可达 的节点集合,借助 bitset 是一个巧妙的技巧!
(完)
相关阅读:- 最小高度树 - 拓扑排序的变形应用


