问题描述 ¶
leetcode 昨天的每日一题,有点难度:
给你一颗含有 $n$ 个节点、$n-1$ 条无向边的树,问选择哪些节点为根的时候,树的高度最小? 其中,树的高度是指从树根到叶子的最长路径上的边的数目。
-- 310. 最小高度树
比如,下图中选取 $1$ 号节点作为根时,树高最小。
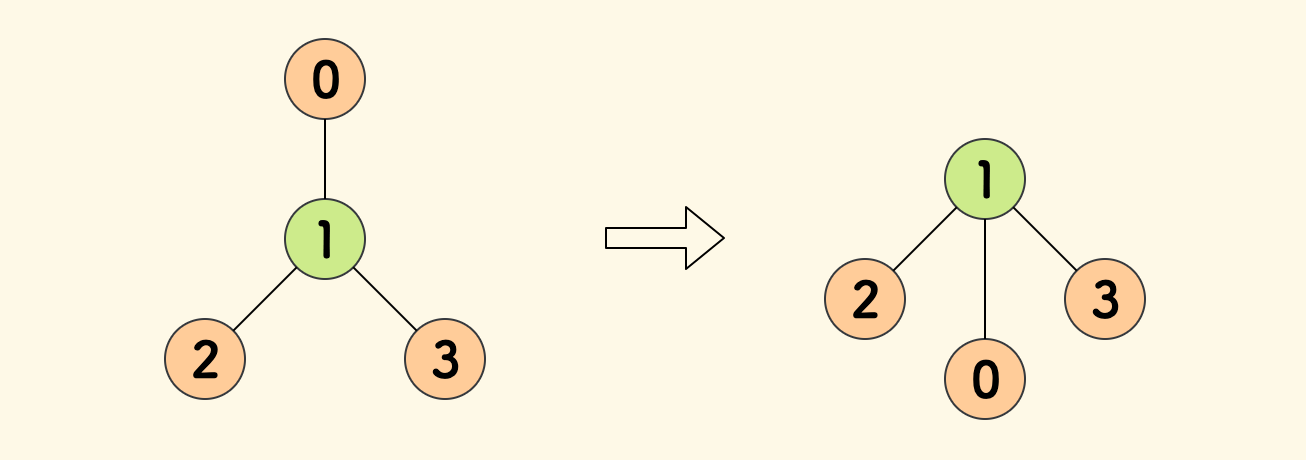
看到「不定根」问题,第一直觉是采用「换根 DP」,但是这个换根不大好想,反而拓扑排序的解法更直接。
拓扑排序法 ¶
前置知识:拓扑排序。
下图是一颗无向树、分别用不同节点作为根时的情况。
可以观察到一个规律:靠近中心的点作为树根时的树高才会更小。
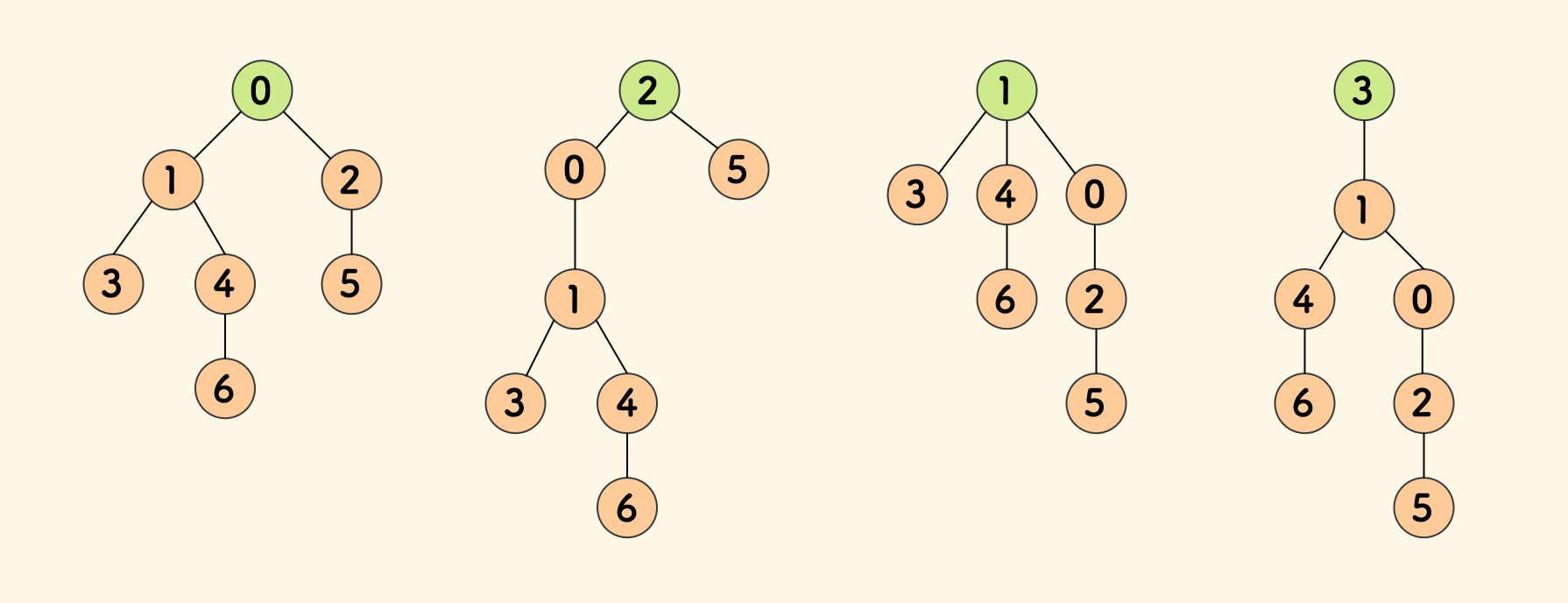
一个节点作为根时,形成的「树高」由其到最边缘节点的最大距离决定。所以要想使这个「树高」尽量地小,应该让它距离各个边缘节点更均衡,所以应更靠近中心。
那么,主要思路就是,可以从图的边缘,逐层向内找,最后一层的节点就是答案。
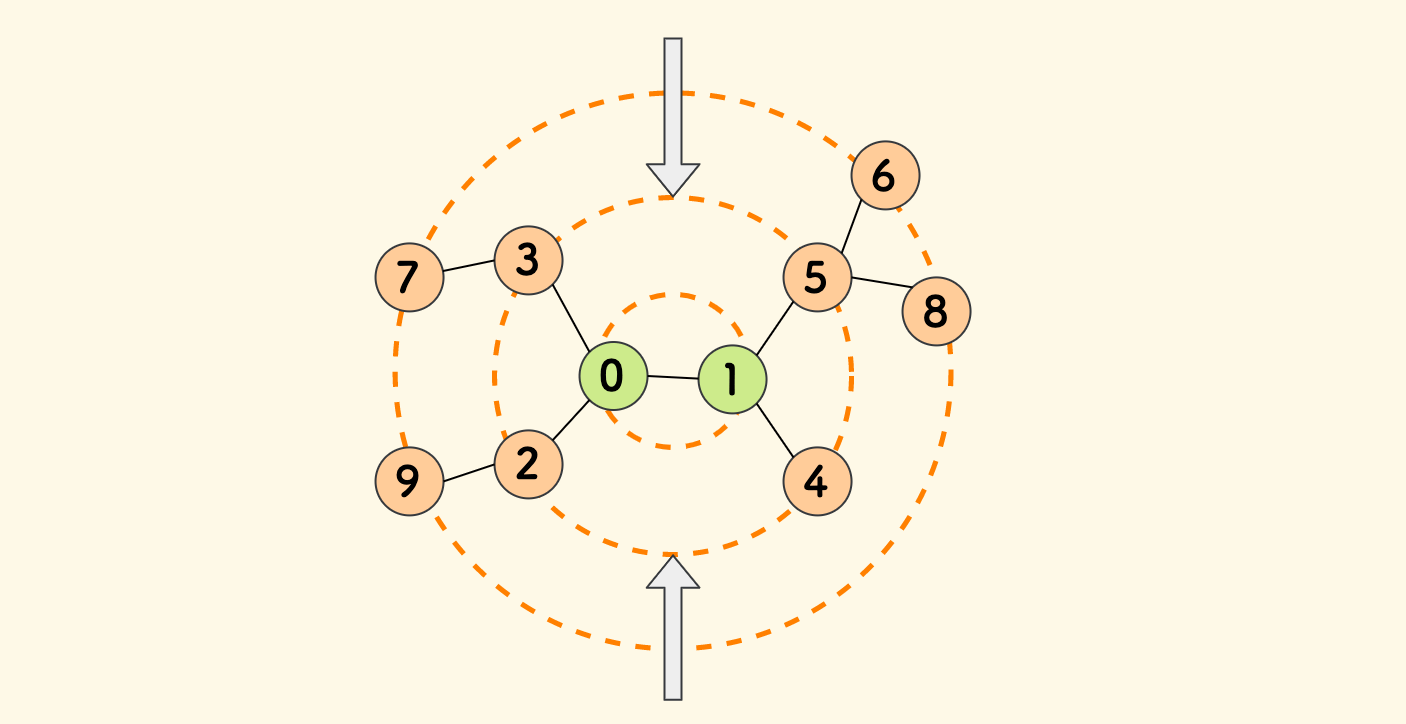
由于是无向图,所以建边的时候建两条,正向和反向。
这个「图的边缘」的节点如何寻找?实际上是,入度恰好为 1 的点。
不断剔除入度为 1 的节点,直到最后一层。
其实是拓扑排序的变形,不再是寻找入度为 0 的点了,而是寻找入度为 1 的点。
下图演示了这个过程:
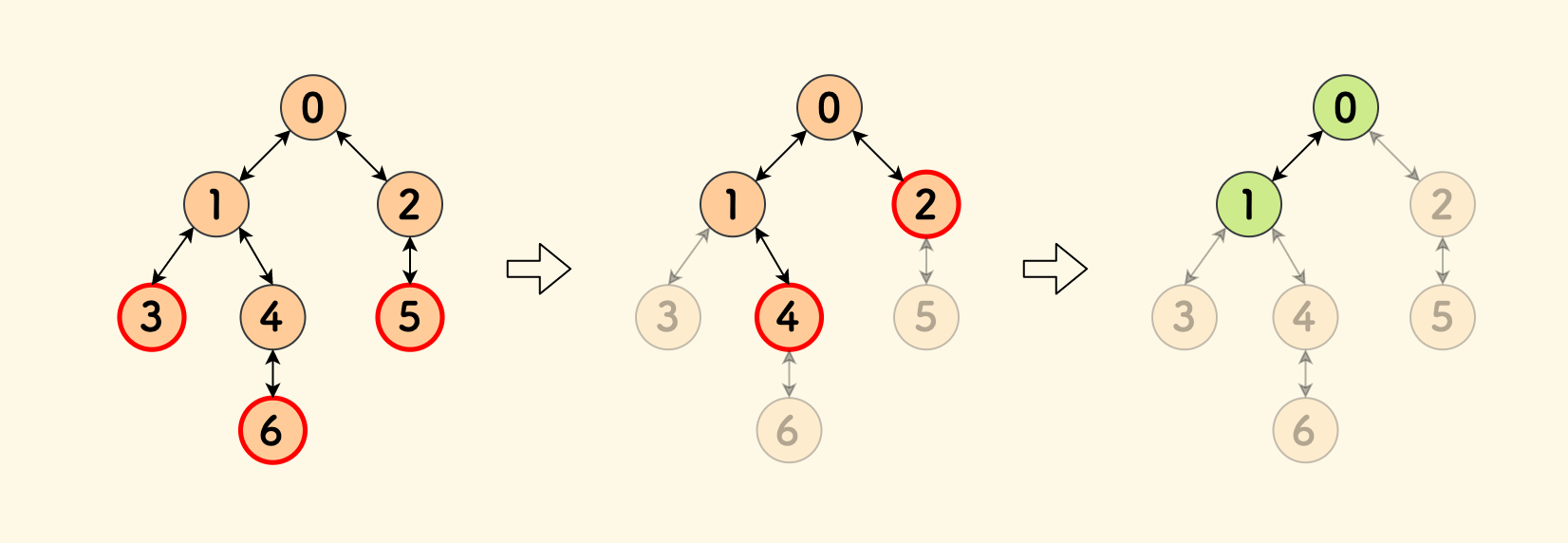
代码实现见下方:
最小高度树 - 拓扑变形 - C++ 代码
class Solution {
public:
vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {
// 特判: 单个节点
if (edges.empty()) return {0};
// 预处理边, 因为是无向,所以建两个
vector<vector<int>> ed(n);
for (auto& e : edges) {
ed[e[0]].push_back(e[1]);
ed[e[1]].push_back(e[0]);
}
// 入度表
vector<int> deg(n, 0);
for (int x = 0; x < n; x++)
for (auto y : ed[x]) ++deg[y];
// 添加入度为 1 的点
queue<int> q;
for (int x = 0; x < n; x++)
if (deg[x] == 1) q.push(x);
// 计算层数
int lv = 0;
// 层序, 最后一层的是最小高度树的节点
vector<int> ans;
while (q.size()) {
int k = q.size();
ans.clear();
while (k--) {
auto x = q.front();
ans.push_back(x);
q.pop();
for (auto y : ed[x])
if (--deg[y] == 1) q.push(y);
}
lv++;
}
return ans;
}
};
换根法 ¶
前置知识:换根 DP。
这是个「不定根」的树上问题,而且题面简洁,一眼「换根 DP」。
但是实际做起来,没那么简单,我觉得这个比一般的换根要难想。
存边
因为是无向图,建图的时候每个无向边作为正反两个有向边存储:
最小高度树 - 换根法 - 存边 - C++ 代码
vector<vector<int>> ed(n);
for (auto& e : edges) {
ed[e[0]].push_back(e[1]);
ed[e[1]].push_back(e[0]);
}
第一次扫描
首先,以 $0$ 号节点为根,计算出每个节点 $x$ 为根的子树的高度 $h(x)$。
这一步比较容易做,只需要一次 dfs 就可以,这是一个简单的树形 DP,从子树向父节点转移。
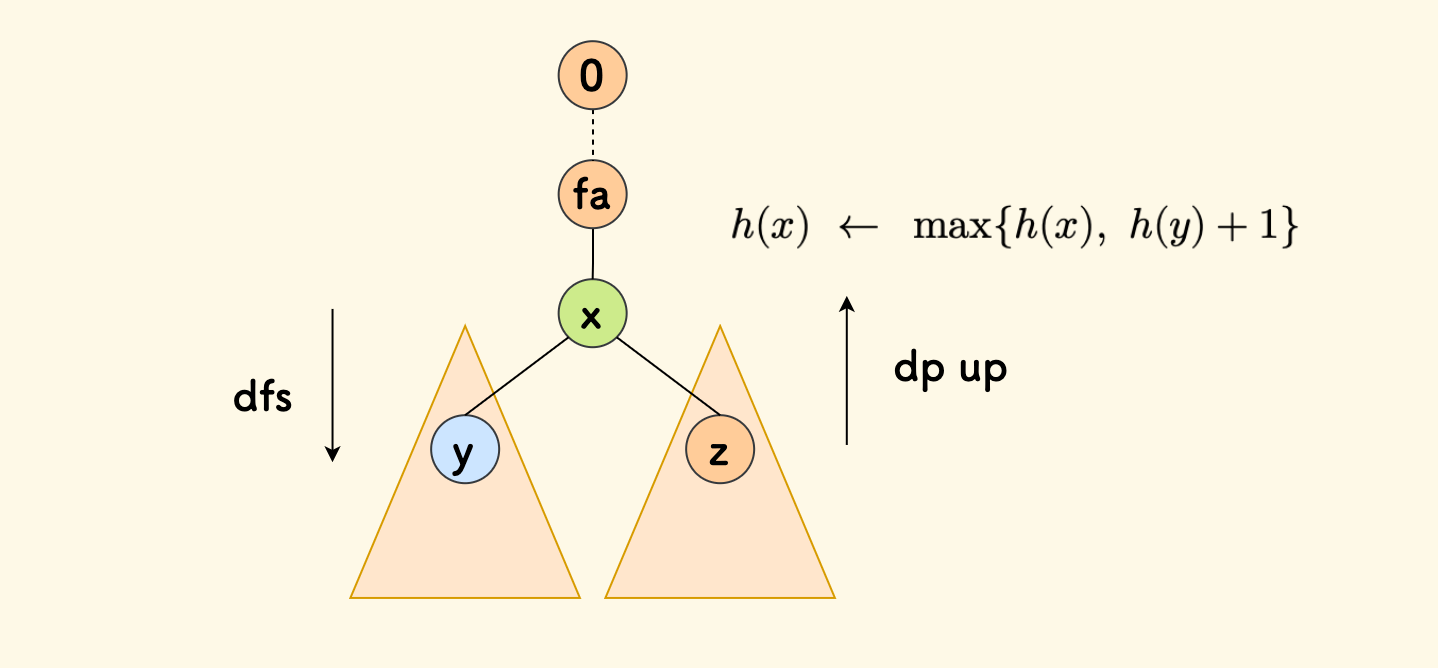
目前的第一次 dfs 的函数 up 代码实现如下:
最小高度树 - 换根法 - 第一次扫描 - C++ 代码
vector<int> h(n, 0);
vector<bool> vis(n, false); // 访问数组, 避免回环
function<void(int)> up = [&](int x) {
vis[x] = true;
for (auto y : ed[x]) {
if (vis[y]) continue;
up(y); // 先处理子树 y
h[x] = max(h[x], h[y]+1);
}
};
up(0);
第二次扫描
我们需要求解以每个节点 $x$ 为根时整颗树的树高 $f(x)$。
第一次扫描结束后,$0$ 号节点的 $h(0)$ 就是 $f(0)$。
现在考虑第二次扫描,仍从 $0$ 号节点开始 dfs,前序向下修正各个节点的 DP 值,这是换根法的一般套路。 即假定父节点 $x$ 的答案已经计算正确,然后换根到子节点 $y$,看下如何计算出以 $y$ 为根的树高。
已经知道下图中蓝色圈的高度 $h(y)$,但是要考虑下红色圈 $Z$ 的情况,它由 $x$ 以及原来的上游部分、$y$ 的兄弟子树 $z$ (可能有多个)组成。
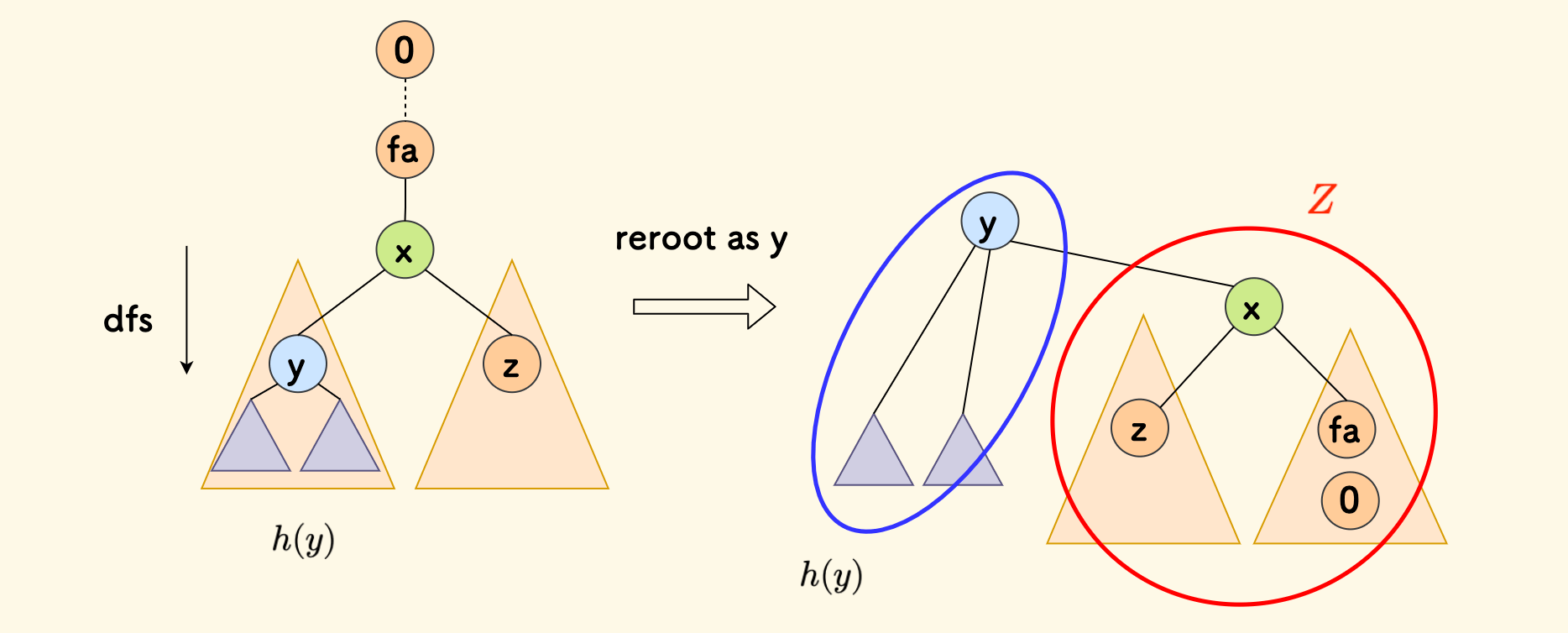
因为树高是由 $y$ 可以到达的最远节点的距离来决定的,但是这时你会发现,这个「最远节点」将会出现在原本的 $y$,还是 $Z$ 中,是无法确定的,信息是不足的。 这里面需要进一步知道 $y$ 最高的兄弟子树 $z$、祖先方向的距离。
定义 $u(y)$ 是节点 $y$ 往上游(也就是经过边 $(y,x)$ )能到达的最远距离。
那么,以 $y$ 为根的树高 $f(y)$ 就是「向下走」和「向上走」之中的最大距离:
\[f(y) = \max { \{ h(y), u(y) \}}\]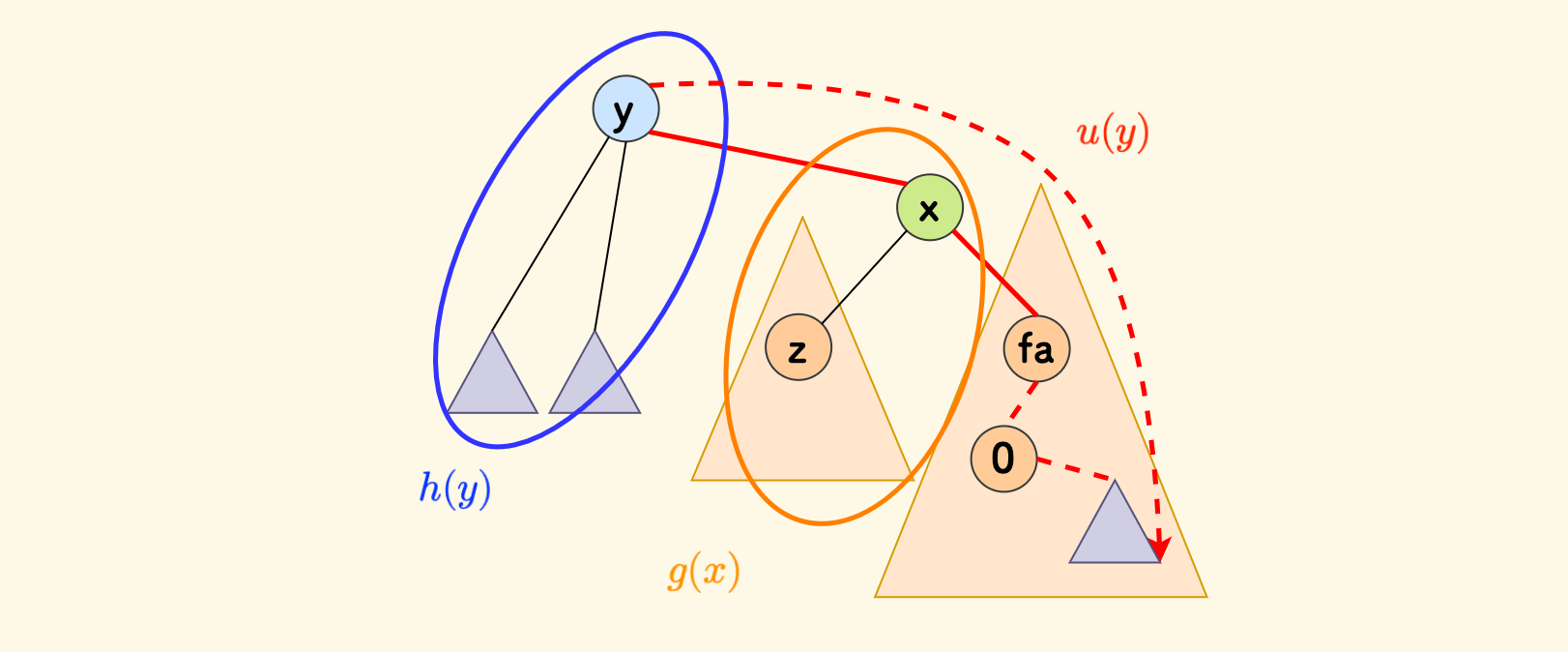
所以,只需要求解 $u$ 函数就可以了。
我们的换根 DP 不再直接推导答案,而是推导中间结果 $u$ 。
最开始,$u(0)$ 一定是 $0$。现在假定已经求出 $u(x)$,来前序推导子节点结果 $u(y)$。
容易知道,因为要么走兄弟 $z$ 、要么走祖先 $fa$,所以 $u(y)$ 一定是 $\max{\{h(z)+1,u(x)\}}+1$。
这其中的不确定量是兄弟子树 $z$ 的高度。
如果 $y$ 是 $x$ 的 唯一最高子树,就是说,$x$ 的树高只由一个子节点 $y$ 来决定。
这个 $z$ 要选择地尽量高,也就是次高的子树。我们可以提前记录 $x$ 的次树高。
次树高定义为 $g(x)$,意思是第一次扫描时,节点 $x$ 向前走的第二远的距离,允许和树高 $h(x)$ 并列。

此时的转移方程是:
\[u(y) = \max { \{ u(x), g(x) \}} + 1\]否则,如果 $y$ 不是 $x$ 的唯一最高子树,那么肯定存在一个最高子树在它的兄弟之中。
这时的 $z$ 选取最高子树,再算上边 $(x,z)$,就是 $h(x)$,此时的转移方程是:
\[u(y) = \max { \{ u(x), h(x) \}} + 1\]
区分 $y$ 是不是唯一的最高子树,只是为了找出它的兄弟中最高的子树 $z$ 的高度该如何表达。
其实我们选择维护的也不是兄弟子树 $z$ 的信息、而是 $x$ 的最高和次高,这是等价的,不用多 $+1$ 一次,还能兼容 $y$ 没有兄弟子树的情况。
这其中,如何判断 $y$ 是否是唯一最高子树:
- $y$ 是 $x$ 的一个最高子树,那么肯定 $x$ 只比 $y$ 高 $1$ 个单位。
- 同时,$x$ 的次高不和最高并列,那么 $y$ 就是唯一的最高子树。
用代码来表达:
if (h[x] != g[x] && h[x] == h[y] + 1) {
// y 是 x 的唯一最高子树
}
至此,可以完整实现第二次扫描了:
最小高度树 - 换根法 - 第二次扫描 - C++ 代码
// u[x] 表示向上走(经过边 (y,x) ) 的最大路径长度
vector<int> u(n, 0);
// f[x] 是以 x 为根的树高,即答案
vector<int> f(n, 0);
// 从根 0 出发前序 dp,注意情况访问数组
fill(vis.begin(), vis.end(), false);
function<void(int)> down = [&](int x) {
vis[x] = true;
for (auto y : ed[x]) {
if (vis[y]) continue;
if (h[x] != g[x] && h[x] == h[y] + 1)
// y 是 x 的唯一最高子树, 经过 z 时取次高
u[y] = max(u[x], g[x]) + 1;
else // 否则 y 之外必然有一个最高子树,经过 z 时取最高
u[y] = max(u[x], h[x]) + 1;
f[y] = max(u[y], h[y]);
down(y);
}
};
f[0] = h[0];
down(0);
改进第一次扫描
还剩下一个余留问题,就是要修改一下第一次扫描,把次高也一并预先计算:
最小高度树 - 换根法 - 第一次扫描(改进) - C++ 代码
// h(x) 表示以 0 为根的时候的子树 x 的高
// g(x) 表示以 0 为根的时候的子树 x 的次高, 允许并列
vector<int> h(n, 0), g(n, 0);
vector<bool> vis(n, false);
function<void(int)> up = [&](int x) {
vis[x] = true;
for (auto y : ed[x]) {
if (vis[y]) continue;
up(y); // 先处理子树 y
if (h[x] < h[y] + 1) {
g[x] = h[x];
h[x] = h[y] + 1;
} else if (g[x] < h[y] + 1) { // 这里注意别丢
g[x] = h[y] + 1;
}
}
};
up(0);
最终取 $f$ 的最小值,收集一下答案即可,代码略。
在这个题目中,换根法远比拓扑排序法要难,这个换根还有点「非典型」。
(完)
相关阅读:

