字符串匹配 - KMP 算法原理和实现

KMP 算法是用来在字符串中搜索一个子字符串的算法。

本文内容较多，需要读者静心阅读。

内容目录：

KMP 算法主体思路
头尾公共长度 - Next 数组
C 语言实现
复杂度分析

问题 ¶

在长度为 n 的字符串 s 中搜索长度为 m 的子串 p 的位置。

本文以 ABCDABCABCABABCABCDA 为主串，ABCABCD 为子串。

简单匹配 ¶

易知，简单匹配方法如下：

将子串 p 依次对齐到 s 的每个字符的位置。
迭代子串进行比对，如果全部匹配，则完成匹配。

此方法的代码省略，其时间复杂度是 O(m * n) 。

KMP 算法过程 ¶

算法思路 ¶

将上面简单匹配的过程展开，如下图 1.1 所示，其中绿色的部分表示字符比对成功，红色表示比对失败。图中每一次比对，都会将子串 p 右移一位，然后子串从头开始匹配。

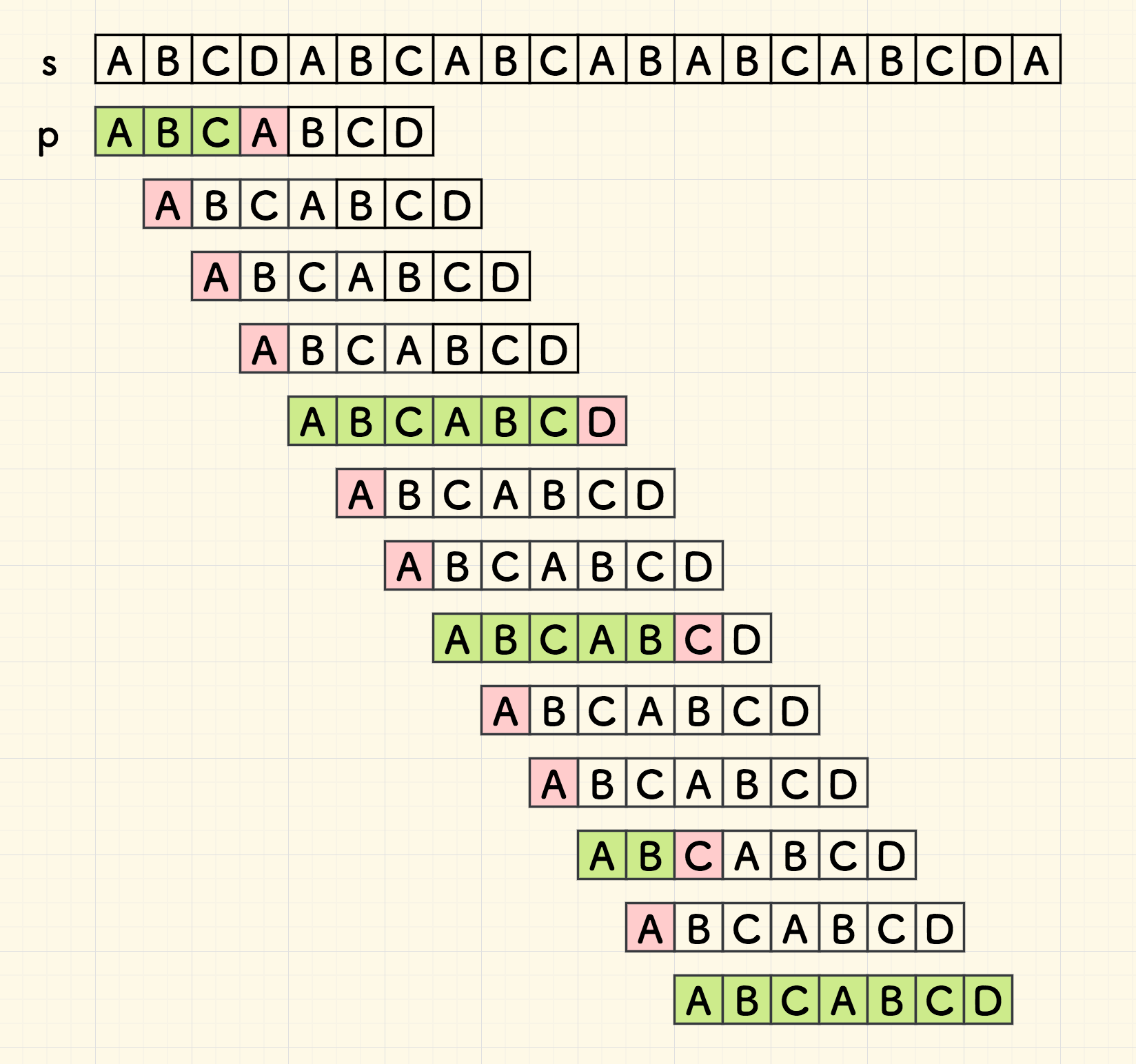
下面将考虑如何减少比对的次数。

考虑第一次失配的状态，如下图 1.2 所示，此时绿色的部分是目前匹配成功的部分。

将说明，接下来的两次比对，可以跳过。

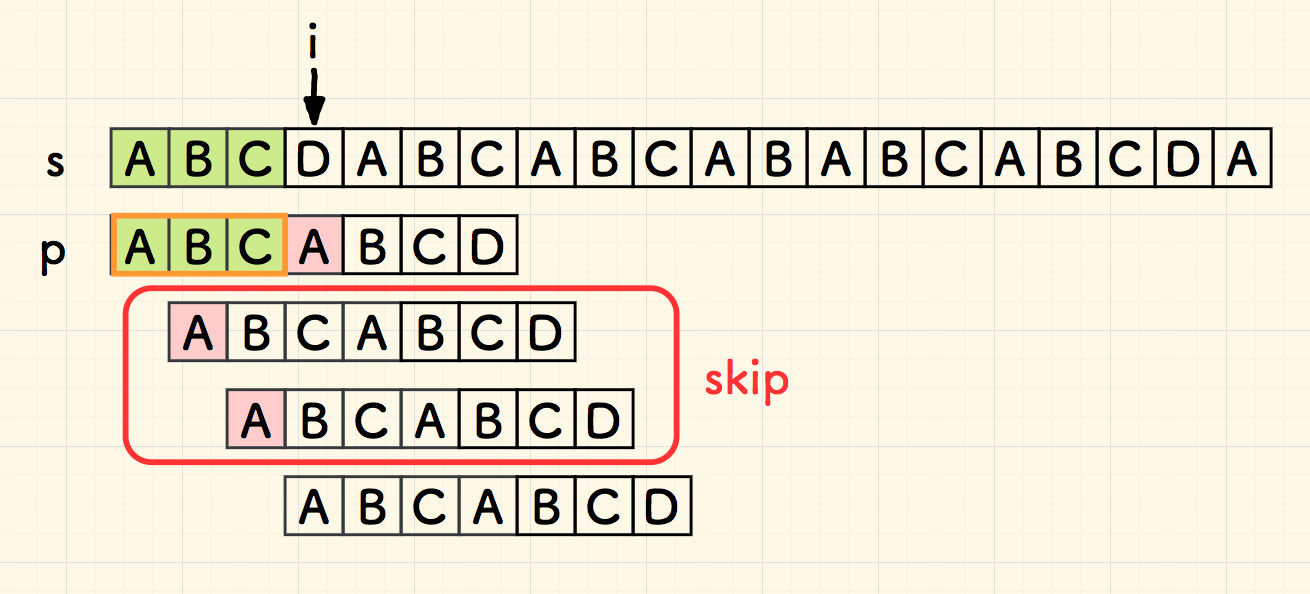
原因在于，右移后的重叠部分 overlap 都无法匹配，整个子串 p 就不必比对了。

下面考虑第二次失配的状态，如下图 1.4 所示，同样的思路可以知道，中间的两次比对可以跳过。

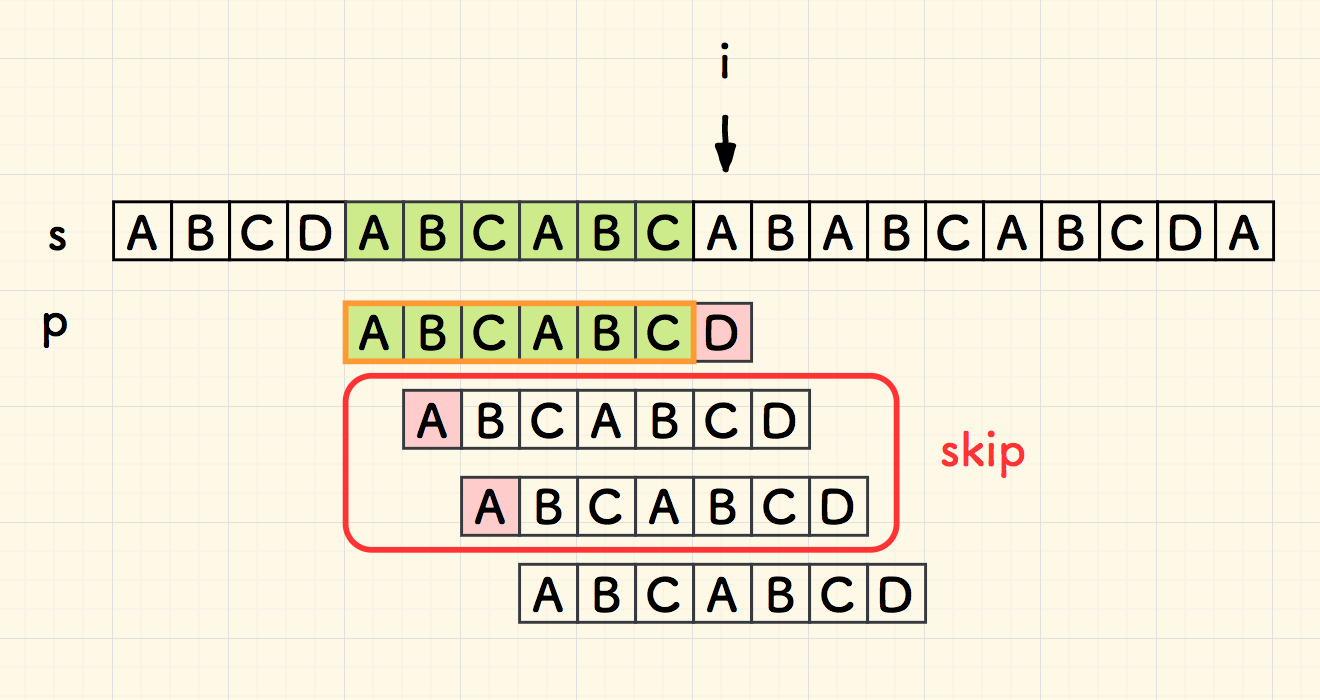
原因仍然在于，因为重叠部分 overlap 无法匹配，整个子串 p 必然无法匹配。

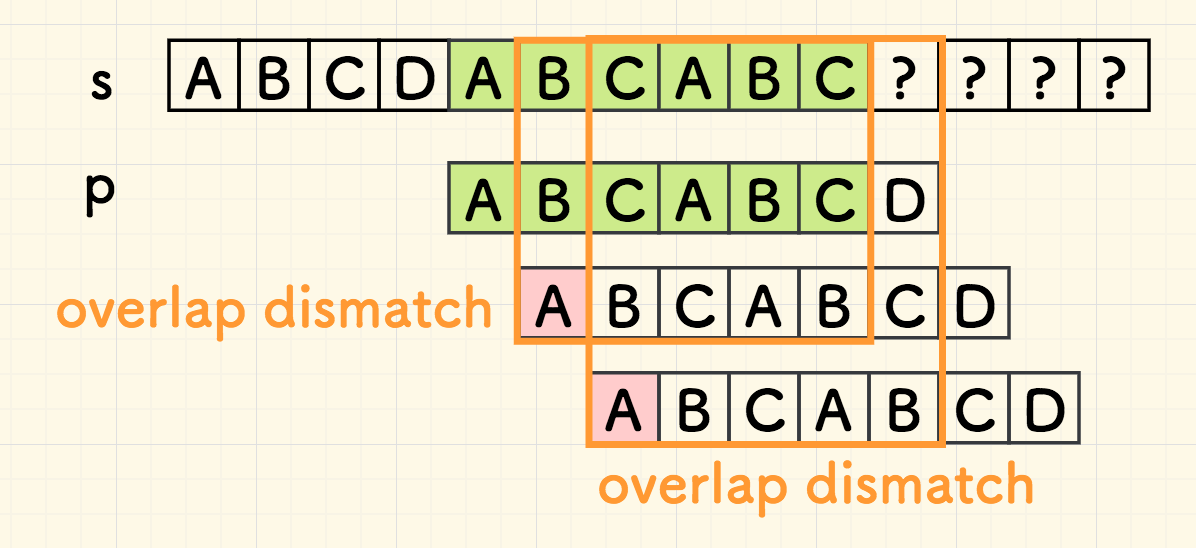
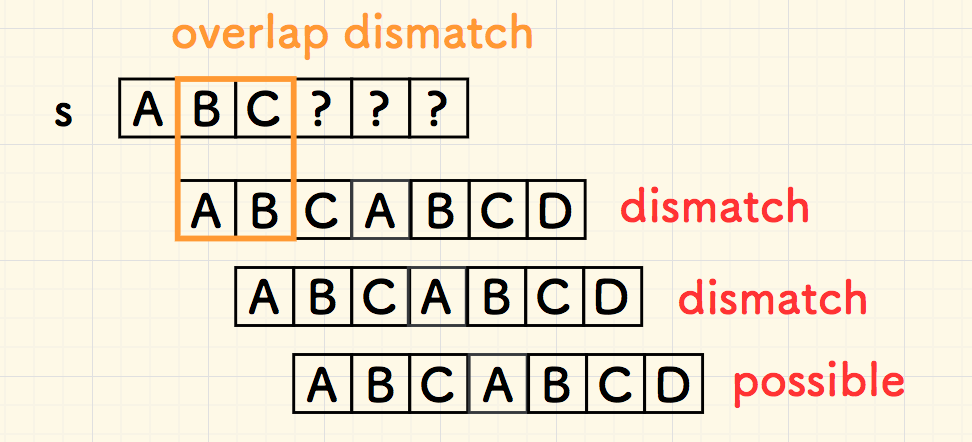
但是，下面一次移动，就无法如此断言。因为重叠部分 overlap 是匹配的，意味着尾端的 ABC 有可能作为下一次比对的开头，那么有必要进行进一步的比对。

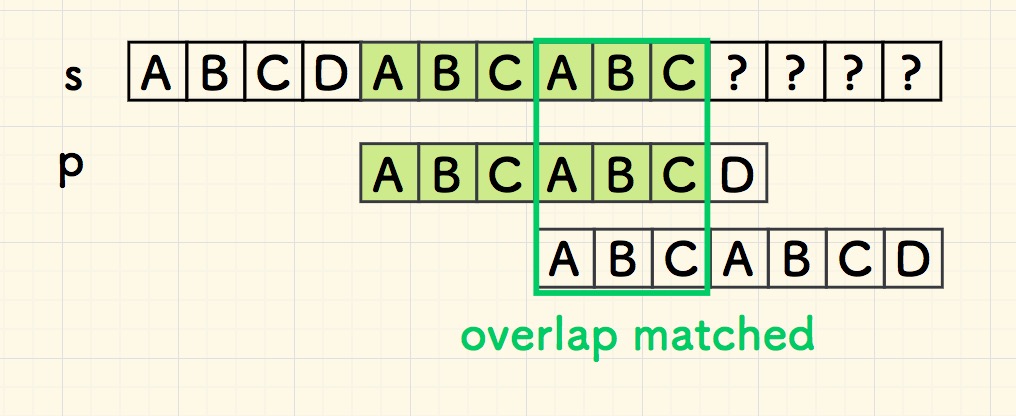
以上所说的重叠部分 overlap 是什么？

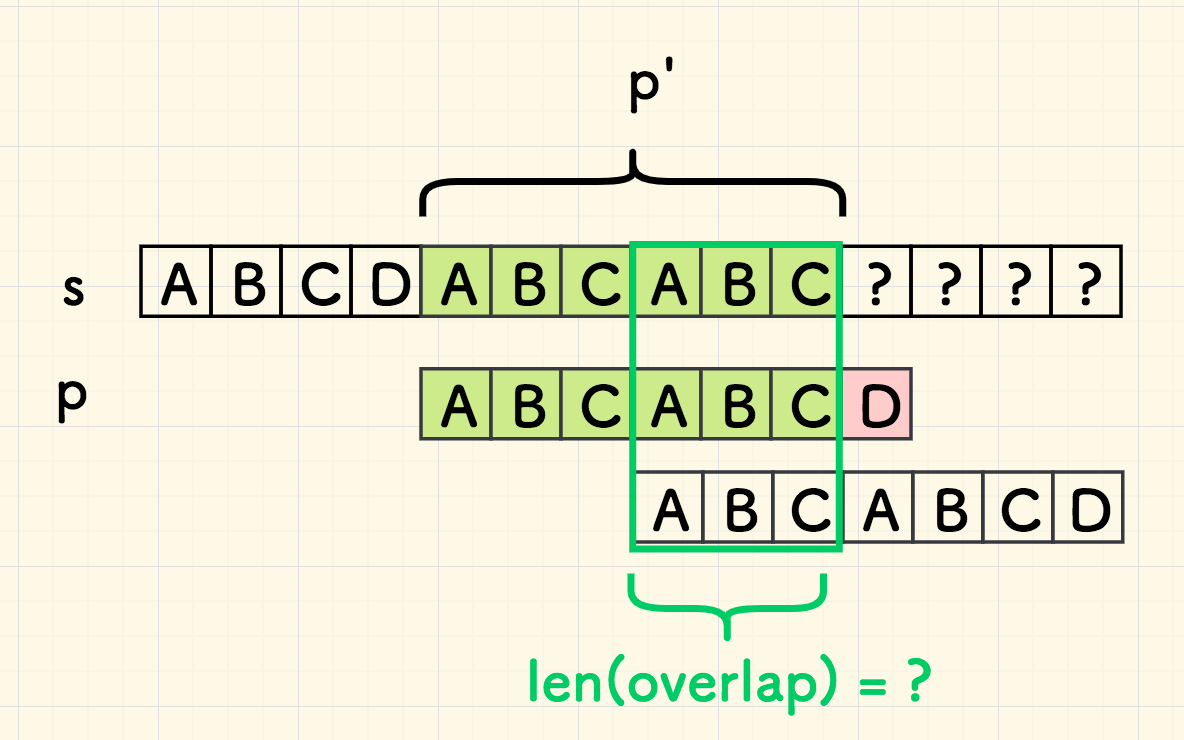
在刚刚失配时，假设已经匹配成功的部分是 p' ，它是 p 的一个子串，那么重叠部分是p' 尾部和右移 p' 后的头部交叉：

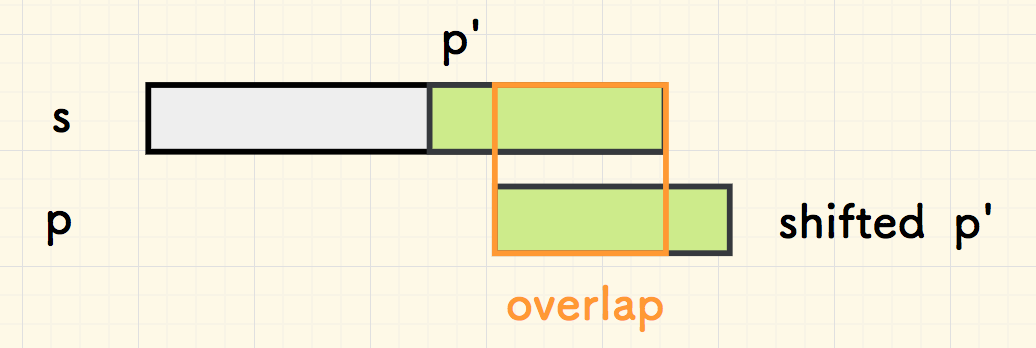
如果 p' 的尾部和头部是无重叠的，则可以开心地跳跃 len(p') 个字符。否则，如果 p' 的尾巴和头有匹配的部分，假如匹配了 len(overlap) 个字符，那么只可以向右跳跃 len(p') - len(overlap) 个字符。

按照这个结论，算法过程优化为下图的样子：

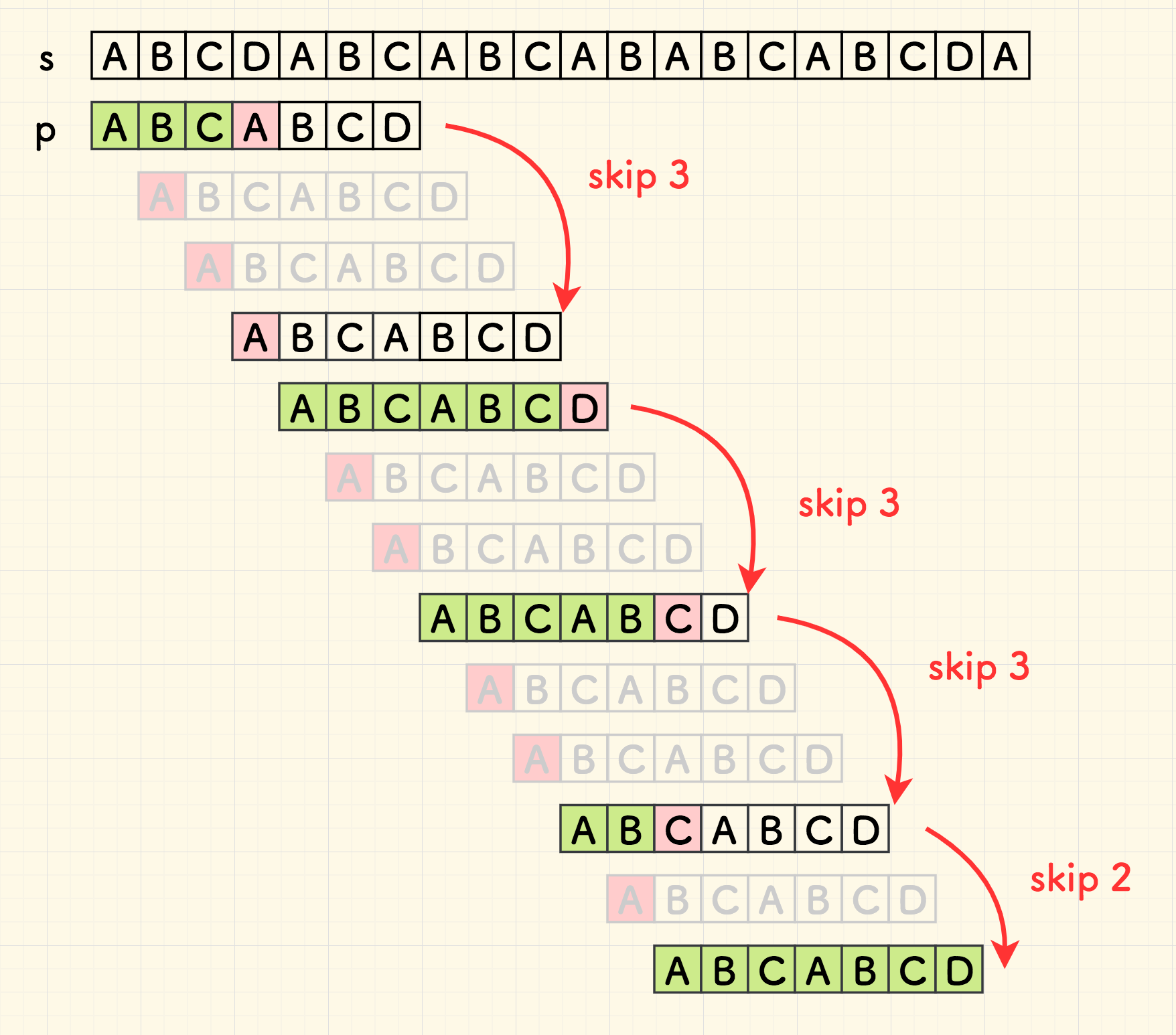
此外，因为重叠部分 overlap 已经是匹配的，所以，移动 p 后，不必回溯到 p 的起点再去匹配一次，直接从失配处继续匹配即可。

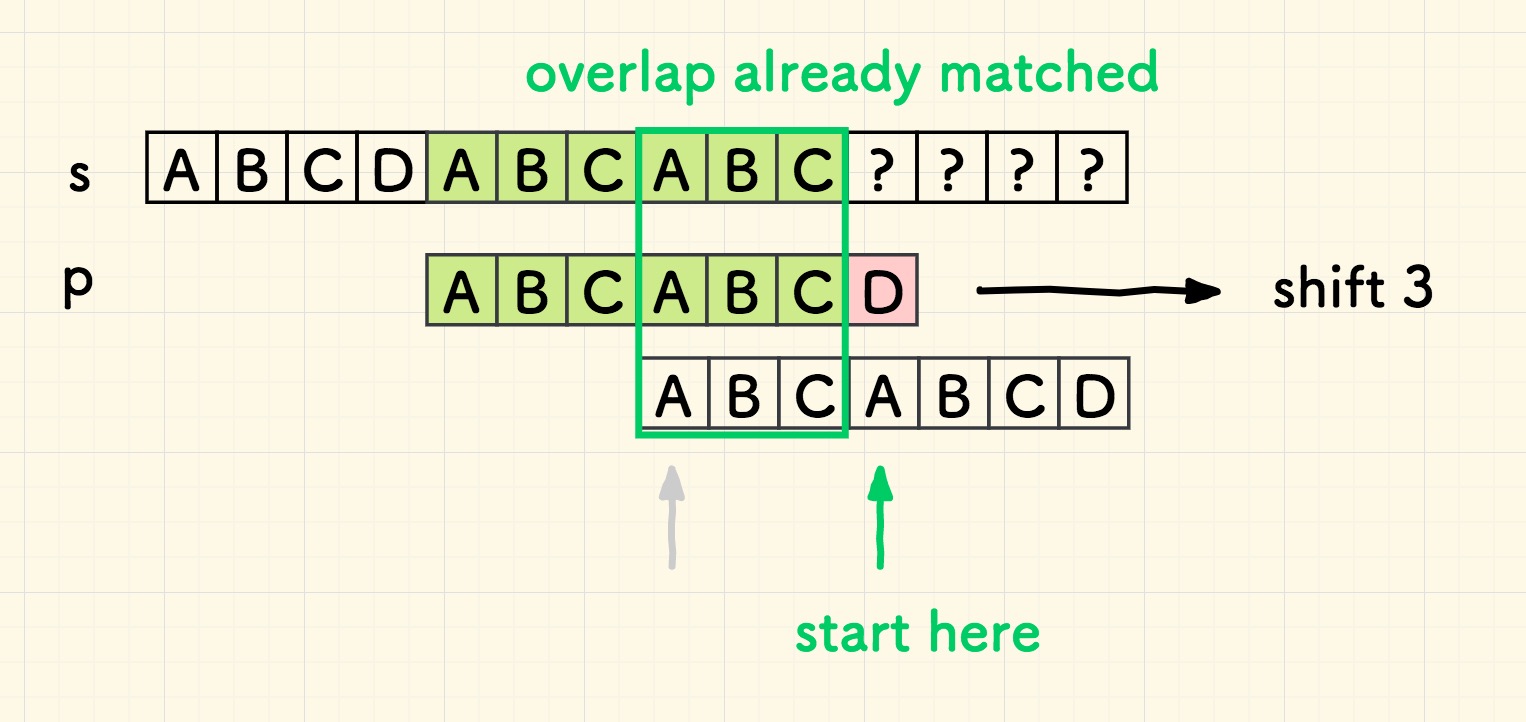
如此，最终的算法过程则是下图的样子，可以看到，主串 s 的遍历无需回溯，只需要在失配的时候回溯子串就好了。

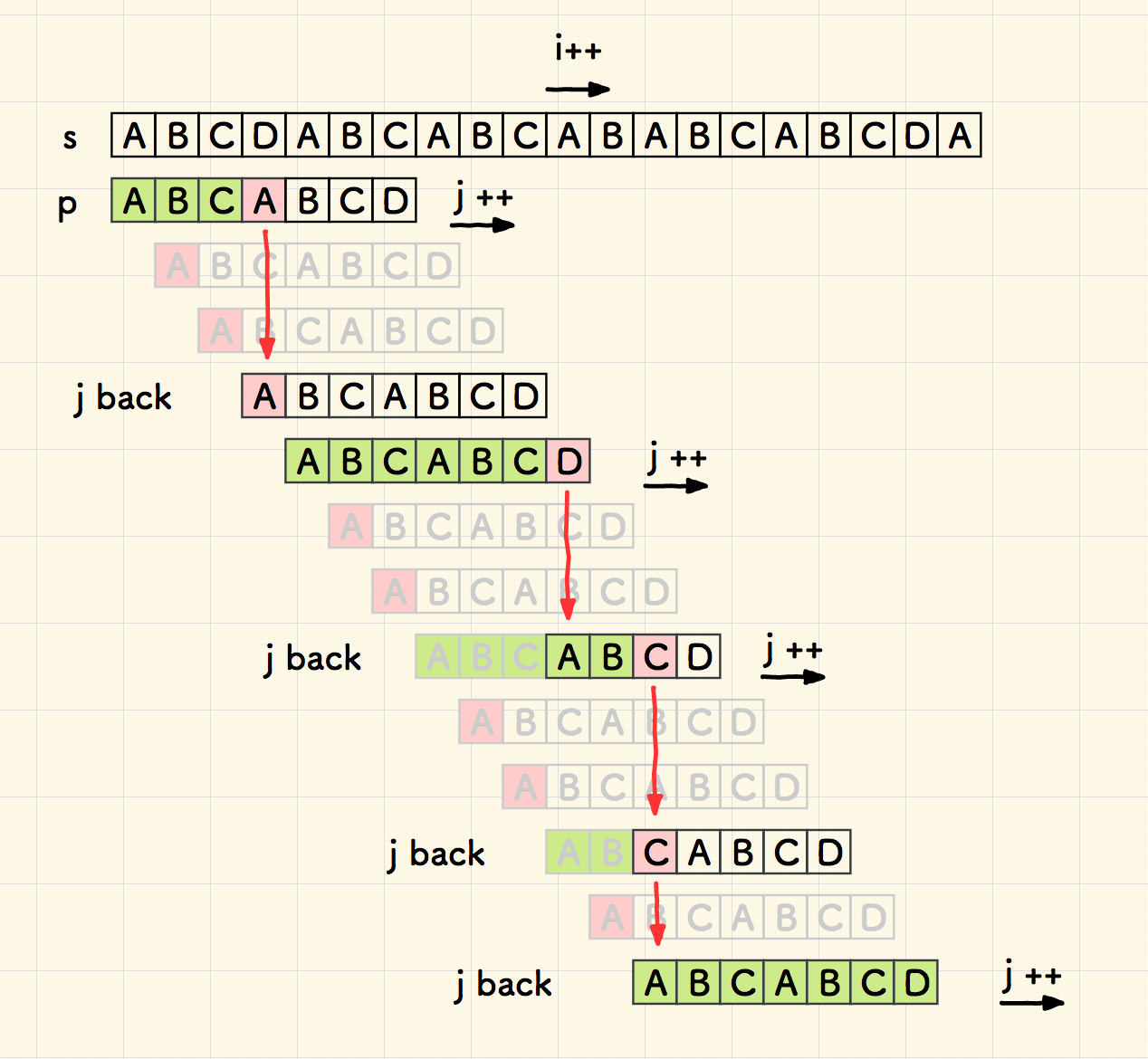
而子串回溯时， j 应该跳到的位置，恰好可以用已经匹配好的子串 p' 的头尾重叠部分的长度 len(overlap) 来表达：

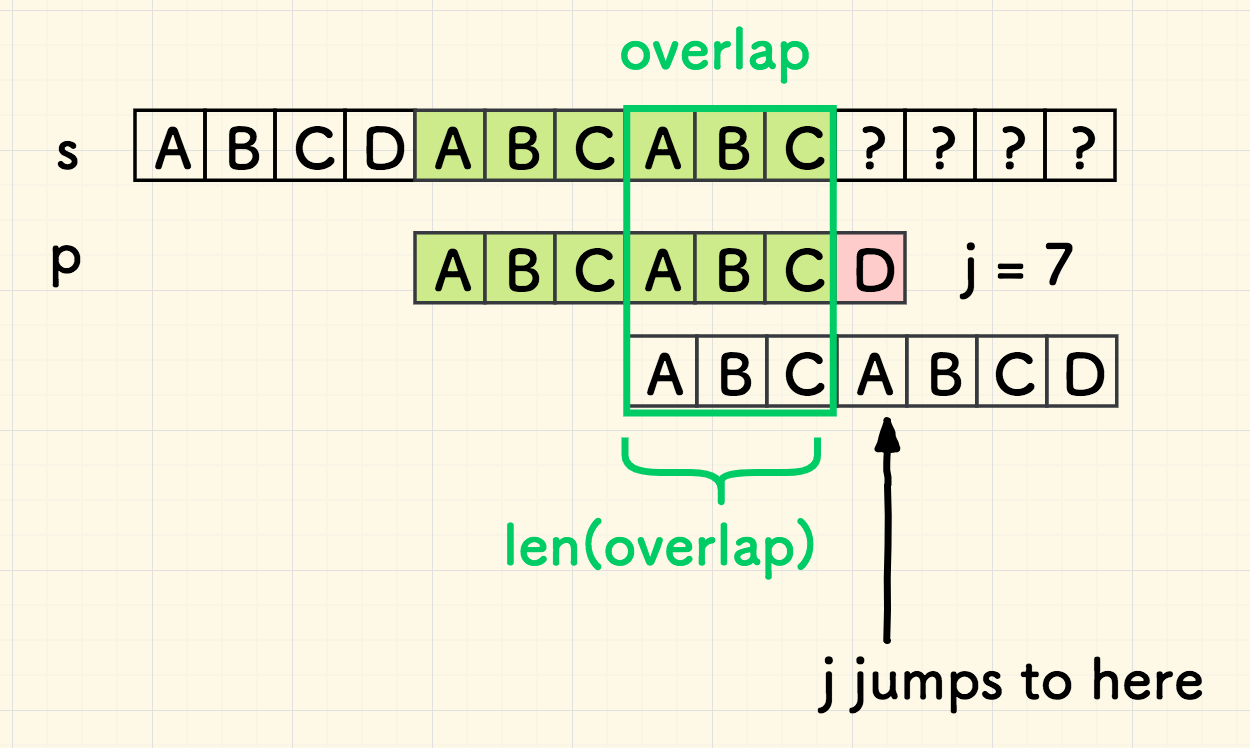
失配时，子串回溯的位置是可以跳跃的，目标位置恰好是已经匹配好的子串的头尾重叠部分的长度 。这是 KMP 整个算法的核心思路，也将应用到下面所讲的预处理环节。

接下来讨论，如何求解重叠部分的长度。

头尾公共长度 ¶

现在的问题是，对于子串 p 的每一个前缀子串 p' ，如何找到它的头部和尾部的重叠部分的长度？

我们观察一下本文例子中的 p' 的情况和对应的 overlap 长度。下图 2.1 中左边的是 p 的每一个前缀子串，右边是头尾重叠部分的长度：

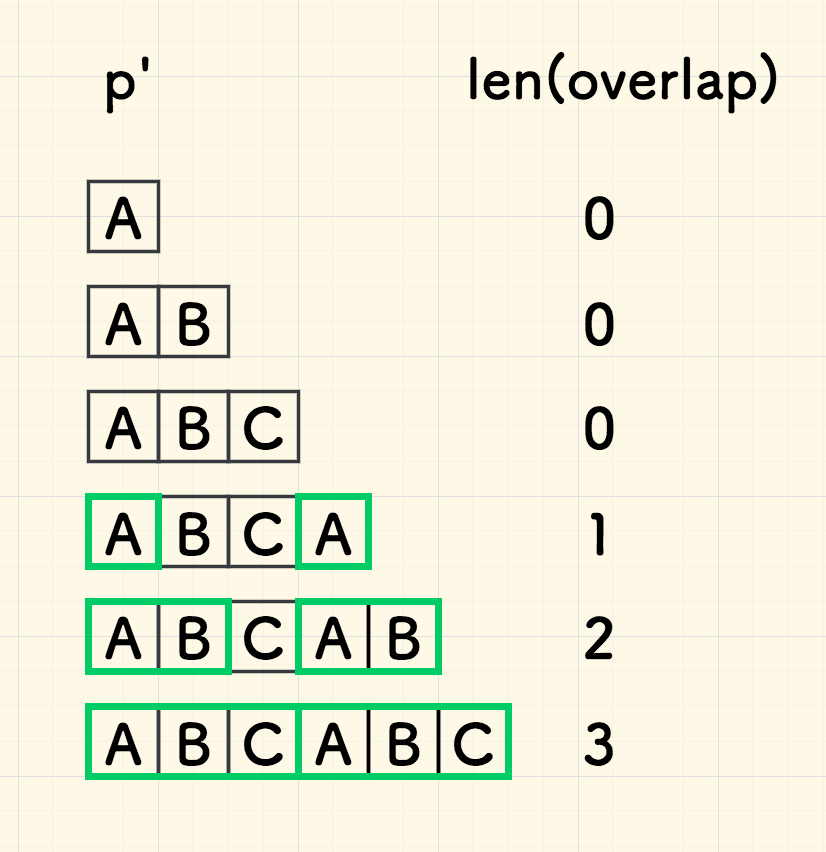
采用归纳法分析，假设 p'(j) 表示长度为 j 的子串，其重叠部分长度为函数 f(j)。我们考虑对它的右面新增一个字符，形成新的子串 p'(j+1)：

如果新增的字符和原来重叠部分后的字符相同，就是说 新的字符扩展了公共缀
因此 f(j+1) = f(j) + 1 ，如下图 2.2 所示：
图 2.2 - 新增一个字符 C 后，重叠部分变长
否则，情况要稍加分析，同时也是 KMP 算法中最为出彩的一笔。
为方便说明，采用一个新的子串 p 为 ABACABABC ，作为示例。
观察下面的情况，新增的字符没有扩展公共缀，但是，也形成了一个稍短的公共缀：
图 2.3 - 新增一个字符 C 后，形成一个稍短的公共缀的情况
当新增的字符没有扩展公共缀的时候，可以退而求其次，从失配处开始，一步一步向前寻找是否可以匹配到一个更短一些的公共缀。
会发现，这个过程十分类似 KMP 匹配的过程，非常神奇。
图 2.4 - 向前找是否可以和更短的串形成公共缀
上图中的 k 是下标，代表着拿 p[k] 和新增字符进行比对，初始为第一次失配的位置 f(j) 。
从前面的分析可以知道，当在 k 处失配时，可以直接跳到 f(k) 处继续比对。
也就是，跳到当前已经匹配好的部分（下图中的 "ABA" ）的头尾重叠部分（下图中为 "A" ）的长度（下图中为 1 ）处。：
图 2.5 - 应用 KMP 的核心思路，比对过程是可以跳跃的
又因为采用的是归纳法，所有 f(k) 的值都是已计算过的。
因此，本情况下的算法步骤则是：
- 初始化 k = f(j) 。
- 比对字符 p[k] 和新增的字符，失配则应用 KMP 跳转规则 k → f(k) ，继续比对。
- 直到两个字符匹配：
  因 f(k) 的跳转位置保证了失配处之前的字符串是匹配好的，意味着形成了一个新的公共缀。
  k 是新公共缀的尾巴位置，所以新公共缀长度是 k+1 ，即得 f(j+1) 。
特殊地，一直失配时，无法形成新的公共缀， f(j+1) = 0 ，下图是一个示例。
图 2.6 - 当没有形成任何公共缀的时候

遂形成递推关系，这里所说的 f(j) 就是 next 数组，它指明了失配时，子串回溯的目标位置。

KMP 算法 next 数组计算中对 KMP 核心思路的再一次使用，应该是算法中最为精妙的设计了。

C 语言实现 ¶

根据上面的分析的两种情况，可以得出计算 next 数组的代码实现：

Next 数组计算 - C 语言实现（简化前）

// ComputeNext 为长度为 m 的搜索串 p 计算 next 数组.
// next 数组的含义：
// 取字符串 p 的位置 j 之前的前缀字符串 p'，其头尾的最大公共长度即 next[j].
// 在 KMP 中，next 数组的值的应用为，在 j 处失配时的跳转位置是 next[j].
// 此处采用归纳方法实现
void ComputeNext(char *p, int m, int next[]) {
    // 初始为 0
    next[0] = 0;
    if (m <= 1) return;

    // p' 是单个字符时，认为它无公共头尾
    next[1] = 0;

    int j = 2;

    while (j < m) {
        // last 是上一次计算得出的 next 值
        int last = next[j - 1];

        // ch 是归纳本次结果时新增的尾巴字符
        char ch = p[j - 1];

        if (ch == p[last]) {
            // 当 ch 和原公共缀后面的一个字符相等
            // 说明新增字符扩展了公共缀，则长度加一
            next[j] = last + 1;
        } else {
            // 否则，观察新增字符 ch 是否和原公共后缀的一部分形成新的公共缀
            // 向前找出第一次匹配的位置 k
            int k = last;

            while (ch != p[k] && k != 0) {
                // 再次应用 KMP 的跳转规则：
                // 失配处跳转 k -> next[k]
                k = next[k];
            }

            if (k == 0 && p[0] != ch) {
                // 未找到任何公共缀
                next[j] = 0;
            } else {
                // ch 和某子串的尾巴匹配，形成新的公共缀
                // k 是匹配的尾巴坐标，因此新公共缀长度是 k + 1
                next[j] = k + 1;
            }
        }

        j++;
    }
}

可以对上面代码进行简化：

Next 数组计算 - C 语言实现（简化后）

// next[j] 的含义是位置 j 之前的字符串的头尾重叠部分的长度
void ComputeNext(char *p, int m, int next[]) {
    if (m > 0) next[0] = 0;
    if (m > 1) next[1] = 0;

    for (int j = 2; j < m; j++) {
        char ch = p[j - 1];
        int k = next[j - 1];
        // 向前跳跃匹配前缀
        while (k != 0 && ch != p[k]) k = next[k];
        next[j] = 0;  // 找不到默认为 0
        // 找到了，长度是 匹配位置 + 1
        if (ch == p[k]) next[j] = k + 1;
    }
}

KMP 查找过程 - C 语言实现

// KMP 从长度为 n 的字符串 s 中查找长度为 m 的字符串 p ，返回其位置.
// 找不到则返回 -1
int KMP(char *s, int n, char *p, int m) {
    // 预处理 next 数组
    int next[m];
    ComputeNext(p, m, next);

    // i 遍历 s
    // j 遍历 p
    int i = 0;
    int j = 0;

    while (i < n) {
        // 匹配
        if (s[i] == p[j]) {
            if (j == m - 1) {
                // 子串匹配到尾部，说明命中
                // 返回匹配的起始位置
                return i + 1 - m;
            } else {
                // 否则，则继续匹配
                i++;
                j++;
            }
        } else {
            if (j == 0) {
                // j 已经在串首, 说明第一个字符不匹配
                // 不必再回溯子串，主串迭代进 1
                i++;
            } else {
                // 失配，j 回溯
                // 回溯的目标位置，已经匹配到的子串的头尾公共部分的长度处
                j = next[j];
            }
        }
    }

    return -1;  // 查找失败
}

复杂度分析 ¶

从算法的总体过程可以看出：

查找过程
由图1.8 可知，红绿色的方格是迭代点位。
因为主串不回溯，失配时，j 回溯后会再原地匹配一次。
所以，查找过程的迭代次数 = 横向的 i 迭代次数 + 纵向的重新匹配次数。
即 n + 失配时重新匹配次数，小于 2n 。

预处理过程

现分析 Next 数组计算的代码实现，亦可参考其伪代码：

Next 数组计算的伪代码

function ComputeNext
    while j < m // 外层循环
        last = next[j-1]
        if ch == p[last]
            // 第一个分支：扩展了公共缀的情况
        else
            // 第二个分支：向前找新公共缀的情况
            k = last
            while ...  // 内层循环
                k = next[k]
            next[j] = k + 1