KMP 算法的简明解释

KMP 算法是非常精妙的字符串匹配算法。

本文将重温 KMP 算法，做一个更简明、更完备的解释。

核心思路 ¶

假设要在长度为 n 的主串 S 中查找长度为 m 的子串 P，容易给出一个时间复杂度为 O(n*m) 的简单版字符串匹配算法:

简单版字符串匹配算法 NaiveStrStr

int NaiveStrStr(char *s, int n, char *p, int m) {
    for (int i = 0; i < n; i++) {
        int j;
        for (j = 0; j < m; j++)
            if (p[j] != s[i + j]) break;
        if (j == m) return i;
    }
    return -1;
}

它的做法是，每当失配，P 都会右移一格，再从头继续匹配。

问题在于，主串迭代变量 i 和子串迭代变量 j 都进行了不必要的回溯。

因为，失配位置左侧的绿色部分是比较过的、是匹配的。

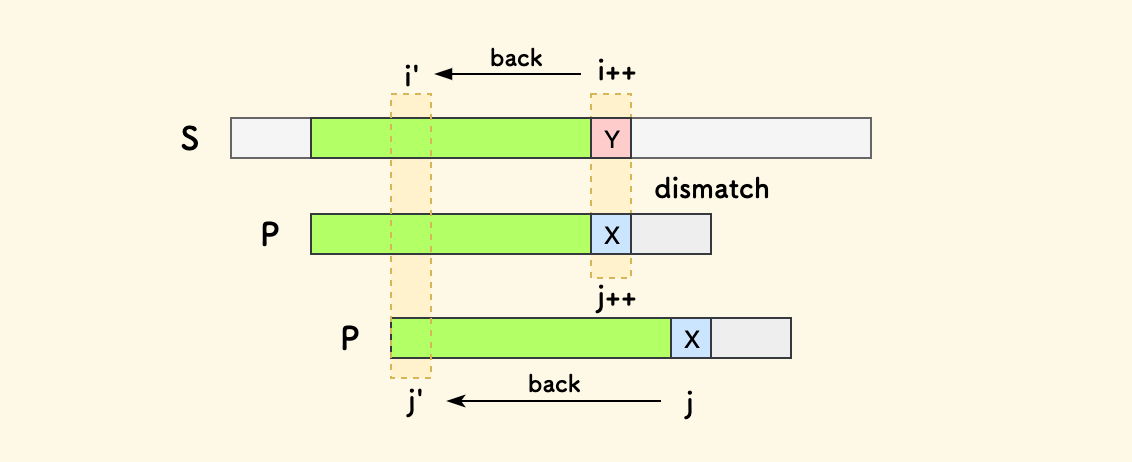
KMP 的改进在于：不必回溯 i，而且 j 也可能不必回溯到串首。

也就是，不必循规蹈矩地每次只右移一格，而是可以跳跃地右移。

要想在右移后匹配成功，那至少下图中 T 和 H 两个部分要相等。而且右移要足够谨慎，不至于错过匹配点，因此还要找尽可能长的 T 和 H。

如果事先知道这样的 T 和 H，主串迭代变量 i 就不必回溯，只需回溯 j 即可。

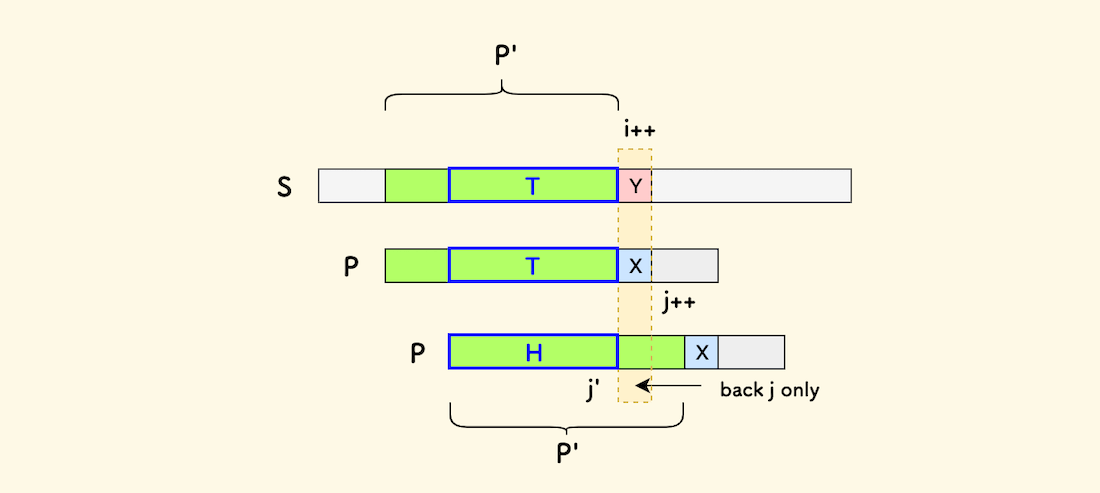
把左侧绿色部分、已经匹配好的子串叫做 P'，它是 P 的一个真子串。

而 T 和 H 则分别是 P' 的尾部和头部子串，要找最长的、相等的它们，就是找 P' 的最大头尾重叠部分。

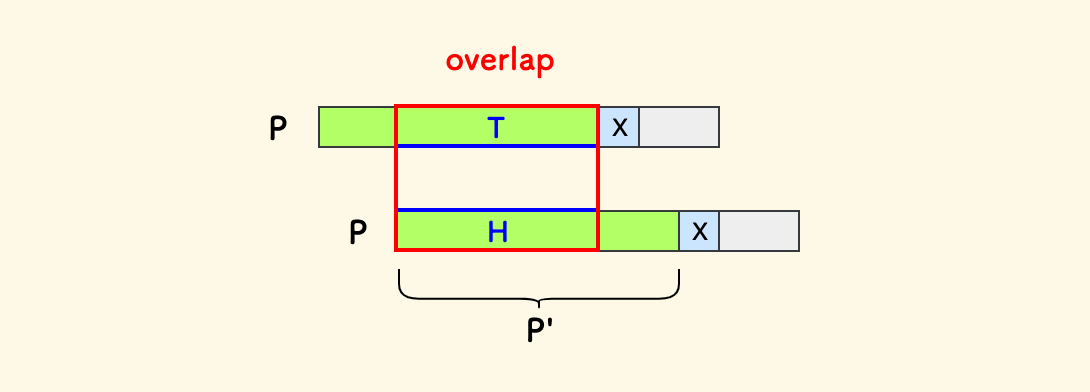
现在的结论是，失配时，可以直接把 j 回溯到已经匹配的 P' 的最大头尾重叠部分后面，继续匹配过程，而不必回溯 i。

overlap 函数推导 ¶

接下来的问题是，如何求解子串 P 的每一个真子串的最大头尾重叠部分的长度呢？

把以位置 j 结尾的子串叫做 P'(j)，其最大头尾重叠部分的长度叫做函数 overlap(j)。

现在来到 KMP 算法最精彩的部分，将再一次应用 KMP 算法的核心思路。

将采用归纳法，如果已知 k = overlap(j)，将如何求解 overlap(j+1) 的值？

下图中，先将字符串右移，把相等的绿色部分对齐，来到 ① 号状态。

现在看红色框中的情况：重叠部分可能会得到扩展，也可能会缩短。

如果字符 Y 和 X 相等，就扩展了 overlap，长度加一。

否则，继续右移 P'(j+1)，来到 ② 号状态，尝试找新的头尾重叠部分。

此时，如果字符 Y 和 X' 相等，那么 overlap(j+1) 就是以 X' 结尾的字符串的长度。

问题是，要右移多少来到 ② 号状态？

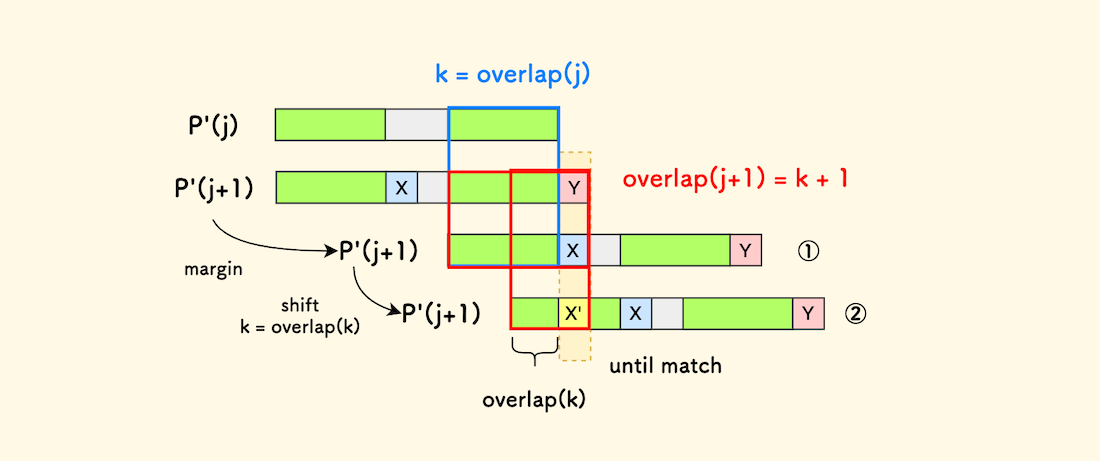
回顾前面 KMP 的核心思路，失配时，可以直接右移到已经匹配好的子串的最大头尾重叠部分的后面，继续比较。

已经匹配好的部分是 P'(k)，那么下一次右移到位置是 overlap(k)。

套娃出现了。

不断取 k = overlap(k)，直到 Y 和某个 X 字符匹配上了，就计算出来了 overlap(j+1)。

而且，扩展的情况，也是统一的, 用伪代码来体现这个过程:

预处理 Overlap 函数 - 伪代码

for j < m:
    k = overlap(j)    // ①

    while Y != P[k]:
        k = overlap(k)  // ②

    overlap(j+1) = k+1

用 C 代码来体现这个过程：

预处理 Overlap 函数 - C 语言

void BuildOverlap(char *p, int m, int overlap[]) {
    if (m > 0) overlap[0] = 0;
    if (m > 1) overlap[1] = 0;

    for (int j = 2; j < m; j++) {
        overlap[j] = 0;  // 默认是 0
        char y = p[j - 1];
        int k = overlap[j - 1];
        while (k != 0 && y != p[k]) k = overlap[k];
        if (y == p[k]) overlap[j] = k + 1;
    }
}

这其实就是常说的 KMP 的失配函数，虽然它有两层循环，但是其时间复杂度却是线性的 O(m) 。

头尾重叠部分是一个真子串，所以一定有 overlap(k) < k，所以内层循环每次迭代时 k 至少减少 1。又因为，每次内层循环的起点是 overlap(j-1)，结束于 overlap(j)-1，所以内层循环的次数不超过二者之差。那么所有内层循环的总迭代次数不超过 overlap(m-1) ，它是小于 m 的。因此预处理函数的内外层循环的总迭代次数不超过 2m。

KMP 最妙之处，就是对同一思路的两次利用。

也有一种思路是把 overlap 函数表达为状态机，不过我觉得没有失配函数的思路简洁。

很有趣的是，预处理过程只和子串相关，和主串无关。与其说我们是在主串中查找子串，不如说是拿着子串来检验主串。

最后，KMP 的主体过程，已经比较清晰： KMP C 实现代码 on Github

（完）